Магнитный монополь

Гипотетическая частица с одним магнитным полюсом

Невозможно сделать магнитные монополи из стержневого магнита . Если стержневой магнит разрезать пополам, то не получится, что у одной половины будет северный полюс, а у другой — южный. Вместо этого у каждой части будут свои северный и южный полюса. Магнитный монополь не может быть создан из обычной материи, такой как атомы и электроны , но вместо этого будет новой элементарной частицей .

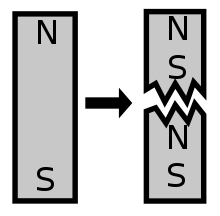
В физике элементарных частиц магнитный монополь — это гипотетическая элементарная частица , которая является изолированным магнитом с одним магнитным полюсом (северный полюс без южного или наоборот). ^{[1] [2]} Магнитный монополь имел бы чистый северный или южный «магнитный заряд». Современный интерес к этой концепции проистекает из теорий частиц , в частности, теории великого объединения и теории суперструн , которые предсказывают их существование. ^{[3] [4] [ необходима полная цитата ]} Известные элементарные частицы, имеющие электрический заряд, являются электрическими монополями.

Магнетизм в стержневых магнитах и ​​электромагнитах не вызван магнитными монополями, и, действительно, нет известных экспериментальных или наблюдательных доказательств того, что магнитные монополи существуют.

Некоторые системы конденсированного вещества содержат эффективные (неизолированные) магнитные монопольные квазичастицы [ ^5] или содержат явления, которые математически аналогичны магнитным монополям ^{[6] .}

Историческая справка

Ранняя наука и классическая физика

Многие ранние ученые приписывали магнетизм магнитов двум различным «магнитным жидкостям» («эффлувиям»), жидкости северного полюса на одном конце и жидкости южного полюса на другом, которые притягивали и отталкивали друг друга по аналогии с положительным и отрицательным электрическим зарядом . ^{[7] [8]} Однако более глубокое понимание электромагнетизма в девятнадцатом веке показало, что магнетизм магнитов правильно объясняется не магнитными монопольными жидкостями, а скорее комбинацией электрических токов , магнитного момента электрона и магнитных моментов других частиц. Закон Гаусса для магнетизма , одно из уравнений Максвелла , является математическим утверждением о том, что магнитные монополи не существуют. Тем не менее, Пьер Кюри указал в 1894 году ^[9] , что магнитные монополи, вероятно, могут существовать, несмотря на то, что до сих пор их не наблюдали.

Квантовая механика

Квантовая теория магнитного заряда началась с работы физика Поля Дирака в 1931 году. [ ^10] В этой работе Дирак показал, что если во Вселенной существуют какие-либо магнитные монополи, то весь электрический заряд во Вселенной должен быть квантован (условие квантования Дирака). ^[11] Электрический заряд , по сути, квантован, что согласуется с существованием монополей (но не доказывает его). ^[11]

После статьи Дирака было проведено несколько систематических поисков монополей. Эксперименты 1975 ^[12] и 1982 ^[13] дали кандидатные события, которые изначально были интерпретированы как монополи, но теперь считаются неубедительными. ^[14] Таким образом, вопрос о том, существуют ли монополи, остается открытым. Дальнейшие достижения в теоретической физике элементарных частиц , в частности, разработки в теориях великого объединения и квантовой гравитации , привели к более убедительным аргументам (подробно изложенным ниже) в пользу того, что монополи действительно существуют. Джозеф Полчински , теоретик струн, описал существование монополей как «одну из самых надежных ставок, которую можно сделать относительно физики, которая еще не наблюдалась». ^[15] Эти теории не обязательно не соответствуют экспериментальным данным. В некоторых теоретических моделях магнитные монополи вряд ли будут наблюдаться, потому что они слишком массивны, чтобы создаваться в ускорителях частиц (см. § Поиски магнитных монополей ниже), а также слишком редки во Вселенной, чтобы попасть в детектор частиц с большой вероятностью. ^[15]

Некоторые системы конденсированного вещества предлагают структуру, внешне похожую на магнитный монополь, известную как трубка потока . Концы трубки потока образуют магнитный диполь , но поскольку они движутся независимо, их можно рассматривать для многих целей как независимые квазичастицы магнитного монополя . С 2009 года многочисленные новостные сообщения из популярных СМИ ^{[16] [17]} неправильно описывали эти системы как долгожданное открытие магнитных монополей, но эти два явления связаны друг с другом лишь поверхностно. ^{[18] [19]} Эти системы конденсированного вещества остаются областью активных исследований. (См. § «Монополи» в системах конденсированного вещества ниже.)

Полюса и магнетизм в обычной материи

Вся материя, изолированная на сегодняшний день, включая каждый атом в периодической таблице и каждую частицу в Стандартной модели , имеет нулевой магнитный монопольный заряд. Поэтому обычные явления магнетизма и магнитов не вытекают из магнитных монополей.

Вместо этого магнетизм в обычной материи обусловлен двумя источниками. Во-первых, электрические токи создают магнитные поля согласно закону Ампера . Во-вторых, многие элементарные частицы имеют собственный магнитный момент , наиболее важным из которых является магнитный дипольный момент электрона , который связан с его квантово-механическим спином .

Математически магнитное поле объекта часто описывается в терминах мультипольного расширения . Это выражение поля как суммы компонентных полей с определенными математическими формами. Первый член в разложении называется монопольным членом, второй называется дипольным членом , затем квадрупольным членом , затем октупольным членом и так далее. Любой из этих членов может присутствовать в мультипольном разложении электрического поля , например. Однако в мультипольном разложении магнитного поля «монопольный» член всегда равен нулю (для обычной материи). Магнитный монополь, если он существует, будет обладать определяющим свойством создания магнитного поля, монопольный член которого не равен нулю.

Магнитный диполь — это то, магнитное поле которого преимущественно или точно описывается термином магнитного диполя мультипольного расширения. Термин диполь означает два полюса , что соответствует тому факту, что дипольный магнит обычно содержит северный полюс с одной стороны и южный полюс с другой стороны. Это аналогично электрическому диполю , который имеет положительный заряд с одной стороны и отрицательный заряд с другой. Однако электрический диполь и магнитный диполь принципиально совершенно различны. В электрическом диполе, сделанном из обычной материи, положительный заряд состоит из протонов , а отрицательный заряд — из электронов , но магнитный диполь не имеет различных типов материи, создающих северный полюс и южный полюс. Вместо этого два магнитных полюса возникают одновременно из совокупного эффекта всех токов и собственных моментов по всему магниту. Из-за этого два полюса магнитного диполя всегда должны иметь равную и противоположную силу, и два полюса не могут быть отделены друг от друга.

Уравнения Максвелла

Уравнения электромагнетизма Максвелла связывают электрические и магнитные поля друг с другом и с распределением электрического заряда и тока. Стандартные уравнения предусматривают электрический заряд, но постулируют нулевой магнитный заряд и ток. За исключением этого ограничения, уравнения симметричны относительно взаимозамены электрического и магнитного полей . Уравнения Максвелла симметричны, когда заряд и плотность электрического тока везде равны нулю, как в вакууме.

Уравнения Максвелла также можно записать в полностью симметричной форме, если допустить «магнитный заряд», аналогичный электрическому заряду. ^[20] При включении переменной для плотности магнитного заряда, скажем, ρ _m , в уравнениях также появляется переменная « плотность магнитного тока », j _m .

Если магнитный заряд не существует (или существует, но отсутствует в некоторой области пространства), то все новые члены в уравнениях Максвелла равны нулю, а расширенные уравнения сводятся к обычным уравнениям электромагнетизма, таким как ∇ ⋅ B = 0 (где ∇⋅ — оператор дивергенции , а B — плотность магнитного потока ).

Поля E и поля B обусловлены электрическим зарядом (черный/белый) и магнитным зарядом (красный/синий). [ 21 ^{] [22]}

В гауссовых единицах СГС

Расширенные уравнения Максвелла в единицах СГС-Гаусса выглядят следующим образом: ^[23]

В этих уравнениях ρ _m — плотность магнитного заряда , j _m — плотность магнитного тока , а q _m — магнитный заряд пробной частицы, все они определяются аналогично связанным величинам электрического заряда и тока; v — скорость частицы, а c — скорость света . Для всех других определений и подробностей см. уравнения Максвелла . Для уравнений в безразмерной форме удалите множители  c .

В единицах СИ

В Международной системе величин, используемой с СИ , существуют два соглашения для определения магнитного заряда q _m , каждое из которых имеет разные единицы: вебер (Вб) и ампер -метр (А⋅м). Преобразование между ними выглядит так: q _m ^[Вб] = μ ₀ q _m ^[А⋅м] , поскольку единицы измерения следующие: 1 Вб = 1 Гн⋅А = (1 Гн⋅м ⁻¹ )(1 А⋅м) , где Гн — это генри — единица индуктивности в системе СИ .

Уравнения Максвелла тогда принимают следующие формы (используя те же обозначения, что и выше): ^{[примечания 1]}

Потенциальная формулировка

Уравнения Максвелла можно также выразить через потенциалы следующим образом:

где

${\displaystyle \Box =\nabla ^{2}-{\frac {1}{c^{2}}}{\frac {\partial ^{2}}{{\partial t}^{2}}}}$

Формулировка тензора

Уравнения Максвелла на языке тензоров делают лоренц-ковариантность понятной. Мы вводим электромагнитные тензоры и предварительные четырехвекторы в этой статье следующим образом:

где:

• Сигнатура метрики Минковского — (+ − − −) .
• Электромагнитный тензор и его дуальный по Ходжу тензор являются антисимметричными тензорами :

  ${\displaystyle F^{\alpha \beta }=-F^{\beta \alpha },\quad {\tilde {F}}^{\alpha \beta }=-{\tilde {F}}^{\beta \alpha }}$

Обобщенные уравнения: ^{[25] [26]}

В качестве альтернативы, ^{[27] [28]}

где ε ^αβμν — символ Леви-Чивита .

Трансформация дуальности

Обобщенные уравнения Максвелла обладают определенной симметрией, называемой преобразованием дуальности . Можно выбрать любой действительный угол ξ и одновременно изменить поля и заряды повсюду во Вселенной следующим образом (в гауссовых единицах): ^[29]

где штрихованные величины — это заряды и поля до преобразования, а нештрихованные величины — после преобразования. Поля и заряды после этого преобразования по-прежнему подчиняются тем же уравнениям Максвелла.

Из-за преобразования дуальности невозможно однозначно решить, имеет ли частица электрический заряд, магнитный заряд или и то, и другое, просто наблюдая за ее поведением и сравнивая его с уравнениями Максвелла. Например, это всего лишь соглашение, а не требование уравнений Максвелла, что электроны имеют электрический заряд, но не магнитный; после преобразования ξ = π /2 все будет наоборот. Ключевым эмпирическим фактом является то, что все когда-либо наблюдавшиеся частицы имеют одинаковое отношение магнитного заряда к электрическому заряду. ^[29] Преобразования дуальности могут изменить отношение на любое произвольное числовое значение, но не могут изменить то, что все частицы имеют одинаковое отношение. Поскольку это так, можно сделать преобразование дуальности, которое устанавливает это отношение равным нулю, так что все частицы не имеют магнитного заряда. Этот выбор лежит в основе «обычных» определений электричества и магнетизма. ^[29]

Квантование Дирака

Одним из определяющих достижений квантовой теории была работа Поля Дирака по разработке релятивистского квантового электромагнетизма. До его формулировки наличие электрического заряда просто «вставлялось» в уравнения квантовой механики (КМ), но в 1931 году Дирак показал, что дискретный заряд естественным образом «выпадает» из КМ. ^[30] То есть, мы можем сохранить форму уравнений Максвелла и по-прежнему иметь магнитные заряды.

Рассмотрим систему, состоящую из одного стационарного электрического монополя (например, электрона) и одного стационарного магнитного монополя, которые не будут оказывать друг на друга никаких сил. Классически, электромагнитное поле, окружающее их, имеет плотность импульса, заданную вектором Пойнтинга , и оно также имеет полный угловой момент , который пропорционален произведению q _e q _m , и не зависит от расстояния между ними.

Однако квантовая механика диктует, что угловой момент квантуется как кратное ħ , поэтому произведение q _e q _m также должно быть квантовано. Это означает, что если бы во вселенной существовал хотя бы один магнитный монополь и форма уравнений Максвелла была бы верна, то все электрические заряды были бы квантованы .

Хотя в приведенном выше примере можно было бы просто интегрировать по всему пространству, чтобы найти полный угловой момент, Дирак выбрал другой подход. Это привело его к новым идеям. Он рассмотрел точечный магнитный заряд, магнитное поле которого ведет себя как ⁠кв _м/г  ²⁠ и направлен в радиальном направлении, расположенном в начале координат. Поскольку дивергенция B равна нулю всюду, за исключением геометрического места магнитного монополя при r = 0 , можно локально определить векторный потенциал таким образом, чторотор векторного потенциала A равен магнитному полю B.

Однако векторный потенциал не может быть определен глобально точно, поскольку дивергенция магнитного поля пропорциональна дельта -функции Дирака в начале координат. Мы должны определить один набор функций для векторного потенциала на «северном полушарии» (полупространство z ​​> 0 над частицей), а другой набор функций для «южного полушария». Эти два векторных потенциала согласованы на «экваторе» (плоскость z = 0 через частицу), и они отличаются калибровочным преобразованием . Волновая функция электрически заряженной частицы («зондового заряда»), которая вращается вокруг «экватора», обычно изменяется на фазу, как в эффекте Ааронова–Бома . Эта фаза пропорциональна электрическому заряду q _e зонда, а также магнитному заряду q _m источника. Дирак первоначально рассматривал электрон , волновая функция которого описывается уравнением Дирака .

Поскольку электрон возвращается в ту же точку после полного обхода вокруг экватора, фаза φ его волновой функции e ^iφ должна быть неизменной, что подразумевает, что фаза φ, добавленная к волновой функции, должна быть кратна 2 π . Это известно как условие квантования Дирака . В различных единицах это условие можно выразить как:

где ε ₀ — диэлектрическая проницаемость вакуума , ħ = h /2 π — приведенная постоянная Планка , c — скорость света , а — набор целых чисел . ${\displaystyle \mathbb {Z} }$

Гипотетическое существование магнитного монополя означало бы, что электрический заряд должен быть квантован в определенных единицах; также существование электрических зарядов подразумевает, что магнитные заряды гипотетических магнитных монополей, если они существуют, должны быть квантованы в единицах, обратно пропорциональных элементарному электрическому заряду.

В то время было неясно, существует ли такая вещь, или даже должна ли она существовать. В конце концов, могла бы появиться другая теория, которая объяснила бы квантование заряда без необходимости в монополе. Концепция оставалась чем-то вроде диковинки. Однако за время, прошедшее с момента публикации этой основополагающей работы, не появилось никакого другого широко принятого объяснения квантования заряда. (Концепция локальной калибровочной инвариантности — см. Калибровочная теория — дает естественное объяснение квантования заряда, не прибегая к необходимости в магнитных монополях; но только если калибровочная группа U(1) компактна, в этом случае мы в любом случае имеем магнитные монополи.)

Если максимально расширить определение векторного потенциала для южного полушария, то он будет определен всюду, за исключением полубесконечной линии, протянутой от начала координат в направлении к северному полюсу. Эта полубесконечная линия называется струной Дирака , и ее влияние на волновую функцию аналогично влиянию соленоида в эффекте Ааронова–Бома . Условие квантования исходит из требования, чтобы фазы вокруг струны Дирака были тривиальными, что означает, что струна Дирака должна быть нефизической. Струна Дирака является всего лишь артефактом используемой координатной карты и не должна восприниматься всерьез.

Монополь Дирака является сингулярным решением уравнения Максвелла (поскольку требует удаления мировой линии из пространства-времени); в более сложных теориях он заменяется гладким решением, таким как монополь 'т Хоофта–Полякова .

Топологическая интерпретация

струна Дирака

Калибровочная теория, такая как электромагнетизм, определяется калибровочным полем, которое связывает элемент группы с каждым путем в пространстве-времени. Для бесконечно малых путей элемент группы близок к тождеству, тогда как для более длинных путей элемент группы является последовательным произведением бесконечно малых элементов группы по пути.

В электродинамике группа — это U(1) , единичные комплексные числа при умножении. Для бесконечно малых путей элемент группы равен 1 + iA _μ dx ^μ , что подразумевает, что для конечных путей, параметризованных s , элемент группы равен:

${\displaystyle \prod _{s}\left(1+ieA_{\mu }{dx^{\mu } \over ds}\,ds\right)=\exp \left(ie\int A\cdot dx\right).}$

Отображение путей в элементы группы называется петлей Вильсона или голономией , а для калибровочной группы U(1) это фазовый множитель, который приобретает волновая функция заряженной частицы при прохождении ею пути. Для петли:

${\displaystyle e\oint _{\partial D}A\cdot dx=e\int _{D}(\nabla \times A)\,dS=e\int _{D}B\,dS.}$

Так что фаза, которую получает заряженная частица, когда движется по петле, является магнитным потоком через петлю. Когда небольшой соленоид имеет магнитный поток, существуют интерференционные полосы для заряженных частиц, которые движутся вокруг соленоида или вокруг разных сторон соленоида, которые обнаруживают его присутствие.

Но если все заряды частиц являются целыми кратными e , соленоиды с потоком 2 π / e не имеют интерференционных полос, поскольку фазовый фактор для любой заряженной частицы равен exp(2 π i ) = 1. Такой соленоид, если он достаточно тонкий, квантово-механически невидим. Если бы такой соленоид нёс поток 2 π / e , то при утечке потока из одного из его концов он был бы неотличим от монополя.

Решение монополя Дирака на самом деле описывает бесконечно малый линейный соленоид, заканчивающийся в точке, а местоположение соленоида является сингулярной частью решения, струной Дирака. Струны Дирака связывают монополи и антимонополи противоположного магнитного заряда, хотя в версии Дирака струна просто уходит в бесконечность. Струна ненаблюдаема, поэтому вы можете поместить ее куда угодно, и, используя два координатных пятна, поле в каждом пятне можно сделать несингулярным, сдвинув струну туда, где ее нельзя увидеть.

Теории великого объединения

В калибровочной группе U(1) с квантованным зарядом группа представляет собой окружность радиуса 2 π / e . Такая калибровочная группа U(1) называется компактной . Любая U(1), которая исходит из теории великого объединения (GUT), компактна — потому что только компактные высшие калибровочные группы имеют смысл. Размер калибровочной группы является мерой обратной константы связи, так что в пределе калибровочной группы большого объема взаимодействие любого фиксированного представления стремится к нулю.

Случай калибровочной группы U(1) является особым случаем, поскольку все ее неприводимые представления имеют одинаковый размер — заряд больше на целое число, но поле по-прежнему является просто комплексным числом — так что в теории калибровочного поля U(1) можно принять декомпактифицированный предел без противоречия. Квант заряда становится малым, но каждая заряженная частица имеет огромное количество квантов заряда, поэтому ее заряд остается конечным. В некомпактной теории калибровочной группы U(1) заряды частиц в общем случае не являются целыми кратными одной единицы. Поскольку квантование заряда является экспериментальной определенностью, ясно, что калибровочная группа электромагнетизма U(1) компактна.

GUT приводят к компактным калибровочным группам U(1), поэтому они объясняют квантование заряда способом, который кажется логически независимым от магнитных монополей. Однако объяснение по сути то же самое, потому что в любой GUT, которая распадается на калибровочную группу U(1) на больших расстояниях, есть магнитные монополи.

Аргумент топологический:

1. Голономия калибровочного поля отображает петли в элементы калибровочной группы. Бесконечно малые петли отображаются в элементы группы, бесконечно близкие к тождественному.
2. Если представить себе большую сферу в космосе, можно деформировать бесконечно малую петлю, которая начинается и заканчивается на северном полюсе, следующим образом: растянуть петлю по западному полушарию, пока она не станет большим кругом (который все еще начинается и заканчивается на северном полюсе), затем дать ей сжаться до маленькой петли, проходя по восточному полушарию. Это называется лассо сферы .
3. Лассо — это последовательность петель, поэтому голономия отображает ее в последовательность групповых элементов, непрерывный путь в калибровочной группе. Поскольку петля в начале лассо совпадает с петлей в конце, путь в группе замкнут.
4. Если групповой путь, связанный с процедурой лассо, обвивается вокруг U(1), сфера содержит магнитный заряд. Во время лассо голономия изменяется на величину магнитного потока через сферу.
5. Поскольку голономия в начале и в конце тождественна, полный магнитный поток квантуется. Магнитный заряд пропорционален числу витков N , магнитный поток через сферу равен 2 π N / e . Это условие квантования Дирака, и это топологическое условие, которое требует, чтобы конфигурации калибровочных полей U(1) на больших расстояниях были согласованы.
6. Когда калибровочная группа U(1) получается из разрыва компактной группы Ли , путь, который обвивает группу U(1) достаточное количество раз, топологически тривиален в большой группе. В не-U(1) компактной группе Ли покрывающее пространство является группой Ли с той же алгеброй Ли , но где все замкнутые петли стягиваемы . Группы Ли однородны, так что любой цикл в группе можно перемещать так, чтобы он начинался в тождестве, затем его подъем в покрывающую группу заканчивался в P , что является подъемом тождества. Обойдя петлю дважды, вы попадаете в P2 , три раза в P3 , все подъемы тождества. Но существует только конечное число подъемов тождества, потому что подъемы не могут накапливаться. Это число раз ^{, которое нужно обойти петлю, чтобы сделать} ее стягиваемой, мало, например, если группа GUT — это SO(3), покрывающая группа — это SU(2), и обхода любой петли дважды достаточно.
7. Это означает, что в группе GUT есть непрерывная конфигурация калибровочного поля, позволяющая конфигурации монополя U(1) раскручиваться на коротких расстояниях, ценой того, что она не остается в U(1). Чтобы сделать это с минимально возможной энергией, следует оставить только калибровочную группу U(1) в окрестности одной точки, которая называется ядром монополя . За пределами ядра монополь имеет только энергию магнитного поля.

Следовательно, монополь Дирака является топологическим дефектом в компактной калибровочной теории U(1). Когда нет GUT, дефектом является сингулярность — ядро ​​сжимается в точку. Но когда есть какой-то регулятор короткого расстояния в пространстве-времени, монополи имеют конечную массу. Монополи возникают в решетке U(1) , и там размер ядра равен размеру решетки. В общем, ожидается, что они возникнут всякий раз, когда есть регулятор короткого расстояния.

Теория струн

Во Вселенной квантовая гравитация обеспечивает регулятор. Когда гравитация включена, монопольная сингулярность может быть черной дырой, и для большого магнитного заряда и массы масса черной дыры равна заряду черной дыры, так что масса магнитной черной дыры не бесконечна. Если черная дыра может полностью распасться излучением Хокинга , самые легкие заряженные частицы не могут быть слишком тяжелыми. ^[32] Самый легкий монополь должен иметь массу, меньшую или сравнимую с его зарядом в натуральных единицах .

Итак, в последовательной голографической теории, единственным известным примером которой является теория струн , всегда существуют монополи с конечной массой. Для обычного электромагнетизма верхняя граница массы не очень полезна, поскольку она примерно того же размера, что и масса Планка .

Математическая формулировка

В математике (классическое) калибровочное поле определяется как связь над главным G-расслоением над пространством-временем. G — это калибровочная группа, и она действует на каждое волокно расслоения по отдельности.

Связность на G -расслоении подскажет вам, как склеить волокна в соседних точках M. Она начинается с непрерывной группы симметрии G , которая действует на волокно F , а затем связывает элемент группы с каждым бесконечно малым путем. Групповое умножение вдоль любого пути подскажет вам, как перейти от одной точки на расслоении к другой, связав элемент G с путем , действующим на волокно F.

В математике определение расслоения призвано подчеркнуть топологию, поэтому понятие связи добавляется как запоздалая мысль. В физике связь является фундаментальным физическим объектом. Одно из фундаментальных наблюдений в теории характеристических классов в алгебраической топологии состоит в том, что многие гомотопические структуры нетривиальных главных расслоений могут быть выражены как интеграл некоторого полинома по любой связи над ним. Обратите внимание, что связь над тривиальным расслоением никогда не может дать нам нетривиальное главное расслоение.

Если пространство-время является пространством всех возможных связей G -расслоения, то оно связно . Но рассмотрим, что происходит, когда мы удаляем из пространства-времени временную мировую линию . Полученное пространство-время гомотопически эквивалентно топологической сфере S ² . ${\displaystyle \mathbb {R} ^{4}}$

Главное G -расслоение над S ² определяется покрытием S ² двумя картами , каждая из которых гомеоморфна открытому 2-шару, так что их пересечение гомеоморфно полосе S ¹ × I . 2-шары гомотопически тривиальны, а полоса гомотопически эквивалентна окружности S ¹ . Таким образом, топологическая классификация возможных соединений сводится к классификации функций перехода. Функция перехода отображает полосу в G , а различные способы отображения полосы в G задаются первой гомотопической группой G .

Итак, в формулировке G -расслоения калибровочная теория допускает монополи Дирака при условии, что G не является односвязной , всякий раз, когда существуют пути, которые обходят группу, которая не может быть деформирована до постоянного пути (пути, образ которого состоит из одной точки). U(1), которая имеет квантованные заряды, не является односвязной и может иметь монополи Дирака, в то время как , ее универсальная накрывающая группа , является односвязной, не имеет квантованных зарядов и не допускает монополи Дирака. Математическое определение эквивалентно физическому определению при условии, что — следуя Дираку — калибровочные поля разрешены, которые определены только по лоскутам, и калибровочные поля на разных лоскутах склеиваются после калибровочного преобразования. ${\displaystyle \mathbb {R} }$

Полный магнитный поток есть не что иное, как первое число Черна главного пучка, и зависит только от выбора главного пучка, а не от конкретной связи над ним. Другими словами, это топологический инвариант.

Этот аргумент для монополей является переформулировкой аргумента лассо для чистой теории U(1). Он обобщается на d + 1 измерений с d ≥ 2 несколькими способами. Один из способов — расширить все на дополнительные измерения, так что монополи U(1) станут листами размерности d − 3 . Другой способ — исследовать тип топологической сингулярности в точке с гомотопической группой π _{d −2} (G) .

Теории великого объединения

В последние годы новый класс теорий также предположил существование магнитных монополей.

В начале 1970-х годов успехи квантовой теории поля и калибровочной теории в развитии электрослабой теории и математики сильного ядерного взаимодействия побудили многих теоретиков попытаться объединить их в единую теорию, известную как Великая унифицированная теория (GUT). Было предложено несколько GUT, большинство из которых подразумевали наличие реальной магнитной монопольной частицы. Точнее, GUT предсказывали ряд частиц, известных как дионы , из которых наиболее базовым состоянием был монополь. Заряд магнитных монополей, предсказываемый GUT, составляет либо 1, либо 2 гД , в зависимости от теории.

Большинство частиц, появляющихся в любой квантовой теории поля, нестабильны, и они распадаются на другие частицы в различных реакциях, которые должны удовлетворять различным законам сохранения . Стабильные частицы стабильны, потому что нет более легких частиц, на которые они могут распадаться и все еще удовлетворять законам сохранения. Например, электрон имеет лептонное число , равное единице, и электрический заряд, равный единице, и нет более легких частиц, которые сохраняют эти значения. С другой стороны, мюон , по сути тяжелый электрон, может распадаться на электрон плюс два кванта энергии, и, следовательно, он нестабилен.

Дионы в этих GUT также стабильны, но по совершенно другой причине. Ожидается, что дионы существуют как побочный эффект «замораживания» условий ранней Вселенной или нарушения симметрии . В этом сценарии дионы возникают из-за конфигурации вакуума в определенной области Вселенной, согласно первоначальной теории Дирака. Они остаются стабильными не из-за условия сохранения, а потому, что нет более простого топологического состояния, в которое они могут распасться.

Масштаб длины, на котором существует эта особая вакуумная конфигурация, называется корреляционной длиной системы. Корреляционная длина не может быть больше, чем допускает причинность , поэтому корреляционная длина для создания магнитных монополей должна быть по крайней мере такой же большой, как размер горизонта, определяемый метрикой расширяющейся Вселенной . Согласно этой логике, должен быть по крайней мере один магнитный монополь на объем горизонта, как это было, когда произошло нарушение симметрии.

Космологические модели событий, последовавших за Большим взрывом, делают прогнозы о том, каким был объем горизонта, что приводит к прогнозам о современной плотности монополей. Ранние модели предсказывали огромную плотность монополей, что явно противоречит экспериментальным данным. ^{[33] [34]} Это называлось « проблемой монополей ». Ее широко признанное решение заключалось не в изменении предсказания физики частиц о монополях, а скорее в изменении космологических моделей, используемых для вывода их современной плотности. В частности, более поздние теории космической инфляции радикально уменьшают предсказанное число магнитных монополей до плотности, достаточно малой, чтобы неудивительно, что люди никогда не видели ни одного. ^[35] Это решение «проблемы монополей» считалось успехом теории космической инфляции . (Однако, конечно, это будет заметным успехом только в том случае, если предсказание монополя в физике элементарных частиц верно. ^[36] ) По этим причинам монополи стали предметом пристального внимания в 1970-х и 1980-х годах, наряду с другими «приближаемыми» предсказаниями теорий Великого объединения, такими как распад протона .

Многие из других частиц, предсказанных этими GUT, были за пределами возможностей обнаружения текущими экспериментами. Например, широкий класс частиц, известных как X- и Y-бозоны , как предсказано, опосредует связь электрослабых и сильных сил, но эти частицы чрезвычайно тяжелые и находятся далеко за пределами возможностей любого разумного ускорителя частиц для их создания.

Поиск магнитных монополей

Экспериментальные поиски магнитных монополей можно отнести к одной из двух категорий: те, которые пытаются обнаружить уже существующие магнитные монополи, и те, которые пытаются создать и обнаружить новые магнитные монополи.

Прохождение магнитного монополя через катушку провода индуцирует в катушке чистый ток. Это не относится к магнитному диполю или магнитному полюсу более высокого порядка, для которых чистый индуцированный ток равен нулю, и, следовательно, эффект может быть использован в качестве однозначного теста на наличие магнитных монополей. В проводе с конечным сопротивлением индуцированный ток быстро рассеивает свою энергию в виде тепла, но в сверхпроводящей петле индуцированный ток является долгоживущим. Используя высокочувствительное «сверхпроводящее квантовое интерференционное устройство» ( SQUID ), можно, в принципе, обнаружить даже один магнитный монополь.

Согласно стандартной инфляционной космологии, магнитные монополи, созданные до инфляции, должны были бы быть разбавлены до чрезвычайно низкой плотности сегодня. Магнитные монополи также могли быть созданы термически после инфляции, в период повторного нагрева. Однако текущие границы температуры повторного нагрева охватывают 18 порядков величины, и, как следствие, плотность магнитных монополей сегодня не очень хорошо ограничена теорией.

Было проведено много поисков уже существующих магнитных монополей. Хотя было зафиксировано одно волнующее событие, Бласом Кабрерой Наварро в ночь на 14 февраля 1982 года (поэтому его иногда называют « Монополь Дня святого Валентина » ^[37] ), никогда не было воспроизводимых доказательств существования магнитных монополей. ^[13] Отсутствие таких событий накладывает верхний предел на количество монополей, равный примерно одному монополю на 10 ²⁹ нуклонов .

Другой эксперимент в 1975 году привел к объявлению об обнаружении движущегося магнитного монополя в космических лучах группой под руководством П. Буфорда Прайса . ^{[12] Позднее Прайс отказался от своего заявления, и} Луис Уолтер Альварес предложил возможное альтернативное объяснение . ^[38] В его статье было показано, что путь события космических лучей, который, как утверждалось, был вызван магнитным монополем, может быть воспроизведен путем, по которому ядро ​​платины распадается сначала на осмий , а затем на тантал .

Коллайдеры частиц высокой энергии использовались для попытки создания магнитных монополей. Из-за сохранения магнитного заряда магнитные монополи должны создаваться парами, один северный и один южный. Из-за сохранения энергии могут быть созданы только магнитные монополи с массой менее половины энергии центра масс сталкивающихся частиц. Помимо этого, очень мало известно теоретически о создании магнитных монополей в столкновениях частиц высокой энергии. Это связано с их большим магнитным зарядом, который сводит на нет все обычные вычислительные методы. Как следствие, поиски магнитных монополей на основе коллайдеров пока не могут предоставить нижние границы массы магнитных монополей. Однако они могут предоставить верхние границы вероятности (или поперечного сечения) образования пар как функции энергии.

Эксперимент ATLAS на Большом адронном коллайдере в настоящее время имеет самые строгие ограничения по сечению для магнитных монополей с 1 и 2 зарядами Дирака, созданных посредством образования пар Дрелла–Яна . Группа под руководством Венди Тейлор ищет эти частицы на основе теорий, которые определяют их как долгоживущие (они не распадаются быстро), а также как высокоионизирующие (их взаимодействие с веществом преимущественно ионизирующее). В 2019 году поиск магнитных монополей в детекторе ATLAS сообщил о своих первых результатах из данных, собранных в результате столкновений LHC Run 2 при энергии центра масс 13 ТэВ, что при 34,4 фб ⁻¹ является крупнейшим проанализированным набором данных на сегодняшний день. ^[39]

Эксперимент MoEDAL , установленный на Большом адронном коллайдере, в настоящее время ищет магнитные монополи и большие суперсимметричные частицы, используя детекторы ядерных треков и алюминиевые стержни вокруг детектора VELO LHCb . Частицы, которые он ищет, повреждают пластиковые листы , из которых состоят детекторы ядерных треков, вдоль своего пути, с различными идентификационными признаками. Кроме того, алюминиевые стержни могут улавливать достаточно медленно движущиеся магнитные монополи. Затем стержни можно анализировать, пропуская их через SQUID.

«Монополи» в конденсированных системах

Начиная примерно с 2003 года различные группы физиков конденсированного состояния использовали термин «магнитный монополь» для описания другого и в значительной степени не связанного между собой явления. ^{[18] [19]}

Настоящий магнитный монополь был бы новой элементарной частицей и нарушил бы закон Гаусса для магнетизма ∇⋅ B = 0. Монополя такого рода, которые помогли бы объяснить закон квантования заряда , сформулированный Полем Дираком в 1931 году, ^[40] никогда не наблюдались в экспериментах. ^{[41] [42]}

Монополи, изучаемые группами конденсированных сред, не обладают ни одним из этих свойств. Они не являются новой элементарной частицей, а скорее представляют собой возникающее явление в системах обычных частиц ( протонов , нейтронов , электронов , фотонов ); другими словами, они являются квазичастицами . Они не являются источниками для B -поля (т. е. они не нарушают ∇⋅ B = 0 ); вместо этого они являются источниками для других полей, например, H -поля , ^[5] « B ​​* -поля» (связанного со сверхтекучей вихревой силой), ^{[6] [43]} или различных других квантовых полей. ^[44] Они не имеют прямого отношения к теориям великого объединения или другим аспектам физики элементарных частиц и не помогают объяснить квантование заряда — за исключением случаев, когда исследования аналогичных ситуаций могут помочь подтвердить, что используемый математический анализ является обоснованным. ^[45]

В физике конденсированного состояния имеется ряд примеров , когда коллективное поведение приводит к возникновению явлений, которые в некоторых отношениях напоминают магнитные монополи, ^{[17] [46] [47] [48]} , среди которых наиболее заметны материалы со спиновым льдом . ^{[5] [49]} Хотя их не следует путать с гипотетическими элементарными монополями, существующими в вакууме, они, тем не менее, обладают схожими свойствами и могут быть исследованы с использованием схожих методов.

Некоторые исследователи используют термин «магнетизм» для описания манипуляции магнитными монопольными квазичастицами в спиновом льду ^{[50] [51]} [ ^{49] [52]} по аналогии со словом «электричество».

Одним из примеров работы над квазичастицами магнитного монополя является статья, опубликованная в журнале Science в сентябре 2009 года, в которой исследователи описали наблюдение квазичастиц, напоминающих магнитные монополи. Монокристалл спинового льда титаната диспрозия был охлажден до температуры от 0,6 до 2,0 кельвина . Используя наблюдения за рассеянием нейтронов , было показано, что магнитные моменты выстраиваются в переплетенные трубчатые пучки, напоминающие струны Дирака . На дефекте , образованном концом каждой трубки, магнитное поле выглядит как поле монополя. Используя приложенное магнитное поле для нарушения симметрии системы, исследователи смогли контролировать плотность и ориентацию этих струн. Также был описан вклад в теплоемкость системы от эффективного газа этих квазичастиц. ^{[16] [53]} Это исследование было удостоено премии Europhysics Prize 2012 по физике конденсированного состояния.

В другом примере, статья в выпуске Nature Physics от 11 февраля 2011 года описывает создание и измерение долгоживущих магнитных монопольных квазичастичных токов в спиновом льду. Прикладывая импульс магнитного поля к кристаллу титаната диспрозия при 0,36 К, авторы создали релаксирующий магнитный ток, который длился несколько минут. Они измерили ток с помощью электродвижущей силы, которую он индуцировал в соленоиде, соединенном с чувствительным усилителем, и количественно описали его с помощью химической кинетической модели точечных зарядов, подчиняющихся механизму Онзагера-Вина диссоциации и рекомбинации носителей. Таким образом, они вывели микроскопические параметры движения монополя в спиновом льду и определили различные роли свободных и связанных магнитных зарядов. ^[52]

В сверхтекучих жидкостях существует поле B * , связанное со сверхтекучей вихревой силой, которое математически аналогично магнитному полю B . Из-за сходства поле B * называют «синтетическим магнитным полем». В январе 2014 года сообщалось, что монопольные квазичастицы ^[54] для поля B * были созданы и изучены в спинорном конденсате Бозе–Эйнштейна. ^[6] Это первый пример квазимагнитного монополя, наблюдаемого в системе, управляемой квантовой теорией поля. ^[45]

Обновления теоретических и экспериментальных исследований материи можно найти в отчетах Дж. Джакомелли (2000) и С. Балестры (2011) в разделе «Библиография».

Смотрите также

• Уравнения Богомольного
• струна Дирака
• Дион
• Феликс Эренхафт
• Проблема плоскостности
• Закон Гаусса для магнетизма
• Теория Гинзбурга–Ландау
• Массив Хальбаха
• Проблема горизонта
• Инстантон
• Проблема магнитного монополя
• Мерон
• Солитон
• Монополь 'т Хоофта–Полякова
• Монополь У–Яна
• Магнитный ток

Примечания

1. Для соглашения, где магнитный заряд имеет единицу измерения Вебер, см. Jackson 1999. В частности, для уравнений Максвелла см. раздел 6.11, уравнение (6.150), стр. 273, а для закона силы Лоренца см. стр. 290, упражнение 6.17(a). Для соглашения, где магнитный заряд имеет единицу измерения ампер-метр, см. arXiv :physics/0508099v1, уравнение (4), например.

Ссылки

1. Хупер, Дэн (6 октября 2009 г.). Темный космос: в поисках недостающей массы и энергии нашей Вселенной. Harper Collins. ISBN 9780061976865– через Google Книги.
2. "Обзор группы по исследованию частиц и поиску магнитного монополя" (PDF) . lbl.gov .
3. Вэнь, Сяо-Ган; Виттен, Эдвард, «Электрические и магнитные заряды в моделях суперструн», Nuclear Physics B , том 261, стр. 651–677
4. С. Коулмен, «Магнитный монополь 50 лет спустя», перепечатано в Aspects of Symmetry
5. Кастельново, К.; Мёсснер, Р.; Сонди, С.Л. (3 января 2008 г.). «Магнитные монополи в спиновом льду». Nature . 451 (7174): 42–45. arXiv : 0710.5515 . Bibcode :2008Natur.451...42C. doi :10.1038/nature06433. PMID  18172493. S2CID  2399316.
6. Ray, MW; Ruokokoski, E.; Kandel, S.; Möttönen, M.; Hall, DS (2014). «Наблюдение монополей Дирака в синтетическом магнитном поле». Nature . 505 (7485): 657–660. arXiv : 1408.3133 . Bibcode :2014Natur.505..657R. doi :10.1038/nature12954. ISSN  0028-0836. PMID  24476889. S2CID  918213.
7. Чисхолм, Хью (26 июня 2018 г.). «Британская энциклопедия: словарь искусств, наук, литературы и общей информации». [Кембридж] University Press – через Google Books.
8. Мэги, Уильям Фрэнсис (26 июня 2018 г.). «Принципы физики: Разработано для использования в качестве учебника общей физики». Century Company – через Google Books.
9. Пьер Кюри (1894). «Sur la possibilité d'existence de la Conductabilité Magnetique et du Magnetisme Free» [О возможном существовании магнитной проводимости и свободного магнетизма]. Séances de la Société Française de Physique (на французском языке). Париж: 76–77.
10. Дирак, Поль (1931). «Квантованные сингулярности в электромагнитном поле». Труды Королевского общества A. 133 ( 821). Лондон: 60. Bibcode : 1931RSPSA.133...60D. doi : 10.1098/rspa.1931.0130.
11. Конспект лекций Роберта Литтлджона, Калифорнийский университет в Беркли, 2007–2008 гг.
12. Price, PB; Shirk, EK; Osborne, WZ; Pinsky, LS (25 августа 1975 г.). «Доказательства обнаружения движущегося магнитного монополя». Physical Review Letters . 35 (8): 487–490. Bibcode : 1975PhRvL..35..487P. doi : 10.1103/PhysRevLett.35.487.
13. Cabrera, Blas (17 мая 1982 г.). «Первые результаты сверхпроводящего детектора для движущихся магнитных монополей». Physical Review Letters . 48 (20): 1378–1381. Bibcode :1982PhRvL..48.1378C. doi :10.1103/PhysRevLett.48.1378.
14. Милтон стр. 60
15. Polchinski, Joseph (1 февраля 2004 г.). «Монополи, дуальность и теория струн». International Journal of Modern Physics A . 19 (supp01): 145–154. arXiv : hep-th/0304042 . Bibcode :2004IJMPA..19S.145P. doi :10.1142/S0217751X0401866X. S2CID  831833.
16. "Впервые обнаружены магнитные монополи в реальном магните". Science Daily . 4 сентября 2009 г. Получено 4 сентября 2009 г.
17. Создание магнитных монополей и другой экзотики в лаборатории, Symmetry Breaking , 29 января 2009 г. Получено 31 января 2009 г.
18. "Магнитные монополи обнаружены в спиновых льдах", Physics World , 3 сентября 2009 г. "Олег Чернышёв из Университета Джонса Хопкинса [исследователь в этой области] предупреждает, что теория и эксперименты специфичны для спиновых льдов и вряд ли прольют свет на магнитные монополи, как предсказывал Дирак".
19. Gibney, Elizabeth (29 января 2014 г.). "Квантовое облако имитирует магнитный монополь". Nature . doi :10.1038/nature.2014.14612. S2CID  124109501. Это не первый случай, когда физики создают аналоги монополей. В 2009 году физики наблюдали магнитные монополи в кристаллическом материале, называемом спиновым льдом, который при охлаждении до почти абсолютного нуля, по-видимому, заполняется классическими монополями размером с атом. Они являются магнитными в истинном смысле, но не могут изучаться по отдельности. Похожие аналоги также были обнаружены в других материалах, например, в сверхтекучем гелии. ... Стивен Брамвелл, физик из Университетского колледжа Лондона, который был пионером в работе над монополями в спиновых льдах, говорит, что [эксперимент 2014 года под руководством Дэвида Холла] впечатляет, но то, что он наблюдал, не является монополем Дирака в том смысле, в каком его понимают многие люди. «Здесь есть математическая аналогия, аккуратная и красивая. Но это не магнитные монополи».
20. Гриффитс, Дэвид Дж. (2013). Введение в электродинамику (Четвертое изд.). Бостон: Pearson. С. 339. ISBN 978-0-321-85656-2.
21. Паркер, К. Б. (1994). Энциклопедия физики Макгроу-Хилла (2-е изд.). Макгроу-Хилл. ISBN 978-0-07-051400-3.
22. Мэнсфилд, М.; О'Салливан, К. (2011). Понимание физики (4-е изд.). John Wiley & Sons. ISBN 978-0-47-0746370.
23. Moulin, F. (2001). «Магнитные монополи и сила Лоренца». Nuovo Cimento B. 116 ( 8): 869–877. arXiv : math-ph/0203043 . Bibcode : 2001NCimB.116..869M.
24. Риндлер, Вольфганг (ноябрь 1989 г.). «Относительность и электромагнетизм: сила, действующая на магнитный монополь». American Journal of Physics . 57 (11): 993–994. Bibcode : 1989AmJPh..57..993R. doi : 10.1119/1.15782.
25. Heras, JA; Baez, G. (2009). «Ковариантная формулировка уравнений Максвелла, выраженная в форме, независимой от конкретных единиц». European Journal of Physics . 30 (1): 23–33. arXiv : 0901.0194 . Bibcode :2009EJPh...30...23H. doi :10.1088/0143-0807/30/1/003. S2CID  14707446.
26. Moulin, F. (2002). «Магнитные монополи и сила Лоренца». Nuovo Cimento B. 116 ( 8): 869–877. arXiv : math-ph/0203043 . Bibcode : 2001NCimB.116..869M.
27. Shanmugadhasan, S (1952). «Динамическая теория магнитных монополей». Canadian Journal of Physics . 30 (3): 218–225. Bibcode : 1952CaJPh..30..218S. doi : 10.1139/p52-021.
28. Фрайбергер, Дэвид (февраль 1989). «Об обобщенном электромагнетизме и алгебре Дирака» (PDF) . Основы физики . 19 (2): 125–159. Bibcode :1989FoPh...19..125F. CiteSeerX 10.1.1.382.3733 . doi :10.1007/bf00734522. S2CID  13909166. 
29. Джексон 1999, раздел 6.11.
30. Фармелло, Грэм (2009). Самый странный человек: Скрытая жизнь Поля Дирака, Квантовый гений . Лондон: Faber and Faber. С. 185–9. ISBN 978-0-571-22278-0.[Опубликовано в Соединенных Штатах под названием « Самый странный человек: тайная жизнь Поля Дирака, мистика атома» . ISBN 978-0-465-01827-7 .] 
31. Джексон 1999, раздел 6.11, уравнение (6.153), стр. 275
32. Аркани-Хамед, Нима; Мотл, Любош; Николис, Альберто; Вафа, Кумрун (2007). «Струнный ландшафт, черные дыры и гравитация как самая слабая сила». Журнал физики высоких энергий . 2007 (6): 060. arXiv : hep-th/0601001 . Bibcode : 2007JHEP...06..060A. doi : 10.1088/1126-6708/2007/06/060. S2CID  16415027.
33. Зельдович, Я. Б.; Хлопов, М. Ю. (1978). «О концентрации реликтовых монополей во Вселенной». Phys. Lett . B79 (3): 239–41. Bibcode :1978PhLB...79..239Z. doi :10.1016/0370-2693(78)90232-0.
34. Прескилл, Джон (1979). «Космологическое производство сверхтяжелых магнитных монополей» (PDF) . Phys. Rev. Lett . 43 (19): 1365–1368. Bibcode :1979PhRvL..43.1365P. doi :10.1103/PhysRevLett.43.1365.
35. Прескилл, Джон (1984). «Магнитные монополи». Annu. Rev. Nucl. Part. Sci . 34 (1): 461–530. Bibcode :1984ARNPS..34..461P. doi : 10.1146/annurev.ns.34.120184.002333 .
36. Риз, Мартин. (1998). Before the Beginning (Нью-Йорк: Basic Books) стр. 185 ISBN 0-201-15142-1 
37. Brumfiel, Geoff (6 мая 2004 г.). «Физика: игра в ожидание». Nature . 429 (6987): 10–11. Bibcode :2004Natur.429...10B. doi : 10.1038/429010a . PMID  15129249. S2CID  4425841.
38. Альварес, Луис В. "Анализ зарегистрированного магнитного монополя". В Kirk, WT (ред.). Труды международного симпозиума 1975 года по взаимодействию лептонов и фотонов при высоких энергиях . Международный симпозиум по взаимодействию лептонов и фотонов при высоких энергиях, 21 августа 1975 г., стр. 967. Архивировано из оригинала 4 февраля 2009 г. Получено 25 мая 2008 г.
39. Aad, Georges el al (2020). «Поиск магнитных монополей и стабильных объектов с высоким электрическим зарядом в столкновениях протонов с энергией 13 ТэВ с помощью детектора ATLAS». Phys. Rev. Lett . 124 (3): 031802. arXiv : 1905.10130 . Bibcode : 2020PhRvL.124c1802A. doi : 10.1103/PhysRevLett.124.031802. PMID  32031842.
40. «Квантованные сингулярности в электромагнитном поле» Поль Дирак , Труды Королевского общества , 29 мая 1931 г. Получено 1 февраля 2014 г.
41. Магнитные монополи, отчет от Particle data group , обновлен в августе 2015 г. Д. Милстедом и Э. Дж. Вайнбергом. «На сегодняшний день не было подтвержденных наблюдений экзотических частиц, обладающих магнитным зарядом».
42. Arttu Rajantie (2016). "Поиск магнитных монополей". Physics Today . 69 (10): 40. Bibcode :2016PhT....69j..40R. doi : 10.1063/PT.3.3328 . Магнитные монополи также вдохновили физиков конденсированного состояния на открытие аналогичных состояний и возбуждений в таких системах, как спиновые льды и конденсаты Бозе-Эйнштейна. Однако, несмотря на важность этих разработок в их собственных областях, они не решают вопрос о существовании реальных магнитных монополей. Поэтому поиск продолжается.
43. T. Ollikainen; K. Tiurev; A. Blinova; W. Lee; DS Hall; M. Möttönen (2017). "Экспериментальная реализация монополя Дирака через распад изолированного монополя". Phys. Rev. X . 7 (2): 021023. arXiv : 1611.07766 . Bibcode :2017PhRvX...7b1023O. doi :10.1103/PhysRevX.7.021023. S2CID  54028181.
44. Якабойлу, Э.; Дойхерт, А.; Лемешко, М. (6 декабря 2017 г.). «Возникновение неабелевых магнитных монополей в проблеме квантовой примеси». Physical Review Letters . 119 (23): 235301. arXiv : 1705.05162 . Bibcode :2017PhRvL.119w5301Y. doi :10.1103/PhysRevLett.119.235301. PMID  29286703. S2CID  206304158.
45. Элизабет Гибни (29 января 2014 г.). "Квантовое облако имитирует магнитный монополь". Nature . doi :10.1038/nature.2014.14612. S2CID  124109501.
46. Чжун, Фан; Нагоса, Наото; Такахаши, Мэй С.; Асамицу, Ацуши; Матье, Роланд; Огасавара, Такеши; Ямада, Хироюки; Кавасаки, Масаси; Токура, Ёсинори; Теракура, Киёюки (2003). «Аномальный эффект Холла и магнитные монополи в импульсном пространстве». Наука . 302 (5642): 92–95. arXiv : cond-mat/0310232 . Бибкод : 2003Sci...302...92F. дои : 10.1126/science.1089408. PMID  14526076. S2CID  41607978.
47. Qi, X.-L.; Li, R.; Zang, J.; Zhang, S.-C. (2009). «Индуцирование магнитного монополя с топологическими поверхностными состояниями». Science . 323 (5918): 1184–1187. arXiv : 0811.1303 . Bibcode :2009Sci...323.1184Q. doi :10.1126/science.1167747. PMID  19179491. S2CID  206517194.
48. «Обнаружены искусственные магнитные монополи». sciencedaily.com .
49. Bramwell, ST; Giblin, SR; Calder, S.; Aldus, R.; Prabhakaran, D.; Fennell, T. (15 октября 2009 г.). «Измерение заряда и тока магнитных монополей в спиновом льду». Nature . 461 (7266): 956–959. arXiv : 0907.0956 . Bibcode :2009Natur.461..956B. doi :10.1038/nature08500. PMID  19829376. S2CID  4399620.
50. "'Магнитность' наблюдалась и измерялась впервые". Science Daily . 15 октября 2009 г. Получено 10 июня 2010 г.
51. MJP Gingras (2009). «Наблюдение монополей в магнитном аналоге льда». Science . 326 (5951): 375–376. arXiv : 1005.3557 . doi :10.1126/science.1181510. PMID  19833948. S2CID  31038263.
52. Giblin, SR; Bramwell, ST; Holdsworth, PCW; Prabhakaran, D.; Terry, I. (13 февраля 2011 г.). «Создание и измерение долгоживущих магнитных монопольных токов в спиновом льду». Nature Physics . 7 (3): 252–258. Bibcode :2011NatPh...7..252G. doi :10.1038/nphys1896.
53. DJP Morris; DA Tennant; SA Grigera; B. Klemke; C. Castelnovo; R. Moessner; C. Czter-nasty; M. Meissner; KC Rule; J.-U. Hoffmann; K. Kiefer; S. Gerischer; D. Slobinsky & RS Perry (3 сентября 2009 г.) [2009-07-09]. "Струны Дирака и магнитные монополи в спиновом льду Dy ₂ Ti ₂ O ₇ ". Science . 326 (5951): 411–4. arXiv : 1011.1174 . Bibcode :2009Sci...326..411M. doi :10.1126/science.1178868. PMID  19729617. S2CID  206522398.
54. Пиетиля, Вилле; Мёттонен, Микко (2009). «Создание монополей Дирака в спинорных конденсатах Бозе – Эйнштейна». Физ. Преподобный Летт . 103 (3): 030401. arXiv : 0903.4732 . Бибкод : 2009PhRvL.103c0401P. doi : 10.1103/physrevlett.103.030401. ПМИД  19659254.

Библиография

• Атья, М. Ф.; Хитчин, Н. (1988). Геометрия и динамика магнитных монополей . Princeton University Press. ISBN 0-691-08480-7.
• Балестра, С. (2011), Библиография магнитного монополя-II , arXiv : 1105.5587
• Brau, CA (2004). Современные проблемы классической электродинамики . Oxford University Press. ISBN 978-0-19-514665-3.
• Хитчин, Нью-Джерси; Мюррей, М.К. (1988). «Спектральные кривые и метод ADHM». Comm. Math. Phys . 114 (3): 463–474. Bibcode :1988CMaPh.114..463H. doi :10.1007/BF01242139. S2CID  123573860.
• Джакомелли, Г. (2000), Библиография по магнитным монополям (PDF)
• Джексон, Дж. Д. (1999). Классическая электродинамика (3-е изд.). Wiley. ISBN 978-0-471-30932-1.
• Лакава, Ф. (2022). Классическая электродинамика: от зарядов изображения до массы фотона и магнитных монополей (2-е изд.). Springer. ISBN 978-3-031-05098-5.
• Лехнер, К. (2018). Классическая электродинамика: современная перспектива . Springer. ISBN 978-3-319-91808-2.
• Лохак, Г.; Штумпф, Х. (2015). Лептонный магнитный монополь: теория и эксперименты . Elsevier. ISBN 978-0-12-802463-8.
• Milton, KA (2006). «Теоретический и экспериментальный статус магнитных монополей». Reports on Progress in Physics . 69 (6): 1637–1711. arXiv : hep-ex/0602040 . Bibcode :2006RPPh...69.1637M. doi :10.1088/0034-4885/69/6/R02. S2CID  119061150.
• Шнир, Я. М. (2005). Магнитные монополи . Springer. ISBN 978-3-540-25277-1.
• Sutcliffe, PM (1997). "BPS monopoles". Int. J. Mod. Phys. A . 12 (26): 4663–4706. arXiv : hep-th/9707009 . Bibcode :1997IJMPA..12.4663S. doi :10.1142/S0217751X97002504. S2CID  16765577.
• Вонсовский, С. В. (1975). Магнетизм элементарных частиц. Издательство «Мир».

Внешние ссылки

В статье использованы материалы из книги Н. Хитчина (2001) [1994], «Магнитный монополь», Энциклопедия математики , EMS Press, которая распространяется по лицензии Creative Commons Attribution/Share-Alike и GNU Free Documentation License .