Тетраэдр

Тетраэдрические объекты

В геометрии тетраэдр ( мн.: тетраэдры или тетраэдры ) , также известный как треугольная пирамида , представляет собой многогранник, состоящий из четырех треугольных граней , шести прямых ребер и четырех вершин . Тетраэдр — самый простой из всех обычных выпуклых многогранников . ^[1]

Тетраэдр — это трехмерный случай более общего понятия евклидова симплекса , поэтому его также можно назвать 3-симплексом .

Тетраэдр — одна из разновидностей пирамиды , представляющая собой многогранник с плоским многоугольным основанием и треугольными гранями, соединяющими основание с общей точкой. В случае тетраэдра основанием является треугольник ( основанием можно считать любую из четырех граней), поэтому тетраэдр также известен как «треугольная пирамида».

Как и все выпуклые многогранники , тетраэдр можно сложить из одного листа бумаги. У него есть две такие сети . ^[1]

Для любого тетраэдра существует сфера (называемая описанной сферой ), на которой лежат все четыре вершины, и другая сфера ( сфера ) , касающаяся граней тетраэдра. ^[2]

Правильный тетраэдр

Правильный тетраэдр — это тетраэдр, у которого все четыре грани представляют собой равносторонние треугольники . Это одно из пяти правильных Платоновых тел , известных с античности.

В правильном тетраэдре все грани имеют одинаковый размер и форму (конгруэнтны), а все ребра имеют одинаковую длину.

Пять тетраэдров раскладываются на плоскости, при этом самые высокие трехмерные точки обозначаются цифрами 1, 2, 3, 4 и 5. Затем эти точки соединяются друг с другом, и остается тонкий объем пустого пространства , где находятся пять тетраэдров. углы кромок не совсем совпадают.

Сами по себе правильные тетраэдры не образуют мозаику (заполняют пространство), но если их чередовать с правильными октаэдрами в соотношении два тетраэдра к одному октаэдру, они образуют чередующиеся кубические соты , которые представляют собой мозаику. Некоторые тетраэдры, которые не являются правильными, включая ортосхему Шлефли и тетраэдр Хилла , могут образовывать мозаику.

Правильный тетраэдр самодуален, то есть двойственным ему является другой правильный тетраэдр. Сложная фигура, состоящая из двух таких двойных тетраэдров , образует звездчатый октаэдр или звездчатый октаэдр.

Координаты правильного тетраэдра

Следующие декартовы координаты определяют четыре вершины тетраэдра с длиной ребра 2, с центром в начале координат и двумя ребрами уровня:

\left(\pm 1,0,-{\frac {1}{\sqrt {2}}}\right)\quad {\mbox{and}}\quad \left(0,\pm 1, {\frac {1}{\sqrt {2}}}\right)

Выраженные симметрично четырьмя точками на единичной сфере , центр тяжести в начале координат и нижняя грань, параллельная плоскости , вершины: $xy$

$v_{1}=\left({\sqrt {\frac {8}{9}}},0,-{\frac {1}{3}}\right)$

$v_{2}=\left(-{\sqrt {\frac {2}{9}}},{\sqrt {\frac {2}{3}}},-{\frac {1} 3}}\вправо)$

$v_{3}=\left(-{\sqrt {\frac {2}{9}}},-{\sqrt {\frac {2}{3}}},-{\frac {1} {3}}\вправо)$

$v_{4}=(0,0,1)$

с длиной ребра . ${\sqrt {\frac {8}{3}}}$

Еще один набор координат основан на чередующемся кубе или полукубе с длиной ребра 2. Эта форма имеет диаграмму Коксетера. и символ Шлефли h{4,3}. Тетраэдр в этом случае имеет длину ребра 2 √ 2 . Инвертирование этих координат создает двойственный тетраэдр, а пара вместе образует звездчатый октаэдр, вершины которого совпадают с вершинами исходного куба.

Тетраэдр: (1,1,1), (1,−1,−1), (−1,1,−1), (−1,−1,1)

Двойной тетраэдр: (−1,−1,−1), (−1,1,1), (1,−1,1), (1,1,−1)

Углы и расстояния

Для правильного тетраэдра с длиной ребра a :

По отношению к базовой плоскости наклон грани (2 √ 2 ) в два раза больше наклона ребра ( √ 2 ), что соответствует тому факту, что горизонтальное расстояние, пройденное от основания до вершины вдоль ребра, в два раза больше, чем вдоль ребра. медиана лица. Другими словами, если C — центр тяжести основания, расстояние от C до вершины основания в два раза больше, чем от C до середины ребра основания. Это следует из того, что медианы треугольника пересекаются в его центроиде, и эта точка делит каждый из них на два отрезка, один из которых вдвое длиннее другого (см. доказательство ).

Для правильного тетраэдра с длиной стороны a , радиусом R описывающей его сферы и расстояниями d _i от произвольной точки трехмерного пространства до четырех его вершин имеем ^[6]

{\begin{aligned}{\frac {d_{1}^{4}+d_{2}^{4}+d_{3}^{4}+d_{4}^{4}}{ 4}}+{\frac {16R^{4}}{9}}&=\left({\frac {d_{1}^{2}+d_{2}^{2}+d_{3}^ {2}+d_{4}^{2}}{4}}+{\frac {2R^{2}}{3}}\right)^{2};\\4\left(a^{4 }+d_{1}^{4}+d_{2}^{4}+d_{3}^{4}+d_{4}^{4}\right)&=\left(a^{2} +d_{1}^{2}+d_{2}^{2}+d_{3}^{2}+d_{4}^{2}\right)^{2}.\end{aligned}}

Изометрии правильного тетраэдра

Вершины куба можно сгруппировать в две группы по четыре, каждая из которых образует правильный тетраэдр (см. выше, а также анимацию , показывающую один из двух тетраэдров в кубе). Симметрии правильного тетраэдра наполовину соответствуют симметрии куба: те, которые отображают тетраэдры в себя, а не друг в друга.

Тетраэдр — единственное платоновское тело, которое не отображается в себя посредством точечной инверсии .

Правильный тетраэдр имеет 24 изометрии, образующие группу симметрии T _d , [3,3], (*332) , изоморфную симметрической группе S ₄ . Их можно классифицировать следующим образом:

T , [3,3] ⁺ , (332) изоморфна знакопеременной группе , A ₄ (единица и 11 собственных вращений) со следующими классами сопряженности (в скобках указаны перестановки вершин или, соответственно, граней, и представление единичного кватерниона ):
- личность (личность; 1)
- поворот вокруг оси через вершину, перпендикулярную противоположной плоскости, на угол ±120°: 4 оси, по 2 на ось, вместе 8 ((1 2 3) и т. д.;1 ± я ± j ± к/2)
- поворот на угол 180° так, что край сопоставляется с противоположным краем: 3 ((1 2)(3 4) и т. д.; i , j , k )
отражения в плоскости, перпендикулярной краю: 6
отражения в плоскости в сочетании с поворотом на 90° вокруг оси, перпендикулярной плоскости: 3 оси, по 2 на каждую ось, всего 6; эквивалентно, это повороты на 90 ° в сочетании с инверсией ( x отображается в − x ): повороты соответствуют поворотам куба вокруг осей лицом к лицу.

Ортогональные проекции правильного тетраэдра

Правильный тетраэдр имеет две специальные ортогональные проекции : одна с центром в вершине или, что то же самое, на грани, а другая с центром на ребре. Первый соответствует плоскости Кокстера _А2 .

Сечение правильного тетраэдра

Два косо перпендикулярных противоположных края правильного тетраэдра определяют набор параллельных плоскостей. Когда одна из этих плоскостей пересекает тетраэдр, в результате получается прямоугольник . ^[7] Когда пересекающая плоскость находится рядом с одним из краев, прямоугольник получается длинным и тонким. На полпути между двумя краями пересечение представляет собой квадрат . Соотношение сторон прямоугольника меняется на противоположное, когда вы проходите эту половину пути. Для пересечения квадрата средней точки результирующая граничная линия аналогично пересекает каждую грань тетраэдра. Если тетраэдр разделить пополам в этой плоскости, обе половины станут клиньями .

Это свойство также применимо к тетрагональным дисфеноидам при применении к двум специальным парам ребер.

Сферическая черепица

Тетраэдр также можно представить в виде сферической мозаики и спроецировать на плоскость посредством стереографической проекции . Эта проекция является равноугольной , сохраняя углы, но не площади или длины. Прямые линии на сфере проецируются на плоскость в виде дуг окружностей.

Спиральная укладка

Правильные тетраэдры могут быть уложены лицом к лицу в киральную апериодическую цепочку, называемую спиралью Бурдейка – Кокстера .

В четырех измерениях все выпуклые правильные 4-многогранники с тетраэдрическими ячейками ( 5-ячеечный , 16-ячеечный и 600-ячеечный ) могут быть построены как мозаики 3-сферы с помощью этих цепочек, которые становятся периодическими в трехмерном пространстве. пространство граничной поверхности 4-многогранника.

Неправильные тетраэдры

Тетраэдры, у которых нет четырех равносторонних граней, классифицируются и называются в зависимости от симметрии, которой они обладают.

Если все три пары противоположных ребер тетраэдра перпендикулярны , то он называется ортоцентрическим тетраэдром . Когда только одна пара противоположных ребер перпендикулярна, он называется полуортоцентрическим тетраэдром .

Изодинамический тетраэдр — это тетраэдр, в котором чевианы , соединяющие вершины с центрами противоположных граней, совпадают .

Изогонический тетраэдр имеет совпадающие чевианы, соединяющие вершины с точками контакта противоположных граней с вписанной сферой тетраэдра.

Трехпрямоугольный тетраэдр

В трехпрямоугольном тетраэдре три грани при одной вершине являются прямыми углами , как в углу куба.

Кеплер открыл связь между кубом, правильным тетраэдром и трехпрямоугольным тетраэдром. ^[8]

дисфеноид

Дисфеноид — это тетраэдр с четырьмя равными треугольниками в качестве граней ; у треугольников обязательно все углы острые. Правильный тетраэдр является частным случаем дисфеноида. Другие названия той же формы включают бисфеноид , равнобедренный тетраэдр и равносторонний тетраэдр .

Ортосхемы

3-ортосхема – это тетраэдр, все четыре грани которого представляют собой прямоугольные треугольники . ^[а] Ортосхема — это неправильный симплекс , который представляет собой выпуклую оболочку дерева , в котором все ребра взаимно перпендикулярны. В трехмерной ортосхеме дерево состоит из трех перпендикулярных ребер, соединяющих все четыре вершины по линейному пути, совершающему два поворота под прямым углом. 3-ортосхема представляет собой тетраэдр, имеющий по два прямых угла в каждой из двух вершин, поэтому другое ее название — двупрямоугольный тетраэдр . Его еще называют четырехпрямоугольным тетраэдром, потому что он содержит четыре прямых угла. ^[9]

Коксетер также называет четырехпрямоугольные тетраэдры характеристическими тетраэдрами из-за их неотъемлемой связи с правильными многогранниками и их группами симметрии. ^{[10] Например,}для куба характерен частный случай 3-ортосхемы с перпендикулярными ребрами одинаковой длины , что означает, что куб можно разделить на экземпляры этой ортосхемы. Если три его перпендикулярных ребра имеют единичную длину, то остальные ребра имеют длину два √ 2 и одно длиной √ 3 , поэтому все его ребра являются ребрами или диагоналями куба. Кубможно разбить на шесть таких 3-ортосхем.четырьмя разными способами, все шесть которых окружают одну и ту же диагональ куба √ 3 . Куб также можно разбить на 48 меньших экземпляров той же самой характеристической 3-ортосхемы (только одним способом, по всем плоскостям симметрии одновременно). ^[б] Характерный тетраэдр куба является примером тетраэдра Герона .

Каждый правильный многогранник, включая правильный тетраэдр, имеет свою характерную ортосхему . ^[c] Существует 3-ортосхема, которая является характерным тетраэдром правильного тетраэдра . Правильный тетраэдрподразделяется на 24 экземпляра своего характерного тетраэдра.по своим плоскостям симметрии. ^[д]

Если длина ребра правильного тетраэдра 𝒍 = 2, то шесть ребер его характеристического тетраэдра имеют длины , , вокруг его внешней грани прямоугольного треугольника (ребра, противоположные характеристическим углам 𝟀, 𝝉, 𝟁), ^[e] плюс , , (ребра, которые — характерные радиусы правильного тетраэдра). Трехреберный путь вдоль ортогональных ребер ортосхемы равен , , : сначала от вершины тетраэдра к центру ребра тетраэдра, затем поворот на 90° к центру грани тетраэдра, затем поворот на 90° к центру тетраэдра. Ортосхема имеет четыре разные грани прямоугольного треугольника. Внешняя грань представляет собой треугольник 60-90-30 , который составляет одну шестую грани тетраэдра. Тремя внутренними гранями тетраэдра являются: прямоугольный треугольник с ребрами , , , прямоугольный треугольник с ребрами , , , и прямоугольный треугольник с ребрами , , . ${\sqrt {\tfrac {4}{3}}}$ $1$ ${\sqrt {\tfrac {1}{3}}}$ ${\sqrt {\tfrac {3}{2}}}$ ${\sqrt {\tfrac {1}{2}}}$ ${\sqrt {\tfrac {1}{6}}}$ $1$ ${\sqrt {\tfrac {1}{3}}}$ ${\sqrt {\tfrac {1}{6}}}$ $1$ ${\sqrt {\tfrac {3}{2}}}$ ${\sqrt {\tfrac {1}{2}}}$ ${\sqrt {\tfrac {1}{3}}}$ ${\sqrt {\tfrac {1}{2}}}$ ${\sqrt {\tfrac {1}{6}}}$ ${\sqrt {\tfrac {4}{3}}}$ ${\sqrt {\tfrac {3}{2}}}$ ${\sqrt {\tfrac {1}{6}}}$

Тетраэдры, заполняющие пространство

Заполняющий пространство тетраэдр упаковывается с прямо конгруэнтными или энантиоморфными ( зеркальными ) копиями самого себя в пространстве плитки. ^[14] Куб можно разрезать на шесть 3-ортосхем, три левые и три правые (по одному на каждой грани куба), причем кубы могут заполнять пространство, поэтому характеристическая 3-ортосхема куба представляет собой тетраэдр, заполняющий пространство в этом смысле. ^[f] Дисфеноид может представлять собой заполняющий пространство тетраэдр в прямо конгруэнтном смысле, как в дисфеноидных тетраэдрических сотах . Однако правильные тетраэдры не могут заполнить пространство сами по себе. ^[г]

Фундаментальные домены

Неправильный тетраэдр, который является фундаментальной областью ^[15] группы симметрии , является примером тетраэдра Гурса . Тетраэдры Гурса порождают все правильные многогранники (и многие другие однородные многогранники) посредством зеркальных отражений, процесс, называемый калейдоскопической конструкцией Витхоффа .

Для многогранников конструкция Витхоффа располагает три зеркала под углом друг к другу, как в калейдоскопе . В отличие от цилиндрического калейдоскопа, зеркала Витгофа расположены на трех гранях тетраэдра Гурса так, что все три зеркала пересекаются в одной точке. ^[час]

Среди тетраэдров Гурса, образующих трехмерные соты , мы можем распознать ортосхему (характерный тетраэдр куба), двойную ортосхему (характерный тетраэдр куба, связанный с его зеркальным изображением) и заполняющий пространство дисфеноид, показанный на рисунке. выше. ^[10] Дисфеноид представляет собой двойную ортосхему, приклеенную лицом к своему зеркальному изображению (четверная ортосхема). Таким образом, все три тетраэдра Гурса и все многогранники, которые они порождают отражениями, можно разбить на характерные тетраэдры куба .

Изометрии неправильных тетраэдров

Изометрия неправильного (немаркированного) тетраэдра зависит от геометрии тетраэдра, возможны 7 случаев. В каждом случае формируется трехмерная точечная группа . Две другие изометрии (C ₃ , [3] ⁺ ) и (S ₄ , [2 ⁺ ,4 ⁺ ]) могут существовать, если включена маркировка грани или края. Для каждого типа ниже включены тетраэдрические диаграммы, ребра которых окрашены в соответствии с изометрической эквивалентностью, а уникальные ребра выделены серым цветом.

Общие свойства

Объем

Объем тетраэдра определяется формулой объема пирамиды:

V={\frac {1}{3}}A_{0}\,h\,

где A ₀ — площадь основания , а h — высота от основания до вершины. Это справедливо для каждого из четырех вариантов основания, поэтому расстояния от вершин до противоположных граней обратно пропорциональны площадям этих граней.

Для тетраэдра с вершинами a = ( a ₁ , a ₂ , a ₃ ) , b = ( b ₁ , b ₂ , b ₃ ) , c = ( c ₁ , c ₂ , c ₃ ) и d = ( d ₁ , d ₂ , d ₃ ) , объем1/6| det ( а - d , б - d , c - d )| или любая другая комбинация пар вершин, образующая односвязный граф . Это можно переписать, используя скалярное произведение и перекрестное произведение , что даст

V={\frac {|(\mathbf {a} -\mathbf {d} )\cdot ((\mathbf {b} -\mathbf {d} )\times (\mathbf {c} -\mathbf {d} ))|}{6}}.

Если начало системы координат выбрано совпадающим с вершиной d , то d = 0 , поэтому

V={\frac {|\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )|}{6}},

где a , b и c представляют три ребра, которые пересекаются в одной вершине, а a · ( b × c ) — скалярное тройное произведение . Сравнивая эту формулу с той, которая используется для вычисления объема параллелепипеда , приходим к выводу, что объем тетраэдра равен1/6объема любого параллелепипеда, имеющего с ним три сходящихся ребра.

Абсолютное значение скалярного тройного произведения можно представить в виде следующих абсолютных значений определителей:

6\cdot V={\begin{Vmatrix}\mathbf {a} &\mathbf {b} &\mathbf {c} \end{Vmatrix}}

или где выражаются как векторы-строки или столбцы.

6\cdot V={\begin{Vmatrix}\mathbf {a} \\\mathbf {b} \\\mathbf {c} \end{Vmatrix}}

{\begin{cases}\mathbf {a} =(a_{1},a_{2},a_{3}),\\\mathbf {b} =(b_{1},b_{2},b_{3}),\\\mathbf {c} =(c_{1},c_{2},c_{3}),\end{cases}}

Следовательно

36\cdot V^{2}={\begin{vmatrix}\mathbf {a^{2}} &\mathbf {a} \cdot \mathbf {b} &\mathbf {a} \cdot \mathbf {c} \\\mathbf {a} \cdot \mathbf {b} &\mathbf {b^{2}} &\mathbf {b} \cdot \mathbf {c} \\\mathbf {a} \cdot \mathbf {c} &\mathbf {b} \cdot \mathbf {c} &\mathbf {c^{2}} \end{vmatrix}}

где

{\begin{cases}\mathbf {a} \cdot \mathbf {b} =ab\cos {\gamma },\\\mathbf {b} \cdot \mathbf {c} =bc\cos {\alpha },\\\mathbf {a} \cdot \mathbf {c} =ac\cos {\beta }.\end{cases}}

который дает

V={\frac {abc}{6}}{\sqrt {1+2\cos {\alpha }\cos {\beta }\cos {\gamma }-\cos ^{2}{\alpha }-\cos ^{2}{\beta }-\cos ^{2}{\gamma }}},\,

где α , β , γ — плоские углы, входящие в вершину d . Угол α — это угол между двумя ребрами, соединяющими вершину d с вершинами b и c . Угол β действует для вершин a и c , а угол γ определяется положением вершин a и b .

Если мы не требуем, чтобы d = 0, то

6\cdot V=\left|\det \left({\begin{matrix}a_{1}&b_{1}&c_{1}&d_{1}\\a_{2}&b_{2}&c_{2}&d_{2}\\a_{3}&b_{3}&c_{3}&d_{3}\\1&1&1&1\end{matrix}}\right)\right|\,.

Учитывая расстояния между вершинами тетраэдра, объем можно вычислить с помощью определителя Кэли – Менгера :

288\cdot V^{2}={\begin{vmatrix}0&1&1&1&1\\1&0&d_{12}^{2}&d_{13}^{2}&d_{14}^{2}\\1&d_{12}^{2}&0&d_{23}^{2}&d_{24}^{2}\\1&d_{13}^{2}&d_{23}^{2}&0&d_{34}^{2}\\1&d_{14}^{2}&d_{24}^{2}&d_{34}^{2}&0\end{vmatrix}}

где индексы i , j ∈ {1, 2, 3, 4} обозначают вершины { a , b , c , d }, а d _ij — попарное расстояние между ними, т. е. длина ребра, соединяющего две вершины. Отрицательное значение определителя означает, что тетраэдр невозможно построить с заданными расстояниями. Эта формула, иногда называемая формулой Тартальи , по существу принадлежит художнику Пьеро делла Франческа в 15 веке как трехмерный аналог формулы Герона I века для площади треугольника. ^[16]

Пусть $a, b, c$ — три ребра, пересекающиеся в одной точке, а $x, y, z —$ противоположные ребра. Пусть $V$ — объем тетраэдра; тогда ^[17]

V={\frac {\sqrt {4a^{2}b^{2}c^{2}-a^{2}X^{2}-b^{2}Y^{2}-c^{2}Z^{2}+XYZ}}{12}}

где

{\begin{aligned}X&=b^{2}+c^{2}-x^{2},\\Y&=a^{2}+c^{2}-y^{2},\\Z&=a^{2}+b^{2}-z^{2}.\end{aligned}}

В приведенной выше формуле используются шесть длин ребер, а в следующей формуле используются три длины ребер и три угла.

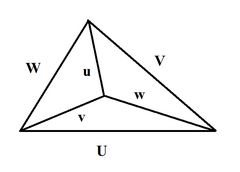
V={\frac {abc}{6}}{\sqrt {1+2\cos {\alpha }\cos {\beta }\cos {\gamma }-\cos ^{2}{\alpha }-\cos ^{2}{\beta }-\cos ^{2}{\gamma }}}

Формула типа Герона для объема тетраэдра

Если $U$ , $V$ , $W$ , $u$ , $v$ , $w$ — длины ребер тетраэдра (первые три образуют треугольник; $u$ напротив $U$ , $v$ напротив $V$ , $w$ напротив $W$ ), то ^[18]

V={\frac {\sqrt {\,(-p+q+r+s)\,(p-q+r+s)\,(p+q-r+s)\,(p+q+r-s)}}{192\,u\,v\,w}}

где

{\begin{aligned}p&={\sqrt {xYZ}},&q&={\sqrt {yZX}},&r&={\sqrt {zXY}},&s&={\sqrt {xyz}},\end{aligned}}

{\begin{aligned}X&=(w-U+v)\,(U+v+w),&x&=(U-v+w)\,(v-w+U),\\Y&=(u-V+w)\,(V+w+u),&y&=(V-w+u)\,(w-u+V),\\Z&=(v-W+u)\,(W+u+v),&z&=(W-u+v)\,(u-v+W).\end{aligned}}

Делитель объема

Любая плоскость, содержащая бимедиану (соединитель середин противоположных ребер) тетраэдра, делит объем тетраэдра пополам. ^[19]

Неевклидов объем

Для тетраэдров в гиперболическом пространстве или в трехмерной эллиптической геометрии двугранные углы тетраэдра определяют его форму и, следовательно, его объем. В этих случаях объем определяется формулой Мураками–Яно . ^[20] Однако в евклидовом пространстве масштабирование тетраэдра изменяет его объем, но не двугранные углы, поэтому такой формулы не может существовать.

Расстояние между краями

Любые два противоположных ребра тетраэдра лежат на двух наклонных линиях , а расстояние между ребрами определяется как расстояние между двумя наклонными линиями. Пусть d будет расстоянием между наклонными линиями, образованными противоположными краями a и b − c , как рассчитано здесь . Тогда другая формула объема имеет вид

V={\frac {d|(\mathbf {a} \times \mathbf {(b-c)} )|}{6}}.

Свойства, аналогичные свойствам треугольника

Тетраэдр обладает многими свойствами, аналогичными свойствам треугольника, включая внутреннюю сферу, описанную сферу, средний тетраэдр и эксферу. Он имеет соответствующие центры, такие как инцентр, центр описанной окружности, эксцентры, центр Шпикера и такие точки, как центроид. Однако обычно нет ортоцентра в смысле пересекающихся высот. ^[21]

Гаспар Монж нашел центр, который существует в каждом тетраэдре, теперь известный как точка Монжа : точка, в которой пересекаются шесть средних плоскостей тетраэдра. Средняя плоскость определяется как плоскость, ортогональная ребру, соединяющему любые две вершины, которая также содержит центр тяжести противоположного ребра, образованного соединением двух других вершин. Если высоты тетраэдра пересекаются, то точка Монжа и ортоцентр совпадают, что дает класс ортоцентрического тетраэдра .

Ортогональная линия, проведенная из точки Монжа к любой грани, пересекает эту грань в средней точке отрезка между ортоцентром этой грани и основанием высоты, опущенной из противоположной вершины.

Отрезок, соединяющий вершину тетраэдра с центроидом противоположной грани, называется медианой , а отрезок, соединяющий середины двух противоположных ребер, называется бимедианой тетраэдра . Следовательно, в тетраэдре четыре медианы и три бимедианы. Все эти семь сегментов линий совпадают в точке, называемой центроидом тетраэдра. ^[22] Кроме того, четыре медианы разделены центроидом в соотношении 3:1 (см. теорему Коммандино ). Центр тяжести тетраэдра — это середина между его точкой Монжа и центром описанной окружности. Эти точки определяют линию Эйлера тетраэдра, аналогичную линии Эйлера треугольника.

Окружность девяти точек общего треугольника имеет аналог в описанной сфере среднего тетраэдра тетраэдра. Это сфера с двенадцатью точками , и помимо центроидов четырех граней эталонного тетраэдра она проходит через четыре замещающие точки Эйлера , по одной трети пути от точки Монжа к каждой из четырех вершин. Наконец, он проходит через четыре базовые точки ортогональных линий, пропущенных из каждой точки Эйлера, к грани, не содержащей вершину, породившую точку Эйлера. ^[23]

Центр Т двенадцатиточечной сферы также лежит на линии Эйлера. В отличие от своего треугольного аналога, этот центр находится на трети расстояния от точки M Монжа к центру описанной окружности. Кроме того, линия, ортогональная к выбранной грани, проходящая через T , компланарна двум другим линиям, ортогональным к той же грани. Первый — это ортогональная линия, проходящая через соответствующую точку Эйлера к выбранной грани. Вторая — ортогональная линия, проходящая через центр тяжести выбранной грани. Эта ортогональная линия, проходящая через центр двенадцати точек, лежит посередине между ортогональной линией точки Эйлера и центроидальной ортогональной линией. Более того, для любой грани двенадцатиточечный центр лежит в середине соответствующей точки Эйлера и ортоцентра этой грани.

Радиус двенадцатиточечной сферы составляет одну треть радиуса описанной опорного тетраэдра.

Между углами, образованными гранями общего тетраэдра, существует связь, определяемая формулой ^[24]:

{\begin{vmatrix}-1&\cos {(\alpha _{12})}&\cos {(\alpha _{13})}&\cos {(\alpha _{14})}\\\cos {(\alpha _{12})}&-1&\cos {(\alpha _{23})}&\cos {(\alpha _{24})}\\\cos {(\alpha _{13})}&\cos {(\alpha _{23})}&-1&\cos {(\alpha _{34})}\\\cos {(\alpha _{14})}&\cos {(\alpha _{24})}&\cos {(\alpha _{34})}&-1\\\end{vmatrix}}=0\,

где αij _— угол между гранями i и j .

Геометрическая медиана координат положения вершин тетраэдра и его изогонический центр связаны при обстоятельствах, аналогичных наблюдаемым для треугольника. Лоренц Линделеф обнаружил, что любому данному тетраэдру соответствует точка, теперь известная как изогонический центр O , в которой телесные углы, образуемые гранями, равны, имеют общее значение π sr и в которой углы, образуемые противоположными гранями, равны. края равны. ^[25] Телесный угол π sr составляет одну четверть угла, образуемого всем пространством. Когда все телесные углы в вершинах тетраэдра меньше π sr, O лежит внутри тетраэдра, а поскольку сумма расстояний от O до вершин минимальна, O совпадает с геометрической медианой M вершин. . В случае, если телесный угол в одной из вершин v равен ровно π sr, то O и M совпадают с v . Однако если тетраэдр имеет вершину v с телесным углом больше π sr, M по-прежнему соответствует v , но O лежит вне тетраэдра.

Геометрические отношения

Тетраэдр – это 3- симплекс . В отличие от других платоновых тел, все вершины правильного тетраэдра равноудалены друг от друга (это единственно возможное расположение четырех равноудаленных точек в трехмерном пространстве).

Тетраэдр — треугольная пирамида , а правильный тетраэдр — самодвойственный .

Правильный тетраэдр можно вложить внутрь куба двумя способами: каждая вершина является вершиной куба, а каждое ребро — диагональю одной из граней куба. Для одного такого вложения декартовы координаты вершин равны

(+1, +1, +1);

(-1, -1, +1);

(-1, +1, -1);

(+1, −1, −1).

В результате получается тетраэдр с длиной ребра 2 √ 2 с центром в начале координат. Для другого тетраэдра (двойственного первому ) поменяйте местами все знаки. Объединение вершин этих двух тетраэдров представляет собой вершины куба, демонстрируя, что правильный тетраэдр представляет собой 3- демикуб .

Объем этого тетраэдра составляет одну треть объема куба. Объединение обоих тетраэдров дает правильное многогранное соединение , называемое соединением двух тетраэдров или стеллой-октангулой .

Внутренняя часть стеллы-октангула представляет собой октаэдр , и соответственно правильный октаэдр является результатом отрезания от правильного тетраэдра четырех правильных тетраэдров половины линейного размера (т. е. спрямления тетраэдра).

Приведенное выше вложение делит куб на пять тетраэдров, один из которых правильный. Фактически пять — это минимальное количество тетраэдров, необходимое для составления куба. Чтобы увидеть это, начиная с базового тетраэдра с 4 вершинами, каждый добавленный тетраэдр добавляет не более 1 новой вершины, поэтому необходимо добавить как минимум еще 4, чтобы получился куб с 8 вершинами.

Вписывание тетраэдров внутрь правильного соединения из пяти кубов дает еще два правильных соединения, содержащих пять и десять тетраэдров.

Правильные тетраэдры сами по себе не могут мозаику пространства , хотя этот результат кажется достаточно вероятным, чтобы Аристотель утверждал, что это возможно. Однако два правильных тетраэдра можно соединить с октаэдром, получив ромбоэдр , который может замостить пространство как тетраэдрически-октаэдрические соты .

Однако известно несколько неправильных тетраэдров, копии которых могут замостить пространство, например, характерная ортосхема куба и дисфеноид дисфеноидной тетраэдральной соты . Полный список остается открытой проблемой. ^[26]

Если ослабить требование, чтобы все тетраэдры имели одинаковую форму, можно замостить пространство, используя только тетраэдры, разными способами. Например, можно разделить октаэдр на четыре одинаковых тетраэдра и снова соединить их с двумя правильными. (В качестве примечания: эти два типа тетраэдров имеют одинаковый объем.)

Тетраэдр уникален среди однородных многогранников тем, что не имеет параллельных граней.

Закон синусов для тетраэдров и пространство всех форм тетраэдров.

Следствием обычного закона синусов является то, что в тетраэдре с вершинами O , A , B , C имеем

\sin \angle OAB\cdot \sin \angle OBC\cdot \sin \angle OCA=\sin \angle OAC\cdot \sin \angle OCB\cdot \sin \angle OBA.\,

Можно рассматривать две стороны этого тождества как соответствующие ориентации поверхности по часовой стрелке и против часовой стрелки.

Помещение любой из четырех вершин в роль O дает четыре таких тождества, но не более трех из них являются независимыми: если стороны трех из них, направленные по часовой стрелке, умножаются и получается, что произведение равно произведению стороны одних и тех же трех тождеств «против часовой стрелки», а затем с обеих сторон сокращаются общие множители, в результате получается четвертое тождество.

Три угла являются углами некоторого треугольника тогда и только тогда, когда их сумма равна 180 ° (π радиан). Какое условие на 12 углов необходимо и достаточно, чтобы они были 12 углами некоторого тетраэдра? Очевидно, что сумма углов любой стороны тетраэдра должна быть равна 180°. Поскольку таких треугольников четыре, существует четыре таких ограничения на суммы углов, и число степеней свободы тем самым уменьшается с 12 до 8. Четыре соотношения, заданные этим законом синуса, еще больше уменьшают количество степеней свободы: 8 до не 4, а до 5, поскольку четвертое ограничение не является независимым от первых трех. Таким образом, пространство всех форм тетраэдров пятимерно. ^[27]

Закон косинусов для тетраэдров

Пусть { P ₁ , P ₂ , P ₃ , P ₄ } — точки тетраэдра. Пусть Δ _i будет площадью грани, противоположной вершине Pi _, и пусть θ _ij будет двугранным углом между двумя гранями тетраэдра, прилегающими к ребру P _i P _j .

Закон косинусов для этого тетраэдра ^[28] , который связывает площади граней тетраэдра с двугранными углами вокруг вершины, определяется следующим соотношением:

\Delta _{i}^{2}=\Delta _{j}^{2}+\Delta _{k}^{2}+\Delta _{l}^{2}-2(\Delta _{j}\Delta _{k}\cos \theta _{il}+\Delta _{j}\Delta _{l}\cos \theta _{ik}+\Delta _{k}\Delta _{l}\cos \theta _{ij})

Внутренняя точка

Пусть P — любая внутренняя точка тетраэдра объёма V , вершины которого — A , B , C и D , а площади противоположных граней — F _a , F _b , F _c и F _d . Тогда ^[29]^{: с.62, #1609}

PA\cdot F_{\mathrm {a} }+PB\cdot F_{\mathrm {b} }+PC\cdot F_{\mathrm {c} }+PD\cdot F_{\mathrm {d} }\geq 9V.

Для вершин A , B , C и D , внутренней точки P и оснований J , K , L и M перпендикуляров от P к граням и предположим, что грани имеют равные площади, тогда ^[29]^{: стр.226 , #215}

PA+PB+PC+PD\geq 3(PJ+PK+PL+PM).

Внутренний радиус

Обозначая внутренний радиус тетраэдра как r , а внутренние радиусы его треугольных граней как _ri для i = 1, 2, 3, 4, имеем ^[29]^{: с.81, #1990}

{\frac {1}{r_{1}^{2}}}+{\frac {1}{r_{2}^{2}}}+{\frac {1}{r_{3}^{2}}}+{\frac {1}{r_{4}^{2}}}\leq {\frac {2}{r^{2}}},

с равенством тогда и только тогда, когда тетраэдр правильный.

Если A ₁ , A ₂ , A ₃ и A ₄ обозначают площадь каждой грани, значение r определяется выражением

r={\frac {3V}{A_{1}+A_{2}+A_{3}+A_{4}}}

Эта формула получается в результате разделения тетраэдра на четыре тетраэдра, точками которых являются три точки одной из исходных граней и центр инцентра. Поскольку четыре субтетраэдра заполняют объем, имеем . $V={\frac {1}{3}}A_{1}r+{\frac {1}{3}}A_{2}r+{\frac {1}{3}}A_{3}r+{\frac {1}{3}}A_{4}r$

Окружной радиус

Обозначим радиус описанной тетраэдра через R. Пусть a , b , c — длины трех ребер, которые встречаются в вершине, а A , B , C — длины противоположных ребер. Пусть V — объем тетраэдра. Тогда ^[30]^[31]

R={\frac {\sqrt {(aA+bB+cC)(aA+bB-cC)(aA-bB+cC)(-aA+bB+cC)}}{24V}}.

Окружной центр

Центр описанной окружности тетраэдра можно найти как пересечение трех биссектрис. Биссектриса определяется как плоскость с центром и ортогонально ребру тетраэдра. С помощью этого определения центр описанной окружности $C$ тетраэдра с вершинами $x 0$ , $x 1$ , $x 2$ , $x 3$ можно сформулировать как матрично-векторное произведение: ^[32]

{\begin{aligned}C&=A^{-1}B&{\text{where}}&\ &A=\left({\begin{matrix}\left[x_{1}-x_{0}\right]^{T}\\\left[x_{2}-x_{0}\right]^{T}\\\left[x_{3}-x_{0}\right]^{T}\end{matrix}}\right)&\ &{\text{and}}&\ &B={\frac {1}{2}}\left({\begin{matrix}\|x_{1}\|^{2}-\|x_{0}\|^{2}\\\|x_{2}\|^{2}-\|x_{0}\|^{2}\\\|x_{3}\|^{2}-\|x_{0}\|^{2}\end{matrix}}\right)\\\end{aligned}}

В отличие от центроида, центр описанной окружности не всегда может лежать внутри тетраэдра. Аналогично тупоугольному треугольнику, в тупоугольном тетраэдре центр описанной окружности находится за пределами объекта.

центроид

Центр масс тетраэдра вычисляется как среднее арифметическое его четырех вершин, см. Центроид .

Лица

Сумма площадей любых трех граней больше площади четвертой грани. ^[29]^{: с.225, #159}

Целые тетраэдры

Существуют тетраэдры, имеющие целочисленные длины ребер, площади граней и объем. Их называют тетраэдрами Герона . В одном примере одно ребро равно 896, противоположное ребро — 990, а остальные четыре ребра — 1073; две грани представляют собой равнобедренные треугольники с площадями436 800 , а два других — равнобедренные с площадями47 120 , а объем124 185 600 . ^[33]

Тетраэдр может иметь целочисленный объем и последовательные целые числа в качестве ребер, например, тетраэдр с ребрами 6, 7, 8, 9, 10 и 11 и объемом 48. ^[34]

Родственные многогранники и соединения

Правильный тетраэдр можно рассматривать как треугольную пирамиду .

Правильный тетраэдр можно рассматривать как вырожденный многогранник, однородную двуугольную антипризму , где базовые многоугольники являются уменьшенными двуугольниками .

Правильный тетраэдр можно рассматривать как вырожденный многогранник, однородный двуугольный трапецоэдр , содержащий 6 вершин, с двумя наборами коллинеарных ребер.

Процесс усечения, примененный к тетраэдру, дает серию однородных многогранников . Усечение ребер до точек дает октаэдр в виде выпрямленного тетраэдра. Процесс завершается биректификацией, уменьшая исходные грани до точек и снова создавая самодвойственный тетраэдр.

Этот многогранник топологически связан как часть последовательности правильных многогранников с символами Шлефли {3, n }, продолжающейся в гиперболическую плоскость .

Тетраэдр топологически связан с серией правильных многогранников и мозаик с вершинными фигурами третьего порядка .

Из пяти пересекающихся тетраэдров можно построить интересный многогранник . Это соединение пяти тетраэдров известно уже сотни лет. Это явление регулярно встречается в мире оригами . Соединение двадцати вершин образует правильный додекаэдр . Существуют как левосторонние , так и правосторонние формы, которые являются зеркальным отражением друг друга. Наложение обеих форм дает соединение десяти тетраэдров , в котором десять тетраэдров расположены как пять пар звездочек-октангулов . Стелла-октангула представляет собой соединение двух тетраэдров в двойном положении, а восемь ее вершин определяют куб как их выпуклую оболочку.

Квадратный осоэдр — это еще один многогранник с четырьмя гранями, но у него нет треугольных граней.

Многогранник Силасси и тетраэдр — единственные два известных многогранника, в которых каждая грань имеет общее ребро с другой гранью. Более того, многогранник Часара (сам по себе является двойственным многограннику Силасси) и тетраэдр - единственные два известных многогранника, в которых каждая диагональ лежит на сторонах.

Приложения

Численный анализ

В численном анализе сложные трехмерные формы обычно разбиваются на многоугольную сетку неправильных тетраэдров или аппроксимируются ею в процессе составления уравнений для анализа методом конечных элементов, особенно при численном решении уравнений в частных производных . Эти методы имеют широкое практическое применение в вычислительной гидродинамике , аэродинамике , электромагнитных полях , гражданском строительстве , химической инженерии , военно-морской архитектуре и технике и в смежных областях.

Строительная инженерия

Тетраэдр с жесткими краями по своей природе является жестким. По этой причине его часто используют для придания жесткости рамным конструкциям, таким как пространственные рамы .

Авиация

На некоторых аэродромах большая рама в форме тетраэдра с двумя сторонами, покрытыми тонким материалом, установлена на вращающейся оси и всегда направлена против ветра. Он построен достаточно большим, чтобы его можно было увидеть с воздуха, и иногда его подсвечивают. Его цель - служить пилотам ориентиром для указания направления ветра. ^[35]

Химия

Форма тетраэдра встречается в природе в ковалентно связанных молекулах. Все sp ³ -гибридизированные атомы окружены атомами (или неподеленными электронными парами ) в четырех углах тетраэдра. Например, в молекуле метана ( CH
₄) или ион аммония ( NH⁺
₄), четыре атома водорода окружают центральный атом углерода или азота с тетраэдрической симметрией. По этой причине один из ведущих журналов по органической химии называется «Тетраэдр» . Центральный угол между любыми двумя вершинами идеального тетраэдра равен arccos(−1/3), или примерно 109,47°. ^[5]

Вода , Ч
₂O также имеет тетраэдрическую структуру с двумя атомами водорода и двумя неподеленными парами электронов вокруг центральных атомов кислорода. Однако его тетраэдрическая симметрия не идеальна, поскольку неподеленные пары отталкиваются сильнее, чем одиночные связи O–H.

Четвертичные диаграммы состояния смесей химических веществ изображаются графически в виде тетраэдров.

Однако четверичные фазовые диаграммы в технике связи представляются графически в двухмерной плоскости.

Электричество и электроника

Если шесть одинаковых резисторов спаять вместе , образуя тетраэдр, то сопротивление, измеренное между любыми двумя вершинами, будет вдвое меньше сопротивления одного резистора. ^[36]^[37]

Поскольку кремний является наиболее распространенным полупроводником, используемым в твердотельной электронике , а валентность кремния равна четырем, тетраэдрическая форма четырех химических связей в кремнии оказывает сильное влияние на то, как формируются кристаллы кремния и какую форму они принимают.

Цветовое пространство

Тетраэдры используются в алгоритмах преобразования цветового пространства специально для случаев, когда ось яркости сегментирует цветовое пространство по диагонали (например, RGB, CMY). ^[38]

Игры

Царская игра Ура , датируемая 2600 годом до нашей эры, проводилась с использованием набора четырехгранных игральных костей.

Особенно в ролевых играх это твердое тело известно как 4-гранный кубик , один из наиболее распространенных многогранных кубиков , число которого появляется вокруг нижней или верхней вершины. Некоторые головоломки, похожие на кубик Рубика, имеют четырехгранную форму, например Пираминкс и Пираморфикс .

Геология

Гипотеза тетраэдра , первоначально опубликованная Уильямом Лоутианом Грином для объяснения образования Земли, ^[39] была популярна в начале 20 века. ^[40]^[41]

Тетраэдрический граф

Скелет тетраэдра (состоящий из вершин и ребер) образует граф с 4 вершинами и 6 ребрами. Это частный случай полного графа K ₄ и графа-колеса W ₄ . ^[43] Это один из 5 платоновых графов , каждый из которых представляет собой скелет своего Платонового тела .

Смотрите также

Спираль Бурдейка – Кокстера
Конфигурация Мёбиуса
Кальтроп
Демигиперкуб и симплекс – n -мерные аналоги
Пентахорон – 4-х мерный аналог
Синергетика (Фуллер)
Тетраэдрический воздушный змей
Тетраэдрическое число
Упаковка тетраэдра
Треугольная дипирамида - построена путем соединения двух тетраэдров по одной грани.
Трехпрямоугольный тетраэдр
Ортосхема

Примечания

^ 3-ортосхема не является дисфеноидом, поскольку ее противоположные края не имеют одинаковой длины. Невозможно построить дисфеноид с гранями прямоугольного или тупоугольного треугольника.
^ Для правильного k -многогранника диаграмма Кокстера-Дынкина характеристической k- ортосхемы представляет собой диаграмму k -многогранника без кольца образующих точек . Правильный k- многогранник подразделяется по его ( k -1)-элементам симметрии на g экземпляров его характеристической k -ортосхемы, окружающей его центр, где g — порядок группы симметрии k -многогранника . ^[11]
^ Правильный многогранник размерности k имеет характеристическую k -ортосхему, а также характеристическую ( k -1)-ортосхему. Правильный многогранник имеет характеристический тетраэдр (3-ортосхему), на который он подразделяется плоскостями симметрии, а также характеристический треугольник (2-ортосхема), на который подразделяется его поверхность линиями симметрии его граней. После разделения его поверхности на характерные прямоугольные треугольники, окружающие центр каждой грани, его внутреннюю часть можно разделить на характерные тетраэдры, добавив радиусы, соединяющие вершины поверхностных прямоугольных треугольников с центром многогранника. ^[12] Образованные таким образом внутренние треугольники также будут прямоугольными.
^ 24 характеристических тетраэдра правильного тетраэдра встречаются в двух зеркальных формах, по 12 в каждой.
^ ab (Коксетер 1973) использует греческую букву 𝝓 (фи) для обозначения одного из трех характеристических углов 𝟀, 𝝓, 𝟁 правильного многогранника. Поскольку 𝝓 обычно используется для обозначения константы золотого сечения ≈ 1,618, для которой Коксетер использует 𝝉 (тау), мы переворачиваем соглашения Кокстера и используем 𝝉 для обозначения характеристического угла.
^ Характерная ортосхема куба — один из тетраэдров Хилла , семейства тетраэдров, заполняющих пространство. Все заполняющие пространство тетраэдры равны ножницам кубу. Каждый выпуклый многогранник ножницеобразен ортосхеме. Каждый правильный выпуклый многогранник (платоново тело) можно разбить на некоторое четное количество экземпляров его характеристической ортосхемы.
^ Тетраэдро -октаэдрические соты заполняют пространство чередующимися ячейками правильного тетраэдра и ячейками правильного октаэдра в соотношении 2:1.
^ Диаграмма Кокстера -Динкина сгенерированного многогранника содержит три узла , представляющие три зеркала. На схеме закодирован двугранный угол между каждой парой зеркал, а также расположение единственной образующей точки , которая умножается зеркальными отражениями в вершины многогранника. Для правильного многогранника диаграмма Кокстера-Дынкина порождающей характеристической ортосхемы представляет собой диаграмму порожденного многогранника без маркировки образующей точки.

Библиография

Кеплер, Иоганн (1619). Harmonices Mundi (Гармония мира) . Иоганн Планк.
Коксетер, HSM (1973). Правильные многогранники (3-е изд.). Нью-Йорк: Дувр.

Внешние ссылки

Викискладе есть медиафайлы по теме Тетраэдра .

Вайсштейн, Эрик В. «Тетраэдр». Математический мир .
Бесплатные бумажные модели тетраэдра и многих других многогранников.
Удивительный, заполняющий пространство, неправильный тетраэдр, который также включает описание «вращающегося кольца тетраэдров», также известного как калейдоцикл .