История квантовой механики

10 самых влиятельных фигур в истории квантовой механики . Слева направо: Макс Планк , Альберт Эйнштейн , Нильс Бор , Луи де Бройль , Макс Борн , Поль Дирак , Вернер Гейзенберг , Вольфганг Паули , Эрвин Шредингер , Ричард Фейнман .

История квантовой механики является фундаментальной частью истории современной физики . Главные главы этой истории начинаются с появления квантовых идей для объяснения отдельных явлений — излучения черного тела, фотоэлектрического эффекта, спектров солнечного излучения — эпохи, называемой Старыми или Старыми квантовыми теориями. ^[1] Основываясь на технологии, разработанной в классической механике , изобретение волновой механики Эрвином Шредингером и расширение многими другими, запускают «современную» эпоху, начинающуюся около 1925 года. Работа Поля Дирака по релятивистской квантовой теории привела его к исследованию квантовых теорий излучения, достигнув кульминации в квантовой электродинамике , первой квантовой теории поля . История квантовой механики продолжается в истории квантовой теории поля . История квантовой химии , теоретической основы химической структуры , реакционной способности и связи , переплетается с событиями, обсуждаемыми в этой статье.

Термин «квантовая механика» был придуман (на немецком языке Quantenmechanik ) группой физиков, включая Макса Борна, Вернера Гейзенберга и Вольфганга Паули , в Гёттингенском университете в начале 1920-х годов и впервые был использован в статье Борна «Zur Quantenmechanik» в 1925 году . ^{[2] [3]}

Слово квантовый происходит от латинского слова «сколько» (как и количество ). Что-то, что квантуется , как энергия гармонических осцилляторов Планка, может принимать только определенные значения. Например, в большинстве стран деньги эффективно квантуются, причем квант денег является монетой наименьшего номинала в обращении. Механика — это раздел науки, который занимается воздействием сил на объекты. Таким образом, квантовая механика — это часть механики, которая занимается объектами, для которых квантуются определенные свойства.

Триумф и смута в конце классической эпохи

Открытия XIX века , как успехи, так и неудачи, подготовили почву для появления квантовой механики.

Волновая теория света

Начиная с 1670 года и на протяжении более трех десятилетий Исаак Ньютон разрабатывал и отстаивал свою корпускулярную теорию , утверждая, что идеально прямые линии отражения демонстрируют корпускулярную природу света, поскольку в то время ни одна волновая теория не демонстрировала движение по прямым линиям. ^{[1] : 19} Он объяснил преломление, постулируя, что частицы света ускоряются в поперечном направлении при входе в более плотную среду. Примерно в то же время современники Ньютона Роберт Гук и Христиан Гюйгенс , а позднее Огюстен-Жан Френель , математически уточнили волновую точку зрения, показав, что если свет распространяется с разной скоростью в разных средах, преломление можно легко объяснить как зависящее от среды распространение световых волн. Полученный принцип Гюйгенса-Френеля оказался чрезвычайно успешным в воспроизведении поведения света и согласовался с открытием Томасом Юнгом интерференции волн света в его эксперименте с двумя щелями в 1801 году. ^[4] Волновая точка зрения не сразу вытеснила лучевую и корпускулярную, но начала доминировать в научном мышлении о свете в середине 19-го века, поскольку она могла объяснить явления поляризации, которые не могли объяснить альтернативные теории. ^[5]

Джеймс Клерк Максвелл обнаружил, что он может применить свои ранее открытые уравнения Максвелла , вместе с небольшой модификацией, для описания самораспространяющихся волн осциллирующих электрических и магнитных полей. Быстро стало очевидно, что видимый свет, ультрафиолетовый свет и инфракрасный свет являются электромагнитными волнами разной частоты. ^{[1] : 272} Эта теория стала критическим ингредиентом в начале квантовой механики.

Возникновение атомной теории

В начале 19 века химические исследования Джона Дальтона и Амедео Авогадро придали вес атомной теории материи, идее, которую Джеймс Клерк Максвелл , Людвиг Больцман и другие развили, чтобы создать кинетическую теорию газов . Успехи кинетической теории придали еще большее доверие идее о том, что материя состоит из атомов, однако у теории также были недостатки, которые могли быть устранены только с развитием квантовой механики. ^[6] Существование атомов не было общепринятым среди физиков и химиков; Эрнст Мах , например, был убежденным антиатомистом. ^[7]

Диаграмма молекулы _I2 , предложенная Людвигом Больцманом в 1898 году, показывающая атомную «чувствительную область» (α, β) перекрытия.

Самые ранние намеки на проблемы в классической механике были высказаны в связи с температурной зависимостью свойств газов. ^[8] Людвиг Больцман предположил в 1877 году, что уровни энергии физической системы, такой как молекула , могут быть дискретными (а не непрерывными). Обоснование Больцмана наличия дискретных уровней энергии в молекулах, таких как молекулы йода, берет свое начало в его теориях статистической термодинамики и статистической механики и было подкреплено математическими аргументами, как это было и двадцать лет спустя с первой квантовой теорией, выдвинутой Максом Планком.

Электроны

В последние дни 1800-х годов Дж. Дж. Томсон установил, что электроны несут отрицательный заряд, противоположный, но такой же размер, как у иона водорода, имея массу более чем в тысячу раз меньшую. Было известно, что многие такие электроны связаны с каждым атомом. ^{[1] : 365}

Теория излучения

При понижении температуры пик кривой излучения черного тела смещается в сторону более длинных волн и также имеет более низкую интенсивность. Кривые излучения черного тела (1862) слева также сравниваются с ранней классической предельной моделью Рэлея и Джинса (1900), показанной справа. Коротковолновая сторона кривых была уже аппроксимирована в 1896 году законом распределения Вина .

На протяжении 1800-х годов многие исследования изучали детали спектра интенсивности в зависимости от частоты для света, излучаемого пламенем, Солнцем или раскаленными объектами. ^{[1] : 367} Формула Ридберга эффективно суммировала темные линии, видимые в спектре, но он не предоставил физической модели для их объяснения. Спектр, излучаемый раскаленными объектами, можно было объяснить на высоких или низких длинах волн, но эти две теории различались.

Старая квантовая теория

Квантовая механика развивалась в два отдельных этапа. Первый этап, известный как старая квантовая теория , начался около 1900 года с радикально новыми подходами к объяснению физических явлений, не понятых классической механикой 1800-х годов. ^[1]

Макс Планк вводит кванты для объяснения излучения черного тела

Портрет Планка в молодости, ок. 1878 г.

Горячие металлические изделия. Желто-оранжевое свечение — это видимая часть теплового излучения, испускаемого из-за высокой температуры. Все остальное на снимке также светится тепловым излучением, но менее ярко и на более длинных волнах, чем может обнаружить человеческий глаз. Камера дальнего инфракрасного диапазона может наблюдать это излучение.

Тепловое излучение — это электромагнитное излучение, испускаемое поверхностью объекта за счет внутренней энергии объекта. Если объект достаточно нагрет, он начинает излучать свет в красном конце видимого спектра , поскольку он становится раскаленным докрасна.

Нагревание его далее приводит к изменению цвета с красного на желтый, белый и синий, поскольку он излучает свет на все более коротких длинах волн (более высоких частотах). Идеальный излучатель также является идеальным поглотителем: когда он холодный, такой объект выглядит идеально черным, потому что он поглощает весь падающий на него свет и не излучает ничего. Следовательно, идеальный тепловой излучатель известен как черное тело , а излучение, которое он испускает, называется излучением черного тела .

Прогнозы количества теплового излучения различных частот, испускаемого телом. Правильные значения, предсказанные законом Планка (зеленый), в сравнении с классическими значениями закона Рэлея-Джинса (красный) и приближения Вина (синий).

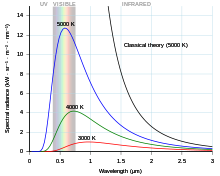
К концу 19 века тепловое излучение было довольно хорошо охарактеризовано экспериментально. Было создано несколько формул, которые могли описывать некоторые экспериментальные измерения теплового излучения: то, как длина волны, на которой излучение наиболее сильно, изменяется с температурой, дается законом смещения Вина , общая мощность, излучаемая на единицу площади, дается законом Стефана-Больцмана . Лучшим теоретическим объяснением экспериментальных результатов был закон Рэлея-Джинса, который хорошо согласуется с экспериментальными результатами на больших длинах волн (или, что эквивалентно, на низких частотах), но сильно не согласен на коротких длинах волн (или на высоких частотах). Фактически, на коротких длинах волн классическая физика предсказывала, что энергия будет излучаться горячим телом с бесконечной скоростью. Этот результат, который явно неверен, известен как ультрафиолетовая катастрофа . Однако классическая физика привела к закону Рэлея-Джинса , который, как показано на рисунке, хорошо согласуется с экспериментальными результатами на низких частотах, но сильно не согласен на высоких частотах. Физики искали единую теорию, которая объясняла бы все экспериментальные результаты.

Интенсивность излучения абсолютно черного тела в зависимости от цвета и температуры. Радужная полоса представляет видимый свет; объекты с температурой 5000 К «раскаляются добела» за счет смешивания различных цветов видимого света. Справа находится невидимый инфракрасный свет. Классическая теория (черная кривая для 5000 К) не работает; другие кривые верны и предсказаны законом Планка.

Первая модель, которая смогла объяснить полный спектр теплового излучения, была предложена Максом Планком в 1900 году. ^[9] Он предложил математическую модель, в которой тепловое излучение находилось в равновесии с набором гармонических осцилляторов . Чтобы воспроизвести экспериментальные результаты, ему пришлось предположить, что каждый осциллятор излучает целое число единиц энергии на своей единственной характерной частоте, а не способен излучать любое произвольное количество энергии. Другими словами, энергия, излучаемая осциллятором, была квантована . Квант энергии для каждого осциллятора, согласно Планку, был пропорционален частоте осциллятора; константа пропорциональности теперь известна как постоянная Планка .

Закон Планка был первой квантовой теорией в физике, и Планк получил Нобелевскую премию в 1918 году «в знак признания заслуг, которые он оказал развитию физики, открыв кванты энергии». ^[10] В то время, однако, Планк считал, что квантование было чисто эвристической математической конструкцией, а не (как сейчас считается) фундаментальным изменением в нашем понимании мира. ^[11]

Альберт Эйнштейн применяет кванты для объяснения фотоэлектрического эффекта

Свет падает на поверхность слева. Если частота света достаточно высока, т. е. если он обеспечивает достаточную энергию, отрицательно заряженные электроны вылетают из металла.

В 1887 году Генрих Герц заметил, что когда свет с достаточной частотой попадает на металлическую поверхность, поверхность испускает катодные лучи . ^{[1] : I:362} Десять лет спустя Дж. Дж. Томсон показал, что многочисленные сообщения о катодных лучах на самом деле были «корпускулами», и их быстро стали называть электронами . В 1902 году Филипп Ленард обнаружил, что максимально возможная энергия выброшенного электрона не связана с его интенсивностью . ^[12] Это наблюдение противоречит классическому электромагнетизму, который предсказывает, что энергия электрона должна быть пропорциональна интенсивности падающего излучения. ^{[13] : 24}

Альберт Эйнштейн около 1905 г.

В 1905 году Альберт Эйнштейн предположил, что хотя непрерывные модели света работают исключительно хорошо для усредненных по времени оптических явлений, для мгновенных переходов энергия в свете может происходить из конечного числа квантов энергии. ^[14] Во вступительном разделе своей квантовой статьи от марта 1905 года «Об эвристической точке зрения относительно излучения и преобразования света» Эйнштейн утверждает:

Согласно рассматриваемому здесь предположению, при распространении светового луча из точки энергия не распределяется непрерывно по все увеличивающимся пространствам, а состоит из конечного числа «квантов энергии», которые локализованы в точках пространства, движутся без деления и могут быть поглощены или сгенерированы только как единое целое.

Это утверждение было названо самым революционным предложением, написанным физиком двадцатого века. ^[15] Энергия одного кванта света частоты определяется как частота, умноженная на постоянную Планка : ${\displaystyle f}$ ${\displaystyle h}$

${\displaystyle E=hf}$

Эйнштейн предположил, что квант света передает всю свою энергию одному электрону, сообщая ему максимум энергии hf . Поэтому только частота света определяет максимальную энергию, которая может быть сообщена электрону; интенсивность фотоэмиссии пропорциональна интенсивности светового луча. ^[14]

Эйнштейн утверждал, что для удаления электрона из металла требуется определенное количество энергии, называемое работой выхода и обозначаемое φ . ^[16] Это количество энергии различно для каждого металла. Если энергия квантов света меньше работы выхода, то они не несут достаточной энергии для удаления электрона из металла. Пороговая частота, f ₀ , — это частота квантов света, энергия которых равна работе выхода:

${\displaystyle \varphi =hf_{0}.}$

Если f больше f ₀ , то энергии hf достаточно для удаления электрона. Выброшенный электрон имеет кинетическую энергию E _k , которая, самое большее, равна световой энергии за вычетом энергии, необходимой для удаления электрона из металла:

${\displaystyle E_{\text{k}}=hf-\varphi =h(f-f_{0}).}$

Описание Эйнштейном света как состоящего из квантов энергии расширило понятие Планка о квантованной энергии, которое заключается в том, что один квант заданной частоты, f , выдает инвариантное количество энергии, hf . В природе одиночные кванты встречаются редко. Солнце и источники излучения, доступные в 19 веке, излучают огромное количество энергии каждую секунду. Постоянная Планка , h , настолько мала, что количество энергии в каждом кванте, hf , очень-очень мало. Свет, который мы видим, включает в себя многие триллионы таких квантов.

Квантование материи: модель атома Бора

К началу 20-го века доказательства требовали модели атома с диффузным облаком отрицательно заряженных электронов, окружающих небольшое, плотное, положительно заряженное ядро . Эти свойства предполагали модель, в которой электроны вращаются вокруг ядра, как планеты, вращающиеся вокруг звезды. Классическая модель атома называется планетарной моделью, или иногда моделью Резерфорда — в честь Эрнеста Резерфорда , который предложил ее в 1911 году на основе эксперимента Гейгера-Марсдена с золотой фольгой , который впервые продемонстрировал существование ядра. Однако было также известно, что атом в этой модели будет нестабильным: согласно классической теории, вращающиеся электроны испытывают центростремительное ускорение и, следовательно, должны испускать электромагнитное излучение, потеря энергии также заставляет их двигаться по спирали к ядру, сталкиваясь с ним за доли секунды.

Вторая, связанная с этим загадка — спектр излучения атомов. Когда газ нагревается, он испускает свет только на дискретных частотах. Например, видимый свет, испускаемый водородом, состоит из четырех разных цветов, как показано на рисунке ниже. Интенсивность света на разных частотах также различна. Напротив, белый свет состоит из непрерывного излучения во всем диапазоне видимых частот. К концу девятнадцатого века простое правило, известное как формула Бальмера, показало, как частоты различных линий связаны друг с другом, хотя и без объяснения, почему это так, или без каких-либо предсказаний относительно интенсивностей. Формула также предсказывала некоторые дополнительные спектральные линии в ультрафиолетовом и инфракрасном свете, которые не наблюдались в то время. Эти линии были позже обнаружены экспериментально, что повысило уверенность в значении формулы.

Спектр излучения водорода . При возбуждении водородный газ испускает свет четырех различных цветов (спектральных линий) в видимом спектре, а также ряд линий в инфракрасном и ультрафиолетовом диапазонах.

Математическая формула, описывающая спектр излучения водорода

В 1885 году швейцарский математик Иоганн Бальмер открыл, что каждая длина волны λ (лямбда) в видимом спектре водорода связана с некоторым целым числом n уравнением

${\displaystyle \lambda =B\left({\frac {n^{2}}{n^{2}-4}}\right)\qquad \qquad n=3,4,5,6}$

где B — константа Бальмера, определенная как 364,56 нм.

В 1888 году Иоганнес Ридберг обобщил и значительно увеличил объяснительную полезность формулы Бальмера. Он предсказал, что λ связана с двумя целыми числами n и m согласно тому, что сейчас известно как формула Ридберга : ^[17]

${\displaystyle {\frac {1}{\lambda }}=R\left({\frac {1}{m^{2}}}-{\frac {1}{n^{2}}}\right),}$

где R — постоянная Ридберга , равная 0,0110 нм ⁻¹ , а n должно быть больше m .

Формула Ридберга учитывает четыре видимые длины волн водорода, устанавливая m = 2 и n = 3, 4, 5, 6. Она также предсказывает дополнительные длины волн в спектре излучения: для m = 1 и для n > 1 спектр излучения должен содержать определенные ультрафиолетовые длины волн, а для m = 3 и n > 3 он должен также содержать определенные инфракрасные длины волн. Экспериментальное наблюдение этих длин волн произошло два десятилетия спустя: в 1908 году Луи Пашен нашел некоторые из предсказанных инфракрасных длин волн, а в 1914 году Теодор Лайман нашел некоторые из предсказанных ультрафиолетовых длин волн. ^[17]

И формула Бальмера, и формула Ридберга включают целые числа: в современных терминах они подразумевают, что некоторое свойство атома квантуется. Понимание того, что именно это свойство и почему оно квантуется, было важной частью развития квантовой механики, как показано в остальной части этой статьи.

В 1905 году Альберт Эйнштейн использовал кинетическую теорию для объяснения броуновского движения . Французский физик Жан Батист Перрен использовал модель из статьи Эйнштейна для экспериментального определения массы и размеров атомов, тем самым дав прямое эмпирическое подтверждение атомной теории. ^{[ необходима цитата ]}

Квантовая модель атома водорода Нильса Бора 1913 года.

В 1913 году Нильс Бор предложил новую модель атома , которая включала квантованные электронные орбиты: электроны все еще вращаются вокруг ядра, как планеты вращаются вокруг Солнца, но им разрешено находиться только на определенных орбитах, а не на орбитах на произвольном расстоянии. ^[18] Когда атом испускает (или поглощает) энергию, электрон не движется по непрерывной траектории с одной орбиты вокруг ядра на другую, как можно было бы ожидать в классическом смысле. Вместо этого электрон мгновенно перескакивает с одной орбиты на другую, испуская испускаемый свет в форме фотона. ^[19] Возможные энергии фотонов, испускаемых каждым элементом, определяются разницей в энергии между орбитами, и поэтому спектр излучения для каждого элемента будет содержать ряд линий. ^[20]

Нильс Бор в молодости

Начиная всего лишь с одного простого предположения о правиле, которому должны подчиняться орбиты, модель Бора смогла связать наблюдаемые спектральные линии в спектре излучения водорода с ранее известными константами. В модели Бора электрону не разрешалось непрерывно излучать энергию и врезаться в ядро: как только он оказывался на ближайшей разрешенной орбите, он был стабилен навсегда. Модель Бора не объясняла, почему орбиты должны быть квантованы таким образом, и не могла делать точных предсказаний для атомов с более чем одним электроном или объяснять, почему некоторые спектральные линии ярче других.

Некоторые фундаментальные предположения модели Бора вскоре оказались неверными, но ключевой результат, что дискретные линии в спектрах излучения обусловлены некоторым свойством электронов в атомах, которые квантуются, является правильным. То, как на самом деле ведут себя электроны, разительно отличается от атома Бора и от того, что мы видим в мире нашего повседневного опыта; эта современная квантово-механическая модель атома обсуждается ниже.

Более подробное объяснение модели Бора

Бор предположил, что момент импульса L электрона квантуется:

${\displaystyle L=n{\frac {h}{2\pi }}=n\hbar }$

где n — целое число, а h и ħ — постоянная Планка и приведенная постоянная Планка соответственно. Исходя из этого предположения, закон Кулона и уравнения кругового движения показывают, что электрон с n единицами углового момента вращается вокруг протона на расстоянии r, заданном формулой

${\displaystyle r={\frac {n^{2}h^{2}}{4\pi ^{2}k_{e}me^{2}}}}$,

где k _e — постоянная Кулона , m — масса электрона, а e — заряд электрона . Для простоты это записывается как

${\displaystyle r=n^{2}a_{0},\!}$

где a ₀ , называемый радиусом Бора , равен 0,0529 нм. Радиус Бора — это радиус наименьшей разрешенной орбиты.

Энергия электрона является суммой его кинетической и потенциальной энергий. Электрон имеет кинетическую энергию в силу своего фактического движения вокруг ядра и потенциальную энергию в силу своего электромагнитного взаимодействия с ядром. В модели Бора эта энергия может быть рассчитана и определяется как

${\displaystyle E=-{\frac {k_{\mathrm {e} }e^{2}}{2a_{0}}}{\frac {1}{n^{2}}}}$.

Таким образом, предположение Бора о том, что момент импульса квантуется, означает, что электрон может находиться только на определенных орбитах вокруг ядра и что он может иметь только определенные энергии. Следствием этих ограничений является то, что электрон не врезается в ядро: он не может непрерывно излучать энергию и не может приблизиться к ядру ближе, чем на ₀ (радиус Бора).

Электрон теряет энергию, мгновенно перескакивая с исходной орбиты на более низкую орбиту; дополнительная энергия излучается в виде фотона. И наоборот, электрон, поглощающий фотон, приобретает энергию, поэтому он перескакивает на орбиту, которая находится дальше от ядра.

Каждый фотон от светящегося атомарного водорода обусловлен движением электрона с более высокой орбиты с радиусом r _n на более низкую орбиту r _m . Энергия E _γ этого фотона представляет собой разницу энергий E _n и E _m электрона:

${\displaystyle E_{\gamma }=E_{n}-E_{m}={\frac {k_{\mathrm {e} }e^{2}}{2a_{0}}}\left({\frac {1}{m^{2}}}-{\frac {1}{n^{2}}}\right)}$

Поскольку уравнение Планка показывает, что энергия фотона связана с его длиной волны соотношением E _γ = hc / λ , длины волн света, которые могут быть испущены, определяются выражением

${\displaystyle {\frac {1}{\lambda }}={\frac {k_{\mathrm {e} }e^{2}}{2a_{0}hc}}\left({\frac {1}{m^{2}}}-{\frac {1}{n^{2}}}\right).}$

Это уравнение имеет ту же форму, что и формула Ридберга, и предсказывает, что константа R должна быть задана как

${\displaystyle R={\frac {k_{\mathrm {e} }e^{2}}{2a_{0}hc}}.}$

Таким образом, модель атома Бора может предсказать спектр излучения водорода в терминах фундаментальных констант. Модель может быть легко модифицирована для учета спектра излучения любой системы, состоящей из ядра и одного электрона (то есть ионов , таких как He ⁺ или O ⁷⁺ , которые содержат только один электрон), но не может быть распространена на атом с двумя электронами, такой как нейтральный гелий. Однако она не смогла сделать точных предсказаний для многоэлектронных атомов или объяснить, почему некоторые спектральные линии ярче других.

Важный шаг в развитии квантовой теории был сделан на первом Сольвеевском конгрессе 1911 года. Там ведущие физики научного сообщества встретились, чтобы обсудить проблему «Излучение и кванты». К этому времени была опубликована модель атома Эрнеста Резерфорда ^{[21] [22],} но большая часть обсуждения, касающегося атомной структуры, вращалась вокруг квантовой модели Артура Хааса 1910 года. Кроме того, на Сольвеевском конгрессе в 1911 году Хендрик Лоренц предложил после доклада Эйнштейна о квантовой структуре, чтобы энергия ротатора была равна nhv. ^{[23] [24] : 244} За этим последовали другие квантовые модели, такие как модель Джона Уильяма Николсона 1912 года, которая была ядерной и дискретизированной по угловому моменту. ^{[25] [26] [27]} Николсон ввел спектры в свою атомную модель, используя колебания электронов в ядерном атоме перпендикулярно плоскости орбиты, тем самым поддерживая стабильность. Атомные спектры Николсона идентифицировали много неотнесенных линий в солнечных и туманных спектрах. ^{[25] [28] [29] [24] : 278}

В 1913 году Бор объяснил спектральные линии атома водорода , снова используя квантование, в своей статье от июля 1913 года « О строении атомов и молекул» , в которой он обсуждал и цитировал модель Николсона. ^{[30] [31] [27]} В модели Бора атом водорода изображается как тяжелое, положительно заряженное ядро, вращающееся вокруг легкого, отрицательно заряженного электрона. Электрон может существовать только на определенных, дискретно разделенных орбитах, обозначенных их угловым моментом , который ограничен целым кратным приведенной постоянной Планка . Ключевой успех модели заключался в объяснении формулы Ридберга для спектральных линий излучения атомарного водорода с использованием переходов электронов между орбитами. ^{[24] : 276} Хотя формула Ридберга была известна экспериментально, она не получила теоретического обоснования, пока не была введена модель Бора. Модель Бора не только объяснила причины структуры формулы Ридберга, но и дала обоснование фундаментальным физическим константам, составляющим эмпирические результаты формулы.

Более того, применение квантовой теории Планка к электрону позволило Штефану Прокопиу в 1911–1913 годах, а затем Нильсу Бору в 1913 году вычислить магнитный момент электрона , который позже был назван « магнетоном »; подобные квантовые вычисления, но с численно совершенно другими значениями, впоследствии стали возможны как для магнитных моментов протона, так и для нейтрона , которые на три порядка меньше, чем у электрона.

Эти теории, хотя и были успешными, были строго феноменологическими : в то время не было строгого обоснования квантования , за исключением, возможно, обсуждения Анри Пуанкаре теории Планка в его статье 1912 года « О теории квантов» . ^{[32] [33]} Они известны как старая квантовая теория .

Квантование спина

Квантовый спин против классического магнита в эксперименте Штерна-Герлаха

Квантование орбитального углового момента электрона в сочетании с магнитным моментом электрона предполагало, что атомы с магнитным моментом должны демонстрировать квантованное поведение в магнитном поле. В 1922 году Отто Штерн и Вальтер Герлах решили проверить эту теорию. Они нагревали серебро в вакуумной трубке, оснащенной серией узких выровненных щелей, создавая молекулярный пучок атомов серебра. Они пропустили этот пучок через неоднородное магнитное поле . Вместо непрерывного узора атомов серебра они обнаружили два пучка. ^[34]

Относительно своего северного полюса, направленного вверх, вниз или где-то посередине, в классической механике магнит, брошенный через магнитное поле, может быть отклонен на малое или большое расстояние вверх или вниз. Атомы, которые Штерн и Герлах выстреливали через магнитное поле, действовали аналогично. Однако, в то время как магниты могли отклоняться на переменные расстояния, атомы всегда отклонялись бы на постоянное расстояние либо вверх, либо вниз. Это подразумевало, что свойство атома, которое соответствует ориентации магнита, должно быть квантовано, принимая одно из двух значений (либо вверх, либо вниз), в отличие от свободного выбора под любым углом.

Выбор ориентации магнитного поля, используемого в эксперименте Штерна–Герлаха, произволен. В показанной здесь анимации поле вертикальное, поэтому атомы отклоняются либо вверх, либо вниз. Если магнит повернуть на четверть оборота, атомы отклоняются либо влево, либо вправо. Использование вертикального поля показывает, что спин вдоль вертикальной оси квантуется, а использование горизонтального поля показывает, что спин вдоль горизонтальной оси квантуется.

Результаты эксперимента Штерна-Герлаха стали сенсацией, особенно потому, что ведущие ученые, включая Эйнштейна и Пауля Эренфеста, утверждали, что атомы серебра должны иметь случайную ориентацию в условиях эксперимента: квантование не должно было наблюдаться. ^[34] Прошло по меньшей мере пять лет, прежде чем эта загадка была разрешена: квантование наблюдалось, но оно не было связано с орбитальным угловым моментом.

В 1925 году Ральф Крониг предположил, что электроны ведут себя так, как будто они вращаются вокруг своей оси или «спинируются». ^{[35] : 56} Спин генерирует крошечный магнитный момент, который разделяет энергетические уровни, ответственные за спектральные линии, в соответствии с существующими измерениями. Два электрона на одной и той же орбитали занимают различные квантовые состояния , если они «вращаются» в противоположных направлениях, тем самым удовлетворяя принципу исключения . К сожалению, теория имела два существенных недостатка: два значения, вычисленные Кронигом, были ошибочны в два раза. Старшие коллеги Кронига отговорили его работу, и она так и не была опубликована.

Десять месяцев спустя голландские физики Джордж Уленбек и Сэмюэл Гоудсмит из Лейденского университета опубликовали свою теорию самовращения электрона. ^[36] Модель, как и модель Кронига, была по сути классической, но привела к квантовому предсказанию.

Гипотеза материальных волн де Бройля

Луи де Бройль в 1929 году. Де Бройль получил Нобелевскую премию по физике за предсказание того, что материя ведет себя как волна, сделанное в его докторской диссертации 1924 года.

В 1924 году Луи де Бройль опубликовал прорывную гипотезу: материя обладает волновыми свойствами. Основываясь на предложении Эйнштейна о том, что фотоэлектрический эффект может быть описан с использованием квантованных переносов энергии, и на отдельном предложении Эйнштейна из специальной теории относительности о том, что масса в состоянии покоя эквивалентна энергии посредством , де Бройль предположил, что движущаяся материя, по-видимому, имеет связанную волну с длиной волны , где — импульс материи от движения. ^{[37] [38]} Требуя, чтобы его длина волны охватывала атом, он объяснил квантование орбит Бора. ^{[1] : 217} Одновременно это показало, что волновое поведение света по сути является квантовым эффектом. ^{[1] : 216} ${\displaystyle E=m_{0}c^{2}}$ ${\displaystyle \lambda =h/p}$ ${\displaystyle p}$

Де Бройль расширил модель атома Бора , показав, что электрон на орбите вокруг ядра можно рассматривать как обладающий волнообразными свойствами. В частности, электрон наблюдается только в ситуациях, которые допускают стоячую волну вокруг ядра . Примером стоячей волны является струна скрипки, которая закреплена на обоих концах и может вибрировать. Волны, создаваемые струнным инструментом, по-видимому, колеблются на месте, перемещаясь от гребня к впадине в движении вверх и вниз. Длина волны стоячей волны связана с длиной вибрирующего объекта и граничными условиями. Например, поскольку струна скрипки закреплена на обоих концах, она может нести стоячие волны с длинами волн , где l — длина, а n — положительное целое число. Де Бройль предположил, что разрешенными электронными орбитами являются те, для которых окружность орбиты будет целым числом длин волн. Таким образом, длина волны электрона определяет, что возможны только орбиты Бора определенных расстояний от ядра. В свою очередь, на любом расстоянии от ядра, меньшем определенного значения, было бы невозможно установить орбиту. Минимально возможное расстояние от ядра называется радиусом Бора. ^[39] Трактовка атома Бора де Бройлем в конечном итоге оказалась неудачной, но его гипотеза послужила отправной точкой для волнового уравнения Шредингера. ${\textstyle {\frac {2l}{n}}}$

Материя, ведущая себя как волна, была впервые экспериментально продемонстрирована для электронов: пучок электронов может демонстрировать дифракцию , как и пучок света или волна на воде. Через три года после того, как де Бройль опубликовал свою гипотезу, две разные группы продемонстрировали дифракцию электронов. В Университете Абердина Джордж Пейджет Томсон и Александр Рид пропускали пучок электронов через тонкую целлулоидную пленку, а затем через металлические пленки и наблюдали предсказанные интерференционные картины. (Александр Рид, аспирант Томсона, провел первые эксперименты, но вскоре погиб в аварии на мотоцикле ^[40] и редко упоминается.) В Bell Labs Клинтон Джозеф Дэвиссон и Лестер Хэлберт Джермер отражали электронный пучок от образца никеля в своем эксперименте, наблюдая четко определенные пучки, предсказанные волновыми моделями, возвращающиеся из кристалла. ^{[1] : II:218} Де Бройль был удостоен Нобелевской премии по физике в 1929 году за свою гипотезу; В 1937 году Томсон и Дэвиссон разделили Нобелевскую премию по физике за свою экспериментальную работу.

Основываясь на подходе де Бройля, современная квантовая механика родилась в 1925 году, когда немецкие физики Вернер Гейзенберг, Макс Борн и Паскуаль Йордан ^{[41] [42]} разработали матричную механику , а австрийский физик Эрвин Шредингер изобрел волновую механику и нерелятивистское уравнение Шредингера как приближение обобщенного случая теории де Бройля. ^[43] Впоследствии Шредингер показал, что оба подхода эквивалентны. Первыми приложениями квантовой механики к физическим системам были алгебраическое определение спектра водорода Вольфгангом Паули ^[44] и рассмотрение двухатомных молекул Люси Менсинг . ^[45]

Развитие современной квантовой механики

Конец первой эры квантовой механики был вызван публикацией де Бройлем своей гипотезы о волнах материи , ^{[1] : 268} что привело к открытию Шредингером волновой механики для материи. Точные предсказания спектра поглощения водорода обеспечили широкое признание новой квантовой теории. ^{[1] : 275}

Матричная механика

В 1925 году Вернер Гейзенберг попытался решить одну из проблем, которую модель Бора оставила без ответа, объяснив интенсивности различных линий в спектре излучения водорода. С помощью ряда математических аналогий он выписал квантово-механический аналог для классического вычисления интенсивностей. ^[46] Вскоре после этого коллега Гейзенберга Макс Борн понял, что метод Гейзенберга по вычислению вероятностей переходов между различными уровнями энергии лучше всего можно выразить с помощью математической концепции матриц .

Гейзенберг сформулировал раннюю версию принципа неопределенности в 1927 году, проанализировав мысленный эксперимент , в котором пытались одновременно измерить положение и импульс электрона . Однако Гейзенберг не дал точных математических определений того, что означает «неопределенность» в этих измерениях, шаг, который вскоре был сделан Эрлом Гессе Кеннардом , Вольфгангом Паули и Германом Вейлем . ^{[47] [48]}

Шредингер и волновая механика

В первой половине 1926 года, основываясь на гипотезе де Бройля, Эрвин Шредингер разработал уравнение, описывающее поведение квантово-механической волны. ^[49] Математическая модель, названная уравнением Шредингера в честь ее создателя, является центральной в квантовой механике, определяет разрешенные стационарные состояния квантовой системы и описывает, как квантовое состояние физической системы изменяется со временем. ^[50] Сама волна описывается математической функцией, известной как « волновая функция ». Шредингер сказал, что волновая функция обеспечивает «средства для предсказания вероятности результатов измерений». ^[51]

Шредингеру удалось рассчитать энергетические уровни водорода, рассматривая электрон атома водорода как классическую волну, движущуюся в яме электрического потенциала, созданного протоном. Этот расчет точно воспроизвел энергетические уровни модели Бора.

В мае 1926 года Шредингер доказал, что матричная механика Гейзенберга и его собственная волновая механика делают одинаковые предсказания о свойствах и поведении электрона; математически эти две теории имели общую базовую форму. Тем не менее, эти двое не согласились с интерпретацией их общей теории. Например, Гейзенберг принял теоретическое предсказание скачков электронов между орбиталями в атоме, ^[52] но Шредингер надеялся, что теория, основанная на непрерывных волнообразных свойствах, сможет избежать того, что он назвал (перефразируя Вильгельма Вина ) «этой чепухой о квантовых скачках». ^[53] В конце концов, подход Гейзенберга победил, и квантовые скачки были подтверждены. ^[54]

Копенгагенская интерпретация

Институт Нильса Бора в Копенгагене, который был центром исследований квантовой механики и смежных дисциплин в 1920-х и 1930-х годах. Большинство самых известных в мире физиков-теоретиков провели там время.

Бор, Гейзенберг и другие пытались объяснить, что на самом деле означают эти экспериментальные результаты и математические модели. Термин «копенгагенская интерпретация» был применен к их взглядам в ретроспективе, сглаживая различия между ними. ^{[55] [56] [57] [58] [59] [60]} Хотя не существует окончательного утверждения «копенгагенской» интерпретации, следующие идеи широко рассматриваются как ее характерные.

1. Система полностью описывается квантовым состоянием (Гейзенберг)
2. То, как квантовое состояние изменяется со временем, описывается волновым уравнением — уравнением Шредингера , придающим свету и материи волновые характеристики.
3. Атомные взаимодействия являются прерывистыми (Планк называл их « квантом действия »).
4. Описание природы по сути вероятностно. Вероятность события, например, когда на экране появляется частица в двухщелевом эксперименте, связана с квадратом абсолютного значения амплитуды ее волновой функции. ( Правило Борна , принадлежащее Максу Борну , которое придает физический смысл волновой функции в копенгагенской интерпретации: амплитуда вероятности )
5. Значения несовместимых пар свойств системы не могут быть известны одновременно. ( Принцип неопределенности Гейзенберга )
6. Материя, как и свет, проявляет корпускулярно-волновой дуализм. Эксперимент может продемонстрировать корпускулярно-подобные свойства материи или ее волновые свойства; но не оба одновременно. ( Принцип дополнительности Бора ^[61] )
7. Измерительные приборы по сути являются классическими устройствами и измеряют классические свойства, такие как положение и импульс.
8. Квантово-механическое описание больших систем должно максимально приближаться к классическому описанию. ( Принцип соответствия Бора и Гейзенберга)

Применение к атому водорода

Модель атома Бора была по сути планетарной, с электронами, вращающимися вокруг ядерного «солнца». Однако принцип неопределенности гласит, что электрон не может одновременно иметь точное местоположение и скорость, как это делает планета. Вместо классических орбит, электроны, как говорят, населяют атомные орбитали . Орбиталь — это «облако» возможных местоположений, в которых может быть обнаружен электрон, распределение вероятностей, а не точное местоположение. ^[62] Каждая орбиталь является трехмерной, а не двумерной орбитой, и часто изображается как трехмерная область, в которой существует 95-процентная вероятность обнаружения электрона. ^[63]

Шредингеру удалось вычислить энергетические уровни водорода, рассматривая электрон атома водорода как волну, представленную « волновой функцией » Ψ , в потенциальной яме V , созданной протоном. Решения уравнения Шредингера ^{[ необходимо разъяснение ]} представляют собой распределения вероятностей для положений и местоположений электронов. Орбитали имеют ряд различных форм в трех измерениях. Энергии различных орбиталей можно вычислить , и они точно соответствуют энергетическим уровням модели Бора.

В картине Шредингера каждый электрон обладает четырьмя свойствами:

1. «Орбитальное» обозначение, указывающее, является ли частица-волна той, которая находится ближе к ядру с меньшей энергией, или той, которая находится дальше от ядра с большей энергией;
2. «Форма» орбиты, сферическая или иная;
3. «Наклон» орбитали, определяющий магнитный момент орбитали вокруг оси z .
4. «Спин» электрона.

Общее название этих свойств — квантовое состояние электрона. Квантовое состояние можно описать, присвоив каждому из этих свойств число; они известны как квантовые числа электрона . Квантовое состояние электрона описывается его волновой функцией. Принцип исключения Паули требует, чтобы никакие два электрона в атоме не могли иметь одинаковые значения всех четырех чисел.

Формы атомных орбиталей. Ряды: 1 s , 2 p , 3 d и 4 f . Слева направо . Цвета показывают фазу волновой функции. ${\displaystyle m=-l,\ldots ,l}$

Первое свойство, описывающее орбиталь, — это главное квантовое число n , которое совпадает с таковым в модели Бора. n обозначает уровень энергии каждой орбитали. Возможные значения n — целые числа:

${\displaystyle n=1,2,3\ldots }$

Следующее квантовое число, азимутальное квантовое число , обозначаемое l , описывает форму орбитали. Форма является следствием углового момента орбитали. Угловой момент представляет собой сопротивление вращающегося объекта ускорению или замедлению под воздействием внешней силы. Азимутальное квантовое число представляет собой орбитальный угловой момент электрона вокруг его ядра. Возможные значения для l — целые числа от 0 до n − 1 (где n — главное квантовое число электрона):

${\displaystyle l=0,1,\ldots ,n-1.}$

Форма каждой орбитали обычно обозначается буквой, а не ее азимутальным квантовым числом. Первая форма ( l =0) обозначается буквой s ( мнемоническое обозначение — « s сфера»). Следующая форма обозначается буквой p и имеет форму гантели. Другие орбитали имеют более сложную форму (см. атомная орбиталь ) и обозначаются буквами d , f , g и т. д.

Третье квантовое число, магнитное квантовое число , описывает магнитный момент электрона и обозначается как m _l (или просто m ). Возможные значения для m _l — целые числа от − l до l (где l — азимутальное квантовое число электрона):

${\displaystyle m_{l}=-l,-(l-1),\ldots ,0,\ldots ,(l-1),l.}$

Магнитное квантовое число измеряет компоненту углового момента в определенном направлении. Выбор направления произволен; условно выбирается направление z.

Четвертое квантовое число, спиновое квантовое число (относящееся к «ориентации» спина электрона), обозначается m _s и принимает значения + 1 ⁄ 2 или − 1 ⁄ 2 .

Химик Лайнус Полинг писал в качестве примера:

В случае атома гелия с двумя электронами на орбитали 1 s принцип исключения Паули требует, чтобы два электрона различались по значению одного квантового числа. Их значения n , l и m _l одинаковы. Соответственно, они должны различаться по значению m _s , которое может иметь значение + 1 ⁄ 2 для одного электрона и − 1 ⁄ 2 для другого." ^[62]

Именно базовая структура и симметрия атомных орбиталей, а также способ, которым электроны их заполняют, приводят к организации периодической таблицы . То, как атомные орбитали на разных атомах объединяются, образуя молекулярные орбитали, определяет структуру и прочность химических связей между атомами.

Пионерами квантовой химии были физики Вальтер Гайтлер и Фриц Лондон , опубликовавшие в 1927 году исследование ковалентной связи молекулы водорода. Впоследствии квантовая химия была развита большим количеством ученых, включая американского химика-теоретика Лайнуса Полинга из Калифорнийского технологического института и Джона К. Слейтера, в различные теории, такие как теория молекулярных орбиталей или теория валентности.

Дирак, теория относительности и развитие формальных методов

Начиная примерно с 1927 года, Поль Дирак начал процесс объединения квантовой механики со специальной теорией относительности , предложив уравнение Дирака для электрона. Уравнение Дирака достигает релятивистского описания волновой функции электрона, которое не удалось получить Шредингеру. Оно предсказывает спин электрона и привело Дирака к предсказанию существования позитрона . Он также был пионером в использовании теории операторов, включая влиятельную нотацию скобок , как описано в его знаменитом учебнике 1930 года. В тот же период венгерский эрудит Джон фон Нейман сформулировал строгую математическую основу для квантовой механики как теорию линейных операторов в гильбертовых пространствах, как описано в его не менее знаменитом учебнике 1932 года . Эти, как и многие другие работы периода основания, до сих пор актуальны и широко используются.

Квантовая теория поля

Начиная с 1927 года исследователи пытались применить квантовую механику к полям вместо отдельных частиц, что привело к появлению квантовых теорий поля. Ранние исследователи в этой области включают П. А. М. Дирака , В. Паули, В. Вайскопфа и П. Джордана . Эта область исследований достигла кульминации в формулировке квантовой электродинамики Р. П. Фейнманом , Ф. Дайсоном , Дж. Швингером и С. Томонагой в 1940-х годах. Квантовая электродинамика описывает квантовую теорию электронов, позитронов и электромагнитного поля и послужила моделью для последующих квантовых теорий поля . ^{[41] [42] [64]}

Диаграмма Фейнмана глюонного излучения в квантовой хромодинамике

Теория квантовой хромодинамики была сформулирована в начале 1960-х годов. Теория, какой мы ее знаем сегодня, была сформулирована Политцером , Гроссом и Вильчеком в 1975 году.

Опираясь на новаторские работы Швингера , Хиггса и Голдстоуна , физики Глэшоу , Вайнберг и Салам независимо друг от друга показали, как слабое ядерное взаимодействие и квантовую электродинамику можно объединить в единое электрослабое взаимодействие , за что они получили Нобелевскую премию по физике 1979 года.

Квантовая информация

Квантовая информатика развивалась в последние десятилетия 20-го века, начиная с таких теоретических результатов, как теорема Холево , концепция обобщенных измерений или POVM , предложение Беннета и Брассара о квантовом распределении ключей и алгоритм Шора .

Основополагающие эксперименты

• Двухщелевой эксперимент Томаса Юнга, демонстрирующий волновую природу света. (ок. 1801 г.)
• Анри Беккерель открывает радиоактивность . (1896)
• Эксперименты Дж. Дж. Томсона с электронно-лучевой трубкой (открытие электрона и его отрицательного заряда). (1897)
• Изучение излучения черного тела в период с 1850 по 1900 год, которое невозможно было объяснить без квантовых концепций.
• Фотоэлектрический эффект : Эйнштейн объяснил его в 1905 году (и позже получил за него Нобелевскую премию), используя концепцию фотонов, частиц света с квантованной энергией.
• Эксперимент Роберта Милликена с каплей масла , показавший, что электрический заряд существует в виде квантов (целых единиц). (1909)
• Эксперимент Эрнеста Резерфорда с золотой фольгой опроверг модель атома «пудинг с изюмом» , которая предполагала, что масса и положительный заряд атома распределены почти равномерно. Это привело к планетарной модели атома (1911).
• Эксперимент Джеймса Франка и Густава Герца по столкновению электронов показал, что поглощение энергии атомами ртути квантуется. (1914)
• Отто Штерн и Вальтер Герлах проводят эксперимент Штерна–Герлаха , демонстрирующий квантовую природу спина частицы . (1920)
• Артур Комптон и эксперимент по комптоновскому рассеянию (1923)
• Клинтон Дэвиссон и Лестер Джермер демонстрируют волновую природу электрона ^[65] в эксперименте по дифракции электронов . (1927)
• Карл Дэвид Андерсон, открыв позитрон (1932), подтвердил теоретическое предсказание Поля Дирака об этой частице (1928)
• Эксперимент Лэмба – Резерфорда открыл сдвиг Лэмба (1947), что привело к развитию квантовой электродинамики.
• Клайд Л. Коуэн и Фредерик Райнес подтверждают существование нейтрино в эксперименте с нейтрино . (1955)
• Двухщелевой эксперимент Клауса Йонссона с электронами. (1961)
• Квантовый эффект Холла , открытый в 1980 году Клаусом фон Клитцингом . Квантовая версия эффекта Холла позволила определить новый практический стандарт для электрического сопротивления и провести чрезвычайно точное независимое определение постоянной тонкой структуры .
• Экспериментальная проверка квантовой запутанности Джоном Клаузером и Стюартом Фридманом . (1972)
• Эксперимент с интерферометром Маха -Цендера, проведенный Полом Квятом , Гарольдом Винфуртером, Томасом Герцогом, Антоном Цайлингером и Марком Касевичем, обеспечивающий экспериментальную проверку испытательной установки бомбы Элицура-Вайдмана и доказывающий возможность измерения без взаимодействия . (1994)

Смотрите также

• История научного портала
• Портал ядерных технологий
• Физический портал

• Золотой век физики
• Мысленные эксперименты Эйнштейна
• История квантовой теории поля
• История химии
• История молекулярной теории
• История термодинамики
• Хронология атомной и субатомной физики

Ссылки

1. Уиттекер, Эдмунд Т. (1989). История теорий эфира и электричества. 2: Современные теории, 1900 - 1926 (Переиздание). Нью-Йорк: Dover Publ. ISBN 978-0-486-26126-3.
2. Макс Борн, Моя жизнь: воспоминания лауреата Нобелевской премии , Тейлор и Фрэнсис, Лондон, 1978. («Мы все больше и больше убеждались в необходимости радикального изменения основ физики, т. е. нового типа механики, для которого мы использовали термин квантовая механика. Это слово впервые появляется в физической литературе в моей статье...»)
3. Федак, Уильям А.; Прентис, Джеффри Дж. (2009-02-01). "Статья Борна и Джордана 1925 года "О квантовой механике"" (PDF) . American Journal of Physics . 77 (2): 128–139. Bibcode :2009AmJPh..77..128F. doi :10.1119/1.3009634. ISSN  0002-9505.
4. Янг, Томас (1804). «Бейкеровская лекция: эксперименты и вычисления относительно физической оптики». Philosophical Transactions of the Royal Society . 94 : 1–16. Bibcode : 1804RSPT...94....1Y. doi : 10.1098/rstl.1804.0001 . S2CID  110408369.
5. Бухвальд, Джед (1989). Возникновение волновой теории света: оптическая теория и эксперимент в начале девятнадцатого века . Чикаго: Издательство Чикагского университета. ISBN 978-0-226-07886-1. OCLC  18069573.
6. Фейнман, Ричард; Лейтон, Роберт; Сэндс, Мэтью (1964). Лекции Фейнмана по физике. Том 1. Калифорнийский технологический институт. ISBN 978-0201500646. Получено 30 сентября 2021 г. .
7. Pojman, Paul (2020), "Ernst Mach", в Zalta, Edward N. (ред.), The Stanford Encyclopedia of Philosophy (зима 2020 г.), Metaphysics Research Lab, Stanford University , получено 30 сентября 2021 г.
8. "Фейнмановские лекции по физике. Том I. Гл. 40: Принципы статистической механики". www.feynmanlectures.caltech.edu . Получено 10.03.2024 .
9. Этот результат был опубликован (на немецком языке) как Planck, Max (1901). «Ueber das Gesetz der Energieverteilung im Normalspectrum». Энн. Физ. 309 (3): 553–63. Бибкод : 1901АнП...309..553П. дои : 10.1002/andp.19013090310 . . Английский перевод: "О законе распределения энергии в нормальном спектре". Архивировано из оригинала 18 апреля 2008 г.
10. "Нобелевская премия по физике 1918 года". Нобелевский фонд . Получено 01.08.2009 .
11. Kragh, Helge (1 декабря 2000 г.). «Макс Планк: нерешительный революционер». PhysicsWorld.com. Архивировано из оригинала 1 апреля 2012 г. Получено 7 декабря 2009 г.
12. Уитон, Брюс Р. (1978). «Филипп Ленард и фотоэлектрический эффект, 1889-1911». Исторические исследования в области физических наук . 9 : 299–322. doi :10.2307/27757381. JSTOR  27757381.
13. Хокинг, Стивен (6 ноября 2001 г.) [5 ноября 2001 г.]. Вселенная в двух словах. Том 55. Импи, CD Bantam Spectra (опубликовано в апреле 2002 г.). стр. 80~. doi :10.1063/1.1480788. ISBN 978-0553802023. S2CID  120382028. Архивировано из оригинала 21 сентября 2020 г. . Получено 14 декабря 2020 г. – через Random House Audiobooks. {{cite book}}: |journal=игнорируется ( помощь ) Альтернативный URL
14. Эйнштейн, Альберт (1905). «Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt». Аннален дер Физик . 17 (6): 132–48. Бибкод : 1905АнП...322..132Е. дои : 10.1002/andp.19053220607 ., переведено на английский язык как On a Heuristic Viewpoint Concerning the Production and Transformation of Light Архивировано 11 июня 2009 года в Wayback Machine . Термин «фотон» был введен в 1926 году.
15. Фолсинг, Альбрехт (1997), Альберт Эйнштейн: Биография , пер. Эвальд Озерс , Викинг
16. Тейлор, JR; Зафиратос, CD; Дабсон, MA (2004). Современная физика для ученых и инженеров . Prentice Hall. стр. 127–29. ISBN 0135897890.
17. Taylor, JR; Zafiratos, CD; Dubson, MA (2004). Современная физика для ученых и инженеров . Prentice Hall. стр. 147–48. ISBN 0135897890.
18. МакЭвой, Дж. П.; Сарате, О. (2004). Введение в квантовую теорию . Totem Books. стр. 70–89, [89]. ISBN 1840465778.
19. World Book.Inc (2007). "22". World Book Encyclopedia (Электронная репродукция). The World Book encyclopedia. Vol. 22 (3 ed.). Chicago, Illinois: World Book. p. 6. ISBN 978-0716601074. OCLC  894799866. Архивировано из оригинала 30 января 2017 г. Получено 14 декабря 2020 г. .Альтернативный URL-адрес
20. Wittke, JP; Dicke, RH (1 июня 1961 г.) [1960]. "11". В Holladay, WG (ред.). Introduction to Quantum Mechanics (электронная книга). Том 16. Нэшвилл, Теннесси: ADDISON WESLEY LONGMAN INC (опубликовано 1 января 1978 г.). стр. 10. doi : 10.1063/1.3057610. ISBN 978-0201015102. OCLC  53473 . Получено 14 декабря 2020 г. – через Университет Вандербильта.
21. Лахтакия, А. (1996). Модели и модельеры водорода: Фалес, Томсон, Резерфорд, Бор, Зоммерфельд, Гоудсмит, Гейзенберг, Шредингер, Дирак, Сальхофер . Singapore River Edge, NJ: World Scientific. ISBN 981-02-2302-1. OCLC  35643527.
22. Резерфорд, Э. (1911). «LXXIX. Рассеяние α- и β-частиц материей и структура атома». Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал . 21 (125). Informa UK Limited: 669–688. doi :10.1080/14786440508637080. ISSN  1941-5982.
23. Оригинальные материалы Сольвеевской конференции 1911 года, опубликованные в 1912 году. THÉORIE DU RAYONNEMENT ET LES QUANTA. ДОКЛАДЫ И ДИСКУССИИ DELA Réunion в Брюсселе, с 30 октября по 3 ноября 1911 года, Sous les Auspices dk ME SOLVAY. Публикации по ММ. П. ЛАНЖЕВЕН и М. де БРОЛЬЕ. Перевод с французского, стр.447.
24. Heilbron, John L.; Kuhn, Thomas S. (1969-01-01). «Происхождение атома Бора». Исторические исследования в области физических наук . 1. University of California Press: vi–290. doi :10.2307/27757291. ISSN  0073-2672. JSTOR  27757291.
25. Heilbron, John L. (2013). «Путь к квантовому атому». Nature . 498 (7452). Springer Science and Business Media LLC: 27–30. doi :10.1038/498027a. ISSN  0028-0836. PMID  23739408. S2CID  4355108.
26. Дж. В. Николсон, Месяц. Нет. Рой. Астр. Соц. lxxxii. стр. 49,130, 677, 693, 729 (1912).
27. McCormmach, Russell (1966). «Атомная теория Джона Уильяма Николсона». Архив истории точных наук . 3 (2). Springer Science and Business Media LLC: 160–184. doi :10.1007/bf00357268. ISSN  0003-9519. S2CID  120797894.
28. Николсон, Дж. У. (1912-06-14). «Конституция солнечной короны. II». Ежемесячные уведомления Королевского астрономического общества . 72 (8). Oxford University Press (OUP): 677–693. doi : 10.1093/mnras/72.8.677 . ISSN  0035-8711.
29. Николсон, Дж. У. (1912). «Конституция солнечной короны. III». Ежемесячные уведомления Королевского астрономического общества . 72 (9). Oxford University Press (OUP): 729–740. doi : 10.1093/mnras/72.9.729 . ISSN  0035-8711.
30. Т. Хиросиге и С. Нисио, «Формирование теории атомного строения Бора», Jap. Studies Hist. Sci, № 3 (1964), 6-28;
31. Дж. Л. Хейлброн, История атомных моделей от открытия электрона до зарождения квантовой механики, дисс. (Калифорнийский университет, Беркли, 1964).
32. Маккормах, Рассел (весна 1967 г.), «Анри Пуанкаре и квантовая теория», Isis , 58 (1): 37–55, doi :10.1086/350182, S2CID  120934561
33. Айронс, FE (август 2001 г.), «Доказательство Пуанкаре 1911–12 гг. квантовой прерывности, интерпретируемое как применимое к атомам», American Journal of Physics , 69 (8): 879–84, Bibcode : 2001AmJPh..69..879I, doi : 10.1119/1.1356056
34. Фридрих, Бржетислав; Хершбах, Дадли (декабрь 2003 г.). «Штерн и Герлах: как плохая сигара помогла переориентировать атомную физику». Physics Today . 56 (12): 53–59. Bibcode : 2003PhT....56l..53F. doi : 10.1063/1.1650229 . ISSN  0031-9228.
35. Багготт, Дж. Э. (2013). Квантовая история: история за 40 мгновений (Впечатление: 3-е изд.). Оксфорд: Oxford Univ. Press. ISBN 978-0-19-965597-7.
36. Пайс, Абрахам. «Джордж Уленбек и открытие спина электрона». Physics Today 42.12 (1989): 34-40.
37. Aczel, Amir D., Запутанность , стр. 51 и далее. (Penguin, 2003) ISBN 978-1551926476 
38. МакЭвой, Дж. П.; Сарате, О. (2004). Введение в квантовую теорию . Totem Books. стр. 114. ISBN 1840465778.
39. МакЭвой, Дж. П.; Сарате, О. (2004). Введение в квантовую теорию . Totem Books. стр. 87. ISBN 1840465778.
40. Наварро, Жауме (2010). «Дифракция электронов у Томсона: ранние отклики на квантовую физику в Британии». Британский журнал истории науки . 43 (2): 245–275. doi :10.1017/S0007087410000026. ISSN  0007-0874.
41. Эдвардс, Дэвид А. (1979). «Математические основы квантовой механики». Synthese . 42 (1). Springer Science and Business Media LLC: 1–70. doi :10.1007/bf00413704. ISSN  0039-7857. S2CID  46969028.
42. Edwards, David A. (1981). "Математические основы квантовой теории поля: фермионы, калибровочные поля и суперсимметрия, часть I: теории решеточных полей". International Journal of Theoretical Physics . 20 (7). Springer Science and Business Media LLC: 503–517. Bibcode : 1981IJTP...20..503E. doi : 10.1007/bf00669437. ISSN  0020-7748. S2CID  120108219.
43. Ханле, П. А. (декабрь 1977 г.), «Реакция Эрвина Шрёдингера на тезис Луи де Бройля о квантовой теории», Isis , 68 (4): 606–609, doi :10.1086/351880, S2CID  121913205
44. Паули, Вольфганг (1 мая 1926). «Über das Wasserstoffspektrum vom Standpunkt der neuen Quantenmechanik». Zeitschrift für Physik (на немецком языке). 36 (5): 336–363. Бибкод : 1926ZPhy...36..336P. дои : 10.1007/BF01450175. ISSN  0044-3328. S2CID  128132824.
45. Менсинг, Люси (1 ноября 1926). «Die Rotations-Schwingungsbanden nach der Quantenmechanik». Zeitschrift für Physik (на немецком языке). 36 (11): 814–823. Бибкод : 1926ZPhy...36..814M. дои : 10.1007/BF01400216. ISSN  0044-3328. S2CID  123240532.
46. Ван дер Варден, Б. Л. (1967). Источники квантовой механики . Минеола, Нью-Йорк: Dover Publications. стр. 261–76. Получено 29 июля 1925 г.См. статью Вернера Гейзенберга «Квантовая теоретическая переинтерпретация кинематических и механических соотношений», стр. 261–76.
47. Буш, Пол ; Лахти, Пекка; Вернер, Рейнхард Ф. (17 октября 2013 г.). «Доказательство соотношения ошибки и возмущения Гейзенберга». Physical Review Letters . 111 (16): 160405. arXiv : 1306.1565 . Bibcode : 2013PhRvL.111p0405B. doi : 10.1103/PhysRevLett.111.160405. ISSN  0031-9007. PMID  24182239. S2CID  24507489.
48. Appleby, David Marcus (6 мая 2016 г.). «Квантовые ошибки и возмущения: ответ Бушу, Лахти и Вернеру». Entropy . 18 (5): 174. arXiv : 1602.09002 . Bibcode :2016Entrp..18..174A. doi : 10.3390/e18050174 .
49. Nobel Prize Organization. "Erwin Schrödinger – Biographical" . Получено 28 марта 2014 г. Его великое открытие, волновое уравнение Шредингера, было сделано в конце этой эпохи — в первой половине 1926 г.
50. "Уравнение Шредингера (Физика)", Encyclopaedia Britannica
51. Эрвин Шредингер, «Современная ситуация в квантовой механике», стр. 9. «Этот перевод был первоначально опубликован в Proceedings of the American Philosophical Society, 124, 323–38, а затем появился как раздел I.11 части I квантовой теории и измерений (редакторы JA Wheeler и WH Zurek, Princeton University Press, NJ 1983). Эту статью можно скачать здесь: Эрвин Шредингер. «Перевод статьи Шредингера «Парадокс кота»». Перевод Джона Д. Триммера. Архивировано из оригинала 13.11.2010.
52. Гейзенберг, В. (1955). Развитие интерпретации квантовой теории, стр. 12–29 в книге « Нильс Бор и развитие физики: эссе, посвященные Нильсу Бору по случаю его семидесятилетия» , под редакцией Паули, В. при содействии Розенфельда, Л. и Вайскопфа, В. , Пергамон, Лондон, стр. 13: «единичный квантовый скачок... имеет «фактическую» природу».
53. W. Moore, Schrödinger: Life and Thought , Cambridge University Press (1989), стр. 222. См. стр. 227 собственных слов Шредингера.
54. Глейк, Джеймс (21 октября 1986 г.). «Физики наконец-то увидели квантовый скачок собственными глазами». The New York Times . Получено 30 ноября 2019 г.
55. Фэй, Ян (2019). «Копенгагенская интерпретация квантовой механики». В Zalta, Edward N. (ред.). Стэнфордская энциклопедия философии . Исследовательская лаборатория метафизики, Стэнфордский университет.
56. Camilleri, K.; Schlosshauer, M. (2015). «Нильс Бор как философ эксперимента: бросает ли теория декогеренции вызов учению Бора о классических концепциях?». Исследования по истории и философии современной физики . 49 : 73–83. arXiv : 1502.06547 . Bibcode : 2015SHPMP..49...73C. doi : 10.1016/j.shpsb.2015.01.005. S2CID  27697360.
57. Омнес, Роланд (1999). «Копенгагенская интерпретация». Понимание квантовой механики . Princeton University Press. стр. 41–54. doi :10.2307/j.ctv173f2pm.9. S2CID  203390914.
58. Шайбе, Эрхард (1973). Логический анализ квантовой механики . Pergamon Press. ISBN 9780080171586. OCLC  799397091. [T]Нет смысла искать Копенгагенскую интерпретацию как единую и последовательную логическую структуру. Такие термины, как «Копенгагенская интерпретация» или «Копенгагенская школа», основаны на истории развития квантовой механики; они образуют упрощенный и часто удобный способ ссылки на идеи ряда физиков, сыгравших важную роль в становлении квантовой механики и сотрудничавших с Бором в его Институте или принимавших участие в дискуссиях в решающие годы. При более внимательном рассмотрении довольно легко увидеть, что эти идеи расходятся в деталях и что, в частности, взгляды Бора, духовного лидера школы, образуют отдельную сущность, которую теперь можно понять только путем тщательного изучения как можно большего числа соответствующих публикаций самого Бора.
59. Перес, Эшер (2002). "Эксперимент Поппера и интерпретация Копенгагена". Исследования по истории и философии современной физики . 33 : 23. arXiv : quant-ph/9910078 . Bibcode : 1999quant.ph.10078P. doi : 10.1016/S1355-2198(01)00034-X. Кажется, существует по крайней мере столько же различных интерпретаций Копенгагена, сколько людей, использующих этот термин; возможно, их больше.
60. Мермин, Н. Дэвид (2017-01-01). «Почему QBism не является копенгагенской интерпретацией и что Джон Белл мог подумать об этом». В Bertlmann, Reinhold; Zeilinger, Anton (ред.). Quantum [Un]Speakables II . The Frontiers Collection. Springer International Publishing. стр. 83–93. arXiv : 1409.2454 . doi :10.1007/978-3-319-38987-5_4. ISBN 9783319389851. S2CID  118458259.
61. Бор, Н. (1928). «Квантовый постулат и недавнее развитие атомной теории». Nature . 121 (3050): 580–590. Bibcode :1928Natur.121..580B. doi : 10.1038/121580a0 . Доступно в сборнике ранних трудов Бора « Теория атома и описание природы» (1934).
62. Pauling, Linus (1960). Природа химической связи (3-е изд.). Itahca, NY: Cornell University Press. стр. 47. ISBN 0801403332. Получено 1 марта 2016 г.
63. "Орбитальный (химия и физика)", Encyclopaedia Britannica
64. С. Ауян, Как возможна квантовая теория поля?, Oxford University Press, 1995.
65. Эксперимент Дэвиссона–Джермера, демонстрирующий волновую природу электрона.

Дальнейшее чтение

• Bacciagaluppi, Guido; Valentini, Antony (2009), Квантовая теория на перепутье: переосмысление конференции Solvay 1927 года , Кембридж, Великобритания: Cambridge University Press, стр. 9184, arXiv : quant-ph/0609184 , Bibcode : 2006quant.ph..9184B, ISBN 978-0-521-81421-8, OCLC  227191829
• Бернстайн, Джереми (2009), Quantum Leaps, Кембридж, Массачусетс: Belknap Press of Harvard University Press, ISBN 978-0-674-03541-6
• Гринбергер, Дэниел, Хентшель, Клаус , Вайнерт, Фридель (ред.) Справочник по квантовой физике. Концепции, эксперименты, история и философия , Нью-Йорк: Springer, 2009. ISBN 978-3-540-70626-7 . 
• Джаммер, Макс (1966), Концептуальное развитие квантовой механики , Нью-Йорк: McGraw-Hill, OCLC  534562
• Джаммер, Макс (1974), Философия квантовой механики: интерпретации квантовой механики в исторической перспективе , Нью-Йорк: Wiley, ISBN 0-471-43958-4, OCLC  969760
• А. Уитакер. Новый квантовый век: от теоремы Белла к квантовым вычислениям и телепортации , Oxford University Press, 2011, ISBN 978-0-19-958913-5 
• Стивен Хокинг. Мечты, из которых сделаны вещи , Running Press, 2011, ISBN 978-0-76-243434-3 
• А. Дуглас Стоун. Эйнштейн и квант, поиски доблестного шваба , Princeton University Press, 2006.

Внешние ссылки