треугольник Рело

Изогнутый треугольник постоянной ширины

Граница треугольника Рело — это кривая постоянной ширины, основанная на равностороннем треугольнике. Все точки на стороне равноудалены от противоположной вершины.

Треугольник Рёло [ʁœlo] — это изогнутый треугольник с постоянной шириной , самая простая и известная кривая постоянной ширины, кроме круга. ^[1] Он образован пересечением трех круглых дисков , каждый из которых имеет свой центр на границе двух других. Постоянная ширина означает, что расстояние между любыми двумя параллельными опорными линиями одинаково, независимо от их ориентации. Поскольку его ширина постоянна, треугольник Рёло является одним из ответов на вопрос «Какую форму, кроме круга, можно придать крышке люка , чтобы она не могла упасть через отверстие?» ^[2]

Они названы в честь Франца Рёло , ^[3] немецкого инженера 19-го века, который был пионером в изучении машин для перевода одного типа движения в другой, и который использовал треугольники Рёло в своих проектах. ^[4] Однако эти формы были известны и до его времени, например, дизайнерам готических церковных окон, Леонардо да Винчи , который использовал его для проекции карты , и Леонарду Эйлеру в его исследовании форм постоянной ширины. Другие применения треугольника Рёло включают придание формы гитарным медиаторам , гайкам пожарного гидранта , карандашам и сверлам для сверления скругленных квадратных отверстий, а также в графическом дизайне в формах некоторых знаков и корпоративных логотипов.

Среди фигур постоянной ширины с заданной шириной треугольник Рёло имеет минимальную площадь и самый острый (наименьший) возможный угол (120°) в своих углах. По нескольким числовым показателям он дальше всего от того, чтобы быть центрально-симметричным . Он обеспечивает самую большую фигуру постоянной ширины, избегая точек целочисленной решетки , и тесно связан с формой четырехугольника, максимизируя отношение периметра к диаметру. Он может выполнять полный поворот внутри квадрата, в то же время все время касаясь всех четырех сторон квадрата, и имеет наименьшую возможную площадь среди фигур с этим свойством. Однако, хотя он покрывает большую часть квадрата в этом процессе вращения, он не может покрыть небольшую часть площади квадрата, вблизи его углов. Из-за этого свойства вращения внутри квадрата треугольник Рёло также иногда называют ротором Рёло . ^[5]

Треугольник Рёло является первым из последовательности многоугольников Рёло , границы которых представляют собой кривые постоянной ширины, образованные из правильных многоугольников с нечетным числом сторон. Некоторые из этих кривых использовались в качестве форм монет . Треугольник Рёло также может быть обобщен в трех измерениях несколькими способами: тетраэдр Рёло (пересечение четырех шаров , центры которых лежат на правильном тетраэдре ) не имеет постоянной ширины, но может быть изменен путем скругления его ребер для образования тетраэдра Мейсснера , который имеет ее. С другой стороны, поверхность вращения треугольника Рёло также имеет постоянную ширину.

Строительство

Чтобы построить треугольник Рело

Треугольник Рело может быть построен либо непосредственно из трех окружностей , либо путем округления сторон равностороннего треугольника . ^[6]

Построение из трех окружностей можно выполнить с помощью одного циркуля , даже не нуждаясь в линейке. По теореме Мора-Маскерони то же самое справедливо в более общем смысле для любой конструкции с помощью циркуля и линейки , ^[7] но построение для треугольника Рело особенно просто. Первый шаг — отметить две произвольные точки плоскости (которые в конечном итоге станут вершинами треугольника) и с помощью циркуля нарисовать окружность с центром в одной из отмеченных точек, проходящую через другую отмеченную точку. Затем рисуется вторая окружность того же радиуса с центром в другой отмеченной точке и проходящая через первую отмеченную точку. Наконец, рисуется третья окружность, снова того же радиуса, с центром в одной из двух точек пересечения двух предыдущих окружностей, проходящая через обе отмеченные точки. ^[8] Центральная область в полученном расположении трех окружностей будет треугольником Рело. ^[6]

В качестве альтернативы, треугольник Рело может быть построен из равностороннего треугольника T путем рисования трех дуг окружностей, каждая из которых имеет центр в одной из вершин T и соединяет две другие вершины. ^[9] Или, что эквивалентно, он может быть построен как пересечение трех дисков с центрами в вершинах T , с радиусом , равным длине стороны T. ^[10]

Математические свойства

Параллельные опорные линии треугольника Рело

Самым основным свойством треугольника Рёло является то, что он имеет постоянную ширину, что означает, что для каждой пары параллельных опорных линий (двух линий одинакового наклона, которые обе касаются фигуры, не пересекая ее) две линии имеют одинаковое евклидово расстояние друг от друга, независимо от ориентации этих линий. ^[9] В любой паре параллельных опорных линий одна из двух линий обязательно коснется треугольника в одной из его вершин. Другая опорная линия может коснуться треугольника в любой точке на противоположной дуге, и их расстояние (ширина треугольника Рёло) равно радиусу этой дуги. ^[11]

Первым математиком, открывшим существование кривых постоянной ширины и заметившим, что треугольник Рело имеет постоянную ширину, возможно, был Леонард Эйлер . ^[5] В работе, которую он представил в 1771 году и опубликовал в 1781 году под названием De curvis triangularibus , Эйлер изучал криволинейные треугольники, а также кривые постоянной ширины, которые он назвал орбиформами. ^{[12] [13]}

Крайние меры

По многим показателям треугольник Рело является одной из самых экстремальных кривых постоянной ширины.

По теореме Бляшке-Лебега треугольник Рело имеет наименьшую возможную площадь среди всех кривых заданной постоянной ширины. Эта площадь равна

${\displaystyle {\frac {1}{2}}(\pi -{\sqrt {3}})s^{2}\approx 0.705s^{2},}$

где s — постоянная ширина. Один из методов вывода этой формулы площади — разбить треугольник Рело на внутренний равносторонний треугольник и три криволинейные области между этим внутренним треугольником и дугами, образующими треугольник Рело, а затем сложить площади этих четырех множеств. С другой стороны, кривая постоянной ширины, которая имеет максимально возможную площадь, представляет собой круглый диск , площадь которого составляет . ^[14] ${\displaystyle \pi s^{2}/4\approx 0.785s^{2}}$

Углы, образованные каждой парой дуг в углах треугольника Рёло, все равны 120°. Это самый острый возможный угол в любой вершине любой кривой постоянной ширины. ^[9] Кроме того, среди кривых постоянной ширины треугольник Рёло — это тот, в который вписаны как самые большие, так и самые маленькие равносторонние треугольники. ^[15] Самый большой равносторонний треугольник, вписанный в треугольник Рёло, — это тот, который соединяет его три угла, а самый маленький — это тот, который соединяет три середины его сторон. Подмножество треугольника Рёло, состоящее из точек, принадлежащих трем или более диаметрам, является внутренней частью большего из этих двух треугольников; оно имеет большую площадь, чем множество точек трех диаметров любой другой кривой постоянной ширины. ^[16]

Центрально-симметричные фигуры внутри и снаружи треугольника Рело, используемые для измерения его асимметрии.

Хотя треугольник Рёло имеет шестигранную диэдральную симметрию , такую ​​же, как и равносторонний треугольник , он не имеет центральной симметрии . Треугольник Рёло является наименее симметричной кривой постоянной ширины согласно двум различным мерам центральной асимметрии, мере Ковнера–Безиковича (отношение площади к наибольшей центрально-симметричной форме, охватываемой кривой) и мере Эстермана (отношение площади к наименьшей центрально-симметричной форме, охватывающей кривую). Для треугольника Рёло две центрально-симметричные формы, которые определяют меры асимметрии, обе являются шестиугольными , хотя внутренняя имеет изогнутые стороны. ^[17] Треугольник Рёло имеет диаметры, которые делят его площадь более неравномерно, чем любая другая кривая постоянной ширины. То есть максимальное отношение площадей по обе стороны от диаметра, еще одна мера асимметрии, больше для треугольника Рёло, чем для других кривых постоянной ширины. ^[18]

Среди всех форм постоянной ширины, которые избегают всех точек целочисленной решетки , самая большая ширина — это треугольник Рело. Одна из его осей симметрии параллельна осям координат на полуцелой прямой. Его ширина, приблизительно 1,54, является корнем полинома степени 6 с целочисленными коэффициентами. ^{[17] [19] [20]}

Так же, как круг может быть окружен шестью конгруэнтными кругами, которые касаются его, также возможно расположить семь конгруэнтных треугольников Рело так, чтобы они все соприкасались с центральным треугольником Рело того же размера. Это максимально возможное число для любой кривой постоянной ширины. ^[21]

Равнодиагональный воздушный змей , максимизирующий отношение периметра к диаметру, вписанный в треугольник Рело .

Среди всех четырехугольников , фигура, имеющая наибольшее отношение периметра к диаметру , — это равнодиагональный воздушный змей , который можно вписать в треугольник Рело. ^[22]

Другие меры

По теореме Барбье все кривые одинаковой постоянной ширины, включая треугольник Рело, имеют равные периметры . В частности, этот периметр равен периметру круга с такой же шириной, который равен . ^{[23] [24] [9]} ${\displaystyle \pi s}$

Радиусы наибольшей вписанной окружности треугольника Рело шириной s и описанной окружности того же треугольника равны

${\displaystyle \displaystyle \left(1-{\frac {1}{\sqrt {3}}}\right)s\approx 0.423s\quad {\text{and}}\quad \displaystyle {\frac {s}{\sqrt {3}}}\approx 0.577s}$

соответственно; сумма этих радиусов равна ширине треугольника Рело. В более общем смысле, для каждой кривой постоянной ширины, наибольшая вписанная окружность и наименьшая описанная окружность являются концентрическими, а их радиусы в сумме равны постоянной ширине кривой. ^[25]

Нерешенная задача по математике :

Насколько плотно треугольники Рело могут быть упакованы на плоскости?

(еще нерешенные проблемы по математике)

Оптимальная плотность упаковки треугольника Рело на плоскости остается недоказанной, но предполагается, что она равна

${\displaystyle {\frac {2(\pi -{\sqrt {3}})}{{\sqrt {15}}+{\sqrt {7}}-{\sqrt {12}}}}\approx 0.923,}$

что является плотностью одной возможной двойной решетчатой ​​упаковки для этих форм. Лучшая доказанная верхняя граница плотности упаковки составляет приблизительно 0,947. ^[26] Также было высказано предположение, но не доказано, что треугольники Рело имеют самую высокую плотность упаковки среди всех кривых постоянной ширины. ^[27]

Вращение внутри квадрата

Вращение треугольника Рело внутри квадрата, показывающее также кривую, описываемую центром треугольника.

Любая кривая постоянной ширины может образовать ротор внутри квадрата , форму, которая может совершать полный оборот, оставаясь внутри квадрата и все время касаясь всех четырех сторон квадрата. Однако треугольник Рело является ротором с минимально возможной площадью. ^[9] При вращении его ось не остается фиксированной в одной точке, а вместо этого следует кривой, образованной частями четырех эллипсов . [ ^28] Из-за своих углов в 120° вращающийся треугольник Рело не может достичь некоторых точек вблизи более острых углов в вершинах квадрата, а вместо этого покрывает форму со слегка закругленными углами, также образованную эллиптическими дугами. ^[9]

В любой точке этого вращения два угла треугольника Рёло касаются двух смежных сторон квадрата, в то время как третий угол треугольника вычерчивает кривую около противоположной вершины квадрата. Форма, вычерченная вращающимся треугольником Рёло, покрывает приблизительно 98,8% площади квадрата. ^[29]

В качестве контрпримера

Первоначальная мотивация Рело к изучению треугольника Рело заключалась в том, чтобы представить контрпример, показывающий, что трех одноточечных контактов может быть недостаточно для фиксации плоского объекта в одном положении. ^[30] Существование треугольников Рело и других кривых постоянной ширины показывает, что одни лишь измерения диаметра не могут подтвердить, что объект имеет круглое поперечное сечение. ^[31]

В связи с проблемой вписанного квадрата Эгглстон (1958) заметил, что треугольник Рело представляет собой пример формы постоянной ширины, в которую не может быть вписан никакой правильный многоугольник с более чем четырьмя сторонами, за исключением правильного шестиугольника, и он описал небольшую модификацию этой формы, которая сохраняет ее постоянную ширину, но также препятствует вписыванию в нее правильных шестиугольников. Он обобщил этот результат на три измерения, используя цилиндр с той же формой, что и его поперечное сечение . ^[32]

Приложения

Достигая углов

Несколько типов машин имеют форму треугольника Рело, поскольку он позволяет вращаться внутри квадрата.

Квадратное сверло Watts Brothers Tool Works имеет форму треугольника Рёло, модифицированного вогнутостями для формирования режущих поверхностей. При установке в специальный патрон, который позволяет сверлу не иметь фиксированного центра вращения, оно может сверлить отверстие, которое почти квадратное. ^[33] Хотя оно было запатентовано Генри Уоттсом в 1914 году, подобные сверла, изобретенные другими, использовались и раньше. ^[9] Другие многоугольники Рёло используются для сверления пятиугольных, шестиугольных и восьмиугольных отверстий. ^{[9] [33]}

Робот-пылесос RULO от Panasonic имеет форму треугольника Рёло, что облегчает уборку пыли в углах комнат. ^{[34] [35]}

Вращающиеся цилиндры

Сравнение цилиндрического и треугольного ролика Рело

Другой класс применений треугольника Рело включает цилиндрические объекты с поперечным сечением в виде треугольника Рело. Несколько карандашей производятся в этой форме, а не в более традиционных круглых или шестиугольных корпусах. ^[36] Обычно их рекламируют как более удобные или способствующие правильному захвату, а также как менее склонные скатываться со стола (поскольку центр тяжести движется вверх и вниз больше, чем катящийся шестиугольник).

Треугольник Рёло (вместе со всеми другими кривыми постоянной ширины ) может катиться , но из него получается плохое колесо, поскольку оно не катится вокруг фиксированного центра вращения. Объект на роликах, имеющих поперечные сечения в виде треугольника Рёло, будет катиться плавно и ровно, но ось, прикрепленная к колесам в виде треугольника Рёло, будет подпрыгивать вверх и вниз три раза за оборот. ^{[9] [37]} Эта концепция была использована в научно-фантастическом рассказе Пола Андерсона под названием «Трехугольное колесо». ^{[11] [38]} Велосипед с плавающими осями и рамой, поддерживаемой ободом колеса в форме треугольника Рёло, был построен и продемонстрирован в 2009 году китайским изобретателем Гуаном Байхуа, которого вдохновили карандаши такой же формы. ^[39]

Конструкция механизма

Механизм подачи кинопленки в советском 8-мм кинопроекторе «Луч-2» на основе треугольника Рёло

Другой класс приложений треугольника Рело включает использование его в качестве части механической связи , которая может преобразовывать вращение вокруг фиксированной оси в возвратно-поступательное движение . ^[10] Эти механизмы изучал Франц Рело. При содействии компании Густава Фойгта Рело построил около 800 моделей механизмов, несколько из которых включали треугольник Рело. ^[40] Рело использовал эти модели в своих пионерских научных исследованиях их движения. ^[41] Хотя большинство моделей Рело–Фойгта были утеряны, 219 из них были собраны в Корнельском университете , включая девять основанных на треугольнике Рело. ^{[40] [42]} Однако использование треугольников Рело в проектировании механизмов предшествовало работам Рело; например, некоторые паровые двигатели еще с 1830 года имели кулачок в форме треугольника Рело. ^{[43] [44]}

Одно из применений этого принципа возникает в кинопроекторе . В этом приложении необходимо продвигать пленку рывками, пошагово, при этом каждый кадр пленки останавливается на долю секунды перед линзой проектора, а затем гораздо быстрее пленка перемещается к следующему кадру. Это можно сделать с помощью механизма, в котором вращение треугольника Рело внутри квадрата используется для создания шаблона движения для привода, который быстро тянет пленку к каждому новому кадру, а затем останавливает движение пленки, пока кадр проецируется. ^[45]

Ротор двигателя Ванкеля имеет форму криволинейного треугольника, который часто приводится в качестве примера треугольника Рёло. ^{[3] [5] [9] [44]} Однако его изогнутые стороны несколько более плоские, чем у треугольника Рёло, и поэтому он не имеет постоянной ширины. ^[46]

Архитектура

Треугольное окно Рёло церкви Богоматери в Брюгге, Бельгия

В готической архитектуре , начиная с конца 13-го века или начала 14-го века, ^[47] треугольник Рёло стал одной из нескольких криволинейных форм, часто используемых для окон, оконных узоров и других архитектурных украшений. ^[3] Например, в английской готической архитектуре эта форма была связана с декорированным периодом, как в его геометрическом стиле 1250–1290 годов, так и продолжалась в его криволинейном стиле 1290–1350 годов. ^[47] Он также появляется в некоторых окнах Миланского собора . ^[48] В этом контексте форму иногда называют сферическим треугольником , ^{[47] [49] [50]} который не следует путать со сферическим треугольником, означающим треугольник на поверхности сферы . При использовании в готической церковной архитектуре треугольная форма треугольника Рёло может рассматриваться и как символ Троицы , [ ^51] и как «акт оппозиции форме круга». ^[52]

Треугольник Рёло также использовался в других архитектурных стилях. Например, Леонардо да Винчи набросал эту форму в качестве плана укрепления. ^[42] Современные здания, которые, как утверждается, использовали планировку в форме треугольника Рёло, включают в себя Аудиториум Массачусетского технологического института , Кёльнский треугольник , Дунайскую башню , Торре-де-Кольсерола и Музей Mercedes-Benz . ^[53] Однако во многих случаях это просто скругленные треугольники с другой геометрией, чем треугольник Рёло.

Картографирование

Другим ранним применением треугольника Рёло была карта мира да Винчи, созданная около 1514 года. На ней сферическая поверхность Земли была разделена на восемь октантов, каждый из которых был сплющен в форме треугольника Рёло. ^{[54] [55] [56]}

Карта мира Леонардо да Винчи в восьми квадрантах треугольника Рёло

Похожие карты, также основанные на треугольнике Рёло, были опубликованы Оронсом Фине в 1551 году и Джоном Ди в 1580 году. ^[56]

Другие объекты

Треугольные медиаторы Reuleaux

Многие гитарные медиаторы используют треугольник Рёло, так как его форма сочетает в себе острый кончик, обеспечивающий сильную артикуляцию, с широким кончиком, создающим тёплый тембр. Поскольку все три точки формы пригодны для использования, его легче ориентировать, и он изнашивается медленнее по сравнению с медиатором с одним кончиком. ^[57]

Незаконное использование пожарного гидранта, Филадельфия, 1996 г., и более нового пожарного гидранта в Филадельфии с гайкой в ​​форме треугольника Рёло для предотвращения такого использования.

Треугольник Рёло использовался в качестве формы поперечного сечения гайки клапана пожарного гидранта . Постоянная ширина этой формы затрудняет открытие пожарного гидранта с помощью стандартных гаечных ключей с параллельными губками; вместо этого необходим ключ специальной формы. Это свойство позволяет открывать пожарные гидранты только пожарным (у которых есть специальный ключ), а не другим людям, пытающимся использовать гидрант в качестве источника воды для других целей. ^[58]

Субмиллиметровая антенная решетка , семь из восьми антенн которой расположены примерно по треугольнику Рело.

Следуя предложению Кето (1997), ^[59] антенны Субмиллиметровой решетки , радиоволновой астрономической обсерватории на Мауна-Кеа на Гавайях , расположены на четырех вложенных треугольниках Рело. ^{[60] [61]} Размещение антенн на кривой постоянной ширины приводит к тому, что обсерватория имеет одинаковое пространственное разрешение во всех направлениях и обеспечивает круговой луч наблюдения. Как наиболее асимметричная кривая постоянной ширины, треугольник Рело приводит к наиболее равномерному покрытию плоскости для преобразования Фурье сигнала от решетки. ^{[59] [61]} Антенны можно перемещать из одного треугольника Рело в другой для различных наблюдений в соответствии с желаемым угловым разрешением каждого наблюдения. ^{[60] [61]} Точное размещение антенн на этих треугольниках Рело было оптимизировано с помощью нейронной сети . В некоторых местах построенная обсерватория отклоняется от предпочтительной формы треугольника Рело, поскольку эта форма была невозможна в пределах данного места. ^[61]

Знаки и логотипы

Формы щитов, используемые для многих знаков и корпоративных логотипов, представляют собой закругленные треугольники. Однако лишь некоторые из них являются треугольниками Рёло.

Корпоративный логотип Petrofina (Fina), бельгийской нефтяной компании с основными операциями в Европе, Северной Америке и Африке, использовал треугольник Рёло с названием Fina с 1950 года до слияния Petrofina с Total SA (сегодня TotalEnergies ) в 2000 году. ^{[62] [63]} Другой корпоративный логотип, обрамленный треугольником Рёло, указывающий на юг компас пивоварни Bavaria , был частью преобразования дизайнерской компании Total Identity, которая выиграла премию SAN 2010 Advertiser of the Year. ^[64] Треугольник Рёло также используется в логотипе Colorado School of Mines . ^[65]

В Соединенных Штатах Национальная система троп и Система велосипедных маршрутов США обозначают маршруты треугольниками Рёло на знаках. ^[66]

В природе

Треугольник Рело как центральный пузырь в математической модели четырехпузырькового плоского кластера мыльных пузырей

Согласно законам Плато , дуги окружностей в двумерных кластерах мыльных пузырей встречаются под углом 120°, таким же углом, который находится в углах треугольника Рело. Основываясь на этом факте, можно построить кластеры, в которых некоторые пузырьки принимают форму треугольника Рело. ^[67]

Форма была впервые выделена в кристаллической форме в 2014 году в виде дисков треугольника Рёло. ^[68] Основные диски нитрата висмута с формой треугольника Рёло были образованы в результате гидролиза и осаждения нитрата висмута в системе этанол–вода в присутствии 2,3-бис(2-пиридил)пиразина.

Обобщения

Треугольные кривые постоянной ширины с гладкими, а не острыми углами могут быть получены как геометрическое место точек на фиксированном расстоянии от треугольника Рело. ^[69] Другие обобщения треугольника Рело включают поверхности в трех измерениях, кривые постоянной ширины с более чем тремя сторонами и множества Янмути, которые представляют собой крайние примеры неравенства между шириной, диаметром и вписанным радиусом.

Трехмерная версия

Четыре шара пересекаются, образуя тетраэдр Рёло.

Пересечение четырех шаров радиуса s с центрами в вершинах правильного тетраэдра с длиной стороны s называется тетраэдром Рело , но его поверхность не является поверхностью постоянной ширины . ^[70] Однако его можно превратить в поверхность постоянной ширины, называемую тетраэдром Мейсснера , заменив три его дуги кромок кривыми поверхностями, поверхностями вращения дуги окружности. Альтернативно, поверхность вращения треугольника Рело через одну из его осей симметрии образует поверхность постоянной ширины с минимальным объемом среди всех известных поверхностей вращения заданной постоянной ширины. ^[71]

Полигоны Рело

Треугольник Рёло может быть обобщен до правильных или неправильных многоугольников с нечетным числом сторон, что дает многоугольник Рёло , кривую постоянной ширины, образованную дугами окружностей постоянного радиуса. Постоянная ширина этих форм позволяет использовать их в качестве монет, которые могут использоваться в монетоприемниках. ^[9] Хотя монеты этого типа в общем обращении обычно имеют более трех сторон, треугольник Рёло использовался для памятной монеты с Бермудских островов . ^[53]

Аналогичные методы можно использовать для заключения произвольного простого многоугольника в кривую постоянной ширины, ширина которой равна диаметру данного многоугольника. Полученная форма состоит из дуг окружности (максимум столько же, сколько сторон многоугольника), может быть построена алгоритмически за линейное время и может быть нарисована с помощью циркуля и линейки. ^[72] Хотя все многоугольники Рело имеют нечетное количество сторон дуг окружности, можно построить формы постоянной ширины с четным количеством сторон дуг окружности различных радиусов. ^[73]

Наборы Янмути

Множества Яньмути определяются как выпуклые оболочки равностороннего треугольника вместе с тремя дугами окружностей, центрированными в вершинах треугольника и охватывающими тот же угол, что и треугольник, с равными радиусами, которые не больше длины стороны треугольника. Таким образом, когда радиус достаточно мал, эти множества вырождаются в сам равносторонний треугольник, но когда радиус максимально велик, они равны соответствующему треугольнику Рело. Каждая фигура с шириной w , диаметром d и вписанным радиусом r (радиусом наибольшего возможного круга, содержащегося в фигуре) подчиняется неравенству

${\displaystyle w-r\leq {\frac {d}{\sqrt {3}}},}$

и это неравенство становится равенством для множеств Янмути, показывая, что его нельзя улучшить. ^[74]

Связанные цифры

Трикветра переплетена, образуя узел-трилистник

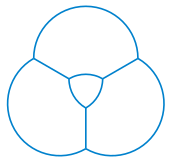
В классическом представлении трехмножественной диаграммы Венна в виде трех перекрывающихся кругов центральная область (представляющая элементы, принадлежащие всем трем множествам) принимает форму треугольника Рело. ^[3] Те же три круга образуют один из стандартных рисунков колец Борромео , трех взаимно связанных колец, которые, однако, не могут быть реализованы как геометрические круги. ^[75] Части этих же кругов используются для формирования трикветра , фигуры из трех перекрывающихся полукругов (каждые два из которых образуют символ vesica piscis ), которая снова имеет треугольник Рело в своем центре; ^[76] так же, как три круга диаграммы Венна могут быть переплетены, чтобы сформировать кольца Борромео, три дуги окружности трикветра могут быть переплетены, чтобы сформировать узел трилистника . ^[77]

Родственники треугольника Рёло возникают в задаче поиска минимальной формы периметра, которая охватывает фиксированное количество площади и включает три заданные точки на плоскости. Для широкого диапазона выбора параметра площади оптимальным решением этой задачи будет изогнутый треугольник, три стороны которого являются дугами окружностей с равными радиусами. В частности, когда три точки равноудалены друг от друга, а площадь равна площади треугольника Рёло, треугольник Рёло является оптимальным ограждением. ^[78]

Круглые треугольники — это треугольники с дугообразными краями, включая треугольник Рело, а также другие формы. Дельтовидная кривая — это еще один тип криволинейного треугольника, но в нем кривые, заменяющие каждую сторону равностороннего треугольника, вогнутые, а не выпуклые. Он не состоит из дуг окружностей, но может быть образован путем вкатывания одного круга в другой с радиусом в три раза большим. ^[79] Другие плоские формы с тремя изогнутыми сторонами включают арбелос , который образован тремя полукругами с коллинеарными концами, ^[80] и треугольник Безье . ^[81]

Треугольник Рело также можно интерпретировать как стереографическую проекцию одной треугольной грани сферического тетраэдра , треугольника Шварца с параметрами со сферическими углами меры и сторонами сферической длины ^{[67] [82]} ${\displaystyle {\tfrac {3}{2}},{\tfrac {3}{2}},{\tfrac {3}{2}}}$ ${\displaystyle 120^{\circ }}$ ${\displaystyle {\arccos }{\bigl (}{-{\tfrac {1}{3}}}{\bigr )}.}$

Ссылки

1. Гарднер (2014) называет его самым простым, а Грубер (1983, стр. 59) называет его «самым печально известным».
2. Клее, Виктор (1971), «Формы будущего», Двухгодичный математический журнал колледжа , 2 (2): 14–27, doi : 10.2307/3026963, JSTOR  3026963.
3. Альсина, Клауди; Нельсен, Роджер Б. (2011), Иконы математики: исследование двадцати ключевых образов , Dolciani Mathematical Expositions, т. 45, Математическая ассоциация Америки, стр. 155, ISBN 978-0-88385-352-8.
4. Moon, FC (2007), Машины Леонардо да Винчи и Франца Рёло: Кинематика машин от эпохи Возрождения до XX века , История механизмов и машиноведения, т. 2, Springer, ISBN 978-1-4020-5598-0.
5. Брайант, Джон; Сангвин, Крис (2011), Насколько круглый ваш круг?: Где встречаются инженерия и математика , Princeton University Press, стр. 190, ISBN 978-0-691-14992-9.
6. Hann, Michael (2014), Структура и форма в дизайне: критические идеи для творческой практики, A&C Black, стр. 34, ISBN 978-1-4725-8431-1.
7. Хунгербюлер, Норберт (1994), «Короткое элементарное доказательство теоремы Мора-Маскерони», American Mathematical Monthly , 101 (8): 784–787, CiteSeerX 10.1.1.45.9902 , doi :10.2307/2974536, JSTOR  2974536, MR  1299166 .
8. Эта конструкция кратко описана Маором и Йостом (2014) и ее можно увидеть, например, в видео «Веселье с треугольниками Рёло» Алекса Франке от 21 августа 2011 года.
9. Гарднер, Мартин (2014), «Глава 18: Кривые постоянной ширины», Узлы и кольца Борромео, повторные плитки и восемь королев , Новая математическая библиотека Мартина Гарднера, т. 4, Cambridge University Press, стр. 223–245, ISBN 978-0-521-75613-6.
10. Klee, Victor ; Wagon, S. (1991), Старые и новые нерешенные проблемы в плоской геометрии и теории чисел, Dolciani Mathematical Expositions, т. 11, Cambridge University Press, стр. 21, ISBN 978-0-88385-315-3.
11. Maor, Eli; Jost, Eugen (2014), «46 Треугольник Рёло», Beautiful Geometry, Princeton University Press, стр. 154–156, ISBN 978-1-4008-4833-1.
12. Райх, Карин (2007), «Вклад Эйлера в дифференциальную геометрию и ее восприятие», в Брэдли, Роберт Э.; Сандифер, Эд (ред.), Леонард Эйлер: жизнь, работа и наследие , Исследования по истории и философии математики, т. 5, Elsevier, стр. 479–502, doi :10.1016/S0928-2017(07)80026-0, ISBN 9780444527288. См. в частности раздел 1.4, «Orbiforms, 1781», стр. 484–485.
13. Эйлер, Леонард (1781), «De curvis triangularibus», Acta Academiae Scientiarum Imperialis Petropolitanae (на латыни), 1778 : 3–30. См., в частности, стр. 7 для определения орбиформ.
14. Грубер, Питер М. (1983), Выпуклость и ее применения, Birkhäuser, стр. 67, ISBN 978-3-7643-1384-5
15. Грубер (1983, стр. 76)
16. Макеев, В. В. (2000), "Экстремальное свойство треугольника Рело", Зап. Научн. Сем. С.-Петербург. Отдел. Мат. Инст. Стеклов. (ПОМИ) , 267 (Геом. и Тополь. 5): 152–155, 329, doi : 10.1023/A:1021287302603 , MR  1809823, S2CID  116027099.
17. Finch, Steven R. (2003), "8.10 Константы треугольника Рело" (PDF) , Математические константы, Энциклопедия математики и ее приложений, Cambridge University Press, стр. 513–514, ISBN 978-0-521-81805-6.
18. Громер, Х.; Валлен, Л. Дж. (2001), «Мера асимметрии для областей постоянной ширины», Beiträge zur Algebra und Geometrie , 42 (2): 517–521, MR  1865537.
19. Грубер (1983, стр. 78)
20. Sallee, GT (1969), «Максимальный набор постоянной ширины в решетке», Pacific Journal of Mathematics , 28 (3): 669–674, doi : 10.2140/pjm.1969.28.669 , MR  0240724.
21. Фейес Тот, Л. (1967), «О числе равных дисков, которые могут касаться другого такого же типа», Studia Scientiarum Mathematicarum Hungarica , 2 : 363–367, MR  0221388; Шопп, Дж. (1970), «Über die Newtonsche Zahl einer Scheibe konstanter Breite», Studia Scientiarum Mathematicarum Hungarica (на немецком языке), 5 : 475–478, MR  0285983.
22. Болл, Д.Г. (1973), «Обобщение числа π», The Mathematical Gazette , 57 (402): 298–303, doi : 10.2307/3616052, JSTOR  3616052, S2CID  125396664; Гриффитс, Дэвид; Калпин, Дэвид (1975), «Пи-оптимальные многоугольники», The Mathematical Gazette , 59 (409): 165–175, doi :10.2307/3617699, JSTOR  3617699, S2CID  126325288.
23. Лэй, Стивен Р. (2007), Выпуклые множества и их приложения, Довер, Теорема 11.11, стр. 81–82, ISBN 978-0-486-45803-8.
24. Барбье, Э. (1860), «Заметка о проблеме l'aiguille et le jeu du Joint couvert» (PDF) , Journal de Mathématiques Pures et Appliquées , 2 ^e série (на французском языке), 5 : 273–286. См. в частности стр. 283–285.
25. Лэй (2007), Теорема 11.8, стр. 80–81.
26. Слепой, Г.; Блинд, Р. (1983), «Eine Abschätzung für die Dichte der dichtesten Packung mit Reuleaux-Dreiecken», Studia Scientiarum Mathematicarum Hungarica (на немецком языке), 18 (2–4): 465–469, MR  0787951. См. также Блайнд Г.; Блинд, Р. (1987), «Reguläre Packungen mit Reuleaux-Dreiecken», Результаты по математике (на немецком языке), 11 (1–2): 1–7, doi : 10.1007/BF03323256, MR  0880190, S2CID  121633860.
27. Резникофф, Говард Л. (2015), О кривых и поверхностях постоянной ширины , arXiv : 1504.06733 , Bibcode : 2015arXiv150406733R.
28. Глейфтнер, Винфрид; Цайтлер, Герберт (май 2000 г.), «Треугольник Рёло и его центр масс», Результаты по математике , 37 (3–4): 335–344, doi :10.1007/bf03322004, S2CID  119600507.
29. Пиковер, Клиффорд А. (2009), «Треугольник Рёло», Математическая книга: от Пифагора до 57-го измерения, 250 вех в истории математики, Sterling Publishing Company, стр. 266, ISBN 978-1-4027-5796-9.
30. Мун (2007), стр. 239.
31. Грановский, ВА; Сирая, ТН, «Метрологическая прослеживаемость и качество измерений промышленных испытаний», в Павезе, Ф.; Бер, М.; Фильц, Дж.-Р.; Форбс, А.Б.; Пендрилл, Л.; Широно, К. (ред.), Передовые математические и вычислительные инструменты в метрологии и испытаниях IX , World Scientific, стр. 194–201. См. в частности стр. 200.
32. Эгглстон, Х. Г. (1958), «Фигуры, вписанные в выпуклые множества», American Mathematical Monthly , 65 (2): 76–80, doi : 10.2307/2308878, JSTOR  2308878, MR  0097768.
33. Как сверлить квадратные, шестигранные, восьмигранные, пятигранные отверстия , Уилмердинг, Пенсильвания: Watts Brothers Tool Works , 1950–1951(Брошюра на 27 страницах).
34. Мотидзуки, Такаши (22 января 2015 г.), «Panasonic выпускает треугольный робот-пылесос», Japan Real Time, Wall Street Journal.
35. Коксворт, Бен (3 марта 2015 г.), «Panasonic выходит на рынок роботов-пылесосов с треугольным Rulo», Gizmag.
36. Гэмбер, Джонни (26 апреля 2006 г.), «Обзор Staedtler Noris Ergosoft HB», Pencil Revolution , заархивировано из оригинала 25.05.2015 , извлечено 22.05.2015.
37. Масферрер Леон, Клаудия; фон Вутенау Майер, Себастьян (декабрь 2005 г.), «Изобретая колесо заново: некруглые колеса», The Mathematical Intelligencer , 27 (4): 7–13, doi :10.1007/bf02985852.
38. Андерсон, Пол (октябрь 1963 г.), «Трехугольное колесо», Analog , стр. 50–69.
39. Демпстер, Тайра (17 июня 2009 г.), Китаец изобретает велосипед, Reuters
40. Moon, Francis C. (июль 1999 г.), The Reuleaux Collection of Kinematic Mechanisms at Cornell University (PDF) , Библиотека Корнелльского университета, архивировано из оригинала (PDF) 14 июня 2020 г..
41. Хендерсон, Дэвид В.; Таймина, Дайна (2007), «Ощущение значений в геометрии», в Синклер, Натали ; Пимм, Дэвид; Хиггинсон, Уильям (ред.), Математика и эстетика: новые подходы к древнему родству , CMS Books in Mathematics, Springer, стр. 58–83, doi : 10.1007/978-0-387-38145-9_4, hdl : 1813/2714 , ISBN 978-0-387-38145-9. См. в частности стр. 81.
42. Moon (2007, стр. 241).
43. Мун (2007, стр. 240)
44. Peterson, Ivars (19 октября 1996 г.), «Rolling with Reuleaux», MathTrek , ScienceNews. Перепечатано в Peterson, Ivars (2002), Mathematical Treks: From Surreal Numbers to Magic Circles, MAA spectrum, Mathematical Association of America , стр. 141–144, ISBN 978-0-88385-537-9.
45. Лэй (2007), стр. 83.
46. Грубер (1983, стр. 80); Нэш, Дэвид Х. (март 1977), «Геометрия роторного двигателя», Mathematics Magazine , 50 (2): 87–89, doi :10.1080/0025570x.1977.11976621; Бадр, О.; Наик, С.; О'Каллаган, П.У.; Проберт, С.Д. (1991), «Роторные двигатели Ванкеля как расширительные устройства в паровых двигателях с циклом Ренкина», Applied Energy , 39 (1): 59–76, doi :10.1016/0306-2619(91)90063-4.
47. Харт, Стивен (2010), Средневековый церковный оконный узор в Англии, Boydell & Brewer Ltd, стр. 63–64, ISBN 978-1-84383-533-2.
48. Маркетти, Елена; Коста, Луиза Росси (2014), «Какие геометрии в Миланском соборе?», в Уильямс, Ким; Оствальд, Майкл Дж. (ред.), Архитектура и математика от античности до будущего, том I: античность до 1500-х годов , Birkhäuser, стр. 509–534, doi :10.1007/978-3-319-00137-1_35
49. Паркер, Джон Генри (1850), Словарь терминов, используемых в греческой, римской, итальянской и готической архитектуре, т. 1 (5-е изд.), Лондон: Дэвид Роуг, стр. 202.
50. Берчетт, Э.С. (1876), Практическая геометрия плоскости, Лондон и Глазго: William Collins, Sons, and Co., Подпись к иллюстрации LV, рис. 6.
51. Дюран, Гийом (1906), Символизм церквей и церковных украшений: перевод первой книги Rationale Divinorum Officiorum (3-е изд.), Гиббингс, стр. lxxxviii.
52. Франкл, Пол; Кроссли, Пол (2000), Готическая архитектура, история искусства Pelican, т. 19, Издательство Йельского университета, стр. 146, ISBN 978-0-300-08799-4.
53. Конти, Джузеппе; Паолетти, Рафаэлла (октябрь 2019 г.), «Треугольник Рело в архитектуре и приложениях», в Магнаги-Дельфино, Паола; Меле, Джампьеро; Норандо, Туллия (ред.), Лица геометрии: от Агнеси до Мирзахани , Конспект лекций по сетям и системам, Springer, стр. 79–89, doi : 10.1007/978-3-030-29796-1_7, S2CID  209976466
54. Снайдер, Джон П. (1997), Сплющивание Земли: две тысячи лет картографических проекций, Издательство Чикагского университета, стр. 40, ISBN 978-0-226-76747-5.
55. Кеунинг, Йоханнес (январь 1955 г.), «История проекций географических карт до 1600 г.», Imago Mundi , 12 (1): 1–24, doi : 10.1080/03085695508592085, JSTOR  1150090.
56. Bower, David I. (февраль 2012 г.), «Необычная проекция для одной из карт Джона Ди 1580 года» (PDF) , The Cartographic Journal , 49 (1): 55–61, doi : 10.1179/1743277411y.0000000015, S2CID  129873912.
57. Hoover, Will (ноябрь 1995), Picks!: Красочная сага о винтажных целлулоидных гитарных медиаторах , Backbeat Books, стр. 32–33, ISBN 978-0-87930-377-8.
58. Мартини, Хорст; Монтехано, Луис; Оливерос, Дебора (2019), Тела постоянной ширины: введение в выпуклую геометрию с приложениями , Birkhäuser, стр. 3, doi :10.1007/978-3-030-03868-7, ISBN 978-3-030-03866-3, MR  3930585, S2CID  127264210
59. Keto, Eric (1997), «Формы кросс-корреляционных интерферометров», The Astrophysical Journal , 475 (2): 843–852, Bibcode : 1997ApJ...475..843K, doi : 10.1086/303545.
60. Blundell, Raymond (2007), "Субмиллиметровый массив" (PDF) , Proc. 2007 IEEE/MTT-S International Microwave Symposium , стр. 1857–1860, doi :10.1109/mwsym.2007.380132, ISBN 978-1-4244-0687-6, S2CID  41312640.
61. Хо, Пол TP; Моран, Джеймс М.; Ло, Квок Юнг (2004), "Субмиллиметровый массив", The Astrophysical Journal , 616 (1): L1–L6, arXiv : astro-ph/0406352 , Bibcode : 2004ApJ...616L...1H, doi : 10.1086/423245, S2CID  115133614.
62. Гвиллиан, Сэм (16 мая 2015 г.), Интересные вещи: кривые постоянной ширины, Newport City Radio, архивировано с оригинала 16 июня 2016 г.
63. "История логотипа Fina: от Petrofina до Fina", Total: Групповая презентация , Total SA, заархивировано из оригинала 26 декабря 2012 г. , извлечено 31 октября 2015 г..
64. "Глобально: Бавария, фундаментальная операция по ребрендингу в Баварии", Total Identity , заархивировано из оригинала 2015-06-30 , извлечено 2015-06-27{{citation}}: CS1 maint: неподходящий URL ( ссылка )
65. Фишер, Роланд Б. (весна 2002 г.), «M-blems: Explaining the logo» (PDF) , Mines: The Magazine of Colorado School of Mines , т. 92, № 2, стр. 29, архивировано из оригинала 10 июля 2010 г.{{citation}}: CS1 maint: неподходящий URL ( ссылка )
66. Линдли, Джеффри А. (1 июня 2012 г.), «Информация: MUTCD — Временное одобрение на необязательное использование альтернативного дизайна знака велосипедного маршрута США (M1-9) (IA-15)», Руководство по унифицированным устройствам управления дорожным движением на улицах и автомагистралях: Ресурсы , Министерство транспорта США, Федеральное управление шоссейных дорог , получено 20 августа 2018 г.
67. Modes, Carl D.; Kamien, Randall D. (2013), "Сферические пены в плоском пространстве", Soft Matter , 9 (46): 11078–11084, arXiv : 0810.5724 , Bibcode : 2013SMat....911078M, doi : 10.1039/c3sm51585k, S2CID  96591302.
68. Ng, CHB; Fan, WY (2014), «Треугольные диски Рело: новая форма на блоке», Журнал Американского химического общества , 136 (37): 12840–12843, doi :10.1021/ja506625y, PMID  25072943.
69. Банчофф, Томас; Гиблин, Питер (1994), «О геометрии кусочно-круговых кривых», American Mathematical Monthly , 101 (5): 403–416, doi :10.2307/2974900, JSTOR  2974900, MR  1272938.
70. Вебер, Кристоф (2009), Какое отношение это тело имеет к шару? (PDF)У Вебера также есть фильмы обоих типов вращения тел Мейснера, а также интерактивные изображения.
71. Кампи, Стефано; Колесанти, Андреа; Грончи, Паоло (1996), «Минимальные задачи для объемов выпуклых тел», Уравнения в частных производных и их приложения: Сборник статей в честь Карло Пуччи , Lecture Notes in Pure and Applied Mathematics, № 177, Марсель Деккер, стр. 43–55.
72. Чандру, В.; Венкатараман, Р. (1991), «Круговые оболочки и орбиформы простых многоугольников», Труды второго ежегодного симпозиума ACM-SIAM по дискретным алгоритмам (SODA '91) , Филадельфия, Пенсильвания, США: Общество промышленной и прикладной математики, стр. 433–440, ISBN 978-0-89791-376-8.
73. Петерсон, Брюс Б. (1973), «Свойства пересечения кривых постоянной ширины», Illinois Journal of Mathematics , 17 (3): 411–420, doi : 10.1215/ijm/1256051608 , MR  0320885.
74. Эрнандес Сифре, MA (2000), «Существует ли плоское выпуклое множество с заданной шириной, диаметром и вписанным радиусом?», American Mathematical Monthly , 107 (10): 893–900, doi :10.2307/2695582, JSTOR  2695582, MR  1806918.
75. Линдстрем, Бернт; Зеттерстрем, Ханс-Олов (1991), «Круги Борромео невозможны», American Mathematical Monthly , 98 (4): 340–341, doi : 10.2307/2323803, JSTOR  2323803.
76. Вайсштейн, Эрик В. , «Трикетра», MathWorld
77. Хой, Джессика; Миллетт, Кеннет С. (2014), «Математический анализ завязывания узлов и соединений в картеле Леонардо да Винчи в Академии Винчиа» (PDF) , Журнал математики и искусств.
78. Курант, Ричард ; Роббинс, Герберт (1996), Что такое математика? Элементарный подход к идеям и методам (2-е изд.), Oxford University Press, стр. 378–379, ISBN 978-0-19-975487-8.
79. Локвуд, Э. Х. (1961), «Глава 8: Дельтовидная мышца», Книга кривых , Издательство Кембриджского университета
80. Маккей, Дж. С. (февраль 1884 г.), «Нож сапожника», Труды Эдинбургского математического общества , 3 :2, doi : 10.1017/s0013091500037196.
81. Bruijns, J. (1998), «Квадратичные треугольники Безье как примитивы для рисования», Труды семинара ACM SIGGRAPH/EUROGRAPHICS по графическому оборудованию (HWWS '98) , Нью-Йорк, США: ACM, стр. 15–24, doi :10.1145/285305.285307, ISBN 978-1-58113-097-3, S2CID  28967106.
82. Веннингер, Магнус Дж. (2014), Сферические модели, Дувр, стр. 134, ISBN 978-0-486-14365-1.

Внешние ссылки

• Вайсштейн, Эрик В. , «Треугольник Рело», MathWorld