Клеточный автомат ( мн. ч. клеточный автомат , сокр. CA ) — дискретная модель вычислений, изучаемая в теории автоматов . Клеточные автоматы также называют клеточными пространствами , тесселяционными автоматами , однородными структурами , клеточными структурами , тесселяционными структурами и итеративными массивами . [2] Клеточные автоматы нашли применение в различных областях, включая физику , теоретическую биологию и моделирование микроструктур .
Клеточный автомат состоит из регулярной сетки ячеек , каждая из которых находится в одном из конечного числа состояний , например, включено и выключено (в отличие от связанной решетки карт ). Сетка может иметь любое конечное число измерений. Для каждой ячейки определяется набор ячеек, называемый ее окрестностью , относительно указанной ячейки. Начальное состояние (время t = 0) выбирается путем назначения состояния для каждой ячейки. Новое поколение создается (увеличение t на 1) в соответствии с некоторым фиксированным правилом (обычно математической функцией) [3] , которое определяет новое состояние каждой ячейки с точки зрения текущего состояния ячейки и состояний ячеек в ее окрестности. Обычно правило обновления состояния ячеек одинаково для каждой ячейки и не меняется со временем, а применяется ко всей сетке одновременно, [4] хотя известны исключения, такие как стохастический клеточный автомат и асинхронный клеточный автомат .
Первоначально эта концепция была открыта в 1940-х годах Станиславом Уламом и Джоном фон Нейманом , когда они были современниками в Лос-Аламосской национальной лаборатории . Хотя некоторые изучали ее в 1950-х и 1960-х годах, только в 1970-х годах и после появления Игры жизни Конвея , двумерного клеточного автомата, интерес к этой теме вышел за рамки академических кругов. В 1980-х годах Стивен Вольфрам занялся систематическим изучением одномерных клеточных автоматов, или того, что он называет элементарными клеточными автоматами ; его научный сотрудник Мэтью Кук показал, что одно из этих правил является полным по Тьюрингу .
Основные классификации клеточных автоматов, как их обозначил Вольфрам, пронумерованы от одного до четырех. Это, по порядку, автоматы, в которых шаблоны обычно стабилизируются в однородность , автоматы, в которых шаблоны эволюционируют в в основном стабильные или колеблющиеся структуры, автоматы, в которых шаблоны эволюционируют, по-видимому, хаотическим образом, и автоматы, в которых шаблоны становятся чрезвычайно сложными и могут сохраняться в течение длительного времени, со стабильными локальными структурами. Этот последний класс считается вычислительно универсальным или способным имитировать машину Тьюринга . Специальные типы клеточных автоматов являются обратимыми , где только одна конфигурация приводит непосредственно к последующей, и тотальными , в которых будущее значение отдельных ячеек зависит только от общего значения группы соседних ячеек. Клеточные автоматы могут имитировать различные системы реального мира, включая биологические и химические.
Один из способов моделирования двумерного клеточного автомата — бесконечный лист миллиметровой бумаги вместе с набором правил для ячеек. Каждый квадрат называется «ячейкой», а каждая ячейка имеет два возможных состояния: черное и белое. Окрестность ячейки — это близлежащие, обычно смежные, ячейки. Два наиболее распространенных типа окрестностей — это окрестность фон Неймана и окрестность Мура . [5] Первая, названная в честь основателя теории клеточных автоматов, состоит из четырех ортогонально смежных ячеек. [5] Последняя включает окрестность фон Неймана, а также четыре диагонально смежные ячейки. [5] Для такой ячейки и ее окрестностей Мура существует 512 (= 2 9 ) возможных шаблонов. Для каждого из 512 возможных шаблонов таблица правил будет определять, будет ли центральная ячейка черной или белой в следующем временном интервале. Игра «Жизнь» Конвея — популярная версия этой модели. Другим распространенным типом соседства является расширенное соседство фон Неймана , которое включает две ближайшие ячейки в каждом ортогональном направлении, всего восемь. [5] Общее уравнение для общего числа возможных автоматов имеет вид k k s , где k — число возможных состояний ячейки, а s — число соседних ячеек (включая саму ячейку, которую нужно вычислить), используемых для определения следующего состояния ячейки. [6] Таким образом, в двумерной системе с соседством Мура общее число возможных автоматов будет равно 2 2 9 , или1,34 × 10 154 .
Обычно предполагается, что каждая ячейка во вселенной начинается в одном и том же состоянии, за исключением конечного числа ячеек в других состояниях; присвоение значений состояния называется конфигурацией . [ 7] В более общем смысле, иногда предполагается, что вселенная изначально покрыта периодическим узором, и только конечное число ячеек нарушает этот узор. Последнее предположение распространено в одномерных клеточных автоматах.

Клеточные автоматы часто моделируются на конечной сетке, а не на бесконечной. В двух измерениях вселенная была бы прямоугольником, а не бесконечной плоскостью. Очевидная проблема с конечными сетками заключается в том, как обрабатывать ячейки на краях. То, как они обрабатываются, повлияет на значения всех ячеек в сетке. Один из возможных методов — позволить значениям в этих ячейках оставаться постоянными. Другой метод — по-разному определять соседства для этих ячеек. Можно сказать, что у них меньше соседей, но тогда также придется определять новые правила для ячеек, расположенных на краях. Эти ячейки обычно обрабатываются с периодическими граничными условиями , что приводит к тороидальному расположению: когда кто-то выходит сверху, он входит в соответствующую позицию снизу, а когда кто-то выходит слева, он входит справа. (По сути, это имитирует бесконечную периодическую мозаику, и в области уравнений с частными производными иногда называется периодическими граничными условиями.) Это можно визуализировать как склеивание левого и правого краев прямоугольника для формирования трубки, а затем склеивание верхнего и нижнего краев трубки для формирования тора ( формы бублика). Вселенные других измерений обрабатываются аналогично. Это решает граничные проблемы с окрестностями, но еще одним преимуществом является то, что это легко программируется с помощью функций модульной арифметики . Например, в одномерном клеточном автомате, подобном примерам ниже, окрестность ячейки x i t равна { x i −1 t −1 , x i t −1 , x i +1 t −1 }, где t — временной шаг (вертикальный), а i — индекс (горизонтальный) в одном поколении.
Станислав Улам , работая в Национальной лаборатории Лос-Аламоса в 1940-х годах, изучал рост кристаллов, используя простую решетчатую сеть в качестве своей модели. [8] В то же время Джон фон Нейман , коллега Улама в Лос-Аламосе, работал над проблемой самовоспроизводящихся систем . [9] Первоначальный проект фон Неймана был основан на идее того, что один робот строит другого робота. Этот проект известен как кинематическая модель. [10] [11] Разрабатывая этот проект, фон Нейман пришел к пониманию большой сложности создания самовоспроизводящегося робота и больших затрат на обеспечение робота «морем деталей», из которых можно построить его репликанта. Нейман написал статью под названием «Общая и логическая теория автоматов» для симпозиума Хиксона в 1948 году. [9] Улам был тем, кто предложил использовать дискретную систему для создания редукционистской модели самовоспроизводства. [12] [13] Нильс Аалль Барричелли выполнил многие из самых ранних исследований этих моделей искусственной жизни .

Улам и фон Нейман создали метод расчета движения жидкости в конце 1950-х годов. Движущей идеей метода было рассматривать жидкость как группу дискретных единиц и вычислять движение каждой на основе поведения ее соседей. [14] Так родилась первая система клеточных автоматов. Подобно решетчатой сети Улама, клеточные автоматы фон Неймана являются двумерными, а его саморепликатор реализован алгоритмически. Результатом стал универсальный копировщик и конструктор, работающий в клеточном автомате с небольшим соседством (только те ячейки, которые соприкасаются, являются соседями; для клеточных автоматов фон Неймана только ортогональные ячейки) и с 29 состояниями на ячейку. [15] Фон Нейман дал доказательство существования того, что определенный шаблон будет создавать бесконечные копии себя в пределах данной клеточной вселенной, спроектировав конфигурацию из 200 000 ячеек, которая могла бы это делать. [15] Эта конструкция известна как модель тесселяции и называется универсальным конструктором фон Неймана . [16]
Также в 1940-х годах Норберт Винер и Артуро Розенблют разработали модель возбудимых сред с некоторыми характеристиками клеточного автомата. [17] Их конкретной мотивацией было математическое описание проведения импульсов в сердечных системах. Однако их модель не является клеточным автоматом, поскольку среда, в которой распространяются сигналы, непрерывна, а волновые фронты представляют собой кривые. [17] [18] Истинная клеточная автоматная модель возбудимых сред была разработана и изучена Дж. М. Гринбергом и С. П. Гастингсом в 1978 году; см. Клеточный автомат Гринберга-Гастингса . Оригинальная работа Винера и Розенблюта содержит много идей и продолжает цитироваться в современных исследовательских публикациях по сердечной аритмии и возбудимым системам. [19]
В 1960-х годах клеточные автоматы изучались как особый тип динамической системы , и впервые была установлена связь с математической областью символической динамики . В 1969 году Густав А. Хедлунд собрал множество результатов, следуя этой точке зрения [20], в работе, которая до сих пор считается основополагающей для математического изучения клеточных автоматов. Наиболее фундаментальным результатом является характеристика в теореме Кертиса–Хедлунда–Линдона множества глобальных правил клеточных автоматов как множества непрерывных эндоморфизмов пространств сдвига .
В 1969 году немецкий пионер компьютеров Конрад Цузе опубликовал свою книгу «Вычисление пространства» , в которой предположил, что физические законы вселенной дискретны по своей природе и что вся вселенная является результатом детерминированного вычисления на одном клеточном автомате; «Теория Цузе» стала основой области исследований, называемой цифровой физикой . [21]
Также в 1969 году компьютерный ученый Элви Рэй Смит завершил докторскую диссертацию в Стэнфорде по теории клеточных автоматов, первой математической трактовке КА как общего класса компьютеров. Многие статьи появились из этой диссертации: он показал эквивалентность окрестностей различных форм, как свести Мура к окрестностям фон Неймана или как свести любую окрестность к окрестностям фон Неймана. [22] Он доказал , что двумерные КА являются универсальными для вычислений, ввел одномерные КА и показал, что они также являются универсальными для вычислений, даже с простыми окрестностями. [23] Он показал, как включить сложное доказательство фон Неймана универсальности построения (и, следовательно, самовоспроизводящихся машин) в следствие универсальности вычислений в одномерном КА. [24] Задуманный как введение к немецкому изданию книги фон Неймана о КА, он написал обзор области с десятками ссылок на статьи многих авторов во многих странах за десятилетие или около того работы, которые часто игнорируются современными исследователями КА. [25]
В 1970-х годах широко известен, особенно среди раннего компьютерного сообщества, двумерный клеточный автомат с двумя состояниями под названием Game of Life . Изобретенный Джоном Конвеем и популяризированный Мартином Гарднером в статье в Scientific American , [26] его правила следующие:
Несмотря на свою простоту, система достигает впечатляющего разнообразия поведения, колеблющегося между кажущейся случайностью и порядком. Одной из наиболее очевидных особенностей Игры Жизни является частое появление планеров , расположений ячеек, которые по сути перемещаются по сетке. Можно организовать автомат так, чтобы планеры взаимодействовали для выполнения вычислений, и после многих усилий было показано, что Игра Жизни может эмулировать универсальную машину Тьюринга . [27] Это рассматривалось как в основном развлекательная тема, и было сделано мало последующих работ за пределами исследования особенностей Игры Жизни и нескольких связанных с ней правил в начале 1970-х годов. [28]
Стивен Вольфрам начал работать над клеточными автоматами независимо в середине 1981 года после того, как рассмотрел, как сложные узоры, по-видимому, формируются в природе в нарушение Второго закона термодинамики . [29] Его исследования изначально были вызваны желанием моделировать системы, такие как нейронные сети , обнаруженные в мозге. [29] Он опубликовал свою первую статью в Reviews of Modern Physics , исследующую элементарные клеточные автоматы ( в частности , Правило 30 ) в июне 1983 года. [2] [29] Неожиданная сложность поведения этих простых правил заставила Вольфрама заподозрить, что сложность в природе может быть обусловлена аналогичными механизмами. [29] Однако его исследования привели его к пониманию того, что клеточные автоматы плохо подходят для моделирования нейронных сетей. [29] Кроме того, в этот период Вольфрам сформулировал концепции внутренней случайности и вычислительной неприводимости , [30] и предположил, что правило 110 может быть универсальным — факт, доказанный позже научным сотрудником Вольфрама Мэтью Куком в 1990-х годах. [31]
Вольфрам в своей работе «Новый вид науки» и нескольких работах середины 1980-х годов определил четыре класса, на которые можно разделить клеточные автоматы и несколько других простых вычислительных моделей в зависимости от их поведения. В то время как более ранние исследования клеточных автоматов были направлены на выявление типов шаблонов для конкретных правил, классификация Вольфрама была первой попыткой классифицировать сами правила. В порядке сложности классы следующие:
Эти определения являются качественными по своей природе и оставляют некоторое пространство для интерпретации. По словам Вольфрама, "...почти с любой общей схемой классификации неизбежно существуют случаи, которые по одному определению относятся к одному классу, а по другому — к другому. И так же обстоит дело с клеточными автоматами: иногда существуют правила..., которые показывают некоторые черты одного класса и некоторые — другого". [34] Классификация Вольфрама была эмпирически сопоставлена с кластеризацией сжатых длин выходов клеточных автоматов. [35]
Было предпринято несколько попыток классифицировать клеточные автоматы в формально строгие классы, вдохновленные классификацией Вольфрама. Например, Кулик и Ю предложили три четко определенных класса (и четвертый для автоматов, не соответствующих ни одному из них), которые иногда называют классами Кулика–Ю; принадлежность к ним оказалась неразрешимой . [36] [37] [38] Класс 2 Вольфрама можно разбить на две подгруппы стабильных (с фиксированной точкой) и осциллирующих (периодических) правил. [39]
Идея о том, что существует 4 класса динамических систем, изначально принадлежит лауреату Нобелевской премии по химии Илье Пригожину , который выделил эти 4 класса термодинамических систем: (1) системы в термодинамическом равновесии, (2) пространственно/временно однородные системы, (3) хаотические системы и (4) сложные далекие от равновесия системы с диссипативными структурами (см. рисунок 1 в статье Николиса, ученика Пригожина, 1974 года). [40]
Клеточный автомат обратим , если для каждой текущей конфигурации клеточного автомата существует ровно одна прошлая конфигурация ( прообраз ). [41] Если рассматривать клеточный автомат как функцию, отображающую конфигурации в конфигурации, обратимость подразумевает, что эта функция является биективной . [41] Если клеточный автомат обратим, его поведение, обращенное во времени, также можно описать как клеточный автомат; этот факт является следствием теоремы Кертиса–Хедлунда–Линдона , топологической характеристики клеточных автоматов. [42] [43] Для клеточных автоматов, в которых не каждая конфигурация имеет прообраз, конфигурации без прообразов называются шаблонами Эдемского сада . [44]
Для одномерных клеточных автоматов известны алгоритмы для принятия решения о том, является ли правило обратимым или необратимым. [45] [46] Однако для клеточных автоматов двух или более измерений обратимость неразрешима ; то есть не существует алгоритма, который принимает в качестве входных данных правило автомата и гарантированно правильно определяет, является ли автомат обратимым. Доказательство Джаркко Кари связано с проблемой замощения плитками Вана . [47]
Обратимые клеточные автоматы часто используются для моделирования таких физических явлений, как динамика газа и жидкости, поскольку они подчиняются законам термодинамики . Такие клеточные автоматы имеют правила, специально сконструированные так, чтобы быть обратимыми. Такие системы изучались Томмазо Тоффоли , Норманом Марголусом и другими. Несколько методов могут быть использованы для явного построения обратимых клеточных автоматов с известными обратными. Два распространенных из них - клеточный автомат второго порядка и блочный клеточный автомат , оба из которых подразумевают изменение определения клеточного автомата каким-либо образом. Хотя такие автоматы не строго удовлетворяют определению, данному выше, можно показать, что их можно эмулировать обычными клеточными автоматами с достаточно большими окрестностями и числом состояний, и поэтому их можно считать подмножеством обычных клеточных автоматов. И наоборот, было показано, что каждый обратимый клеточный автомат можно эмулировать блочным клеточным автоматом. [48] [49]
Особый класс клеточных автоматов — это тоталистические клеточные автоматы. Состояние каждой клетки в тоталистическом клеточном автомате представлено числом (обычно целым числом, взятым из конечного набора), а значение клетки в момент времени t зависит только от суммы значений клеток в ее окрестности (возможно, включая саму клетку) в момент времени t − 1. [50] [51] Если состояние клетки в момент времени t зависит как от ее собственного состояния, так и от суммы ее соседей в момент времени t − 1, то клеточный автомат правильно называть внешним тоталистическим . [51] Игра Конвея «Жизнь» является примером внешнего тоталистического клеточного автомата со значениями клеток 0 и 1; внешние тоталистические клеточные автоматы с той же структурой соседства Мура, что и у «Жизни», иногда называются клеточным автоматом, подобным жизни . [52] [53]
Существует множество возможных обобщений концепции клеточного автомата.
Один из способов — использовать что-то, кроме прямоугольной (кубической и т. д. ) сетки. Например, если плоскость вымощена правильными шестиугольниками , эти шестиугольники можно использовать в качестве ячеек. Во многих случаях полученные клеточные автоматы эквивалентны автоматам с прямоугольными сетками со специально разработанными окрестностями и правилами. Другой вариант — сделать саму сетку нерегулярной, например, с помощью плиток Пенроуза . [54]
Также правила могут быть вероятностными, а не детерминированными. Такие клеточные автоматы называются вероятностными клеточными автоматами . Вероятностное правило дает для каждого шаблона в момент времени t вероятности того, что центральная ячейка перейдет в каждое возможное состояние в момент времени t + 1. Иногда используется более простое правило, например: «Правило — это Игра Жизни, но на каждом временном шаге существует вероятность 0,001%, что каждая ячейка перейдет в противоположный цвет».
Соседство или правила могут меняться со временем или в пространстве. Например, изначально новое состояние ячейки может определяться горизонтально соседними ячейками, но для следующего поколения будут использоваться вертикальные ячейки.
В клеточных автоматах новое состояние клетки не зависит от нового состояния других клеток. Это можно изменить так, что, например, блок клеток 2 на 2 может определяться им самим и клетками, соседствующими с ним.
Существуют непрерывные автоматы . Они похожи на тотальные клеточные автоматы, но вместо того, чтобы правило и состояния были дискретными ( например, таблица, использующая состояния {0,1,2}), используются непрерывные функции, и состояния становятся непрерывными (обычно значения в [0,1] ). Состояние местоположения — это конечное число действительных чисел. Некоторые клеточные автоматы могут давать диффузию в жидких образцах таким образом.
Непрерывные пространственные автоматы имеют континуум местоположений. Состояние местоположения — это конечное число действительных чисел. Время также непрерывно, и состояние развивается в соответствии с дифференциальными уравнениями. Одним из важных примеров являются реакционно-диффузионные текстуры, дифференциальные уравнения, предложенные Аланом Тьюрингом для объяснения того, как химические реакции могут создавать полосы на зебрах и пятна на леопардах. [55] Когда они аппроксимируются клеточными автоматами, они часто дают похожие узоры. Макленнан [1] рассматривает непрерывные пространственные автоматы как модель вычислений.
Известны примеры непрерывных пространственных автоматов, которые демонстрируют распространяющиеся явления, аналогичные планерам в Игре Жизни. [56]
Автоматы переписывания графов являются расширениями клеточных автоматов, основанными на системах переписывания графов . [57]
Простейший нетривиальный клеточный автомат будет одномерным, с двумя возможными состояниями на ячейку, и соседями ячейки, определенными как смежные ячейки по обе стороны от нее. Ячейка и ее два соседа образуют соседство из 3 ячеек, поэтому существует 2 3 = 8 возможных шаблонов для соседства. Правило состоит в решении для каждого шаблона, будет ли ячейка 1 или 0 в следующем поколении. Тогда существует 2 8 = 256 возможных правил. [6]
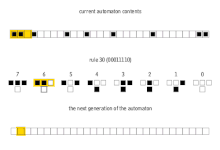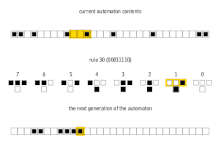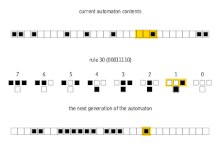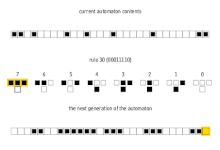
Эти 256 клеточных автоматов обычно называются их кодом Wolfram , стандартным соглашением об именовании, изобретенным Wolfram, которое дает каждому правилу номер от 0 до 255. В ряде статей анализировались и сравнивались различные случаи среди 256 клеточных автоматов (многие из них тривиально изоморфны). Клеточные автоматы правила 30 , правила 90 , правила 110 и правила 184 особенно интересны. На изображениях ниже показана история правил 30 и 110, когда начальная конфигурация состоит из 1 (в верхней части каждого изображения), окруженной нулями. Каждая строка пикселей представляет поколение в истории автомата, причем t = 0 является верхней строкой. Каждый пиксель окрашен в белый цвет для 0 и в черный для 1.

Правило 30 демонстрирует поведение класса 3 , то есть даже простые входные шаблоны, такие как показанные, приводят к хаотичным, на первый взгляд случайным историям.

Правило 110, как и Игра Жизни, демонстрирует то, что Вольфрам называет поведением класса 4 , которое не является ни полностью случайным, ни полностью повторяющимся. Локализованные структуры появляются и взаимодействуют различными сложными на вид способами. В ходе разработки A New Kind of Science , будучи научным сотрудником Вольфрама в 1994 году, Мэтью Кук доказал, что некоторые из этих структур были достаточно богаты, чтобы поддерживать универсальность . Этот результат интересен, поскольку правило 110 является чрезвычайно простой одномерной системой и ее трудно спроектировать для выполнения определенного поведения. Таким образом, этот результат предоставляет значительную поддержку мнению Вольфрама о том, что системы класса 4 по своей сути, вероятно, являются универсальными. Кук представил свое доказательство на конференции Института Санта-Фе по клеточным автоматам в 1998 году, но Вольфрам заблокировал включение доказательства в протоколы конференции, поскольку Вольфрам не хотел, чтобы доказательство было объявлено до публикации A New Kind of Science . [58] В 2004 году доказательство Кука было наконец опубликовано в журнале Вольфрама Complex Systems (т. 15, № 1), спустя более десяти лет после того, как Кук его придумал. Правило 110 стало основой для некоторых из самых маленьких универсальных машин Тьюринга. [59]
Элементарное правило клеточного автомата задается 8 битами, и все элементарные правила клеточного автомата можно считать расположенными на вершинах 8-мерного единичного гиперкуба . Этот единичный гиперкуб является пространством правил клеточного автомата. Для клеточных автоматов следующего ближайшего соседа правило задается 2 5 = 32 битами, а пространство правил клеточного автомата является 32-мерным единичным гиперкубом. Расстояние между двумя правилами можно определить числом шагов, необходимых для перемещения из одной вершины, которая представляет первое правило, и другой вершины, представляющей другое правило, вдоль ребра гиперкуба . Это расстояние от правила до правила также называется расстоянием Хэмминга .
Пространство правил клеточного автомата позволяет нам задать вопрос о том, являются ли правила с похожим динамическим поведением «близкими» друг к другу. Графическое рисование гиперкуба высокой размерности на двумерной плоскости остается сложной задачей, и одним грубым локатором правила в гиперкубе является число бит-1 в 8-битной строке для элементарных правил (или 32-битной строке для правил следующего ближайшего соседа). Рисование правил в различных классах Wolfram в этих срезах пространства правил показывает, что правила класса 1, как правило, имеют меньшее число бит-1, таким образом, располагаясь в одной области пространства, тогда как правила класса 3, как правило, имеют большую долю (50%) бит-1. [39]
Для большего пространства правил клеточного автомата показано, что правила класса 4 расположены между правилами класса 1 и класса 3. [60] Это наблюдение является основой для фразы « граница хаоса» и напоминает фазовый переход в термодинамике .

Клеточные автоматы осуществляют — или могут моделировать — ряд биологических процессов.
Вот некоторые примеры биологических явлений, моделируемых клеточными автоматами с простым пространством состояний:
Кроме того, биологические явления, требующие явного моделирования скоростей агентов (например, те, которые участвуют в коллективной миграции клеток ), могут быть смоделированы клеточными автоматами с более сложным пространством состояний и правилами, такими как биологические клеточные автоматы решеточного газа . К ним относятся явления, имеющие большое медицинское значение, такие как:
Реакция Белоусова -Жаботинского является пространственно-временным химическим осциллятором , который можно моделировать с помощью клеточного автомата. В 1950-х годах А. М. Жаботинский (продолжая работу Б. П. Белоусова ) обнаружил, что если смешать тонкий однородный слой смеси малоновой кислоты , подкисленного бромата и соли церия и оставить его нетронутым, то в среде будут распространяться завораживающие геометрические узоры, такие как концентрические круги и спирали. В разделе «Компьютерные развлечения» выпуска Scientific American за август 1988 года [69] А. К. Дьюдни обсудил клеточный автомат [70], разработанный Мартином Герхардтом и Хайке Шустер из Университета Билефельда (Германия). Этот автомат создает волновые узоры, которые напоминают узоры в реакции Белоусова-Жаботинского.

Вероятностные клеточные автоматы используются в статистической и конденсированной физике для изучения таких явлений, как динамика жидкости и фазовые переходы. Модель Изинга является прототипическим примером, в котором каждая ячейка может находиться в одном из двух состояний, называемых «вверх» и «вниз», создавая идеализированное представление магнита . Регулируя параметры модели, можно изменять долю ячеек, находящихся в одном и том же состоянии, способами, которые помогают объяснить, как ферромагнетики размагничиваются при нагревании. Более того, результаты изучения фазового перехода размагничивания могут быть перенесены на другие фазовые переходы, такие как испарение жидкости в газ; эта удобная перекрестная применимость известна как универсальность . [71] [72] Фазовый переход в двумерной модели Изинга и других системах в ее классе универсальности представляет особый интерес, поскольку для его глубокого понимания требуется конформная теория поля . [73] Другие клеточные автоматы, которые имели значение в физике, включают автоматы решеточного газа , которые моделируют потоки жидкости.
Процессоры клеточных автоматов являются физическими реализациями концепций КА, которые могут обрабатывать информацию вычислительно. Элементы обработки располагаются в регулярной сетке идентичных ячеек. Сетка обычно представляет собой квадратную мозаику или тесселяцию двух или трех измерений; другие мозаики возможны, но пока не используются. Состояния ячеек определяются только взаимодействием с соседними соседними ячейками. Не существует средств для прямой связи с ячейками, расположенными дальше. [74] Одной из таких конфигураций массива процессоров клеточных автоматов является систолический массив . Взаимодействие ячеек может осуществляться через электрический заряд, магнетизм, вибрацию ( фононы в квантовых масштабах) или любые другие физически полезные средства. Это можно сделать несколькими способами, так что между элементами не нужны никакие провода. Это очень не похоже на процессоры, используемые в большинстве компьютеров сегодня ( конструкции фон Неймана ), которые разделены на секции с элементами, которые могут общаться с удаленными элементами по проводам.
Правило 30 изначально было предложено как возможный блочный шифр для использования в криптографии . Двумерные клеточные автоматы могут быть использованы для построения генератора псевдослучайных чисел . [75]
Клеточные автоматы были предложены для криптографии с открытым ключом . Односторонняя функция является эволюцией конечного CA, обратную которой, как полагают, трудно найти. Учитывая правило, любой может легко вычислить будущие состояния, но, по-видимому, очень сложно вычислить предыдущие состояния. Клеточные автоматы также применялись для разработки кодов исправления ошибок . [76]
Другие проблемы, которые можно решить с помощью клеточных автоматов, включают в себя:
Клеточные автоматы использовались в генеративной музыке [77] и эволюционной музыкальной композиции [78] , а также в процедурной генерации ландшафта в видеоиграх. [79]
Определенные типы клеточных автоматов могут быть использованы для создания лабиринтов. [80] Два известных таких клеточных автомата, Maze и Mazectric, имеют строки правил B3/S12345 и B3/S1234. [80] В первом случае это означает, что клетки выживают из одного поколения в другое, если у них есть по крайней мере один и не более пяти соседей . Во втором случае это означает, что клетки выживают, если у них есть от одного до четырех соседей. Если у клетки ровно три соседа, она рождается. Это похоже на игру Конвея «Жизнь» в том, что шаблоны, в которых нет живой клетки, соседствующей с 1, 4 или 5 другими живыми клетками в любом поколении, будут вести себя идентично ей. [80] Однако для больших шаблонов он ведет себя совсем не так, как Жизнь. [80]
Для случайного начального шаблона эти клеточные автоматы, генерирующие лабиринты, будут развиваться в сложные лабиринты с четко определенными стенами, очерчивающими коридоры. Mazecetric, имеющий правило B3/S1234, имеет тенденцию генерировать более длинные и прямые коридоры по сравнению с Maze, с правилом B3/S12345. [80] Поскольку эти правила клеточных автоматов являются детерминированными , каждый сгенерированный лабиринт однозначно определяется его случайным начальным шаблоном. Это существенный недостаток, поскольку лабиринты, как правило, относительно предсказуемы.
Как и некоторые из описанных выше методов, основанных на теории графов, эти клеточные автоматы обычно генерируют лабиринты из единственного начального шаблона; следовательно, обычно будет относительно легко найти путь к начальной ячейке, но сложнее найти путь в любую другую ячейку.Конкретные правила клеточных автоматов включают в себя:
{{cite web}}: CS1 maint: архивная копия как заголовок ( ссылка )