Непрерывная функция

Математическая функция без резких изменений

В математике непрерывная функция — это функция , у которой небольшое изменение аргумента вызывает небольшое изменение значения функции . Это означает, что нет резких изменений стоимости, известных как разрывы . Точнее, функция является непрерывной, если сколь угодно малые изменения ее значения могут быть обеспечены путем ограничения достаточно малых изменений ее аргумента. Разрывная функция – это функция, которая не является непрерывной . До XIX века математики во многом полагались на интуитивные представления о непрерывности и рассматривали только непрерывные функции. Эпсилон -дельта-определение предела было введено для формализации определения непрерывности.

Непрерывность — одна из основных концепций исчисления и математического анализа , где аргументами и значениями функций являются действительные и комплексные числа. Эта концепция была обобщена на функции между метрическими пространствами и между топологическими пространствами. Последние являются наиболее общими непрерывными функциями, и их определение лежит в основе топологии .

Более сильной формой непрерывности является равномерная непрерывность . В теории порядка , особенно в теории областей , родственным понятием непрерывности является непрерывность Скотта .

Например, функция H ( t ) , обозначающая высоту растущего цветка в момент времени t , будет считаться непрерывной. Напротив, функция M ( t ) , обозначающая сумму денег на банковском счете в момент времени t , будет считаться разрывной, поскольку она «скачет» в каждый момент времени, когда деньги вносятся или снимаются.

История

Эпсилон -дельта-определение непрерывности было впервые дано Бернаром Больцано в 1817 году. Огюстен-Луи Коши определил непрерывность следующим образом: бесконечно малое приращение независимой переменной x всегда приводит к бесконечно малому изменению зависимой переменной y ( см., например, «Кур д'Анализ» , стр. 34). Коши определил бесконечно малые величины через переменные величины, и его определение непрерывности во многом соответствует определению бесконечно малых величин, используемому сегодня (см. микронепрерывность ). Формальное определение и различие между точечной непрерывностью и равномерной непрерывностью были впервые даны Больцано в 1830-х годах, но работа не была опубликована до 1930-х годов. Как и Больцано, ^[1] Карл Вейерштрасс ^[2] отрицал непрерывность функции в точке с , если она не определена в точке с и по обе стороны от нее , но Эдуард Гурса ^[3] допускал определение функции только в точке и по одну сторону. из c , и Камилла Джордан ^[4] допускала это, даже если функция была определена только в c . Все три из этих неэквивалентных определений поточечной непрерывности все еще используются. ^[5] Эдуард Гейне дал первое опубликованное определение равномерной непрерывности в 1872 году, но основывал эти идеи на лекциях, прочитанных Питером Густавом Леженом Дирихле в 1854 году ^{. [6]} ${\displaystyle y=f(x)}$ ${\displaystyle \alpha }$ ${\displaystyle f(x+\alpha )-f(x)}$

Реальные функции

Определение

Функция непрерывна в своей области определения ( ), но разрывна, если рассматривать ее как частичную функцию , определенную на действительных числах. ^[7] . ${\displaystyle f(x)={\tfrac {1}{x}}}$ ${\displaystyle \mathbb {R} \setminus \{0\}}$ ${\displaystyle x=0,}$

Действительная функция , которая является функцией преобразования действительных чисел в действительные числа, может быть представлена ​​графиком в декартовой плоскости ; такая функция непрерывна, если, грубо говоря, график представляет собой одну непрерывную кривую , областью определения которой является вся действительная линия. Более математически строгое определение дано ниже. ^[8]

Непрерывность вещественных функций обычно определяют в терминах пределов . Функция f с переменной x непрерывна при действительном числе c , если предел при x стремится к c , равен ${\displaystyle f(x),}$ ${\displaystyle f(c).}$

Существует несколько различных определений (глобальной) непрерывности функции, которые зависят от природы ее области определения .

Функция непрерывна на открытом интервале , если этот интервал содержится в области определения функции и функция непрерывна в каждой точке интервала. Функцию, непрерывную на отрезке (вся действительная прямая ), часто называют просто непрерывной функцией; говорят также, что такая функция всюду непрерывна . Например, все полиномиальные функции всюду непрерывны. ${\displaystyle (-\infty ,+\infty )}$

Функция непрерывна на полуоткрытом или замкнутом интервале; если интервал содержится в области определения функции, функция непрерывна в каждой внутренней точке интервала, а значение функции в каждой конечной точке, принадлежащей интервалу, является пределом значений функции, когда переменная стремится к концу из внутренней части интервала. Например, функция непрерывна во всей своей области определения, которая представляет собой отрезок ${\displaystyle f(x)={\sqrt {x}}}$ ${\displaystyle [0,+\infty ).}$

Многие часто встречающиеся функции являются частичными функциями , область определения которых состоит из всех действительных чисел, за исключением некоторых изолированных точек . Примерами являются функции и Когда они непрерывны в своей области определения, в некоторых контекстах говорят, что они непрерывны, хотя они не непрерывны повсюду. В других контекстах, главным образом, когда кто-то интересуется их поведением вблизи исключительных точек, говорят, что они прерывисты. ${\textstyle x\mapsto {\frac {1}{x}}}$ ${\displaystyle x\mapsto \tan x.}$

Частичная функция разрывна в точке, если точка принадлежит топологическому замыканию своей области определения, и либо точка не принадлежит области определения функции, либо функция не является непрерывной в этой точке. Например, функции и разрывны в точке 0 и остаются разрывными, какое бы значение ни было выбрано для их определения в точке 0 . Точка, в которой функция разрывна, называется разрывом . ${\textstyle x\mapsto {\frac {1}{x}}}$ ${\textstyle x\mapsto \sin({\frac {1}{x}})}$

Используя математическую запись, существует несколько способов определения непрерывных функций в трех упомянутых выше смыслах.

Позволять

$${\displaystyle f:D\to \mathbb {R} }$$

подмножестве ${\displaystyle D}$ ${\displaystyle \mathbb {R} }$

Это подмножество является областью применения f . Некоторые возможные варианты включают в себя ${\displaystyle D}$

• ${\displaystyle D=\mathbb {R} }$: т.е. это весь набор действительных чисел. или, для действительных чисел a и b , ${\displaystyle D}$
• ${\displaystyle D=[a,b]=\{x\in \mathbb {R} \mid a\leq x\leq b\}}$: закрытый интервал , или ${\displaystyle D}$
• ${\displaystyle D=(a,b)=\{x\in \mathbb {R} \mid a<x<b\}}$: открытый интервал . ${\displaystyle D}$

В случае, когда область определяется как открытый интервал и не принадлежит , значения и не имеют значения для непрерывности на . ${\displaystyle D}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle D}$ ${\displaystyle f(a)}$ ${\displaystyle f(b)}$ ${\displaystyle D}$

Определение через пределы функций

Функция f непрерывна в некоторой точке c своей области определения, если предел при приближении x к c через область определения f существует и равен ^[9] В математических обозначениях это записывается как ${\displaystyle f(x),}$ ${\displaystyle f(c).}$

$${\displaystyle \lim _{x\to c}{f(x)}=f(c).}$$

fccf ${\displaystyle f(c).}$

(Здесь мы предположили, что область определения f не имеет изолированных точек .)

Определение с точки зрения окрестностей

Окрестность точки c — это множество, содержащее, по крайней мере, все точки в пределах некоторого фиксированного расстояния от c . Интуитивно понятно, что функция непрерывна в точке c , если диапазон f в окрестности точки c сжимается до одной точки , когда ширина окрестности вокруг точки c сжимается до нуля. Точнее, функция f непрерывна в точке c своей области определения, если для любой окрестности в ее области определения существует такая окрестность, что всякий раз, когда ${\displaystyle f(c)}$ ${\displaystyle N_{1}(f(c))}$ ${\displaystyle N_{2}(c)}$ ${\displaystyle f(x)\in N_{1}(f(c))}$ ${\displaystyle x\in N_{2}(c).}$

Поскольку окрестности определены в любом топологическом пространстве , это определение непрерывной функции применимо не только к действительным функциям, но и тогда, когда область определения и кодомен являются топологическими пространствами , и, таким образом, является наиболее общим определением. Отсюда следует, что функция автоматически непрерывна в каждой изолированной точке своей области определения. Например, каждая вещественная функция целых чисел непрерывна.

Определение в терминах пределов последовательностей

Последовательность exp(1/ n ) сходится к exp(0) = 1

Вместо этого можно потребовать, чтобы для любой последовательности точек в области, сходящейся к c , соответствующая последовательность сходилась к В математической записи ${\displaystyle (x_{n})_{n\in \mathbb {N} }}$ ${\displaystyle \left(f(x_{n})\right)_{n\in \mathbb {N} }}$ ${\displaystyle f(c).}$

$${\displaystyle \forall (x_{n})_{n\in \mathbb {N} }\subset D:\lim _{n\to \infty }x_{n}=c\Rightarrow \lim _{n\to \infty }f(x_{n})=f(c)\,.}$$

Определения Вейерштрасса и Жордана (эпсилон – дельта) непрерывных функций

Иллюстрация ε - δ -определения: при x = 2 любое значение δ ≤ 0,5 удовлетворяет условию определения для ε = 0,5 .

Явно включив определение предела функции, мы получаем автономное определение: Учитывая вышеописанную функцию и элемент области определения , она называется непрерывной в той точке , когда выполняется следующее: Однако для любого положительного действительного числа мал, существует некоторое положительное действительное число такое, что для всех в области со значением удовлетворяет ${\displaystyle f:D\to \mathbb {R} }$ ${\displaystyle x_{0}}$ ${\displaystyle D}$ ${\displaystyle f}$ ${\displaystyle x_{0}}$ ${\displaystyle \varepsilon >0,}$ ${\displaystyle \delta >0}$ ${\displaystyle x}$ ${\displaystyle f}$ ${\displaystyle x_{0}-\delta <x<x_{0}+\delta ,}$ ${\displaystyle f(x)}$

$${\displaystyle f\left(x_{0}\right)-\varepsilon <f(x)<f(x_{0})+\varepsilon .}$$

Альтернативно записанное: непрерывность at означает, что для каждого существует такое, что для всех : ${\displaystyle f:D\to \mathbb {R} }$ ${\displaystyle x_{0}\in D}$ ${\displaystyle \varepsilon >0,}$ ${\displaystyle \delta >0}$ ${\displaystyle x\in D}$

$${\displaystyle \left|x-x_{0}\right|<\delta ~~{\text{ implies }}~~|f(x)-f(x_{0})|<\varepsilon .}$$

Более интуитивно мы можем сказать, что если мы хотим, чтобы все значения оставались в некоторой небольшой окрестности , нам нужно выбрать достаточно маленькую окрестность для значений вокруг . Если мы можем это сделать, независимо от того, насколько мала окрестность, тогда она непрерывна. в ${\displaystyle f(x)}$ ${\displaystyle f\left(x_{0}\right),}$ ${\displaystyle x}$ ${\displaystyle x_{0}.}$ ${\displaystyle f(x_{0})}$ ${\displaystyle f}$ ${\displaystyle x_{0}.}$

Говоря современным языком, это обобщается определением непрерывности функции относительно основы топологии , здесь метрической топологии .

Вейерштрасс требовал, чтобы интервал полностью находился в пределах области , но Джордан снял это ограничение. ${\displaystyle x_{0}-\delta <x<x_{0}+\delta }$ ${\displaystyle D}$

Определение с точки зрения контроля остатка

В доказательствах и численном анализе нам часто необходимо знать, насколько быстро сходятся пределы, или, другими словами, контролировать остаток. Мы можем формализовать это до определения непрерывности. Функция называется функцией управления, если ${\displaystyle C:[0,\infty )\to [0,\infty ]}$

• C не убывает
• ${\displaystyle \inf _{\delta >0}C(\delta )=0}$

Функция называется C -непрерывной в, если существует такая окрестность , что ${\displaystyle f:D\to R}$ ${\displaystyle x_{0}}$ ${\textstyle N(x_{0})}$

$${\displaystyle |f(x)-f(x_{0})|\leq C\left(\left|x-x_{0}\right|\right){\text{ for all }}x\in D\cap N(x_{0})}$$

Функция непрерывна, если она C -непрерывна для некоторой управляющей функции C. ${\displaystyle x_{0}}$

Такой подход естественным образом приводит к уточнению понятия непрерывности за счет ограничения набора допустимых функций управления. Для данного набора функций управления функция является -непрерывной, если она -непрерывна для некоторых . Например, непрерывные функции Липшица и Гёльдера показателя степени α ниже определяются набором функций управления ${\displaystyle {\mathcal {C}}}$ ${\displaystyle {\mathcal {C}}}$ ${\displaystyle C}$ ${\displaystyle C\in {\mathcal {C}}.}$

$${\displaystyle {\mathcal {C}}_{\mathrm {Lipschitz} }=\{C:C(\delta )=K|\delta |,\ K>0\}}$$

$${\displaystyle {\mathcal {C}}_{{\text{Hölder}}-\alpha }=\{C:C(\delta )=K|\delta |^{\alpha },\ K>0\}.}$$

Определение с использованием колебаний

Неспособность функции быть непрерывной в точке количественно выражается ее колебанием .

Непрерывность также можно определить с точки зрения колебаний : функция f непрерывна в точке тогда и только тогда, когда ее колебание в этой точке равно нулю; ^[10] в символах. Преимущество этого определения состоит в том, что оно дает количественную оценку разрыва: колебание показывает, насколько функция разрывна в определенной точке. ${\displaystyle x_{0}}$ ${\displaystyle \omega _{f}(x_{0})=0.}$

Это определение полезно в описательной теории множеств для изучения множества разрывов и непрерывных точек (непрерывные точки представляют собой пересечение множеств, где колебание меньше (следовательно, множество )), и дает быстрое доказательство одного направления Лебега . условие интегрируемости . ^[11] ${\displaystyle \varepsilon }$ ${\displaystyle G_{\delta }}$

Колебание эквивалентно определению путем простой перестановки и использования предела ( lim sup , lim inf ) для определения колебания: если (в данной точке) для данного нет ничего , удовлетворяющего определению, то колебание по крайней мере, и наоборот, если для каждого есть желаемое колебание равно 0. Определение колебания можно естественным образом обобщить на отображения из топологического пространства в метрическое пространство . ${\displaystyle \varepsilon -\delta }$ ${\displaystyle \varepsilon _{0}}$ ${\displaystyle \delta }$ ${\displaystyle \varepsilon -\delta }$ ${\displaystyle \varepsilon _{0},}$ ${\displaystyle \varepsilon }$ ${\displaystyle \delta ,}$

Определение с использованием гиперреальности

Коши определил непрерывность функции в следующих интуитивных терминах: бесконечно малое изменение независимой переменной соответствует бесконечно малому изменению зависимой переменной (см. «Кур анализа» , стр. 34). Нестандартный анализ — это способ сделать это математически строгим. Действительная линия дополняется добавлением бесконечных и бесконечно малых чисел, образуя гипердействительные числа . В нестандартном анализе непрерывность можно определить следующим образом.

Действительная функция f является непрерывной в точке x , если ее естественное расширение на гиперреалы обладает свойством, которое для всех бесконечно малых dx является бесконечно малым ^[12] ${\displaystyle f(x+dx)-f(x)}$

(см. микронепрерывность ). Другими словами, бесконечно малое приращение независимой переменной всегда приводит к бесконечно малому изменению зависимой переменной, что дает современное выражение определению непрерывности Огюстена-Луи Коши .

Построение непрерывных функций

График кубической функции не имеет скачков и дыр. Функция непрерывна.

Проверку непрерывности данной функции можно упростить, проверив одно из вышеперечисленных определяющих свойств строительных блоков данной функции. Несложно показать, что сумма двух функций, непрерывная в некоторой области, непрерывна и в этой области. Данный

$${\displaystyle f,g\colon D\to \mathbb {R} ,}$$

сумма непрерывных функций

$${\displaystyle s=f+g}$$

${\displaystyle s(x)=f(x)+g(x)}$ ${\displaystyle x\in D}$ ${\displaystyle D.}$

То же самое справедливо и для произведения непрерывных функций ,

$${\displaystyle p=f\cdot g}$$

${\displaystyle p(x)=f(x)\cdot g(x)}$ ${\displaystyle x\in D}$ ${\displaystyle D.}$

Комбинируя приведенные выше сохранения непрерывности и непрерывности постоянных функций и тождественной функции на , можно прийти к непрерывности всех полиномиальных функций на , таких как ${\displaystyle I(x)=x}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} }$

$${\displaystyle f(x)=x^{3}+x^{2}-5x+3}$$

График непрерывной рациональной функции . Функция не определена. Вертикальные и горизонтальные линии являются асимптотами . ${\displaystyle x=-2.}$

Точно так же можно показать, что обратная непрерывная функция

$${\displaystyle r=1/f}$$

${\displaystyle r(x)=1/f(x)}$ ${\displaystyle x\in D}$ ${\displaystyle f(x)\neq 0}$ ${\displaystyle D\setminus \{x:f(x)=0\}.}$

Отсюда следует, что, исключая корни частного непрерывных функций ${\displaystyle g,}$

$${\displaystyle q=f/g}$$

${\displaystyle q(x)=f(x)/g(x)}$ ${\displaystyle x\in D}$ ${\displaystyle g(x)\neq 0}$ ${\displaystyle D\setminus \{x:g(x)=0\}}$

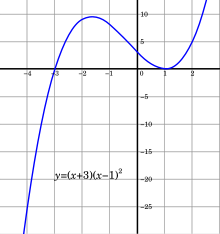
Например, функция (на фото)

$${\displaystyle y(x)={\frac {2x-1}{x+2}}}$$

${\displaystyle x\neq -2}$ ${\displaystyle x=-2}$ ${\displaystyle x=-2}$ ${\displaystyle y.}$ ${\displaystyle F:\mathbb {R} \to \mathbb {R} }$ ${\displaystyle y(x)}$ ${\displaystyle x\neq -2.}$

Функции sinc и cos

Поскольку функция синус непрерывна для всех действительных чисел, функция sinc определена и непрерывна для всех действительных чисел . Однако, в отличие от предыдущего примера, G можно расширить до непрерывной функции для всех действительных чисел, определив значение равным 1, что равно предел, когда x приближается к 0, т. е. ${\displaystyle G(x)=\sin(x)/x,}$ ${\displaystyle x\neq 0.}$ ${\displaystyle G(0)}$ ${\displaystyle G(x),}$

$${\displaystyle G(0)=\lim _{x\to 0}{\frac {\sin x}{x}}=1.}$$

Таким образом, установив

${\displaystyle G(x)={\begin{cases}{\frac {\sin(x)}{x}}&{\text{ if }}x\neq 0\\1&{\text{ if }}x=0,\end{cases}}}$

функция sinc становится непрерывной функцией для всех действительных чисел. Термин «устранимая особенность» используется в таких случаях, когда (пере)определение значений функции так, чтобы они совпадали с соответствующими пределами, делает функцию непрерывной в определенных точках.

Более сложная конструкция непрерывных функций — это композиция функций . Даны две непрерывные функции

$${\displaystyle g:D_{g}\subseteq \mathbb {R} \to R_{g}\subseteq \mathbb {R} \quad {\text{ and }}\quad f:D_{f}\subseteq \mathbb {R} \to R_{f}\subseteq D_{g},}$$

${\displaystyle c=g\circ f:D_{f}\to \mathbb {R} ,}$ ${\displaystyle c(x)=g(f(x)),}$

Эта конструкция позволяет, например, утверждать, что

$${\displaystyle e^{\sin(\ln x)}}$$

${\displaystyle x>0.}$

Примеры разрывных функций

График функции Signum. Это показывает, что . Таким образом, сигнум-функция разрывна в точке 0 (см. раздел 2.1.3). ${\displaystyle \lim _{n\to \infty }\operatorname {sgn} \left({\tfrac {1}{n}}\right)\neq \operatorname {sgn} \left(\lim _{n\to \infty }{\tfrac {1}{n}}\right)}$

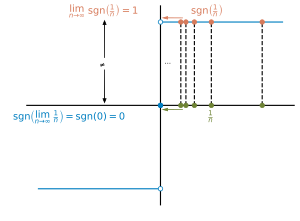
Примером разрывной функции является ступенчатая функция Хевисайда , определяемая формулой ${\displaystyle H}$

$${\displaystyle H(x)={\begin{cases}1&{\text{ if }}x\geq 0\\0&{\text{ if }}x<0\end{cases}}}$$

Выбери, например . Тогда вокруг , то есть нет открытого интервала , который заставил бы все значения находиться в пределах -окрестности , то есть внутри . Интуитивно мы можем думать об этом типе разрыва как о внезапном скачке значений функции. ${\displaystyle \varepsilon =1/2}$ ${\displaystyle \delta }$ ${\displaystyle x=0}$ ${\displaystyle (-\delta ,\;\delta )}$ ${\displaystyle \delta >0,}$ ${\displaystyle H(x)}$ ${\displaystyle \varepsilon }$ ${\displaystyle H(0)}$ ${\displaystyle (1/2,\;3/2)}$

Аналогично, функция Signum или Sign

$${\displaystyle \operatorname {sgn}(x)={\begin{cases}\;\;\ 1&{\text{ if }}x>0\\\;\;\ 0&{\text{ if }}x=0\\-1&{\text{ if }}x<0\end{cases}}}$$

${\displaystyle x=0}$

$${\displaystyle f(x)={\begin{cases}\sin \left(x^{-2}\right)&{\text{ if }}x\neq 0\\0&{\text{ if }}x=0\end{cases}}}$$

${\displaystyle x=0}$

Точечный график функции Томаэ на интервале (0,1). Самая верхняя точка посередине показывает f(1/2) = 1/2.

Помимо правдоподобных непрерывностей и разрывов, подобных описанным выше, существуют также функции с поведением, часто называемым патологическим , например, функция Томаэ ,

$${\displaystyle f(x)={\begin{cases}1&{\text{ if }}x=0\\{\frac {1}{q}}&{\text{ if }}x={\frac {p}{q}}{\text{(in lowest terms) is a rational number}}\\0&{\text{ if }}x{\text{ is irrational}}.\end{cases}}}$$

функция Дирихлеиндикаторная функция

$${\displaystyle D(x)={\begin{cases}0&{\text{ if }}x{\text{ is irrational }}(\in \mathbb {R} \setminus \mathbb {Q} )\\1&{\text{ if }}x{\text{ is rational }}(\in \mathbb {Q} )\end{cases}}}$$

Характеристики

Полезная лемма

Пусть – функция, непрерывная в точке , и такое значение. Тогда в некоторой окрестности ^[13] ${\displaystyle f(x)}$ ${\displaystyle x_{0},}$ ${\displaystyle y_{0}}$ ${\displaystyle f\left(x_{0}\right)\neq y_{0}.}$ ${\displaystyle f(x)\neq y_{0}}$ ${\displaystyle x_{0}.}$

Доказательство: По определению непрерывности, возьмем , то существует такое, что ${\displaystyle \varepsilon ={\frac {|y_{0}-f(x_{0})|}{2}}>0}$ ${\displaystyle \delta >0}$

$${\displaystyle \left|f(x)-f(x_{0})\right|<{\frac {\left|y_{0}-f(x_{0})\right|}{2}}\quad {\text{ whenever }}\quad |x-x_{0}|<\delta }$$

${\displaystyle |x-x_{0}|<\delta }$ ${\displaystyle f(x)=y_{0};}$

$${\displaystyle \left|f(x_{0})-y_{0}\right|<{\frac {\left|f(x_{0})-y_{0}\right|}{2}}.}$$

Теорема о промежуточном значении

Теорема о промежуточном значении — это теорема существования , основанная на свойстве полноты вещественного числа и утверждающая:

Если действительная функция f непрерывна на замкнутом интервале и k — некоторое число между ними , то существует такое число, что ${\displaystyle [a,b],}$ ${\displaystyle f(a)}$ ${\displaystyle f(b),}$ ${\displaystyle c\in [a,b],}$ ${\displaystyle f(c)=k.}$

Например, если в возрасте от двух до шести лет ребенок вырастает с 1 м до 1,5 м, то в какой-то момент между двумя и шестью годами рост ребенка должен был составлять 1,25 м.

Как следствие, если f непрерывна на и и различаются знаком , то в некоторой точке должно равняться нулю . ${\displaystyle [a,b]}$ ${\displaystyle f(a)}$ ${\displaystyle f(b)}$ ${\displaystyle c\in [a,b],}$ ${\displaystyle f(c)}$

Теорема об экстремальных значениях

Теорема о крайнем значении утверждает, что если функция f определена на замкнутом интервале (или любом замкнутом и ограниченном множестве) и непрерывна там, то функция достигает своего максимума, т. е. существует с для всех. То же самое верно и для минимума ф . Эти утверждения, вообще говоря, неверны, если функция определена на открытом интервале (или любом множестве, которое не является одновременно замкнутым и ограниченным), как, например, непрерывная функция , определенная на открытом интервале (0,1), не достигает максимума, будучи неограниченным сверху. ${\displaystyle [a,b]}$ ${\displaystyle c\in [a,b]}$ ${\displaystyle f(c)\geq f(x)}$ ${\displaystyle x\in [a,b].}$ ${\displaystyle (a,b)}$ ${\displaystyle f(x)={\frac {1}{x}},}$

Связь с дифференцируемостью и интегрируемостью

Любая дифференцируемая функция

$${\displaystyle f:(a,b)\to \mathbb {R} }$$

функциязначения

${\displaystyle f(x)=|x|={\begin{cases}\;\;\ x&{\text{ if }}x\geq 0\\-x&{\text{ if }}x<0\end{cases}}}$

всюду непрерывен. Однако оно не дифференцируемо в (но дифференцируемо всюду). Функция Вейерштрасса также всюду непрерывна, но нигде не дифференцируема. ${\displaystyle x=0}$

Производная f′ ( x ) дифференцируемой функции f ( x ) не обязательно должна быть непрерывной. Если f′ ( x ) непрерывно, то f ( x ) называется непрерывно дифференцируемым . Множество таких функций обозначается. В более общем смысле множество функций ${\displaystyle C^{1}((a,b)).}$

$${\displaystyle f:\Omega \to \mathbb {R} }$$

открытого подмножестваffкласс дифференцируемостиГладкость кривых и поверхностей ${\displaystyle \mathbb {R} }$ ${\displaystyle \Omega }$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle C^{n}(\Omega ).}$ ${\displaystyle C^{0},C^{1},C^{2}}$ ${\displaystyle G^{0}}$ ${\displaystyle G^{1}}$ ${\displaystyle G^{2}}$

Любая непрерывная функция

$${\displaystyle f:[a,b]\to \mathbb {R} }$$

,интеграла Риманазнаковая функция

Поточечные и равномерные пределы

Последовательность непрерывных функций , предельная (поточечная) функция которой разрывна. Сближение не является равномерным. ${\displaystyle f_{n}(x)}$ ${\displaystyle f(x)}$

Учитывая последовательность

$${\displaystyle f_{1},f_{2},\dotsc :I\to \mathbb {R} }$$

$${\displaystyle f(x):=\lim _{n\to \infty }f_{n}(x)}$$

поточечным пределомfсходится равномернотеореме о равномерной сходимостипоказательные функциилогарифмыквадратного корнятригонометрические функции ${\displaystyle x\in D,}$ ${\displaystyle f(x)}$ ${\displaystyle \left(f_{n}\right)_{n\in N}.}$ ${\displaystyle f_{n}}$ ${\displaystyle f_{n}}$

Направленность и полунепрерывность

• 
  Непрерывная справа функция
• 
  Непрерывная слева функция

Разрывные функции могут быть ограниченно разрывными, что порождает концепцию направленной непрерывности (или непрерывных функций справа и слева) и полунепрерывности . Грубо говоря, функция непрерывна справа , если при приближении к предельной точке справа не происходит скачка. Формально f называется непрерывным справа в точке c , если выполняется следующее: для любого числа, каким бы малым оно ни было, существует такое число, что для всех x в области со значением будет удовлетворять ${\displaystyle \varepsilon >0}$ ${\displaystyle \delta >0}$ ${\displaystyle c<x<c+\delta ,}$ ${\displaystyle f(x)}$

$${\displaystyle |f(x)-f(c)|<\varepsilon .}$$

Это то же самое условие, что и для непрерывных функций, за исключением того, что оно должно выполняться только для x, строго большего, чем c . Требование этого вместо этого для всех x с дает понятие непрерывных слева функций. Функция непрерывна тогда и только тогда, когда она непрерывна одновременно справа и слева. ${\displaystyle c-\delta <x<c}$

Функция f является полунепрерывной снизу , если, грубо говоря, любые скачки, которые могут произойти, идут только вниз, но не вверх. То есть для любого существует такое число, что для всех x в области значений со значением удовлетворяет ${\displaystyle \varepsilon >0,}$ ${\displaystyle \delta >0}$ ${\displaystyle |x-c|<\delta ,}$ ${\displaystyle f(x)}$

$${\displaystyle f(x)\geq f(c)-\epsilon .}$$

полунепрерывность сверху

Непрерывные функции между метрическими пространствами

Понятие непрерывных вещественнозначных функций можно обобщить на функции между метрическими пространствами . Метрическое пространство — это множество, оснащенное функцией (называемой метрикой ) , которую можно рассматривать как измерение расстояния между любыми двумя элементами в X. Формально метрика — это функция ${\displaystyle X}$ ${\displaystyle d_{X},}$

$${\displaystyle d_{X}:X\times X\to \mathbb {R} }$$

неравенству треугольника ${\displaystyle \left(X,d_{X}\right)}$ ${\displaystyle \left(Y,d_{Y}\right)}$

$${\displaystyle f:X\to Y}$$

последовательностью Коши ${\displaystyle f}$ ${\displaystyle c\in X}$ ${\displaystyle \varepsilon >0,}$ ${\displaystyle \delta >0}$ ${\displaystyle x\in X}$ ${\displaystyle d_{X}(x,c)<\delta }$ ${\displaystyle d_{Y}(f(x),f(c))<\varepsilon .}$ ${\displaystyle \left(x_{n}\right)}$ ${\displaystyle X}$ ${\displaystyle \lim x_{n}=c,}$ ${\displaystyle \lim f\left(x_{n}\right)=f(c).}$ ${\displaystyle f}$ ${\displaystyle c}$ ${\displaystyle \left(x_{n}\right)}$ ${\displaystyle X}$ ${\displaystyle c}$ ${\displaystyle \left(f\left(x_{n}\right)\right)}$ ${\displaystyle c}$ ${\displaystyle f}$

Множество точек, в которых функция между метрическими пространствами непрерывна, является множеством –  это следует из определения непрерывности. ${\displaystyle G_{\delta }}$ ${\displaystyle \varepsilon -\delta }$

Это понятие непрерывности применяется, например, в функциональном анализе . Ключевое утверждение в этой области гласит, что линейный оператор

$${\displaystyle T:V\to W}$$

нормированными векторными пространствамивекторными пространстваминормойограничено ${\displaystyle V}$ ${\displaystyle W}$ ${\displaystyle \|x\|}$ ${\displaystyle K}$

$${\displaystyle \|T(x)\|\leq K\|x\|}$$

${\displaystyle x\in V.}$

Равномерность, непрерывность Гельдера и Липшица

Для непрерывной по Липшицу функции существует двойной конус (показан белым), вершину которого можно перемещать вдоль графика так, что график всегда остается полностью вне конуса.

Понятие непрерывности функций между метрическими пространствами можно усилить различными способами, ограничив зависимость от и c в приведенном выше определении. Интуитивно понятно, что функция f , как указано выше, является равномерно непрерывной, если не зависит от точки c . Точнее, требуется, чтобы для всякого действительного числа существовало такое, что для каждого с имеем: Таким образом, любая равномерно непрерывная функция непрерывна. Обратное утверждение вообще не верно, но справедливо, когда доменное пространство X компактно . Равномерно непрерывные отображения могут быть определены в более общей ситуации равномерных пространств . ^[14] ${\displaystyle \delta }$ ${\displaystyle \varepsilon }$ ${\displaystyle \delta }$ ${\displaystyle \varepsilon >0}$ ${\displaystyle \delta >0}$ ${\displaystyle c,b\in X}$ ${\displaystyle d_{X}(b,c)<\delta ,}$ ${\displaystyle d_{Y}(f(b),f(c))<\varepsilon .}$

Функция является непрерывной по Гельдеру с показателем α (действительным числом), если существует константа K такая, что для всех неравенств ${\displaystyle b,c\in X,}$

$${\displaystyle d_{Y}(f(b),f(c))\leq K\cdot (d_{X}(b,c))^{\alpha }}$$

липшицевой непрерывностьюK ${\displaystyle \alpha =1}$

$${\displaystyle d_{Y}(f(b),f(c))\leq K\cdot d_{X}(b,c)}$$

^[15]теореме Пикара–Линделёфаобыкновенных дифференциальных уравнений ${\displaystyle b,c\in X.}$

Непрерывные функции между топологическими пространствами

Другое, более абстрактное понятие непрерывности — это непрерывность функций между топологическими пространствами , в которых обычно нет формального понятия расстояния, как в случае метрических пространств . Топологическое пространство — это множество X вместе с топологией на X , которая представляет собой набор подмножеств X , удовлетворяющих нескольким требованиям в отношении их объединений и пересечений, которые обобщают свойства открытых шаров в метрических пространствах, но при этом позволяют говорить об окрестностях данной точки. Элементы топологии называются открытыми подмножествами X ( относительно топологии).

Функция

$${\displaystyle f:X\to Y}$$

XYсуществует ${\displaystyle V\subseteq Y,}$

$${\displaystyle f^{-1}(V)=\{x\in X\;|\;f(x)\in V\}}$$

XfXYfXY. ${\displaystyle T_{X}}$

Это эквивалентно условию, что прообразы замкнутых множеств (которые являются дополнениями к открытым подмножествам) в Y замкнуты в X .

Крайний пример: если множеству X задана дискретная топология (в которой каждое подмножество открыто), все функции

$${\displaystyle f:X\to T}$$

TXтопологиейXTT 0

Непрерывность в одной точке

Непрерывность в точке: для каждой окрестности V точки существует окрестность U точки x такая, что ${\displaystyle f(x)}$ ${\displaystyle f(U)\subseteq V}$

Перевод на язык окрестностей -определения непрерывности приводит к следующему определению непрерывности в точке: ${\displaystyle (\varepsilon ,\delta )}$

Функция непрерывна в точке тогда и только тогда, когда для любой окрестности V в Y существует окрестность U такая, что ${\displaystyle f:X\to Y}$ ${\displaystyle x\in X}$ ${\displaystyle f(x)}$ ${\displaystyle x}$ ${\displaystyle f(U)\subseteq V.}$

Это определение эквивалентно тому же утверждению с окрестностями, ограниченными открытыми окрестностями, и может быть переформулировано несколькими способами, используя прообразы , а не изображения.

Кроме того, поскольку каждое множество, содержащее окрестность, также является окрестностью и является самым большим подмножеством U из X , так что это определение можно упростить до: ${\displaystyle f^{-1}(V)}$ ${\displaystyle f(U)\subseteq V,}$

Функция непрерывна в точке тогда и только тогда, когда является окрестностью для каждой окрестности V из Y . ${\displaystyle f:X\to Y}$ ${\displaystyle x\in X}$ ${\displaystyle f^{-1}(V)}$ ${\displaystyle x}$ ${\displaystyle f(x)}$

Поскольку открытое множество — это множество, которое является окрестностью всех своих точек, функция непрерывна в каждой точке X тогда и только тогда, когда она является непрерывной функцией. ${\displaystyle f:X\to Y}$

Если X и Y — метрические пространства, это эквивалентно рассмотрению системы окрестностей открытых шаров с центрами в точках x и f ( x ) вместо всех окрестностей. Это возвращает приведенное выше определение непрерывности в контексте метрических пространств. В общих топологических пространствах нет понятия близости или расстояния. Однако если целевое пространство является хаусдорфовым пространством , то по-прежнему верно, что f непрерывно в точке a тогда и только тогда, когда предел f при приближении x к a равен f ( a ). В изолированной точке каждая функция непрерывна. ${\displaystyle \varepsilon -\delta }$

Данное отображение является непрерывным в том и только в том случае, если всякий раз, когда фильтр на том , который сходится к , в котором выражается записью то обязательно в Если обозначает фильтр окрестности в то непрерывен в том и только в том случае, если в ^[16] Более того, это происходит, если и только если префильтр является базой фильтра для фильтра окрестности из [ ^16] ${\displaystyle x\in X,}$ ${\displaystyle f:X\to Y}$ ${\displaystyle x}$ ${\displaystyle {\mathcal {B}}}$ ${\displaystyle X}$ ${\displaystyle x}$ ${\displaystyle X,}$ ${\displaystyle {\mathcal {B}}\to x,}$ ${\displaystyle f({\mathcal {B}})\to f(x)}$ ${\displaystyle Y.}$ ${\displaystyle {\mathcal {N}}(x)}$ ${\displaystyle x}$ ${\displaystyle f:X\to Y}$ ${\displaystyle x}$ ${\displaystyle f({\mathcal {N}}(x))\to f(x)}$ ${\displaystyle Y.}$ ${\displaystyle f({\mathcal {N}}(x))}$ ${\displaystyle f(x)}$ ${\displaystyle Y.}$

Альтернативные определения

Существует несколько эквивалентных определений топологической структуры ; таким образом, существует несколько эквивалентных способов определения непрерывной функции.

Последовательности и сети

В некоторых контекстах топологию пространства удобно задавать в терминах предельных точек . Это часто достигается путем указания того, когда точка является пределом последовательности . Тем не менее, для некоторых пространств, которые в некотором смысле слишком велики, также указывается, когда точка является пределом более общих наборов точек, индексированных направленным набором , известным как сети . Функция (по Гейне)непрерывна только в том случае, если она переводит пределы последовательностей в пределы последовательностей. В первом случае достаточно сохранения пределов; во втором случае функция может сохранять все пределы последовательностей, но при этом не быть непрерывной, а сохранение сетей является необходимым и достаточным условием.

Подробно, функция является секвенциально непрерывной, если всякий раз, когда последовательность в сходится к пределу , она сходится к Таким образом, секвенциально непрерывные функции «сохраняют последовательные пределы». Любая непрерывная функция секвенциально непрерывна. Если пространство - счетное в первую очередь и имеет место счетный выбор , то верно и обратное: любая функция, сохраняющая последовательные пределы, непрерывна. В частности, если пространство метрическое, секвенциальная непрерывность и непрерывность эквивалентны. Для пространств без первого счета секвенциальная непрерывность может быть строго слабее непрерывности. (Пространства, для которых эти два свойства эквивалентны, называются секвенциальными пространствами .) Это мотивирует рассматривать сети вместо последовательностей в общих топологических пространствах. Непрерывные функции сохраняют пределы сетей, и это свойство характеризует непрерывные функции. ${\displaystyle f:X\to Y}$ ${\displaystyle \left(x_{n}\right)}$ ${\displaystyle X}$ ${\displaystyle x,}$ ${\displaystyle \left(f\left(x_{n}\right)\right)}$ ${\displaystyle f(x).}$ ${\displaystyle X}$ ${\displaystyle X}$

Например, рассмотрим случай вещественных функций одной действительной переменной: ^[17]

Теорема  :  Функция непрерывна тогда и только тогда, когда она секвенциально непрерывна в этой точке. ${\displaystyle f:A\subseteq \mathbb {R} \to \mathbb {R} }$ ${\displaystyle x_{0}}$

Определения оператора замыкания и внутреннего оператора

С точки зрения внутреннего оператора функция между топологическими пространствами непрерывна тогда и только тогда, когда для каждого подмножества ${\displaystyle f:X\to Y}$ ${\displaystyle B\subseteq Y,}$

$${\displaystyle f^{-1}\left(\operatorname {int} _{Y}B\right)~\subseteq ~\operatorname {int} _{X}\left(f^{-1}(B)\right).}$$

С точки зрения оператора замыкания , непрерывно тогда и только тогда, когда для каждого подмножества ${\displaystyle f:X\to Y}$ ${\displaystyle A\subseteq X,}$

$${\displaystyle f\left(\operatorname {cl} _{X}A\right)~\subseteq ~\operatorname {cl} _{Y}(f(A)).}$$

кпростое английское ${\displaystyle x\in X}$ ${\displaystyle A\subseteq X,}$ ${\displaystyle f(x)}$ ${\displaystyle f(A)}$ ${\displaystyle Y.}$ ${\displaystyle x}$ ${\displaystyle A\subseteq X}$ ${\displaystyle x\in \operatorname {cl} _{X}A,}$ ${\displaystyle f}$ ${\displaystyle A\subseteq X,}$ ${\displaystyle f}$ ${\displaystyle A}$ ${\displaystyle f(A).}$ ${\displaystyle f}$ ${\displaystyle x\in X}$ ${\displaystyle x}$ ${\displaystyle A\subseteq X,}$ ${\displaystyle f(x)}$ ${\displaystyle f(A).}$

Вместо определения топологических пространств их открытыми подмножествами любая топология может альтернативно определяться оператором замыкания или внутренним оператором . В частности, карта, которая отправляет подмножество топологического пространства к его топологическому замыканию, удовлетворяет аксиомам замыкания Куратовского . И наоборот, для любого оператора замыкания существует уникальная топология на (в частности, ) такая, что для каждого подмножества равно топологическому замыканию в . Если каждое из множеств и связано с операторами замыкания (оба обозначаются через ), то отображение является непрерывным, если и только если для каждого подмножества ${\displaystyle X}$ ${\displaystyle A}$ ${\displaystyle X}$ ${\displaystyle \operatorname {cl} _{X}A}$ ${\displaystyle A\mapsto \operatorname {cl} A}$ ${\displaystyle \tau }$ ${\displaystyle X}$ ${\displaystyle \tau :=\{X\setminus \operatorname {cl} A:A\subseteq X\}}$ ${\displaystyle A\subseteq X,}$ ${\displaystyle \operatorname {cl} A}$ ${\displaystyle \operatorname {cl} _{(X,\tau )}A}$ ${\displaystyle A}$ ${\displaystyle (X,\tau ).}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle \operatorname {cl} }$ ${\displaystyle f:X\to Y}$ ${\displaystyle f(\operatorname {cl} A)\subseteq \operatorname {cl} (f(A))}$ ${\displaystyle A\subseteq X.}$

Аналогично, карта, которая отправляет подмножество в свою топологическую внутреннюю часть, определяет внутренний оператор . И наоборот, любой внутренний оператор индуцирует уникальную топологию на (в частности, ) такую, что для каждого равна топологической внутренней части в . Если множества и каждый связаны с внутренними операторами (оба обозначаются через ), то отображение непрерывно тогда и только тогда, когда для каждого подмножества ^[18] ${\displaystyle A}$ ${\displaystyle X}$ ${\displaystyle \operatorname {int} _{X}A}$ ${\displaystyle A\mapsto \operatorname {int} A}$ ${\displaystyle \tau }$ ${\displaystyle X}$ ${\displaystyle \tau :=\{\operatorname {int} A:A\subseteq X\}}$ ${\displaystyle A\subseteq X,}$ ${\displaystyle \operatorname {int} A}$ ${\displaystyle \operatorname {int} _{(X,\tau )}A}$ ${\displaystyle A}$ ${\displaystyle (X,\tau ).}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle \operatorname {int} }$ ${\displaystyle f:X\to Y}$ ${\displaystyle f^{-1}(\operatorname {int} B)\subseteq \operatorname {int} \left(f^{-1}(B)\right)}$ ${\displaystyle B\subseteq Y.}$

Фильтры и префильтры

Непрерывность также можно охарактеризовать с точки зрения фильтров . Функция непрерывна тогда и только тогда, когда всякий раз, когда фильтр сходится к точке , предфильтр сходится к Эта характеристика остается верной , если слово «фильтр» заменяется словом «предфильтр». ^[16] ${\displaystyle f:X\to Y}$ ${\displaystyle {\mathcal {B}}}$ ${\displaystyle X}$ ${\displaystyle X}$ ${\displaystyle x\in X,}$ ${\displaystyle f({\mathcal {B}})}$ ${\displaystyle Y}$ ${\displaystyle f(x).}$

Характеристики

Если и непрерывны, то непрерывна и композиция. Если непрерывна и ${\displaystyle f:X\to Y}$ ${\displaystyle g:Y\to Z}$ ${\displaystyle g\circ f:X\to Z.}$ ${\displaystyle f:X\to Y}$

• X компактен , то f ( X ) компактен.
• X связен , то f ( X ) связен .
• X линейно связен , тогда f ( X ) линейно связен.
• X — Линделеф , тогда f ( X ) — Линделеф.
• X сепарабельно , то f ( X ) сепарабельно.

Возможные топологии на фиксированном множестве X частично упорядочены : топология называется более грубой , чем другая топология (обозначение: ), если каждое открытое подмножество относительно также открыто относительно Тогда тождественное отображение ${\displaystyle \tau _{1}}$ ${\displaystyle \tau _{2}}$ ${\displaystyle \tau _{1}\subseteq \tau _{2}}$ ${\displaystyle \tau _{1}}$ ${\displaystyle \tau _{2}.}$

$${\displaystyle \operatorname {id} _{X}:\left(X,\tau _{2}\right)\to \left(X,\tau _{1}\right)}$$

сравнение топологий ${\displaystyle \tau _{1}\subseteq \tau _{2}}$

$${\displaystyle \left(X,\tau _{X}\right)\to \left(Y,\tau _{Y}\right)}$$

более грубой топологиейтонкой топологией ${\displaystyle \tau _{Y}}$ ${\displaystyle \tau _{X}}$

Гомеоморфизмы

Симметричным понятию непрерывного отображения является открытое отображение , для которого открыты образы открытых множеств. Если открытое отображение f имеет обратную функцию , эта обратная функция непрерывна, а если непрерывное отображение g имеет обратную функцию, эта обратная функция открыта. Учитывая биективную функцию f между двумя топологическими пространствами, обратная функция не обязательно должна быть непрерывной. Биективная непрерывная функция с непрерывной обратной функцией называется гомеоморфизмом . ${\displaystyle f^{-1}}$

Если непрерывная биекция имеет областью определения компактное пространство , а ее ко-область — Хаусдорф , то она является гомеоморфизмом.

Определение топологий с помощью непрерывных функций

Дана функция

$${\displaystyle f:X\to S,}$$

XSокончательная топологияSSASXSfгрубееSSffканоническифактор-топологиейотношении эквивалентности,f ${\displaystyle f^{-1}(A)}$

Двойственным образом, для функции f из множества S в топологическое пространство X начальная топология на S определяется путем обозначения открытого множества каждого подмножества A из S такого, что для некоторого открытого подмножества U из X . Если S имеет существующую топологию, f непрерывен относительно этой топологии тогда и только тогда, когда существующая топология тоньше, чем исходная топология на S . Таким образом, исходная топология является самой грубой топологией на S , которая делает f непрерывным. Если f инъективно, эта топология канонически отождествляется с топологией подпространства S , рассматриваемой как подмножество X. ${\displaystyle A=f^{-1}(U)}$

Топология на множестве S однозначно определяется классом всех непрерывных функций во всех топологических пространствах X. Аналогичную идею можно применить и к картам. ${\displaystyle S\to X}$ ${\displaystyle X\to S.}$

Связанные понятия

Если – непрерывная функция из некоторого подмножества топологического пространства, то ${\displaystyle f:S\to Y}$ ${\displaystyle S}$ ${\displaystyle X}$непрерывное расширение to—это любая непрерывная функция,такая чтодля каждой, которая является условием, которое часто записывают какДругими словами, это любая непрерывная функция,ограничивающаясяна.Это понятие используется, например, втеореме о расширении ТитцеиХана – Банаха. теорема. Еслионо не является непрерывным, то оно не может иметь непрерывного продолжения. Еслипространство Хаусдорфаявляетсяплотнымподмножеством,тонепрерывное расширение пространствадо, если оно существует, будет единственным. ТеоремаБлюмбергаутверждает, что если— произвольная функция, то существует ее плотное подмножество,ограничение которогонепрерывно; другими словами, каждую функциюможно ограничить некоторым плотным подмножеством, на котором она непрерывна. ${\displaystyle f}$ ${\displaystyle X}$ ${\displaystyle F:X\to Y}$ ${\displaystyle F(s)=f(s)}$ ${\displaystyle s\in S,}$ ${\displaystyle f=F{\big \vert }_{S}.}$ ${\displaystyle F:X\to Y}$ ${\displaystyle f}$ ${\displaystyle S.}$ ${\displaystyle f:S\to Y}$ ${\displaystyle Y}$ ${\displaystyle S}$ ${\displaystyle X}$ ${\displaystyle f:S\to Y}$ ${\displaystyle X,}$ ${\displaystyle f:\mathbb {R} \to \mathbb {R} }$ ${\displaystyle D}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle f{\big \vert }_{D}:D\to \mathbb {R} }$ ${\displaystyle \mathbb {R} \to \mathbb {R} }$

В различных других математических областях понятие непрерывности используется в разных, но связанных значениях. Например, в теории порядка функция, сохраняющая порядок между конкретными типами частично упорядоченных множеств , является непрерывной, если для каждого направленного подмножества мы имеем Здесь является супремумом относительно упорядочений в и соответственно. Это понятие непрерывности совпадает с топологической непрерывностью, когда частично упорядоченным множествам задана топология Скотта . ^{[19] [20]} ${\displaystyle f:X\to Y}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle A}$ ${\displaystyle X,}$ ${\displaystyle \sup f(A)=f(\sup A).}$ ${\displaystyle \,\sup \,}$ ${\displaystyle X}$ ${\displaystyle Y,}$

В теории категорий функтор

$${\displaystyle F:{\mathcal {C}}\to {\mathcal {D}}}$$

категорияминепрерывным,пределами

$${\displaystyle \varprojlim _{i\in I}F(C_{i})\cong F\left(\varprojlim _{i\in I}C_{i}\right)}$$

аклассомдиаграммы ${\displaystyle I,}$ ${\displaystyle {\mathcal {C}}}$

Пространство непрерывности — это обобщение метрических пространств и частично упорядоченных множеств ^{[21] , [22]} , в котором используется концепция кванталов и которое можно использовать для унификации понятий метрических пространств и областей . ^[23]

Смотрите также

• Непрерывность (математика)
• Абсолютная непрерывность
• Преемственность Дини
• Равнонепрерывность
• Геометрическая непрерывность
• Параметрическая непрерывность
• Классификация несплошностей
• Грубая функция
• Непрерывная функция (теория множеств)
• Непрерывный случайный процесс
• Нормальная функция
• Открытые и закрытые карты
• Кусочно
• Симметрично непрерывная функция

• Функция сохранения направления — аналог непрерывной функции в дискретных пространствах.

Рекомендации

1. Больцано, Бернар (1817). «Rein analytischer Beweis des Lehrsatzes daß zwischen je zwey Werthen, die ein entgegengesetzetes Resultat gewähren, wenigstens eine reelle Wurzel der Gleichung Liege». Прага: Хаазе.
2. Дугак, Пьер (1973), «Элементы анализа Карла Вейерштрасса», Архив истории точных наук , 10 (1–2): 41–176, doi : 10.1007/bf00343406, S2CID  122843140
3. Гурса, Э. (1904), Курс математического анализа , Бостон: Джинн, с. 2
4. Джордан, MC (1893), Cours d'analyse de l'École Polytechnique, vol. 1 (2-е изд.), Париж: Готье-Виллар, с. 46
5. Харпер, Дж. Ф. (2016), «Определение непрерывности действительных функций действительных переменных», Бюллетень BSHM: Журнал Британского общества истории математики , 31 (3): 1–16, doi : 10.1080/17498430.2015.1116053, S2CID  123997123
6. Руснок, П.; Керр-Лоусон, А. (2005), «Больцано и равномерная непрерывность», Historia Mathematica , 32 (3): 303–311, doi : 10.1016/j.hm.2004.11.003
7. Стрэнг, Гилберт (1991). Исчисление. СИАМ. п. 702. ИСБН 0961408820.
8. Спек, Джаред (2014). «Непрерывность и прерывистость» (PDF) . Массачусетский технологический институт Математика . п. 3. Архивировано из оригинала (PDF) 6 октября 2016 г. Проверено 2 сентября 2016 г. Пример 5. Функция непрерывна на и на , т. е. при и иными словами, в каждой точке своей области определения. Однако это не непрерывная функция, поскольку ее область определения не является интервалом. Он имеет единственную точку разрыва, а именно , и бесконечный разрыв там. ${\displaystyle 1/x}$ ${\displaystyle (0,\infty )}$ ${\displaystyle (-\infty ,0),}$ ${\displaystyle x>0}$ ${\displaystyle x<0,}$ ${\displaystyle x=0,}$
9. Ланг, Серж (1997), Анализ бакалавриата , Тексты для бакалавров по математике (2-е изд.), Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-0-387-94841-6, раздел II.4
10. Введение в реальный анализ, обновлено в апреле 2010 г., Уильям Ф. Тренч, теорема 3.5.2, стр. 172
11. Введение в реальный анализ, обновлено в апреле 2010 г., Уильям Ф. Тренч, 3.5 «Более продвинутый взгляд на существование правильного интеграла Римана», стр. 171–177.
12. «Элементарное исчисление». Wisc.edu .
13. Браун, Джеймс Уорд (2009), Комплексные переменные и приложения (8-е изд.), McGraw Hill, стр. 54, ISBN 978-0-07-305194-9
14. Гаал, Стивен А. (2009), Топология множества точек , Нью-Йорк: Dover Publications , ISBN 978-0-486-47222-5, раздел IV.10
15. Searcoid, Mícheál Ó (2006), Метрические пространства, серия Springer по математике для студентов, Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-1-84628-369-7, раздел 9.4
16. Дугунджи 1966, стр. 211–221.
17. Шурман, Джерри (2016). Исчисление и анализ в евклидовом пространстве (иллюстрированное издание). Спрингер. стр. 271–272. ISBN 978-3-319-49314-5.
18. «общая топология - непрерывность и интерьер». Математический обмен стеками .
19. Губо-Ларрек, Жан (2013). Нехаусдорфова топология и теория предметной области: избранные темы топологии множества точек . Издательство Кембриджского университета . ISBN 978-1107034136.
20. Гирц, Г.; Хофманн, К.Х.; Кеймель, К.; Лоусон, доктор юридических наук; Мислов, М.В.; Скотт, DS (2003). Непрерывные решетки и области . Энциклопедия математики и ее приложений. Том. 93. Издательство Кембриджского университета. ISBN 0521803381.
21. Флэгг, RC (1997). «Кванталы и пространства непрерывности». Алгебра Универсалис . 37 (3): 257–276. CiteSeerX 10.1.1.48.851 . дои : 10.1007/s000120050018. S2CID  17603865. 
22. Копперман, Р. (1988). «Все топологии основаны на обобщенных метриках». Американский математический ежемесячник . 95 (2): 89–97. дои : 10.2307/2323060. JSTOR  2323060.
23. Флэгг, Б.; Копперман, Р. (1997). «Пространства непрерывности: согласование областей и метрических пространств». Теоретическая информатика . 177 (1): 111–138. дои : 10.1016/S0304-3975(97)00236-3 .

Библиография

• Дугунджи, Джеймс (1966). Топология . Бостон: Аллин и Бэкон. ISBN 978-0-697-06889-7. ОСЛК  395340485.
• «Непрерывная функция», Математическая энциклопедия , EMS Press , 2001 [1994]