stringtranslate.com

Популяционная генетика

Популяционная генетика — это подраздел генетики , который занимается генетическими различиями внутри и между популяциями , и является частью эволюционной биологии . Исследования в этой отрасли биологии изучают такие явления, как адаптация , видообразование и структура популяции . [1]

Генетика популяций была жизненно важным компонентом в появлении современного эволюционного синтеза . Ее основными основателями были Сьюэлл Райт , Дж. Б. С. Холдейн и Рональд Фишер , которые также заложили основы для смежной дисциплины количественной генетики . Традиционно высоко математическая дисциплина, современная популяционная генетика охватывает теоретические, лабораторные и полевые работы. Генетические модели популяций используются как для статистического вывода из данных о последовательностях ДНК, так и для доказательства/опровержения концепции. [2]

Что отличает популяционную генетику от более новых, более фенотипических подходов к моделированию эволюции, таких как эволюционная теория игр и адаптивная динамика , так это ее акцент на таких генетических явлениях, как доминирование , эпистаз , степень, в которой генетическая рекомбинация нарушает неравновесие сцепления , и случайные явления мутации и генетического дрейфа . Это делает ее пригодной для сравнения с данными по популяционной геномике .

История

Популяционная генетика началась как примирение менделевской наследственности и моделей биостатистики . Естественный отбор вызовет эволюцию только в том случае, если в популяции достаточно генетической изменчивости . До открытия менделевской генетики одной из распространенных гипотез была смешанная наследственность . Но при смешанной наследственности генетическая изменчивость быстро теряется, делая эволюцию путем естественного или полового отбора неправдоподобной. Принцип Харди-Вайнберга дает решение того, как изменчивость поддерживается в популяции с менделевской наследственностью. Согласно этому принципу, частоты аллелей (изменений в гене) будут оставаться постоянными при отсутствии отбора, мутации, миграции и генетического дрейфа. [3]

Следующим ключевым шагом стала работа британского биолога и статистика Рональда Фишера . В серии статей, начавшейся в 1918 году и завершившейся в 1930 году книгой «Генетическая теория естественного отбора» , Фишер показал, что непрерывное изменение, измеряемое биометристами, может быть получено совместным действием многих дискретных генов, и что естественный отбор может изменять частоты аллелей в популяции, что приводит к эволюции. В серии статей, начавшейся в 1924 году, другой британский генетик, Дж. Б. С. Холдейн , разработал математику изменения частоты аллелей в одном локусе гена в широком диапазоне условий. Холдейн также применил статистический анализ к реальным примерам естественного отбора, таким как эволюция березовой пяденицы и промышленный меланизм , и показал, что коэффициенты отбора могут быть больше, чем предполагал Фишер, что приводит к более быстрой адаптивной эволюции в качестве стратегии маскировки после возросшего загрязнения. [4] [5]

Американский биолог Сьюэлл Райт , имевший опыт в экспериментах по разведению животных , сосредоточился на комбинациях взаимодействующих генов и эффектах инбридинга на небольших, относительно изолированных популяциях, которые демонстрировали генетический дрейф. В 1932 году Райт ввел концепцию адаптивного ландшафта и утверждал, что генетический дрейф и инбридинг могут увести небольшую изолированную субпопуляцию от адаптивного пика, позволяя естественному отбору вести ее к другим адаптивным пикам. [ необходима цитата ]

Работа Фишера, Холдейна и Райта основала дисциплину популяционной генетики. Она объединила естественный отбор с менделевской генетикой, что стало первым важным шагом в разработке единой теории того, как работает эволюция. [4] [5] Джон Мейнард Смит был учеником Холдейна, в то время как У. Д. Гамильтон находился под влиянием трудов Фишера. Американец Джордж Р. Прайс работал и с Гамильтоном, и с Мейнардом Смитом. Американец Ричард Левонтин и японец Мотоо Кимура находились под влиянием Райта и Холдейна. [ необходима ссылка ]

Современный синтез

Математика популяционной генетики изначально была разработана как начало современного синтеза . Такие авторы, как Битти [6], утверждали, что популяционная генетика определяет ядро ​​современного синтеза. В течение первых нескольких десятилетий 20-го века большинство полевых натуралистов продолжали верить, что ламаркизм и ортогенез давали лучшее объяснение сложности, которую они наблюдали в живом мире. [7] В ходе современного синтеза эти идеи были очищены, и были сохранены только эволюционные причины, которые могли быть выражены в математической структуре популяционной генетики. [8] Был достигнут консенсус относительно того, какие эволюционные факторы могут влиять на эволюцию, но не относительно относительной важности различных факторов. [8]

Феодосий Добжанский , постдокторант в лаборатории TH Morgan , находился под влиянием работы по генетическому разнообразию русских генетиков, таких как Сергей Четвериков . Он помог преодолеть разрыв между основами микроэволюции, разработанными популяционными генетиками, и закономерностями макроэволюции, наблюдаемыми полевыми биологами, в своей книге 1937 года «Генетика и происхождение видов» . Добжанский исследовал генетическое разнообразие диких популяций и показал, что, вопреки предположениям популяционных генетиков, эти популяции имели большое количество генетического разнообразия с заметными различиями между субпопуляциями. Книга также взяла высокоматематическую работу популяционных генетиков и поместила ее в более доступную форму. Гораздо больше биологов были под влиянием популяционной генетики через Добжанского, чем смогли прочитать высокоматематические работы в оригинале. [9]

В Великобритании Э. Б. Форд , пионер экологической генетики , [10] продолжал в течение 1930-х и 1940-х годов эмпирически демонстрировать силу отбора, обусловленного экологическими факторами, включая способность поддерживать генетическое разнообразие посредством генетических полиморфизмов, таких как группы крови человека . Работа Форда, в сотрудничестве с Фишером, способствовала смещению акцента в ходе современного синтеза в сторону естественного отбора как доминирующей силы. [4] [5] [11] [12]

Нейтральная теория и динамика фиксации происхождения

Первоначальный, современный синтетический взгляд на популяционную генетику предполагает, что мутации обеспечивают обильный исходный материал, и фокусируется только на изменении частоты аллелей в популяциях . [13] Основными процессами, влияющими на частоты аллелей, являются естественный отбор , генетический дрейф , поток генов и повторяющиеся мутации . У Фишера и Райта были некоторые фундаментальные разногласия относительно относительной роли отбора и дрейфа. [14] Наличие молекулярных данных по всем генетическим различиям привело к нейтральной теории молекулярной эволюции . С этой точки зрения многие мутации вредны и поэтому никогда не наблюдаются, а большинство остальных нейтральны, т. е. не находятся под отбором. Поскольку судьба каждой нейтральной мутации оставлена ​​на волю случая (генетический дрейф), направление эволюционных изменений определяется тем, какие мутации происходят, и поэтому не может быть отражено только моделями изменения частоты (существующих) аллелей. [13] [15]

Точка зрения популяционной генетики на фиксацию происхождения обобщает этот подход за пределы строго нейтральных мутаций и рассматривает скорость, с которой происходит конкретное изменение, как произведение скорости мутации и вероятности фиксации . [13]

Четыре процесса

Выбор

Естественный отбор , включающий половой отбор , заключается в том, что некоторые черты повышают вероятность выживания и размножения организма . Популяционная генетика описывает естественный отбор, определяя приспособленность как склонность или вероятность выживания и размножения в определенной среде. Приспособленность обычно задается символом w =1- s, где s — коэффициент отбора . Естественный отбор действует на фенотипы , поэтому популяционно-генетические модели предполагают относительно простые отношения для предсказания фенотипа и, следовательно, приспособленности из аллеля в одном или небольшом количестве локусов. Таким образом, естественный отбор преобразует различия в приспособленности особей с разными фенотипами в изменения частоты аллелей в популяции на протяжении последовательных поколений. [ необходима ссылка ]

До появления популяционной генетики многие биологи сомневались, что небольшие различия в приспособленности достаточны для того, чтобы иметь большое значение для эволюции. [9] Популяционные генетики частично рассмотрели эту проблему, сравнив отбор с генетическим дрейфом . Отбор может преодолеть генетический дрейф, когда s больше 1, деленного на эффективный размер популяции . Когда этот критерий выполняется, вероятность того, что новый выгодный мутант закрепится, приблизительно равна 2s . [16] [17] Время до фиксации такого аллеля составляет приблизительно . [18]

Доминирование

Доминирование означает, что фенотипический и/или фитнес-эффект одного аллеля в локусе зависит от того, какой аллель присутствует во второй копии для этого локуса. Рассмотрим три генотипа в одном локусе со следующими значениями фитнеса [19]

s — коэффициент отбора , h — коэффициент доминирования. Значение h дает следующую информацию:

Эпистаз

Логарифм приспособленности как функция числа вредных мутаций. Синергетический эпистаз представлен красной линией — каждая последующая вредная мутация оказывает большее пропорциональное влияние на приспособленность организма. Антагонистический эпистаз показан синим цветом. Черная линия показывает неэпистатический случай, где приспособленность является произведением вкладов каждого из его локусов .

Эпистаз означает, что фенотипический и/или фитнес-эффект аллеля в одном локусе зависит от того, какие аллели присутствуют в других локусах. Отбор не действует на один локус, а на фенотип, который возникает в результате развития из полного генотипа. [20] Однако многие модели популяционной генетики половых видов являются моделями «одного локуса», где фитнес особи рассчитывается как произведение вкладов каждого из ее локусов — фактически предполагая отсутствие эпистаза.

На самом деле, ландшафт генотипа к приспособленности более сложен. Популяционная генетика должна либо детально смоделировать эту сложность, либо охватить ее каким-то более простым правилом среднего. Эмпирически, полезные мутации, как правило, имеют меньший выигрыш в приспособленности, когда добавляются к генетическому фону, который уже имеет высокую приспособленность: это известно как убывающая отдача эпистаза. [21] Когда вредные мутации также имеют меньший эффект приспособленности на фоне высокой приспособленности, это известно как «синергетический эпистаз». Однако эффект вредных мутаций, как правило, в среднем очень близок к мультипликативному или даже может показывать противоположную картину, известную как «антагонистический эпистаз». [22]

Синергетический эпистаз занимает центральное место в некоторых теориях очищения от мутационной нагрузки [23] и в эволюции полового размножения .

Мутация

Дрозофила меланогастер

Генетический процесс мутации происходит внутри индивидуума, приводя к наследуемым изменениям генетического материала. Этот процесс часто характеризуется описанием начальных и конечных состояний или вида изменения, которое произошло на уровне ДНК (например, мутация T-to-C, делеция 1-bp), генов или белков (например, нулевая мутация, мутация потери функции) или на более высоком фенотипическом уровне (например, мутация красных глаз). Изменения одного нуклеотида часто являются наиболее распространенным типом мутации, но возможны и многие другие типы мутаций , и они происходят с сильно различающимися скоростями, которые могут показывать систематические асимметрии или смещения ( смещение мутации ).

Мутации могут включать в себя большие участки ДНК, которые становятся дублированными , обычно посредством генетической рекомбинации . [24] Это приводит к изменению числа копий в популяции. Дупликации являются основным источником сырья для развития новых генов. [25] Другие типы мутаций иногда создают новые гены из ранее некодирующей ДНК. [26] [27]

В распределении эффектов приспособленности (DFE) для новых мутаций только меньшинство мутаций являются полезными. Мутации с грубыми эффектами обычно вредны. Исследования на мухе Drosophila melanogaster показывают, что если мутация изменяет белок, производимый геном, это, вероятно, будет вредным, причем около 70 процентов этих мутаций имеют разрушительные эффекты, а остальные либо нейтральны, либо слабо полезны. [28]

Этот биологический процесс мутации представлен в популяционно-генетических моделях одним из двух способов: либо как детерминированное давление повторяющейся мутации на частоты аллелей, либо как источник вариации. В детерминированной теории эволюция начинается с предопределенного набора аллелей и продолжается сдвигами в непрерывных частотах, как будто популяция бесконечна. Возникновение мутаций у особей представлено «силой» или «давлением» мутации на уровне популяции, т. е. силой бесчисленных событий мутации с масштабированной величиной u, применяемой к сдвигу частот f(A1) до f(A2). Например, в классической модели баланса мутации и отбора [29] сила давления мутации повышает частоту аллеля, а отбор против его пагубных эффектов снижает частоту, так что баланс достигается в равновесии, заданном (в простейшем случае) как f = u/s.

Эта концепция мутационного давления в основном полезна для рассмотрения последствий вредных мутаций, таких как нагрузка мутаций и ее последствия для эволюции скорости мутаций. [30] Трансформация популяций под действием мутационного давления маловероятна. Холдейн [31]  утверждал, что для этого потребуются высокие скорости мутаций, не встречающие сопротивления со стороны отбора, а Кимура [32] пришел к еще более пессимистическому выводу, что даже это маловероятно, поскольку процесс займет слишком много времени (см. эволюция под действием мутационного давления ).

Однако эволюция под давлением мутаций возможна при некоторых обстоятельствах и уже давно предлагается в качестве возможной причины потери неиспользуемых признаков. [33] Например, пигменты больше не полезны, когда животные живут в темноте пещер, и имеют тенденцию к потере. [34] Экспериментальный пример включает потерю споруляции в экспериментальных популяциях B. subtilis . Спороуляция является сложным признаком, кодируемым многими локусами, так что скорость мутации для потери признака была оценена как необычно высокое значение, . [35] Потеря споруляции в этом случае может произойти из-за повторяющейся мутации, не требуя отбора на потерю способности к споруляции. Когда нет отбора на потерю функции, скорость, с которой развивается потеря, больше зависит от скорости мутации, чем от эффективного размера популяции , [36] указывая на то, что она больше обусловлена ​​мутацией, чем генетическим дрейфом.

Роль мутации как источника новизны отличается от этих классических моделей давления мутаций. Когда популяционно-генетические модели включают зависящий от скорости процесс мутационного введения или возникновения, т. е. процесс, который вводит новые аллели, включая нейтральные и полезные, тогда свойства мутации могут иметь более прямое влияние на скорость и направление эволюции, даже если скорость мутации очень низкая. [37] [38] То есть, спектр мутаций может стать очень важным, в частности мутационные смещения , предсказуемые различия в скоростях возникновения для разных типов мутаций, поскольку смещение при введении вариации может накладывать смещения на ход эволюции. [39]

Мутация играет ключевую роль в других классических и современных теориях, включая храповой механизм Мюллера , субфункционализацию , концепцию Эйгена о катастрофической ошибке и гипотезу мутационной опасности Линча .

Генетический дрейф

Генетический дрейф — это изменение частот аллелей , вызванное случайной выборкой . [40] То есть, аллели у потомства являются случайной выборкой аллелей у родителей. [41] Генетический дрейф может привести к полному исчезновению вариантов генов и, таким образом, снижению генетической изменчивости. В отличие от естественного отбора, который делает варианты генов более распространенными или менее распространенными в зависимости от их репродуктивного успеха, [42] изменения, вызванные генетическим дрейфом, не вызваны давлением окружающей среды или адаптивными факторами и с одинаковой вероятностью могут сделать аллель более распространенным или менее распространенным.

Эффект генетического дрейфа больше для аллелей, присутствующих в нескольких копиях, чем когда аллель присутствует во многих копиях. Популяционная генетика генетического дрейфа описывается с использованием либо процессов ветвления , либо уравнения диффузии, описывающего изменения частоты аллелей. [43] Эти подходы обычно применяются к моделям популяционной генетики Райта-Фишера и Морана . Предполагая, что генетический дрейф является единственной эволюционной силой, действующей на аллель, после t поколений во многих реплицированных популяциях, начиная с частот аллелей p и q, дисперсия частоты аллелей в этих популяциях равна

[44]

Рональд Фишер придерживался мнения, что генетический дрейф играет в лучшем случае незначительную роль в эволюции, и это мнение оставалось доминирующим в течение нескольких десятилетий. Ни одна из точек зрения популяционной генетики никогда не отводила генетическому дрейфу центральную роль как таковому, но некоторые считали генетический дрейф важным в сочетании с другой неселективной силой. Теория смещающегося баланса Сьюэлла Райта утверждала, что сочетание структуры популяции и генетического дрейфа было важным. Нейтральная теория молекулярной эволюции Мотоо Кимуры утверждает, что большинство генетических различий внутри и между популяциями вызваны сочетанием нейтральных мутаций и генетического дрейфа. [45]

Роль генетического дрейфа посредством ошибки выборки в эволюции критиковалась Джоном Х. Гиллеспи [46] и Уиллом Провайном [47], которые утверждают, что отбор на связанных участках является более важной стохастической силой, выполняющей работу, традиционно приписываемую генетическому дрейфу посредством ошибки выборки. Математические свойства генетического проекта отличаются от свойств генетического дрейфа. [48] Направление случайного изменения частоты аллелей автокоррелируется между поколениями. [40]

Поток генов

Поток генов — это перенос аллелей из одной популяции в другую посредством иммиграции особей. В этом примере одна из птиц из популяции A иммигрирует в популяцию B, которая имеет меньше доминирующих аллелей, и посредством спаривания включает свои аллели в другую популяцию.

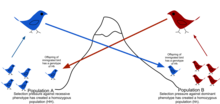
Из-за физических барьеров для миграции, а также ограниченной тенденции особей к перемещению или распространению (неустойчивость) и тенденции оставаться или возвращаться в место рождения ( филопатрия ), естественные популяции редко все скрещиваются, как можно предположить в теоретических случайных моделях ( панмиксия ). [49] Обычно существует географический диапазон, в пределах которого особи более тесно связаны друг с другом, чем те, которые были случайно выбраны из общей популяции. Это описывается как степень, в которой популяция генетически структурирована. [50]

Великая Китайская стена является препятствием для потока генов некоторых наземных видов. [51]

Генетическая структуризация может быть вызвана миграцией из-за исторического изменения климата , расширения ареала видов или текущей доступности среды обитания . Поток генов затрудняется горными хребтами, океанами и пустынями или даже искусственными сооружениями, такими как Великая Китайская стена , которая препятствовала потоку генов растений. [51]

Поток генов — это обмен генами между популяциями или видами, разрушающий структуру. Примерами потока генов внутри вида являются миграция и последующее размножение организмов или обмен пыльцой . Перенос генов между видами включает образование гибридных организмов и горизонтальный перенос генов . Популяционно-генетические модели могут использоваться для определения того, какие популяции демонстрируют значительную генетическую изоляцию друг от друга, и для реконструкции их истории. [52]

Изоляция популяции приводит к инбридинговой депрессии . Миграция в популяцию может привнести новые генетические варианты, [53] потенциально способствуя эволюционному спасению . Если значительная часть особей или гамет мигрирует, это также может изменить частоты аллелей, например, вызывая миграционную нагрузку . [54]

При наличии потока генов для того, чтобы популяции стали новыми видами, необходимы другие барьеры для гибридизации между двумя расходящимися популяциями скрещивающегося вида .

Горизонтальный перенос генов

Текущее древо жизни, показывающее вертикальный и горизонтальный перенос генов

Горизонтальный перенос генов — это перенос генетического материала от одного организма к другому, который не является его потомком; это наиболее распространено среди прокариот . [55] В медицине это способствует распространению устойчивости к антибиотикам , поскольку когда одна бактерия приобретает гены устойчивости, она может быстро передавать их другим видам. [56] Горизонтальный перенос генов от бактерий к эукариотам, таким как дрожжи Saccharomyces cerevisiae и фасолевая жужелица Callosobruchus chinensis, также мог иметь место. [57] [58] Примером крупномасштабных переносов являются эукариотические бделлоидные коловратки , которые, по-видимому, получили ряд генов от бактерий, грибов и растений. [59] Вирусы также могут переносить ДНК между организмами, что позволяет переносить гены даже между биологическими доменами . [60] Крупномасштабный перенос генов также произошел между предками эукариотических клеток и прокариот во время приобретения хлоропластов и митохондрий . [61]

Связь

Если все гены находятся в равновесии сцепления , эффект аллеля в одном локусе может быть усреднен по всему генофонду в других локусах. В действительности, один аллель часто находится в неравновесии сцепления с генами в других локусах, особенно с генами, расположенными поблизости на той же хромосоме. Рекомбинация разрушает это неравновесие сцепления слишком медленно, чтобы избежать генетического автостопа , когда аллель в одном локусе повышается до высокой частоты, потому что он связан с аллелем, находящимся под отбором в соседнем локусе. Сцепление также замедляет скорость адаптации, даже в половых популяциях. [62] [63] [64] Эффект неравновесия сцепления в замедлении скорости адаптивной эволюции возникает из-за комбинации эффекта Хилла-Робертсона (задержки в объединении полезных мутаций) и фонового отбора (задержки в отделении полезных мутаций от вредных автостопщиков ).

Сцепление является проблемой для популяционных генетических моделей, которые обрабатывают один локус гена за раз. Однако его можно использовать как метод обнаружения действия естественного отбора посредством выборочных зачисток .

В крайнем случае бесполой популяции сцепление является полным, и уравнения популяционной генетики могут быть выведены и решены в терминах бегущей волны частот генотипов вдоль простого ландшафта приспособленности . [65] Большинство микробов , таких как бактерии , являются бесполыми. Популяционная генетика их адаптации имеет два контрастных режима. Когда произведение полезной скорости мутации и размера популяции невелико, бесполые популяции следуют «последовательному режиму» динамики фиксации происхождения, причем скорость адаптации сильно зависит от этого продукта. Когда продукт намного больше, бесполые популяции следуют режиму «конкурентных мутаций», причем скорость адаптации в меньшей степени зависит от продукта, характеризующемуся клональной интерференцией и появлением новой полезной мутации до того, как зафиксируется предыдущая .

Приложения

Объяснение уровней генетической изменчивости

Нейтральная теория предсказывает, что уровень нуклеотидного разнообразия в популяции будет пропорционален произведению размера популяции и нейтральной скорости мутации. Тот факт, что уровни генетического разнообразия варьируются гораздо меньше, чем размеры популяции, известен как «парадокс вариации». [66] Хотя высокие уровни генетического разнообразия были одним из первоначальных аргументов в пользу нейтральной теории, парадокс вариации был одним из самых сильных аргументов против нейтральной теории.

Очевидно, что уровни генетического разнообразия значительно различаются в пределах вида в зависимости от локальной скорости рекомбинации, как из-за генетического автостопа , так и фонового отбора . Большинство современных решений парадокса вариации предполагают некоторый уровень отбора на связанных участках. [67] Например, один анализ предполагает, что более крупные популяции имеют более селективные зачистки, которые удаляют больше нейтрального генетического разнообразия. [68] Отрицательная корреляция между скоростью мутаций и размером популяции также может способствовать этому. [69]

История жизни влияет на генетическое разнообразие больше, чем история популяции, например, у r-стратегов генетическое разнообразие больше. [67]

Обнаружение выбора

Модели популяционной генетики используются для вывода о том, какие гены подвергаются отбору. Один из распространенных подходов заключается в поиске областей с высоким неравновесием сцепления и низкой генетической дисперсией вдоль хромосомы, чтобы обнаружить недавние селективные зачистки .

Вторым распространенным подходом является тест Макдональда-Крейтмана , который сравнивает количество вариаций внутри вида ( полиморфизм ) с расхождением между видами (замены) в двух типах сайтов; один из них предполагается нейтральным. Обычно синонимичные сайты считаются нейтральными. [70] Гены, подвергающиеся положительному отбору, имеют избыток расходящихся сайтов по сравнению с полиморфными сайтами. Тест также можно использовать для получения общегеномной оценки доли замен, которые фиксируются положительным отбором, α. [71] [72] Согласно нейтральной теории молекулярной эволюции , это число должно быть близко к нулю. Поэтому высокие числа были интерпретированы как общегеномная фальсификация нейтральной теории. [73]

Демографический вывод

Самый простой тест на структуру популяции у диплоидных видов, размножающихся половым путем, заключается в том, чтобы посмотреть, следуют ли частоты генотипов пропорциям Харди-Вайнберга как функции частот аллелей. Например, в простейшем случае одного локуса с двумя аллелями , обозначенными A и a с частотами p и q , случайное спаривание предсказывает freq( AA ) =  p 2 для гомозигот AA , freq( aa ) =  q 2 для гомозигот aa и freq( Aa ) = 2 pq для гетерозигот . При отсутствии структуры популяции пропорции Харди-Вайнберга достигаются в течение 1–2 поколений случайного спаривания. Чаще всего наблюдается избыток гомозигот, что указывает на структуру популяции. Степень этого избытка можно количественно оценить как коэффициент инбридинга, F .

Индивидуумы могут быть сгруппированы в K субпопуляции. [74] [75] Степень структуры популяции затем может быть рассчитана с использованием F ST , который является мерой доли генетической дисперсии, которая может быть объяснена структурой популяции. Генетическая структура популяции затем может быть связана с географической структурой, и может быть обнаружена генетическая примесь .

Коалесцентная теория связывает генетическое разнообразие в образце с демографической историей популяции, из которой он был взят. Обычно она предполагает нейтральность , и поэтому для таких анализов выбираются последовательности из более нейтрально развивающихся частей геномов. Ее можно использовать для вывода взаимосвязей между видами ( филогенетика ), а также структуры популяции, демографической истории (например, узкие места популяции , рост популяции ), биологического рассеивания , динамики источника-стока [76] и интрогрессии внутри вида.

Другой подход к демографическим выводам основан на спектре частот аллелей . [77]

Эволюция генетических систем

Предполагая, что существуют локусы, которые контролируют саму генетическую систему, создаются популяционно-генетические модели для описания эволюции доминирования и других форм устойчивости , эволюции полового размножения и скорости рекомбинации, эволюции скорости мутаций , эволюции эволюционных конденсаторов , эволюции дорогостоящих сигнальных признаков , эволюции старения и эволюции кооперации . Например, большинство мутаций вредны, поэтому оптимальная скорость мутаций для вида может быть компромиссом между ущербом от высокой скорости вредных мутаций и метаболическими затратами на поддержание систем для снижения скорости мутаций, таких как ферменты репарации ДНК. [78]

Одним из важных аспектов таких моделей является то, что отбор достаточно силен, чтобы удалить вредные мутации и, следовательно, пересилить мутационный уклон в сторону деградации, только если коэффициент отбора s больше, чем обратная величина эффективного размера популяции . Это известно как барьер дрейфа и связано с почти нейтральной теорией молекулярной эволюции . Теория барьера дрейфа предсказывает, что виды с большими эффективными размерами популяции будут иметь высокоорганизованные, эффективные генетические системы, в то время как виды с малыми размерами популяции будут иметь раздутые и сложные геномы, содержащие, например, интроны и транспонируемые элементы . [79] Однако, как это ни парадоксально, виды с большими размерами популяции могут быть настолько терпимы к последствиям определенных типов ошибок, что они развивают более высокие показатели ошибок, например, в транскрипции и трансляции , чем небольшие популяции. [80]

Смотрите также

Ссылки

  1. ^ "Популяционная генетика - Последние исследования и новости". www.nature.com . Получено 29.01.2018 .
  2. ^ Servedio, Maria R. ; Brandvain, Yaniv; Dhole, Sumit; Fitzpatrick, Courtney L.; Goldberg, Emma E.; Stern, Caitlin A.; Van Cleve, Jeremy; Yeh, D. Justin (9 декабря 2014 г.). «Не просто теория — полезность математических моделей в эволюционной биологии». PLOS Biology . 12 (12): e1002017. doi : 10.1371/journal.pbio.1002017 . PMC 4260780 . PMID  25489940. 
  3. ^ Эвенс, У. Дж. (2004). Математическая популяционная генетика (2-е изд.). Нью-Йорк: Springer. ISBN 978-0-387-20191-7.
  4. ^ abc Bowler, Peter J. (2003). Эволюция: история идеи (3-е изд.). Беркли: Издательство Калифорнийского университета. С. 325–339. ISBN 978-0-520-23693-6.
  5. ^ abc Larson, Edward J. (2004). Эволюция: замечательная история научной теории (ред. Modern Library). Нью-Йорк: Modern Library. стр. 221–243. ISBN 978-0-679-64288-6.
  6. ^ Битти, Джон (1986). «Синтез и синтетическая теория». Интеграция научных дисциплин . Наука и философия. Том 2. Springer Netherlands. С. 125–135. doi :10.1007/978-94-010-9435-1_7. ISBN 9789024733422.
  7. ^ Mayr, Ernst ; Provine, William B., ред. (1998). Эволюционный синтез: перспективы объединения биологии ([New ed]. ред.). Кембридж, Массачусетс: Harvard University Press. стр. 295–298. ISBN 9780674272262.
  8. ^ ab Provine, WB (1988). «Прогресс в эволюции и смысл жизни». Эволюционный прогресс . Издательство Чикагского университета. С. 49–79.
  9. ^ ab Provine, William B. (1978). «Роль математических популяционных генетиков в эволюционном синтезе 1930-х и 1940-х годов». Исследования по истории биологии . 2 : 167–192. PMID  11610409.
  10. ^ Форд, ЭБ (1975) [1964]. Экологическая генетика (4-е изд.). Лондон: Chapman and Hall. С. 1 и далее.
  11. ^ Майр, Эрнст (1988). К новой философии биологии: наблюдения эволюциониста . Кембридж, Массачусетс: Belknap Press of Harvard University Press . стр. 402. ISBN 978-0-674-89665-9.
  12. ^ Mayr, Ernst ; Provine, William B., ред. (1998). Эволюционный синтез: перспективы объединения биологии ([New ed]. ред.). Кембридж, Массачусетс: Harvard University Press. стр. 338–341. ISBN 9780674272262.
  13. ^ abc McCandlish, David M.; Stoltzfus, Arlin (сентябрь 2014 г.). «Моделирование эволюции с использованием вероятности фиксации: история и последствия». The Quarterly Review of Biology . 89 (3): 225–252. doi :10.1086/677571. PMID  25195318. S2CID  19619966.
  14. ^ Кроу, Джеймс Ф. (2010). «Райт и Фишер об инбридинге и случайном дрейфе». Генетика . 184 (3): 609–611. doi : 10.1534/genetics.109.110023 . ISSN  0016-6731. PMC 2845331. PMID 20332416  . 
  15. ^ Касильяс, Соня; Барбадилья, Антонио (2017). «Молекулярная популяционная генетика». Генетика . 205 (3): 1003–1035. doi : 10.1534/genetics.116.196493. ПМК 5340319 . ПМИД  28270526. 
  16. ^ Холдейн, Дж. Б. С. (1927). «Математическая теория естественного и искусственного отбора, часть V: отбор и мутация». Математические труды Кембриджского философского общества . 23 (7): 838–844. Bibcode :1927PCPS...23..838H. doi :10.1017/S0305004100015644. S2CID  86716613.
  17. ^ Орр, HA (2010). «Популяционная генетика полезных мутаций». Philosophical Transactions of the Royal Society B: Biological Sciences . 365 (1544): 1195–1201. doi :10.1098/rstb.2009.0282. PMC 2871816. PMID  20308094 . 
  18. ^ Hermisson, J.; Pennings, PS (2005). «Мягкие развертки: молекулярная популяционная генетика адаптации из постоянных генетических вариаций». Genetics . 169 (4): 2335–2352. doi :10.1534/genetics.104.036947. PMC 1449620 . PMID  15716498. 
  19. ^ Джиллеспи, Джон (2004). Генетика популяций: краткое руководство (2-е изд.). Издательство Университета Джонса Хопкинса. ISBN 978-0-8018-8008-7.
  20. ^ Мико, И. (2008). "Эпистаз: взаимодействие генов и эффекты фенотипа". Nature Education . 1 (1): 197.
  21. ^ Бергер, Д.; Постма, Э. (13 октября 2014 г.). «Смещенные оценки эпистаза убывающей отдачи? Пересмотр эмпирических доказательств». Генетика . 198 (4): 1417–1420. doi :10.1534/genetics.114.169870. PMC 4256761. PMID  25313131 . 
  22. ^ Kouyos, Roger D.; Silander, Olin K.; Bonhoeffer, Sebastian (июнь 2007 г.). «Эпистаз между вредными мутациями и эволюцией рекомбинации». Trends in Ecology & Evolution . 22 (6): 308–315. Bibcode : 2007TEcoE..22..308K. doi : 10.1016/j.tree.2007.02.014. PMID  17337087.
  23. ^ Кроу, Дж. Ф. (5 августа 1997 г.). «Высокая скорость спонтанных мутаций: представляет ли она риск для здоровья?». Труды Национальной академии наук Соединенных Штатов Америки . 94 (16): 8380–8386. Bibcode : 1997PNAS...94.8380C. doi : 10.1073 /pnas.94.16.8380 . PMC 33757. PMID  9237985. 
  24. ^ Hastings, PJ; Lupski, JR; Rosenberg, SM; Ira, G. (2009). «Механизмы изменения числа копий генов». Nature Reviews Genetics . 10 (8): 551–564. doi :10.1038/nrg2593. PMC 2864001. PMID  19597530 . 
  25. ^ M., Long; Betrán, E.; Thornton, K.; Wang, W. (ноябрь 2003 г.). «Происхождение новых генов: взгляд из молодых и старых». Nat. Rev. Genet . 4 (11): 865–75. doi :10.1038/nrg1204. PMID  14634634. S2CID  33999892.
  26. ^ Лю, Н.; Окамура, К.; Тайлер, Д.М.; Филлипс; Чунг; Лай (2008). «Эволюция и функциональная диверсификация генов микроРНК животных». Cell Research . 18 (10): 985–996. doi :10.1038/cr.2008.278. PMC 2712117. PMID  18711447 . 
  27. ^ McLysaght, Aoife; Hurst, Laurence D. (25 июля 2016 г.). «Открытые вопросы в изучении генов de novo: что, как и почему». Nature Reviews Genetics . 17 (9): 567–578. doi :10.1038/nrg.2016.78. PMID  27452112. S2CID  6033249.
  28. ^ Sawyer, SA; Parsch, J.; Zhang, Z.; Hartl, DL (2007). «Распространенность положительного отбора среди почти нейтральных аминокислотных замен у Drosophila». Труды Национальной академии наук . 104 (16): 6504–6510. Bibcode : 2007PNAS..104.6504S. doi : 10.1073/pnas.0701572104 . ISSN  0027-8424. PMC 1871816. PMID 17409186  . 
  29. ^ Кроу, Джеймс Ф.; Кимура, Мотоо (1970). Введение в теорию популяционной генетики (ред. [Переиздание]). Нью-Джерси: Blackburn Press. ISBN 9781932846126.
  30. ^ Линч, Майкл (август 2010 г.). «Эволюция скорости мутаций». Trends in Genetics . 26 (8): 345–352. doi :10.1016/j.tig.2010.05.003. PMC 2910838. PMID 20594608  . 
  31. ^ JBS Haldane (1932). Причины эволюции . Longmans, Green and Co., Нью-Йорк.
  32. ^ М. Кимура (1980). «Среднее время до фиксации мутантного аллеля в конечной популяции под постоянным давлением мутаций: исследования аналитическими, численными и псевдовыборочными методами». Proc Natl Acad Sci USA . 77 (1): 522–526. Bibcode :1980PNAS...77..522K. doi : 10.1073/pnas.77.1.522 . PMC 348304 . PMID  16592764. 
  33. ^ Холдейн, Дж. Б. С. (1933). «Роль, которую играют повторяющиеся мутации в эволюции». American Naturalist . 67 (708): 5–19. doi :10.1086/280465. JSTOR  2457127. S2CID  84059440.
  34. ^ Протас, Мередит; Конрад, М.; Гросс, Дж. Б.; Табин, К.; Боровски, Р. (2007). «Регрессивная эволюция мексиканской пещерной тетра, Astyanax mexicanus». Current Biology . 17 (5): 452–454. Bibcode : 2007CBio...17..452P. doi : 10.1016/j.cub.2007.01.051. PMC 2570642. PMID  17306543. 
  35. ^ H. Maughan, J. Masel, CW Birky, Jr. и WL Nicholson (2007). «Роль накопления мутаций и отбора в потере споруляции в экспериментальных популяциях Bacillus subtilis». Genetics . 177 (2): 937–48. doi :10.1534/genetics.107.075663. PMC 2034656 . PMID  17720926. {{cite journal}}: CS1 maint: multiple names: authors list (link)
  36. ^ Masel, J. ; King, OD; Maughan, H. (2007). «Потеря адаптивной пластичности в течение длительных периодов экологического застоя». American Naturalist . 169 (1): 38–46. doi :10.1086/510212. PMC 1766558 . PMID  17206583. 
  37. ^ K. Gomez, J. Bertram и J. Masel (2020). «Смещение мутаций может формировать адаптацию в больших бесполых популяциях, испытывающих клональную интерференцию». Proc. R. Soc. B . 287 (1937): 20201503. doi :10.1098/rspb.2020.1503. PMC 7661309 . PMID  33081612. 
  38. ^ AV Cano, H. Rozhonova, A. Stoltzfus, DM McCandlish и JL Payne (2022-02-10). "Смещение мутаций формирует спектр адаптивных замен". Proc Natl Acad Sci USA . 119 (7). Bibcode : 2022PNAS..11919720C. doi : 10.1073/pnas.2119720119 . PMC 8851560. PMID  35145034 . {{cite journal}}: CS1 maint: multiple names: authors list (link)
  39. ^ Штольцфус, А.; Ямпольский, Л.Ю. (2009). «Восхождение на вероятную вершину: мутация как причина неслучайности в эволюции». Журнал наследственности . 100 (5): 637–647. doi : 10.1093/jhered/esp048 . PMID  19625453.
  40. ^ ab Masel, J. (2011). «Генетический дрейф». Current Biology . 21 (20): R837–R838. Bibcode : 2011CBio...21.R837M. doi : 10.1016/j.cub.2011.08.007 . PMID  22032182.
  41. ^ Футуйма, Дуглас (1998). Эволюционная биология . Sinauer Associates . стр. Глоссарий. ISBN 978-0-87893-189-7.
  42. ^ Аверс, Шарлотта (1989). Процесс и закономерность в эволюции . Oxford University Press.
  43. ^ Wahl, LM (2011). «Фиксация при изменении N и s: классические подходы дают элегантные новые результаты». Genetics . 188 (4): 783–785. doi :10.1534/genetics.111.131748. PMC 3176088 . PMID  21828279. 
  44. ^ Бартон, Николас Х.; Бриггс, Дерек Э.Г.; Эйзен, Джонатан А.; Голдштейн, Дэвид Б.; Патель, Нипам Х. (2007). Эволюция . Cold Spring Harbor Laboratory Press. стр. 417. ISBN 978-0-87969-684-9.
  45. ^ Футуйма, Дуглас (1998). Эволюционная биология . Sinauer Associates . стр. 320. ISBN 978-0-87893-189-7.
  46. ^ Gillespie, JH (2000). «Генетический дрейф в бесконечной популяции: модель псевдоавтостопа». Genetics . 155 (2): 909–919. doi :10.1093/genetics/155.2.909. PMC 1461093 . PMID  10835409. 
  47. ^ Провайн, Уильям Б. Заблуждение о «случайном генетическом дрейфе» . CreateSpace.
  48. ^ Неер, Ричард А.; Шрайман, Борис И. (август 2011 г.). «Генетический проект и квазинейтральность в крупных факультативно половых популяциях». Genetics . 188 (4): 975–996. arXiv : 1108.1635 . doi :10.1534/genetics.111.128876. ISSN  0016-6731. PMC 3176096 . PMID  21625002. 
  49. ^ Бастон, П. М.; Пилкингтон, Дж. Г.; и др. (2007). «Состоят ли группы рыб-клоунов из близких родственников? Анализ изменений микросателлитной ДНК у Amphiprion percula ». Молекулярная экология . 12 (3): 733–742. doi :10.1046/j.1365-294X.2003.01762.x. PMID  12675828. S2CID  35546810.
  50. ^ Repaci, V.; Stow, AJ; Briscoe, DA (2007). «Тонкомасштабная генетическая структура, совместное основание и множественное спаривание у австралийской аллодапиновой пчелы ( Ramphocinclus brachyurus )». Журнал зоологии . 270 (4): 687–691. doi :10.1111/j.1469-7998.2006.00191.x.
  51. ^ ab Su, H.; Qu, L.-J.; He, K.; Zhang, Z.; Wang, J; Chen, Z.; Gu, H. (2003). «Великая Китайская стена: физическое препятствие для потока генов?». Наследственность . 90 (3): 212–219. doi :10.1038/sj.hdy.6800237. ISSN  0018-067X. PMID  12634804. S2CID  13367320.
  52. ^ Gravel, S. (2012). «Модели популяционной генетики местного происхождения». Genetics . 1202 (2): 607–619. arXiv : 1202.4811 . Bibcode :2012arXiv1202.4811G. doi :10.1534/genetics.112.139808. PMC 3374321 . PMID  22491189. 
  53. ^ Морьян, К.; Ризеберг, Л. (2004). «Как виды развиваются коллективно: влияние потока генов и отбора на распространение выгодных аллелей». Молекулярная экология . 13 (6): 1341–56. Bibcode : 2004MolEc..13.1341M. doi : 10.1111/j.1365-294X.2004.02164.x. PMC 2600545. PMID  15140081. 
  54. ^ Bolnick, Daniel I.; Nosil, Patrik (сентябрь 2007 г.). «Естественный отбор в популяциях, подверженных миграционной нагрузке». Evolution . 61 (9): 2229–2243. doi : 10.1111/j.1558-5646.2007.00179.x . PMID  17767592. S2CID  25685919.
  55. ^ Буше, Ян; Дуади, Кристоф Дж.; Папке, Р. Тейн; Уолш, Дэвид А.; Будро, Мэри Эллен Р.; Несбё, Камилла Л.; Кейс, Ребекка Дж.; Дулиттл, У. Форд (2003). «Локальный перенос генов и происхождение прокариотических групп». Annual Review of Genetics . 37 (1): 283–328. doi :10.1146/annurev.genet.37.050503.084247. ISSN  0066-4197. PMID  14616063.
  56. ^ Уолш, Т. (2006). «Комбинаторная генетическая эволюция мультирезистентности». Current Opinion in Microbiology . 9 (5): 476–82. doi :10.1016/j.mib.2006.08.009. PMID  16942901.
  57. ^ Kondo, N.; Nikoh, N.; Ijichi, N.; Shimada, M.; Fukatsu, T. (2002). «Фрагмент генома эндосимбионта Wolbachia, перенесенный на X-хромосому насекомого-хозяина». Труды Национальной академии наук . 99 (22): 14280–14285. Bibcode : 2002PNAS...9914280K. doi : 10.1073/pnas.222228199 . ISSN  0027-8424. PMC 137875. PMID 12386340  . 
  58. ^ Спраг, Г. (1991). «Генетический обмен между королевствами». Current Opinion in Genetics & Development . 1 (4): 530–533. doi :10.1016/S0959-437X(05)80203-5. PMID  1822285.
  59. ^ Глэдышев, Е.А.; Месельсон, М.; Архипова, ИР (2008). «Массовый горизонтальный перенос генов у коловраток бделлоидных». Science . 320 (5880): 1210–1213. Bibcode :2008Sci...320.1210G. doi :10.1126/science.1156407. ISSN  0036-8075. PMID  18511688. S2CID  11862013.
  60. ^ Baldo, A.; McClure, M. (1 сентября 1999 г.). «Эволюция и горизонтальный перенос генов, кодирующих dUTPase, у вирусов и их хозяев». Journal of Virology . 73 (9): 7710–7721. doi :10.1128/JVI.73.9.7710-7721.1999. PMC 104298 . PMID  10438861. 
  61. ^ Пул, А.; Пенни, Д. (2007). «Оценка гипотез происхождения эукариот». BioEssays . 29 (1): 74–84. doi :10.1002/bies.20516. PMID  17187354.
  62. ^ Weissman, DB; Hallatschek, O. (15 января 2014 г.). «Скорость адаптации в крупных половых популяциях с линейными хромосомами». Genetics . 196 (4): 1167–1183. doi :10.1534/genetics.113.160705. PMC 3982688 . PMID  24429280. 
  63. ^ Вайсман, Дэниел Б.; Бартон, Николас Х.; МакВин, Джил (7 июня 2012 г.). «Ограничения скорости адаптивной замены в половых популяциях». PLOS Genetics . 8 (6): e1002740. doi : 10.1371/journal.pgen.1002740 . PMC 3369949. PMID  22685419 . 
  64. ^ Neher, RA; Shraiman, BI; Fisher, DS (30 ноября 2009 г.). «Скорость адаптации в крупных сексуальных популяциях». Genetics . 184 (2): 467–481. arXiv : 1108.3464 . doi :10.1534/genetics.109.109009. PMC 2828726 . PMID  19948891. 
  65. ^ Десаи, Майкл М.; Фишер, Дэниел С. (2007). «Баланс отбора полезных мутаций и влияние сцепления на положительный отбор». Генетика . 176 (3): 1759–1798. doi :10.1534/genetics.106.067678. PMC 1931526. PMID  17483432 . 
  66. ^ Левонтин, RC (1973). Генетическая основа эволюционных изменений ([4-е издание.] ред.). Нью-Йорк: Columbia University Press. ISBN 978-0231033923.
  67. ^ ab Эллегрен, Ханс; Гальтье, Николас (6 июня 2016 г.). «Детерминанты генетического разнообразия». Nature Reviews Genetics . 17 (7): 422–433. doi :10.1038/nrg.2016.58. PMID  27265362. S2CID  23531428.
  68. ^ Корбетт-Детиг, Рассел Б.; Хартл, Дэниел Л.; Сэктон, Тимоти Б.; Бартон, Ник Х. (10 апреля 2015 г.). «Естественный отбор ограничивает нейтральное разнообразие среди широкого спектра видов». PLOS Biology . 13 (4): e1002112. doi : 10.1371/journal.pbio.1002112 . PMC 4393120. PMID  25859758 . 
  69. ^ Sung, W.; Ackerman, MS; Miller, SF; Doak, TG; Lynch, M. (17 октября 2012 г.). "Гипотеза барьера дрейфа и эволюция скорости мутаций" (PDF) . Труды Национальной академии наук . 109 (45): 18488–18492. Bibcode :2012PNAS..10918488S. doi : 10.1073/pnas.1216223109 . PMC 3494944 . PMID  23077252. 
  70. ^ Чарльзворт, Дж. Эйр-Уокер (2008). «Тест Макдональда–Крейтмана и слабовредные мутации». Молекулярная биология и эволюция . 25 (6): 1007–1015. doi : 10.1093/molbev/msn005 . PMID  18195052.
  71. ^ Эйр-Уокер, А. (2006). "Геномная скорость адаптивной эволюции" (PDF) . Тенденции в экологии и эволюции . 21 (10): 569–575. Bibcode : 2006TEcoE..21..569E. doi : 10.1016/j.tree.2006.06.015. PMID  16820244.
  72. ^ Смит, NGC; Эйр-Уокер, А. (2002). «Адаптивная эволюция белков у дрозофилы». Nature . 415 (6875): 1022–1024. Bibcode :2002Natur.415.1022S. doi :10.1038/4151022a. PMID  11875568. S2CID  4426258.
  73. ^ Хан, М. В. (2008). «К теории отбора молекулярной эволюции». Эволюция . 62 (2): 255–265. doi : 10.1111/j.1558-5646.2007.00308.x . PMID  18302709. S2CID  5986211.
  74. ^ Притчард, Дж. К.; Стивенс, М.; Доннелли, П. (июнь 2000 г.). «Вывод структуры популяции с использованием данных о многолокусном генотипе». Генетика . 155 (2): 945–959. doi :10.1093/genetics/155.2.945. ISSN  0016-6731. PMC 1461096 . PMID  10835412. 
  75. ^ Верити, Роберт; Николс, Ричард А. (август 2016 г.). «Оценка количества субпопуляций (K) в структурированных популяциях». Генетика . 203 (4): 1827–1839. doi :10.1534/genetics.115.180992. ISSN  0016-6731. PMC 4981280. PMID  27317680 . 
  76. ^ Manlik, Oliver; Chabanne, Delphine; Daniel, Claire; Bejder, Lars; Allen, Simon J.; Sherwin, William B. (13 ноября 2018 г.). «Демография и генетика предполагают изменение динамики источника-стока дельфинов, что имеет значение для сохранения». Marine Mammal Science . 35 (3): 732–759. doi :10.1111/mms.12555. S2CID  92108810.
  77. ^ Гутенкунст, Райан Н.; Эрнандес, Райан Д.; Уильямсон, Скотт Х.; Бустаманте, Карлос Д.; МакВин, Джил (23 октября 2009 г.). «Вывод совместной демографической истории множественных популяций из многомерных данных о частоте однонуклеотидных полиморфизмов». PLOS Genetics . 5 (10): e1000695. arXiv : 0909.0925 . doi : 10.1371/journal.pgen.1000695 . PMC 2760211 . PMID  19851460. 
  78. ^ Sniegowski, P. (2000). «Эволюция скорости мутаций: отделение причин от последствий». BioEssays . 22 (12). Gerrish P.; Johnson T;. Shaver A.: 1057–1066. doi :10.1002/1521-1878(200012)22:12<1057::AID-BIES3>3.0.CO;2-W. PMID  11084621. S2CID  36771934.
  79. ^ Линч, Майкл; Конери, Джон С. (2003). «Истоки сложности генома». Science . 302 (5649): 1401–1404. Bibcode :2003Sci...302.1401L. CiteSeerX 10.1.1.135.974 . doi :10.1126/science.1089370. PMID  14631042. S2CID  11246091. 
  80. ^ Rajon, E.; Masel, J. (3 января 2011 г.). «Эволюция молекулярных коэффициентов ошибок и последствия для эволюционируемости». Труды Национальной академии наук . 108 (3): 1082–1087. Bibcode : 2011PNAS..108.1082R . doi : 10.1073/pnas.1012918108 . PMC 3024668. PMID  21199946. 

Внешние ссылки

На Викискладе есть медиафайлы по теме «Популяционная генетика» .