Второй закон термодинамики

Физический закон для энтропии и тепла

Второй закон термодинамики — это физический закон, основанный на универсальном эмпирическом наблюдении за взаимопревращениями тепла и энергии . Простая формулировка закона заключается в том, что тепло всегда самопроизвольно течет от более горячих к более холодным областям материи (или «вниз по склону» в терминах температурного градиента). Другое утверждение: «Не все тепло может быть преобразовано в работу в циклическом процессе ». ^{[1] [2] [3]}

Второй закон термодинамики устанавливает концепцию энтропии как физического свойства термодинамической системы . Он предсказывает, запрещены ли процессы, несмотря на соблюдение требования сохранения энергии, как выражено в первом законе термодинамики, и предоставляет необходимые критерии для спонтанных процессов . Например, первый закон допускает процесс падения чашки со стола и разбивания об пол, а также допускает обратный процесс объединения осколков чашки и «запрыгивания» обратно на стол, в то время как второй закон допускает первое и отрицает второе. Второй закон можно сформулировать, наблюдая, что энтропия изолированных систем, оставленных на спонтанную эволюцию, не может уменьшаться, поскольку они всегда стремятся к состоянию термодинамического равновесия , в котором энтропия является наивысшей при данной внутренней энергии. ^[4] Увеличение объединенной энтропии системы и окружения объясняет необратимость естественных процессов, часто упоминаемую в концепции стрелы времени . ^{[5] [6]}

Исторически второй закон был эмпирическим открытием , которое было принято в качестве аксиомы термодинамической теории . Статистическая механика дает микроскопическое объяснение закона в терминах вероятностных распределений состояний больших совокупностей атомов или молекул . Второй закон был выражен многими способами. Его первой формулировкой, которая предшествовала надлежащему определению энтропии и была основана на теории теплорода , является теорема Карно , сформулированная французским ученым Сади Карно , который в 1824 году показал, что эффективность преобразования тепла в работу в тепловой машине имеет верхний предел. ^{[7] [8]} Первое строгое определение второго закона, основанное на концепции энтропии, было дано немецким ученым Рудольфом Клаузиусом в 1850-х годах и включало его утверждение о том, что тепло никогда не может перейти от более холодного к более теплому телу без какого-либо другого изменения, связанного с этим, происходящего в то же время.

Второй закон термодинамики позволяет определить понятие термодинамической температуры , но формально это делегировано нулевому закону термодинамики .

Введение

Тепло, перетекающее из горячей воды в холодную

Первый закон термодинамики дает определение внутренней энергии термодинамической системы и выражает ее изменение для замкнутой системы в терминах работы и тепла . ^[9] Его можно связать с законом сохранения энергии . ^[10] Концептуально первый закон описывает фундаментальный принцип, согласно которому системы не потребляют и не «расходуют» энергию, что энергия не создается и не уничтожается, а просто преобразуется из одной формы в другую.

Второй закон касается направления естественных процессов. ^[11] Он утверждает, что естественный процесс протекает только в одном направлении и необратим. То есть, состояние самой естественной системы может быть обращено вспять, но не без увеличения энтропии окружения системы, то есть, как состояние системы, так и состояние ее окружения не могут быть вместе полностью обращены вспять, не подразумевая уничтожения энтропии.

Например, когда путь для проводимости или излучения становится доступным, тепло всегда самопроизвольно течет от более горячего к более холодному телу. Такие явления объясняются с точки зрения изменения энтропии . ^{[12] [13]} Тепловой насос может обратить этот тепловой поток, но процесс обращения и исходный процесс, оба вызывают производство энтропии, тем самым увеличивая энтропию окружения системы. Если изолированная система, содержащая отдельные подсистемы, изначально удерживается во внутреннем термодинамическом равновесии за счет внутреннего разделения непроницаемыми стенками между подсистемами, а затем некоторая операция делает стенки более проницаемыми, то система самопроизвольно эволюционирует, чтобы достичь окончательного нового внутреннего термодинамического равновесия , и ее общая энтропия, , увеличивается. ${\displaystyle S}$

В обратимом или квазистатическом , идеализированном процессе передачи энергии в виде тепла в замкнутую термодинамическую систему интереса (которая допускает вход или выход энергии, но не передачу вещества) из вспомогательной термодинамической системы, бесконечно малое приращение ( ) энтропии системы интереса определяется как результат бесконечно малой передачи тепла ( ) в систему интереса, деленной на общую термодинамическую температуру системы интереса и вспомогательной термодинамической системы: ^[14] ${\displaystyle \mathrm {d} S}$ ${\displaystyle \delta Q}$ ${\displaystyle (T)}$

${\displaystyle \mathrm {d} S={\frac {\delta Q}{T}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{(closed system; idealized, reversible process)}}.}$

Для бесконечно малого количества тепла и бесконечно малого изменения энтропии используются разные обозначения , поскольку энтропия является функцией состояния , тогда как тепло, как и работа, таковой не является. ${\displaystyle (\delta )}$ ${\displaystyle (\mathrm {d} )}$

Для действительно возможного бесконечно малого процесса без обмена массой с окружающей средой второй закон требует, чтобы приращение энтропии системы удовлетворяло неравенству ^{[15] [16]}

${\displaystyle \mathrm {d} S>{\frac {\delta Q}{T_{\text{surr}}}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{(closed system; actually possible, irreversible process).}}}$

Это происходит потому, что общий процесс для этого случая (отсутствие массообмена между системой и ее окружением) может включать работу, выполняемую над системой ее окружением, что может иметь фрикционные или вязкие эффекты внутри системы, потому что может происходить химическая реакция, или потому, что передача тепла фактически происходит только необратимо, обусловленная конечной разницей между температурой системы ( T ) и температурой окружения ( Tsurr ). ^{[17] [} ₁₈ ^]

Равенство по-прежнему применимо к чистому тепловому потоку (только тепловой поток, без изменения химического состава и массы),

${\displaystyle \mathrm {d} S={\frac {\delta Q}{T}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{(actually possible quasistatic irreversible process without composition change).}}}$

что является основой точного определения абсолютной энтропии чистых веществ из измеренных кривых теплоемкости и изменения энтропии при фазовых переходах, т.е. методом калориметрии. ^{[19] [15]}

Вводя набор внутренних переменных для описания отклонения термодинамической системы от состояния химического равновесия в физическое равновесие (с требуемыми четко определенными равномерными давлением P и температурой T ), можно записать равенство ${\displaystyle \xi }$

${\displaystyle \mathrm {d} S={\frac {\delta Q}{T}}-{\frac {1}{T}}\sum _{j}\,\Xi _{j}\,\delta \xi _{j}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{(closed system; actually possible quasistatic irreversible process).}}}$

Второй член представляет собой работу внутренних переменных, которые могут быть возмущены внешними воздействиями, но система не может выполнить никакой положительной работы через внутренние переменные. Это утверждение вводит невозможность обращения эволюции термодинамической системы во времени и может рассматриваться как формулировка второго принципа термодинамики – формулировка, которая, конечно, эквивалентна формулировке принципа в терминах энтропии. ^{[20] [21]}

Нулевой закон термодинамики в его обычной краткой формулировке позволяет распознать, что два тела, находящиеся в отношении теплового равновесия, имеют одинаковую температуру, особенно, что испытуемое тело имеет ту же температуру, что и эталонное термометрическое тело. ^[22] Для тела, находящегося в тепловом равновесии с другим, существует бесконечно много эмпирических температурных шкал, в общем случае соответственно зависящих от свойств конкретного эталонного термометрического тела. Второй закон допускает ^{[ необходимо разъяснение ]} выделенную температурную шкалу, которая определяет абсолютную, термодинамическую температуру , независимую от свойств любого конкретного эталонного термометрического тела. ^{[23] [24]}

Различные положения закона

Второй закон термодинамики может быть выражен многими конкретными способами, ^[25] наиболее известными классическими утверждениями ^[26] являются утверждение Рудольфа Клаузиуса (1854), утверждение лорда Кельвина (1851) и утверждение в аксиоматической термодинамике Константина Каратеодори (1909). Эти утверждения излагают закон в общих физических терминах, ссылаясь на невозможность определенных процессов. Было показано, что утверждения Клаузиуса и Кельвина эквивалентны. ^[27]

принцип Карно

Историческое происхождение ^[28] второго закона термодинамики было в теоретическом анализе Сади Карно потока тепла в паровых двигателях (1824). Центральным элементом этого анализа, теперь известного как двигатель Карно , является идеальная тепловая машина, фиктивно работающая в предельном режиме чрезвычайной медленности, известном как квазистатический, так что передача тепла и работы происходит между подсистемами, которые всегда находятся в своих собственных внутренних состояниях термодинамического равновесия . Он представляет собой теоретический максимальный КПД тепловой машины, работающей между любыми двумя заданными термическими или тепловыми резервуарами при разных температурах. Принцип Карно был признан Карно в то время, когда теория теплорода представляла собой доминирующее понимание природы тепла, до признания первого закона термодинамики и до математического выражения концепции энтропии. Интерпретируемый в свете первого закона, анализ Карно физически эквивалентен второму закону термодинамики и остается действительным сегодня. Вот некоторые примеры из его книги:

... везде, где существует разница температур, может быть создана движущая сила. ^[29]

Производство движущей силы в паровых двигателях обусловлено не фактическим потреблением теплоты, а ее переносом от теплого тела к холодному... ^[30]

Движущая сила тепла не зависит от агентов, используемых для ее создания; ее количество определяется исключительно температурами тел, между которыми в конечном итоге осуществляется передача теплоты. ^[31]

В современных терминах принцип Карно можно сформулировать точнее:

Эффективность квазистатического или обратимого цикла Карно зависит только от температур двух тепловых резервуаров и одинакова, независимо от рабочего вещества. Двигатель Карно, работающий таким образом, является наиболее эффективным возможным тепловым двигателем, использующим эти две температуры. ^{[32] [33] [34] [35] [36] [37]}

заявление Клаузиуса

Немецкий ученый Рудольф Клаузиус заложил основу второго закона термодинамики в 1850 году, исследовав связь между теплопередачей и работой. ^[38] Его формулировка второго закона, опубликованная на немецком языке в 1854 году, известна как утверждение Клаузиуса :

Тепло никогда не может перейти от более холодного тела к более теплому без какого-либо другого изменения, связанного с этим и происходящего в то же самое время. ^[39]

В заявлении Клаузиуса используется концепция «передачи тепла». Как обычно в термодинамических дискуссиях, это означает «чистую передачу энергии в виде тепла» и не относится к сопутствующим передачам в одну или другую сторону.

Тепло не может спонтанно перетекать из холодных областей в горячие без выполнения внешней работы над системой, что очевидно из обычного опыта охлаждения , например. В холодильнике тепло передается от холода к горячему, но только под действием внешнего агента — холодильной системы.

Заявления Кельвина

Лорд Кельвин сформулировал второй закон в нескольких формулировках.

Самодействующая машина не может без посторонней помощи передавать тепло от одного тела к другому, находящемуся при более высокой температуре.

Невозможно посредством неодушевленного материального фактора получить механический эффект от любой части материи, охлаждая ее ниже температуры самого холодного из окружающих предметов. ^[40]

Эквивалентность утверждений Клаузиуса и Кельвина

Вывести утверждение Кельвина из утверждения Клаузиуса

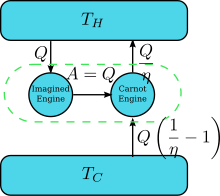
Предположим, что есть двигатель, нарушающий утверждение Кельвина: т. е. тот, который отводит тепло и полностью преобразует его в работу (отведенное тепло полностью преобразуется в работу) циклическим образом без какого-либо другого результата. Теперь соедините его с обращенным двигателем Карно , как показано на правом рисунке. КПД обычного теплового двигателя равен η , поэтому КПД обращенного теплового двигателя равен 1/ η . Чистый и единственный эффект объединенной пары двигателей заключается в передаче тепла из более холодного резервуара в более горячий, что нарушает утверждение Клаузиуса. Это является следствием первого закона термодинамики , поскольку для того, чтобы общая энергия системы оставалась прежней; , поэтому , где (1) используется соглашение о знаках тепла, при котором тепло, входящее в (выходящее) двигатель, является положительным (отрицательным), и (2) получается из определения КПД двигателя, когда работа двигателя не является обратной. Таким образом, нарушение утверждения Кельвина подразумевает нарушение утверждения Клаузиуса, т. е. утверждение Клаузиуса подразумевает утверждение Кельвина. Мы можем доказать аналогичным образом, что утверждение Кельвина подразумевает утверждение Клаузиуса, и, следовательно, эти два утверждения эквивалентны. ${\textstyle \Delta Q=Q\left({\frac {1}{\eta }}-1\right)}$ ${\textstyle {\text{Input}}+{\text{Output}}=0\implies (Q+Q_{c})-{\frac {Q}{\eta }}=0}$ ${\textstyle Q_{c}=Q\left({\frac {1}{\eta }}-1\right)}$ ${\displaystyle {\frac {Q}{\eta }}}$

Предложение Планка

Планк выдвинул следующее положение, выведенное непосредственно из опыта. Иногда это считают его утверждением второго закона, но он считал его отправной точкой для вывода второго закона.

Невозможно построить двигатель, который будет работать в полном цикле и не давать никакого эффекта, кроме производства работы и охлаждения теплового резервуара. ^{[41] [42]}

Связь между утверждением Кельвина и предложением Планка

В учебниках почти принято говорить о «формулировке закона Кельвина–Планка», как, например, в тексте Тер Хаара и Вергеланда . ^[43] Эта версия, также известная как формулировка теплового двигателя , второго закона гласит, что

Невозможно разработать циклически работающее устройство, единственным эффектом которого будет поглощение энергии в виде тепла из одного теплового резервуара и выполнение эквивалентного количества работы . ^[2]

Заявление Планка

Макс Планк сформулировал второй закон следующим образом.

Каждый процесс, происходящий в природе, происходит в том смысле, что сумма энтропий всех тел, принимающих участие в процессе, увеличивается. В пределе, т.е. для обратимых процессов, сумма энтропий остается неизменной. ^{[44] [45] [46]}

Утверждение Планка весьма похоже на утверждение Джорджа Уленбека и Джорджа У. Форда о необратимых явлениях .

... при необратимом или спонтанном переходе из одного состояния равновесия в другое (как, например, выравнивание температуры двух тел A и B, приведенных в соприкосновение) энтропия всегда увеличивается. ^[47]

Принцип Каратеодори

Константин Каратеодори сформулировал термодинамику на чисто математической аксиоматической основе. Его утверждение второго закона известно как Принцип Каратеодори, который можно сформулировать следующим образом: ^[48]

В каждой окрестности любого состояния S адиабатически замкнутой системы существуют состояния, недоступные из S. ^[49]

С помощью этой формулировки он впервые описал концепцию адиабатической доступности и заложил основу для нового подраздела классической термодинамики, часто называемого геометрической термодинамикой . Из принципа Каратеодори следует, что количество энергии, квазистатически переданной в виде тепла, является голономной функцией процесса , другими словами, . ^[50] ${\displaystyle \delta Q=TdS}$

Хотя в учебниках почти принято говорить, что принцип Каратеодори выражает второй закон и рассматривать его как эквивалент утверждений Клаузиуса или Кельвина-Планка, это не так. Чтобы получить все содержание второго закона, принцип Каратеодори необходимо дополнить принципом Планка, что изохорная работа всегда увеличивает внутреннюю энергию замкнутой системы, которая изначально находилась в своем собственном внутреннем термодинамическом равновесии. ^{[18] [51] [52] [53] [ требуется разъяснение ]}

принцип Планка

В 1926 году Макс Планк написал важную работу по основам термодинамики. ^{[52] [54]} Он указал на принцип

Внутренняя энергия замкнутой системы увеличивается за счет адиабатического процесса, на протяжении которого объем системы остается постоянным. ^{[18] [51]}

Эта формулировка не упоминает теплоту и не упоминает температуру, даже энтропию, и не обязательно неявно опирается на эти концепции, но она подразумевает содержание второго закона. Тесно связанное утверждение заключается в том, что «давление трения никогда не производит положительной работы». ^[55] Планк писал: «Производство тепла трением необратимо». ^{[56] [57]}

Не упоминая энтропию, этот принцип Планка сформулирован в физических терминах. Он очень тесно связан с утверждением Кельвина, данным чуть выше. ^[58] Важно, что для системы при постоянном объеме и числе молей энтропия является монотонной функцией внутренней энергии. Тем не менее, этот принцип Планка на самом деле не является предпочтительным утверждением Планка второго закона, которое цитируется выше, в предыдущем подразделе настоящего раздела этой статьи, и опирается на концепцию энтропии.

Утверждение, которое в некотором смысле является дополнительным к принципу Планка, сделано Клаусом Боргнакке и Рихардом Э. Зоннтагом. Они не предлагают его как полное утверждение второго закона:

... существует только один способ, которым можно уменьшить энтропию [закрытой] системы, а именно, отвод тепла от системы. ^[59]

В отличие от только что упомянутого принципа Планка, этот принцип явно относится к изменению энтропии. Удаление материи из системы также может уменьшить ее энтропию.

Связь второго закона с определением температуры

Было показано, что второй закон эквивалентен внутренней энергии U, определяемой как выпуклая функция других экстенсивных свойств системы. ^[60] То есть, когда система описывается путем указания ее внутренней энергии U , экстенсивной переменной, как функции ее энтропии S , объема V и числа молей N , т.е. U = U ( S , V , N ), то температура равна частной производной внутренней энергии по энтропии ^[61] (по сути, эквивалентно первому уравнению TdS для V и N, поддерживаемых постоянными):

${\displaystyle T=\left({\frac {\partial U}{\partial S}}\right)_{V,N}}$

Утверждения второго закона, такие как неравенство Клаузиуса, включающие потоки излучения

Неравенство Клаузиуса, а также некоторые другие утверждения второго закона, должны быть переформулированы, чтобы иметь общую применимость для всех форм теплопередачи, т. е. сценариев, включающих лучистые потоки. Например, подынтегральное выражение (đQ/T) выражения Клаузиуса применяется к теплопроводности и конвекции, а также к случаю идеального бесконечно малого переноса излучения черного тела (BR), но не применяется к большинству сценариев лучистого переноса и в некоторых случаях вообще не имеет физического смысла. Следовательно, неравенство Клаузиуса было переформулировано ^[62] так, чтобы оно было применимо к циклам с процессами, включающими любую форму теплопередачи. Перенос энтропии с лучистыми потоками ( ) рассматривается отдельно от переноса за счет теплопередачи путем теплопроводности и конвекции ( ), где температура оценивается на границе системы, где происходит перенос тепла. Модифицированное неравенство Клаузиуса для всех сценариев теплопередачи может быть тогда выражено как, $\delta S_{\text{NetRad}}$ $\delta Q_{CC}$ $${\displaystyle \int _{\text{cycle}}({\frac {\delta Q_{CC}}{T_{b}}}+\delta S_{\text{NetRad}})<=0}$$

Вкратце, неравенство Клаузиуса гласит, что по завершении цикла изменение свойства состояния S будет равно нулю, поэтому энтропия, которая была произведена во время цикла, должна была быть выведена из системы посредством теплопередачи. (или đ) указывает на интеграцию, зависящую от пути. $\delta$

Из-за присущего всей материи излучения большинство расчетов потока энтропии включают падающие, отраженные и испускаемые потоки излучения. Энергия и энтропия неполяризованного теплового излучения черного тела рассчитываются с использованием выражений спектральной энергии и энтропии излучения, выведенных Максом Планком ^[63] с использованием равновесной статистической механики, где c — скорость света, k — постоянная Больцмана, h — постоянная Планка, ν — частота, а величины K _v и L _v — потоки энергии и энтропии на единицу частоты, площади и телесного угла. При выводе этой спектральной энтропии излучения черного тела с целью вывода формулы энергии черного тела Планк постулировал, что энергия фотона квантуется (отчасти для упрощения математики), тем самым положив начало квантовой теории. $${\displaystyle K_{\nu }={\frac {2h}{c^{2}}}{\frac {\nu ^{3}}{\exp \left({\frac {h\nu }{kT}}\right)-1}},}$$ $${\displaystyle L_{\nu }={\frac {2k\nu ^{2}}{c^{2}}}((1+{\frac {c^{2}K_{\nu }}{2h\nu ^{3}}})\ln(1+{\frac {c^{2}K_{\nu }}{2h\nu ^{3}}})-({\frac {c^{2}K_{\nu }}{2h\nu ^{3}}})\ln({\frac {c^{2}K_{\nu }}{2h\nu ^{3}}}))}$$

Подход неравновесной статистической механики также использовался для получения того же результата, что и у Планка, указывая на то, что он имеет более широкое значение и представляет собой неравновесную энтропию. ^[64] График зависимости K _v от частоты (v) для различных значений температуры ( T) ​​дает семейство энергетических спектров излучения черного тела, а также для спектров энтропии. Для потоков излучения нечерного тела (NBR) спектральная энтропийная яркость L _v находится путем подстановки данных о спектральной энергетической яркости K _{v в выражение} L _v (отмечая, что испускаемые и отраженные потоки энтропии, в общем случае, не являются независимыми). Для излучения NBR, включая излучение серого тела (GR), результирующий испускаемый поток энтропии или яркость L , имеет более высокое отношение энтропии к энергии ( L/K ), чем у BR. То есть поток энтропии излучения NBR дальше отстоит от результата проводимости и конвекции q / T , чем для излучения BR. ^[65] Это наблюдение согласуется с формулами энергии и энтропии излучения черного тела Макса Планка и согласуется с тем фактом, что излучение излучения черного тела представляет собой максимальное излучение энтропии для всех материалов с одинаковой температурой, а также максимальное излучение энтропии для всего излучения с одинаковой энергетической яркостью.

Обобщенное концептуальное изложение принципа второго закона

Анализ второго закона ценен в научном и инженерном анализе, поскольку он обеспечивает ряд преимуществ по сравнению с одним лишь энергетическим анализом, включая основу для определения качества энергии (содержание эксергии ^{[66] [67] [68]} ), понимание фундаментальных физических явлений и улучшение оценки производительности и оптимизации. В результате концептуальное изложение принципа очень полезно в инженерном анализе. Термодинамические системы можно классифицировать по четырем комбинациям энтропии (S) вверх или вниз, и однородности (Y) – между системой и ее средой – вверх или вниз. Эта «особая» категория процессов, категория IV, характеризуется движением в направлении низкого беспорядка и низкой однородности, противодействуя тенденции второго закона к однородности и беспорядку. ^[69]

Четыре категории процессов с учетом увеличения или уменьшения энтропии и увеличения или уменьшения однородности

Второй закон можно концептуально сформулировать ^[69] следующим образом: Материя и энергия имеют тенденцию достигать состояния однородности или внутреннего и внешнего равновесия, состояния максимального беспорядка (энтропии). Реальные неравновесные процессы всегда производят энтропию, вызывая увеличение беспорядка во вселенной, в то время как идеализированные обратимые процессы не производят энтропии, и не известно ни одного процесса, который бы разрушал энтропию. Тенденция системы к достижению однородности может быть нейтрализована, и система может стать более упорядоченной или сложной, путем сочетания двух вещей: источника работы или эксергии и некоторой формы инструкции или интеллекта. Где «эксергия» — это тепловой, механический, электрический или химический рабочий потенциал источника или потока энергии, а «инструкция или интеллект», хотя и субъективны, находятся в контексте набора процессов категории IV.

Рассмотрим пример категории IV роботизированного производства и сборки транспортных средств на заводе. Роботизированное оборудование требует ввода электрической работы и инструкций, но после завершения изготовленные продукты имеют меньшее единообразие с окружающей средой или большую сложность (более высокий порядок) по сравнению с сырьем, из которого они были сделаны. Таким образом, энтропия системы или беспорядок уменьшаются, в то время как тенденция к единообразию между системой и ее средой нейтрализуется. В этом примере инструкции, а также источник работы могут быть внутренними или внешними по отношению к системе, и они могут или не могут пересекать границу системы. Для иллюстрации, инструкции могут быть предварительно закодированы, а электрическая работа может храниться в системе хранения энергии на месте. В качестве альтернативы управление оборудованием может осуществляться посредством удаленного управления через сеть связи, в то время как электрическая работа подается на завод из местной электросети. Кроме того, люди могут напрямую играть, полностью или частично, роль, которую роботизированное оборудование играет в производстве. В этом случае могут быть задействованы инструкции, но интеллект либо напрямую, либо косвенно отвечает за направление или применение работы таким образом, чтобы противодействовать тенденции к беспорядку и единообразию.

Существуют также ситуации, когда энтропия спонтанно уменьшается посредством передачи энергии и энтропии. Когда термодинамические ограничения отсутствуют, энергия или масса, а также сопутствующая энтропия могут спонтанно передаваться из системы в процессе достижения внешнего равновесия или однородности интенсивных свойств системы с ее окружением. Это происходит спонтанно, потому что энергия или масса, переданная из системы в ее окружение, приводит к более высокой энтропии в окружении, то есть это приводит к более высокой общей энтропии системы плюс ее окружение. Обратите внимание, что этот перенос энтропии требует неравновесия в свойствах, таких как разница температур. Одним из примеров этого является охлаждающая кристаллизация воды, которая может происходить, когда окружение системы находится ниже температуры замерзания. Неограниченная передача тепла может происходить спонтанно, приводя к замерзанию молекул воды в кристаллизованную структуру с уменьшенным беспорядком (слипание в определенном порядке из-за молекулярного притяжения). Энтропия системы уменьшается, но система приближается к однородности со своим окружением (категория III).

С другой стороны, рассмотрим охлаждение воды в теплой среде. Из-за охлаждения, по мере того как тепло извлекается из воды, температура и энтропия воды уменьшаются, поскольку система все дальше отходит от однородности с ее теплым окружением или средой (категория IV). Главное, вывод, заключается в том, что охлаждение требует не только источника работы, оно требует спроектированного оборудования, а также предварительно закодированного или прямого оперативного интеллекта или инструкций для достижения желаемого эффекта охлаждения.

Следствия

Вечное движение второго рода

До установления второго закона многие люди, заинтересованные в изобретении вечного двигателя, пытались обойти ограничения первого закона термодинамики , извлекая огромную внутреннюю энергию окружающей среды в качестве мощности машины. Такая машина называется «вечным двигателем второго рода». Второй закон провозгласил невозможность таких машин.

Теорема Карно

Теорема Карно (1824) — это принцип, ограничивающий максимальную эффективность любого возможного двигателя. Эффективность зависит исключительно от разницы температур между горячим и холодным термическими резервуарами. Теорема Карно гласит:

• Все необратимые тепловые двигатели между двумя резервуарами тепла менее эффективны, чем двигатель Карно, работающий между теми же резервуарами.
• Все обратимые тепловые двигатели между двумя резервуарами тепла одинаково эффективны с двигателем Карно, работающим между теми же резервуарами.

В его идеальной модели теплота теплоты, преобразованная в работу, могла быть восстановлена ​​путем обращения движения цикла, концепция, впоследствии известная как термодинамическая обратимость . Карно, однако, далее постулировал, что часть теплоты теряется, не преобразуясь в механическую работу. Следовательно, ни один реальный тепловой двигатель не мог реализовать обратимость цикла Карно и был обречен на меньшую эффективность.

Хотя это и было сформулировано в терминах теплорода (см. устаревшую теорию теплорода ), а не энтропии , это было раннее понимание второго закона.

неравенство Клаузиуса

Теорема Клаузиуса ( 1854) утверждает, что в циклическом процессе

${\displaystyle \oint {\frac {\delta Q}{T_{\text{surr}}}}\leq 0.}$

Равенство выполняется в обратимом случае ^[70] , а строгое неравенство выполняется в необратимом случае, где T _surr — температура термостата (окружающей среды). Обратимый случай используется для введения энтропии функции состояния . Это происходит потому, что в циклических процессах изменение функции состояния равно нулю по сравнению с функциональностью состояния.

Термодинамическая температура

Для произвольной тепловой машины КПД равен:

где W _n — чистая работа, выполненная двигателем за цикл, q _H > 0 — тепло, добавленное к двигателю из горячего резервуара, а q _C = −| q _C | < 0 ^[71] — отработанное тепло, отданное в холодный резервуар от двигателя. Таким образом, эффективность зависит только от соотношения | q _C | / | q _H |.

Теорема Карно утверждает, что все обратимые двигатели, работающие между одними и теми же тепловыми резервуарами, одинаково эффективны. Таким образом, любой обратимый тепловой двигатель, работающий между температурами T _H и T _C, должен иметь одинаковую эффективность, то есть эффективность является функцией только температур:

Кроме того, обратимый тепловой двигатель, работающий между температурами T ₁ и T _3, должен иметь такую ​​же эффективность, как и двигатель, состоящий из двух циклов, один между T ₁ и другой (промежуточной) температурой T ₂ , а второй между T ₂ и T ₃ , где T ₁ > T ₂ > T ₃ . Это происходит потому, что если часть двухтактного двигателя скрыта так, что она распознается как двигатель между резервуарами при температурах T ₁ и T ₃ , то эффективность этого двигателя должна быть такой же, как и у другого двигателя в тех же резервуарах. Если мы выберем двигатели так, чтобы работа, выполняемая однотактным двигателем и двухтактным двигателем, была одинаковой, то эффективность каждого теплового двигателя записывается следующим образом.

${\displaystyle \eta _{1}=1-{\frac {|q_{3}|}{|q_{1}|}}=1-f(T_{1},T_{3})}$,

${\displaystyle \eta _{2}=1-{\frac {|q_{2}|}{|q_{1}|}}=1-f(T_{1},T_{2})}$,

${\displaystyle \eta _{3}=1-{\frac {|q_{3}|}{|q_{2}|}}=1-f(T_{2},T_{3})}$.

Здесь двигатель 1 является однотактным, а двигатели 2 и 3 составляют двухтактный двигатель, в котором имеется промежуточный резервуар при T ₂ . Мы также использовали тот факт, что тепло проходит через промежуточный тепловой резервуар при , не теряя своей энергии. (Т.е. не теряется при прохождении через резервуар при .) Этот факт можно доказать следующим образом. ${\displaystyle q_{2}}$ ${\displaystyle T_{2}}$ ${\displaystyle q_{2}}$ ${\displaystyle T_{2}}$

${\displaystyle {\begin{aligned}&{{\eta }_{2}}=1-{\frac {|{{q}_{2}}|}{|{{q}_{1}}|}}\to |{{w}_{2}}|=|{{q}_{1}}|-|{{q}_{2}}|,\\&{{\eta }_{3}}=1-{\frac {|{{q}_{3}}|}{|{{q}_{2}}^{*}|}}\to |{{w}_{3}}|=|{{q}_{2}}^{*}|-|{{q}_{3}}|,\\&|{{w}_{2}}|+|{{w}_{3}}|=(|{{q}_{1}}|-|{{q}_{2}}|)+(|{{q}_{2}}^{*}|-|{{q}_{3}}|),\\&{{\eta }_{1}}=1-{\frac {|{{q}_{3}}|}{|{{q}_{1}}|}}={\frac {(|{{w}_{2}}|+|{{w}_{3}}|)}{|{{q}_{1}}|}}={\frac {(|{{q}_{1}}|-|{{q}_{2}}|)+(|{{q}_{2}}^{*}|-|{{q}_{3}}|)}{|{{q}_{1}}|}}.\\\end{aligned}}}$

Для обеспечения согласованности последнего уравнения тепло, переданное от двигателя 2 к промежуточному резервуару, должно быть равно теплу, переданному от резервуара к двигателю 3. ${\displaystyle q_{2}}$ ${\displaystyle q_{2}^{*}}$

Затем

${\displaystyle f(T_{1},T_{3})={\frac {|q_{3}|}{|q_{1}|}}={\frac {|q_{2}||q_{3}|}{|q_{1}||q_{2}|}}=f(T_{1},T_{2})f(T_{2},T_{3}).}$

Теперь рассмотрим случай, когда - фиксированная опорная температура: температура тройной точки воды равна 273,16 К; Тогда для любых T ₂ и T ₃ , ${\displaystyle T_{1}}$ ${\displaystyle T_{1}=\mathrm {273.16~K} }$

${\displaystyle f(T_{2},T_{3})={\frac {f(T_{1},T_{3})}{f(T_{1},T_{2})}}={\frac {273.16{\text{ K}}\cdot f(T_{1},T_{3})}{273.16{\text{ K}}\cdot f(T_{1},T_{2})}}.}$

Следовательно, если термодинамическая температура T * определяется как

${\displaystyle T^{*}=273.16{\text{ K}}\cdot f(T_{1},T)}$

тогда функция f , рассматриваемая как функция термодинамических температур, просто равна

${\displaystyle f(T_{2},T_{3})=f(T_{2}^{*},T_{3}^{*})={\frac {T_{3}^{*}}{T_{2}^{*}}},}$

и опорная температура T ₁ * = 273,16 К × f ( T ₁ , T ₁ ) = 273,16 К. (Можно использовать любую опорную температуру и любое положительное числовое значение – выбор здесь соответствует шкале Кельвина .)

Энтропия

Согласно равенству Клаузиуса , для обратимого процесса

${\displaystyle \oint {\frac {\delta Q}{T}}=0}$

Это означает, что линейный интеграл не зависит от пути для обратимых процессов. ${\displaystyle \int _{L}{\frac {\delta Q}{T}}}$

Итак, мы можем определить функцию состояния S , называемую энтропией, которая для обратимого процесса или для чистой теплопередачи удовлетворяет условию

${\displaystyle dS={\frac {\delta Q}{T}}}$

При этом мы можем получить разницу энтропии только путем интегрирования приведенной выше формулы. Чтобы получить абсолютное значение, нам нужен третий закон термодинамики , который гласит, что S = 0 при абсолютном нуле для идеальных кристаллов.

Для любого необратимого процесса, поскольку энтропия является функцией состояния, мы всегда можем связать начальное и конечное состояния с воображаемым обратимым процессом и, интегрируя по этому пути, вычислить разницу в энтропии.

Теперь обратим обратимый процесс и объединим его с указанным необратимым процессом. Применяем неравенство Клаузиуса к этой петле, при этом T _surr — температура окружающей среды,

${\displaystyle -\Delta S+\int {\frac {\delta Q}{T_{\text{surr}}}}=\oint {\frac {\delta Q}{T_{\text{surr}}}}\leq 0}$

Таким образом,

${\displaystyle \Delta S\geq \int {\frac {\delta Q}{T_{\text{surr}}}}}$

где равенство выполняется, если преобразование обратимо. Если процесс является адиабатическим , то , поэтому . ${\displaystyle \delta Q=0}$ ${\displaystyle \Delta S\geq 0}$

Энергия, доступная полезная работа

Важным и показательным идеализированным частным случаем является рассмотрение применения второго закона к сценарию изолированной системы (называемой полной системой или вселенной), состоящей из двух частей: интересующей подсистемы и окружения подсистемы. Это окружение воображается настолько большим, что его можно рассматривать как неограниченный резервуар тепла при температуре T _R и давлении P _R  – так что независимо от того, сколько тепла передается в (или от) подсистемы, температура окружения останется T _R ; и независимо от того, насколько объем подсистемы расширяется (или сжимается), давление окружения останется P _R .

Какие бы изменения dS и dS _R ни происходили в энтропиях подсистемы и окружающей среды по отдельности, энтропия S _tot изолированной полной системы не должна уменьшаться в соответствии со вторым законом термодинамики:

${\displaystyle dS_{\mathrm {tot} }=dS+dS_{\text{R}}\geq 0}$

Согласно первому закону термодинамики , изменение внутренней энергии подсистемы dU равно сумме тепла δq, добавленного к подсистеме, за вычетом любой работы δw, выполненной подсистемой , плюс любая чистая химическая энергия, поступающая в подсистему d Σ μ _iR N _i , так что:

${\displaystyle dU=\delta q-\delta w+d\left(\sum \mu _{iR}N_{i}\right)}$

где μ _iR — химические потенциалы химических веществ во внешней среде.

Теперь тепло, покидающее резервуар и поступающее в подсистему, равно

${\displaystyle \delta q=T_{\text{R}}(-dS_{\text{R}})\leq T_{\text{R}}dS}$

где мы сначала использовали определение энтропии в классической термодинамике (альтернативно, в статистической термодинамике можно вывести связь между изменением энтропии, температурой и поглощенным теплом); а затем неравенство второго закона сверху.

Отсюда следует, что любая сетевая работа δw, выполненная подсистемой, должна подчиняться

${\displaystyle \delta w\leq -dU+T_{\text{R}}dS+\sum \mu _{iR}dN_{i}}$

Полезно разделить работу δw, выполняемую подсистемой, на полезную работу δw _u , которая может быть выполнена подсистемой , сверх работы p _R dV, выполняемой просто подсистемой, расширяющейся против окружающего внешнего давления, что дает следующее соотношение для полезной работы (эксергии), которая может быть выполнена:

${\displaystyle \delta w_{u}\leq -d\left(U-T_{\text{R}}S+p_{\text{R}}V-\sum \mu _{iR}N_{i}\right)}$

Удобно определить правую часть как точную производную термодинамического потенциала, называемую доступностью или эксергией E подсистемы,

${\displaystyle E=U-T_{\text{R}}S+p_{\text{R}}V-\sum \mu _{iR}N_{i}}$

Второй закон, таким образом, подразумевает, что для любого процесса, который можно рассматривать как разделенный просто на подсистему и неограниченный резервуар температуры и давления, с которым он находится в контакте,

${\displaystyle dE+\delta w_{u}\leq 0}$

т.е. изменение эксергии подсистемы плюс полезная работа, выполненная подсистемой (или изменение эксергии подсистемы за вычетом любой работы, дополнительной к той, что выполнена резервуаром давления, выполненной над системой) должно быть меньше или равно нулю.

Подводя итог, можно сказать, что если в качестве системного окружения в реальном мире выбрано соответствующее бесконечному резервуару эталонное состояние, то второй закон предсказывает уменьшение E для необратимого процесса и отсутствие изменений для обратимого процесса.

${\displaystyle dS_{\text{tot}}\geq 0}$эквивалентно ${\displaystyle dE+\delta w_{u}\leq 0}$

Это выражение вместе с соответствующим референтным состоянием позволяет инженеру-конструктору, работающему в макроскопическом масштабе (выше термодинамического предела ), использовать второй закон без прямого измерения или рассмотрения изменения энтропии в полной изолированной системе (см. также Инженер-технолог ). Эти изменения уже были рассмотрены в предположении, что рассматриваемая система может достичь равновесия с референтным состоянием, не изменяя референтное состояние. Эффективность для процесса или набора процессов, которая сравнивает его с обратимым идеалом, также может быть найдена (см. Эффективность эксергии .)

Такой подход ко второму закону широко используется в инженерной практике, экологическом учете , системной экологии и других дисциплинах.

Направление самопроизвольных процессов

Второй закон определяет, запрещен ли предлагаемый физический или химический процесс или он может происходить спонтанно. Для изолированных систем окружающая среда не обеспечивает никакой энергии, и второй закон требует, чтобы энтропия системы сама по себе увеличивалась: Δ S > 0. Примеры спонтанных физических процессов в изолированных системах включают следующее:

• 1) Тепло может передаваться из области с более высокой температурой в область с более низкой температурой (но не наоборот).
• 2) Механическая энергия может быть преобразована в тепловую энергию (но не наоборот).
• 3) Растворенное вещество может перемещаться из области с более высокой концентрацией в область с более низкой концентрацией (но не наоборот).

Однако для некоторых неизолированных систем, которые могут обмениваться энергией с окружающей средой, окружающая среда обменивается с системой достаточным количеством тепла или выполняет достаточную работу над системой, так что процессы происходят в противоположном направлении. Это возможно при условии, что общее изменение энтропии системы плюс окружающая среда положительно, как того требует второй закон: Δ S _tot = Δ S + Δ S _R > 0. Для трех приведенных выше примеров:

• 1) Тепло может быть передано из области с более низкой температурой в область с более высокой температурой в холодильнике или тепловом насосе . Эти машины должны обеспечивать достаточную работу для системы.
• 2) Тепловая энергия может быть преобразована в механическую работу в тепловом двигателе , если при этом в окружающую среду выделяется достаточное количество тепла.
• 3) Растворенное вещество может перемещаться из области с более низкой концентрацией в область с более высокой концентрацией в биохимическом процессе активного транспорта , если достаточная работа обеспечивается градиентом концентрации химического вещества, такого как АТФ, или электрохимическим градиентом .

Второй закон химической термодинамики

Для самопроизвольного химического процесса в замкнутой системе при постоянной температуре и давлении без нефотонной работы неравенство Клаузиуса Δ S > Q/T _surr превращается в условие изменения свободной энергии Гиббса

${\displaystyle \Delta G<0}$

или d G < 0. Для аналогичного процесса при постоянной температуре и объеме изменение свободной энергии Гельмгольца должно быть отрицательным, . Таким образом, отрицательное значение изменения свободной энергии ( G или A ) является необходимым условием для того, чтобы процесс был самопроизвольным. Это наиболее полезная форма второго закона термодинамики в химии, где изменения свободной энергии могут быть рассчитаны из табличных энтальпий образования и стандартных молярных энтропий реагентов и продуктов. ^{[19] [15]} Условие химического равновесия при постоянных T и p без электрической работы: d G = 0. ${\displaystyle \Delta A<0}$

История

Николя Леонар Сади Карно в традиционной форме студента Политехнической школы.

Первая теория преобразования тепла в механическую работу была создана Николя Леонаром Сади Карно в 1824 году. Он первым правильно понял, что эффективность этого преобразования зависит от разницы температур между двигателем и окружающей средой.

Признавая значимость работы Джеймса Прескотта Джоуля о сохранении энергии, Рудольф Клаузиус был первым, кто сформулировал второй закон в 1850 году в такой форме: тепло не переходит самопроизвольно от холодных тел к горячим. Хотя сейчас это общеизвестно, это противоречило популярной в то время калорической теории тепла, которая рассматривала тепло как жидкость. Отсюда он смог вывести принцип Сади Карно и определение энтропии (1865).

Установленное в XIX веке утверждение Кельвина-Планка о втором законе гласит: «Никакое устройство, работающее по циклу, не может получать тепло из одного резервуара и производить чистую работу». Было показано, что это утверждение эквивалентно утверждению Клаузиуса.

Эргодическая гипотеза также важна для подхода Больцмана . Она утверждает, что в течение длительных периодов времени время, проведенное в некоторой области фазового пространства микросостояний с одинаковой энергией, пропорционально объему этой области, т.е. что все доступные микросостояния равновероятны в течение длительного периода времени. Эквивалентно, она утверждает, что среднее по времени и среднее по статистическому ансамблю одинаковы.

Существует традиционная доктрина, начинающаяся с Клаузиуса, что энтропию можно понимать в терминах молекулярного «беспорядка» внутри макроскопической системы . Эта доктрина устарела. ^{[72] [73] [74]}

Отчет, предоставленный Клаузиусом

Рудольф Клаузиус

В 1865 году немецкий физик Рудольф Клаузиус сформулировал то, что он назвал «второй фундаментальной теоремой механической теории тепла » в следующей форме: ^[75]

${\displaystyle \int {\frac {\delta Q}{T}}=-N}$

где Q — тепло, T — температура, а N — «эквивалентная величина» всех некомпенсированных преобразований, участвующих в циклическом процессе. Позже, в 1865 году, Клаузиус придет к определению «эквивалентной величины» как энтропии. Вслед за этим определением, в том же году, самая известная версия второго закона была зачитана в презентации в Философском обществе Цюриха 24 апреля, в которой, в конце своей презентации, Клаузиус заключает:

Энтропия Вселенной стремится к максимуму.

Это утверждение является наиболее известной формулировкой второго закона. Из-за неопределенности его языка, например, вселенная , а также из-за отсутствия конкретных условий, например, открытости, закрытости или изолированности, многие люди считают это простое утверждение тем, что второй закон термодинамики применим практически к любому мыслимому предмету. Это не так; это утверждение является лишь упрощенной версией более расширенного и точного описания.

С точки зрения изменения во времени математическая формулировка второго закона для изолированной системы, подвергающейся произвольному преобразованию, выглядит следующим образом:

${\displaystyle {\frac {dS}{dt}}\geq 0}$

где

S — энтропия системы и

т - время .

Знак равенства применяется после уравновешивания. Альтернативный способ формулировки второго закона для изолированных систем:

${\displaystyle {\frac {dS}{dt}}={\dot {S}}_{\text{i}}}$с ${\displaystyle {\dot {S}}_{\text{i}}\geq 0}$

с суммой скорости производства энтропии всеми процессами внутри системы. Преимущество этой формулировки в том, что она показывает эффект производства энтропии. Скорость производства энтропии является очень важным понятием, поскольку она определяет (ограничивает) эффективность тепловых машин. Умноженная на температуру окружающей среды, она дает так называемую рассеиваемую энергию . ${\displaystyle {\dot {S}}_{\text{i}}}$ ${\displaystyle T_{\text{a}}}$ ${\displaystyle P_{\text{diss}}=T_{\text{a}}{\dot {S}}_{\text{i}}}$

Выражение второго закона для закрытых систем (то есть допускающих теплообмен и движущиеся границы, но не обмен веществ) имеет вид:

${\displaystyle {\frac {dS}{dt}}={\frac {\dot {Q}}{T}}+{\dot {S}}_{\text{i}}}$с ${\displaystyle {\dot {S}}_{\text{i}}\geq 0}$

Здесь,

${\displaystyle {\dot {Q}}}$это поток тепла в систему

${\displaystyle T}$— это температура в точке, где тепло поступает в систему.

Знак равенства имеет место в том случае, если внутри системы происходят только обратимые процессы. Если же происходят необратимые процессы (что имеет место в реальных системах, находящихся в эксплуатации), то имеет место знак >. Если тепло подводится к системе в нескольких местах, то следует взять алгебраическую сумму соответствующих членов.

Для открытых систем (также допускающих обмен веществ):

${\displaystyle {\frac {dS}{dt}}={\frac {\dot {Q}}{T}}+{\dot {S}}+{\dot {S}}_{\text{i}}}$с ${\displaystyle {\dot {S}}_{\text{i}}\geq 0}$

Здесь — поток энтропии в систему, связанный с потоком материи, поступающей в систему. Его не следует путать с производной энтропии по времени. Если материя поступает в нескольких местах, то мы должны взять алгебраическую сумму этих вкладов. ${\displaystyle {\dot {S}}}$

Статистическая механика

Статистическая механика дает объяснение второму закону, постулируя, что материал состоит из атомов и молекул, которые находятся в постоянном движении. Определенный набор положений и скоростей для каждой частицы в системе называется микросостоянием системы , и из-за постоянного движения система постоянно меняет свое микросостояние. Статистическая механика постулирует, что в равновесии каждое микросостояние, в котором может находиться система, имеет одинаковую вероятность возникновения, и когда делается это предположение, это приводит непосредственно к выводу, что второй закон должен выполняться в статистическом смысле. То есть второй закон будет выполняться в среднем со статистическим изменением порядка 1/ √ N, где N — число частиц в системе. Для повседневных (макроскопических) ситуаций вероятность того, что второй закон будет нарушен, практически равна нулю. Однако для систем с небольшим числом частиц термодинамические параметры, включая энтропию, могут показывать значительные статистические отклонения от предсказанных вторым законом. Классическая термодинамическая теория не имеет дела с этими статистическими изменениями.

Вывод из статистической механики

Первый механический аргумент кинетической теории газов о том, что молекулярные столкновения влекут за собой выравнивание температур и, следовательно, тенденцию к равновесию, был выдвинут Джеймсом Клерком Максвеллом в 1860 году; ^[76] Людвиг Больцман в своей H-теореме 1872 года также утверждал, что из-за столкновений газы должны со временем стремиться к распределению Максвелла–Больцмана .

Из-за парадокса Лошмидта , выводы второго закона должны делать предположение относительно прошлого, а именно, что система некоррелирована в какой-то момент в прошлом; это допускает простую вероятностную трактовку. Это предположение обычно рассматривается как граничное условие , и, таким образом, второй закон в конечном итоге является следствием начальных условий где-то в прошлом, вероятно, в начале Вселенной ( Большой взрыв ), хотя были предложены и другие сценарии . ^{[77] [78] [79]}

Учитывая эти предположения, в статистической механике второй закон не является постулатом, а скорее следствием фундаментального постулата , также известного как постулат равной априорной вероятности, при условии, что ясно, что простые вероятностные аргументы применяются только к будущему, в то время как для прошлого имеются вспомогательные источники информации, которые говорят нам, что это была низкая энтропия. ^{[ необходима цитата ]} Первая часть второго закона, которая гласит, что энтропия термически изолированной системы может только увеличиваться, является тривиальным следствием постулата равной априорной вероятности, если мы ограничим понятие энтропии системами в тепловом равновесии. Энтропия изолированной системы в тепловом равновесии, содержащей количество энергии, равна: ${\displaystyle E}$

${\displaystyle S=k_{\mathrm {B} }\ln \left[\Omega \left(E\right)\right]}$

где — число квантовых состояний в малом интервале между и . Здесь — макроскопически малый интервал энергии, который сохраняется фиксированным. Строго говоря, это означает, что энтропия зависит от выбора . Однако в термодинамическом пределе (т.е. в пределе бесконечно большого размера системы) удельная энтропия (энтропия на единицу объема или на единицу массы) не зависит от . ${\displaystyle \Omega \left(E\right)}$ ${\displaystyle E}$ ${\displaystyle E+\delta E}$ ${\displaystyle \delta E}$ ${\displaystyle \delta E}$ ${\displaystyle \delta E}$

Предположим, что у нас есть изолированная система, макроскопическое состояние которой задается рядом переменных. Эти макроскопические переменные могут, например, относиться к общему объему, положениям поршней в системе и т. д. Тогда будет зависеть от значений этих переменных. Если переменная не фиксирована (например, мы не зажимаем поршень в определенном положении), то, поскольку все доступные состояния равновероятны в равновесии, свободная переменная в равновесии будет такой, что максимизируется при заданной энергии изолированной системы ^[80] , поскольку это наиболее вероятная ситуация в равновесии. ${\displaystyle \Omega }$ ${\displaystyle \Omega }$

Если переменная изначально была зафиксирована на некотором значении, то после освобождения и при достижении нового равновесия тот факт, что переменная подстроится так, что будет максимизирована, подразумевает, что энтропия увеличится или останется прежней (если значение, при котором переменная была зафиксирована, окажется равновесным значением). Предположим, мы начинаем с равновесной ситуации и внезапно снимаем ограничение на переменную. Тогда сразу после того, как мы это сделаем, есть несколько доступных микросостояний, но равновесие еще не достигнуто, поэтому фактические вероятности нахождения системы в некотором доступном состоянии еще не равны априорной вероятности . Мы уже видели, что в конечном равновесном состоянии энтропия увеличится или останется прежней относительно предыдущего равновесного состояния. Однако H-теорема Больцмана доказывает, что величина H монотонно увеличивается как функция времени в течение промежуточного неравновесного состояния. ${\displaystyle \Omega }$ ${\displaystyle \Omega }$ ${\displaystyle 1/\Omega }$

Вывод изменения энтропии для обратимых процессов

Вторая часть второго закона гласит, что изменение энтропии системы, подвергающейся обратимому процессу, определяется по формуле:

${\displaystyle dS={\frac {\delta Q}{T}}}$

где температура определяется как:

${\displaystyle {\frac {1}{k_{\mathrm {B} }T}}\equiv \beta \equiv {\frac {d\ln \left[\Omega \left(E\right)\right]}{dE}}}$

См. Микроканонический ансамбль для обоснования этого определения. Предположим, что система имеет некоторый внешний параметр x , который может быть изменен. В общем случае собственные энергетические состояния системы будут зависеть от x . Согласно адиабатической теореме квантовой механики, в пределе бесконечно медленного изменения гамильтониана системы система останется в том же собственном энергетическом состоянии и, таким образом, изменит свою энергию в соответствии с изменением энергии собственного энергетического состояния, в котором она находится.

Обобщенная сила X , соответствующая внешней переменной x , определяется так, что — это работа, выполняемая системой, если x увеличивается на величину dx . Например, если x — это объем, то X — это давление. Обобщенная сила для системы, которая, как известно, находится в собственном энергетическом состоянии, определяется как: ${\displaystyle Xdx}$ ${\displaystyle E_{r}}$

${\displaystyle X=-{\frac {dE_{r}}{dx}}}$

Поскольку система может находиться в любом собственном энергетическом состоянии в пределах интервала , мы определяем обобщенную силу для системы как математическое ожидание приведенного выше выражения: ${\displaystyle \delta E}$

${\displaystyle X=-\left\langle {\frac {dE_{r}}{dx}}\right\rangle \,}$

Чтобы оценить среднее значение, мы разделяем собственные энергетические состояния, подсчитывая, сколько из них имеют значение в диапазоне от и . Называя это число , мы имеем: ${\displaystyle \Omega \left(E\right)}$ ${\displaystyle {\frac {dE_{r}}{dx}}}$ ${\displaystyle Y}$ ${\displaystyle Y+\delta Y}$ ${\displaystyle \Omega _{Y}\left(E\right)}$

${\displaystyle \Omega \left(E\right)=\sum _{Y}\Omega _{Y}\left(E\right)\,}$

Среднее значение, определяющее обобщенную силу, теперь можно записать:

${\displaystyle X=-{\frac {1}{\Omega \left(E\right)}}\sum _{Y}Y\Omega _{Y}\left(E\right)\,}$

Мы можем связать это с производной энтропии по x при постоянной энергии E следующим образом. Предположим, мы изменяем x на x + dx . Тогда изменится, поскольку собственные энергетические состояния зависят от x , заставляя собственные энергетические состояния перемещаться в диапазон между и или из него . Давайте снова сосредоточимся на собственных энергетических состояниях, для которых лежит в диапазоне между и . Поскольку эти собственные энергетические состояния увеличиваются по энергии на Y dx , все такие собственные энергетические состояния, которые находятся в интервале от E – Y dx до E , перемещаются из-под E в-выше E . Существуют ${\displaystyle \Omega \left(E\right)}$ ${\displaystyle E}$ ${\displaystyle E+\delta E}$ ${\textstyle {\frac {dE_{r}}{dx}}}$ ${\displaystyle Y}$ ${\displaystyle Y+\delta Y}$

${\displaystyle N_{Y}\left(E\right)={\frac {\Omega _{Y}\left(E\right)}{\delta E}}Ydx\,}$

такие энергетические собственные состояния. Если , все эти энергетические собственные состояния переместятся в диапазон между и и будут способствовать увеличению . Количество энергетических собственных состояний, которые перемещаются снизу вверх, определяется как . Разница ${\displaystyle Ydx\leq \delta E}$ ${\displaystyle E}$ ${\displaystyle E+\delta E}$ ${\displaystyle \Omega }$ ${\displaystyle E+\delta E}$ ${\displaystyle E+\delta E}$ ${\displaystyle N_{Y}\left(E+\delta E\right)}$

${\displaystyle N_{Y}\left(E\right)-N_{Y}\left(E+\delta E\right)\,}$

Таким образом, это чистый вклад в увеличение . Если Y dx больше, то будут собственные энергетические состояния, которые перемещаются снизу E вверх . Они учитываются как в , так и , поэтому приведенное выше выражение справедливо и в этом случае. ${\displaystyle \Omega }$ ${\displaystyle \delta E}$ ${\displaystyle E+\delta E}$ ${\displaystyle N_{Y}\left(E\right)}$ ${\displaystyle N_{Y}\left(E+\delta E\right)}$

Выражая приведенное выше выражение как производную по E и суммируя по Y, получаем выражение:

${\displaystyle \left({\frac {\partial \Omega }{\partial x}}\right)_{E}=-\sum _{Y}Y\left({\frac {\partial \Omega _{Y}}{\partial E}}\right)_{x}=\left({\frac {\partial \left(\Omega X\right)}{\partial E}}\right)_{x}\,}$

Логарифмическая производная по x, таким образом, определяется выражением: ${\displaystyle \Omega }$

${\displaystyle \left({\frac {\partial \ln \left(\Omega \right)}{\partial x}}\right)_{E}=\beta X+\left({\frac {\partial X}{\partial E}}\right)_{x}\,}$

Первый член интенсивен, т.е. он не масштабируется с размером системы. Напротив, последний член масштабируется как обратный размер системы и, таким образом, исчезнет в термодинамическом пределе. Таким образом, мы обнаружили, что:

${\displaystyle \left({\frac {\partial S}{\partial x}}\right)_{E}={\frac {X}{T}}\,}$

Объединяя это с

${\displaystyle \left({\frac {\partial S}{\partial E}}\right)_{x}={\frac {1}{T}}\,}$

дает:

${\displaystyle dS=\left({\frac {\partial S}{\partial E}}\right)_{x}dE+\left({\frac {\partial S}{\partial x}}\right)_{E}dx={\frac {dE}{T}}+{\frac {X}{T}}dx={\frac {\delta Q}{T}}\,}$

Вывод для систем, описываемых каноническим ансамблем

Если система находится в тепловом контакте с термостатом при некоторой температуре T , то в равновесии распределение вероятностей по собственным значениям энергии задается каноническим ансамблем :

${\displaystyle P_{j}={\frac {\exp \left(-{\frac {E_{j}}{k_{\mathrm {B} }T}}\right)}{Z}}}$

Здесь Z — фактор, нормирующий сумму всех вероятностей к 1, эта функция известна как функция распределения . Рассмотрим теперь бесконечно малое обратимое изменение температуры и внешних параметров, от которых зависят уровни энергии. Из общей формулы для энтропии следует:

${\displaystyle S=-k_{\mathrm {B} }\sum _{j}P_{j}\ln \left(P_{j}\right)}$

что

${\displaystyle dS=-k_{\mathrm {B} }\sum _{j}\ln \left(P_{j}\right)dP_{j}}$

Подставив сюда формулу для канонического ансамбля, получим: ${\displaystyle P_{j}}$

${\displaystyle dS={\frac {1}{T}}\sum _{j}E_{j}dP_{j}={\frac {1}{T}}\sum _{j}d\left(E_{j}P_{j}\right)-{\frac {1}{T}}\sum _{j}P_{j}dE_{j}={\frac {dE+\delta W}{T}}={\frac {\delta Q}{T}}}$

Начальные условия при Большом взрыве

Как было сказано выше, считается, что второй закон термодинамики является результатом начальных условий с очень низкой энтропией при Большом взрыве . Со статистической точки зрения, это были очень особые условия. С другой стороны, они были довольно простыми, поскольку вселенная — или, по крайней мере, та ее часть, из которой развилась наблюдаемая вселенная — кажется, была чрезвычайно однородной. ^[81]

Это может показаться несколько парадоксальным, поскольку во многих физических системах однородные условия (например, смешанные, а не разделенные газы) имеют высокую энтропию. Парадокс решается, как только осознается, что гравитационные системы имеют отрицательную теплоемкость , так что, когда гравитация важна, однородные условия (например, газ однородной плотности) на самом деле имеют более низкую энтропию по сравнению с неоднородными (например, черные дыры в пустом пространстве). ^[82] Еще один подход заключается в том, что Вселенная имела высокую (или даже максимальную) энтропию, учитывая ее размер, но по мере роста Вселенная быстро вышла из термодинамического равновесия, ее энтропия лишь немного увеличилась по сравнению с увеличением максимально возможной энтропии, и, таким образом, она достигла очень низкой энтропии по сравнению с гораздо большим возможным максимумом, учитывая ее более поздний размер. ^[83]

Что касается причины, по которой начальные условия были такими, одно из предположений заключается в том, что космологическая инфляция была достаточна для устранения негладкости, в то время как другое заключается в том, что Вселенная была создана спонтанно , а механизм создания подразумевает начальные условия с низкой энтропией. ^[84]

Живые организмы

Существует два основных способа формулирования термодинамики: (a) через переходы из одного состояния термодинамического равновесия в другое и (b) через циклические процессы, при которых система остается неизменной, в то время как общая энтропия окружающей среды увеличивается. Эти два способа помогают понять процессы жизни. Термодинамика живых организмов рассматривалась многими авторами, включая Эрвина Шредингера (в его книге «Что такое жизнь? ») и Леона Бриллюэна . ^[85]

В достаточном приближении живые организмы можно рассматривать как примеры (b). Примерно, физическое состояние животного циклично по дням, оставляя животное почти неизменным. Животные потребляют пищу, воду и кислород и, в результате метаболизма , выделяют продукты распада и тепло. Растения поглощают лучистую энергию от солнца, которую можно рассматривать как тепло, углекислый газ и воду. Они выделяют кислород. Таким образом, они растут. В конце концов они умирают, и их останки гниют, превращаясь в основном обратно в углекислый газ и воду. Это можно рассматривать как циклический процесс. В целом, солнечный свет исходит от источника с высокой температурой, солнца, и его энергия передается в поглотитель с более низкой температурой, т. е. излучается в космос. Это увеличение энтропии окружающей среды растения. Таким образом, животные и растения подчиняются второму закону термодинамики, рассматриваемому с точки зрения циклических процессов.

Более того, способность живых организмов расти и усложняться, а также формировать корреляции с окружающей средой в форме адаптации и памяти, не противоречит второму закону, а скорее близка к общим результатам, вытекающим из него: согласно некоторым определениям, увеличение энтропии также приводит к увеличению сложности, ^[86] а для конечной системы, взаимодействующей с конечными резервуарами, увеличение энтропии эквивалентно увеличению корреляций между системой и резервуарами. ^[87]

Живые организмы можно рассматривать как открытые системы, поскольку материя входит в них и выходит из них. Термодинамика открытых систем в настоящее время часто рассматривается в терминах переходов из одного состояния термодинамического равновесия в другое или в терминах потоков в приближении локального термодинамического равновесия. Проблема для живых организмов может быть еще более упрощена приближением предположения устойчивого состояния с неизменными потоками. Общие принципы производства энтропии для таких приближений являются предметом текущих исследований .

Гравитационные системы

Обычно системы, для которых гравитация не важна, имеют положительную теплоемкость , что означает, что их температура растет с ростом их внутренней энергии. Поэтому, когда энергия течет от высокотемпературного объекта к низкотемпературному объекту, температура источника уменьшается, а температура стока увеличивается; следовательно, разница температур имеет тенденцию уменьшаться с течением времени.

Это не всегда так для систем, в которых гравитационная сила важна: системы, которые связаны собственной гравитацией, такие как звезды, могут иметь отрицательную теплоемкость. По мере их сжатия и их полная энергия, и их энтропия уменьшаются ^[88], но их внутренняя температура может увеличиваться . Это может быть значительным для протозвезд и даже газовых гигантских планет, таких как Юпитер . Однако, когда включается энтропия излучения черного тела, испускаемого телами, можно показать, что полная энтропия системы увеличивается, даже если энтропия планеты или звезды уменьшается. ^[89]

Неравновесные состояния

Теория классической или равновесной термодинамики идеализирована. Основной постулат или предположение, часто даже не сформулированное явно, заключается в существовании систем в их собственных внутренних состояниях термодинамического равновесия. В общем, область пространства, содержащая физическую систему в данный момент времени, которая может быть обнаружена в природе, не находится в термодинамическом равновесии, если читать в самых строгих терминах. В более свободных терминах, ничто во всей вселенной не находится или никогда не находилось в точном термодинамическом равновесии. ^{[90] [91]}

Для целей физического анализа часто бывает достаточно удобно сделать предположение о термодинамическом равновесии . Такое предположение может опираться на метод проб и ошибок для своего обоснования. Если предположение обосновано, оно часто может быть очень ценным и полезным, поскольку оно делает доступной теорию термодинамики. Элементы предположения о равновесии заключаются в том, что система наблюдается неизменной в течение неопределенно долгого времени, и что в системе так много частиц, что ее корпускулярную природу можно полностью игнорировать. При таком предположении о равновесии, как правило, нет макроскопически обнаруживаемых флуктуаций . Существует исключение, случай критических состояний , которые демонстрируют невооруженным глазом явление критической опалесценции . Для лабораторных исследований критических состояний необходимы исключительно длительные времена наблюдения.

Во всех случаях предположение о термодинамическом равновесии, однажды сделанное, подразумевает, что ни одна предполагаемая «флуктуация» не изменяет энтропию системы.

Легко может случиться, что физическая система демонстрирует внутренние макроскопические изменения, которые достаточно быстры, чтобы сделать недействительным предположение о постоянстве энтропии. Или что физическая система имеет так мало частиц, что корпускулярная природа проявляется в наблюдаемых флуктуациях. Тогда предположение о термодинамическом равновесии должно быть отвергнуто. Не существует безусловного общего определения энтропии для неравновесных состояний. ^[92]

Существуют промежуточные случаи, в которых предположение о локальном термодинамическом равновесии является очень хорошим приближением, ^{[93] [94] [95] [96],} но, строго говоря, это все еще приближение, а не теоретически идеальный вариант.

Для неравновесных ситуаций в целом может быть полезно рассмотреть статистические механические определения других величин, которые можно удобно назвать «энтропией», но их не следует путать или объединять с термодинамической энтропией, правильно определенной для второго закона. Эти другие величины действительно принадлежат статистической механике, а не термодинамике, первичной области второго закона.

Физика макроскопически наблюдаемых флуктуаций выходит за рамки данной статьи.

Стрела времени

Второй закон термодинамики — это физический закон, который не симметричен изменению направления времени. Это не противоречит симметриям, наблюдаемым в фундаментальных законах физики (в частности, симметрии CPT ), поскольку второй закон статистически применяется к асимметричным по времени граничным условиям. ^[97] Второй закон был связан с разницей между движением вперед и назад во времени или с принципом, согласно которому причина предшествует следствию ( причинная стрела времени , или причинность ). ^[98]

Необратимость

Необратимость в термодинамических процессах является следствием асимметричного характера термодинамических операций, а не каких-либо внутренне необратимых микроскопических свойств тел. Термодинамические операции являются макроскопическими внешними вмешательствами, налагаемыми на участвующие тела, а не вытекающими из их внутренних свойств. Существуют известные «парадоксы», которые возникают из-за неспособности распознать это.

Парадокс Лошмидта

Парадокс Лошмидта , также известный как парадокс обратимости, представляет собой возражение, согласно которому невозможно вывести необратимый процесс из симметричной во времени динамики, описывающей микроскопическую эволюцию макроскопической системы.

По мнению Шредингера, «теперь совершенно очевидно, каким образом вам следует переформулировать закон энтропии — или, если на то пошло, все другие необратимые утверждения — так, чтобы их можно было вывести из обратимых моделей. Вы не должны говорить об одной изолированной системе, а по крайней мере о двух, которые вы можете на данный момент считать изолированными от остального мира, но не всегда друг от друга». ^[99] Две системы изолированы друг от друга стеной, пока она не будет удалена термодинамической операцией, как предусмотрено законом. Термодинамическая операция навязывается извне, не подчиняясь обратимым микроскопическим динамическим законам, которые управляют составляющими систем. Она является причиной необратимости. Формулировка закона в настоящей статье соответствует совету Шредингера. Причинно-следственная связь логически предшествует второму закону, а не выводится из него.

Теорема о возвращении Пуанкаре

Теорема о возвращении Пуанкаре рассматривает теоретическое микроскопическое описание изолированной физической системы. Это можно рассматривать как модель термодинамической системы после того, как термодинамическая операция удалила внутреннюю стенку. Система через достаточно долгое время вернется в микроскопически определенное состояние, очень близкое к исходному. Время возвращения Пуанкаре — это промежуток времени, прошедший до возвращения. Оно чрезвычайно велико, вероятно, больше, чем жизнь вселенной, и чувствительно зависит от геометрии стенки, которая была удалена термодинамической операцией. Теорема о возвращении может восприниматься как явно противоречащая второму закону термодинамики. Однако более очевидно, что это просто микроскопическая модель термодинамического равновесия в изолированной системе, образованной удалением стенки между двумя системами. Для типичной термодинамической системы время возвращения настолько велико (во много раз больше, чем время жизни вселенной), что для всех практических целей невозможно наблюдать возвращение. Тем не менее, можно было бы представить, что можно было бы дождаться повторения Пуанкаре, а затем снова вставить стенку, которая была удалена термодинамической операцией. Тогда очевидно, что появление необратимости обусловлено полной непредсказуемостью повторения Пуанкаре, учитывая только то, что начальное состояние было состоянием термодинамического равновесия, как это имеет место в макроскопической термодинамике. Даже если бы можно было дождаться его, у нас нет практической возможности выбрать правильный момент, в который нужно снова вставить стенку. Теорема о повторении Пуанкаре дает решение парадокса Лошмидта. Если бы изолированную термодинамическую систему можно было бы контролировать в течение все большего числа кратных среднего времени повторения Пуанкаре, термодинамическое поведение системы стало бы инвариантным относительно обращения времени.

Джеймс Клерк Максвелл

демон Максвелла

Джеймс Клерк Максвелл представил себе один контейнер, разделенный на две части, A и B. Обе части заполнены одним и тем же газом при одинаковой температуре и размещены рядом друг с другом, разделенные стенкой. Наблюдая за молекулами с обеих сторон, воображаемый демон охраняет микроскопический люк в стене. Когда молекула, движущаяся быстрее среднего, из A летит к люку, демон открывает его, и молекула летит из A в B. Средняя скорость молекул в B увеличится, в то время как в A они в среднем замедлятся. Поскольку средняя молекулярная скорость соответствует температуре, температура уменьшается в A и увеличивается в B , вопреки второму закону термодинамики. ^[100]

Один из ответов на этот вопрос был предложен в 1929 году Лео Силардом , а позднее Леоном Бриллюэном . Силард указал, что реальному демону Максвелла понадобятся некоторые средства измерения скорости молекул, и что процесс получения информации потребует затрат энергии. ^[101] Аналогичным образом Бриллюэн продемонстрировал, что уменьшение энтропии, вызванное демоном, будет меньше энтропии, произведенной при выборе молекул на основе их скорости. ^[100]

«Демон» Максвелла многократно изменяет проницаемость стенки между A и B. Таким образом, он выполняет термодинамические операции в микроскопическом масштабе, а не просто наблюдает обычные спонтанные или естественные макроскопические термодинамические процессы. ^[101]

Цитаты

Закон, что энтропия всегда возрастает, занимает, я думаю, верховное положение среди законов природы . Если кто-то указывает вам, что ваша любимая теория вселенной не согласуется с уравнениями Максвелла , — тем хуже для уравнений Максвелла. Если же окажется, что она противоречит наблюдениям, — ну, эти экспериментаторы иногда что-то путают. Но если ваша теория окажется противоречащей второму закону термодинамики, я не могу дать вам никакой надежды; вам ничего не остается, кроме как рухнуть в глубочайшем унижении.

—  Сэр Артур Стэнли Эддингтон , Природа физического мира (1927)

Формулировок второго закона было почти столько же, сколько и его обсуждений.

—  Философ/Физик П. У. Бриджмен , (1941)

Клаузиус является автором пророческого изречения: «Энергия Вселенной постоянна; энтропия Вселенной стремится к максимуму». Цели континуальной термомеханики далеки от объяснения «Вселенной», но в рамках этой теории мы можем легко вывести явное утверждение, в некотором роде напоминающее Клаузиуса, но относящееся только к скромному объекту: изолированному телу конечного размера.

—  Трусделл, К. , Манкастер, Р. Г. (1980). Основы кинетической теории Максвелла простого одноатомного газа, рассматриваемые как раздел рациональной механики , Academic Press, Нью-Йорк, ISBN  0-12-701350-4 , стр. 17.

Смотрите также

• Нулевой закон термодинамики
• Первый закон термодинамики
• Третий закон термодинамики
• Неравенство Клаузиуса–Дюгема
• Теорема флуктуации
• Тепловая смерть вселенной
• История термодинамики
• равенство Яжинского
• Законы термодинамики
• Максимальная энтропия термодинамики
• Квантовая термодинамика
• Размышления о движущей силе огня
• Релятивистская теплопроводность
• Термодиод
• Термодинамическое равновесие

Ссылки

1. Райхл, Линда (1980). Современный курс статистической физики . Эдвард Арнольд. стр. 9. ISBN 0-7131-2789-9.
2. Rao, YVC (1997). Химическая инженерия Термодинамика . Universities Press. стр. 158. ISBN 978-81-7371-048-3.
3. Янг, Х. Д.; Фридман, Р. А. (2004). Университетская физика , 11-е издание. Пирсон. стр. 764.
4. "5.2 Аксиоматические утверждения законов термодинамики". www.web.mit.edu . Массачусетский технологический институт .
5. {Дэвид Сэнборн Скотт, Стрела времени, Международный журнал водородной энергетики, том 28, выпуск 2, 2003, страницы 147-149, ISSN 0360-3199}
6. Кэрролл, Шон (2010). От вечности к настоящему: поиск окончательной теории времени . Даттон. ISBN 978-0-525-95133-9.
7. Джаффе, Р. Л.; Тейлор, В. (2018). Физика энергии. Кембридж, Великобритания: Cambridge University Press. стр. 150, № 259, 772, 743. ISBN 978-1-107-01665-1.
8. Дэвид Л. Чандлер (2011-05-19). «Объяснение: предел Карно».
9. Планк, М. (1897/1903), стр. 40–41.
10. Мюнстер А. (1970), стр. 8–9, 50–51.
11. Мандл 1988
12. Планк, М. (1897/1903), стр. 79–107.
13. Бейлин, М. (1994), Раздел 71, стр. 113–154.
14. Бейлин, М. (1994), стр. 120.
15. Мортимер, RG (2008). Физическая химия. Elsevier Science. стр. 120. ISBN 978-0-12-370617-1.
16. Ферми, Э. (2012). Термодинамика. Dover Books on Physics. Dover Publications. стр. 48. ISBN 978-0-486-13485-7.
17. Адкинс, CJ (1968/1983), стр. 75.
18. Мюнстер, А. (1970), стр. 45.
19. Oxtoby, D. W; Gillis, HP, Butler, LJ (2015). Principles of Modern Chemistry , Brooks Cole. стр. 617. ISBN 978-1305079113 
20. Покровский В.Н. (2005) Расширенная термодинамика в дискретно-системном подходе, Eur. J. Phys. т. 26, 769–781.
21. Покровский, Владимир Н. (2013). «Вывод основных соотношений неравновесной термодинамики». ISRN Термодинамика . 2013 : 1–9. doi : 10.1155/2013/906136 .
22. JS Dugdale (1996). Энтропия и ее физическое значение . Тейлор и Фрэнсис. стр. 13. ISBN 978-0-7484-0569-5. Этот закон является основой температуры.
23. Земанский, MW (1968), стр. 207–209.
24. Куинн, Т.Дж. (1983), стр. 8.
25. "Концепция и положения Второго закона". web.mit.edu . Получено 2010-10-07 .
26. Либ и Ингвасон (1999).
27. Рао (2004), стр. 213.
28. Карно, С. (1824/1986).
29. Карно, С. (1824/1986), стр. 51.
30. Карно, С. (1824/1986), стр. 46.
31. Карно, С. (1824/1986), стр. 68.
32. Трусделл, К. (1980), Глава 5.
33. Адкинс, CJ (1968/1983), стр. 56–58.
34. Мюнстер, А. (1970), стр. 11.
35. Кондепуди Д., Пригожин И. (1998), стр. 67–75.
36. Лебон, Г., Джоу, Д., Касас-Васкес, Дж. (2008), стр. 10.
37. Eu, BC (2002), стр. 32–35.
38. Клаузиус (1850).
39. Клаузиус (1854), стр. 86.
40. Томсон (1851).
41. Планк, М. (1897/1903), стр. 86.
42. Робертс, Дж. К., Миллер, А. Р. (1928/1960), стр. 319.
43. тер Хаар, Д. , Вергеланд, Х. (1966), с. 17.
44. Планк, М. (1897/1903), стр. 100.
45. Планк, М. (1926), стр. 463, перевод Уффинка, Дж. (2003), стр. 131.
46. Roberts, JK, Miller, AR (1928/1960), стр. 382. Этот источник частично дословно цитирует утверждение Планка, но не цитирует Планка. Этот источник называет утверждение принципом возрастания энтропии.
47. Уленбек, GE , Форд, GW (1963), стр. 16.
48. Каратеодори, К. (1909).
49. Бухдаль, HA (1966), стр. 68.
50. Сычев, В. В. (1991). Дифференциальные уравнения термодинамики . Тейлор и Фрэнсис. ISBN 978-1-56032-121-7.
51. Lieb & Yngvason (1999), стр. 49.
52. Планк, М. (1926).
53. Бухдаль, HA (1966), стр. 69.
54. Уффинк, Дж. (2003), стр. 129–132.
55. Трусделл, К. , Манкастер, Р. Г. (1980). Основы кинетической теории Максвелла простого одноатомного газа, рассматриваемые как раздел рациональной механики , Academic Press, Нью-Йорк, ISBN 0-12-701350-4 , стр. 15. 
56. Планк, М. (1897/1903), стр. 81.
57. Планк, М. (1926), стр. 457, перевод редактора Википедии.
58. Либ, Э.Х., Ингвасон, Дж. (2003), с. 149.
59. Боргнакке, К., Sonntag., RE (2009), стр. 304.
60. Grubbström, Robert W. (1985). «К обобщенной концепции эксергии». В Van Gool, W.; Bruggink, JJC (ред.). Энергия и время в экономических и физических науках . North-Holland. стр. 41–56. ISBN 978-0-444-87748-2.
61. Каллен, Х. Б. (1960/1985), Термодинамика и введение в термостатистику , (первое издание 1960 г.), второе издание 1985 г., John Wiley & Sons, Нью-Йорк, ISBN 0-471-86256-8 , стр. 146–148. 
62. Райт, С. Э. (декабрь 2007 г.). «Неравенство Клаузиуса, исправленное для теплопередачи с участием излучения». Международный журнал инженерных наук . 45 (12): 1007–1016. doi :10.1016/j.ijengsci.2007.08.005. ISSN  0020-7225.
63. Планк, Макс (1914). «Перевод Мортона Маузиуса, Теория теплового излучения». Dover Publications, Нью-Йорк .
64. Ландсберг, ПТ; Тонге, Г (апрель 1979). «Термодинамика преобразования разбавленного излучения». Журнал физики A: Mathematical and General . 12 (4): 551–562. Bibcode : 1979JPhA...12..551L. doi : 10.1088/0305-4470/12/4/015. ISSN  0305-4470.
65. Райт (2001). «Об энтропии лучистого теплообмена в инженерной термодинамике». Int. J. Eng. Sci . 39 (15): 1691–1706. doi :10.1016/S0020-7225(01)00024-6.
66. Райт, SE; Розен, MA; Скотт, DS; Хэддоу, JB (январь 2002 г.). «Поток эксергии лучистого теплопереноса для особого случая излучения черного тела». Exergy . 2 (1): 24–33. doi :10.1016/s1164-0235(01)00040-1. ISSN  1164-0235.
67. Райт, SE; Розен, MA; Скотт, DS; Хэддоу, JB (январь 2002 г.). «Поток эксергии лучистого теплопереноса с произвольным спектром». Exergy . 2 (2): 69–77. doi :10.1016/s1164-0235(01)00041-3. ISSN  1164-0235.
68. Райт, Шон Э.; Розен, Марк А. (2004-02-01). «Эксергетическая эффективность и содержание эксергии в земном солнечном излучении». Журнал солнечной энергетики . 126 (1): 673–676. doi :10.1115/1.1636796. ISSN  0199-6231.
69. Wright, SE (февраль 2017 г.). «Обобщенное и явное концептуальное утверждение принципа второго закона термодинамики». International Journal of Engineering Science . 111 : 12–18. doi :10.1016/j.ijengsci.2016.11.002. ISSN  0020-7225.
70. Теорема Клаузиуса в Wolfram Research
71. Планк, М. (1945). Трактат по термодинамике . Dover Publications. стр. §90. ур. (39) и (40).
72. Денби, К. Г., Денби, Дж. С. (1985). Энтропия в связи с неполным знанием , Cambridge University Press, Кембридж, Великобритания, ISBN 0-521-25677-1 , стр. 43–44. 
73. Гранди, У. Т., младший (2008). Энтропия и временная эволюция макроскопических систем , Oxford University Press, Оксфорд, ISBN 978-0-19-954617-6 , стр. 55–58. 
74. Entropy Sites — Руководство Содержание выбрано Фрэнком Л. Ламбертом
75. Клаузиус (1867).
76. Gyenis, Balazs (2017). «Максвелл и нормальное распределение: красочная история вероятности, независимости и тенденции к равновесию». Исследования по истории и философии современной физики . 57 : 53–65. arXiv : 1702.01411 . Bibcode :2017SHPMP..57...53G. doi :10.1016/j.shpsb.2017.01.001. S2CID  38272381.
77. Хокинг, SW (1985). «Стрела времени в космологии». Phys. Rev. D. 32 ( 10): 2489–2495. Bibcode : 1985PhRvD..32.2489H. doi : 10.1103/PhysRevD.32.2489. PMID  9956019.
78. Грин, Брайан (2004). Ткань космоса . Альфред А. Кнопф. стр. 171. ISBN 978-0-375-41288-2.
79. Лебовиц, Джоэл Л. (сентябрь 1993 г.). «Энтропия Больцмана и стрела времени» (PDF) . Physics Today . 46 (9): 32–38. Bibcode :1993PhT....46i..32L. doi :10.1063/1.881363 . Получено 22.02.2013 .
80. Янг, Х. Д.; Фридман, Р. А. (2004). Университетская физика , 11-е издание. Пирсон. стр. 731.
81. Кэрролл, С. (2017). Общая картина: о происхождении жизни, смысле и самой вселенной. Penguin.
82. Грин, Б. (2004). Ткань космоса: пространство, время и текстура реальности. Кнопф.
83. Дэвис, ПК (1983). Инфляция и асимметрия времени во Вселенной. Nature, 301(5899), 398–400.
84. Физики обсуждают идею Хокинга о том, что у Вселенной не было начала. Wolchover, N. Quantmagazine, 6 июня 2019 г. Получено 28 ноября 2020 г.
85. Бриллюэн, Л. (2013). Наука и теория информации. Dover Books on Physics. Dover Publications, Incorporated. ISBN 978-0-486-49755-6. Получено 26 марта 2021 г. .
86. Ladyman, James; Lambert, James; Wiesner, Karoline (19 июня 2012 г.). «Что такое сложная система?». European Journal for Philosophy of Science . 3 (1). Springer Science and Business Media LLC: 33–67. doi :10.1007/s13194-012-0056-8. ISSN  1879-4912. S2CID  18787276.
87. Эспозито, Массимилиано; Линденберг, Катя ; Ван ден Брок, Кристиан (15 января 2010 г.). «Производство энтропии как корреляция между системой и резервуаром». New Journal of Physics . 12 (1): 013013. arXiv : 0908.1125 . Bibcode : 2010NJPh...12a3013E. doi : 10.1088/1367-2630/12/1/013013 . ISSN  1367-2630.
88. Баез, Джон (7 августа 2000 г.). «Может ли гравитация уменьшить энтропию?». Кафедра математики Калифорнийского университета в Риверсайде . Калифорнийский университет в Риверсайде . Получено 7 июня 2020 г. ... гравитационно связанный шар газа имеет отрицательную удельную теплоемкость!
89. Баез, Джон (7 августа 2000 г.). «Может ли гравитация уменьшить энтропию?». Калифорнийский университет в Риверсайде, кафедра математики . Калифорнийский университет в Риверсайде . Получено 7 июня 2020 г.
90. Гранди, У. Т. (младший) (2008), стр. 151.
91. Каллен, Х.Б. (1960/1985), стр. 15.
92. Либ, Э.Х., Ингвасон, Дж. (2003), с. 190.
93. Дьярмати, И. (1967/1970), стр. 4-14.
94. Глансдорф, П., Пригожин, И. (1971).
95. Мюллер, И. (1985).
96. Мюллер, И. (2003).
97. Каллендер, Крейг (29 июля 2011 г.). «Термодинамическая асимметрия во времени». Стэнфордская энциклопедия философии .
98. Холливелл, Дж. Дж. и др. (1994). Физические истоки асимметрии времени . Кембридж. ISBN 978-0-521-56837-1.глава 6
99. Шрёдингер, Э. (1950), с. 192.
100. "Демон Максвелла | физика | Britannica". www.britannica.com . Получено 14.03.2023 .
101. Norton, John (3 июля 2013 г.). «All Shook Up: Fluctuations, Maxwell's Demon and the Thermodynamics of Computation». Entropy . 15 (12): 4432–4483. Bibcode :2013Entrp..15.4432N. doi : 10.3390/e15104432 .

Источники

• Adkins, CJ (1983). Равновесная термодинамика (1-е изд. 1968, 3-е изд.). Cambridge UK: Cambridge University Press. ISBN 0-521-25445-0. OCLC  9132054.
• Аткинс, П. В. , де Паула, Дж. (2006). Физическая химия Аткинса , восьмое издание, WH Freeman, Нью-Йорк, ISBN 978-0-7167-8759-4 . 
• Аттард, П. (2012). Неравновесная термодинамика и статистическая механика: основы и приложения , Oxford University Press, Оксфорд, Великобритания, ISBN 978-0-19-966276-0 . 
• Байерлейн, Р. (1999). Тепловая физика , Cambridge University Press, Кембридж, Великобритания, ISBN 0-521-59082-5 . 
• Бейлин, М. (1994). Обзор термодинамики , Американский институт физики, Нью-Йорк, ISBN 0-88318-797-3 . 
• Бланделл, Стивен Дж .; Бланделл, Кэтрин М. (2010). Концепции в тепловой физике (2-е изд.). Оксфорд: Oxford University Press . doi :10.1093/acprof:oso/9780199562091.001.0001. ISBN 9780199562107. OCLC  607907330.
• Больцман, Л. (1896/1964). Лекции по теории газа , перевод С. Г. Браша, Издательство Калифорнийского университета, Беркли.
• Боргнакке К., Sonntag., RE (2009). Основы термодинамики , седьмое издание, Wiley, ISBN 978-0-470-04192-5 . 
• Бухдаль, HA (1966). Концепции классической термодинамики , Cambridge University Press, Кембридж, Великобритания.
• Бриджмен, П. У. (1943). Природа термодинамики , Издательство Гарвардского университета, Кембридж, Массачусетс.
• Каллен, Х. Б. (1960/1985). Термодинамика и введение в термостатистику , (1-е издание 1960 г.) 2-е издание 1985 г., Wiley, Нью-Йорк, ISBN 0-471-86256-8 . 
• К. Каратеодори (1909). «Untersuchungen über die Grundlagen der Thermodynamik». Математические Аннален . 67 (3): 355–386. дои : 10.1007/bf01450409. S2CID  118230148. Архивировано из оригинала 4 марта 2016 г. Проверено 18 февраля 2014 г. Аксиома II: In jeder beliebigen Umgebung eines willkürlich vorgeschriebenen Anfangszustandes gibt es Zustände, die durch adiabatische Zustandsänderungen nicht beliebig Approimiert Werden Können. (стр.363). Перевод можно найти здесь. Также наиболее надежный перевод можно найти у Кестина, Дж. (1976). Второй закон термодинамики , Доуден, Хатчинсон и Росс, Страудсбург, Пенсильвания.
• Карно, С. (1824/1986). Размышления о движущей силе огня, Manchester University Press, Manchester UK, ISBN 0-7190-1741-6 . Также здесь. 
• Чепмен, С. , Коулинг, Т.Г. (1939/1970). Математическая теория неоднородных газов. Отчет о кинетической теории вязкости, теплопроводности и диффузии в газах , третье издание 1970, Cambridge University Press, Лондон.
• Клаузиус, Р. (1850). «Ueber Die Bewegende Kraft Der Wärme Und Die Gesetze, Welche Sich Daraus Für Die Wärmelehre Selbst Ableiten Lassen». Аннален дер Физик . 79 (4): 368–397, 500–524. Бибкод : 1850АнП...155..500С. дои : 10.1002/andp.18501550403. hdl : 2027/uc1.$b242250 . Проверено 26 июня 2012 г.Перевод на английский: Клаузиус, Р. (июль 1851 г.). «О движущей силе тепла и законах, касающихся самой природы тепла, которые из нее выводятся». London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science . 4th. 2 (VIII): 1–21, 102–119. doi :10.1080/14786445108646819 . Получено 26 июня 2012 г.
• Клаузиус, Р. (1854). «Über eine veränderte Form des zweiten Hauptsatzes der mechanischen Wärmetheorie» (PDF) . Аннален дер Физик . xciii (12): 481–506. Бибкод : 1854АнП...169..481С. дои : 10.1002/andp.18541691202. Архивировано из оригинала (PDF) 24 марта 2014 года . Проверено 24 марта 2014 г.Перевод на английский: Клаузиус, Р. (июль 1856 г.). «О модифицированной форме второй фундаментальной теоремы в механической теории тепла». London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science . 4th. 2 : 86 . Получено 24 марта 2014 г.Перепечатано в: Клаузиус, Р. (1867). Механическая теория тепла – с ее приложениями к паровой машине и физическим свойствам тел. Лондон: Джон ван Ворст . Получено 19 июня 2012 г. Издания : PwR_Sbkwa8IC.
• Денби, К. (1954/1981). Принципы химического равновесия. С приложениями в химии и химической инженерии , четвертое издание, Cambridge University Press, Кембридж, Великобритания, ISBN 0-521-23682-7 . 
• Eu, BC (2002). Обобщенная термодинамика. Термодинамика необратимых процессов и обобщенная гидродинамика , Kluwer Academic Publishers, Дордрехт, ISBN 1-4020-0788-4 . 
• Гиббс, Дж. У. (1876/1878). О равновесии гетерогенных веществ, Trans. Conn. Acad. , 3 : 108–248, 343–524, перепечатано в The Collected Works of J. Willard Gibbs, Ph.D, LL. D. , под редакцией WR Longley, RG Van Name, Longmans, Green & Co., Нью-Йорк, 1928, том 1, стр. 55–353.
• Griem, HR (2005). Принципы плазменной спектроскопии (Кембриджские монографии по физике плазмы) , Cambridge University Press, Нью-Йорк ISBN 0-521-61941-6 . 
• Глансдорф, П., Пригожин, И. (1971). Термодинамическая теория структуры, устойчивости и флуктуаций , Wiley-Interscience, Лондон, 1971, ISBN 0-471-30280-5 . 
• Грэнди, Уолтер Т. (2008). Энтропия и временная эволюция макроскопических систем. Оксфорд, Нью-Йорк: Oxford University Press. ISBN 978-0-19-954617-6. OCLC  190843367.
• Гревен А., Келлер Г., Варнеке (редакторы) (2003). Энтропия , Издательство Принстонского университета, Принстон, штат Нью-Джерси, ISBN 0-691-11338-6 . 
• Гуггенхайм, Э.А. (1949). «Статистическая основа термодинамики», Исследования , 2 : 450–454.
• Гуггенхайм, Э. А. (1967). Термодинамика. Расширенный курс для химиков и физиков , пятое пересмотренное издание, Северная Голландия, Амстердам.
• Дьярмати, И. (1967/1970) Неравновесная термодинамика. Теория поля и вариационные принципы , перевод Э. Дьярмати и В. Ф. Хайнца, Springer, Нью-Йорк.
• Киттель, К. , Кремер, Х. (1969/1980). Теплофизика , второе издание, Фримен, Сан-Франциско, Калифорния, ISBN 0-7167-1088-9 . 
• Кондепуди, Д., Пригожин, И. (1998). Современная термодинамика: от тепловых двигателей до диссипативных структур , John Wiley & Sons, Чичестер, ISBN 0-471-97393-9 . 
• Лебон Г., Жу Д., Касас-Васкес Дж. (2008). Понимание неравновесной термодинамики: основы, приложения, границы , Springer-Verlag, Берлин, ISBN 978-3-540-74252-4 . 
• Либ, Э. Х.; Ингвасон, Дж. (1999). «Физика и математика второго закона термодинамики». Physics Reports . 310 (1): 1–96. arXiv : cond-mat/9708200 . Bibcode : 1999PhR...310....1L. doi : 10.1016/S0370-1573(98)00082-9. S2CID  119620408.
• Либ Э.Х., Ингвасон Дж. (2003). Энтропия классической термодинамики, стр. 147–195, глава 8 книги «Энтропия» , Гревен А., Келлер Г., Варнеке (редакторы) (2003).
• Мандл, Ф. (1988). Статистическая физика (второе изд.). Wiley & Sons . ISBN 978-0-471-91533-1.
• Максвелл, Дж. К. (1867). «О динамической теории газов». Phil. Trans. R. Soc. Lond . 157 : 49–88. doi :10.1098/rstl.1867.0004. S2CID  96568430.
• Мюллер, И. (1985). Термодинамика , Питман, Лондон, ISBN 0-273-08577-8 . 
• Мюллер, И. (2003). Энтропия в неравновесии, стр. 79–109, глава 5 книги «Энтропия» , Гревен А., Келлер Г., Варнеке (редакторы) (2003).
• Мюнстер, А. (1970), Классическая термодинамика , перевод Э. С. Хальберштадта, Wiley–Interscience, Лондон, ISBN 0-471-62430-6 . 
• Пиппард, А. Б. (1957/1966). Элементы классической термодинамики для продвинутых студентов-физиков , оригинальная публикация 1957 г., переиздание 1966 г., Cambridge University Press, Кембридж, Великобритания.
• Планк, М. (1897/1903). Трактат по термодинамике, перевод А. Огга, Longmans Green, Лондон, стр. 100.
• Планк. М. (1914). Теория теплового излучения, перевод Масиуса М. второго немецкого издания, P. Blakiston's Son & Co., Филадельфия.
• Планк, М. (1926). Über die Begründung des zweiten Hauptsatzes der Thermodynamik, Sitzungsberichte der Preussischen Akademie der Wissenschaften: Physikalisch-mathematische Klasse : 453–463.
• Покровский В.Н. (2005) Расширенная термодинамика в дискретно-системном подходе, Eur. J. Phys. vol. 26, 769–781.
• Покровский, Владимир Н. (2013). «Вывод основных соотношений неравновесной термодинамики». ISRN Термодинамика . 2013 : 1–9. doi : 10.1155/2013/906136 .
• Куинн, Т. Дж. (1983). Температура , Academic Press, Лондон, ISBN 0-12-569680-9 . 
• Рао, YVC (2004). Введение в термодинамику. Universities Press. стр. 213. ISBN 978-81-7371-461-0.
• Робертс, Дж. К., Миллер, А. Р. (1928/1960). Тепло и термодинамика , (первое издание 1928), пятое издание, Blackie & Son Limited, Глазго.
• Шредингер, Э. (1950). Необратимость, Proc. R. Ir. Acad. , A53 : 189–195.
• тер Хаар, Д. , Вергеланд, Х. (1966). Элементы термодинамики , Addison-Wesley Publishing, Reading MA.
• Томсон, В. (1851). «О динамической теории тепла с численными результатами, выведенными из эквивалента тепловой единицы г-на Джоуля и наблюдений М. Реньо над паром». Труды Королевского общества Эдинбурга . XX (часть II): 261–268, 289–298.Также опубликовано в Thomson, W. (декабрь 1852 г.). «О динамической теории тепла с численными результатами, выведенными из эквивалента тепловой единицы г-на Джоуля и наблюдений М. Реньо над паром». Philos. Mag . 4. IV (22): 13. Получено 25 июня 2012 г.
• Томсон, У. (1852). О всеобщей тенденции в природе к рассеиванию механической энергии. Philosophical Magazine, Ser. 4, стр. 304.
• Тиса, Л. (1966). Обобщенная термодинамика , MIT Press, Кембридж, Массачусетс.
• Трусделл, К. (1980). Трагикомическая история термодинамики 1822–1854 , Springer, Нью-Йорк, ISBN 0-387-90403-4 . 
• Уффинк, Дж. (2001). Обманите себя во втором законе термодинамики, Stud. Hist. Phil. Mod. Phys. , 32 (3): 305–394.
• Уффинк, Дж. (2003). Необратимость и второй закон термодинамики, Глава 7 Энтропии , Гревен, А., Келлер, Г., Варнеке (редакторы) (2003), Princeton University Press, Princeton NJ, ISBN 0-691-11338-6 . 
• Уленбек, GE , Форд, GW (1963). Лекции по статистической механике , Американское математическое общество, Провиденс, Род-Айленд.
• Земанский, М. В. (1968). Тепло и термодинамика. Учебник для среднего уровня , пятое издание, McGraw-Hill Book Company, Нью-Йорк.

Дальнейшее чтение

• Goldstein, Martin, and Inge F., 1993. Холодильник и Вселенная . Harvard Univ. Press. Главы 4–9 содержат введение во второй закон, немного менее техническое, чем эта запись. ISBN 978-0-674-75324-2 
• Leff, Harvey S., и Rex, Andrew F. (ред.) 2003. Maxwell's Demon 2: Entropy, classic and quantum information, computing . Bristol UK; Philadelphia PA: Institute of Physics . ISBN 978-0-585-49237-7 
• Холливелл, Дж. Дж. (1994). Физические истоки асимметрии времени . Кембридж. ISBN 978-0-521-56837-1.(технический).
• Карно, Сади (1890). Терстон, Роберт Генри (ред.). Размышления о движущей силе тепла и о машинах, приспособленных для развития этой силы . Нью-Йорк: J. Wiley & Sons.(полный текст издания 1897 г.) (html Архивировано 18 августа 2007 г. на Wayback Machine )
• Стивен Джей Клайн (1999). Вся правда об энтропии и интерпретативной термодинамике , Ла-Каньяда, Калифорния: DCW Industries. ISBN 1-928729-01-0 . 
• Костич, М. (2011). Возвращаясь ко второму закону деградации энергии и генерации энтропии: от гениальных рассуждений Сади Карно к целостному обобщению . Труды конференции AIP. Том 1411. С. 327–350. Bibcode : 2011AIPC.1411..327K. CiteSeerX  10.1.1.405.1945 . doi : 10.1063/1.3665247. ISBN 978-0-7354-0985-9. {{cite book}}: |journal=проигнорировано ( помощь ) также в [1].

Внешние ссылки

• Стэнфордская энциклопедия философии : «Философия статистической механики» – Лоуренс Склар.
• Второй закон термодинамики в курсе Массачусетского технологического института «Единая термодинамика и движение» от проф. З.С. Спаковски
• ET Jaynes , 1988, «Эволюция принципа Карно», в GJ Erickson и CR Smith (ред.) Maximum-Entropy and Bayesian Methods in Science and Engineering , Vol,.1: p. 267.
• Каратеодори, К., «Исследование основ термодинамики», перевод Д. Х. Дельфенича
• Второй закон термодинамики, обсуждение на BBC Radio 4 с Джоном Гриббином, Питером Аткинсом и Моникой Грейди ( In Our Time , 16 декабря 2004 г.)
• Журнал Международного общества истории философии науки, 2012 г.