Корреляция

Статистическая концепция

Несколько наборов точек ( x ,  y ) с коэффициентом корреляции Пирсона x и y для каждого набора. Корреляция отражает шумность и направление линейной связи (верхний ряд), но не наклон этой связи (средний) и не многие аспекты нелинейных связей (нижний). Примечание: фигура в центре имеет наклон 0, но в этом случае коэффициент корреляции не определен, поскольку дисперсия Y равна нулю.

В статистике корреляция или зависимость — это любая статистическая связь, причинная или нет, между двумя случайными величинами или двумерными данными . Хотя в самом широком смысле «корреляция» может указывать на любой тип ассоциации, в статистике она обычно относится к степени, в которой пара переменных линейно связана . Знакомые примеры зависимых явлений включают корреляцию между ростом родителей и их потомства, а также корреляцию между ценой товара и количеством, которое потребители готовы купить, как это изображено на так называемой кривой спроса .

Корреляции полезны, поскольку они могут указывать на предсказательную связь, которую можно использовать на практике. Например, электроэнергетическая компания может производить меньше электроэнергии в мягкий день на основе корреляции между спросом на электроэнергию и погодой. В этом примере существует причинно-следственная связь , поскольку экстремальные погодные условия заставляют людей использовать больше электроэнергии для отопления или охлаждения. Однако, в целом, наличие корреляции недостаточно для вывода о наличии причинно-следственной связи (т. е. корреляция не подразумевает причинно-следственную связь ).

Формально случайные величины являются зависимыми , если они не удовлетворяют математическому свойству вероятностной независимости . В неформальном выражении корреляция является синонимом зависимости . Однако при использовании в техническом смысле корреляция относится к любому из нескольких конкретных типов математических отношений между условным ожиданием одной переменной при условии, что другая не является постоянной при изменении обусловливающей переменной ; в широком смысле корреляция в этом конкретном смысле используется, когда связана с некоторым образом (например, линейно, монотонно или, возможно, в соответствии с некоторой конкретной функциональной формой, такой как логарифмическая). По сути, корреляция является мерой того, как две или более переменных связаны друг с другом. Существует несколько коэффициентов корреляции , часто обозначаемых или , измеряющих степень корреляции. Наиболее распространенным из них является коэффициент корреляции Пирсона , который чувствителен только к линейной связи между двумя переменными (которая может присутствовать, даже если одна переменная является нелинейной функцией другой). Другие коэффициенты корреляции, такие как ранговая корреляция Спирмена , были разработаны, чтобы быть более надежными, чем коэффициент Пирсона, то есть более чувствительными к нелинейным связям. ^{[1] [2] [3]} Взаимная информация также может применяться для измерения зависимости между двумя переменными. ${\displaystyle E(Y|X=x)}$ ${\displaystyle x}$ ${\displaystyle \rho }$ ${\displaystyle r}$

Коэффициент момента произведения Пирсона

Примеры диаграмм рассеяния различных наборов данных с различными коэффициентами корреляции

Наиболее известной мерой зависимости между двумя величинами является коэффициент корреляции Пирсона (PPMCC), или «коэффициент корреляции Пирсона», обычно называемый просто «коэффициентом корреляции». Он получается путем взятия отношения ковариации двух рассматриваемых переменных нашего числового набора данных, нормализованного к квадратному корню их дисперсий. Математически, ковариация двух переменных просто делится на произведение их стандартных отклонений . Карл Пирсон разработал коэффициент из похожей, но немного другой идеи Фрэнсиса Гальтона . ^[4]

Коэффициент корреляции Пирсона-момента пытается установить линию наилучшего соответствия через набор данных из двух переменных, по сути, выкладывая ожидаемые значения, а полученный коэффициент корреляции Пирсона указывает, насколько далеко фактический набор данных находится от ожидаемых значений. В зависимости от знака нашего коэффициента корреляции Пирсона, мы можем получить либо отрицательную, либо положительную корреляцию, если между переменными нашего набора данных есть какая-либо связь. ^{[ необходима цитата ]}

Коэффициент корреляции популяции между двумя случайными величинами с ожидаемыми значениями и стандартными отклонениями определяется как: ${\displaystyle \rho _{X,Y}}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle \mu _{X}}$ ${\displaystyle \mu _{Y}}$ ${\displaystyle \sigma _{X}}$ ${\displaystyle \sigma _{Y}}$

$${\displaystyle \rho _{X,Y}=\operatorname {corr} (X,Y)={\operatorname {cov} (X,Y) \over \sigma _{X}\sigma _{Y}}={\operatorname {E} [(X-\mu _{X})(Y-\mu _{Y})] \over \sigma _{X}\sigma _{Y}},\quad {\text{if}}\ \sigma _{X}\sigma _{Y}>0.}$$

где — оператор ожидаемого значения , означает ковариацию , а — широко используемая альтернативная запись для коэффициента корреляции. Корреляция Пирсона определяется только в том случае, если оба стандартных отклонения конечны и положительны. Альтернативная формула, чисто в терминах моментов, выглядит так: ${\displaystyle \operatorname {E} }$ ${\displaystyle \operatorname {cov} }$ ${\displaystyle \operatorname {corr} }$

$${\displaystyle \rho _{X,Y}={\operatorname {E} (XY)-\operatorname {E} (X)\operatorname {E} (Y) \over {\sqrt {\operatorname {E} (X^{2})-\operatorname {E} (X)^{2}}}\cdot {\sqrt {\operatorname {E} (Y^{2})-\operatorname {E} (Y)^{2}}}}}$$

Корреляция и независимость

Следствием неравенства Коши–Шварца является то, что абсолютное значение коэффициента корреляции Пирсона не больше 1. Таким образом, значение коэффициента корреляции находится в диапазоне от −1 до +1. Коэффициент корреляции равен +1 в случае совершенной прямой (возрастающей) линейной связи (корреляции), −1 в случае совершенной обратной (убывающей) линейной связи ( антикорреляции ) ^[5] и некоторому значению в открытом интервале во всех остальных случаях, что указывает на степень линейной зависимости между переменными. По мере приближения к нулю связь становится слабее (ближе к некоррелированному). Чем ближе коэффициент к −1 или 1, тем сильнее корреляция между переменными. ${\displaystyle (-1,1)}$

Если переменные независимы , коэффициент корреляции Пирсона равен 0. Однако, поскольку коэффициент корреляции обнаруживает только линейные зависимости между двумя переменными, обратное не обязательно верно. Коэффициент корреляции, равный 0, не означает, что переменные независимы ^{[ требуется цитата ]} .

$${\displaystyle {\begin{aligned}X,Y{\text{ independent}}\quad &\Rightarrow \quad \rho _{X,Y}=0\quad (X,Y{\text{ uncorrelated}})\\\rho _{X,Y}=0\quad (X,Y{\text{ uncorrelated}})\quad &\nRightarrow \quad X,Y{\text{ independent}}\end{aligned}}}$$

Например, предположим, что случайная величина симметрично распределена относительно нуля, и . Тогда полностью определяется , так что и совершенно зависимы, но их корреляция равна нулю; они некоррелированы . Однако в особом случае, когда и совместно нормальны , некоррелированность эквивалентна независимости. ${\displaystyle X}$ ${\displaystyle Y=X^{2}}$ ${\displaystyle Y}$ ${\displaystyle X}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle X}$ ${\displaystyle Y}$

Несмотря на то, что некоррелированные данные не обязательно подразумевают независимость, можно проверить, являются ли случайные величины независимыми, если их взаимная информация равна 0.

Коэффициент корреляции выборки

При наличии ряда измерений пары, проиндексированной , коэффициент корреляции выборки может быть использован для оценки корреляции Пирсона популяции между и . Коэффициент корреляции выборки определяется как ${\displaystyle n}$ ${\displaystyle (X_{i},Y_{i})}$ ${\displaystyle i=1,\ldots ,n}$ ${\displaystyle \rho _{X,Y}}$ ${\displaystyle X}$ ${\displaystyle Y}$

${\displaystyle r_{xy}\quad {\overset {\underset {\mathrm {def} }{}}{=}}\quad {\frac {\sum \limits _{i=1}^{n}(x_{i}-{\bar {x}})(y_{i}-{\bar {y}})}{(n-1)s_{x}s_{y}}}={\frac {\sum \limits _{i=1}^{n}(x_{i}-{\bar {x}})(y_{i}-{\bar {y}})}{\sqrt {\sum \limits _{i=1}^{n}(x_{i}-{\bar {x}})^{2}\sum \limits _{i=1}^{n}(y_{i}-{\bar {y}})^{2}}}},}$

где и — выборочные средние значения и , а и — скорректированные выборочные стандартные отклонения и . ${\displaystyle {\overline {x}}}$ ${\displaystyle {\overline {y}}}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle s_{x}}$ ${\displaystyle s_{y}}$ ${\displaystyle X}$ ${\displaystyle Y}$

Эквивалентные выражения для являются ${\displaystyle r_{xy}}$

${\displaystyle {\begin{aligned}r_{xy}&={\frac {\sum x_{i}y_{i}-n{\bar {x}}{\bar {y}}}{ns'_{x}s'_{y}}}\\[5pt]&={\frac {n\sum x_{i}y_{i}-\sum x_{i}\sum y_{i}}{{\sqrt {n\sum x_{i}^{2}-(\sum x_{i})^{2}}}~{\sqrt {n\sum y_{i}^{2}-(\sum y_{i})^{2}}}}}.\end{aligned}}}$

где и — нескорректированные выборочные стандартные отклонения и . ${\displaystyle s'_{x}}$ ${\displaystyle s'_{y}}$ ${\displaystyle X}$ ${\displaystyle Y}$

Если и являются результатами измерений, содержащими ошибку измерения, то реалистичные пределы коэффициента корреляции составляют не от −1 до +1, а меньший диапазон. ^[6] Для случая линейной модели с одной независимой переменной коэффициент детерминации (R в квадрате) равен квадрату , коэффициента момента произведения Пирсона. ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle r_{xy}}$

Пример

Рассмотрим совместное распределение вероятностей X и Y, приведенное в таблице ниже.

Для этого совместного распределения предельные распределения следующие:

${\displaystyle \mathrm {P} (X=x)={\begin{cases}{\frac {1}{3}}&\quad {\text{for }}x=0\\{\frac {2}{3}}&\quad {\text{for }}x=1\end{cases}}}$

${\displaystyle \mathrm {P} (Y=y)={\begin{cases}{\frac {1}{3}}&\quad {\text{for }}y=-1\\{\frac {1}{3}}&\quad {\text{for }}y=0\\{\frac {1}{3}}&\quad {\text{for }}y=1\end{cases}}}$

Это дает следующие ожидания и отклонения:

${\displaystyle \mu _{X}={\frac {2}{3}}}$

${\displaystyle \mu _{Y}=0}$

${\displaystyle \sigma _{X}^{2}={\frac {2}{9}}}$

${\displaystyle \sigma _{Y}^{2}={\frac {2}{3}}}$

Поэтому:

${\displaystyle {\begin{aligned}\rho _{X,Y}&={\frac {1}{\sigma _{X}\sigma _{Y}}}\mathrm {E} [(X-\mu _{X})(Y-\mu _{Y})]\\[5pt]&={\frac {1}{\sigma _{X}\sigma _{Y}}}\sum _{x,y}{(x-\mu _{X})(y-\mu _{Y})\mathrm {P} (X=x,Y=y)}\\[5pt]&={\frac {3{\sqrt {3}}}{2}}\left(\left(1-{\frac {2}{3}}\right)(-1-0){\frac {1}{3}}+\left(0-{\frac {2}{3}}\right)(0-0){\frac {1}{3}}+\left(1-{\frac {2}{3}}\right)(1-0){\frac {1}{3}}\right)=0.\end{aligned}}}$

Коэффициенты ранговой корреляции

Коэффициенты ранговой корреляции , такие как коэффициент ранговой корреляции Спирмена и коэффициент ранговой корреляции Кендалла (τ), измеряют степень, в которой при увеличении одной переменной другая переменная имеет тенденцию к увеличению, не требуя, чтобы это увеличение было представлено линейной зависимостью. Если при увеличении одной переменной другая уменьшается , коэффициенты ранговой корреляции будут отрицательными. Обычно эти коэффициенты ранговой корреляции рассматривают как альтернативы коэффициенту Пирсона, используемые либо для уменьшения объема вычислений, либо для того, чтобы сделать коэффициент менее чувствительным к ненормальности распределений. Однако эта точка зрения имеет мало математической основы, поскольку коэффициенты ранговой корреляции измеряют другой тип связи, чем коэффициент корреляции Пирсона по продукту-моменту , и их лучше всего рассматривать как меры другого типа ассоциации, а не как альтернативную меру коэффициента корреляции популяции. ^{[7] [8]}

Чтобы проиллюстрировать природу ранговой корреляции и ее отличие от линейной корреляции, рассмотрим следующие четыре пары чисел : ${\displaystyle (x,y)}$

(0, 1), (10, 100), (101, 500), (102, 2000).

По мере того как мы переходим от каждой пары к следующей, увеличивается , и то же самое происходит . Это отношение является идеальным, в том смысле, что увеличение всегда сопровождается увеличением . Это означает, что у нас есть идеальная ранговая корреляция, и оба коэффициента корреляции Спирмена и Кендалла равны 1, тогда как в этом примере коэффициент корреляции произведения-момента Пирсона равен 0,7544, что указывает на то, что точки далеки от того, чтобы лежать на прямой линии. Точно так же, если всегда уменьшается при увеличении , коэффициенты ранговой корреляции будут равны −1, в то время как коэффициент корреляции произведения-момента Пирсона может быть или не быть близким к −1, в зависимости от того, насколько близки точки к прямой линии. Хотя в крайних случаях идеальной ранговой корреляции оба коэффициента равны (оба +1 или оба −1), обычно это не так, и поэтому значения двух коэффициентов нельзя осмысленно сравнивать. ^[7] Например, для трех пар (1, 1) (2, 3) (3, 2) коэффициент Спирмена равен 1/2, а коэффициент Кендалла равен 1/3. ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle y}$ ${\displaystyle x}$

Другие меры зависимости между случайными величинами

Информация, предоставляемая коэффициентом корреляции, недостаточна для определения структуры зависимости между случайными величинами. ^[9] Коэффициент корреляции полностью определяет структуру зависимости только в очень частных случаях, например, когда распределение является многомерным нормальным распределением . (См. диаграмму выше.) В случае эллиптических распределений он характеризует (гипер-)эллипсы равной плотности; однако он не характеризует полностью структуру зависимости (например, степени свободы многомерного t-распределения определяют уровень хвостовой зависимости).

Для непрерывных переменных были введены несколько альтернативных мер зависимости, чтобы устранить недостаток корреляции Пирсона, заключающийся в том, что она может быть равна нулю для зависимых случайных величин (см. ^[10] и ссылки в нем для обзора). Все они имеют важное свойство, что значение нуля подразумевает независимость. Это привело некоторых авторов ^{[10] [11]} к рекомендации их повседневного использования, в частности, корреляции расстояния . ^{[12] [13]} Другой альтернативной мерой является коэффициент рандомизированной зависимости. ^[14] RDC является вычислительно эффективной, основанной на копуле мерой зависимости между многомерными случайными величинами и инвариантна относительно нелинейного масштабирования случайных величин.

Один важный недостаток альтернативных, более общих мер заключается в том, что при использовании для проверки того, связаны ли две переменные, они, как правило, имеют меньшую мощность по сравнению с корреляцией Пирсона, когда данные следуют многомерному нормальному распределению. ^[10] Это следствие теоремы о теореме об отсутствии бесплатных обедов . Чтобы обнаружить все виды взаимосвязей, эти меры должны пожертвовать мощностью по отношению к другим взаимосвязям, особенно для важного особого случая линейной связи с гауссовыми маргинальными значениями, для которых корреляция Пирсона является оптимальной. Другая проблема касается интерпретации. В то время как корреляция Персона может быть интерпретирована для всех значений, альтернативные меры, как правило, могут быть интерпретированы осмысленно только в крайних случаях. ^[15]

Для двух бинарных переменных отношение шансов измеряет их зависимость и принимает диапазон неотрицательных чисел, возможно, бесконечность: ⁠ ⁠ ${\displaystyle [0,+\infty ]}$ . Связанные статистики, такие как Y Юла и Q Юла, нормализуют это до диапазона, подобного корреляции ⁠ ⁠ ${\displaystyle [-1,1]}$ . Отношение шансов обобщается логистической моделью для моделирования случаев, когда зависимые переменные являются дискретными и может быть одна или несколько независимых переменных.

Коэффициент корреляции , взаимная информация на основе энтропии , полная корреляция , двойная полная корреляция и полихорическая корреляция также способны обнаруживать более общие зависимости, как и рассмотрение копулы между ними, в то время как коэффициент детерминации обобщает коэффициент корреляции до множественной регрессии .

Чувствительность к распределению данных

Степень зависимости между переменными X и Y не зависит от масштаба, в котором выражены переменные. То есть, если мы анализируем связь между X и Y , большинство мер корреляции не затрагиваются преобразованием X в a + bX и Y в c + dY , где a , b , c и d являются константами ( b и d положительны). Это справедливо как для некоторых статистик корреляции, так и для их популяционных аналогов. Некоторые статистики корреляции, такие как коэффициент ранговой корреляции, также инвариантны к монотонным преобразованиям маргинальных распределений X и/ или Y.

Коэффициенты корреляции Пирсона / Спирмена между X и Y показаны, когда диапазоны двух переменных не ограничены, а диапазон X ограничен интервалом (0,1).

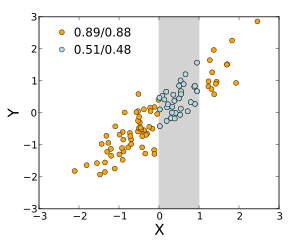
Большинство мер корреляции чувствительны к способу, которым отбираются X и Y. Зависимости, как правило, сильнее, если рассматривать более широкий диапазон значений. Таким образом, если мы рассмотрим коэффициент корреляции между ростом отцов и их сыновей по всем взрослым мужчинам и сравним его с тем же коэффициентом корреляции, рассчитанным для отцов, рост которых составляет от 165 см до 170 см, то в последнем случае корреляция будет слабее. Было разработано несколько методов, которые пытаются скорректировать ограничение диапазона в одной или обеих переменных, и они обычно используются в метаанализе; наиболее распространенными являются уравнения случая II и случая III Торндайка. ^[16]

Различные используемые меры корреляции могут быть неопределенными для определенных совместных распределений X и Y. Например, коэффициент корреляции Пирсона определяется в терминах моментов и, следовательно, будет неопределенным, если моменты не определены. Меры зависимости, основанные на квантилях , всегда определены. Выборочная статистика, предназначенная для оценки популяционных мер зависимости, может иметь или не иметь желаемые статистические свойства, такие как несмещенность или асимптотическая согласованность , основанные на пространственной структуре популяции, из которой были отобраны данные.

Чувствительность к распределению данных может быть использована с выгодой. Например, масштабированная корреляция предназначена для использования чувствительности к диапазону с целью выделения корреляций между быстрыми компонентами временных рядов . ^[17] Уменьшая диапазон значений контролируемым образом, корреляции в длительной временной шкале отфильтровываются и выявляются только корреляции в краткосрочной временной шкале.

Матрицы корреляции

Матрица корреляции случайных величин — это матрица , элемент которой ${\displaystyle n}$ ${\displaystyle X_{1},\ldots ,X_{n}}$ ${\displaystyle n\times n}$ ${\displaystyle C}$ ${\displaystyle (i,j)}$

${\displaystyle c_{ij}:=\operatorname {corr} (X_{i},X_{j})={\frac {\operatorname {cov} (X_{i},X_{j})}{\sigma _{X_{i}}\sigma _{X_{j}}}},\quad {\text{if}}\ \sigma _{X_{i}}\sigma _{X_{j}}>0.}$

Таким образом, все диагональные элементы тождественно равны единице . Если используемые меры корреляции являются коэффициентами момента произведения, матрица корреляции совпадает с матрицей ковариации стандартизированных случайных величин для . Это применимо как к матрице корреляций популяции (в этом случае это стандартное отклонение популяции), так и к матрице корреляций выборки (в этом случае обозначает стандартное отклонение выборки). Следовательно, каждая из них обязательно является положительно-полуопределенной матрицей . Более того, матрица корреляции строго положительно определена , если ни одна переменная не может иметь все свои значения, точно сгенерированные как линейная функция значений других. ${\displaystyle X_{i}/\sigma (X_{i})}$ ${\displaystyle i=1,\dots ,n}$ ${\displaystyle \sigma }$ ${\displaystyle \sigma }$

Матрица корреляции симметрична, поскольку корреляция между и такая же, как корреляция между и . ${\displaystyle X_{i}}$ ${\displaystyle X_{j}}$ ${\displaystyle X_{j}}$ ${\displaystyle X_{i}}$

Например, корреляционная матрица появляется в одной из формул для коэффициента множественной детерминации — меры качества соответствия во множественной регрессии .

В статистическом моделировании корреляционные матрицы, представляющие взаимосвязи между переменными, классифицируются по различным корреляционным структурам, которые различаются по таким факторам, как количество параметров, необходимых для их оценки. Например, в сменной корреляционной матрице все пары переменных моделируются как имеющие одинаковую корреляцию, поэтому все недиагональные элементы матрицы равны друг другу. С другой стороны, авторегрессионная матрица часто используется, когда переменные представляют временной ряд, поскольку корреляции, вероятно, будут больше, когда измерения ближе по времени. Другие примеры включают независимые, неструктурированные, M-зависимые и Теплица .

В разведочном анализе данных иконография корреляций заключается в замене корреляционной матрицы диаграммой, где «замечательные» корреляции представлены сплошной линией (положительная корреляция) или пунктирной линией (отрицательная корреляция).

Ближайшая действительная корреляционная матрица

В некоторых приложениях (например, при построении моделей данных только на основе частично наблюдаемых данных) требуется найти «ближайшую» матрицу корреляции к «приблизительной» матрице корреляции (например, матрице, которая обычно не имеет полуопределенной положительности из-за способа ее вычисления).

В 2002 году Хайэм ^[18] формализовал понятие близости, используя норму Фробениуса , и предложил метод вычисления ближайшей корреляционной матрицы с использованием алгоритма проекции Дайкстры , реализация которого доступна в виде онлайн-API. ^[19]

Это вызвало интерес к предмету, и в последующие годы были получены новые теоретические (например, вычисление матрицы ближайшей корреляции с факторной структурой ^[20] ) и численные (например, использование метода Ньютона для вычисления матрицы ближайшей корреляции ^{[21] ) результаты.}

Некоррелированность и независимость случайных процессов

Аналогично для двух стохастических процессов и : Если они независимы, то они некоррелированы. ^{[22] : стр. 151} Противоположность этому утверждению может быть неверной. Даже если две переменные некоррелированы, они могут не быть независимыми друг от друга. ${\displaystyle \left\{X_{t}\right\}_{t\in {\mathcal {T}}}}$ ${\displaystyle \left\{Y_{t}\right\}_{t\in {\mathcal {T}}}}$

Распространенные заблуждения

Корреляция и причинно-следственная связь

Общепринятое изречение о том, что « корреляция не подразумевает причинно-следственную связь », означает, что корреляция сама по себе не может быть использована для вывода причинно-следственной связи между переменными. ^[23] Это изречение не следует понимать так, что корреляции не могут указывать на потенциальное существование причинно-следственных связей. Однако причины, лежащие в основе корреляции, если таковые имеются, могут быть косвенными и неизвестными, а высокие корреляции также пересекаются с отношениями идентичности ( тавтологиями ), где не существует причинно-следственного процесса. Следовательно, корреляция между двумя переменными не является достаточным условием для установления причинно-следственной связи (в любом направлении).

Корреляция между возрастом и ростом у детей достаточно прозрачна с точки зрения причин, но корреляция между настроением и здоровьем у людей менее прозрачна. Приводит ли улучшение настроения к улучшению здоровья, или хорошее здоровье к хорошему настроению, или и то, и другое? Или в основе обоих лежит какой-то другой фактор? Другими словами, корреляция может быть принята в качестве доказательства возможной причинно-следственной связи, но не может указывать на то, какой может быть причинно-следственная связь, если таковая имеется.

Простые линейные корреляции

Квартет Энскомба : четыре набора данных с одинаковой корреляцией 0,816

Коэффициент корреляции Пирсона показывает силу линейной связи между двумя переменными, но его значение, как правило, не характеризует полностью их связь. ^[24] В частности, если условное среднее значение заданной , обозначенное , не является линейным по , то коэффициент корреляции не будет полностью определять вид . ${\displaystyle Y}$ ${\displaystyle X}$ ${\displaystyle \operatorname {E} (Y\mid X)}$ ${\displaystyle X}$ ${\displaystyle \operatorname {E} (Y\mid X)}$

На соседнем изображении показаны диаграммы рассеяния квартета Энскомба , набора из четырех различных пар переменных, созданных Фрэнсисом Энскомбом . ^[25] Четыре переменные имеют одинаковое среднее значение (7,5), дисперсию (4,12), корреляцию (0,816) и линию регрессии ( ). Однако, как можно видеть на графиках, распределение переменных сильно различается. Первая из них (вверху слева) кажется распределенной нормально и соответствует тому, чего можно было бы ожидать при рассмотрении двух переменных, коррелированных и следующих предположению о нормальности. Вторая (вверху справа) распределена не нормально; хотя можно наблюдать очевидную связь между двумя переменными, она не линейна. В этом случае коэффициент корреляции Пирсона не указывает на то, что существует точная функциональная связь: только на степень, в которой эта связь может быть аппроксимирована линейной связью. В третьем случае (внизу слева) линейная связь идеальна, за исключением одного выброса , который оказывает достаточное влияние, чтобы снизить коэффициент корреляции с 1 до 0,816. Наконец, четвертый пример (внизу справа) демонстрирует еще один случай, когда одного выброса достаточно для получения высокого коэффициента корреляции, даже если связь между двумя переменными не является линейной. ${\displaystyle y}$ ${\textstyle y=3+0.5x}$

Эти примеры показывают, что коэффициент корреляции, как сводная статистика , не может заменить визуальное изучение данных. Иногда говорят, что примеры демонстрируют, что корреляция Пирсона предполагает, что данные следуют нормальному распределению , но это верно лишь отчасти. ^[4] Корреляция Пирсона может быть точно рассчитана для любого распределения, имеющего конечную ковариационную матрицу , которая включает большинство распределений, встречающихся на практике. Однако коэффициент корреляции Пирсона (взятый вместе с выборочным средним и дисперсией) является достаточной статистикой только в том случае, если данные взяты из многомерного нормального распределения . В результате коэффициент корреляции Пирсона полностью характеризует связь между переменными тогда и только тогда, когда данные взяты из многомерного нормального распределения.

Двумерное нормальное распределение

Если пара случайных величин подчиняется двумерному нормальному распределению , то условное среднее является линейной функцией , а условное среднее является линейной функцией Коэффициент корреляции между и и маргинальные средние значения и дисперсии и определяют эту линейную зависимость: ${\displaystyle \ (X,Y)\ }$ ${\displaystyle \operatorname {\boldsymbol {\mathcal {E}}} (X\mid Y)}$ ${\displaystyle Y}$ ${\displaystyle \operatorname {\boldsymbol {\mathcal {E}}} (Y\mid X)}$ ${\displaystyle \ X~.}$ ${\displaystyle \ \rho _{X,Y}\ }$ ${\displaystyle \ X\ }$ ${\displaystyle \ Y\ ,}$ ${\displaystyle \ X\ }$ ${\displaystyle \ Y\ }$

${\displaystyle \operatorname {\boldsymbol {\mathcal {E}}} (Y\mid X)=\operatorname {\boldsymbol {\mathcal {E}}} (Y)+\rho _{X,Y}\cdot \sigma _{Y}\cdot {\frac {\ X-\operatorname {\boldsymbol {\mathcal {E}}} (X)\ }{\sigma _{X}}}\ ,}$

где и — ожидаемые значения и соответственно, а и — стандартные отклонения и соответственно. ${\displaystyle \operatorname {\boldsymbol {\mathcal {E}}} (X)}$ ${\displaystyle \operatorname {\boldsymbol {\mathcal {E}}} (Y)}$ ${\displaystyle \ X\ }$ ${\displaystyle \ Y\ ,}$ ${\displaystyle \ \sigma _{X}\ }$ ${\displaystyle \ \sigma _{Y}\ }$ ${\displaystyle \ X\ }$ ${\displaystyle \ Y\ ,}$

Эмпирическая корреляция представляет собой оценку коэффициента корреляции. Оценка распределения для определяется по формуле ${\displaystyle r}$ ${\displaystyle \ \rho ~.}$ ${\displaystyle \ \rho \ }$

$${\displaystyle \pi (\rho \mid r)={\frac {\ \Gamma (N)\ }{\ {\sqrt {2\pi \ }}\cdot \Gamma (N-{\tfrac {\ 1\ }{2}})\ }}\cdot {\bigl (}1-r^{2}{\bigr )}^{\frac {\ N\ -2\ }{2}}\cdot {\bigl (}1-\rho ^{2}{\bigr )}^{\frac {\ N-3\ }{2}}\cdot {\bigl (}1-r\rho {\bigr )}^{-N+{\frac {\ 3\ }{2}}}\cdot F_{\mathsf {Hyp}}\left(\ {\tfrac {\ 3\ }{2}},-{\tfrac {\ 1\ }{2}};N-{\tfrac {\ 1\ }{2}};{\frac {\ 1+r\rho \ }{2}}\ \right)\ }$$

где — гипергеометрическая функция Гаусса . ${\displaystyle \ F_{\mathsf {Hyp}}\ }$

Эта плотность является как байесовской апостериорной плотностью, так и точной оптимальной плотностью распределения уверенности . ^{[26] [27]}

Смотрите также

• Математический портал

• Автокорреляция
• Каноническая корреляция
• Коэффициент детерминации
• Коинтеграция
• Коэффициент корреляции конкордантности
• Кофенетическая корреляция
• Корреляционное ослабление
• Корреляционная функция
• Корреляционный разрыв
• Ковариация
• Ковариация и корреляция
• Кросс-корреляция
• Экологическая корреляция
• Необъясненная доля дисперсии
• Генетическая корреляция
• Лямбда Гудмана и Краскала
• Иконография корреляций
• Иллюзорная корреляция
• Межклассовая корреляция
• Внутриклассовая корреляция
• Лифт (интеллектуальный анализ данных)
• Средняя зависимость
• Проблема изменяемой площади
• Множественная корреляция
• Коэффициент точечно-бисериальной корреляции
• Коэффициент количества квадрантов
• Ложная корреляция
• Статистическое корреляционное отношение
• Субнезависимость

Ссылки

1. Крокстон, Фредерик Эмори; Коуден, Дадли Джонстон; Кляйн, Сидней (1968) Прикладная общая статистика , Питман. ISBN  9780273403159 (стр. 625)
2. Дитрих, Корнелиус Франк (1991) Неопределенность, калибровка и вероятность: статистика научных и промышленных измерений 2-е издание, А. Хиглер. ISBN 9780750300605 (стр. 331) 
3. Эйткен, Александр Крейг (1957) Статистическая математика 8-е издание. Оливер и Бойд. ISBN 9780050013007 (стр. 95) 
4. Rodgers, JL; Nicewander, WA (1988). «Тринадцать способов взглянуть на коэффициент корреляции». The American Statistician . 42 (1): 59–66. doi :10.1080/00031305.1988.10475524. JSTOR  2685263.
5. Доуди, С. и Уэрден, С. (1983). «Статистика для исследований», Wiley. ISBN 0-471-08602-9 стр. 230 
6. Фрэнсис, Д.П.; Коутс А.Дж.; Гибсон Д. (1999). «Насколько высоким может быть коэффициент корреляции?». Int J Cardiol . 69 (2): 185–199. doi :10.1016/S0167-5273(99)00028-5. PMID  10549842.
7. Yule, GU и Kendall, MG (1950), «Введение в теорию статистики», 14-е издание (5-е издание, 1968 г.). Charles Griffin & Co., стр. 258–270
8. Кендалл, МГ (1955) «Методы ранговой корреляции», Чарльз Гриффин и компания.
9. Махдави Дамгани Б. (2013). «Не вводящая в заблуждение ценность выводимой корреляции: введение в модель коинтеляции». Wilmott Magazine . 2013 (67): 50–61. doi :10.1002/wilm.10252.
10. Карч, Джулиан Д.; Перес-Алонсо, Андрес Ф.; Бергсма, Вичер П. (2024-08-04). "За пределами корреляции Пирсона: современные непараметрические тесты независимости для психологических исследований". Многомерные поведенческие исследования . doi : 10.1080/00273171.2024.2347960.{{cite journal}}: CS1 maint: date and year (link)
11. Саймон, Ноа; Тибширани, Роберт (2014). «Комментарий к статье «Обнаружение новых ассоциаций в больших наборах данных» Решефа и др., Science, 16 декабря 2011 г.». стр. 3. arXiv : 1401.7645 [stat.ME].
12. Székely, GJ Rizzo; Bakirov, NK (2007). «Измерение и проверка независимости с помощью корреляции расстояний». Annals of Statistics . 35 (6): 2769–2794. arXiv : 0803.4101 . doi : 10.1214/009053607000000505. S2CID  5661488.
13. Székely, GJ; Rizzo, ML (2009). «Броуновская ковариация расстояний». Annals of Applied Statistics . 3 (4): 1233–1303. arXiv : 1010.0297 . doi : 10.1214/09-AOAS312. PMC 2889501. PMID 20574547  . 
14. Лопес-Пас Д. и Хенниг П. и Шёлькопф Б. (2013). «Рандомизированный коэффициент зависимости», « Конференция по нейронным системам обработки информации » Перепечатка
15. Реймхерр, Мэтью; Николае, Дэн Л. (2013). «О количественной оценке зависимости: структура для разработки интерпретируемых показателей». Статистическая наука . 28 (1): 116–130. arXiv : 1302.5233 . doi : 10.1214/12-STS405.
16. Торндайк, Роберт Лэдд (1947). Проблемы и методы исследования (Отчет № 3) . Вашингтон, округ Колумбия: Издательство правительства США.
17. Николич, Д.; Мурешан, Р. К.; Фэн, В.; Сингер, В. (2012). «Масштабированный корреляционный анализ: лучший способ вычисления кросс-коррелограммы». European Journal of Neuroscience . 35 (5): 1–21. doi :10.1111/j.1460-9568.2011.07987.x. PMID  22324876. S2CID  4694570.
18. Хайэм, Николас Дж. (2002). «Вычисление ближайшей корреляционной матрицы — проблема из области финансов». Журнал численного анализа IMA . 22 (3): 329–343. CiteSeerX 10.1.1.661.2180 . doi :10.1093/imanum/22.3.329. 
19. "Portfolio Optimizer". portfoliooptimizer.io . Получено 2021-01-30 .
20. Борсдорф, Рудигер; Хайэм, Николас Дж.; Рэйдан, Маркос (2010). «Вычисление матрицы ближайшей корреляции с факторной структурой» (PDF) . SIAM J. Matrix Anal. Appl . 31 (5): 2603–2622. doi :10.1137/090776718.
21. Qi, HOUDUO; Sun, DEFENG (2006). «Квадратично сходящийся метод Ньютона для вычисления ближайшей корреляционной матрицы». SIAM J. Matrix Anal. Appl . 28 (2): 360–385. doi :10.1137/050624509.
22. Пак, Кун Ил (2018). Основы вероятности и стохастических процессов с приложениями к коммуникациям . Springer. ISBN 978-3-319-68074-3.
23. Олдрич, Джон (1995). «Истинные и ложные корреляции у Пирсона и Юла». Статистическая наука . 10 (4): 364–376. doi : 10.1214/ss/1177009870 . JSTOR  2246135.
24. Махдави Дамгани, Бабак (2012). «Вводящая в заблуждение ценность измеренной корреляции». Журнал Уилмотт . 2012 (1): 64–73. дои : 10.1002/wilm.10167. S2CID  154550363.
25. Anscombe, Francis J. (1973). «Графики в статистическом анализе». The American Statistician . 27 (1): 17–21. doi :10.2307/2682899. JSTOR  2682899.
26. Таралдсен, Гуннар (2021). «Плотность уверенности для корреляции». Санкхья А. 85 : 600–616. doi : 10.1007/s13171-021-00267-y . ISSN  0976-8378. S2CID  244594067.
27. Таральдсен, Гуннар (2020). Уверенность в корреляции. Researchgate.net (препринт). дои : 10.13140/RG.2.2.23673.49769.

Дальнейшее чтение

• Коэн, Дж.; Коэн П.; Уэст, С.Г. и Эйкен, Л.С. (2002). Прикладной множественный регрессионный/корреляционный анализ для поведенческих наук (3-е изд.). Psychology Press. ISBN 978-0-8058-2223-6.
• «Корреляция (в статистике)», Энциклопедия математики , EMS Press , 2001 [1994]
• Oestreicher, J. & DR (26 февраля 2015 г.). Plague of Equals: научный триллер о международных болезнях, политике и открытии лекарств . Калифорния: Omega Cat Press. стр. 408. ISBN 978-0963175540.

Внешние ссылки

• Страница MathWorld о коэффициенте(ах) (кросс-)корреляции выборки
• Вычислите значимость между двумя корреляциями для сравнения двух значений корреляции.
• "A MATLAB Toolbox for computing Weighted Correlation Coefficients". Архивировано из оригинала 24 апреля 2021 г.
• Доказательство того, что выборочная двумерная корреляция имеет пределы плюс или минус 1
• Интерактивное флэш-моделирование корреляции двух нормально распределенных переменных от Юхи Пуранена.
• Корреляционный анализ. Биомедицинская статистика
• R-Psychologist Correlation визуализация корреляции между двумя числовыми переменными