Законы формы

1969 non-fiction book by G. Spencer-Brown

«Законы формы» (далее LoF ) — книга Г. Спенсера-Брауна , опубликованная в 1969 году, которая находится на грани между математикой и философией . LoF описывает три различные логические системы :

• «Первичная арифметика» (описанная в Главе 4 LoF ), модели которой включают Булеву арифметику ;
• «Первичная алгебра » (глава 6 LoF ), модели которой включают двухэлементную булеву алгебру (далее сокращенно 2 ), булеву логику и классическое исчисление высказываний ;
• «Уравнения второй степени» (глава 11), интерпретации которых включают конечные автоматы и ограниченную рекурсивную арифметику Алонзо Чёрча (RRA).

«Граничную алгебру» Мегуайр (2011) ^[1] называет объединением первичной алгебры и первичной арифметики. В «Законах формы » иногда вольно упоминается как «первичная алгебра», так и LoF .

Книга

В предисловии говорится, что работа была впервые исследована в 1959 году, и Спенсер Браун цитирует Бертрана Рассела как человека, поддержавшего его начинание. Он также благодарит Дж. К. П. Миллера из Лондонского университетского колледжа за помощь с корректурой и предоставление других рекомендаций. В 1963 году Спенсер Браун был приглашен Гарри Фростом, штатным преподавателем физических наук на кафедре заочных исследований Лондонского университета , для чтения курса по математике логики.

LoF возник из работы по электронной инженерии, которую его автор проделал около 1960 года, и из последующих лекций по математической логике, которые он читал под эгидой программы расширения Лондонского университета . LoF появился в нескольких изданиях. Вторая серия изданий появилась в 1972 году с «Предисловием к первому американскому изданию», в котором подчеркивалось использование самореферентных парадоксов, ^[2] и самым последним был немецкий перевод 1997 года. LoF никогда не выходил из печати.

Мистическая и декламационная проза LoF и ее любовь к парадоксам делают ее сложным чтением для всех. Спенсер-Браун находился под влиянием Витгенштейна и Р. Д. Лэйнга . LoF также перекликается с рядом тем из произведений Чарльза Сандерса Пирса , Бертрана Рассела и Альфреда Норта Уайтхеда .

Работа оказала любопытное воздействие на некоторые классы ее читателей; например, на неясных основаниях было заявлено, что вся книга написана операциональным способом, давая инструкции читателю вместо того, чтобы рассказывать ему, что «есть», и что в соответствии с интересом Г. Спенсера-Брауна к парадоксам, единственное предложение, которое утверждает, что что-то есть , — это утверждение, которое говорит, что такие утверждения не используются в этой книге. ^[3] Кроме того, в заявлении утверждается, что за исключением этого одного предложения книгу можно рассматривать как пример E-Prime . То, что побудило к такому заявлению, неясно, либо с точки зрения стимула, логической заслуги, либо по сути, потому что книга регулярно и естественно использует глагол to be повсюду и во всех его грамматических формах, как можно увидеть как в оригинале, так и в цитатах, показанных ниже. ^[4]

Прием

Якобы работа по формальной математике и философии, LoF стала чем-то вроде культовой классики : ее похвалил Хайнц фон Ферстер, когда он рецензировал ее для Whole Earth Catalog . ^[5] Те, кто согласен, указывают на LoF как на воплощение загадочной «математики сознания », ее алгебраический символизм, улавливающий (возможно, даже «самый») неявный корень познания : способность «различать». LoF утверждает, что первичная алгебра обнаруживает поразительные связи между логикой , булевой алгеброй и арифметикой, а также философией языка и разума .

Стаффорд Бир написал в рецензии для Nature : «Когда думаешь обо всем, что Рассел пережил шестьдесят лет назад, чтобы написать « Начала» , и обо всем, что мы, его читатели, претерпели, борясь с этими тремя огромными томами, это почти грустно» ^{[6] .}

Банашевски (1977) ^[7] утверждает, что первичная алгебра — это не что иное, как новая нотация для булевой алгебры. Действительно, двухэлементная булева алгебра 2 может рассматриваться как предполагаемая интерпретация первичной алгебры. Однако нотация первичной алгебры:

• Полностью использует двойственность , характерную не только для булевых алгебр , но и для всех решеток ;
• Подчеркивает, как синтаксически различные утверждения в логике и 2 могут иметь одинаковую семантику ;
• Значительно упрощает вычисления в булевой алгебре, а также доказательства в сентенциальной и силлогистической логике .

Более того, синтаксис первичной алгебры может быть расширен до формальных систем, отличных от 2 и сентенциальной логики, что приводит к граничной математике (см. § Сопутствующие работы ниже).

LoF оказал влияние, среди прочих, на Хайнца фон Ферстера , Луи Кауфмана , Никласа Лумана , Умберто Матурану , Франциско Варелу и Уильяма Брикена. Некоторые из этих авторов модифицировали первичную алгебру различными интересными способами.

LoF утверждал, что некоторые известные математические гипотезы, имеющие давнюю историю, такие как теорема о четырех красках , Великая теорема Ферма и гипотеза Гольдбаха , доказуемы с использованием расширений первичной алгебры. Спенсер-Браун в конечном итоге распространил предполагаемое доказательство теоремы о четырех красках, но оно было встречено скептически. ^[8]

Форма (Глава 1)

Символ:

Также называемый «меткой» или «крестом», является неотъемлемой чертой Законов Формы. В неповторимой и загадочной манере Спенсера-Брауна, Метка символизирует корень познания , т. е. дуалистическая Метка указывает на способность отличать «это» от «всего остального, кроме этого».

В LoF крест обозначает рисунок «различия» и может рассматриваться как означающий следующее одновременно:

• Процесс проведения границы вокруг чего-либо, тем самым отделяя его от всего остального;
• То, что становится отличным от всего, проводя границу;
• Переход с одной стороны границы на другую.

Все три способа подразумевают действие со стороны когнитивной сущности (например, человека), проводящей различие. Как говорит LoF :

«Первая команда:

• Проведите различие

вполне можно выразить такими способами, как:

• Пусть будет различие,
• Найдите различие,
• Увидьте различие,
• Опишите различие,
• Определите различие,

Или:

• Давайте проведем различие». ( LoF , Примечания к главе 2)

Контрапунктом состояния Marked является состояние Unmarked, которое есть просто ничто, пустота или невыразимая бесконечность, представленная пустым пространством. Это просто отсутствие Креста. Никакого различия не было сделано, и ничего не было пересечено. Состояние Marked и пустота являются двумя первобытными значениями Законов Формы.

Крест можно рассматривать как обозначение различия между двумя состояниями, одно из которых «рассматривается как символ», а другое таковым не считается. Из этого факта возникает любопытный резонанс с некоторыми теориями сознания и языка . Парадоксально, но Форма одновременно является Наблюдателем и Наблюдаемым, а также творческим актом осуществления наблюдения. LoF (исключая заднюю материю) заканчивается словами:

...первое различие: Знак и наблюдатель не только взаимозаменяемы, но и по форме идентичны.

К. С. Пирс пришёл к схожему выводу в 1890-х годах; см. § Сопутствующие работы.

Основная арифметика (глава 4)

Синтаксис первичной арифметики выглядит следующим образом. Есть только два атомарных выражения :

• Пустой Крест  ;
• Вся или часть пустой страницы («пустота»).

Существует два индуктивных правила:

• Крест может быть написан над любым выражением;
• Любые два выражения могут быть объединены .

Семантика первичной арифметики, возможно, представляет собой не что иное, как единственное явное определение в LoF : «Различие есть совершенное воздержание».

Пусть «неотмеченное состояние» будет синонимом пустоты. Пусть пустой Крест обозначает «отмеченное состояние». Пересечься — значит перейти от одного значения, неотмеченного или отмеченного состояния, к другому. Теперь мы можем сформулировать «арифметические» аксиомы A1 и A2, которые обосновывают первичную арифметику (и, следовательно, все Законы Формы):

"A1. Закон призыва". Призыв дважды из состояния неотличим от призыва один раз. Проведение различия дважды имеет тот же эффект, что и проведение его один раз. Например, сказать «Да будет свет», а затем сказать «Да будет свет» еще раз, то же самое, что сказать это один раз. Формально:

${\displaystyle \ =}$

"A2. Закон скрещивания". После скрещивания из немаркированного состояния в маркированное повторное скрещивание ("ре-кроссинг") из маркированного состояния возвращает в немаркированное состояние. Следовательно, ре-кроссинг аннулирует скрещивание. Формально:

${\displaystyle \ =}$

В обоих A1 и A2 выражение справа от '=' имеет меньше символов, чем выражение слева от '='. Это говорит о том, что каждое первичное арифметическое выражение может быть упрощено путем повторного применения A1 и A2 до одного из двух состояний: отмеченного или неотмеченного. Это действительно так, и результатом является «упрощение» выражения. Две фундаментальные метатеоремы первичной арифметики утверждают, что:

• Каждое конечное выражение имеет уникальное упрощение. (T3 в LoF );
• Начиная с начального отмеченного или неотмеченного состояния, «усложнение» выражения путем конечного числа повторных применений A1 и A2 не может привести к выражению, упрощение которого отличается от начального состояния. (T4 в LoF ).

Таким образом, отношение логической эквивалентности разделяет все первичные арифметические выражения на два класса эквивалентности : те, которые упрощаются до Креста, и те, которые упрощаются до пустоты.

A1 и A2 имеют свободные аналоги в свойствах последовательных и параллельных электрических цепей, а также в других способах представления процессов на диаграммах, включая блок-схемы. A1 соответствует параллельному соединению, а A2 — последовательному соединению, при этом следует понимать, что проведение различия соответствует изменению способа соединения двух точек в цепи, а не просто добавлению проводов.

Первичная арифметика аналогична следующим формальным языкам математики и информатики :

• Язык Дика с нулевым алфавитом;
• Простейший контекстно-свободный язык в иерархии Хомского ;
• Система перезаписи , которая является строго нормализующей и конфлюэнтной .

Фраза «исчисление показаний» в LoF является синонимом «первичной арифметики».

Понятие канона

Концепцией, свойственной LoF, является понятие «канон». Хотя LoF формально не определяет канон, следующие два отрывка из Примечаний к гл. 2 подходят:

Более важные структуры приказа иногда называются канонами . Они представляют собой способы, которыми руководящие предписания, по-видимому, группируются в созвездия, и, таким образом, никоим образом не являются независимыми друг от друга. Канон отличается тем, что находится вне (т. е. описывает) строящуюся систему, но приказ построить (например, «провести различие»), даже если он может иметь центральное значение, не является каноном. Канон — это приказ или набор приказов, разрешать или допускать, но не строить или создавать.

...основной формой математической коммуникации является не описание, а предписание... Музыка является схожей формой искусства, композитор даже не пытается описать набор звуков, которые он имеет в виду, и тем более набор чувств, вызываемых ими, но записывает набор команд, которые, если они соблюдаются исполнителем, могут привести к воспроизведению для слушателя первоначального опыта композитора.

Эти отрывки относятся к различию в металогике между объектным языком, формальным языком обсуждаемой логической системы, и метаязыком , языком (часто естественным языком), отличным от объектного языка, используемым для изложения и обсуждения объектного языка. Первая цитата, по-видимому, утверждает, что каноны являются частью метаязыка. Вторая цитата, по-видимому, утверждает, что утверждения на объектном языке по сути являются командами, адресованными автором читателю. Ни одно из утверждений не выполняется в стандартной металогике.

Первичная алгебра (глава 6)

Синтаксис

Дано любое допустимое первичное арифметическое выражение, вставьте в одно или несколько мест любое количество латинских букв с необязательными числовыми индексами; результатом будет первичная алгебраическая формула . Буквы, используемые таким образом в математике и логике , называются переменными . Первичная алгебраическая переменная указывает место, где можно записать примитивное значение или его дополнение . Несколько экземпляров одной и той же переменной обозначают несколько мест одного и того же примитивного значения.

Правила, регулирующие логическую эквивалентность

Знак '=' может связывать два логически эквивалентных выражения; результатом является уравнение . Под "логически эквивалентным" подразумевается, что два выражения имеют одинаковое упрощение. Логическая эквивалентность — это отношение эквивалентности над множеством формул первичной алгебры, управляемое правилами R1 и R2. Пусть "C" и "D" — формулы, каждая из которых содержит по крайней мере один экземпляр подформулы A :

• R1 , Подстановка равных . Заменить один или несколько экземпляров A в C на B , получив в результате E. Если A = B , то C = E.
• R2 , Равномерная замена . Заменить все вхождения A в C и D на B . C становится E , а D становится F . Если C = D , то E = F . Обратите внимание, что A = B не обязательно.

R2 очень часто используется в демонстрациях начальной алгебры (см. ниже), почти всегда молча. Эти правила регулярно используются в логике и большей части математики, почти всегда неосознанно.

Первичная алгебра состоит из уравнений , т. е. пар формул, связанных инфиксным оператором '='. R1 и R2 позволяют преобразовывать одно уравнение в другое. Следовательно, первичная алгебра является эквациональной формальной системой, подобной многим алгебраическим структурам , включая булеву алгебру , которые являются разновидностями . Эквациональная логика была распространена до Principia Mathematica (например, Peirce, ^1,2,3 Johnson 1892), и имеет современных сторонников (Gries and Schneider 1993).

Традиционная математическая логика состоит из тавтологических формул, обозначенных префиксом турникет . Чтобы обозначить, что первичная алгебраическая формула A является тавтологией , просто напишите " A = ". Если заменить '=' в R1 и R2 на двуусловный , полученные правила сохранят силу в традиционной логике. Однако традиционная логика в основном опирается на правило modus ponens ; таким образом, традиционная логика является степенной . Эквационально-потенциальная дихотомия вычленяет многое из того, что отличает математическую логику от остальной математики.

Инициалы

Инициал — это первичное алгебраическое уравнение, проверяемое процедурой принятия решения , и как таковое не является аксиомой . LoF устанавливает инициалы :

Отсутствие чего-либо справа от знака «=» является преднамеренным.

J2 — это известный распределительный закон пропозициональной логики и булевой алгебры .

Другой набор инициалов, более удобный для вычислений, выглядит так:

Именно благодаря C2 первичная алгебра является решеткой . В силу J1a она является дополненной решеткой , верхняя граница которой равна . По J0 , является соответствующей нижней границей и единичным элементом . J0 также является алгебраической версией A2 и проясняет смысл, в котором псевдонимы с пустой страницей.

T13 в LoF обобщает C2 следующим образом. Любая первичная алгебраическая (или сентенциальная логическая) формула B может рассматриваться как упорядоченное дерево с ветвями . Тогда:

T13 : Подформула A может быть скопирована по желанию на любую глубину B, большую, чем глубина A , при условии, что A и ее копия находятся в одной и той же ветви B. Кроме того, если в одной и той же ветви B имеется несколько экземпляров A , все экземпляры, кроме самого поверхностного, являются избыточными.

Хотя доказательство T13 потребует индукции , интуиция, лежащая в его основе, должна быть ясна.

C2 или его эквивалент называется:

• «Поколение» в LoF ;
• «Исключение» у Джонсона (1892);
• «Проникновение» в творчестве Уильяма Брикена.

Возможно, первым примером аксиомы или правила с силой C2 было «Правило (де)итерации», объединяющее T13 и AA=A , из экзистенциальных графов К. С. Пирса .

LoF утверждает, что конкатенация может быть прочитана как коммутация и ассоциация по умолчанию и, следовательно, не должна явно предполагаться или демонстрироваться. (Пирс сделал похожее утверждение о своих экзистенциальных графах .) Пусть период будет временной нотацией для установления группировки. То, что конкатенация коммутирует и ассоциирует, может быть затем продемонстрировано из:

• Исходное AC.D = CD.A и следствие AA = A (Byrne 1946). Этот результат справедлив для всех решеток , поскольку AA = A является простым следствием закона поглощения , который справедлив для всех решеток;
• Начальные AC.D = AD.C и J0 . Поскольку J0 выполняется только для решеток с нижней границей, этот метод выполняется только для ограниченных решеток (которые включают первичную алгебру и 2 ). Коммутативность тривиальна; просто положим A = . Ассоциативность: AC.D = CA.D = CD.A = A.CD .

Доказав ассоциативность, точку можно отбросить.

Инициалы в Meguire (2011) — это AC.D = CD.A , называемые B1 ; B2 , J0 выше; B3 , J1a выше; и B4 , C2. По замыслу эти инициалы очень похожи на аксиомы для абелевой группы , G1-G3 ниже.

Теория доказательств

Первичная алгебра содержит три вида доказанных утверждений:

• Следствие — это первичное алгебраическое уравнение, проверенное демонстрацией . Демонстрация состоит из последовательности шагов , каждый шаг обоснован начальным или ранее продемонстрированным следствием.
• Теорема — это утверждение на метаязыке, подтвержденное доказательством , т. е. аргументом, сформулированным на метаязыке и принимаемым подготовленными математиками и логиками.
• Начальный , определенный выше. Демонстрации и доказательства ссылаются на начальный, как если бы он был аксиомой.

Различие между следствием и теоремой сохраняется для всех формальных систем, включая математику и логику, но обычно не делается явным. Демонстрация или процедура принятия решения могут быть выполнены и проверены компьютером. Доказательство теоремы не может быть выполнено .

Пусть A и B — формулы первичной алгебры . Демонстрация A = B может происходить двумя способами:

• Изменяйте A пошагово, пока не получите B , или наоборот;
• Упростить обаик . Это известно как «расчет».

После того, как A = B продемонстрировано, A = B может быть использовано для обоснования шагов в последующих демонстрациях. Для демонстраций и вычислений первичной алгебры часто требуется не более J1a , J2 , C2 и следствий( C3 в LoF ),( C1 ) и АА = А ( C5 ).

Последствие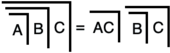, C7' в LoF , позволяет использовать алгоритм , описанный в доказательстве LoF T14, который преобразует произвольную формулу первичной алгебры в эквивалентную формулу, глубина которой не превышает двух. Результатом является нормальная форма , аналог первичной алгебры конъюнктивной нормальной формы . LoF (T14–15) доказывает аналог первичной алгебры известной теоремы булевой алгебры о том, что каждая формула имеет нормальную форму.

Пусть A будет подформулой некоторой формулы B. В паре с C3 J1a можно рассматривать как условие замыкания для вычислений: B является тавтологией тогда и только тогда, когда A и ( A ) оба появляются в глубине 0 формулы B. Связанное условие появляется в некоторых версиях естественной дедукции . Демонстрация с помощью вычислений часто немного больше, чем:

• Повторный вызов T13 для устранения избыточных подформул;
• Удаление любых подформул, имеющих вид.

Последний шаг расчета всегда вызывает J1a .

LoF включает в себя элегантные новые доказательства следующей стандартной метатеории :

• Полнота : все следствия первичной алгебры можно продемонстрировать из инициалов (T17).
• Независимость : J1 не может быть продемонстрирована на основе J2 и наоборот (T18).

То, что сентенциальная логика является полной, преподается в каждом первом университетском курсе математической логики . Но университетские курсы по булевой алгебре редко упоминают полноту 2 .

Интерпретации

Если состояния Marked и Unmarked считываются как булевы значения 1 и 0 (или True и False ), первичная алгебра интерпретирует 2 (или сентенциальную логику ). LoF показывает, как первичная алгебра может интерпретировать силлогизм . Каждая из этих интерпретаций обсуждается в подразделе ниже. Расширение первичной алгебры таким образом, чтобы она могла интерпретировать стандартную логику первого порядка , еще не сделано, но бета- экзистенциальные графы Пирса предполагают , что это расширение осуществимо.

Двухэлементная булева алгебра 2

Первичная алгебра — это элегантная минималистская запись для двухэлементной булевой алгебры 2. Пусть:

• Одна из интерпретаций конкатенации : логическое соединение (+) или встреча (×) ;
• Дополнение к A интерпретирует​
• 0 (1) интерпретирует пустую метку, если join (meet) интерпретирует конкатенацию (поскольку бинарная операция, примененная к нулю операндов, может рассматриваться как равная элементу идентичности этой операции; или, другими словами, отсутствующий операнд может рассматриваться как действующий по умолчанию как элемент идентичности).

Если join (meet) интерпретирует AC , то meet (join) интерпретирует . Следовательно, первичная алгебра и 2 изоморфны, за исключением одной детали: дополнение первичной алгебры может быть нулевым, в этом случае оно обозначает примитивное значение. По модулю этой детали 2 является моделью первичной алгебры. Первичная арифметика предполагает следующую арифметическую аксиоматизацию 2 : 1+1=1+0=0+1=1=~0 и 0+0=0=~1. ${\displaystyle {\overline {{\overline {A|}}\ \ {\overline {C|}}{\Big |}}}}$

Множество — это булева область или носитель . На языке универсальной алгебры первичная алгебра — это алгебраическая структура типа . Выразительная адекватность штриха Шеффера указывает на то, что первичная алгебра также является алгеброй типа . В обоих случаях тождествами являются J1a, J0, C2 и ACD=CDA . Поскольку первичная алгебра и 2 изоморфны , 2 можно рассматривать как алгебру типа . Это описание 2 проще обычного, а именно алгебры типа . ${\displaystyle \ B=\{}$ ${\displaystyle ,}$ ${\displaystyle \ \}}$ ${\displaystyle \langle B,-\ -,{\overline {-\ |}},{\overline {\ \ |}}\rangle }$ ${\displaystyle \langle 2,1,0\rangle }$ ${\displaystyle \langle B,{\overline {-\ -\ |}},{\overline {\ \ |}}\rangle }$ ${\displaystyle \langle 2,0\rangle }$ ${\displaystyle \langle B,+,\lnot ,1\rangle }$ ${\displaystyle \langle 2,1,0\rangle }$ ${\displaystyle \langle B,+,\times ,\lnot ,1,0\rangle }$ ${\displaystyle \langle 2,2,1,0,0\rangle }$

Две возможные интерпретации являются дуальными друг другу в булевом смысле. (В булевой алгебре замена AND ↔ OR и 1 ↔ 0 в уравнении дает одинаково допустимое уравнение.) Тождества остаются инвариантными независимо от выбранной интерпретации, поэтому преобразования или режимы вычисления остаются теми же; только интерпретация каждой формы будет отличаться. Пример: J1a — это. Интерпретируя сопоставление как ИЛИ и как 1, это переводится в , что является истинным. Интерпретируя сопоставление как И и как 0, это переводится в , что также является истинным (и двойственным к ). ${\displaystyle \neg A\lor A=1}$ ${\displaystyle \neg A\land A=0}$ ${\displaystyle \neg A\lor A=1}$

дуальность оператор-операнд

Отмеченное состояние, , является как оператором (например, дополнением), так и операндом (например, значением 1). Это можно аккуратно суммировать, определив две функции и для отмеченного и неотмеченного состояния соответственно: пусть и , где — (возможно, пустой) набор булевых значений. ${\displaystyle m(x)}$ ${\displaystyle u(x)}$ ${\displaystyle m(x)=1-\max(\{0\}\cup x)}$ ${\displaystyle u(x)=\max(\{0\}\cup x)}$ ${\displaystyle x}$

Это показывает, что либо значение 0, либо оператор OR, в то время как либо значение 1, либо оператор NOR, в зависимости от того, является ли множество пустым или нет. Как отмечено выше, существует двойственная форма этих функций, меняющих местами AND ↔ OR и 1 ↔ 0. ${\displaystyle u}$ ${\displaystyle m}$ ${\displaystyle x}$

Логика предложений

Пусть пустая страница обозначает Ложь , а Крест читается как Нет . Тогда первичная арифметика имеет следующее сентенциальное чтение:

 =   Ложь

 =   Истина  =   не Ложь

 =   Неправда  =   Ложь

Первичная алгебра интерпретирует сентенциальную логику следующим образом. Буква представляет любое данное сентенциальное выражение. Таким образом:

интерпретирует Не А

интерпретирует A или B

интерпретирует Not A Or B или If A Then B.

интерпретирует Не (Не А или Не Б)

или нет (если A, то не B)

или А и В.

Таким образом, любое выражение в сентенциальной логике имеет первичную алгебраическую трансляцию. Эквивалентно, первичная алгебра интерпретирует сентенциальную логику. При задании каждой переменной в состояниях Marked или Unmarked этот первичный алгебраический трансляционный перевод сводится к первичному арифметическому выражению, которое можно упростить. Повторение этого упражнения для всех возможных назначений двух примитивных значений каждой переменной показывает, является ли исходное выражение тавтологическим или выполнимым . Это пример процедуры принятия решения , более или менее в духе обычных таблиц истинности. При заданной некоторой первичной алгебраической формуле, содержащей N переменных, эта процедура принятия решения требует упрощения 2 ^N первичных арифметических формул. Для менее утомительной процедуры принятия решения, более соответствующей духу «анализа истинностных значений» Куайна, см. Meguire (2003) .

Шварц (1981) доказал, что первичная алгебра эквивалентна — синтаксически , семантически и теоретически доказательно — классическому исчислению высказываний . Аналогично можно показать, что первичная алгебра синтаксически эквивалентна выражениям, построенным обычным способом из классических значений истинности true и false , логических связок NOT, OR и AND и скобок.

Интерпретация неотмеченного состояния как ложного полностью произвольна; это состояние может быть с таким же успехом прочитано как истинное . Все, что требуется, это чтобы интерпретация конкатенации изменилась с ИЛИ на И. IF A THEN B теперь переводится каквместо. В более общем смысле, первичная алгебра является «самодвойственной » , что означает, что любая формула первичной алгебры имеет два сентенциальных или булевых прочтения, каждое из которых является дуальным по отношению к другому. Другим следствием самодвойственности является нерелевантность законов Де Моргана ; эти законы изначально встроены в синтаксис первичной алгебры .

Теперь проявляется истинная природа различия между первичной алгеброй с одной стороны и 2 и сентенциальной логикой с другой. В последних формализмах дополнение / отрицание, действующее на «ничто», не является правильно сформированным. Но пустой Крест — это правильно сформированное выражение первичной алгебры , обозначающее состояние Marked, примитивное значение. Следовательно, непустой Крест — это оператор , в то время как пустой Крест — это операнд, поскольку он обозначает примитивное значение. Таким образом, первичная алгебра показывает, что до сих пор различные математические концепции оператора и операнда на самом деле являются просто разными гранями одного фундаментального действия — проведения различия.

Силлогизмы

Приложение 2 к LoF показывает, как перевести традиционные силлогизмы и сориты в первичную алгебру . Действительный силлогизм — это просто тот, чей перевод первичной алгебры упрощается до пустого Креста. Пусть A * обозначает литерал , т. е. либо A , либо , безразлично. Тогда каждый силлогизм, который не требует, чтобы один или несколько терминов предполагались непустыми, является одной из 24 возможных перестановок обобщения Барбары , чей эквивалент первичной алгебры — . Эти 24 возможных перестановки включают 19 силлогистических форм, считающихся действительными в аристотелевской и средневековой логике . Этот перевод первичной алгебры силлогистической логики также предполагает, что первичная алгебра может интерпретировать монадическую и терминальную логику , и что первичная алгебра имеет сходство с булевыми схемами терминов Куайна (1982: Часть II). ${\displaystyle {\overline {A|}}}$ ${\displaystyle {\overline {A^{*}\ B|}}\ \ {\overline {{\overline {B|}}\ C^{*}{\Big |}}}\ A^{*}\ C^{*}}$

Пример расчета

Следующее вычисление нетривиальной теоремы Лейбница Praeclarum Theorema иллюстрирует доказательную силу первичной алгебры . Пусть C1 будет = A , C2 будет , C3 будет , J1a будет , и пусть OI означает, что переменные и подформулы были переупорядочены таким образом, что это допускают коммутативность и ассоциативность. ${\displaystyle {\overline {{\overline {A|}}{\Big |}}}}$ ${\displaystyle A\ {\overline {A\ B|}}=A\ {\overline {B|}}}$ ${\displaystyle {\overline {\ \ |}}\ A={\overline {\ \ |}}}$ ${\displaystyle {\overline {A|}}\ A={\overline {\ \ |}}}$

Отношение к магмам

Первичная алгебра воплощает точку зрения, отмеченную Хантингтоном в 1933 году: Булева алгебра требует, в дополнение к одной унарной операции , одну, а не две, бинарные операции . Отсюда редко отмечаемый факт, что булевы алгебры являются магмами . (Магмы назывались группоидами, пока последний термин не был присвоен теорией категорий .) Чтобы увидеть это, отметим, что первичная алгебра является коммутативной :

• Полугруппа , поскольку первичное алгебраическое сопоставление коммутирует и ассоциирует ;
• Моноид с единичным элементом , в силу J0 .

Группы также требуют унарной операции , называемой инверсией , группового аналога булевого дополнения . Пустьобозначим обратный элемент a . Пусть обозначим элемент групповой идентичности . Тогда группы и первичная алгебра имеют одинаковые сигнатуры , а именно они обе являются алгебрами типа 〈2,1,0〉. Следовательно, первичная алгебра является граничной алгеброй . Аксиомы для абелевой группы в граничной нотации следующие: ${\displaystyle \langle -\ -,{\overline {-\ |}},{\overline {\ \ |}}\rangle }$

• G1 . abc = acb (предполагая ассоциацию слева);
• Г2 .
• Г3 ..

Из G1 и G2 можно вывести коммутативность и ассоциативность конкатенации, как указано выше. Обратите внимание, что G3 и J1a идентичны. G2 и J0 были бы идентичны, если    =    заменил A2 . Это определяющее арифметическое тождество теории групп в граничной нотации.

Первичная алгебра отличается от абелевой группы двумя способами:

• Из A2 следует, что ≠ . Если бы первичная алгебра была группой , то = выполнялось бы, и одно из    a  =     или    a   =  a    должно быть следствием первичной алгебры . Обратите внимание, чтоиявляются взаимными первичными алгебраическими дополнениями, как того требует теория групп, так что это справедливо как для теории групп, так и для первичной алгебры ; ${\displaystyle {\overline {\ {\overline {\ {\overline {\ \ |}}\ {\Big |}}}\ {\Bigg |}}}={\overline {\ \ |}}}$
• C2 наиболее четко разграничивает первичную алгебру от других магм, поскольку C2 позволяет продемонстрировать закон поглощения , определяющий решетки , и распределительный закон, являющийся центральным для булевой алгебры .

Оба утверждения A2 и C2 вытекают из того, что B является упорядоченным множеством .

Уравнения второй степени (глава 11)

Глава 11 LoF вводит уравнения второй степени , состоящие из рекурсивных формул, которые можно рассматривать как имеющие «бесконечную» глубину. Некоторые рекурсивные формулы упрощаются до отмеченного или неотмеченного состояния. Другие «колеблются» бесконечно между двумя состояниями в зависимости от того, является ли заданная глубина четной или нечетной. В частности, некоторые рекурсивные формулы можно интерпретировать как колеблющиеся между истинным и ложным в течение последовательных интервалов времени, и в этом случае считается, что формула имеет «мнимое» значение истинности. Таким образом, поток времени может быть введен в первичную алгебру .

Turney (1986) показывает, как эти рекурсивные формулы можно интерпретировать с помощью Restricted Recursive Arithmetic (RRA) Алонзо Чёрча . Чёрч представил RRA в 1955 году как аксиоматическую формализацию конечных автоматов . Turney (1986) представляет общий метод перевода уравнений второй степени в RRA Чёрча, иллюстрируя свой метод с помощью формул E1 , E2 и E4 в главе 11 LoF . Этот перевод в RRA проливает свет на названия, которые Спенсер-Браун дал E1 и E4 , а именно «память» и «счётчик». Таким образом, RRA формализует и проясняет понятие LoF о мнимом значении истинности.

Связанная работа

Готфрид Лейбниц в меморандумах, не опубликованных до конца 19-го и начала 20-го веков, изобрел булеву логику . Его нотация была изоморфна нотации LoF : конкатенация читалась как конъюнкция , а «не-( X )» читалось как дополнение X . Признание пионерской роли Лейбница в алгебраической логике было предвосхищено Льюисом (1918) и Решером (1954). Но полное признание достижений Лейбница пришлось ждать работы Вольфганга Ленцена, опубликованной в 1980-х годах и рассмотренной в Lenzen (2004).

Чарльз Сандерс Пирс (1839–1914) предвосхитил возникновение элементарной алгебры в трех направлениях работы:

1. Две статьи, написанные им в 1886 году, предложили логическую алгебру, использующую только один символ, стример , почти идентичный Кресту LoF . Семантика стримера идентична семантике Креста, за исключением того, что Пирс никогда не писал стример без ничего под ним. Отрывок из одной из этих статей был опубликован в 1976 году, ^[9] но они не были опубликованы полностью до 1993 года. ^[10]
2. В статье энциклопедии 1902 года ^[11] Пирс записал булеву алгебру и сентенциальную логику в стиле этой записи, за исключением того, что он использовал два стиля скобок, переключаясь между «(», «)» и «[», «]» с каждым увеличением глубины формулы.
3. Синтаксис его альфа- экзистенциальных графов — это просто конкатенация , читаемая как конъюнкция , и обрамление овалами, читаемое как отрицание . ^[12] Если конкатенацию первичной алгебры читать как конъюнкция , то эти графы изоморфны первичной алгебре (Кауфман 2001).

По иронии судьбы, LoF цитирует том 4 «Собрания статей» Пирса, источник формализмов в (2) и (3) выше. (1)-(3) были практически неизвестны в то время (1960-е) и в том месте (Великобритания), где был написан LoF . Семиотика Пирса , о которой LoF умалчивает, все еще может пролить свет на философские аспекты LoF .

Кауфман (2001) обсуждает другую нотацию, похожую на LoF , из статьи 1917 года Жана Никода , ученика Бертрана Рассела .

Вышеуказанные формализмы, как и первичная алгебра , являются примерами граничной математики , т. е. математики, синтаксис которой ограничен буквами и скобками (ограничительными устройствами). Минималистский синтаксис такого рода — это «граничная нотация». Граничная нотация свободна от инфиксных операторов, префиксных или постфиксных операторных символов. Очень известные фигурные скобки ('{', '}') теории множеств можно рассматривать как граничную нотацию.

Работы Лейбница, Пирса и Никода не содержат метатеории, поскольку они писали об этом до знаменательной статьи Эмиля Поста 1920 года (на которую ссылается LoF ), доказывающей полноту пропозициональной логики , и до того, как Гильберт и Лукасевич показали, как доказать независимость аксиом с помощью моделей .

Крейг (1979) утверждал, что мир и то, как люди воспринимают и взаимодействуют с этим миром, имеет богатую булеву структуру. Крейг был ортодоксальным логиком и авторитетом в области алгебраической логики .

Второе поколение когнитивной науки появилось в 1970-х годах, после написания LoF . О когнитивной науке и ее связи с булевой алгеброй, логикой и теорией множеств см. Lakoff (1987) (см. индексные записи в разделе «Примеры схем изображений: контейнер») и Lakoff и Núñez (2001). Ни одна из книг не ссылается на LoF .

Биологи и когнитивные ученые Умберто Матурана и его ученик Франциско Варела обсуждают LoF в своих работах, которые определяют «различение» как фундаментальный когнитивный акт. Психолог из Беркли и когнитивный ученый Элеанор Рош много писала о тесно связанном понятии категоризации.

Другие формальные системы, имеющие возможное сходство с первичной алгеброй, включают:

• Мереология , которая обычно имеет решетчатую структуру, очень похожую на структуру булевой алгебры. Для некоторых авторов мереология — это просто модель булевой алгебры и , следовательно, также и первичной алгебры.
• Мереотопология , которая по своей сути богаче булевой алгебры;
• Система Уайтхеда (1934), фундаментальным примитивом которой является «индикация».

Первичная арифметика и алгебра являются минималистским формализмом для сентенциальной логики и булевой алгебры. Другие минималистские формализмы, имеющие силу теории множеств, включают:

• Лямбда -исчисление ;
• Комбинаторная логика с двумя ( S и K ) или даже одним ( X ) примитивными комбинаторами;
• Математическая логика, сделанная всего с тремя примитивными понятиями: одним связующим, НЕ-И (чьим первичным алгебраическим переводом является или, дуально, ), универсальной квантификацией и одной бинарной атомарной формулой , обозначающей принадлежность к множеству . Это система Куайна (1951). ${\displaystyle {\overline {A\ \ B\ |}}}$ ${\displaystyle {\overline {A|}}\ \ {\overline {B|}}}$
• Бета - экзистенциальные графы с одним бинарным предикатом, обозначающим принадлежность множеству. Это еще предстоит изучить. Альфа -графы, упомянутые выше, являются частным случаем бета - графов.

Издания

• 1969. Лондон: Allen & Unwin, твердый переплет.
• 1972. Crown Publishers, твердый переплет: ISBN  0-517-52776-6
• 1973. Bantam Books, мягкая обложка. ISBN 0-553-07782-1 
• 1979. EP Dutton, мягкая обложка. ISBN 0-525-47544-3 
• 1994. Портленд, штат Орегон: Cognizer Company, мягкая обложка. ISBN 0-9639899-0-1 
• Немецкий перевод 1997 года под названием Gesetze der Form . Любек: Bohmeier Verlag. ISBN 3-89094-321-7 
• 2008 Bohmeier Verlag, Лейпциг, 5-е международное издание. ISBN 978-3-89094-580-4 

Смотрите также

• Булева алгебра  – Алгебраические манипуляции с «истиной» и «ложью»
• Булевы алгебры, канонически определенные  – Техническая трактовка булевых алгебр
• Граф сущности  – тип диаграммной записи для пропозициональной логикиPages displaying short descriptions of redirect targets
• Экзистенциальный граф  – тип диаграммной записи для пропозициональной логики
• Знак и пробел  – состояния сигнала связи
• Программирование и метапрограммирование  – научно-популярная книга Джона К. Лилли, изданная в 1968 году.
• Исчисление высказываний  – Раздел логики
• Двухэлементная булева алгебра  – Булева алгебра
• Список тем по булевой алгебре

Примечания

1. Meguire, P. (2011) Граничная алгебра: более простой подход к базовой логике и булевой алгебре. Саарбрюккен: VDM Publishing Ltd. 168 стр.
2. Шёнвальдер-Кунц, Татьяна; Вилле, Катрин; Хёльшер, Томас; Спенсер Браун, Джордж (2009). «Джордж Спенсер Браун: Eine Einführung в законах формы , 2. Auflage» . Висбаден: VS Verlag für Sozialwissenschaften. ISBN 978-3-531-16105-1.
3. Феликс Лау: Die Form der Paradoxie , 2005 Carl-Auer Verlag, ISBN 9783896703521 
4. Джордж Спенсер-Браун. Законы формы. 1969, Издательство Джорджа Аллена и Анвина. SBN 04 510028 4
5. Мюллер, Альберт (2008). «Вычисление реальности. Лекция Хайнца фон Ферстера на конференции AUM в 1973 году» (PDF) . Основы конструктивизма . 4 (1): 62–69.
6. Бир, Стаффорд (1969). «Maths Created». Nature . 223 (5213): 1392–1393. Bibcode : 1969Natur.223.1392B. doi : 10.1038/2231392b0. S2CID  5223774.
7. Б. Банашевски (июль 1977 г.). «О законах формы Г. Спенсера Брауна». Notre Dame Journal of Formal Logic . 18 (3): 507–509. doi : 10.1305/ndjfl/1093888028 .
8. Для сочувственной оценки см. Kauffman (2001).
9. "Qualitative Logic", MS 736 (c. 1886) в Eisele, Carolyn, ред. 1976. Новые элементы математики Чарльза С. Пирса . Том 4, Математическая философия . (Гаага) Мутон: 101-15.1
10. "Qualitative Logic", MS 582 (1886) в Kloesel, Christian et al., eds., 1993. Writings of Charles S. Peirce: A Chronological Edition , Vol. 5, 1884–1886 . Indiana University Press : 323-71. "The Logic of Relatives: Qualitative and Quantitative", MS 584 (1886) в Kloesel, Christian et al., eds., 1993. Writings of Charles S. Peirce: A Chronological Edition, Vol. 5, 1884–1886 . Indiana University Press: 372-78.
11. Перепечатано в Peirce, CS (1933) Collected Papers of Charles Sanders Peirce , Vol. 4 , Charles Hartshorne and Paul Weiss , eds. Harvard University Press . Пункты 378–383
12. Экзистенциальные графы подробно описаны в Peirce, CS (1933) Collected Papers, Vol. 4 , Charles Hartshorne and Paul Weiss , eds. Harvard University Press. Paragraphs 347–529.

Библиография

• Босток, Дэвид, 1997. Промежуточный уровень логики . Oxford Univ. Press.
• Бирн, Ли, 1946, «Две формулировки булевой алгебры», Бюллетень Американского математического общества : 268–71.
• Крейг, Уильям (1979). «Булева логика и повседневный физический мир». Труды и выступления Американской философской ассоциации . 52 (6): 751–78. doi :10.2307/3131383. JSTOR  3131383.
• Дэвид Грайс и Шнайдер, Ф. Б., 1993. Логический подход к дискретной математике . Springer-Verlag.
• Уильям Эрнест Джонсон , 1892, «Логическое исчисление», Mind 1 (ns): 3–30.
• Луис Х. Кауфман, 2001, «Математика К. С. Пирса», Кибернетика и человеческое познание 8: 79–110.
• ------, 2006, «Переформулировка теоремы о цвете карты».
• ------, 2006a. «Законы формы – исследование математики и ее основ». Черновик книги (отсюда и большой).
• Ленцен, Вольфганг, 2004, «Логика Лейбница» в книге Габбея, Д. и Вудса, Дж., ред., « Восход современной логики: от Лейбница до Фреге» (Справочник по истории логики – т. 3) . Амстердам: Elsevier, 1–83.
• Лакофф, Джордж , 1987. Женщины, огонь и опасные вещи . Издательство Чикагского университета.
• -------- и Рафаэль Э. Нуньес , 2001. Откуда берется математика : как воплощенный разум воплощает математику в жизнь . Основные книги.
• Meguire, PG (2003). «Открытие граничной алгебры: упрощенная нотация для булевой алгебры и функторы истинности». International Journal of General Systems . 32 : 25–87. CiteSeerX  10.1.1.106.634 . doi :10.1080/0308107031000075690. S2CID  9460101.
• --------, 2011. Граничная алгебра: более простой подход к базовой логике и булевой алгебре . VDM Publishing Ltd. ISBN 978-3639367492 . Источник большей части этой записи, включая нотацию, которая заключает в скобки то, что LoF помещает под крест. Избегает более спекулятивных аспектов LoF . 
• Уиллард Куайн , 1951. Математическая логика , 2-е изд. Издательство Гарвардского университета.
• --------, 1982. Методы логики , 4-е изд. Издательство Гарвардского университета.
• Решер, Николас (1954). «Интерпретация Лейбницем его логических исчислений». Журнал символической логики . 18 (1): 1–13. doi :10.2307/2267644. JSTOR  2267644. S2CID  689315.
• Шварц, Дэниел Г. (1981). «Изоморфизмы законов формы Г. Спенсера-Брауна и исчисления самореференции Ф. Варелы». Международный журнал общих систем . 6 (4): 239–55. doi :10.1080/03081078108934802.
• Turney, PD (1986). « Законы формы и конечные автоматы». International Journal of General Systems . 12 (4): 307–18. doi :10.1080/03081078608934939.
• AN Whitehead , 1934, «Указание, классы, число, валидация», Mind 43 (ns): 281–97, 543. Исправления на стр. 543 многочисленны и важны, и более поздние переиздания этой статьи не включают их.
• Дирк Бекер (редактор) (1993), Калькюль дер Форм. Зуркамп; Дирк Беккер (редактор), «Проблема формы» . Зуркамп.
• Дирк Беккер (ред.) (1999), Проблемы формы , Издательство Стэнфордского университета.
• Дирк Беккер (ред.) (2013), Математика формы, Социология наблюдателей , Кибернетика и человеческое познание, т. 20, № 3-4.
• Луис Х. Кауфман (ред.) (2019), Кибернетика и человеческое знание, т. 26, № 2-3. Специальный выпуск, Законы формы: Спенсер-Браун в Эсалене, 1973 .

Внешние ссылки

• Законы формы, архив сайта Ричарда Шоупа.
• Доклады Спенсера-Брауна в Эсалене, 1973 г. Самореферентные формы вводятся в разделе под названием «Степень уравнений и теория типов».
• Аудиозапись вступительного заседания конференции АУМ 1973 года в Эсалене.
• Луис Х. Кауфман, «Ящичная алгебра, граничная математика, логика и законы формы».
• Киссель, Маттиас, «Несистематическое, но легкое для понимания введение в законы формы».
• Форум «Законы формы», где с 2002 года обсуждаются основные положения алгебры и связанные с ней формализмы.
• Встреча с GSB Моше Кляйна
• «Отметка знака», введение в идеи Законов Формы простыми шагами
• Исчисление БФ и квадратный корень отрицания Луиса Кауфмана и Артура Коллингса; оно расширяет законы формы, добавляя мнимое логическое значение. (Мнимые логические значения вводятся в главе 11 книги « Законы формы »).
• Курс «Законы формы» — бесплатный онлайн-курс, знакомящий слушателей с основной частью текста «Законов формы» Леона Конрада, последнего ученика Спенсера-Брауна, изучавшего это произведение вместе с автором.