Ковариантность и контравариантность векторов

Поведение вектора при изменении координат

А вектор, v , представленный в терминах

касательный базис

  е ₁ , е ₂ , е ₃ к координатные кривые ( слева ),

двойной базис, ковекторный базис или обратный базис

  е ¹ , е ² , е ³ к координатные поверхности ( справа ),

в 3-мерных общих криволинейных координатах ( q ¹ , q ² , q ³ ) , кортеж чисел для определения точки в пространстве положений . Обратите внимание, что базис и кобазис совпадают только тогда, когда базис ортонормальный . ^{[1] [ указать ]}

В физике , особенно в полилинейной алгебре и тензорном анализе , ковариантность и контравариантность описывают, как количественное описание определенных геометрических или физических объектов изменяется при изменении базиса . ^[2] Вкратце, контравариантный вектор — это список чисел, который преобразуется противоположно изменению базиса, а ковариантный вектор — это список чисел, который преобразуется таким же образом. Контравариантные векторы часто называют просто векторами , а ковариантные векторы называют ковекторами или дуальными векторами . Термины ковариантный и контравариантный были введены Джеймсом Джозефом Сильвестром в 1851 году. ^{[3] [4]}

Криволинейные системы координат , такие как цилиндрические или сферические координаты , часто используются в физических и геометрических задачах. С любой системой координат связан естественный выбор базиса координат для векторов, основанных на каждой точке пространства, а ковариантность и контравариантность особенно важны для понимания того, как изменяется координатное описание вектора при переходе из одной системы координат в другую. Тензоры — это объекты в полилинейной алгебре , которые могут иметь аспекты как ковариантности, так и контравариантности.

Введение

В физике вектор обычно возникает как результат измерения или серии измерений и представляется в виде списка (или кортежа ) чисел, например:

${\displaystyle (v_{1},v_{2},v_{3}).}$

Числа в списке зависят от выбора системы координат . Например, если вектор представляет положение относительно наблюдателя ( вектор положения ), то система координат может быть получена из системы жестких стержней или опорных осей, вдоль которых измеряются компоненты v ₁ , v ₂ и v ₃ . Для того чтобы вектор представлял геометрический объект, необходимо иметь возможность описать, как он выглядит в любой другой системе координат. То есть компоненты векторов будут определенным образом трансформироваться при переходе из одной системы координат в другую.

Простым иллюстративным случаем является евклидов вектор . Для вектора, как только определен набор базисных векторов, компоненты этого вектора всегда будут изменяться противоположно компонентам базисных векторов. Поэтому этот вектор определяется как контравариантный тензор. Возьмем, к примеру, стандартный вектор положения. При изменении масштаба осей отсчета с метров на сантиметры (то есть делении масштаба осей отсчета на 100, так что базисные векторы теперь имеют длину в метрах), компоненты измеренного вектора положения умножаются на 100. Компоненты вектора изменяют масштаб обратно пропорционально изменениям масштаба осей отсчета, и, следовательно, вектор называется контравариантным тензором. ${\displaystyle .01}$

Вектор , который является примером контравариантного тензора, имеет компоненты, которые преобразуются обратно преобразованию осей отсчета (с примерами преобразований, включая вращение и растяжение ). Сам вектор не изменяется при этих операциях ; вместо этого компоненты вектора изменяются таким образом, что отменяют изменение пространственных осей. Другими словами, если оси отсчета были повернуты в одном направлении, компонентное представление вектора повернулось бы точно в противоположном направлении. Аналогично, если оси отсчета были растянуты в одном направлении, компоненты вектора, уменьшились бы точно компенсирующим образом. Математически, если система координат претерпевает преобразование, описываемое обратимой матрицей M , так что базисные векторы преобразуются согласно , то компоненты вектора v в исходном базисе ( ) должны быть аналогично преобразованы с помощью . Компоненты вектора часто представляются расположенными в столбце. ${\displaystyle n\times n}$ ${\displaystyle {\begin{bmatrix}\mathbf {e} _{1}^{\prime }\ \mathbf {e} _{2}^{\prime }\ ...\ \mathbf {e} _{n}^{\prime }\end{bmatrix}}={\begin{bmatrix}\mathbf {e} _{1}\ \mathbf {e} _{2}\ ...\ \mathbf {e} _{n}\end{bmatrix}}M}$ ${\displaystyle v^{i}}$ ${\displaystyle {\begin{bmatrix}v^{1}{^{\prime }}\\v^{2}{^{\prime }}\\...\\v^{n}{^{\prime }}\end{bmatrix}}=M^{-1}{\begin{bmatrix}v^{1}\\v^{2}\\...\\v^{n}\end{bmatrix}}}$

Напротив, ковектор имеет компоненты, которые преобразуются подобно осям отсчета. Он находится в двойственном векторном пространстве и представляет собой линейное отображение векторов в скаляры. Оператор скалярного произведения, включающий векторы, является хорошим примером ковектора. Для иллюстрации предположим, что у нас есть ковектор, определенный как , где — вектор. Компоненты этого ковектора в некотором произвольном базисе равны , причем являются базисными векторами в соответствующем векторном пространстве. (Это можно вывести, заметив, что мы хотим получить правильный ответ для операции скалярного произведения при умножении на произвольный вектор , с компонентами ). Ковариантность этих компонентов ковектора затем видна, заметив, что если преобразование, описанное обратимой матрицей M, было применено к базисным векторам в соответствующем векторном пространстве, , то компоненты ковектора преобразуются с той же матрицей , а именно, . Компоненты ковектора часто представляются расположенными в ряд. ${\displaystyle \mathbf {v} \ \cdot }$ ${\displaystyle \mathbf {v} }$ ${\displaystyle {\begin{bmatrix}\mathbf {v} \cdot \mathbf {e} _{1}&\mathbf {v} \cdot \mathbf {e} _{2}&...&\mathbf {v} \cdot \mathbf {e} _{n}\end{bmatrix}}}$ ${\displaystyle {\begin{bmatrix}\mathbf {e} _{1}\ \mathbf {e} _{2}\ ...\ \mathbf {e} _{n}\end{bmatrix}}}$ ${\displaystyle \mathbf {w} }$ ${\displaystyle {\begin{bmatrix}w^{1}\\w^{2}\\...\\w^{n}\end{bmatrix}}}$ ${\displaystyle n\times n}$ ${\displaystyle {\begin{bmatrix}\mathbf {e} _{1}^{\prime }\ \mathbf {e} _{2}^{\prime }\ ...\ \mathbf {e} _{n}^{\prime }\end{bmatrix}}={\begin{bmatrix}\mathbf {e} _{1}\ \mathbf {e} _{2}\ ...\ \mathbf {e} _{n}\end{bmatrix}}M}$ ${\displaystyle \mathbf {v} \ \cdot }$ ${\displaystyle M}$ ${\displaystyle {\begin{bmatrix}\mathbf {v} \cdot \mathbf {e} _{1}^{\prime }&\mathbf {v} \cdot \mathbf {e} _{2}^{\prime }&...&\mathbf {v} \cdot \mathbf {e} _{n}^{\prime }\end{bmatrix}}={\begin{bmatrix}\mathbf {v} \cdot \mathbf {e} _{1}&\mathbf {v} \cdot \mathbf {e} _{2}&...&\mathbf {v} \cdot \mathbf {e} _{n}\end{bmatrix}}M}$

Третье понятие, связанное с ковариантностью и контравариантностью, — это инвариантность . Скаляр (также называемый тензором типа 0 или ранга 0) — это объект, который не меняется с изменением базиса. Примером физической наблюдаемой величины , которая является скаляром, является масса частицы. Единственное скалярное значение массы не зависит от изменений базисных векторов и, следовательно, называется инвариантом . Величина вектора (например, расстояния ) — еще один пример инварианта, поскольку она остается фиксированной, даже если геометрические компоненты вектора изменяются. (Например, для вектора положения длиной метры, если все декартовы базисные векторы изменяются с метров в длину на метры в длину, длина вектора положения остается неизменной в метрах, хотя все компоненты вектора увеличатся в множитель ). Скалярное произведение вектора и ковектора инвариантно, поскольку у одного есть компоненты, которые изменяются с изменением базиса, а у другого есть компоненты, которые изменяются противоположно, и эти два эффекта взаимно уничтожаются. Таким образом, можно сказать, что ковекторы двойственны векторам. ${\displaystyle 3}$ ${\displaystyle 1}$ ${\displaystyle .01}$ ${\displaystyle 3}$ ${\displaystyle 100}$

Итак, подведем итог:

• Вектор или касательный вектор имеет компоненты, которые контрвариантны с изменением базиса для компенсации. То есть матрица, которая преобразует компоненты вектора, должна быть обратной матрице, которая преобразует базисные векторы. Компоненты векторов (в отличие от компонентов ковекторов) называются контрвариантными . В обозначениях Эйнштейна (неявное суммирование по повторяющемуся индексу) контрвариантные компоненты обозначаются верхними индексами, как в

  ${\displaystyle \mathbf {v} =v^{i}\mathbf {e} _{i}}$

• Ковектор или котангенс вектор имеет компоненты, которые ковариантны с изменением базиса в соответствующем (исходном) векторном пространстве. То есть компоненты должны быть преобразованы той же матрицей, что и изменение базисной матрицы в соответствующем (исходном) векторном пространстве. Компоненты ковекторов (в отличие от компонентов векторов) называются ковариантными . В обозначениях Эйнштейна ковариантные компоненты обозначаются нижними индексами, как в

  ${\displaystyle \mathbf {w} =w_{i}\mathbf {e} ^{i}.}$

• Скалярное произведение вектора и ковектора — это скаляр , который инвариантен. Это дуальное спаривание векторов и ковекторов. ${\displaystyle v^{i}w_{i}}$

Определение

Ковариантные и контравариантные компоненты вектора, когда базис не ортогонален.

Общая формулировка ковариантности и контравариантности относится к тому, как компоненты координатного вектора преобразуются при изменении базиса ( пассивное преобразование ). Таким образом, пусть V будет векторным пространством размерности n над полем скаляров S , и пусть каждое из f = ( X ₁ , ..., X _n ) и f ′ = ( Y ₁ , ..., Y _n ) будет базисом V . ^{[примечание 1]} Также пусть изменение базиса с f на f ′ задается как

для некоторой обратимой n × n матрицы A с элементами . Здесь каждый вектор Y _j базиса f ′ является линейной комбинацией векторов X _i базиса f , так что ${\displaystyle a_{j}^{i}}$

${\displaystyle Y_{j}=\sum _{i}a_{j}^{i}X_{i}.}$

Контравариантное преобразование

Вектор в V однозначно выражается как линейная комбинация элементов базиса f : ${\displaystyle v}$ ${\displaystyle X_{i}}$

где v ⁱ [ f ] — элементы поля S, известные как компоненты v в базисе f . Обозначим вектор-столбец компонентов v через v [ f ]:

${\displaystyle \mathbf {v} [\mathbf {f} ]={\begin{bmatrix}v^{1}[\mathbf {f} ]\\v^{2}[\mathbf {f} ]\\\vdots \\v^{n}[\mathbf {f} ]\end{bmatrix}}}$

так что ( 2 ) можно переписать как матричное произведение

${\displaystyle v=\mathbf {f} \,\mathbf {v} [\mathbf {f} ].}$

Вектор v также может быть выражен через базис f ′, так что

${\displaystyle v=\mathbf {f'} \,\mathbf {v} [\mathbf {f'} ].}$

Однако, поскольку сам вектор v инвариантен относительно выбора базиса,

${\displaystyle \mathbf {f} \,\mathbf {v} [\mathbf {f} ]=v=\mathbf {f'} \,\mathbf {v} [\mathbf {f'} ].}$

Инвариантность v в сочетании с соотношением ( 1 ) между f и f ′ подразумевает, что

${\displaystyle \mathbf {f} \,\mathbf {v} [\mathbf {f} ]=\mathbf {f} A\,\mathbf {v} [\mathbf {f} A],}$

давая правило преобразования

${\displaystyle \mathbf {v} [\mathbf {f'} ]=\mathbf {v} [\mathbf {f} A]=A^{-1}\mathbf {v} [\mathbf {f} ].}$

С точки зрения компонентов,

${\displaystyle v^{i}[\mathbf {f} A]=\sum _{j}{\tilde {a}}_{j}^{i}v^{j}[\mathbf {f} ]}$

где коэффициенты являются элементами обратной матрицы A. ${\displaystyle {\tilde {a}}_{j}^{i}}$

Поскольку компоненты вектора v преобразуются с обратной матрицей A , говорят, что эти компоненты преобразуются контравариантно при смене базиса.

Способ, которым А связывает две пары, изображен на следующей неформальной диаграмме с помощью стрелки. Переворот стрелки указывает на контравариантное изменение:

${\displaystyle {\begin{aligned}\mathbf {f} &\longrightarrow \mathbf {f'} \\v[\mathbf {f} ]&\longleftarrow v[\mathbf {f'} ]\end{aligned}}}$

Ковариантное преобразование

Линейный функционал α на V однозначно выражается через свои компоненты (элементы в S ) в базисе f как

${\displaystyle \alpha (X_{i})=\alpha _{i}[\mathbf {f} ],\quad i=1,2,\dots ,n.}$

Эти компоненты представляют собой действие α на базисные векторы X _i базиса f .

При замене базиса с f на f ′ (через 1 ) компоненты преобразуются так, что

Обозначим вектор-строку компонентов α через α [ f ]:

${\displaystyle \mathbf {\alpha } [\mathbf {f} ]={\begin{bmatrix}\alpha _{1}[\mathbf {f} ],\alpha _{2}[\mathbf {f} ],\dots ,\alpha _{n}[\mathbf {f} ]\end{bmatrix}}}$

так что ( 3 ) можно переписать как матричное произведение

${\displaystyle \alpha [\mathbf {f} A]=\alpha [\mathbf {f} ]A.}$

Поскольку компоненты линейного функционала α преобразуются вместе с матрицей A , говорят, что эти компоненты преобразуются ковариантно при смене базиса.

Способ, которым А связывает две пары, изображен на следующей неформальной диаграмме с помощью стрелки. Ковариантная связь обозначена, поскольку стрелки идут в одном направлении:

${\displaystyle {\begin{aligned}\mathbf {f} &\longrightarrow \mathbf {f'} \\\alpha [\mathbf {f} ]&\longrightarrow \alpha [\mathbf {f'} ]\end{aligned}}}$

Если бы вместо этого использовалось представление в виде столбчатого вектора, закон преобразования был бы транспонированным

${\displaystyle \alpha ^{\mathrm {T} }[\mathbf {f} A]=A^{\mathrm {T} }\alpha ^{\mathrm {T} }[\mathbf {f} ].}$

Координаты

Выбор базиса f на векторном пространстве V однозначно определяет набор координатных функций на V посредством

${\displaystyle x^{i}[\mathbf {f} ](v)=v^{i}[\mathbf {f} ].}$

Координаты на V , следовательно, контравариантны в том смысле, что

${\displaystyle x^{i}[\mathbf {f} A]=\sum _{k=1}^{n}{\tilde {a}}_{k}^{i}x^{k}[\mathbf {f} ].}$

Наоборот, система из n величин v ⁱ , преобразующихся подобно координатам x ⁱ на V, определяет контравариантный вектор (или просто вектор). Система из n величин, преобразующихся противоположно координатам, является тогда ковариантным вектором (или ковектором).

Эта формулировка контравариантности и ковариантности часто более естественна в приложениях, в которых есть координатное пространство ( многообразие ), на котором векторы существуют как касательные векторы или котангенсивные векторы . При наличии локальной системы координат x ⁱ на многообразии опорными осями для системы координат являются векторные поля

${\displaystyle X_{1}={\frac {\partial }{\partial x^{1}}},\dots ,X_{n}={\frac {\partial }{\partial x^{n}}}.}$

Это приводит к появлению кадра f = ( X ₁ , ..., X _n ) в каждой точке координатного пятна.

Если y ⁱ — другая система координат и

${\displaystyle Y_{1}={\frac {\partial }{\partial y^{1}}},\dots ,Y_{n}={\frac {\partial }{\partial y^{n}}},}$

тогда кадр f' связан с кадром f обратной матрицей Якоби перехода координат:

${\displaystyle \mathbf {f} '=\mathbf {f} J^{-1},\quad J=\left({\frac {\partial y^{i}}{\partial x^{j}}}\right)_{i,j=1}^{n}.}$

Или, в индексах,

${\displaystyle {\frac {\partial }{\partial y^{i}}}=\sum _{j=1}^{n}{\frac {\partial x^{j}}{\partial y^{i}}}{\frac {\partial }{\partial x^{j}}}.}$

Касательный вектор по определению является вектором, который является линейной комбинацией парциальных координат . Таким образом, касательный вектор определяется как ${\displaystyle \partial /\partial x^{i}}$

${\displaystyle v=\sum _{i=1}^{n}v^{i}[\mathbf {f} ]X_{i}=\mathbf {f} \ \mathbf {v} [\mathbf {f} ].}$

Такой вектор контравариантен относительно смены системы отсчета. При смене системы координат имеем

${\displaystyle \mathbf {v} \left[\mathbf {f} '\right]=\mathbf {v} \left[\mathbf {f} J^{-1}\right]=J\,\mathbf {v} [\mathbf {f} ].}$

Следовательно, компоненты касательного вектора преобразуются посредством

${\displaystyle v^{i}\left[\mathbf {f} '\right]=\sum _{j=1}^{n}{\frac {\partial y^{i}}{\partial x^{j}}}v^{j}[\mathbf {f} ].}$

Соответственно, система из n величин v ^{i ,} зависящих от координат, преобразующихся указанным образом при переходе от одной системы координат к другой, называется контравариантным вектором.

Ковариантные и контравариантные компоненты вектора с метрикой

Контравариантные компоненты вектора получаются путем проецирования на оси координат. Ковариантные компоненты получаются путем проецирования на нормали к координатным гиперплоскостям.

В конечномерном векторном пространстве V над полем K с симметричной билинейной формой g  : V × V → K (которую можно назвать метрическим тензором ) существует небольшое различие между ковариантными и контравариантными векторами, поскольку билинейная форма позволяет отождествлять ковекторы с векторами. То есть вектор v однозначно определяет ковектор α посредством

${\displaystyle \alpha (w)=g(v,w)}$

для всех векторов w . Наоборот, каждый ковектор α определяет уникальный вектор v этим уравнением. Из-за этой идентификации векторов с ковекторами можно говорить о ковариантных компонентах или контравариантных компонентах вектора, то есть они являются просто представлениями одного и того же вектора с использованием обратного базиса .

Если задан базис f = ( X ₁ , ..., X _n ) множества V , то существует единственный обратный базис f ^# = ( Y ¹ , ..., Y ⁿ ) множества V , определяемый требованием, чтобы

${\displaystyle g(Y^{i},X_{j})=\delta _{j}^{i},}$

дельта Кронекера . В терминах этих базисов любой вектор v можно записать двумя способами:

${\displaystyle {\begin{aligned}v&=\sum _{i}v^{i}[\mathbf {f} ]X_{i}=\mathbf {f} \,\mathbf {v} [\mathbf {f} ]\\&=\sum _{i}v_{i}[\mathbf {f} ]Y^{i}=\mathbf {f} ^{\sharp }\mathbf {v} ^{\sharp }[\mathbf {f} ].\end{aligned}}}$

Компоненты v ⁱ [ f ] являются контравариантными компонентами вектора v в базисе f , а компоненты v _i [ f ] являются ковариантными компонентами v в базисе f . Терминология оправдана, поскольку при смене базиса,

${\displaystyle \mathbf {v} [\mathbf {f} A]=A^{-1}\mathbf {v} [\mathbf {f} ],\quad \mathbf {v} ^{\sharp }[\mathbf {f} A]=A^{T}\mathbf {v} ^{\sharp }[\mathbf {f} ].}$

Евклидова плоскость

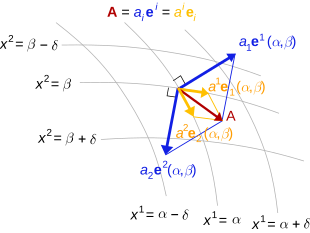
В евклидовой плоскости скалярное произведение позволяет отождествлять векторы с ковекторами. Если является базисом, то двойственный базис удовлетворяет ${\displaystyle \mathbf {e} _{1},\mathbf {e} _{2}}$ ${\displaystyle \mathbf {e} ^{1},\mathbf {e} ^{2}}$

${\displaystyle {\begin{aligned}\mathbf {e} ^{1}\cdot \mathbf {e} _{1}=1,&\quad \mathbf {e} ^{1}\cdot \mathbf {e} _{2}=0\\\mathbf {e} ^{2}\cdot \mathbf {e} _{1}=0,&\quad \mathbf {e} ^{2}\cdot \mathbf {e} _{2}=1.\end{aligned}}}$

Таким образом, e ¹ и e ₂ перпендикулярны друг другу, как и e ² и e ₁ , а длины e ¹ и e ² нормализованы относительно e ₁ и e ₂ соответственно.

Пример

Например, ^[5] предположим, что нам дан базис e1 , e2 _{, состоящий из} пары векторов, образующих угол 45° друг с другом, так что _e1 имеет длину 2, а e2 — длину 1. _Тогда двойственные базисные векторы задаются следующим образом:

• e ² является результатом поворота e ₁ на угол 90° (где направление измеряется, предполагая, что пара e ₁ , e ₂ имеет положительную ориентацию), а затем изменения масштаба таким образом, чтобы выполнялось соотношение e ² ⋅ e ₂ = 1 .
• e ¹ является результатом поворота e ₂ на угол 90°, а затем изменения масштаба таким образом, чтобы выполнялось соотношение e ¹ ⋅ e ₁ = 1 .

Применяя эти правила, находим

${\displaystyle \mathbf {e} ^{1}={\frac {1}{2}}\mathbf {e} _{1}-{\frac {1}{\sqrt {2}}}\mathbf {e} _{2}}$

и

${\displaystyle \mathbf {e} ^{2}=-{\frac {1}{\sqrt {2}}}\mathbf {e} _{1}+2\mathbf {e} _{2}.}$

Таким образом, изменение базисной матрицы при переходе от исходного базиса к обратному базису равно

${\displaystyle R={\begin{bmatrix}{\frac {1}{2}}&-{\frac {1}{\sqrt {2}}}\\-{\frac {1}{\sqrt {2}}}&2\end{bmatrix}},}$

с

${\displaystyle [\mathbf {e} ^{1}\ \mathbf {e} ^{2}]=[\mathbf {e} _{1}\ \mathbf {e} _{2}]{\begin{bmatrix}{\frac {1}{2}}&-{\frac {1}{\sqrt {2}}}\\-{\frac {1}{\sqrt {2}}}&2\end{bmatrix}}.}$

Например, вектор

${\displaystyle v={\frac {3}{2}}\mathbf {e} _{1}+2\mathbf {e} _{2}}$

это вектор с контравариантными компонентами

${\displaystyle v^{1}={\frac {3}{2}},\quad v^{2}=2.}$

Ковариантные компоненты получаются путем приравнивания двух выражений для вектора v :

${\displaystyle v=v_{1}\mathbf {e} ^{1}+v_{2}\mathbf {e} ^{2}=v^{1}\mathbf {e} _{1}+v^{2}\mathbf {e} _{2}}$

так

${\displaystyle {\begin{aligned}{\begin{bmatrix}v_{1}\\v_{2}\end{bmatrix}}&=R^{-1}{\begin{bmatrix}v^{1}\\v^{2}\end{bmatrix}}\\&={\begin{bmatrix}4&{\sqrt {2}}\\{\sqrt {2}}&1\end{bmatrix}}{\begin{bmatrix}v^{1}\\v^{2}\end{bmatrix}}\\&={\begin{bmatrix}6+2{\sqrt {2}}\\2+{\frac {3}{\sqrt {2}}}\end{bmatrix}}\end{aligned}}.}$

Трехмерное евклидово пространство

В трехмерном евклидовом пространстве можно также явно определить двойственный базис для заданного набора базисных векторов e ₁ , e ₂ , e ₃ из E ₃ , которые не обязательно предполагаются ортогональными или имеющими единичную норму. Двойственные базисные векторы:

${\displaystyle \mathbf {e} ^{1}={\frac {\mathbf {e} _{2}\times \mathbf {e} _{3}}{\mathbf {e} _{1}\cdot (\mathbf {e} _{2}\times \mathbf {e} _{3})}};\qquad \mathbf {e} ^{2}={\frac {\mathbf {e} _{3}\times \mathbf {e} _{1}}{\mathbf {e} _{2}\cdot (\mathbf {e} _{3}\times \mathbf {e} _{1})}};\qquad \mathbf {e} ^{3}={\frac {\mathbf {e} _{1}\times \mathbf {e} _{2}}{\mathbf {e} _{3}\cdot (\mathbf {e} _{1}\times \mathbf {e} _{2})}}.}$

_Даже если ei и ei не ортонормальны , они все равно взаимно обратны ^:

${\displaystyle \mathbf {e} ^{i}\cdot \mathbf {e} _{j}=\delta _{j}^{i},}$

Тогда контравариантные компоненты любого вектора v могут быть получены скалярным произведением v с двойственными базисными векторами:

${\displaystyle q^{1}=\mathbf {v} \cdot \mathbf {e} ^{1};\qquad q^{2}=\mathbf {v} \cdot \mathbf {e} ^{2};\qquad q^{3}=\mathbf {v} \cdot \mathbf {e} ^{3}.}$

Аналогично, ковариантные компоненты v могут быть получены из скалярного произведения v с базисными векторами, а именно.

${\displaystyle q_{1}=\mathbf {v} \cdot \mathbf {e} _{1};\qquad q_{2}=\mathbf {v} \cdot \mathbf {e} _{2};\qquad q_{3}=\mathbf {v} \cdot \mathbf {e} _{3}.}$

Тогда v можно выразить двумя (взаимными) способами, а именно:

${\displaystyle \mathbf {v} =q^{i}\mathbf {e} _{i}=q^{1}\mathbf {e} _{1}+q^{2}\mathbf {e} _{2}+q^{3}\mathbf {e} _{3}.}$

или

${\displaystyle \mathbf {v} =q_{i}\mathbf {e} ^{i}=q_{1}\mathbf {e} ^{1}+q_{2}\mathbf {e} ^{2}+q_{3}\mathbf {e} ^{3}}$

Объединяя приведенные выше соотношения, имеем

${\displaystyle \mathbf {v} =(\mathbf {v} \cdot \mathbf {e} ^{i})\mathbf {e} _{i}=(\mathbf {v} \cdot \mathbf {e} _{i})\mathbf {e} ^{i}}$

и мы можем преобразовать между базисом и дуальным базисом с помощью

${\displaystyle q_{i}=\mathbf {v} \cdot \mathbf {e} _{i}=(q^{j}\mathbf {e} _{j})\cdot \mathbf {e} _{i}=(\mathbf {e} _{j}\cdot \mathbf {e} _{i})q^{j}}$

и

${\displaystyle q^{i}=\mathbf {v} \cdot \mathbf {e} ^{i}=(q_{j}\mathbf {e} ^{j})\cdot \mathbf {e} ^{i}=(\mathbf {e} ^{j}\cdot \mathbf {e} ^{i})q_{j}.}$

Если базисные векторы ортонормальны , то они совпадают с дуальными базисными векторами.

Общие евклидовы пространства

В более общем случае, в n -мерном евклидовом пространстве V , если базис есть

${\displaystyle \mathbf {e} _{1},\dots ,\mathbf {e} _{n},}$

обратный базис определяется как (двойные индексы суммируются),

${\displaystyle \mathbf {e} ^{i}=g^{ij}\mathbf {e} _{j}}$

где коэффициенты g ^ij являются элементами обратной матрицы

${\displaystyle g_{ij}=\mathbf {e} _{i}\cdot \mathbf {e} _{j}.}$

Действительно, тогда мы имеем

${\displaystyle \mathbf {e} ^{i}\cdot \mathbf {e} _{k}=g^{ij}\mathbf {e} _{j}\cdot \mathbf {e} _{k}=g^{ij}g_{jk}=\delta _{k}^{i}.}$

Ковариантные и контравариантные компоненты любого вектора

${\displaystyle \mathbf {v} =q_{i}\mathbf {e} ^{i}=q^{i}\mathbf {e} _{i}\,}$

связаны, как указано выше,

${\displaystyle q_{i}=\mathbf {v} \cdot \mathbf {e} _{i}=(q^{j}\mathbf {e} _{j})\cdot \mathbf {e} _{i}=q^{j}g_{ji}}$

и

${\displaystyle q^{i}=\mathbf {v} \cdot \mathbf {e} ^{i}=(q_{j}\mathbf {e} ^{j})\cdot \mathbf {e} ^{i}=q_{j}g^{ji}.}$

Использование в тензорном анализе

Различие между ковариантностью и контравариантностью особенно важно для вычислений с тензорами , которые часто имеют смешанную дисперсию . Это означает, что они имеют как ковариантные, так и контравариантные компоненты, или как векторные, так и ковекторные компоненты. Валентность тензора — это число ковариантных и контравариантных членов, и в нотации Эйнштейна ковариантные компоненты имеют нижние индексы, в то время как контравариантные компоненты имеют верхние индексы. Двойственность между ковариантностью и контравариантностью вмешивается всякий раз, когда векторная или тензорная величина представлена ​​своими компонентами, хотя современная дифференциальная геометрия использует более сложные безиндексные методы для представления тензоров .

В тензорном анализе ковариантный вектор изменяется более или менее обратно пропорционально соответствующему контравариантному вектору. Выражения для длин, площадей и объемов объектов в векторном пространстве могут быть заданы в терминах тензоров с ковариантными и контравариантными индексами. При простых расширениях и сокращениях координат взаимность является точной; при аффинных преобразованиях компоненты вектора смешиваются при переходе между ковариантным и контравариантным выражением.

На многообразии тензорное поле обычно будет иметь несколько верхних и нижних индексов, где широко используется обозначение Эйнштейна. Когда многообразие снабжено метрикой , ковариантные и контравариантные индексы становятся очень тесно связанными друг с другом. Контравариантные индексы можно превратить в ковариантные индексы путем сжатия с метрическим тензором. Обратное возможно путем сжатия с (матричным) обратным метрическому тензору. Обратите внимание, что в общем случае такого соотношения не существует в пространствах, не снабженных метрическим тензором. Более того, с более абстрактной точки зрения, тензор просто «есть», и его компоненты любого вида являются лишь вычислительными артефактами, значения которых зависят от выбранных координат.

Геометрическое объяснение состоит в том, что общий тензор будет иметь как контравариантные, так и ковариантные индексы, поскольку у него есть части, которые находятся как в касательном, так и в кокасательном расслоении .

Контравариантный вектор — это вектор, который преобразуется как , где — координаты частицы в ее собственное время . Ковариантный вектор — это вектор, который преобразуется как , где — скалярное поле. ${\displaystyle {\frac {dx^{\mu }}{d\tau }}}$ ${\displaystyle x^{\mu }\!}$ ${\displaystyle \tau }$ ${\displaystyle {\frac {\partial \varphi }{\partial x^{\mu }}}}$ ${\displaystyle \varphi }$

Алгебра и геометрия

В теории категорий существуют ковариантные функторы и контравариантные функторы . Присвоение дуального пространства векторному пространству является стандартным примером контравариантного функтора. Контравариантные (соотв. ковариантные) векторы являются контравариантными (соотв. ковариантными) функторами из - торсора в фундаментальное представление . Аналогично, тензоры более высокой степени являются функторами со значениями в других представлениях . Однако некоторые конструкции полилинейной алгебры имеют «смешанную» дисперсию, что не позволяет им быть функторами. ${\displaystyle {\text{GL}}(n)}$ ${\displaystyle {\text{GL}}(n)}$ ${\displaystyle {\text{GL}}(n)}$

В дифференциальной геометрии компоненты вектора относительно базиса касательного расслоения ковариантны, если они изменяются при том же линейном преобразовании, что и при изменении базиса. Они контравариантны, если они изменяются при обратном преобразовании. Иногда это является источником путаницы по двум различным, но связанным причинам. Первая заключается в том, что векторы, компоненты которых ковариантны (называемые ковекторами или 1-формами ), на самом деле отступают под действием гладких функций, что означает, что операция назначения пространства ковекторов гладкому многообразию на самом деле является контравариантным функтором. Аналогично векторы, компоненты которых контравариантны, выдвигаются вперед под действием гладких отображений, поэтому операция назначения пространства (контравариантных) векторов гладкому многообразию является ковариантным функтором. Во-вторых, в классическом подходе к дифференциальной геометрии не базисы касательного расслоения являются наиболее примитивными объектами, а скорее изменения в системе координат. Векторы с контравариантными компонентами преобразуются так же, как изменения координат (потому что они фактически изменяются противоположно индуцированному изменению базиса). Аналогично, векторы с ковариантными компонентами преобразуются противоположным образом, как изменения координат.

Смотрите также

• Активная и пассивная трансформация
• Смешанный тензор
• Двухточечный тензор , обобщение, позволяющее индексам ссылаться на несколько векторных баз

Примечания

1. Базис f здесь можно с пользой рассматривать как линейный изоморфизм из R ⁿ в V. Рассматривая f как вектор-строку, элементы которой являются элементами базиса, соответствующий линейный изоморфизм тогда имеет вид ${\displaystyle \mathbf {x} \mapsto \mathbf {f} \mathbf {x} .}$

Цитаты

1. Мизнер, К.; Торн, К. С.; Уилер, Дж. А. (1973). Гравитация . WH Freeman. ISBN  0-7167-0344-0.
2. Франкель, Теодор (2012). Геометрия физики: введение. Кембридж: Cambridge University Press. стр. 42. ISBN 978-1-107-60260-1. OCLC  739094283.
3. Сильвестр, Дж. Дж. (1851). «Об общей теории ассоциированных алгебраических форм». Cambridge and Dublin Mathematical Journal . Том 6. С. 289–293.
4. Sylvester, JJ University Press. Собрание математических работ Джеймса Джозефа Сильвестра . Том 3, 1870–1883. ISBN 978-1107661431. OCLC  758983870.
5. Боуэн, Рэй; Ванг, К.-К. (2008) [1976]. "§3.14 Взаимный базис и изменение базиса". Введение в векторы и тензоры . Довер. стр. 78, 79, 81. ISBN 9780486469140.

Ссылки

• Куссе, Брюс Р.; Вествиг, Эрик А. (2010), Математическая физика: прикладная математика для ученых и инженеров (2-е изд.), Wiley, ISBN 978-3-527-61814-9.
• Арфкен, Джордж Б .; Вебер, Ганс Дж. (2005), Математические методы для физиков (6-е изд.), Харкорт, ISBN 0-12-059876-0.
• Dodson, CTJ; Poston, T. (1991), Тензорная геометрия , Graduate Texts in Mathematics, т. 130 (2-е изд.), Springer, ISBN 978-3-540-52018-4, МР  1223091.
• Греуб, Вернер Хильдберт (1967), Полилинейная алгебра , Die Grundlehren der Mathematischen Wissenschaften, Band 136, Springer, ISBN 9780387038278, МР  0224623.
• Стернберг, Шломо (1983), Лекции по дифференциальной геометрии , Челси, ISBN 978-0-8284-0316-0.
• Сильвестр, Дж. Дж. (1853), «О теории сизигических отношений двух рациональных интегральных функций, включающей приложение к теории функций Штурма и теории наибольшей алгебраической общей меры», Philosophical Transactions of the Royal Society of London , 143 : 407–548, doi : 10.1098/rstl.1853.0018 , JSTOR  108572.
• Вайнрайх, Габриэль (1998), Геометрические векторы , Чикагские лекции по физике, Издательство Чикагского университета, стр. 126, ISBN 9780226890487

Внешние ссылки

• «Ковариантный тензор», Энциклопедия математики , EMS Press , 2001 [1994]
• «Контравариантный тензор», Энциклопедия математики , EMS Press , 2001 [1994]
• Вайсштейн, Эрик В. «Ковариантный тензор». MathWorld .
• Вайсштейн, Эрик В. «Контравариантный тензор». MathWorld .
• Инвариантность, контравариантность и ковариантность
• Даллемонд, Кес; Петерс, Каспер (2010). «Введение в тензорное исчисление» (PDF) .