Сол Крипке

Американский философ и логик (1940–2022)

Сол Аарон Крипке ( / ˈk r ɪ p k i / ; 13 ноября 1940 — 15 сентября 2022) был американским аналитическим философом и логиком . Он был заслуженным профессором философии в аспирантуре Городского университета Нью-Йорка и почетным профессором Принстонского университета . С 1960 - х годов и до своей смерти он был центральной фигурой в ряде областей, связанных с математической и модальной логикой , философией языка и математики , метафизикой , эпистемологией и теорией рекурсии .

Крипке внес значительный и оригинальный вклад в логику , особенно модальную логику. Его главный вклад — семантика для модальной логики, включающая возможные миры , теперь называемая семантикой Крипке . ^[6] Он получил премию Шока 2001 года по логике и философии.

Крипке также частично ответственен за возрождение метафизики и эссенциализма после упадка логического позитивизма , утверждая, что необходимость — это метафизическое понятие, отличное от эпистемического понятия априори , и что существуют необходимые истины , которые известны апостериори , например, что вода — это H2O _. Серия лекций в Принстоне 1970 года, опубликованная в виде книги в 1980 году под названием « Именование и необходимость » , считается одной из важнейших философских работ XX века. Она ввела концепцию имен как жестких десигнаторов , обозначающих (выбирающих, обозначающих, ссылающихся на) один и тот же объект в каждом возможном мире, в отличие от описаний . Она также установила каузальную теорию референции Крипке , оспаривая дескриптивистскую теорию , обнаруженную в концепции смысла Готлоба Фреге и теории описаний Бертрана Рассела . Крипке часто рассматривается как оппозиционер другого великого философа конца 20-го века, который избегал логического позитивизма: У. В. О. Куайна . Куайн отвергал эссенциализм и модальную логику. ^{[7] [8]}

Крипке также дал оригинальное прочтение Людвига Витгенштейна , известного как « Крипкенштейн », в его «Витгенштейне о правилах и частном языке» . Книга содержит его аргумент о следовании правилам, парадокс скептицизма относительно смысла . Большая часть его работ остается неопубликованной или существует только в виде магнитофонных записей и рукописей, распространяемых в частном порядке.

Жизнь и карьера

Сол Крипке был старшим из трех детей, родившихся у Дороти К. Крипке и Майера С. Крипке . ^[9] Его отец был лидером синагоги Бет-Эль, единственной консервативной общины в Омахе , штат Небраска ; его мать писала еврейские образовательные книги для детей. Сол и его две сестры, Мадлен и Нетта, посещали начальную школу Данди и среднюю школу Омахи . Крипке считался вундеркиндом , он самостоятельно выучил древнееврейский язык к шести годам, прочитал все сочинения Шекспира к девяти годам и освоил труды Декарта и сложные математические задачи до окончания начальной школы. ^{[10] [11]} Он написал свою первую теорему о полноте в модальной логике в 17 лет и опубликовал ее год спустя. Окончив среднюю школу в 1958 году, Крипке поступил в Гарвардский университет и окончил его с отличием в 1962 году, получив степень бакалавра по математике. На втором курсе Гарварда он преподавал курс логики для выпускников в соседнем Массачусетском технологическом институте . ^[12] После окончания университета он получил стипендию Фулбрайта , а в 1963 году был принят в Общество стипендиатов . Позже Крипке сказал: «Я бы хотел пропустить колледж. Я познакомился с несколькими интересными людьми, но не могу сказать, что чему-то научился. Я бы, наверное, все равно узнал все, просто читая самостоятельно». ^[13] Его двоюродный брат — Эрик Крипке , известный созданием телешоу « Пацаны » . ^[14]

После недолгого преподавания в Гарварде, Крипке в 1968 году переехал в Рокфеллеровский университет в Нью-Йорке, где преподавал до 1976 года. В 1978 году он занял должность профессора-председателя в Принстонском университете . ^[15] В 1988 году он получил университетскую премию Бермана за выдающиеся достижения в области гуманитарных наук. В 2002 году Крипке начал преподавать в аспирантуре CUNY , а в 2003 году был назначен там почетным профессором философии.

Крипке получил почетные степени от Университета Небраски , Омаха (1977), Университета Джонса Хопкинса (1997), Университета Хайфы , Израиль (1998) и Университета Пенсильвании (2005). Он был членом Американского философского общества и избранным членом Американской академии искусств и наук , а в 1985 году был членом-корреспондентом Британской академии . ^[16] Он выиграл премию Шока по логике и философии в 2001 году. ^[17]

Крипке был женат на философе Маргарет Гилберт .

Крипке умер от рака поджелудочной железы 15 сентября 2022 года в Плейнсборо, штат Нью-Джерси, в возрасте 81 года. ^{[18] [19] [20]}

Работа

Пример модели Крипке для линейной временной логики , конкретная модальная логика

Вклад Крипке в философию включает:

1. Семантика Крипке для модальной и родственных логик , опубликованная в нескольких эссе, начиная с подросткового возраста.
2. Его лекции 1970 года в Принстоне «Именование и необходимость» (опубликованные в 1972 и 1980 годах) существенно перестроили философию языка .
3. Его интерпретация Витгенштейна .
4. Его теория истины .

Он также внес вклад в теорию рекурсии (см. допустимый ординал и теорию множеств Крипке–Платека ).

Модальная логика

Две из ранних работ Крипке, «Теорема о полноте в модальной логике» (1959) ^[21] и «Семантические соображения о модальной логике» (1963), первая из которых была написана, когда он был подростком, были посвящены модальной логике . Наиболее известные логики в модальном семействе построены на основе слабой логики под названием K, названной в честь Крипке. Крипке ввел ныне стандартную семантику Крипке (также известную как реляционная семантика или семантика фреймов) для модальных логик. Семантика Крипке — это формальная семантика для неклассических логических систем. Впервые она была создана для модальных логик, а затем адаптирована к интуиционистской логике и другим неклассическим системам. Открытие семантики Крипке стало прорывом в создании неклассических логик, поскольку модельная теория таких логик отсутствовала до Крипке.

Рамка Крипке или модальная рамка — это пара , где W — непустое множество, а R — бинарное отношение на W. Элементы W называются узлами или мирами , а R известно как отношение доступности . В зависимости от свойств отношения доступности ( транзитивность , рефлексивность и т. д.) соответствующая рамка описывается, в расширении, как транзитивная, рефлексивная и т. д. ${\displaystyle \langle W,R\rangle }$

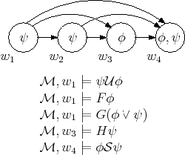
Модель Крипке представляет собой тройку , где — фрейм Крипке, а — отношение между узлами W и модальными формулами, такое, что: ${\displaystyle \langle W,R,\Vdash \rangle }$ ${\displaystyle \langle W,R\rangle }$ ${\displaystyle \Vdash }$

• ${\displaystyle w\Vdash \neg A}$тогда и только тогда, когда , ${\displaystyle w\nVdash A}$
• ${\displaystyle w\Vdash A\to B}$тогда и только тогда, когда или , ${\displaystyle w\nVdash A}$ ${\displaystyle w\Vdash B}$
• ${\displaystyle w\Vdash \Box A}$тогда и только тогда, когда подразумевается . ${\displaystyle \forall u\,(w\;R\;u}$ ${\displaystyle u\Vdash A)}$

Мы читаем как « w удовлетворяет A », « A удовлетворяется в w » или « w заставляет A ». Отношение называется отношением удовлетворения , оценкой или принуждением . Отношение удовлетворения однозначно определяется его значением на пропозициональных переменных. ${\displaystyle w\Vdash A}$ ${\displaystyle \Vdash }$

Формула А действительна в :

• модель , если для всех w  ∈  W , ${\displaystyle \langle W,R,\Vdash \rangle }$ ${\displaystyle w\Vdash A}$
• кадр , если он действителен для всех возможных вариантов , ${\displaystyle \langle W,R\rangle }$ ${\displaystyle \langle W,R,\Vdash \rangle }$ ${\displaystyle \Vdash }$
• класс C фреймов или моделей, если он действителен для каждого члена C.

Мы определяем Thm( C ) как множество всех формул, которые действительны в C . И наоборот, если X — это множество формул, пусть Mod( X ) будет классом всех фреймов, которые проверяют каждую формулу из X .

Модальная логика (т.е. набор формул) L корректна относительно класса фреймов C , если L  ⊆ Thm( C ). L полна относительно C , если L  ⊇ Thm( C ).

Семантика полезна для исследования логики (т. е. системы вывода) только в том случае, если семантическое отношение вывода отражает его синтаксический аналог, отношение следования ( выводимость ). Крайне важно знать, какие модальные логики являются обоснованными и полными относительно класса фреймов Крипке, и для них определить, к какому классу они относятся.

Для любого класса C фреймов Крипке Thm( C ) является нормальной модальной логикой (в частности, теоремы минимальной нормальной модальной логики K верны в любой модели Крипке). Однако обратное, как правило, не выполняется. Существуют неполные нормальные модальные логики Крипке, что не вызывает проблем, поскольку большинство изученных модальных систем являются полными классами фреймов, описываемых простыми условиями.

Нормальная модальная логика L соответствует классу фреймов C , если C  = Mod( L ). Другими словами, C — наибольший класс фреймов, такой что L является звуком относительно C. Отсюда следует, что L является полным по Крипке тогда и только тогда, когда он является полным своего соответствующего класса.

Рассмотрим схему T  : . T действителен в любой рефлексивной рамке : если , то поскольку w R w . С другой стороны, рама, которая подтверждает T, должна быть рефлексивной: зафиксируем w  ∈  W , и определим удовлетворение пропозициональной переменной p следующим образом: если и только если w R u . Тогда , таким образом , через T , что означает w R w с использованием определения . T соответствует классу рефлексивных рамок Крипке. ${\displaystyle \Box A\to A}$ ${\displaystyle \langle W,R\rangle }$ ${\displaystyle w\Vdash \Box A}$ ${\displaystyle w\Vdash A}$   ${\displaystyle u\Vdash p}$   ${\displaystyle w\Vdash \Box p}$ ${\displaystyle w\Vdash p}$   ${\displaystyle \Vdash }$

Часто гораздо проще охарактеризовать соответствующий класс L , чем доказать его полноту, поэтому соответствие служит руководством к доказательствам полноты. Соответствие также используется для демонстрации неполноты модальных логик: предположим, что L ₁  ⊆  L ₂ — нормальные модальные логики, соответствующие одному и тому же классу фреймов, но L ₁ не доказывает все теоремы L ₂ . Тогда L ₁ является неполным по Крипке. Например, схема порождает неполную логику, поскольку соответствует тому же классу фреймов, что и GL (а именно, транзитивным и обратным хорошо обоснованным фреймам), но не доказывает GL - тавтологию . ${\displaystyle \Box (A\equiv \Box A)\to \Box A}$ ${\displaystyle \Box A\to \Box \Box A}$

Канонические модели

Для любой нормальной модальной логики L может быть построена модель Крипке (называемая канонической моделью ), которая точно подтверждает теоремы L , путем адаптации стандартной техники использования максимальных непротиворечивых множеств в качестве моделей. Канонические модели Крипке играют роль, аналогичную конструкции алгебры Линденбаума–Тарского в алгебраической семантике.

Набор формул является L - непротиворечивым , если из них нельзя вывести противоречие, используя аксиомы L и modus ponens . Максимальный L-непротиворечивый набор ( L - MCS для краткости) - это L -непротиворечивый набор, который не имеет собственного L -непротиворечивого надмножества.

Канонической моделью L является модель Крипке , где W — множество всех L - MCS , а отношения R и R имеют следующий вид: ${\displaystyle \langle W,R,\Vdash \rangle }$ ${\displaystyle \Vdash }$

${\displaystyle X\;R\;Y}$тогда и только тогда, когда для каждой формулы , если тогда , ${\displaystyle A}$ ${\displaystyle \Box A\in X}$ ${\displaystyle A\in Y}$

${\displaystyle X\Vdash A}$тогда и только тогда, когда . ${\displaystyle A\in X}$

Каноническая модель является моделью L , поскольку каждая L - MCS содержит все теоремы L. По лемме Цорна каждое L -согласованное множество содержится в L - MCS , в частности, каждая формула, недоказуемая в L, имеет контрпример в канонической модели.

Основное применение канонических моделей — доказательства полноты. Свойства канонической модели K немедленно подразумевают полноту K относительно класса всех фреймов Крипке. Этот аргумент не работает для произвольного L , поскольку нет гарантии, что базовый фрейм канонической модели удовлетворяет условиям фрейма L .

Мы говорим, что формула или набор формул X являются каноническими относительно свойства P фреймов Крипке, если

• X действителен в каждом кадре, который удовлетворяет P ,
• для любой нормальной модальной логики L , содержащей X , базовый фрейм канонической модели L удовлетворяет P.

Объединение канонических наборов формул само является каноническим. Из предыдущего обсуждения следует, что любая логика, аксиоматизированная каноническим набором формул, является полной по Крипке и компактной .

Аксиомы T, 4, D, B, 5, H, G (и, следовательно, любая их комбинация) являются каноническими. GL и Grz не являются каноническими, поскольку они не компактны. Аксиома M сама по себе не является канонической ( Goldblatt , 1991), но объединенная логика S4.1 (на самом деле, даже K4.1 ) является канонической.

В общем случае невозможно решить , является ли данная аксиома канонической. Мы знаем хорошее достаточное условие: Х. Сальквист выделил широкий класс формул (теперь называемых формулами Сальквиста ), таких что:

• формула Сальквиста является канонической,
• класс фреймов, соответствующих формуле Сальквиста, является определимым в первом порядке ,
• существует алгоритм, который вычисляет соответствующее состояние кадра для заданной формулы Сальквиста.

Это мощный критерий: например, все аксиомы, перечисленные выше как канонические, являются (эквивалентными) формулами Салквиста. Логика имеет свойство конечной модели (FMP), если она полна относительно класса конечных фреймов. Применением этого понятия является вопрос разрешимости: из теоремы Поста следует, что рекурсивно аксиоматизированная модальная логика L, имеющая FMP, разрешима, при условии, что разрешимо, является ли заданный конечный фрейм моделью L. В частности, каждая конечно аксиоматизируемая логика с FMP разрешима.

Существуют различные методы установления FMP для заданной логики. Уточнения и расширения конструкции канонической модели часто работают, используя такие инструменты, как фильтрация или распутывание. В качестве другой возможности, доказательства полноты, основанные на исчислениях секвенций без разрезов, обычно производят конечные модели напрямую.

Большинство модальных систем, используемых на практике (включая все перечисленные выше), имеют FMP.

В некоторых случаях мы можем использовать FMP для доказательства полноты Крипке логики: каждая нормальная модальная логика полна относительно класса модальных алгебр, а конечная модальная алгебра может быть преобразована в фрейм Крипке. Например, Роберт Булл доказал с помощью этого метода, что каждое нормальное расширение S4.3 имеет FMP и является полным по Крипке.

Семантика Крипке имеет прямое обобщение на логики с более чем одной модальностью. Фрейм Крипке для языка с как множеством его операторов необходимости состоит из непустого множества W, снабженного бинарными отношениями R _i для каждого i  ∈  I . Определение отношения удовлетворения модифицируется следующим образом: ${\displaystyle \{\Box _{i}\mid \,i\in I\}}$

${\displaystyle w\Vdash \Box _{i}A}$если и только если ${\displaystyle \forall u\,(w\;R_{i}\;u\Rightarrow u\Vdash A).}$

Модели Карлсона

Упрощенная семантика, открытая Тимом Карлсоном, часто используется для полимодальных логик доказуемости . ^[22] Модель Карлсона представляет собой структуру с единственным отношением доступности R и подмножествами D _i  ⊆  W для каждой модальности. Удовлетворение определяется как: ${\displaystyle \langle W,R,\{D_{i}\}_{i\in I},\Vdash \rangle }$

${\displaystyle w\Vdash \Box _{i}A}$если и только если ${\displaystyle \forall u\in D_{i}\,(w\;R\;u\Rightarrow u\Vdash A).}$

Модели Карлсона проще визуализировать и с ними проще работать, чем с обычными полимодальными моделями Крипке; однако существуют полные по Крипке полимодальные логики, которые являются неполными по Карлсону.

В работе Semantical Considerations on Modal Logic , опубликованной в 1963 году, Крипке ответил на затруднение с классической теорией квантификации . Мотивацией подхода, основанного на мировом отношении, было представление возможности того, что объекты в одном мире могут не существовать в другом. Но если использовать стандартные правила квантификаторов, каждый термин должен ссылаться на что-то, что существует во всех возможных мирах. Это кажется несовместимым с нашей обычной практикой использования терминов для обозначения вещей, которые существуют условно.

Крипке ответил на эту трудность, устранив термины. Он привел пример системы, которая использует интерпретацию относительно мира и сохраняет классические правила. Но издержки серьезны. Во-первых, его язык искусственно обеднен, а во-вторых, правила для пропозициональной модальной логики должны быть ослаблены.

Теория возможных миров Крипке использовалась нарратологами (начиная с Павла и Долежела) для понимания «манипулирования читателями альтернативных вариантов развития сюжета или запланированных или придуманных персонажами альтернативных серий действий». Это применение стало особенно полезным в анализе гиперфикции . ^[23]

Интуиционистская логика

Семантика Крипке для интуиционистской логики следует тем же принципам, что и семантика модальной логики, но использует другое определение удовлетворения.

Интуиционистская модель Крипке представляет собой тройку , где — частично упорядоченный фрейм Крипке, и удовлетворяет следующим условиям: ${\displaystyle \langle W,\leq ,\Vdash \rangle }$ ${\displaystyle \langle W,\leq \rangle }$ ${\displaystyle \Vdash }$

• если p — пропозициональная переменная , и , то ( условие персистентности ), ${\displaystyle w\leq u}$ ${\displaystyle w\Vdash p}$ ${\displaystyle u\Vdash p}$
• ${\displaystyle w\Vdash A\land B}$тогда и только тогда, когда и , ${\displaystyle w\Vdash A}$ ${\displaystyle w\Vdash B}$
• ${\displaystyle w\Vdash A\lor B}$тогда и только тогда, когда или , ${\displaystyle w\Vdash A}$ ${\displaystyle w\Vdash B}$
• ${\displaystyle w\Vdash A\to B}$тогда и только тогда, когда для всех , подразумевает , ${\displaystyle u\geq w}$ ${\displaystyle u\Vdash A}$ ${\displaystyle u\Vdash B}$
• нет . ${\displaystyle w\Vdash \bot }$

Интуиционистская логика является обоснованной и полной относительно ее семантики Крипке и обладает свойством конечной модели.

Интуиционистская логика первого порядка

Пусть L — язык первого порядка . Модель Крипке языка L — это тройка , где — интуиционистская рамка Крипке, M _w — (классическая) L -структура для каждого узла w  ∈  W , и следующие условия совместимости выполняются всякий раз, когда u  ≤  v : ${\displaystyle \langle W,\leq ,\{M_{w}\}_{w\in W}\rangle }$ ${\displaystyle \langle W,\leq \rangle }$

• область M _u включена в область M _v ,
• реализации символов функций в M _u и M _v согласуются по элементам M _u ,
• для каждого n -арного предиката P и элементов a ₁ ,..., a _n  ∈  M _u : если P ( a ₁ ,..., a _n ) выполняется в M _u , то он выполняется в M _v .

Учитывая оценку e переменных элементами M _w , мы определяем отношение удовлетворения : ${\displaystyle w\Vdash A[e]}$

• ${\displaystyle w\Vdash P(t_{1},\dots ,t_{n})[e]}$тогда и только тогда, когда выполняется в M _w , ${\displaystyle P(t_{1}[e],\dots ,t_{n}[e])}$
• ${\displaystyle w\Vdash (A\land B)[e]}$тогда и только тогда, когда и , ${\displaystyle w\Vdash A[e]}$ ${\displaystyle w\Vdash B[e]}$
• ${\displaystyle w\Vdash (A\lor B)[e]}$тогда и только тогда, когда или , ${\displaystyle w\Vdash A[e]}$ ${\displaystyle w\Vdash B[e]}$
• ${\displaystyle w\Vdash (A\to B)[e]}$тогда и только тогда, когда для всех , подразумевает , ${\displaystyle u\geq w}$ ${\displaystyle u\Vdash A[e]}$ ${\displaystyle u\Vdash B[e]}$
• нет , ${\displaystyle w\Vdash \bot [e]}$
• ${\displaystyle w\Vdash (\exists x\,A)[e]}$тогда и только тогда, когда существует такое , что , ${\displaystyle a\in M_{w}}$ ${\displaystyle w\Vdash A[e(x\to a)]}$
• ${\displaystyle w\Vdash (\forall x\,A)[e]}$тогда и только тогда, когда для каждого и каждого , . ${\displaystyle u\geq w}$ ${\displaystyle a\in M_{u}}$ ${\displaystyle u\Vdash A[e(x\to a)]}$

Здесь e ( x → a ) — оценка, которая дает x значение a , а в остальном согласуется с e .

Наименование и необходимость

Обложка книги «Именование и необходимость»

Три лекции, которые формируют Naming and Necessity, представляют собой атаку на дескриптивистскую теорию имен . Крипке приписывает варианты дескриптивистских теорий Фреге , Расселу , Витгенштейну и Джону Сёрлу , среди прочих. Согласно дескриптивистским теориям, собственные имена либо синонимичны описаниям, либо имеют свою референцию, определяемую в силу того, что имя связано с описанием или группой описаний, которым объект удовлетворяет однозначно. Крипке отвергает оба этих вида дескриптивизма. Он приводит несколько примеров, претендующих на то, чтобы сделать дескриптивизм неправдоподобным как теорию того, как имена получают свои референции (например, конечно, Аристотель мог умереть в возрасте двух лет и, таким образом, не удовлетворять ни одному из описаний, которые мы связываем с его именем, но было бы неправильно отрицать, что он все еще был Аристотелем).

В качестве альтернативы Крипке изложил каузальную теорию референции , согласно которой имя относится к объекту в силу каузальной связи с объектом, опосредованной сообществами говорящих. Он указывает, что имена собственные, в отличие от большинства описаний, являются жесткими десигнаторами : то есть имя собственное относится к названному объекту в каждом возможном мире , в котором существует объект, в то время как большинство описаний обозначают разные объекты в разных возможных мирах. Например, «Ричард Никсон» относится к одному и тому же человеку в каждом возможном мире, в котором существует Никсон, в то время как «человек, победивший на президентских выборах в Соединенных Штатах в 1968 году» может относиться к Никсону , Хамфри или другим в разных возможных мирах.

Крипке также поднял перспективу апостериорных необходимостей — фактов, которые обязательно истинны , хотя они могут быть познаны только посредством эмпирического исследования. Примерами служат « Геспер есть Фосфор », « Цицерон есть Туллий », «Вода есть H2O _» и другие утверждения об идентичности, где два имени относятся к одному и тому же объекту. По мнению Крипке, кантовские различия между аналитическим и синтетическим, априорным и апостериорным , случайным и необходимым не сопоставляются друг с другом. Скорее, аналитическое/синтетическое — это семантическое различие, априорное / апостериорное — эпистемическое различие, а случайный/необходимый — метафизическое различие.

Наконец, Крипке выдвинул аргумент против материализма идентичности в философии сознания , взгляда, согласно которому каждая ментальная конкретная идентична некоторой физической конкретике. Крипке утверждал, что единственный способ защитить эту идентичность — это апостериорная необходимая идентичность, но что такая идентичность — например, что боль есть активация С-волокон — не может быть необходимой, учитывая (очевидно мыслимую) возможность того, что боль может быть отделена от активации С-волокон, или активация С-волокон может быть отделена от боли. (Подобные аргументы с тех пор выдвигал Дэвид Чалмерс . ^[24] ) В любом случае, теоретик психофизической идентичности, по мнению Крипке, берет на себя диалектическое обязательство объяснить кажущуюся логическую возможность этих обстоятельств, поскольку, по мнению таких теоретиков, они должны быть невозможны.

Крипке прочитал лекции Джона Локка по философии в Оксфорде в 1973 году. Названные «Ссылка и существование» , они во многих отношениях были продолжением « Именования и необходимости» и рассматривали темы вымышленных имен и ошибок восприятия. В 2013 году издательство Oxford University Press опубликовало лекции в виде книги, также озаглавленной «Ссылка и существование» .

В статье 1995 года философ Квентин Смит утверждал, что ключевые концепции новой теории референции Крипке возникли в работе Рут Баркан Маркус более чем десятилетием ранее. ^[25] Смит выделил шесть важных идей в Новой теории, которые, как он утверждал, разработал Маркус: (1) что собственные имена являются прямыми ссылками, которые не состоят из содержащихся определений; (2) что хотя можно выделить отдельную вещь с помощью описания, это описание не эквивалентно собственному имени этой вещи; (3) модальный аргумент о том, что собственные имена являются непосредственно референциальными, а не замаскированными описаниями; (4) формальное модальное логическое доказательство необходимости тождества ; (5) концепция жесткого десигнатора , хотя Крипке ввел этот термин; и (6) апостериорное тождество. Смит утверждал, что Крипке не понял теорию Маркуса в то время, но позже перенял многие из ее ключевых концептуальных тем в своей Новой теории референции.

Другие ученые впоследствии дали подробные ответы, утверждая, что никакого плагиата не было. ^{[26] [27]}

«Загадка веры»

Основные положения Крипке об именах собственных в работе «Именование и необходимость» заключаются в том, что значение имени — это просто объект, на который оно ссылается, и что референт имени определяется причинно-следственной связью между своего рода «крещением» и произнесением имени. Тем не менее, он признает возможность того, что предложения, содержащие имена, могут иметь некоторые дополнительные семантические свойства, ^[28] свойства, которые могли бы объяснить, почему два имени, ссылающиеся на одного и того же человека, могут давать разные значения истинности в предложениях об убеждениях. Например, Лоис Лейн считает, что Супермен может летать, хотя она не верит, что Кларк Кент может летать. Это можно объяснить, если имена «Супермен» и «Кларк Кент», хотя и ссылаются на одного и того же человека, имеют различные семантические свойства.

Но в своей статье «Загадка о вере» (1988) Крипке, кажется, выступает против даже этой возможности. Его аргумент можно реконструировать следующим образом: Идея о том, что два имени, ссылающиеся на один и тот же объект, могут иметь разные семантические свойства, как предполагается, объясняет, что кореферирующие имена ведут себя по-разному в предложениях об убеждениях (как в случае Лоис Лейн). Но то же самое явление происходит даже с кореферирующими именами, которые, очевидно, имеют одинаковые семантические свойства: Крипке предлагает нам представить себе французского, монолингвального мальчика Пьера, который верит, что « Londres est jolie » («Лондон прекрасен»). Пьер переезжает в Лондон, не осознавая, что Лондон = Londres. Затем он изучает английский язык так же, как ребенок изучает язык, то есть не переводя слова с французского на английский. Пьер узнает название «Лондон» из непривлекательной части города, где он живет, и поэтому приходит к убеждению, что Лондон некрасив. Если мнение Крипке верно, то Пьер теперь верит и в то, что Londres — это jolie , и в то, что London — некрасивый. Это не может быть объяснено кореферированием имен с разными семантическими свойствами. По мнению Крипке, это показывает, что приписывание дополнительных семантических свойств именам не объясняет, для чего оно предназначено.

Витгенштейн

Впервые опубликованный в 1982 году труд Крипке «Витгенштейн о правилах и личном языке» утверждает, что центральный аргумент «Философских исследований » Витгенштейна сосредоточен на разрушительном парадоксе следования правилам , который подрывает возможность нашего постоянного следования правилам в нашем использовании языка. Крипке пишет, что этот парадокс является «самой радикальной и оригинальной скептической проблемой, которую философия видела до сих пор», и что Витгенштейн не отвергает аргумент, который приводит к парадоксу следования правилу, но принимает его и предлагает «скептическое решение» для смягчения разрушительных эффектов парадокса.

Большинство комментаторов признают, что «Философские исследования» содержат парадокс следования правилу, как его представляет Крипке, но мало кто согласен с тем, что он приписывает скептическое решение Витгенштейну. Сам Крипке выражает сомнения в «Витгенштейне о правилах и частном языке» относительно того, одобрил бы Витгенштейн его интерпретацию «Философских исследований». Он говорит, что работу следует читать не как попытку дать точное изложение взглядов Витгенштейна, а скорее как изложение аргумента Витгенштейна, «как он поразил Крипке, как он представлял для него проблему».

Слово-портманто «Крипкенштейн» было придумано для интерпретации Крипке « Философских исследований ». Главное значение Крипкенштейна заключалось в четком заявлении о новом виде скептицизма, названном «скептицизмом смысла»: идея о том, что для изолированных индивидов не существует факта, в силу которого они подразумевают одно, а не другое, используя слово. «Скептическое решение» Крипке скептицизма смысла заключается в обосновании смысла поведением сообщества.

Книга Крипке породила большую вторичную литературу, разделенную между теми, кто находит его скептическую проблему интересной и проницательной, и другими, такими как Гордон Бейкер , Питер Хакер и Колин Макгинн , которые утверждают, что его скептицизм смысла является псевдопроблемой, которая вытекает из запутанного, избирательного прочтения Витгенштейна. Позиция Крипке была защищена от этих и других нападок кембриджским философом Мартином Кушем , а исследователь Витгенштейна Дэвид Г. Стерн считает книгу Крипке «самой влиятельной и широко обсуждаемой» работой о Витгенштейне с 1980-х годов. ^[29]

Правда

В своей статье 1975 года «Очерк теории истины» Крипке показал, что язык может последовательно содержать свой собственный предикат истины , что Альфред Тарский , пионер формальных теорий истины, считал невозможным. Подход предполагает, что истина является частично определенным свойством над множеством грамматически правильно сформированных предложений в языке. Крипке показал, как сделать это рекурсивно, начав с множества выражений в языке, которые не содержат предиката истины, и определив предикат истины только над этим сегментом: это действие добавляет новые предложения в язык, и истина, в свою очередь, определяется для всех из них. Однако, в отличие от подхода Тарского, подход Крипке позволяет «истине» быть объединением всех этих стадий определения; после счетной бесконечности шагов язык достигает «фиксированной точки», такой что использование метода Крипке для расширения предиката истины не изменяет язык дальше. Такая фиксированная точка может быть принята в качестве базовой формы естественного языка, содержащего свой собственный предикат истинности. Но этот предикат не определен для любых предложений, которые, так сказать, не «выходят за пределы» более простых предложений, не содержащих предикат истинности. То есть, «„Снег бел“ истинно» является хорошо определенным, как и «„Снег бел“ истинно» является истинным» и так далее, но ни «Это предложение истинно», ни «Это предложение не истинно» не получают условий истинности; они, по терминологии Крипке, «необоснованны».

Сол Крипке читает лекцию о Гёделе в Калифорнийском университете в Санта-Барбаре .

Первая теорема Гёделя о неполноте демонстрирует, что самореференции нельзя избежать наивно, поскольку предложения о, казалось бы, не связанных между собой объектах (таких как целые числа) могут иметь неформальное самореферентное значение, и эта идея — проявленная диагональной леммой — является основой теоремы Тарского о том, что истина не может быть последовательно определена. Но предикат истинности Крипке не дает истинностного значения (истина/ложь) предложениям, таким как построенное в доказательстве Тарского, поскольку можно доказать по индукции , что оно не определено на этапе для каждого конечного . ${\displaystyle n}$ ${\displaystyle n}$

Предложение Крипке проблематично в том смысле, что, хотя язык и содержит предикат «истины» самого себя (по крайней мере частичный), некоторые из его предложений — например, предложение лжеца («это предложение ложно») — имеют неопределенное значение истинности, но язык не содержит своего собственного предиката «неопределенный». Фактически, он не может, так как это создало бы новую версию парадокса лжеца , усиленный парадокс лжеца («это предложение ложно или неопределено»). Таким образом, хотя предложение лжеца не определено в языке, язык не может выразить, что оно не определено. ^[30]

Центр Сола Крипке

Центр Сола Крипке в аспирантуре Городского университета Нью-Йорка занимается сохранением и продвижением работ Крипке. Его директор — Ромина Падро. Центр Сола Крипке проводит мероприятия, связанные с работами Крипке, и создает цифровой архив ранее не публиковавшихся записей лекций Крипке, лекционных заметок и переписки, датируемых 1950-ми годами. ^[31] В своем благоприятном обзоре «Философских проблем » Крипке философ из Стэнфорда Марк Кримминс написал: «Того, что здесь находятся четыре из самых уважаемых и обсуждаемых эссе по философии 1970-х годов, достаточно, чтобы сделать этот первый том сборника статей Сола Крипке обязательным... Восторг читателя будет расти по мере того, как будут появляться намеки на то, что в этой серии, подготовленной Крипке и командой первоклассных редакторов-философов в аспирантуре Городского университета Нью-Йорка, будет еще много всего». ^[32]

Работы

• Именование и необходимость . Кембридж, Массачусетс: Издательство Гарвардского университета, 1972. ISBN  0-674-59845-8
• Витгенштейн о правилах и личном языке: элементарное изложение . Кембридж, Массачусетс: Издательство Гарвардского университета, 1982. ISBN 0-674-95401-7 . 
• Философские проблемы. Сборник статей. Том 1. Нью-Йорк: Oxford University Press, 2011. ISBN 9780199730155 
• Ссылка и существование – Лекции Джона Локка . Нью-Йорк: Oxford University Press, 2013. ISBN 9780199928385 

Награды и признание

• Стипендиат программы Фулбрайта (1962–1963)
• Общество стипендиатов Гарвардского университета (1963–1966).
• Доктор гуманитарных наук, почетная степень, Университет Небраски , 1977.
• Член Американской академии искусств и наук (1978–).
• Член-корреспондент Британской академии (1985–).
• Премия Говарда Бермана, Принстонский университет , 1988.
• Сотрудник Academia Scientiarum et Artium Europaea (1993–).
• Доктор гуманитарных наук, почетная степень, Университет Джонса Хопкинса , 1997 г.
• Доктор гуманитарных наук, почетная степень, Хайфский университет , Израиль, 1998 г.
• Член Норвежской академии наук (2000–).
• Премия Шока по логике и философии, Шведская академия наук , 2001 г.
• Доктор гуманитарных наук, почетная степень, Пенсильванский университет , 2005 г.
• Член Американского философского общества (2005–).

Смотрите также

• Философский портал

• Американская философия
• Список американских философов
• Барри Крипке (персонаж сериала «Теория большого взрыва», который, как полагают, был назван в честь Сола) ^[33]

Ссылки

1. Камминг, Сэм (19 марта 2013 г.). «Имена». В Zalta, Edward N. (ред.). The Stanford Encyclopedia of Philosophy (ред. осень 2016 г.). Исследовательская лаборатория метафизики, Стэнфордский университет.
2. Палмквист, Стивен (декабрь 1987 г.). « Априорное знание в перспективе: (II) Наименование, необходимость и аналитическое апостериори». Обзор метафизики . 41 (2): 255–282.
3. Георг Нортхофф, «Minding the Brain: A Guide to Philosophy and Neuroscience» , Palgrave, стр. 51.
4. Майкл Джудис, Понимание природы права: аргументы в пользу конструктивного концептуального объяснения , Edward Elgar Publishing, 2015, стр. 92.
5. Сол Крипке (1986). «Жесткое обозначение и априорная условность: пересмотр измерительной линейки» (Нотр-Дам).
6. Джерри Фодор, «Вода повсюду вода», London Review of Books , 21 октября 2004 г.
7. Куайн против Крипке о метафизике модальности
8. Что Черепаха сказала Крипке, Ромина Падро
9. Крипке, Саул (2011). Философские проблемы: Сборник статей , том 1. Оксфорд: Oxford University Press. стр. xii. ISBN 978-0-19-973015-5.
10. Чарльз Макграт (28.01.2006). «Философ, 65 лет, читает лекции не о «Что я?», а о «Что я?». The New York Times . Получено 23.01.2008 .
11. Спутник аналитической философии (Blackwell Companions to Philosophy) , А. П. Мартинич (редактор), Э. Дэвид Соса (редактор), 38. Сол Крипке (1940–).
12. "Saul Kripke – The Graduate Center, CUNY". Архивировано из оригинала 2022-01-19 . Получено 2019-08-18 .
13. Макграт, Чарльз (28 января 2006 г.). «Философ, 65 лет, читает лекции не о «Что я?», а о «Что я?». The New York Times .
14. "x.com". X (ранее Twitter) . Получено 2024-06-15 .
15. "Saul Kripke | ​​Жизнь, философия, творчество и факты | Britannica". www.britannica.com . Получено 13 марта 2023 г. .
16. "Fellows of the British Academy". Британская академия . Получено 13 марта 2023 г.
17. "Кунгл. Vetenskapsakademien" . Архивировано из оригинала 08 января 2018 г. Проверено 7 января 2018 г.
18. "Сол Аарон Крипке (1940-2022) – Центр Сола Крипке". 16 сентября 2022 г.
19. Робертс, Сэм (21 сентября 2022 г.). «Сол Крипке, философ, нашедший истину в семантике, умер в возрасте 81 года». The New York Times .
20. "Сол Крипке (1940-2022)". 16 сентября 2022 г.
21. Крипке, Саул А. (март 1959 г.). «Теорема о полноте в модальной логике». Журнал символической логики . 24 (1): 1–14. doi :10.2307/2964568. JSTOR  2964568. S2CID  44300271.
22. Карлсон, Тим (февраль 1986 г.). «Модальные логики с несколькими операторами и интерпретации доказуемости». Israel Journal of Mathematics . 54 (1): 14–24. doi :10.1007/BF02764872. MR  0852465. S2CID  120461106.
23. Флудерник, Моника. «Истории нарративной теории: от структурализма до настоящего времени». Спутник по нарративной теории. Ред. Фелан и Рабинович. Blackwell Publishing, MA:2005.
24. Чалмерс, Дэвид. 1996. Сознательный разум. Oxford University Press, стр. 146–149.
25. Смит, Квентин (2 августа 2001 г.). «Маркус, Крипке и происхождение новой теории референции». Synthese . 104 (2): 179–189. doi :10.1007/BF01063869. S2CID  44151212. Архивировано из оригинала 10 июня 2007 г. Получено 28 мая 2007 г.
26. Стивен Нил (9 февраля 2001 г.). «No Plagiarism Here» (PDF) . Times Literary Supplement . 104 (2): 12–13. doi :10.1007/BF01063869. S2CID  44151212. Архивировано из оригинала (.PDF) 14 июля 2010 г. Получено 13 ноября 2009 г.
27. Джон Берджесс, «Маркус, Крипке и имена» Философские исследования , 84: 1, стр. 1–47.
28. Крипке, 1980, стр. 20
29. Стерн, Дэвид Г. 2006. Философские исследования Витгенштейна: Введение . Cambridge University Press. стр. 2
30. Боландер, Томас (31 августа 2017 г.). «Самореференция». В Zalta, Edward N. (ред.). The Stanford Encyclopedia of Philosophy (ред. осень 2017 г.). Исследовательская лаборатория метафизики, Стэнфордский университет.
31. Веб-сайт Центра Сола Крипке: Большинство этих записей и конспектов лекций были созданы Натаном Салмоном, когда он был студентом, а позднее коллегой Крипке.
32. Кримминс, Марк (30 октября 2013 г.). «Обзор философских проблем: Сборник статей, том 1». Notre Dame Philosophical Reviews .
33. Дэвис, Алекс (13.11.2019). «Теория большого взрыва: в честь кого на самом деле назван Барри Крипке? Раскрыто реальное вдохновение». Express.co.uk . Получено 23.01.2022 .

Дальнейшее чтение

• Ариф Ахмед (2007), Сол Крипке . Нью-Йорк, Нью-Йорк; Лондон: Continuum. ISBN 0-8264-9262-2 . 
• Алан Бергер (редактор) (2011) Сол Крипке. ISBN 978-0-521-85826-7 . 
• Джонатан Берг (2014) Именование, необходимость и многое другое: исследования философских работ Сола Крипке . ISBN 9781137400932 
• Тейлор Бранч (14 августа 1977 г.), «Новые рубежи американской философии». The New York Times Magazine .
• Джон Берджесс (2013), Сол Крипке: Загадки и тайны. ISBN 978-0-7456-5284-9 . 
• GW Fitch (2005), Сол Крипке . ISBN 0-7735-2885-7 . 
• Кристофер Хьюз (2004), Крипке: Имена, Необходимость и Идентичность . ISBN 0-19-824107-0 . 
• Пол У. Хамфрис и Джеймс Х. Фетцер (редакторы) (1998) Новая теория референции: Крипке, Маркус и ее истоки ISBN 978-0-7923-4898-6 
• Мартин Куш (2006), Скептическое руководство по смыслу и правилам: защита Витгенштейна Крипке . Acumben: Publishing Limited.
• Колин Макгинн (1984), Витгенштейн о смысле . ISBN 0631137645 ISBN 978-0631137641 .   
• Гарольд Нунан (2013), Путеводитель по философии Routledge по Крипке и Наименованию и Необходимости . ISBN 978-1135105167 
• Кристофер Норрис (2007), Художественная литература, философия и литературная теория: Настоящий Сол Крипке, пожалуйста, встаньте? Лондон: Continuum
• Консуэло Прети (2002), О Крипке . Уодсворт. ISBN 0-534-58366-0 . 
• Натан Салмон (1981), Ссылка и сущность . ISBN 1-59102-215-0 ISBN 978-1591022152 .   
• Скотт Сомс (2002), За пределами жесткости: незаконченная семантическая программа именования и необходимости . ISBN 0-19-514529-1 . 

Внешние ссылки

• Страница факультета философского факультета аспирантуры CUNY Архивировано 30.09.2009 на Wayback Machine
• Архив Сола Крипке на сайте CUNY Philosophy Commons
• Вторая ежегодная лекция Сола Крипке Джона Берджесса о необходимости происхождения в аспирантуре Городского университета Нью-Йорка, 13 ноября 2012 г.
• Сол Крипке в проекте «Генеалогия математики»
• «Сол Крипке, гениальный логик», короткое, нетехническое интервью Андреаса Саугстада, 25 февраля 2001 г.
• Конференция в честь 65-летия Крипке с видеозаписью его выступления «Первое лицо», 25–26 января 2006 г.
• Видеозапись его выступления «От тезиса Чёрча к теореме об алгоритме первого порядка», 13 июня 2006 г.
• Подкаст его выступления «Неограниченный экспорт и некоторые моральные принципы философии языка», архив 25 ноября 2015 г. на Wayback Machine 21 мая 2008 г.
• Статья Джерри Фодора в London Review of Books, в которой обсуждается работа Крипке. Архивировано 16 апреля 2009 г. на Wayback Machine.
• Чествование гениального философа Городского университета Нью-Йорка, Гэри Шапиро, 27 января 2006 г., The New York Sun.
• информация с сайта «Wisdom Supreme»
• Статья в New York Times о его 65-летии
• Круглый стол, посвященный критике Крипке идентичности разума и тела, со Скоттом Сомсом в качестве основного докладчика, 26 мая 2010 г.