Теория управления

Отделение инженерии и математики

Теория управления — это область инженерии управления и прикладной математики , которая занимается управлением динамическими системами в инженерных процессах и машинах. Цель состоит в том, чтобы разработать модель или алгоритм, управляющий применением системных входов для приведения системы в желаемое состояние, минимизируя любые задержки , перерегулирования или ошибки установившегося состояния и обеспечивая уровень стабильности управления ; часто с целью достижения степени оптимальности .

Для этого требуется контроллер с необходимым корректирующим поведением. Этот контроллер контролирует контролируемую переменную процесса (PV) и сравнивает ее с опорным или заданным значением (SP). Разница между фактическим и желаемым значением переменной процесса, называемая сигналом ошибки , или ошибкой SP-PV, применяется в качестве обратной связи для генерации управляющего воздействия, чтобы привести контролируемую переменную процесса к тому же значению, что и заданное значение. Другими аспектами, которые также изучаются, являются управляемость и наблюдаемость . Теория управления используется в проектировании систем управления для проектирования автоматизации, которая произвела революцию в производстве, авиации, связи и других отраслях промышленности, а также создала новые области, такие как робототехника .

Обычно широко используется диаграммный стиль, известный как блок-схема . В ней передаточная функция , также известная как системная функция или сетевая функция, представляет собой математическую модель связи между входом и выходом, основанную на дифференциальных уравнениях, описывающих систему.

Теория управления берет свое начало в 19 веке, когда Джеймс Клерк Максвелл впервые описал теоретическую основу работы регуляторов . ^[1] Теория управления была далее развита Эдвардом Раутом в 1874 году, Чарльзом Штурмом и в 1895 году Адольфом Гурвицем , которые внесли свой вклад в установление критериев устойчивости управления; и с 1922 года, разработка теории ПИД-регулирования Николасом Минорским . [ ^2] Хотя основное применение математической теории управления заключается в проектировании систем управления , которое занимается проектированием систем управления процессами для промышленности, другие приложения простираются далеко за пределы этого. Как общая теория систем обратной связи, теория управления полезна везде, где возникает обратная связь - таким образом, теория управления также имеет приложения в науках о жизни, компьютерной инженерии, социологии и исследовании операций . ^[3]

История

Центробежный регулятор в двигателе Болтона и Уатта 1788 года

Хотя системы управления различных типов восходят к античности, более формальный анализ этой области начался с динамического анализа центробежного регулятора , проведенного физиком Джеймсом Клерком Максвеллом в 1868 году под названием «О регуляторах» . ^[4] Центробежный регулятор уже использовался для регулирования скорости ветряных мельниц. ^[5] Максвелл описал и проанализировал явление автоколебаний , при котором запаздывания в системе могут приводить к сверхкомпенсации и нестабильному поведению. Это вызвало всплеск интереса к теме, в ходе которого одноклассник Максвелла, Эдвард Джон Раут , абстрагировал результаты Максвелла для общего класса линейных систем. ^[6] Независимо от этого, Адольф Гурвиц проанализировал устойчивость системы с помощью дифференциальных уравнений в 1877 году, что привело к тому, что сейчас известно как теорема Рауса–Гурвица . ^{[7] [8]}

Заметное применение динамического управления было в области пилотируемых полетов. Братья Райт совершили свои первые успешные испытательные полеты 17 декабря 1903 года и отличались своей способностью управлять своими полетами в течение значительных периодов времени (больше, чем способность создавать подъемную силу с помощью аэродинамического профиля, которая была известна). Непрерывное, надежное управление самолетом было необходимо для полетов, длящихся дольше нескольких секунд.

К началу Второй мировой войны теория управления стала важной областью исследований. Ирмгард Флюгге-Лотц разработала теорию прерывистых систем автоматического управления и применила принцип реверберации к разработке автоматического оборудования управления полетом для самолетов. ^{[9] [10]} Другие области применения прерывистого управления включали системы управления огнем , системы наведения и электронику .

Иногда для повышения устойчивости систем используются механические методы. Например, корабельные стабилизаторы — это плавники, установленные под ватерлинией и выступающие сбоку. На современных судах это могут быть активные плавники с гироскопическим управлением, которые способны изменять угол атаки для противодействия качке, вызванной ветром или волнами, действующими на судно.

Космическая гонка также зависела от точного управления космическими аппаратами, и теория управления также находит все большее применение в таких областях, как экономика и искусственный интеллект. Здесь можно сказать, что цель состоит в том, чтобы найти внутреннюю модель , которая подчиняется теореме о хорошем регуляторе . Так, например, в экономике, чем точнее торговая модель (акций или товаров) представляет действия рынка, тем легче она может контролировать этот рынок (и извлекать из него «полезную работу» (прибыль)). В ИИ примером может служить чат-бот, моделирующий состояние дискурса людей: чем точнее он может моделировать состояние человека (например, на горячей линии голосовой поддержки по телефону), тем лучше он может манипулировать человеком (например, выполняя корректирующие действия для решения проблемы, вызвавшей телефонный звонок на линию помощи). Эти последние два примера берут узкую историческую интерпретацию теории управления как набора дифференциальных уравнений, моделирующих и регулирующих кинетическое движение, и расширяют ее до обширного обобщения регулятора, взаимодействующего с растением .

Управление с открытым и закрытым контуром (обратная связь)

По сути, существует два типа контура управления: управление с разомкнутым контуром (прямая связь) и управление с замкнутым контуром (обратная связь).

Электромеханический таймер, обычно используемый для управления в разомкнутом контуре, основанном исключительно на временной последовательности, без обратной связи от процесса.

При управлении с открытым контуром управляющее воздействие контроллера не зависит от «выходного сигнала процесса» (или «регулируемой переменной процесса»). Хорошим примером этого является котел центрального отопления, управляемый только таймером, так что тепло подается в течение постоянного времени, независимо от температуры здания. Управляющим воздействием является включение/выключение котла, но управляемой переменной должна быть температура здания, но это не так, поскольку это управление котлом с открытым контуром, которое не дает замкнутого контура управления температурой.

В управлении с замкнутым контуром управляющее воздействие контроллера зависит от выходного сигнала процесса. В случае аналогии с котлом это будет включать термостат для контроля температуры здания и, таким образом, обратной связи сигнала, чтобы гарантировать, что контроллер поддерживает температуру здания на уровне, установленном на термостате. Таким образом, контроллер с замкнутым контуром имеет контур обратной связи, который гарантирует, что контроллер применяет управляющее воздействие для выдачи выходного сигнала процесса, такого же, как «опорный вход» или «заданное значение». По этой причине контроллеры с замкнутым контуром также называются контроллерами с обратной связью. ^[11]

Определение замкнутой системы управления согласно Британскому институту стандартов : «система управления, имеющая контрольную обратную связь, причем сигнал отклонения, сформированный в результате этой обратной связи, используется для управления действием конечного элемента управления таким образом, чтобы стремиться свести отклонение к нулю». ^[12]

Аналогично; « Система управления с обратной связью — это система, которая стремится поддерживать заданное соотношение одной системной переменной к другой путем сравнения функций этих переменных и использования разницы в качестве средства управления». ^[13]

Классическая теория управления

Пример одного промышленного контура управления, демонстрирующий непрерывное модулированное управление потоком процесса.

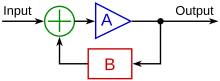
Контроллер с замкнутым контуром или контроллер с обратной связью — это контур управления , который включает обратную связь , в отличие от контроллера с разомкнутым контуром или контроллера без обратной связи . Контроллер с замкнутым контуром использует обратную связь для управления состояниями или выходами динамической системы . Его название происходит от информационного пути в системе: входы процесса (например, напряжение, подаваемое на электродвигатель ) оказывают влияние на выходы процесса (например, скорость или крутящий момент двигателя), которые измеряются датчиками и обрабатываются контроллером; результат (сигнал управления) «возвращается обратно» в качестве входа в процесс, замыкая контур. ^[14]

В случае линейных систем обратной связи контур управления , включающий датчики , алгоритмы управления и исполнительные механизмы, организован в попытке регулировать переменную в заданном значении (SP). Повседневным примером является круиз-контроль на дорожном транспортном средстве; где внешние воздействия, такие как холмы, могут вызвать изменение скорости, и водитель имеет возможность изменить желаемую заданную скорость. Алгоритм ПИД в контроллере восстанавливает фактическую скорость до желаемой скорости оптимальным образом, с минимальной задержкой или перерегулированием , управляя выходной мощностью двигателя транспортного средства. Системы управления, которые включают некоторое восприятие результатов, которых они пытаются достичь, используют обратную связь и могут в некоторой степени адаптироваться к изменяющимся обстоятельствам. Системы управления с разомкнутым контуром не используют обратную связь и работают только заранее заданными способами.

Контроллеры с замкнутым контуром имеют следующие преимущества по сравнению с контроллерами с разомкнутым контуром:

• подавление помех (например, холмов в примере круиз-контроля выше)
• гарантированная производительность даже при наличии неопределенностей модели , когда структура модели не полностью соответствует реальному процессу, а параметры модели неточны
• нестабильные процессы можно стабилизировать
• снижение чувствительности к изменению параметров
• улучшенная производительность отслеживания ссылок
• улучшенное исправление случайных колебаний ^[15]

В некоторых системах замкнутый и разомкнутый контуры управления используются одновременно. В таких системах разомкнутый контур управления называется прямой связью и служит для дальнейшего улучшения характеристик отслеживания опорных сигналов.

Распространенной архитектурой регулятора замкнутого контура является ПИД-регулятор .

Базовый цикл обратной связи

Линейная и нелинейная теория управления

Область теории управления можно разделить на две ветви:

• Линейная теория управления – это относится к системам, состоящим из устройств, которые подчиняются принципу суперпозиции , что примерно означает, что выход пропорционален входу. Они управляются линейными дифференциальными уравнениями . Основной подкласс – это системы, которые, кроме того, имеют параметры, которые не меняются со временем, называемые линейными системами с постоянной скоростью (LTI). Эти системы поддаются мощным математическим методам частотной области большой общности, таким как преобразование Лапласа , преобразование Фурье , Z-преобразование , диаграмма Боде , корневой годограф и критерий устойчивости Найквиста . Они приводят к описанию системы с использованием таких терминов, как полоса пропускания , частотная характеристика , собственные значения , усиление , резонансные частоты , нули и полюса , которые дают решения для реакции системы и методов проектирования для большинства интересующих систем.
• Нелинейная теория управления – охватывает более широкий класс систем, которые не подчиняются принципу суперпозиции, и применяется к более реальным системам, поскольку все реальные системы управления нелинейны. Эти системы часто управляются нелинейными дифференциальными уравнениями . Несколько математических методов, которые были разработаны для их обработки, более сложны и гораздо менее общие, часто применимы только к узким категориям систем. К ним относятсятеория предельных циклов , отображения Пуанкаре , теорема устойчивости Ляпунова и описывающие функции . Нелинейные системы часто анализируются с использованием численных методов на компьютерах, например, путем моделирования их работы с использованием языка моделирования . Если интерес представляют только решения вблизи устойчивой точки, нелинейные системы часто можно линеаризовать , аппроксимируя их линейной системой с использованием теории возмущений , и можно использовать линейные методы. ^[16]

Методы анализа – частотная область и временная область

Математические методы анализа и проектирования систем управления делятся на две категории:

• Частотная область – в этом типе значения переменных состояния , математических переменных , представляющих вход системы, выход и обратную связь, представлены как функции частоты . Входной сигнал и передаточная функция системыпреобразуются из функций времени в функции частоты с помощью преобразования, такого как преобразование Фурье , преобразование Лапласа или Z-преобразование . Преимущество этого метода заключается в том, что он приводит к упрощению математики; дифференциальные уравнения , представляющие систему, заменяются алгебраическими уравнениями в частотной области, которые гораздо проще решать. Однако методы частотной области можно использовать только с линейными системами, как упоминалось выше.
• Представление пространства состояний во временной области – В этом типе значения переменных состояния представлены как функции времени. С помощью этой модели анализируемая система представлена ​​одним или несколькими дифференциальными уравнениями . Поскольку методы частотной области ограничены линейными системами, временная область широко используется для анализа нелинейных систем реального мира. Хотя их сложнее решить, современные методы компьютерного моделирования, такие как языки моделирования, сделали их анализ рутинным.

В отличие от анализа частотной области классической теории управления, современная теория управления использует представление пространства состояний во временной области, ^{[ требуется ссылка ]} математическую модель физической системы как набора входных, выходных и переменных состояния, связанных дифференциальными уравнениями первого порядка. Чтобы абстрагироваться от количества входов, выходов и состояний, переменные выражаются как векторы, а дифференциальные и алгебраические уравнения записываются в матричной форме (последнее возможно только тогда, когда динамическая система линейна). Представление пространства состояний (также известное как «подход во временной области») обеспечивает удобный и компактный способ моделирования и анализа систем с несколькими входами и выходами. При наличии входов и выходов нам в противном случае пришлось бы записывать преобразования Лапласа для кодирования всей информации о системе. В отличие от подхода частотной области, использование представления пространства состояний не ограничивается системами с линейными компонентами и нулевыми начальными условиями. «Пространство состояний» относится к пространству, оси которого являются переменными состояния. Состояние системы может быть представлено как точка внутри этого пространства. ^{[17] [18]}

Системный интерфейс - SISO и MIMO

Системы управления можно разделить на различные категории в зависимости от количества входов и выходов.

• Один вход-один выход (SISO) – Это самый простой и распространенный тип, в котором один выход управляется одним управляющим сигналом. Примерами являются пример круиз-контроля выше или аудиосистема , в которой управляющим входом является входной аудиосигнал, а выходом – звуковые волны из динамика.
• Многоканальный вход-многоканальный выход (MIMO) – Они встречаются в более сложных системах. Например, современные большие телескопы, такие как Keck и MMT, имеют зеркала, состоящие из множества отдельных сегментов, каждый из которых управляется приводом . Форма всего зеркала постоянно корректируется системой управления активной оптикой MIMO с использованием входных данных от нескольких датчиков в фокальной плоскости, чтобы компенсировать изменения формы зеркала из-за теплового расширения, сжатия, напряжений при вращении и искажения волнового фронта из-за турбулентности в атмосфере. Сложные системы, такие как ядерные реакторы и человеческие клетки, моделируются компьютером как большие системы управления MIMO.

Классическая конструкция системы SISO

Область применения классической теории управления ограничена проектированием систем с одним входом и одним выходом (SISO), за исключением случаев анализа подавления помех с использованием второго входа. Анализ системы выполняется во временной области с использованием дифференциальных уравнений , в комплексной области s с помощью преобразования Лапласа или в частотной области путем преобразования из комплексной области s. Можно предположить, что многие системы имеют второй порядок и реакцию системы с одной переменной во временной области. Контроллер, разработанный с использованием классической теории, часто требует настройки на месте из-за неверных приближений проектирования. Тем не менее, из-за более простой физической реализации классических конструкций контроллеров по сравнению с системами, разработанными с использованием современной теории управления, эти контроллеры являются предпочтительными в большинстве промышленных приложений. Наиболее распространенными контроллерами, разработанными с использованием классической теории управления, являются ПИД-регуляторы . Менее распространенная реализация может включать в себя либо опережающий, либо запаздывающий фильтр, либо оба фильтра. Конечной конечной целью является удовлетворение требований, обычно предъявляемых во временной области, называемой откликом на скачок, или иногда в частотной области, называемой откликом разомкнутого контура. Характеристики реакции на скачок, применяемые в спецификации, обычно представляют собой процент перерегулирования, время установления и т. д. Характеристики реакции разомкнутого контура, применяемые в спецификации, обычно представляют собой запас усиления и фазы и полосу пропускания. Эти характеристики можно оценить с помощью моделирования, включая динамическую модель контролируемой системы в сочетании с моделью компенсации.

Современная конструкция системы MIMO

Современная теория управления выполняется в пространстве состояний и может иметь дело с системами с несколькими входами и несколькими выходами (MIMO). Это преодолевает ограничения классической теории управления в более сложных задачах проектирования, таких как управление истребителем, с тем ограничением, что анализ в частотной области невозможен. В современном проектировании система представляется с наибольшим преимуществом в виде набора разъединенных дифференциальных уравнений первого порядка, определенных с использованием переменных состояния . Нелинейные , многомерные, адаптивные и надежные теории управления попадают в это разделение. Матричные методы существенно ограничены для систем MIMO, где линейная независимость не может быть обеспечена во взаимосвязи между входами и выходами. ^{[ необходима цитата ]} Будучи довольно новой, современная теория управления имеет много областей, которые еще предстоит изучить. Такие ученые, как Рудольф Э. Кальман и Александр Ляпунов, хорошо известны среди людей, которые сформировали современную теорию управления.

Темы по теории управления

Стабильность

Устойчивость общей динамической системы при отсутствии входных данных можно описать с помощью критериев устойчивости Ляпунова .

• Линейная система называется устойчивой с ограниченным входом и ограниченным выходом (BIBO), если ее выход остается ограниченным для любого ограниченного входа.
• Устойчивость нелинейных систем , принимающих входной сигнал, называется устойчивостью «вход-состояние» (УВС), которая объединяет устойчивость по Ляпунову и понятие, аналогичное устойчивости по БИБО.

Для простоты в следующих описаниях основное внимание уделяется непрерывным и дискретным линейным системам .

Математически это означает, что для того, чтобы причинная линейная система была устойчивой, все полюса ее передаточной функции должны иметь отрицательные действительные значения, т.е. действительная часть каждого полюса должна быть меньше нуля. Практически говоря, устойчивость требует, чтобы комплексные полюса передаточной функции находились

• в открытой левой половине комплексной плоскости для непрерывного времени, когда для получения передаточной функции используется преобразование Лапласа .
• внутри единичной окружности для дискретного времени, когда используется Z-преобразование .

Разница между двумя случаями обусловлена ​​просто традиционным методом построения графиков функций передачи непрерывного времени и дискретного времени. Непрерывное преобразование Лапласа выполняется в декартовых координатах , где ось является действительной осью, а дискретное Z-преобразование выполняется в круговых координатах , где ось является действительной осью. ${\displaystyle x}$ ${\displaystyle \rho }$

Когда выполняются соответствующие условия, указанные выше, система называется асимптотически устойчивой ; переменные асимптотически устойчивой системы управления всегда уменьшаются от своего начального значения и не показывают перманентных колебаний. Перманентные колебания возникают, когда полюс имеет действительную часть, точно равную нулю (в случае непрерывного времени), или модуль, равный единице (в случае дискретного времени). Если просто устойчивая реакция системы не затухает и не растет со временем и не имеет колебаний, она является предельно устойчивой ; в этом случае передаточная функция системы имеет неповторяющиеся полюса в начале комплексной плоскости (т. е. их действительная и комплексная компоненты равны нулю в случае непрерывного времени). Колебания присутствуют, когда полюса с действительной частью, равной нулю, имеют мнимую часть, не равную нулю.

Если рассматриваемая система имеет импульсную характеристику

${\displaystyle \ x[n]=0.5^{n}u[n]}$

тогда Z-преобразование (см. этот пример ) задается как

${\displaystyle \ X(z)={\frac {1}{1-0.5z^{-1}}}}$

которая имеет полюс в (нулевая мнимая часть ). Эта система BIBO (асимптотически) устойчива, поскольку полюс находится внутри единичной окружности. ${\displaystyle z=0.5}$

Однако, если импульсный отклик был

${\displaystyle \ x[n]=1.5^{n}u[n]}$

тогда Z-преобразование равно

${\displaystyle \ X(z)={\frac {1}{1-1.5z^{-1}}}}$

которая имеет полюс в точке и не является BIBO-устойчивой, поскольку полюс имеет модуль строго больше единицы. ${\displaystyle z=1.5}$

Существует множество инструментов для анализа полюсов системы. Они включают графические системы, такие как корневой годограф , графики Боде или графики Найквиста .

Механические изменения могут сделать оборудование (и системы управления) более устойчивыми. Моряки добавляют балласт, чтобы улучшить устойчивость судов. Круизные суда используют стабилизаторы качки , которые простираются поперечно от борта судна примерно на 30 футов (10 м) и непрерывно вращаются вокруг своих осей, чтобы создавать силы, противодействующие качке.

Управляемость и наблюдаемость

Управляемость и наблюдаемость являются основными проблемами при анализе системы перед принятием решения о наилучшей стратегии управления, которую следует применить, или о том, возможно ли вообще контролировать или стабилизировать систему. Управляемость связана с возможностью принудительного перевода системы в определенное состояние с помощью соответствующего управляющего сигнала. Если состояние неуправляемо, то никакой сигнал никогда не сможет контролировать состояние. Если состояние неуправляемо, но его динамика стабильна, то состояние называется стабилизируемым . Наблюдаемость, напротив, связана с возможностью наблюдения за состоянием системы посредством выходных измерений. Если состояние ненаблюдаемо, контроллер никогда не сможет определить поведение ненаблюдаемого состояния и, следовательно, не может использовать его для стабилизации системы. Однако, подобно условию стабилизируемости выше, если состояние не может наблюдаться, оно все равно может быть обнаруживаемым.

С геометрической точки зрения, если рассматривать состояния каждой переменной системы, которая должна контролироваться, каждое «плохое» состояние этих переменных должно быть контролируемым и наблюдаемым, чтобы обеспечить хорошее поведение в замкнутой системе. То есть, если одно из собственных значений системы не является одновременно контролируемым и наблюдаемым, эта часть динамики останется нетронутой в замкнутой системе. Если такое собственное значение не является стабильным, динамика этого собственного значения будет присутствовать в замкнутой системе, которая, следовательно, будет нестабильной. Ненаблюдаемые полюса отсутствуют в реализации передаточной функции представления пространства состояний, поэтому иногда последнее предпочтительнее в анализе динамических систем.

Решения проблем неконтролируемой или ненаблюдаемой системы включают добавление исполнительных механизмов и датчиков.

Спецификация управления

За последние годы было разработано несколько различных стратегий управления. Они варьируются от крайне общих (ПИД-регулятор) до других, посвященных очень конкретным классам систем (особенно робототехнике или круиз-контролю самолетов).

Проблема управления может иметь несколько спецификаций. Устойчивость, конечно, всегда присутствует. Контроллер должен гарантировать, что замкнутая система устойчива, независимо от устойчивости разомкнутой системы. Неудачный выбор контроллера может даже ухудшить устойчивость разомкнутой системы, чего обычно следует избегать. Иногда желательно получить определенную динамику в замкнутой системе: т. е. чтобы полюса имели , где — фиксированное значение, строго большее нуля, вместо того, чтобы просто спросить, что . ${\displaystyle Re[\lambda ]<-{\overline {\lambda }}}$ ${\displaystyle {\overline {\lambda }}}$ ${\displaystyle Re[\lambda ]<0}$

Другой типичной спецификацией является отклонение ступенчатого возмущения; включение интегратора в цепь разомкнутого контура (т.е. непосредственно перед контролируемой системой) легко достигает этого. Другие классы возмущений требуют включения других типов подсистем.

Другие спецификации "классической" теории управления касаются времени отклика замкнутой системы. К ним относятся время нарастания (время, необходимое системе управления для достижения желаемого значения после возмущения), пиковый выброс (наивысшее значение, достигнутое откликом до достижения желаемого значения) и другие ( время установления , четверть спада). Спецификации частотной области обычно связаны с надежностью (см. далее).

Современные оценки эффективности используют некоторые вариации интегрированной ошибки отслеживания (IAE, ISA, CQI).

Идентификация и надежность модели

Система управления всегда должна обладать некоторым свойством надежности. Надежный контроллер таков, что его свойства не сильно меняются, если его применить к системе, немного отличающейся от математической, использованной для его синтеза. Это требование важно, поскольку ни одна реальная физическая система не ведет себя так, как ряд дифференциальных уравнений, используемых для ее математического представления. Обычно выбирается более простая математическая модель для упрощения вычислений, в противном случае истинная динамика системы может быть настолько сложной, что полная модель невозможна.

Системная идентификация

Процесс определения уравнений, управляющих динамикой модели, называется идентификацией системы . Это можно сделать в автономном режиме: например, выполнив ряд мер, из которых можно вычислить приближенную математическую модель, обычно ее передаточную функцию или матрицу. Однако такая идентификация из выходных данных не может учитывать ненаблюдаемую динамику. Иногда модель строится непосредственно, исходя из известных физических уравнений, например, в случае системы масса-пружина-демпфер мы знаем, что . Даже если предположить, что при проектировании контроллера используется «полная» модель, все параметры, включенные в эти уравнения (называемые «номинальными параметрами»), никогда не известны с абсолютной точностью; система управления должна будет вести себя правильно даже при подключении к физической системе с истинными значениями параметров, далекими от номинальных. ${\displaystyle m{\ddot {x}}(t)=-Kx(t)-\mathrm {B} {\dot {x}}(t)}$

Некоторые передовые методы управления включают в себя процесс идентификации «онлайн» (см. далее). Параметры модели вычисляются («идентифицируются») во время работы самого контроллера. Таким образом, если происходит резкое изменение параметров, например, если рука робота отпускает груз, контроллер автоматически подстраивается, чтобы обеспечить правильную работу.

Анализ

Анализ надежности системы управления SISO (один вход один выход) может быть выполнен в частотной области, учитывая передаточную функцию системы и используя диаграммы Найквиста и Боде . Темы включают запас по усилению и фазе и запас по амплитуде. Для MIMO (много входов и много выходов) и, в целом, более сложных систем управления необходимо рассмотреть теоретические результаты, разработанные для каждого метода управления (см. следующий раздел). То есть, если требуются особые качества надежности, инженер должен переключить свое внимание на метод управления, включив эти качества в его свойства.

Ограничения

Особая проблема надежности — это требование к системе управления работать должным образом при наличии ограничений на вход и состояние. В физическом мире каждый сигнал ограничен. Может случиться, что контроллер будет посылать сигналы управления, которые не могут быть отслежены физической системой, например, пытаясь вращать клапан с чрезмерной скоростью. Это может привести к нежелательному поведению замкнутой системы или даже повредить или сломать приводы или другие подсистемы. Для решения этой проблемы доступны специальные методы управления: управление с прогнозированием модели (см. ниже) и системы защиты от срабатывания . Последняя состоит из дополнительного блока управления, который гарантирует, что сигнал управления никогда не превысит заданный порог.

Системные классификации

Управление линейными системами

Для систем MIMO размещение полюсов может быть выполнено математически с использованием представления пространства состояний системы с открытым контуром и вычисления матрицы обратной связи, назначающей полюса в желаемых позициях. В сложных системах это может потребовать возможностей компьютерного расчета и не всегда может гарантировать надежность. Кроме того, все состояния системы в общем случае не измеряются, поэтому наблюдатели должны быть включены и включены в проект размещения полюсов.

Управление нелинейными системами

Процессы в таких отраслях, как робототехника и аэрокосмическая промышленность, обычно имеют сильную нелинейную динамику. В теории управления иногда возможно линеаризировать такие классы систем и применять линейные методы, но во многих случаях может быть необходимо разработать с нуля теории, позволяющие управлять нелинейными системами. Такие, например, как линеаризация обратной связи , бэкстепинг , управление скользящим режимом , управление линеаризацией траектории, обычно используют результаты, основанные на теории Ляпунова . Дифференциальная геометрия широко использовалась в качестве инструмента для обобщения известных концепций линейного управления на нелинейный случай, а также для демонстрации тонкостей, которые делают его более сложной проблемой. Теория управления также использовалась для расшифровки нейронного механизма, который управляет когнитивными состояниями. ^[19]

Децентрализованное управление системами

Когда система управляется несколькими контроллерами, проблема заключается в децентрализованном управлении. Децентрализация полезна во многих отношениях, например, она помогает системам управления работать на большей географической территории. Агенты в децентрализованных системах управления могут взаимодействовать, используя каналы связи, и координировать свои действия.

Детерминированные и стохастические системы управления

Стохастическая задача управления — это задача, в которой эволюция переменных состояния подвергается случайным шокам извне системы. Детерминированная задача управления не подвержена внешним случайным шокам.

Основные стратегии контроля

Каждая система управления должна гарантировать в первую очередь устойчивость поведения замкнутого контура. Для линейных систем это может быть достигнуто путем прямого размещения полюсов. Нелинейные системы управления используют специальные теории (обычно основанные на теории Александра Ляпунова ) для обеспечения устойчивости без учета внутренней динамики системы. Возможность выполнения различных спецификаций зависит от рассматриваемой модели и выбранной стратегии управления.

Перечень основных методов контроля

• Оптимальное управление — это особый метод управления, в котором управляющий сигнал оптимизирует определенный «индекс стоимости»: например, в случае спутника — реактивные тяги, необходимые для вывода его на желаемую траекторию, которая потребляет наименьшее количество топлива. Два метода проектирования оптимального управления широко используются в промышленных приложениях, поскольку было показано, что они могут гарантировать устойчивость замкнутого контура. Это управление с прогнозированием моделей (MPC) и линейно-квадратично-гауссовское управление (LQG). Первый может более явно учитывать ограничения на сигналы в системе, что является важной особенностью во многих промышленных процессах. Однако структура «оптимального управления» в MPC является лишь средством достижения такого результата, поскольку она не оптимизирует истинный индекс производительности замкнутой системы управления. Вместе с ПИД-регуляторами системы MPC являются наиболее широко используемым методом управления в управлении процессами .
• Надежное управление явно имеет дело с неопределенностью в своем подходе к проектированию контроллера. Контроллеры, разработанные с использованием надежных методов управления, как правило, способны справляться с небольшими различиями между истинной системой и номинальной моделью, используемой для проектирования. ^[20] Ранние методы Боде и других были довольно надежными; методы пространства состояний, изобретенные в 1960-х и 1970-х годах, иногда оказывались недостаточно надежными. Примерами современных надежных методов управления являются формирование петли H-infinity, разработанное Дунканом Макфарлейном и Кейтом Гловером , управление скользящим режимом (SMC), разработанное Вадимом Уткиным , и безопасные протоколы, разработанные для управления большими гетерогенными популяциями электрических нагрузок в приложениях Smart Power Grid. ^[21] Надежные методы направлены на достижение надежной производительности и/или стабильности при наличии небольших ошибок моделирования.
• Стохастическое управление имеет дело с проектированием управления с неопределенностью в модели. В типичных задачах стохастического управления предполагается, что в модели и контроллере существуют случайные шумы и помехи, и проектирование управления должно учитывать эти случайные отклонения.
• Адаптивное управление использует онлайн-идентификацию параметров процесса или изменение коэффициентов усиления контроллера, тем самым получая сильные свойства надежности. Адаптивное управление было впервые применено в аэрокосмической промышленности в 1950-х годах и добилось особого успеха в этой области.
• Иерархическая система управления — это тип системы управления , в которой набор устройств и управляющего программного обеспечения организован в иерархическое дерево . Когда связи в дереве реализуются компьютерной сетью , то эта иерархическая система управления также является формой сетевой системы управления .
• Интеллектуальное управление использует различные подходы к вычислениям на основе ИИ, такие как искусственные нейронные сети , байесовская вероятность , нечеткая логика , ^[22] машинное обучение , эволюционные вычисления и генетические алгоритмы или комбинацию этих методов, например, нейро-нечеткие алгоритмы, для управления динамической системой .
• Самоорганизованный контроль критичности можно определить как попытки вмешаться в процессы, посредством которых самоорганизованная система рассеивает энергию.

Люди в системах и контроле

Многие активные и исторические деятели внесли значительный вклад в теорию управления, в том числе:

• Пьер-Симон Лаплас изобрел Z-преобразование в своей работе по теории вероятностей , которое теперь используется для решения задач теории управления в дискретном времени. Z-преобразование является эквивалентом преобразования Лапласа в дискретном времени, названного в его честь.
• Ирмгард Флюгге-Лотц разработала теорию прерывистого автоматического управления и применила ее к системам автоматического управления самолетами .
• Александр Ляпунов в 1890-х годах знаменует начало теории устойчивости .
• Гарольд С. Блэк изобрел концепцию усилителей с отрицательной обратной связью в 1927 году. В 1930-х годах ему удалось разработать стабильные усилители с отрицательной обратной связью.
• В 1930-х годах Гарри Найквист разработал критерий устойчивости Найквиста для систем с обратной связью.
• Ричард Беллман разработал динамическое программирование в 1940-х годах. ^[23]
• Уоррен Э. Диксон , теоретик управления и профессор
• Кириакос Г. Вамвудакис разработал синхронные алгоритмы обучения с подкреплением для решения задач оптимального управления и теории игр.
• Андрей Колмогоров стал одним из разработчиков фильтра Винера-Колмогорова в 1941 году.
• Норберт Винер был одним из разработчиков фильтра Винера-Колмогорова и ввел термин «кибернетика» в 1940-х годах.
• В 1950-х годах Джон Р. Рагаццини ввел цифровое управление и использование Z-преобразования в теории управления (изобретенного Лапласом).
• Лев Понтрягин ввел принцип максимума и принцип «бэнг-бэнг» .
• Пьер-Луи Лионс разработал решения для измерения вязкости в методах стохастического управления и оптимального управления .
• Рудольф Э. Кальман был пионером подхода пространства состояний к системам и управлению. Ввел понятия управляемости и наблюдаемости . Разработал фильтр Калмана для линейной оценки.
• Али Х. Найфех , который внес один из главных вкладов в нелинейную теорию управления и опубликовал множество книг по методам возмущений.
• Ян К. Виллемс Ввел понятие диссипативности как обобщение функции Ляпунова на системы вход/состояние/выход. Построение функции хранения, как называется аналог функции Ляпунова, привело к изучению линейного матричного неравенства (ЛМН) в теории управления. Он был пионером поведенческого подхода к математической теории систем.

Смотрите также

• Портал системной науки

Примеры систем управления

• Автоматизация
• Контроллер безработицы
• Системы с распределенными параметрами
• Дробный контроль
• H-образная бесконечная петля-формирование
• Иерархическая система управления
• Модель предиктивного управления
• Оптимальное управление
• Управление процессом
• Надежный контроль
• Сервомеханизм
• Пространство состояний (элементы управления)
• Контроль векторов

Темы по теории управления

• Метод диаграммы коэффициентов
• Реконфигурация управления
• Обратная связь
• H бесконечность
• Генкелевское сингулярное значение
• Теорема Кренера
• Компенсатор опережения-запаздывания
• Обратная связь по второстепенному циклу
• Многоконтурная обратная связь
• Положительные системы
• Радиальная базисная функция
• Корневой локус
• Графики потока сигналов
• Стабильный многочлен
• Государственное пространственное представительство
• Устойчивое состояние
• Переходный ответ
• Переходное состояние
• Недостаточное срабатывание
• Параметризация Юлы–Кучеры
• Метод аппроксимации цепи Маркова

Другие похожие темы

• Адаптивная система
• Автоматизация и дистанционное управление
• График облигаций
• Контрольная техника
• Цикл управления–обратной связи–прерывания
• Контроллер (теория управления)
• Кибернетика
• Интеллектуальное управление
• Теория математических систем
• Усилитель с отрицательной обратной связью
• Схема управления
• Люди в системах и контроле
• Теория перцептивного контроля
• Теория систем

Ссылки

1. Максвелл, Дж. К. (1868). «О губернаторах» (PDF) . Труды Королевского общества . 100. Архивировано (PDF) из оригинала 19 декабря 2008 г.
2. Минорский, Николас (1922). «Курсовая устойчивость автоматически управляемых тел». Журнал Американского общества военно-морских инженеров . 34 (2): 280–309. doi :10.1111/j.1559-3584.1922.tb04958.x.
3. Земля. «Каталог der Deutschen Nationalbibliothek (Официальный контроль)». портал.dnb.de . Проверено 26 апреля 2020 г.
4. Максвелл, Дж. К. (1868). «О губернаторах». Труды Лондонского королевского общества . 16 : 270–283. doi :10.1098/rspl.1867.0055. JSTOR  112510.
5. Фернандес-Кара, Э.; Суазуа, Э. «Теория управления: история, математические достижения и перспективы». Boletin de la Sociedad Sociedad Espanola de Matematica Aplicada. CiteSeerX 10.1.1.302.5633 . ISSN  1575-9822. 
6. Раут, Э. Дж.; Фуллер, А. Т. (1975). Устойчивость движения . Тейлор и Фрэнсис.
7. Раут, Э. Дж. (1877). Трактат об устойчивости данного состояния движения, особенно устойчивого движения: особенно устойчивого движения. Macmillan and co.
8. Гурвиц, А. (1964). «Об условиях, при которых уравнение имеет корни только с отрицательными действительными частями». Избранные статьи по математическим тенденциям в теории управления .
9. Flugge-Lotz, Irmgard; Titus, Harold A. (октябрь 1962 г.). «Оптимальное и квазиоптимальное управление системами третьего и четвертого порядка» (PDF) . Stanford University Technical Report (134): 8–12. Архивировано из оригинала (PDF) 27 апреля 2019 г.
10. Халлион, Ричард П. (1980). Сичерман, Барбара; Грин, Кэрол Хёрд; Кантров, Айлин; Уокер, Харриетт (ред.). Известные американские женщины: современный период: биографический словарь . Кембридж, Массачусетс: Belknap Press of Harvard University Press. стр. 241–242. ISBN 9781849722704.
11. "Обратная связь и системы управления" - JJ Di Steffano, AR Stubberud, IJ Williams. Серия набросков Шаумса, McGraw-Hill 1967
12. Майр, Отто (1970). Истоки управления с обратной связью . Клинтон, MA США: The Colonial Press, Inc.
13. Майр, Отто (1969). Истоки управления с обратной связью . Клинтон, MA США: The Colonial Press, Inc.
14. Беххофер, Джон (31 августа 2005 г.). «Обратная связь для физиков: учебное эссе по управлению». Reviews of Modern Physics . 77 (3): 783–836. doi :10.1103/RevModPhys.77.783.
15. Cao, FJ; Feito, M. (10 апреля 2009 г.). "Термодинамика систем с обратной связью". Physical Review E. 79 ( 4): 041118. arXiv : 0805.4824 . doi : 10.1103/PhysRevE.79.041118.
16. "точка обрезки".
17. Дональд М. Виберг (1971). Пространство состояний и линейные системы . Серия очерков Шаума. McGraw Hill. ISBN 978-0-07-070096-3.
18. Террелл, Уильям (1999). «Некоторые фундаментальные теории управления I: Управляемость, наблюдаемость и двойственность —И— Некоторые фундаментальные теории управления II: Линеаризация обратной связи нелинейных систем с одним входом». American Mathematical Monthly . 106 (9): 705–719 и 812–828. doi :10.2307/2589614. JSTOR  2589614.
19. Гу Ши; и др. (2015). «Управляемость структурных мозговых сетей (статья № 8414)». Nature Communications . 6 (6): 8414. arXiv : 1406.5197 . Bibcode :2015NatCo...6.8414G. doi :10.1038/ncomms9414. PMC 4600713 . PMID  26423222. Здесь мы используем инструменты из теорий управления и сетей, чтобы предложить механистическое объяснение того, как мозг перемещается между когнитивными состояниями, взятое из сетевой организации микроструктуры белого вещества 
20. Мелби, Пол и др. (2002). «Надежность адаптации в управляемых саморегулирующихся хаотических системах». Fluctuation and Noise Letters . 02 (4): L285–L292. doi :10.1142/S0219477502000919.
21. NA Синицын. S. Kundu, S. Backhaus (2013). «Безопасные протоколы для генерации импульсов мощности с гетерогенными популяциями термостатически контролируемых нагрузок». Energy Conversion and Management . 67 : 297–308. arXiv : 1211.0248 . Bibcode : 2013ECM....67..297S. doi : 10.1016/j.enconman.2012.11.021. S2CID  32067734.
22. Лю, Цзе; Уилсон Ван; Фарид Голнараги; Эрик Кубица (2010). «Новая нечеткая структура для управления нелинейными системами». Нечеткие множества и системы . 161 (21): 2746–2759. doi :10.1016/j.fss.2010.04.009.
23. Ричард Беллман (1964). «Теория управления». Scientific American . Т. 211, № 3. С. 186–200. doi :10.1038/scientificamerican0964-186.

Дальнейшее чтение

• Левин, Уильям С., ред. (1996). Справочник по контролю . Нью-Йорк: CRC Press. ISBN 978-0-8493-8570-4.
• Karl J. Åström; Richard M. Murray (2008). Системы обратной связи: Введение для ученых и инженеров (PDF) . Princeton University Press. ISBN 978-0-691-13576-2.
• Кристофер Килиан (2005). Современные технологии управления . Thompson Delmar Learning. ISBN 978-1-4018-5806-3.
• Ванневар Буш (1929). Анализ операционных цепей . John Wiley and Sons, Inc.
• Роберт Ф. Стенгель (1994). Оптимальное управление и оценка . Dover Publications. ISBN 978-0-486-68200-6.
• Франклин и др. (2002). Управление динамическими системами с обратной связью (4-е изд.). Нью-Джерси: Prentice Hall. ISBN 978-0-13-032393-4.
• Джозеф Л. Хеллерстайн; Дон М. Тилбери ; Суджай Парекх (2004). Управление вычислительными системами с обратной связью . John Wiley and Sons. ISBN 978-0-471-26637-2.
• Дидерих Хинрихсен и Энтони Дж. Притчард (2005). Математическая теория систем I – Моделирование, Анализ пространства состояний, Устойчивость и надежность . Springer. ISBN 978-3-540-44125-0.
• Зонтаг, Эдуардо (1998). Математическая теория управления: детерминированные конечномерные системы. Второе издание (PDF) . Springer. ISBN 978-0-387-98489-6.
• Гудвин, Грэм (2001). Проектирование системы управления . Prentice Hall. ISBN 978-0-13-958653-8.
• Кристоф Бассо (2012). Проектирование контуров управления для линейных и импульсных источников питания: учебное пособие. Artech House. ISBN 978-1608075577.
• Борис Дж. Лурье; Пол Дж. Энрайт (2019). Классическое управление с обратной связью в нелинейных многоконтурных системах (3-е изд.). CRC Press. ISBN 978-1-1385-4114-6.

Для химической инженерии

• Luyben, William (1989). Моделирование, имитация и управление процессами для инженеров-химиков . McGraw Hill. ISBN 978-0-07-039159-8.

Внешние ссылки

• Учебники по управлению для Matlab, набор проработанных примеров управления, решенных несколькими различными методами.
• Настройка управления и передовой опыт
• Расширенные структуры управления, бесплатные онлайн-симуляторы, объясняющие теорию управления