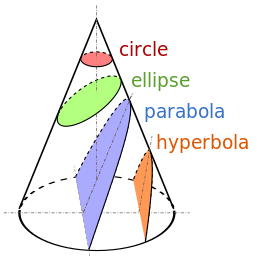
Коническое сечение

Кривая от конуса, пересекающего плоскость

Черные границы цветных областей — конические сечения. Не показана другая половина гиперболы, которая находится на не показанной другой половине двойного конуса.

Конические сечения, визуализированные с помощью фонарика

На этой диаграмме поясняются различные углы секущих плоскостей, которые приводят к различным свойствам трех типов конических сечений.

Коническое сечение , коническая или квадратичная кривая — это кривая, полученная из поверхности конуса, пересекающей плоскость . Три типа конического сечения — это гипербола , парабола и эллипс ; окружность — это частный случай эллипса, хотя иногда ее называли четвертым типом. Древнегреческие математики изучали конические сечения, достигнув кульминации около 200 г. до н. э. в систематической работе Аполлония Пергского об их свойствах.

Конические сечения в евклидовой плоскости обладают различными отличительными свойствами, многие из которых могут быть использованы в качестве альтернативных определений. Одно из таких свойств определяет некруглую конику ^[1] как множество тех точек, расстояния которых до некоторой конкретной точки, называемой фокусом , и некоторой конкретной линии, называемой директрисой , находятся в фиксированном отношении, называемом эксцентриситетом . Тип коники определяется значением эксцентриситета. В аналитической геометрии конику можно определить как плоскую алгебраическую кривую степени 2; то есть как множество точек, координаты которых удовлетворяют квадратному уравнению с двумя переменными, которое можно записать в виде Геометрические свойства коники можно вывести из ее уравнения. ${\displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0.}$

В евклидовой плоскости три типа конических сечений кажутся совершенно разными, но имеют много общих свойств. При расширении евклидовой плоскости с включением линии на бесконечности, получая проективную плоскость , кажущееся различие исчезает: ветви гиперболы встречаются в двух точках на бесконечности, превращая ее в одну замкнутую кривую; а два конца параболы встречаются, превращая ее в замкнутую кривую, касательную к линии на бесконечности. Дальнейшее расширение, путем расширения действительных координат для допуска комплексных координат, дает возможность увидеть это объединение алгебраически.

Евклидова геометрия

Типы конических сечений:
1: Окружность        2: Эллипс
3: Парабола  4: Гипербола

Конические сечения изучаются уже тысячи лет и являются богатым источником интересных и красивых результатов в евклидовой геометрии .

Определение

Коника — это кривая, полученная пересечением плоскости , называемой секущей , с поверхностью двойного конуса (конуса с двумя лопастями ). Обычно предполагается, что конус является прямым круговым конусом для простоты описания, но это не обязательно; подойдет любой двойной конус с некоторым круговым сечением. Плоскости, проходящие через вершину конуса, будут пересекать конус в точке, линии или паре пересекающихся линий. Они называются вырожденными кониками, и некоторые авторы вообще не считают их кониками. Если не указано иное, «коника» в этой статье будет относиться к невырожденной конике.

Существует три типа коник: эллипс , парабола и гипербола . Окружность является особым видом эллипса, хотя исторически Аполлоний считал ее четвертым типом. Эллипсы возникают, когда пересечение конуса и плоскости представляет собой замкнутую кривую . Окружность получается, когда секущая плоскость параллельна плоскости образующей окружности конуса; для прямого конуса это означает, что секущая плоскость перпендикулярна оси. Если секущая плоскость параллельна ровно одной образующей линии конуса, то коника неограниченна и называется параболой . В оставшемся случае фигура является гиперболой : плоскость пересекает обе половины конуса, создавая две отдельные неограниченные кривые.

Сравните также сферическое сечение (пересечение плоскости со сферой, в результате которого получается окружность или точка) и сферическое коническое сечение (пересечение эллиптического конуса с концентрической сферой).

Эксцентриситет, фокус и директриса

Конические сечения переменного эксцентриситета , разделяющие фокус и линию директрисы, включая эллипс (красный, e = 1/2 ), параболу (зеленый, e = 1 ) и гиперболу (синий, e = 2 ). Коника эксцентриситета 0 на этом рисунке представляет собой бесконечно малую окружность с центром в фокусе, а коника эксцентриситета ∞ представляет собой бесконечно мало разделенную пару линий.

Окружность конечного радиуса имеет бесконечно удаленную директрису, в то время как пара линий конечного расстояния имеют бесконечно удаленный фокус.

В качестве альтернативы можно определить коническое сечение исключительно в терминах плоской геометрии: это геометрическое место всех точек P , расстояние которых до фиксированной точки F (называемой фокусом ) является постоянным кратным e (называемым эксцентриситетом ) расстояния от P до фиксированной линии L (называемой директрисой ). При 0 < e < 1 мы получаем эллипс, при e = 1 — параболу, а при e > 1 — гиперболу.

Окружность является предельным случаем и не определяется фокусом и директрисой в евклидовой плоскости. Эксцентриситет окружности определяется как нулевой, а ее фокус является центром окружности, но ее директриса может быть взята только как линия на бесконечности в проективной плоскости. ^[2]

Эксцентриситет эллипса можно рассматривать как меру того, насколько эллипс отклоняется от круговой формы. ^[3]

Если угол между поверхностью конуса и его осью равен , а угол между секущей плоскостью и осью равен , то эксцентриситет равен ^[4] ${\displaystyle \beta }$ ${\displaystyle \alpha ,}$ ${\displaystyle {\frac {\cos \alpha }{\cos \beta }}.}$

Доказательство того, что указанные выше кривые, определяемые свойством фокус-директрисы, совпадают с кривыми, полученными при пересечении конуса плоскостями, облегчается использованием сфер Данделена . ^[5]

В качестве альтернативы эллипс можно определить в терминах двух фокусных точек, как геометрическое место точек, для которых сумма расстояний до двух фокусов равна 2 a ; в то время как гипербола является геометрическим местом, для которого разность расстояний равна 2 a . (Здесь a — большая полуось, определенная ниже.) Парабола также может быть определена в терминах ее фокуса и линии latus rectum (параллельной директрисе и проходящей через фокус): это геометрическое место точек, расстояние которых до фокуса плюс или минус расстояние до прямой равно 2 a ; плюс, если точка находится между директрисой и latus rectum, и минус в противном случае.

Конические параметры

Конические параметры в случае эллипса

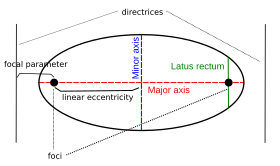
Помимо эксцентриситета ( e ), фокусов и директрисы, с коническим сечением связаны различные геометрические характеристики и длины.

Главная ось — это линия, соединяющая фокусы эллипса или гиперболы, а ее середина — центр кривой . Парабола не имеет центра.

Линейный эксцентриситет ( c ) — это расстояние между центром и фокусом.

Широкая прямая кость — это хорда, параллельная директрисе и проходящая через фокус; ее половина длины — полуширокая прямая кость ( ℓ ).

Фокальный параметр ( p ) — это расстояние от фокуса до соответствующей директрисы.

Большая ось — это хорда между двумя вершинами: самая длинная хорда эллипса, самая короткая хорда между ветвями гиперболы. Ее половина длины — большая полуось ( a ). Когда эллипс или гипербола находятся в стандартном положении, как в уравнениях ниже, с фокусами на оси x и центром в начале координат, вершины конического сечения имеют координаты (− a , 0) и ( a , 0) , с неотрицательным .

Малая ось — это наименьший диаметр эллипса, а его половина длины — это малая полуось ( b ), то же значение b, что и в стандартном уравнении ниже. По аналогии, для гиперболы параметр b в стандартном уравнении также называется малой полуосью.

Имеют место следующие соотношения: ^[6]

• ${\displaystyle \ \ell =pe}$
• ${\displaystyle \ c=ae}$
• ${\displaystyle \ p+c={\frac {a}{e}}}$

Для коник в стандартном положении эти параметры имеют следующие значения, принимая . ${\displaystyle a,b>0}$

Стандартные формы в декартовых координатах

Стандартные формы эллипса

Стандартные формы параболы

Стандартные формы гиперболы

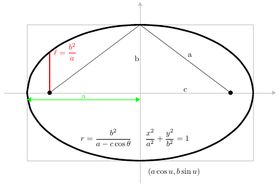
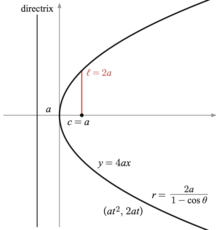
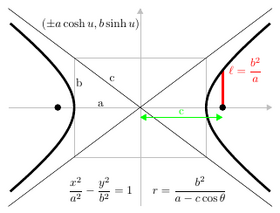
После введения декартовых координат свойство фокуса-директрисы может быть использовано для получения уравнений, которым удовлетворяют точки конического сечения. ^[7] С помощью изменения координат ( вращение и перенос осей ) эти уравнения могут быть приведены к стандартным формам . ^[8] Для эллипсов и гипербол стандартная форма имеет ось x в качестве главной оси и начало координат (0,0) в качестве центра. Вершины - (± a , 0) и фокусы (± c , 0) . Определим b уравнениями c ² = a ² − b ² для эллипса и c ² = a ² + b ² для гиперболы. Для окружности c = 0 , поэтому a ² = b ² , с радиусом r = a = b . Для параболы стандартная форма имеет фокус на оси x в точке ( a , 0) и директрису - прямую с уравнением x = − a . В стандартной форме парабола всегда проходит через начало координат.

Для прямоугольной или равносторонней гиперболы, асимптоты которой перпендикулярны, существует альтернативная стандартная форма, в которой асимптоты являются осями координат, а линия x = y является главной осью. Фокусы тогда имеют координаты ( c , c ) и (− c , − c ) . ^[9]

• Круг:

  ${\displaystyle x^{2}+y^{2}=a^{2},}$

• Эллипс:

  ${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1,}$

• Парабола:

  ${\displaystyle y^{2}=4ax,{\text{ with }}a>0,}$

• Гипербола:

  ${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1,}$

• Прямоугольная гипербола: ^[10]

  ${\displaystyle xy=c^{2}.}$

Первые четыре из этих форм симметричны относительно как оси x , так и оси y (для окружности, эллипса и гиперболы) или только относительно оси x (для параболы). Прямоугольная гипербола, однако, симметрична относительно линий y = x и y = − x .

Эти стандартные формы можно записать параметрически как:

• Круг :

  ${\displaystyle (a\cos \theta ,a\sin \theta ),}$

• Эллипс :

  ${\displaystyle (a\cos \theta ,b\sin \theta ),}$

• Парабола :

  ${\displaystyle (at^{2},2at),}$

• Гипербола :

  ${\displaystyle (a\sec \theta ,b\tan \theta ),{\text{ or }}(\pm a\cosh \psi ,b\sinh \psi )}$,

• Прямоугольная гипербола :

  ${\displaystyle \left(dt,{\frac {d}{t}}\right),{\text{ where }}d={\frac {c}{\sqrt {2}}}.}$

Общая декартова форма

В декартовой системе координат график квадратного уравнения с двумя переменными всегда является коническим сечением (хотя оно может быть вырожденным), [ ^a] и все конические сечения возникают таким образом. Наиболее общее уравнение имеет вид ^[11]

${\displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0,}$

где все коэффициенты — действительные числа , а A, B, C не все равны нулю.

Матричная запись

Приведенное выше уравнение можно записать в матричной форме как ^[12] $${\displaystyle {\begin{pmatrix}x&y\end{pmatrix}}{\begin{pmatrix}A&B/2\\B/2&C\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}+{\begin{pmatrix}D&E\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}+F=0.}$$

Общее уравнение можно также записать как $${\displaystyle {\begin{pmatrix}x&y&1\end{pmatrix}}{\begin{pmatrix}A&B/2&D/2\\B/2&C&E/2\\D/2&E/2&F\end{pmatrix}}{\begin{pmatrix}x\\y\\1\end{pmatrix}}=0.}$$

Эта форма является специализацией однородной формы, используемой в более общей области проективной геометрии (см. ниже).

Дискриминант

Конические сечения, описываемые этим уравнением, можно классифицировать по значению , называемому дискриминантом уравнения. ^[13] Таким образом, дискриминант равен − 4Δ, где Δ — определитель матрицы ${\displaystyle B^{2}-4AC}$ ${\displaystyle \left|{\begin{matrix}A&B/2\\B/2&C\end{matrix}}\right|.}$

Если коника невырожденная , то: ^[14]

• если B ² − 4 AC < 0 , уравнение представляет собой эллипс ;
  • если A = C и B = 0 , уравнение представляет собой окружность , которая является частным случаем эллипса;
• если B ² − 4 AC = 0 , уравнение представляет собой параболу ;
• если B ² − 4 AC > 0 , уравнение представляет собой гиперболу ;
  • если A + C = 0 , уравнение представляет собой прямоугольную гиперболу .

В используемых здесь обозначениях A и B являются коэффициентами полиномов, в отличие от некоторых источников , которые обозначают большую и малую полуоси как A и B.

Инварианты

Дискриминант B ² – 4 AC квадратного уравнения конического сечения (или, что эквивалентно, определитель AC – B ² /4 матрицы 2 × 2) и величина A + C ( след матрицы 2 × 2) инвариантны относительно произвольных вращений и перемещений осей координат, ^{[14] [15] [16]} , как и определитель матрицы 3 × 3 выше. ^{[17] : стр. 60–62} Постоянный член F и сумма D ² + E ² инвариантны только относительно вращения. ^{[17] : стр. 60–62}

Эксцентриситет по коэффициентам

Когда коническое сечение записывается алгебраически как

${\displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0,\,}$

эксцентриситет можно записать как функцию коэффициентов квадратного уравнения. ^[18] Если 4 AC = B ^{2 ,} то коника является параболой, а ее эксцентриситет равен 1 (при условии, что она невырожденная). В противном случае, предполагая, что уравнение представляет собой либо невырожденную гиперболу, либо эллипс, эксцентриситет определяется как

${\displaystyle e={\sqrt {\frac {2{\sqrt {(A-C)^{2}+B^{2}}}}{\eta (A+C)+{\sqrt {(A-C)^{2}+B^{2}}}}}},}$

где η = 1 , если определитель матрицы 3 × 3 выше отрицательный, и η = −1, если этот определитель положительный.

Можно также показать ^{[17] : стр. 89,} что эксцентриситет является положительным решением уравнения

${\displaystyle \Delta e^{4}+[(A+C)^{2}-4\Delta ]e^{2}-[(A+C)^{2}-4\Delta ]=0,}$

где снова Это имеет ровно одно положительное решение — эксцентриситет — в случае параболы или эллипса, тогда как в случае гиперболы оно имеет два положительных решения, одним из которых является эксцентриситет. ${\displaystyle \Delta =AC-{\frac {B^{2}}{4}}.}$

Преобразование в каноническую форму

В случае эллипса или гиперболы уравнение

${\displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0\,}$

можно преобразовать в каноническую форму в преобразованных переменных как ^[19] ${\displaystyle {\tilde {x}},{\tilde {y}}}$

${\displaystyle {\frac {{\tilde {x}}^{2}}{-S/(\lambda _{1}^{2}\lambda _{2})}}+{\frac {{\tilde {y}}^{2}}{-S/(\lambda _{1}\lambda _{2}^{2})}}=1,}$

или эквивалентно

${\displaystyle {\frac {{\tilde {x}}^{2}}{-S/(\lambda _{1}\Delta )}}+{\frac {{\tilde {y}}^{2}}{-S/(\lambda _{2}\Delta )}}=1,}$

где и — собственные значения матрицы , то есть решения уравнения ${\displaystyle \lambda _{1}}$ ${\displaystyle \lambda _{2}}$ ${\displaystyle \left({\begin{matrix}A&B/2\\B/2&C\end{matrix}}\right)}$

${\displaystyle \lambda ^{2}-(A+C)\lambda +(AC-(B/2)^{2})=0}$

— и является определителем матрицы 3 × 3, приведенной выше, и является снова определителем матрицы 2 × 2. В случае эллипса квадраты двух полуосей задаются знаменателями в канонической форме. ${\displaystyle S}$ ${\displaystyle \Delta =\lambda _{1}\lambda _{2}}$

Полярные координаты

Развитие конического сечения по мере увеличения эксцентриситета e

В полярных координатах коническое сечение с одним фокусом в начале координат и, если таковое имеется, другим при отрицательном значении (для эллипса) или положительном значении (для гиперболы) на оси x задается уравнением

${\displaystyle r={\frac {l}{1+e\cos \theta }},}$

где e — эксцентриситет, а l — полуширота прямой кишки.

Как и выше, при e = 0 график представляет собой окружность, при 0 < e < 1 график представляет собой эллипс, при e = 1 — параболу, а при e > 1 — гиперболу.

Полярная форма уравнения конического сечения часто используется в динамике , например, для определения орбит объектов, вращающихся вокруг Солнца. ^[20]

Характеристики

Так же, как две (различные) точки определяют прямую, пять точек определяют конику . Формально, если заданы любые пять точек на плоскости в общем линейном положении , то есть нет трех коллинеарных , то через них проходит единственная коника, которая будет невырожденной; это верно как для евклидовой плоскости, так и для ее расширения, реальной проективной плоскости. Действительно, если заданы любые пять точек, через них проходит коника, но если три из точек коллинеарны, то коника будет вырожденной (приводимой, поскольку она содержит прямую) и может быть не единственной; см. дальнейшее обсуждение .

Четыре точки на плоскости в общем линейном положении определяют единственную конику, проходящую через первые три точки и имеющую четвертую точку в качестве своего центра. Таким образом, знание центра эквивалентно знанию двух точек на конике для определения кривой. ^[21]

Кроме того, коника определяется любой комбинацией k точек в общем положении, через которые она проходит, и 5 – k прямых, которые касаются ее, для 0 ≤ k ≤5. ^[22]

Любая точка плоскости находится либо на нулевой, либо на одной, либо на двух касательных линиях конического сечения. Точка, лежащая только на одной касательной линии, находится на коническом сечении. Точка, лежащая ни на одной касательной линии, называется внутренней точкой конического сечения, а точка, лежащая на двух касательных линиях, — внешней точкой .

Все конические сечения разделяют свойство отражения , которое можно сформулировать так: Все зеркала в форме невырожденного конического сечения отражают свет, исходящий или идущий к одному фокусу, к другому фокусу или от него. В случае параболы второй фокус нужно рассматривать как бесконечно далекий, так что лучи света, идущие к второму фокусу или от него, параллельны. ^{[23] [24]}

Теорема Паскаля касается коллинеарности трех точек, которые построены из набора из шести точек на любой невырожденной конике. Теорема также справедлива для вырожденных коник, состоящих из двух прямых, но в этом случае она известна как теорема Паппуса .

Невырожденные конические сечения всегда « гладкие ». Это важно для многих приложений, таких как аэродинамика, где гладкая поверхность требуется для обеспечения ламинарного течения и предотвращения турбулентности .

История

Менехм и ранние произведения

Считается, что первое определение конического сечения было дано Менехмом (умер в 320 г. до н. э.) как часть его решения Делосской проблемы ( Удвоение куба ). ^{[b] [25]} Его работа не сохранилась, даже названия, которые он использовал для этих кривых, и известны только по вторичным источникам. ^[26] Определение, используемое в то время, отличается от общепринятого сегодня. Конусы строились путем вращения прямоугольного треугольника вокруг одного из его катетов так, что гипотенуза образовывала поверхность конуса (такая линия называется образующей). Три типа конусов определялись их углами при вершине (измеряемыми удвоенным углом, образованным гипотенузой и катетом, вращающимся вокруг прямоугольного треугольника). Затем коническое сечение определялось путем пересечения одного из этих конусов с плоскостью, проведенной перпендикулярно образующей. Тип конического сечения определяется типом конуса, то есть углом, образованным при вершине конуса: если угол острый, то коническое сечение является эллипсом; если угол прямой, то коническое сечение является параболой; а если угол тупой, то коническое сечение является гиперболой (но только одной ветвью кривой). ^[27]

Говорят, что Евклид (ок. 300 г. до н. э.) написал четыре книги о конических сечениях, но они также были утеряны. ^[28] Известно, что Архимед (умер около  212 г. до н. э.) изучал конические сечения, определив площадь, ограниченную параболой и хордой в «Квадратуре параболы» . Его основной интерес был связан с измерением площадей и объемов фигур, связанных с коническими сечениями, и часть этой работы сохранилась в его книге о телах вращения конических сечений « О коноидах и сфероидах» . ^[29]

Аполлоний Пергский

Диаграмма из « Конических проекций » Аполлония в арабском переводе IX века.

Наибольший прогресс в изучении конических сечений древними греками был достигнут благодаря Аполлонию Пергскому (умер около  190 г. до н. э.), чей восьмитомный труд « Конические сечения » обобщил и значительно расширил существующие знания. ^[30] Изучение Аполлонием свойств этих кривых позволило показать, что любая плоскость, пересекающая фиксированный двойной конус (двухсторонний), независимо от его угла, даст коническое сечение в соответствии с более ранним определением, что привело к определению, которое обычно используется сегодня. Окружности, не строившиеся более ранним методом, также могут быть получены таким образом. Это может объяснить, почему Аполлоний считал окружности четвертым типом конического сечения, различие, которое больше не проводится. Аполлоний использовал названия «эллипс», «парабола» и «гипербола» для этих кривых, заимствуя терминологию из более ранней пифагорейской работы о площадях. ^[31]

Паппу Александрийскому (умер около  350 г. н. э.) приписывают разъяснение важности концепции фокуса конического сечения и детализацию связанной с ней концепции директрисы, включая случай параболы (которая отсутствует в известных трудах Аполлония) ^{[32] .}

Исламский мир

Работа Аполлония была переведена на арабский язык, и большая часть его работы сохранилась только в арабской версии. Исламские математики нашли применение этой теории, в частности, персидский математик и поэт Омар Хайям , ^[33] который нашел геометрический метод решения кубических уравнений с использованием конических сечений. ^{[34] [35]}

За столетие до более известной работы Хайяма Абу аль-Джуд использовал конические сечения для решения уравнений четвертой и третьей степени, ^[36] хотя его решение не охватывало все случаи. ^[37]

Инструмент для черчения конических сечений был впервые описан в 1000 году нашей эры Аль-Кухи . ^{[38] [39]}

Европа

Таблица конических сечений, Энциклопедия , 1728 г.

Иоганн Кеплер расширил теорию конических сечений с помощью « принципа непрерывности », предшественника концепции пределов. Кеплер впервые использовал термин «фокусы» в 1604 году. ^[40]

Жирар Дезарг и Блез Паскаль разработали теорию коник, используя раннюю форму проективной геометрии , и это помогло дать толчок изучению этой новой области. В частности, Паскаль открыл теорему, известную как hexagrammum mysticum, из которой можно вывести многие другие свойства коник.

Рене Декарт и Пьер Ферма оба применили свою недавно открытую аналитическую геометрию к изучению конических сечений. Это имело эффект сведения геометрических проблем конических сечений к проблемам алгебры. Однако именно Джон Уоллис в своем трактате 1655 года Tractatus de sectionibus conicis впервые определил конические сечения как примеры уравнений второй степени. ^[41] Написанная ранее, но опубликованная позже, Elementa Curvarum Linearum Яна де Витта начинается с кинематического построения конических сечений Кеплером , а затем развивает алгебраические уравнения. Эта работа, которая использует методологию Ферма и обозначения Декарта, была описана как первый учебник по этому предмету. ^[42] Де Витт изобрел термин «директриса». ^[42]

Приложения

Конические сечения важны в астрономии : орбиты двух массивных объектов, которые взаимодействуют в соответствии с законом всемирного тяготения Ньютона, являются коническими сечениями, если их общий центр масс считается находящимся в состоянии покоя. Если они связаны вместе, они оба будут описывать эллипсы; если они разъединяются, они оба будут следовать параболам или гиперболам. См. задачу двух тел .

Отражательные свойства конических сечений используются в конструкции прожекторов, радиотелескопов и некоторых оптических телескопов. ^[43] Прожектор использует параболическое зеркало в качестве отражателя с колбой в фокусе; похожая конструкция используется для параболического микрофона . 4,2-метровый оптический телескоп Гершеля на острове Ла-Пальма, на Канарских островах, использует первичное параболическое зеркало для отражения света в направлении вторичного гиперболического зеркала, которое отражает его снова в фокус за первым зеркалом.

В реальной проективной плоскости

Конические сечения имеют некоторые очень похожие свойства в евклидовой плоскости, и причины этого становятся яснее, когда коники рассматриваются с точки зрения более крупной геометрии. Евклидова плоскость может быть вложена в действительную проективную плоскость , а коники могут рассматриваться как объекты в этой проективной геометрии. Один из способов сделать это — ввести однородные координаты и определить конику как множество точек, координаты которых удовлетворяют неприводимому квадратному уравнению с тремя переменными (или, что эквивалентно, нулям неприводимой квадратичной формы ). Более технически, множество точек, которые являются нулями квадратичной формы (с любым числом переменных), называется квадрикой , а неприводимые квадрики в двумерном проективном пространстве (то есть имеющие три переменные) традиционно называются кониками.

Евклидова плоскость R2 вкладывается в действительную проективную плоскость путем присоединения прямой на бесконечности (и соответствующих ей точек на бесконечности ) так, что все прямые параллельного класса пересекаются на этой прямой. С другой стороны, начиная ^с действительной проективной плоскости, евклидова плоскость получается путем выделения некоторой прямой как прямой на бесконечности и удаления ее и всех ее точек.

Пересечение в бесконечности

В проективном пространстве над любым делением, но в частности над действительными или комплексными числами, все невырожденные коники эквивалентны, и поэтому в проективной геометрии говорят о «конике», не указывая тип. То есть, существует проективное преобразование, которое сопоставит любую невырожденную конику с любой другой невырожденной коникой. ^[44]

Три типа конических сечений снова появятся в аффинной плоскости, полученной путем выбора линии проективного пространства в качестве линии на бесконечности. Затем три типа определяются тем, как эта линия на бесконечности пересекает конику в проективном пространстве. В соответствующем аффинном пространстве получается эллипс, если коника не пересекает линию на бесконечности, парабола, если коника пересекает линию на бесконечности в одной двойной точке, соответствующей оси, и гипербола, если коника пересекает линию на бесконечности в двух точках, соответствующих асимптотам. ^[45]

Однородные координаты

В однородных координатах коническое сечение можно представить в виде:

${\displaystyle Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}=0.}$

Или в матричной записи

${\displaystyle \left({\begin{matrix}x&y&z\end{matrix}}\right)\left({\begin{matrix}A&B/2&D/2\\B/2&C&E/2\\D/2&E/2&F\end{matrix}}\right)\left({\begin{matrix}x\\y\\z\end{matrix}}\right)=0.}$

Матрица 3 × 3, представленная выше, называется матрицей конического сечения .

Некоторые авторы предпочитают записывать общее однородное уравнение в виде

${\displaystyle Ax^{2}+2Bxy+Cy^{2}+2Dxz+2Eyz+Fz^{2}=0,}$

(или какая-то ее вариация) так, чтобы матрица конического сечения имела более простой вид,

${\displaystyle M=\left({\begin{matrix}A&B&D\\B&C&E\\D&E&F\end{matrix}}\right),}$

но в данной статье это обозначение не используется. ^[c]

Если определитель матрицы конического сечения равен нулю, то коническое сечение вырождено.

Поскольку умножение всех шести коэффициентов на один и тот же ненулевой скаляр дает уравнение с тем же набором нулей, можно рассматривать коники, представленные как ( A , B , C , D , E , F ), как точки в пятимерном проективном пространстве. ${\displaystyle \mathbf {P} ^{5}.}$

Проективное определение окружности

Метрические концепции евклидовой геометрии (концепции, связанные с измерением длин и углов) не могут быть немедленно расширены на действительную проективную плоскость. ^[d] Они должны быть переопределены (и обобщены) в этой новой геометрии. Это можно сделать для произвольных проективных плоскостей , но чтобы получить действительную проективную плоскость как расширенную евклидову плоскость, необходимо сделать некоторые конкретные выборы. ^[46]

Зафиксируем произвольную линию в проективной плоскости, которая будет называться абсолютной линией . Выберем две различные точки на абсолютной линии и назовем их абсолютными точками . Несколько метрических понятий могут быть определены со ссылкой на эти выборы. Например, если задана линия, содержащая точки A и B , середина отрезка AB определяется как точка C , которая является проективным гармоническим сопряжением точки пересечения AB и абсолютной линии относительно A и B.

Коника в проективной плоскости, которая содержит две абсолютные точки, называется окружностью . Поскольку пять точек определяют конику, окружность (которая может быть вырожденной) определяется тремя точками. Чтобы получить расширенную евклидову плоскость, абсолютная прямая выбирается как прямая в бесконечности евклидовой плоскости, а абсолютные точки — это две особые точки на этой прямой, называемые круговыми точками в бесконечности . Прямые, содержащие две точки с действительными координатами, не проходят через круговые точки в бесконечности, поэтому в евклидовой плоскости окружность, согласно этому определению, определяется тремя точками, которые не являются коллинеарными . ^[47]

Было упомянуто, что окружности на евклидовой плоскости не могут быть определены свойством фокуса-директрисы. Однако, если рассматривать бесконечную линию как директрису, то, приняв эксцентриситет равным e = 0, окружность будет обладать свойством фокуса-директрисы, но она все еще не будет определена этим свойством. ^[48] В этой ситуации нужно быть осторожным, чтобы правильно использовать определение эксцентриситета как отношение расстояния точки на окружности до фокуса (длина радиуса) к расстоянию этой точки до директрисы (это расстояние бесконечно), что дает предельное значение, равное нулю.

Проективное коническое определение Штейнера

Определение поколения Штейнера конического сечения

Синтетический (безкоординатный) подход к определению конических сечений в проективной плоскости был предложен Якобом Штейнером в 1867 году.

• Даны два пучка прямых в двух точках (все прямые содержат и соответственно) и проективное , но не перспективное отображение на . Тогда точки пересечения соответствующих прямых образуют невырожденное проективное коническое сечение. ^{[49] [50] [51]} [ ^52] ${\displaystyle B(U),B(V)}$ ${\displaystyle U,V}$ ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle \pi }$ ${\displaystyle B(U)}$ ${\displaystyle B(V)}$

Перспективное отображение карандаша на карандаш — это биекция (соответствие 1-1) , при котором соответствующие прямые пересекаются по фиксированной прямой , которая называется осью перспективы . ${\displaystyle \pi }$ ${\displaystyle B(U)}$ ${\displaystyle B(V)}$ ${\displaystyle a}$ ${\displaystyle \pi }$

Проективное отображение — это конечная последовательность перспективных отображений.

Так как проективное отображение в проективной плоскости над полем ( папповой плоскостью ) однозначно определяется заданием образов трех прямых, ^[53] для генерации Штейнера конического сечения, помимо двух точек, должны быть заданы только образы трех прямых. Эти 5 элементов (2 точки, 3 прямые) однозначно определяют коническое сечение. ${\displaystyle U,V}$

Линейные коники

Согласно принципу двойственности в проективной плоскости, двойственной для каждой точки является прямая, а двойственной для геометрического места точек (множества точек, удовлетворяющих некоторому условию) называется огибающей прямых . Используя определение Штейнера коники (это геометрическое место точек теперь будет называться точечной коникой ) как пересечения соответствующих лучей двух связанных пучков, легко дуализировать и получить соответствующую огибающую, состоящую из соединений соответствующих точек двух связанных диапазонов (точек на прямой) на разных базисах (прямых, на которых находятся точки). Такая огибающая называется прямой коникой (или двойственной коникой).

В вещественной проективной плоскости точечная коника обладает тем свойством, что каждая прямая пересекает ее в двух точках (которые могут совпадать или быть комплексными), и любой набор точек с этим свойством является точечной коникой. Из этого следует двойственно, что прямая коника имеет две свои прямые через каждую точку, и любая огибающая прямых с этим свойством является прямой коникой. В каждой точке точечной коники есть единственная касательная прямая, и двойственно, на каждой прямой прямой коники есть единственная точка, называемая точкой контакта . Важная теорема утверждает, что касательные линии точечной коники образуют прямую конику, и двойственно, точки контакта прямой коники образуют точечную конику. ^[54]

Определение фон Штаудта

Карл Георг Кристиан фон Штаудт определил конику как множество точек, заданное всеми абсолютными точками полярности , имеющей абсолютные точки. Фон Штаудт ввел это определение в Geometrie der Lage (1847) как часть своей попытки удалить все метрические концепции из проективной геометрии.

Полярность , π , проективной плоскости P — это инволютивная биекция между точками и прямыми P , которая сохраняет отношение инцидентности . Таким образом, полярность связывает точку Q с прямой q посредством π ( Q ) = q и π ( q ) = Q . Согласно Жергонну, q называется полярой Q, а Q — полюсом q . [ 55 ] Абсолютная точка ( или прямая ) полярности — это та , ^{которая} инцидентна ее поляре ( полюсу). ^[e]

Коника фон Штаудта в вещественной проективной плоскости эквивалентна конике Штейнера . ^[56]

Конструкции

Никакая непрерывная дуга конического сечения не может быть построена с помощью циркуля и линейки. Однако существует несколько построений с помощью циркуля и линейки для любого количества отдельных точек на дуге.

Один из них основан на обратной теореме Паскаля, а именно, если точки пересечения противоположных сторон шестиугольника коллинеарны, то шесть вершин лежат на конике. В частности, если заданы пять точек, A , B , C , D , E и прямая, проходящая через E , скажем EG , можно построить точку F , которая лежит на этой прямой и находится на конике, определяемой пятью точками. Пусть AB пересекает DE в L , BC пересекает EG в M и пусть CD пересекает LM в N . Тогда AN пересекает EG в требуемой точке F . ^[57] Изменяя прямую, проходящую через E , можно построить столько дополнительных точек на конике, сколько необходимо.

Метод параллелограмма для построения эллипса

Другой метод, основанный на конструкции Штейнера и полезный в инженерных приложениях, — это метод параллелограмма, в котором коническое сечение строится точка за точкой путем соединения определенных равноотстоящих точек на горизонтальной и вертикальной линиях. ^[58] В частности, для построения эллипса с помощью уравнения ⁠х ²/а ²⁠ + ⁠г ²/б ²⁠ = 1 , сначала постройте прямоугольник ABCD с вершинами A ( a , 0), B ( a , 2 b ), C (− a , 2 b ) и D (− a , 0) . Разделите сторону BC на n равных отрезков и используйте параллельную проекцию относительно диагонали AC , чтобы сформировать равные отрезки на стороне AB (длины этих отрезков будут ⁠б/а⁠ умножить на длину отрезков на BC ). На стороне BC обозначим левые концы отрезков с A ₁ по An _, начиная с B и идя к C . На стороне AB обозначим верхние концы D ₁ по D _{n ,} начиная с A и идя к B . Точки пересечения AA _i ∩ DD _i для 1 ≤ i ≤ n будут точками эллипса между A и P (0, b ) . Обозначение связывает прямые карандаша, проходящие через A, с прямыми карандаша, проходящим через D , проективно, но не перспективно. Искомая коника получается этим построением, поскольку три точки A , D и P и две касательные (вертикальные прямые в A и D ) однозначно определяют конику. Если вместо большой и малой осей эллипса использовать другой диаметр (и его сопряженный диаметр), то при построении используется параллелограмм, который не является прямоугольником, что и дало название методу. Объединение линий пучков может быть продолжено для получения других точек эллипса. Построения для гипербол ^[59] и парабол ^[60] аналогичны.

Еще один общий метод использует свойство полярности для построения касательной оболочки конического сечения (прямоугольного конического сечения). ^[61]

В комплексной проективной плоскости

В комплексной плоскости C ² эллипсы и гиперболы неотличимы: можно рассматривать гиперболу как эллипс с мнимой длиной оси. Например, эллипс становится гиперболой при замене геометрически комплексного вращения, что дает . Таким образом, существует 2-сторонняя классификация: эллипс/гипербола и парабола. Продлевая кривые до комплексной проективной плоскости, это соответствует пересечению прямой на бесконечности либо в 2 различных точках (соответствующих двум асимптотам), либо в 1 двойной точке (соответствующей оси параболы); таким образом, действительная гипербола является более наводящим на размышления действительным образом для комплексного эллипса/гиперболы, поскольку она также имеет 2 (действительных) пересечения с прямой на бесконечности. ${\displaystyle x^{2}+y^{2}=1}$ ${\displaystyle y=iw,}$ ${\displaystyle x^{2}-w^{2}=1}$

Дальнейшее объединение происходит в комплексной проективной плоскости CP2 : невырожденные коники невозможно отличить друг от друга, поскольку любую из них можно перевести в любую другую с помощью ^{проективного} линейного преобразования .

Можно доказать, что в CP ² два конических сечения имеют четыре общие точки (если учитывать кратность ), поэтому имеется от 1 до 4 точек пересечения . Возможные точки пересечения: четыре различных точки, две особые точки и одна двойная точка, две двойные точки, одна особая точка и одна с кратностью 3, одна точка с кратностью 4. Если какая-либо точка пересечения имеет кратность > 1, то две кривые называются касательными . Если имеется точка пересечения с кратностью не менее 3, то две кривые называются соприкасающимися . Если имеется только одна точка пересечения с кратностью 4, то две кривые называются сверхсоприкасающимися . ^[62]

Более того, каждая прямая пересекает каждое коническое сечение дважды. Если точка пересечения двойная, то линия является касательной . Пересекаясь с прямой на бесконечности, каждое коническое сечение имеет две точки на бесконечности. Если эти точки действительны, кривая является гиперболой ; если они мнимо сопряженные, то это эллипс ; если есть только одна двойная точка, то это парабола . Если точки на бесконечности являются циклическими точками (1, i , 0) и (1, – i , 0) , то коническое сечение является окружностью . Если коэффициенты конического сечения действительны, то точки на бесконечности являются либо действительными, либо комплексно сопряженными .

Вырожденные случаи

Что следует считать вырожденным случаем конического сечения, зависит от используемого определения и геометрической настройки конического сечения. Некоторые авторы определяют коническое сечение как двумерное невырожденное квадрико. При такой терминологии вырожденных коник нет (только вырожденные квадрико), но мы будем использовать более традиционную терминологию и избегать этого определения.

В евклидовой плоскости, используя геометрическое определение, вырожденный случай возникает, когда секущая плоскость проходит через вершину конуса. Вырожденная коника — это либо: точка , когда плоскость пересекает конус только в вершине; прямая , когда плоскость касается конуса (она содержит ровно одну образующую конуса); или пара пересекающихся прямых (две образующие конуса). ^[63] Они соответствуют предельным формам эллипса, параболы и гиперболы соответственно.

Если коника в евклидовой плоскости определяется нулями квадратного уравнения (то есть как квадрика), то вырожденные коники — это: пустое множество , точка или пара прямых, которые могут быть параллельны, пересекаться в точке или совпадать. Случай пустого множества может соответствовать либо паре комплексно сопряженных параллельных прямых, таких как в уравнении, либо мнимому эллипсу , например, в уравнении Мнимый эллипс не удовлетворяет общему определению вырожденности и , таким образом, обычно не считается вырожденным. ^[64] Случай двух прямых возникает, когда квадратичное выражение разлагается на два линейных множителя, нули каждого из которых дают прямую. В случае, когда множители одинаковы, соответствующие прямые совпадают, и мы называем прямую двойной прямой (прямой с кратностью 2), и это предыдущий случай касательной секущей плоскости. ${\displaystyle x^{2}+1=0,}$ ${\displaystyle x^{2}+y^{2}+1=0.}$

В действительной проективной плоскости, поскольку параллельные прямые встречаются в точке на бесконечности, случай параллельных прямых евклидовой плоскости можно рассматривать как пересекающиеся прямые. Однако, поскольку точка пересечения является вершиной конуса, сам конус вырождается в цилиндр , т. е. с вершиной в бесконечности. Другие сечения в этом случае называются цилиндрическими сечениями . ^[65] Невырожденные цилиндрические сечения являются эллипсами (или окружностями).

При рассмотрении с точки зрения комплексной проективной плоскости вырожденные случаи действительной квадрики (т. е. квадратное уравнение имеет действительные коэффициенты) можно рассматривать как пару прямых, возможно совпадающих. Пустым множеством может быть прямая на бесконечности, рассматриваемая как двойная прямая, (действительная) точка — пересечение двух комплексно-сопряженных прямых , а другие случаи, как упоминалось ранее.

Чтобы отличить вырожденные случаи от невырожденных (включая пустое множество с последним) с помощью матричной записи, пусть β будет определителем матрицы 3 × 3 конического сечения, то есть β = ( AC − ⁠Б ²/4⁠ ) ​​Ф + ⁠КРОВАТЬ − CD ² − AE ²/4⁠ ; и пусть α = B ² − 4 AC будет дискриминантом. Тогда коническое сечение невырождено тогда и только тогда, когда β ≠ 0 . Если β = 0, мы имеем точку, когда α < 0 , две параллельные прямые (возможно, совпадающие) когда α = 0 , или две пересекающиеся прямые, когда α > 0 . ^[66]

Карандаш из коник

(Невырожденная) коника полностью определяется пятью точками в общем положении (никаких трех коллинеарных ) на плоскости, а система коник, проходящих через фиксированный набор из четырех точек (снова на плоскости и никаких трех коллинеарных), называется пучком коник . ^[67] Четыре общие точки называются базовыми точками пучка. Через любую точку, отличную от базовой точки, проходит одна коника пучка. Это понятие обобщает пучок окружностей . ^[68]

Пересечение двух конических сечений

Решения системы двух уравнений второй степени с двумя переменными можно рассматривать как координаты точек пересечения двух общих конических сечений. В частности, две коники могут не иметь ни одной, либо иметь две или четыре возможно совпадающие точки пересечения. Эффективный метод нахождения этих решений использует однородное матричное представление конических сечений , т.е. симметричную матрицу 3 × 3 , которая зависит от шести параметров.

Процедура определения точек пересечения выполняется следующим образом, где коники представлены матрицами: ^[69]

• учитывая две коники и , рассмотрим пучок коник, заданный их линейной комбинацией ${\displaystyle C_{1}}$ ${\displaystyle C_{2}}$ ${\displaystyle \lambda C_{1}+\mu C_{2}.}$
• определить однородные параметры , которые соответствуют вырожденной конике пучка. Это можно сделать, наложив условие и решив для и . Они оказываются решениями уравнения третьей степени. ${\displaystyle (\lambda ,\mu )}$ ${\displaystyle \det(\lambda C_{1}+\mu C_{2})=0}$ ${\displaystyle \lambda }$ ${\displaystyle \mu }$
• Для данной вырожденной коники определите две, возможно совпадающие, прямые, ее составляющие. ${\displaystyle C_{0}}$
• пересечь каждую идентифицированную линию с одной из двух исходных коник; этот шаг можно эффективно выполнить, используя двойственное коническое представление ${\displaystyle C_{0}}$
• точки пересечения будут представлять решения исходной системы уравнений.

Обобщения

Коники могут быть определены над другими полями (то есть в других папповских геометриях ). Однако следует соблюдать осторожность, когда поле имеет характеристику 2, поскольку некоторые формулы не могут быть использованы. Например, матричные представления, использованные выше, требуют деления на 2.

Обобщением невырожденной коники в проективной плоскости является овал . Овал — это множество точек, обладающее следующими свойствами, которые присущи коникам: 1) любая прямая не пересекает овал ни в одной, ни в одной точке, 2) в любой точке овала существует единственная касательная.

Обобщение фокусных свойств коник на случай, когда имеется более двух фокусов, приводит к множествам, называемым обобщенными кониками .

Пересечение эллиптического конуса со сферой представляет собой сферическую конику , которая имеет много общих свойств с плоскими кониками.

В других областях математики

Классификация на эллиптические, параболические и гиперболические широко распространена в математике и часто делит поле на резко различающиеся подполя. Классификация в основном возникает из-за наличия квадратичной формы (в двух переменных это соответствует связанному дискриминанту ), но может также соответствовать эксцентриситету.

Классификации квадратичных форм:

Квадратичные формы

Квадратичные формы над действительными числами классифицируются по закону инерции Сильвестра , а именно по их положительному индексу, нулевому индексу и отрицательному индексу: квадратичную форму от n переменных можно преобразовать в диагональную форму , как где число коэффициентов +1, k, является положительным индексом, число коэффициентов −1, ℓ , является отрицательным индексом, а остальные переменные являются нулевым индексом m, поэтому от двух переменных ненулевые квадратичные формы классифицируются как: ${\displaystyle x_{1}^{2}+x_{2}^{2}+\cdots +x_{k}^{2}-x_{k+1}^{2}-\cdots -x_{k+\ell }^{2},}$ ${\displaystyle k+\ell +m=n.}$

• ${\displaystyle x^{2}+y^{2}}$– положительно-определенные (отрицательные также включены), соответствующие эллипсам,
• ${\displaystyle x^{2}}$– вырожденные, соответствующие параболам, и
• ${\displaystyle x^{2}-y^{2}}$– неопределенный, соответствующий гиперболам.

В случае двух переменных квадратичные формы классифицируются по дискриминанту, аналогично коническим, но в более высоких измерениях более полезной является классификация как определенная (все положительные или все отрицательные), вырожденная (некоторые нули) или неопределенная (смесь положительных и отрицательных, но без нулей). Эта классификация лежит в основе многих последующих.

Кривизна

Гауссова кривизна поверхности описывает бесконечно малую геометрию и может быть в каждой точке либо положительной — эллиптическая геометрия , либо нулевой — евклидова геометрия (плоская, парабола), либо отрицательной — гиперболическая геометрия ; бесконечно мало, до второго порядка поверхность выглядит как график (или 0), или . Действительно, по теореме об униформизации каждая поверхность может быть принята глобально (в каждой точке) положительно искривленной, плоской или отрицательно искривленной. В более высоких измерениях тензор кривизны Римана является более сложным объектом, но многообразия с постоянной секционной кривизной являются интересными объектами изучения и имеют поразительно разные свойства, как обсуждалось в секционная кривизна . ${\displaystyle x^{2}+y^{2},}$ ${\displaystyle x^{2}}$ ${\displaystyle x^{2}-y^{2}}$

Уравнения с частными производными второго порядка

Уравнения с частными производными (УЧП) второго порядка классифицируются в каждой точке как эллиптические, параболические или гиперболические, соответственно, поскольку их члены второго порядка соответствуют эллиптической, параболической или гиперболической квадратичной форме. Поведение и теория этих различных типов УЧП разительно отличаются — показательными примерами являются то, что уравнение Пуассона является эллиптическим, уравнение теплопроводности является параболическим, а волновое уравнение является гиперболическим.

Классификации эксцентриситета включают в себя:

Преобразования Мёбиуса

Действительные преобразования Мёбиуса (элементы PSL ₂ ( R ) или его двукратного покрытия, SL ₂ ( R ) ) классифицируются как эллиптические, параболические или гиперболические соответственно, поскольку их полуслед является или зеркально отражает классификацию по эксцентриситету. ${\displaystyle 0\leq |\operatorname {tr} |/2<1,}$ ${\displaystyle |\operatorname {tr} |/2=1,}$ ${\displaystyle |\operatorname {tr} |/2>1,}$

Отношение дисперсии к среднему значению

Отношение дисперсии к среднему классифицирует несколько важных семейств дискретных распределений вероятностей : постоянное распределение как круговое (эксцентриситет 0), биномиальные распределения как эллиптические, распределения Пуассона как параболические и отрицательные биномиальные распределения как гиперболические. Это подробно рассматривается в кумулянтах некоторых дискретных распределений вероятностей .

В этом интерактивном SVG-изображении перемещайтесь влево и вправо по SVG-изображению, чтобы вращать двойной конус.

Смотрите также

• Конфокальные конические сечения
• Циркумконический и инконический
• Директорский круг
• Эллиптическая система координат
• Равноудалённый набор
• Параболические координаты
• Квадратичная функция
• Сферический конический

Примечания

1. Пустое множество включено как вырожденная коника, поскольку оно может возникнуть как решение этого уравнения.
2. Согласно Плутарху , это решение было отвергнуто Платоном на том основании, что его нельзя было получить, используя только линейку и циркуль, однако эта интерпретация утверждения Плутарха подверглась критике. Boyer 2004, стр. 14, сноска 14.
3. Эта форма уравнения не обобщается на поля характеристики два.
4. Рассмотрим нахождение середины отрезка прямой, одна из конечных точек которого находится на бесконечности.
5. Коксетер и несколько других авторов используют термин «самосопряженный» вместо «абсолютный».

Ссылки

1. Ивс 1963, стр. 319
2. Браннан, Эсплен и Грей 1999, с. 13
3. Коэн, Д., Предварительное исчисление: с тригонометрией единичной окружности ( Стэмфорд : Thomson Brooks/Cole , 2006), стр. 844.
4. Томас и Финни 1979, стр. 434
5. Браннан, Эсплен и Грей 1999, с. 19; Кендиг 2005, стр. 86, 141.
6. Браннан, Эсплен и Грей 1999, стр. 13–16.
7. Браннан, Эсплен и Грей 1999, стр. 11–16.
8. Проттер и Морри 1970, стр. 314–328, 585–589.
9. Проттер и Морри 1970, стр. 290–314.
10. Уилсон и Трейси 1925, стр. 130
11. Проттер и Морри 1970, с. 316
12. Браннан, Эсплен и Грей 1999, с. 30
13. Фанчи, Джон Р. (2006), Освежение знаний по математике для ученых и инженеров, John Wiley and Sons, стр. 44–45, ISBN 0-471-75715-2, Раздел 3.2, стр. 45
14. Проттер и Морри 1970, с. 326
15. Уилсон и Трейси 1925, стр. 153
16. Петтофреццо, Энтони, Матрицы и преобразования , Dover Publ., 1966, стр. 110.
17. Spain, B., Analytical Conics (Mineola, NY: Dover, 2007). Первоначально опубликовано в 1957 году издательством Pergamon .
18. Аюб, Аюб Б., «Эксцентриситет конического сечения», The College Mathematics Journal 34(2), март 2003 г., 116–121.
19. Аюб, А.Б., «Повторный взгляд на центральные конические сечения», Mathematics Magazine 66(5), 1993, 322–325.
20. Браннан, Эсплен и Грей 1999, с. 17
21. Уитворт, Уильям Аллен . Трилинейные координаты и другие методы современной аналитической геометрии двух измерений , Forgotten Books, 2012 (оригинал Deighton, Bell, and Co., 1866), стр. 203.
22. Pamfilos, Париж (2014). «Галерея коник по пяти элементам» (PDF) . Forum Geometricorum . 14 : 295–348.
23. Браннан, Эсплен и Грей 1999, с. 28
24. Даунс 2003, стр. 36 и далее.
25. Бойер 2004, стр. 17–18.
26. Бойер 2004, стр. 18
27. Кац 1998, стр. 117
28. Хит, Т.Л., Тринадцать книг «Начал» Евклида , т. I, Дувр, 1956, стр. 16.
29. Ивс 1963, стр. 28
30. Аполлоний Пергский, «Трактат о конических сечениях», под редакцией Т. Л. Хита (Кембридж: Издательство Кембриджского университета, 2013).
31. Ивс 1963, стр. 30.
32. Бойер 2004, стр. 36.
33. Тернер, Говард Р. (1997). Наука в средневековом исламе: иллюстрированное введение. Издательство Техасского университета . стр. 53. ISBN 0-292-78149-0.
34. Бойер, К. Б. и Мерцбах, У. К. , История математики ( Хобокен : John Wiley & Sons, Inc. , 1968), стр. 219.
35. Ван дер Варден, Б.Л. , Геометрия и алгебра в древних цивилизациях ( Берлин / Гейдельберг : Springer Verlag , 1983), стр. 73.
36. Сидоли, Натан; Бруммелен, Глен Ван (2013-10-30). Из Александрии через Багдад: обзоры и исследования древнегреческих и средневековых исламских математических наук в честь Дж. Л. Берггрена . Springer Science & Business Media. стр. 110. ISBN 978-3-642-36736-6.
37. Waerden, Bartel L. van der (2013-06-29). История алгебры: от аль-Хорезми до Эмми Нётер . Springer Science & Business Media. стр. 29. ISBN 978-3-642-51599-6.
38. Стиллвелл, Джон (2010). Математика и ее история (3-е изд.). Нью-Йорк: Springer. С. 30. ISBN 978-1-4419-6052-8.
39. "Аполлоний Пергский Конические книги с первой по седьмую" (PDF) . Архивировано из оригинала (PDF) 17 мая 2013 года . Получено 10 июня 2011 года .
40. Кац 1998, стр. 126.
41. Бойер 2004, стр. 110.
42. Boyer 2004, стр. 114.
43. Браннан, Эсплен и Грей 1999, с. 27
44. Artzy 2008, стр. 158, Thm 3-5.1
45. Арци 2008, стр. 159
46. Фолкнер 1952, стр. 71
47. Фолкнер 1952, стр. 72
48. Ивс 1963, стр. 320
49. Коксетер 1993, стр. 80
50. Хартманн, стр. 38
51. Мерсерв 1983, стр. 65
52. Vorlesungen über Synthetische Geometrie Якоба Штайнера , Б. Г. Тойбнер, Лейпциг, 1867 г. (из Google Книги: (немецкий) Часть II следует за Частью I), Часть II, стр. 96
53. Хартманн, стр. 19
54. Фолкнер 1952, стр. 48–49.
55. Коксетер 1964, стр. 60
56. Коксетер 1964, стр. 80
57. Фолкнер 1952, стр. 52–53.
58. Даунс 2003, стр. 5
59. Даунс 2003, стр. 14
60. Даунс 2003, стр. 19
61. Акопян и Заславский 2007, стр. 70
62. Вильчинский, Э. Дж. (1916), «Некоторые замечания об историческом развитии и будущих перспективах дифференциальной геометрии плоских кривых», Bull. Amer. Math. Soc. , 22 (7): 317–329, doi : 10.1090/s0002-9904-1916-02785-6.
63. Браннан, Эсплен и Грей 1999, с. 6
64. Корн, GA, & Корн, TM , Математический справочник для ученых и инженеров: определения, теоремы и формулы для справки и обзора ( Mineola, NY : Dover Publications , 1961), стр. 42.
65. "MathWorld: Цилиндрическое сечение".
66. Лоуренс, Дж. Деннис (1972), Каталог специальных плоских кривых , Довер, стр. 63, ISBN 0-486-60288-5
67. Фолкнер 1952, стр. 64.
68. Бергер, М. , Раскрытая геометрия: лестница Иакова к современной высшей геометрии (Берлин/Гейдельберг: Springer, 2010), стр. 127.
69. Рихтер-Геберт 2011, стр. 196

Библиография

• Акопян, АВ; Заславский, АА (2007). Геометрия конических сечений . Американское математическое общество . ISBN 978-0-8218-4323-9.
• Арци, Рафаэль (2008) [1965], Линейная геометрия , Дувр, ISBN 978-0-486-46627-9
• Бойер, Карл Б. (2004) [1956], История аналитической геометрии, Дувр, ISBN 978-0-486-43832-0
• Бреннан, Дэвид А.; Эсплен, Мэтью Ф.; Грей, Джереми Дж. (1999), Геометрия, Cambridge University Press, ISBN 978-0-521-59787-6
• Коксетер, HSM (1964), Проективная геометрия, Блейсделл, ISBN 9780387406237
• Коксетер, HSM (1993), Реальная проективная плоскость , Springer Science & Business Media
• Даунс, Дж. В. (2003) [1993], Практические конические сечения: геометрические свойства эллипсов, парабол и гипербол, Довер, ISBN 0-486-42876-1
• Ивс, Говард (1963), Обзор геометрии (Том первый) , Бостон: Аллин и Бэкон
• Глезер, Георг; Штахель, Хельмут; Оденал, Борис (2016), Вселенная конических сечений: от древних греков до достижений 21-го века , Берлин: Springer
• Хартманн, Эрих, Плоская круговая геометрия, введение в плоскости Мёбиуса, Лагерра и Минковского (PDF) , получено 20 сентября 2014 г.(PDF; 891 кБ).
• Кац, Виктор Дж. (1998), История математики / Введение (2-е изд.), Эддисон Уэсли Лонгман, ISBN 978-0-321-01618-8
• Кендиг, Кит (2005), Конические многоугольники , Математическая ассоциация Америки , ISBN 978-0-88385-335-1
• Фолкнер, TE (1952), Проективная геометрия (2-е изд.), Эдинбург: Oliver and Boyd, ISBN 9780486154893
• Мерсерв, Брюс Э. (1983) [1959], Основные понятия геометрии, Дувр, ISBN 0-486-63415-9
• Проттер, Мюррей Х.; Моррей, Чарльз Б. младший (1970), College Calculus with Analytic Geometry (2-е изд.), Reading: Addison-Wesley , LCCN  76087042
• Richter-Gebert, Jürgen (2011). Перспективы проективной геометрии: путеводитель по реальной и комплексной геометрии . Springer. ISBN 9783642172854.
• Сэмюэл, Пьер (1988), Проективная геометрия , Тексты для бакалавров по математике (Лекции по математике), Нью-Йорк: Springer-Verlag, ISBN 0-387-96752-4
• Томас, Джордж Б.; Финни, Росс Л. (1979), Исчисление и аналитическая геометрия (пятое изд.), Addison-Wesley, стр. 434, ISBN 0-201-07540-7
• Уилсон, WA; Трейси, JI (1925), Аналитическая геометрия (пересмотренное издание), DC Heath and Company

Внешние ссылки

• Вайсштейн, Эрик В. «Коническое сечение». MathWorld .
• Встречаемость коник. Коники в природе и в других местах.