Квантовые вычисления

Технология, использующая квантовую механику

Представление кубита в виде сферы Блоха . Состояние — это точка на поверхности сферы, на полпути между полюсами и . ${\displaystyle |\psi \rangle =\alpha |0\rangle +\beta |1\rangle }$ ${\displaystyle |0\rangle }$ ${\displaystyle |1\rangle }$

Квантовый компьютер — это компьютер , который использует квантово-механические явления. В малых масштабах физическая материя проявляет свойства как частиц, так и волн , и квантовые вычисления используют это поведение с помощью специализированного оборудования. Классическая физика не может объяснить работу этих квантовых устройств, а масштабируемый квантовый компьютер мог бы выполнять некоторые вычисления экспоненциально быстрее ^[a], чем любой современный «классический» компьютер. Теоретически крупномасштабный квантовый компьютер мог бы взломать некоторые широко используемые схемы шифрования и помочь физикам в выполнении физических симуляций ; однако, текущее состояние дел в значительной степени экспериментально и непрактично, с несколькими препятствиями для полезных приложений.

Основная единица информации в квантовых вычислениях, кубит (или «квантовый бит»), выполняет ту же функцию, что и бит в классических вычислениях. Однако, в отличие от классического бита, который может находиться в одном из двух состояний (двоичном ) , кубит может существовать в суперпозиции своих двух «базисных» состояний, что в общих чертах означает, что он находится в обоих состояниях одновременно. При измерении кубита результатом является вероятностный выход классического бита. Если квантовый компьютер манипулирует кубитом определенным образом, эффекты интерференции волн могут усилить желаемые результаты измерений. Разработка квантовых алгоритмов включает создание процедур, которые позволяют квантовому компьютеру выполнять вычисления эффективно и быстро.

Квантовые компьютеры пока не пригодны для реальной работы. Физическая разработка высококачественных кубитов оказалась сложной задачей. Если физический кубит недостаточно изолирован от окружающей среды, он страдает от квантовой декогеренции , внося шум в вычисления. Национальные правительства вложили значительные средства в экспериментальные исследования, направленные на разработку масштабируемых кубитов с более длительным временем когерентности и более низким уровнем ошибок. Примерами реализаций являются сверхпроводники (которые изолируют электрический ток , устраняя электрическое сопротивление ) и ионные ловушки (которые удерживают одну атомную частицу с помощью электромагнитных полей ).

В принципе, классический компьютер может решать те же вычислительные задачи, что и квантовый компьютер, если дать ему достаточно времени. Квантовое преимущество проявляется в форме временной сложности, а не вычислимости , и теория квантовой сложности показывает, что некоторые квантовые алгоритмы экспоненциально эффективнее самых известных классических алгоритмов. Крупномасштабный квантовый компьютер теоретически может решать вычислительные задачи, неразрешимые классическим компьютером за любое разумное время. Эта концепция дополнительных возможностей была названа « квантовым превосходством ». Хотя такие заявления привлекли значительное внимание к дисциплине, практические случаи ее использования в краткосрочной перспективе остаются ограниченными.

История

В течение многих лет области квантовой механики и компьютерной науки формировали отдельные академические сообщества. ^[1] Современная квантовая теория была разработана в 1920-х годах для объяснения дуализма волна-частица, наблюдаемого в атомных масштабах, ^[2] а цифровые компьютеры появились в последующие десятилетия, чтобы заменить человеческие компьютеры для утомительных вычислений. ^[3] Обе дисциплины имели практическое применение во время Второй мировой войны ; компьютеры играли важную роль в военной криптографии , ^[4] а квантовая физика была необходима для ядерной физики, используемой в Манхэттенском проекте . ^[5]

Когда физики применили квантово-механические модели к вычислительным задачам и заменили цифровые биты на кубиты , области квантовой механики и компьютерной науки начали сближаться. В 1980 году Пол Бениофф представил квантовую машину Тьюринга , которая использует квантовую теорию для описания упрощенного компьютера. ^[6] Когда цифровые компьютеры стали быстрее, физики столкнулись с экспоненциальным ростом накладных расходов при моделировании квантовой динамики , ^[7] что побудило Юрия Манина и Ричарда Фейнмана независимо друг от друга предположить, что аппаратное обеспечение, основанное на квантовых явлениях, может быть более эффективным для компьютерного моделирования. ^{[8] [9] [10]} В статье 1984 года Чарльз Беннетт и Жиль Брассар применили квантовую теорию к протоколам криптографии и продемонстрировали, что квантовое распределение ключей может повысить информационную безопасность . ^{[11] [12]}

Затем появились квантовые алгоритмы для решения проблем оракула , такие как алгоритм Дойча в 1985 году, ^[13] алгоритм Бернштейна-Вазирани в 1993 году, ^[14] и алгоритм Саймона в 1994 году. ^[15] Эти алгоритмы не решали практических задач, но математически демонстрировали, что можно получить больше информации, запросив черный ящик с квантовым состоянием в суперпозиции , что иногда называют квантовым параллелизмом . ^[16]

Питер Шор (на фото 2017 года) в 1994 году показал, что масштабируемый квантовый компьютер сможет взломать шифрование RSA .

Питер Шор развил эти результаты в своем алгоритме 1994 года для взлома широко используемых протоколов шифрования RSA и Диффи-Хеллмана , ^[17] который привлек значительное внимание к области квантовых вычислений. ^[18] В 1996 году алгоритм Гровера установил квантовое ускорение для широко применяемой задачи неструктурированного поиска. ^{[19] [20]} В том же году Сет Ллойд доказал, что квантовые компьютеры могут моделировать квантовые системы без экспоненциальных накладных расходов, присутствующих в классических симуляциях, ^[21] подтвердив гипотезу Фейнмана 1982 года. ^[22]

На протяжении многих лет экспериментаторы создавали небольшие квантовые компьютеры, используя захваченные ионы и сверхпроводники . ^[23] В 1998 году двухкубитный квантовый компьютер продемонстрировал осуществимость технологии, ^{[24] [25]} а последующие эксперименты увеличили количество кубитов и снизили частоту ошибок. ^[23]

В 2019 году Google AI и NASA объявили, что достигли квантового превосходства с помощью 54-кубитной машины, выполнив вычисления, которые невозможны для любого классического компьютера. ^{[26] [27] [28]} Однако обоснованность этого утверждения все еще активно исследуется. ^{[29] [30]}

В декабре 2023 года физики впервые сообщили о запутанности отдельных молекул, которая может иметь важное применение в квантовых вычислениях. ^[31]

Квантовая обработка информации

Инженеры-компьютерщики обычно описывают работу современного компьютера в терминах классической электродинамики . В этих «классических» компьютерах некоторые компоненты (например, полупроводники и генераторы случайных чисел ) могут полагаться на квантовое поведение, но эти компоненты не изолированы от своего окружения, поэтому любая квантовая информация быстро декогерирует . В то время как программисты могут полагаться на теорию вероятностей при разработке рандомизированного алгоритма , квантово-механические понятия, такие как суперпозиция и интерференция, в значительной степени не имеют отношения к анализу программ .

Квантовые программы , напротив, полагаются на точное управление когерентными квантовыми системами. Физики описывают эти системы математически, используя линейную алгебру . Комплексные числа моделируют амплитуды вероятности , векторы моделируют квантовые состояния , а матрицы моделируют операции, которые могут быть выполнены над этими состояниями. Программирование квантового компьютера, таким образом, является вопросом составления операций таким образом, чтобы полученная программа вычисляла полезный результат в теории и была реализуема на практике.

Как описывает физик Чарли Беннетт взаимосвязь между квантовыми и классическими компьютерами, ^[32]

Классический компьютер — это квантовый компьютер... поэтому мы не должны спрашивать: «Откуда берутся квантовые ускорения?» Мы должны сказать: «Ну, все компьютеры квантовые. ... Откуда берутся классические замедления?»

Квантовая информация

Так же, как бит является основным понятием классической теории информации, кубит является фундаментальной единицей квантовой информации . Один и тот же термин кубит используется для обозначения абстрактной математической модели и любой физической системы, представленной этой моделью. Классический бит, по определению, существует в одном из двух физических состояний, которые можно обозначить как 0 и 1. Кубит также описывается состоянием, и два состояния часто записываются и служат квантовыми аналогами классических состояний 0 и 1. Однако квантовые состояния и принадлежат векторному пространству , что означает, что их можно умножать на константы и складывать вместе, и результатом снова является допустимое квантовое состояние. Такая комбинация известна как суперпозиция и . [ ^{33] [34]} ${\displaystyle |0\rangle }$ ${\displaystyle |1\rangle }$ ${\displaystyle |0\rangle }$ ${\displaystyle |1\rangle }$ ${\displaystyle |0\rangle }$ ${\displaystyle |1\rangle }$

Двумерный вектор математически представляет состояние кубита. Физики обычно используют обозначение Дирака для квантово-механической линейной алгебры , записывая « ket psi » для вектора, помеченного . Поскольку кубит является системой с двумя состояниями, любое состояние кубита принимает вид , где и являются стандартными базисными состояниями , ^[b] а и являются амплитудами вероятности , которые в общем случае являются комплексными числами . ^[34] Если либо или равно нулю, кубит фактически является классическим битом; когда оба не равны нулю, кубит находится в суперпозиции. Такой вектор квантового состояния действует аналогично (классическому) вектору вероятности , с одним ключевым отличием: в отличие от вероятностей, амплитуды вероятности не обязательно являются положительными числами. ^[36] Отрицательные амплитуды допускают деструктивную интерференцию волн. ${\displaystyle |\psi \rangle }$ ${\displaystyle \psi }$ ${\displaystyle \alpha |0\rangle +\beta |1\rangle }$ ${\displaystyle |0\rangle }$ ${\displaystyle |1\rangle }$ ${\displaystyle \alpha }$ ${\displaystyle \beta }$ ${\displaystyle \alpha }$ ${\displaystyle \beta }$

Когда кубит измеряется в стандартном базисе , результатом является классический бит. Правило Борна описывает квадратичное соответствие между амплитудами и вероятностями — при измерении кубита состояние коллапсирует до с вероятностью , или до с вероятностью . Любое допустимое состояние кубита имеет коэффициенты и такие, что . Например, измерение кубита даст либо или с равной вероятностью. ${\displaystyle \alpha |0\rangle +\beta |1\rangle }$ ${\displaystyle |0\rangle }$ ${\displaystyle |\alpha |^{2}}$ ${\displaystyle |1\rangle }$ ${\displaystyle |\beta |^{2}}$ ${\displaystyle \alpha }$ ${\displaystyle \beta }$ ${\displaystyle |\alpha |^{2}+|\beta |^{2}=1}$ ${\displaystyle 1/{\sqrt {2}}|0\rangle +1/{\sqrt {2}}|1\rangle }$ ${\displaystyle |0\rangle }$ ${\displaystyle |1\rangle }$

Каждый дополнительный кубит удваивает размерность пространства состояний . ^[35] Например, вектор ⁠1/√2⁠ |00⟩ + ⁠1/√2⁠ |01⟩ представляет двухкубитное состояние, тензорное произведение кубита |0⟩ на кубит ⁠1/√2⁠ |0⟩ + ⁠1/√2⁠ |1⟩ . Этот вектор занимает четырехмерное векторное пространство , охватывающее базисные векторы |00⟩ , |01⟩ , |10⟩ , и |11⟩ . Состояние Белла ⁠1/√2⁠ |00⟩ + ⁠1/√2⁠ |11⟩ невозможно разложить на тензорное произведение двух отдельных кубитов — два кубита запутаны , поскольку их амплитуды вероятности коррелируют . В общем случае векторное пространство для системы из n кубитов имеет размерность 2 ⁿ , и это затрудняет моделирование квантовой системы на классическом компьютере: для представления системы из 100 кубитов требуется хранить 2 ¹⁰⁰ классических значений.

Унитарные операторы

Состояние этой однокубитовой квантовой памяти можно изменять, применяя квантовые логические вентили , аналогично тому, как можно изменять классическую память с помощью классических логических вентилей . Одним из важных вентилей как для классических, так и для квантовых вычислений является вентиль НЕ, который может быть представлен матрицей . Математически применение такого логического вентиля к вектору квантового состояния моделируется с помощью умножения матриц . Таким образом $${\displaystyle X:={\begin{pmatrix}0&1\\1&0\end{pmatrix}}.}$$

${\displaystyle X|0\rangle =|1\rangle }$и . ${\displaystyle X|1\rangle =|0\rangle }$

Математику однокубитных вентилей можно расширить для работы с многокубитной квантовой памятью двумя важными способами. Один способ — просто выбрать кубит и применить этот вентиль к целевому кубиту, оставив остальную часть памяти нетронутой. Другой способ — применить вентиль к его цели только в том случае, если другая часть памяти находится в желаемом состоянии. Эти два варианта можно проиллюстрировать с помощью другого примера. Возможные состояния двухкубитной квантовой памяти: Управляемый вентиль НЕ (CNOT) можно представить с помощью следующей матрицы: Как математическое следствие этого определения, , , , и . Другими словами, CNOT применяет вентиль НЕ ( из предыдущего) ко второму кубиту тогда и только тогда, когда первый кубит находится в состоянии . Если первый кубит находится в состоянии , то ничего не происходит ни с одним из кубитов. $${\displaystyle |00\rangle :={\begin{pmatrix}1\\0\\0\\0\end{pmatrix}};\quad |01\rangle :={\begin{pmatrix}0\\1\\0\\0\end{pmatrix}};\quad |10\rangle :={\begin{pmatrix}0\\0\\1\\0\end{pmatrix}};\quad |11\rangle :={\begin{pmatrix}0\\0\\0\\1\end{pmatrix}}.}$$ $${\displaystyle \operatorname {CNOT} :={\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&0&1\\0&0&1&0\end{pmatrix}}.}$$ ${\textstyle \operatorname {CNOT} |00\rangle =|00\rangle }$ ${\textstyle \operatorname {CNOT} |01\rangle =|01\rangle }$ ${\textstyle \operatorname {CNOT} |10\rangle =|11\rangle }$ ${\textstyle \operatorname {CNOT} |11\rangle =|10\rangle }$ ${\textstyle X}$ ${\textstyle |1\rangle }$ ${\textstyle |0\rangle }$

Подводя итог, квантовые вычисления можно описать как сеть квантовых логических вентилей и измерений. Однако любое измерение может быть отложено до конца квантовых вычислений, хотя эта отсрочка может потребовать вычислительных затрат, поэтому большинство квантовых схем представляют собой сеть, состоящую только из квантовых логических вентилей и без измерений.

Квантовый параллелизм

Квантовый параллелизм — это эвристика, согласно которой квантовые компьютеры можно рассматривать как оценивающие функцию для нескольких входных значений одновременно. Этого можно достичь, подготовив квантовую систему в суперпозиции входных состояний и применив унитарное преобразование, которое кодирует оцениваемую функцию. Результирующее состояние кодирует выходные значения функции для всех входных значений в суперпозиции, что позволяет вычислять несколько выходов одновременно. Это свойство является ключевым для ускорения многих квантовых алгоритмов. Однако «параллелизм» в этом смысле недостаточен для ускорения вычисления, поскольку измерение в конце вычисления дает только одно значение. Чтобы быть полезным, квантовый алгоритм должен также включать в себя какой-то другой концептуальный ингредиент. ^{[37] [38]}

Квантовое программирование

Существует ряд моделей квантовых вычислений, различающихся по основным элементам, на которые разлагается вычисление.

Вентильная матрица

Квантовая схема, реализующая вентили Тоффоли из более примитивных вентилей

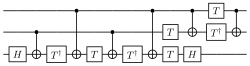
Квантовая матрица вентилей разлагает вычисления на последовательность квантовых вентилей с несколькими кубитами . Квантовое вычисление можно описать как сеть квантовых логических вентилей и измерений. Однако любое измерение может быть отложено до конца квантового вычисления, хотя эта отсрочка может потребовать вычислительных затрат, поэтому большинство квантовых схем представляют собой сеть, состоящую только из квантовых логических вентилей и без измерений.

Любое квантовое вычисление (которое в приведенном выше формализме является любой унитарной матрицей размера над кубитами) может быть представлено как сеть квантовых логических вентилей из довольно небольшого семейства вентилей. Выбор семейства вентилей, который позволяет эту конструкцию, известен как универсальный набор вентилей , поскольку компьютер, который может запускать такие схемы, является универсальным квантовым компьютером . Один из таких общих наборов включает все однокубитные вентили, а также вентиль CNOT, указанный выше. Это означает, что любое квантовое вычисление может быть выполнено путем выполнения последовательности однокубитных вентилей вместе с вентилями CNOT. Хотя этот набор вентилей бесконечен, его можно заменить конечным набором вентилей, обратившись к теореме Соловея-Китаева . Реализация булевых функций с использованием малокубитных квантовых вентилей представлена ​​здесь. ^[39] ${\displaystyle 2^{n}\times 2^{n}}$ ${\displaystyle n}$

Квантовые вычисления на основе измерений

Квантовый компьютер, основанный на измерениях, разлагает вычисления на последовательность измерений состояния Белла и однокубитовых квантовых вентилей, применяемых к сильно запутанному начальному состоянию ( состоянию кластера ), используя технику, называемую телепортацией квантовых вентилей .

Адиабатические квантовые вычисления

Адиабатический квантовый компьютер , основанный на квантовом отжиге , разлагает вычисления на медленное непрерывное преобразование начального гамильтониана в конечный гамильтониан, основные состояния которого содержат решение. ^[40]

Нейроморфные квантовые вычисления

Нейроморфные квантовые вычисления (сокращенно «n.quantum computing») — это нетрадиционный тип вычислений, который использует нейроморфные вычисления для выполнения квантовых операций. Было высказано предположение, что квантовые алгоритмы , которые являются алгоритмами, работающими на реалистичной модели квантовых вычислений, могут быть вычислены одинаково эффективно с помощью нейроморфных квантовых вычислений. И традиционные квантовые вычисления, и нейроморфные квантовые вычисления являются нетрадиционными вычислительными подходами к вычислениям, основанными на физике, и не следуют архитектуре фон Неймана . Они оба создают систему (схему), которая представляет рассматриваемую физическую проблему, а затем используют соответствующие физические свойства системы для поиска «минимума». Нейроморфные квантовые вычисления и квантовые вычисления имеют схожие физические свойства во время вычислений.

Топологические квантовые вычисления

Топологический квантовый компьютер разлагает вычисления на сплетение анионов в двумерной решетке. ^[41]

Квантовая машина Тьюринга

Квантовая машина Тьюринга — это квантовый аналог машины Тьюринга . ^[6] Все эти модели вычислений — квантовые схемы, ^[42] односторонние квантовые вычисления , ^[43] адиабатические квантовые вычисления, ^[44] и топологические квантовые вычисления ^[45] — как было показано, эквивалентны квантовой машине Тьюринга; при условии идеальной реализации одного такого квантового компьютера он может моделировать все остальные с не более чем полиномиальными накладными расходами. Эта эквивалентность не обязательно должна соблюдаться для практических квантовых компьютеров, поскольку накладные расходы на моделирование могут быть слишком большими, чтобы быть практичными.

Шумные квантовые вычисления среднего масштаба

Пороговая теорема показывает , как увеличение числа кубитов может смягчить ошибки, ^[46] однако полностью отказоустойчивые квантовые вычисления остаются «довольно далекой мечтой». ^[47] По мнению некоторых исследователей, шумные квантовые машины среднего масштаба ( NISQ ) могут иметь специализированное применение в ближайшем будущем, но шум в квантовых вентилях ограничивает их надежность. ^[47] Ученые из Гарвардского университета успешно создали «квантовые схемы», которые исправляют ошибки более эффективно, чем альтернативные методы, что потенциально может устранить главное препятствие для практических квантовых компьютеров. ^{[48] [49]} Исследовательская группа Гарварда была поддержана MIT , QuEra Computing , Caltech и Принстонским университетом и финансировалась программой DARPA Optimization with Noisy Intermediate-Scale Quantum devices (ONISQ). ^{[50] [51]}

Квантовая криптография и кибербезопасность

Пример схемы квантовой криптосистемы

Квантовые вычисления имеют значительный потенциал применения в области криптографии и кибербезопасности. Квантовая криптография, которая опирается на принципы квантовой механики, предлагает возможность защищенных каналов связи, устойчивых к подслушиванию. Протоколы квантового распределения ключей (QKD), такие как BB84, обеспечивают безопасный обмен криптографическими ключами между сторонами, гарантируя конфиденциальность и целостность связи. Более того, квантовые генераторы случайных чисел (QRNG) могут производить высококачественные случайные числа, которые необходимы для безопасного шифрования.

Однако квантовые вычисления также создают проблемы для традиционных криптографических систем. Алгоритм Шора , квантовый алгоритм для факторизации целых чисел, потенциально может взломать широко используемые схемы криптографии с открытым ключом, такие как RSA, которые полагаются на сложность факторизации больших чисел. Постквантовая криптография, которая включает разработку криптографических алгоритмов, устойчивых к атакам как классических, так и квантовых компьютеров, является активной областью исследований, направленных на решение этой проблемы.

Текущие исследования в области квантовой криптографии и постквантовой криптографии имеют решающее значение для обеспечения безопасности коммуникации и данных в условиях развивающихся возможностей квантовых вычислений. Достижения в этих областях, такие как разработка новых протоколов QKD, улучшение QRNG и стандартизация постквантовых криптографических алгоритмов, будут играть ключевую роль в поддержании целостности и конфиденциальности информации в квантовую эпоху. ^[52]

Коммуникация

Квантовая криптография открывает новые способы безопасной передачи данных; например, квантовое распределение ключей использует запутанные квантовые состояния для установления безопасных криптографических ключей . ^[53] Когда отправитель и получатель обмениваются квантовыми состояниями, они могут гарантировать, что злоумышленник не перехватит сообщение, поскольку любой несанкционированный перехватчик нарушит деликатную квантовую систему и внесет обнаруживаемые изменения. ^[54] С помощью соответствующих криптографических протоколов отправитель и получатель могут таким образом установить общую конфиденциальную информацию, устойчивую к перехвату. ^{[11] [55]}

Современные волоконно-оптические кабели могут передавать квантовую информацию на относительно короткие расстояния. Текущие экспериментальные исследования направлены на разработку более надежного оборудования (например, квантовых повторителей), в надежде масштабировать эту технологию до квантовых сетей на большие расстояния с сквозной запутанностью. Теоретически это может позволить новые технологические приложения, такие как распределенные квантовые вычисления и улучшенное квантовое зондирование . ^{[56] [57]}

Алгоритмы

Прогресс в поиске квантовых алгоритмов обычно фокусируется на этой модели квантовой цепи, хотя существуют исключения, такие как квантовый адиабатический алгоритм . Квантовые алгоритмы можно грубо классифицировать по типу ускорения, достигнутого по сравнению с соответствующими классическими алгоритмами. ^[58]

Квантовые алгоритмы, которые предлагают более чем полиномиальное ускорение по сравнению с самым известным классическим алгоритмом, включают алгоритм Шора для факторизации и связанные с ним квантовые алгоритмы для вычисления дискретных логарифмов , решения уравнения Пелля и, в более общем плане, решения проблемы скрытой подгруппы для абелевых конечных групп. ^[58] Эти алгоритмы зависят от примитива квантового преобразования Фурье . Не было найдено математического доказательства, показывающего, что столь же быстрый классический алгоритм не может быть обнаружен, но данные свидетельствуют о том, что это маловероятно. ^[59] Некоторые проблемы оракула, такие как проблема Саймона и проблема Бернштейна–Вазирани , действительно дают доказуемое ускорение, хотя это относится к модели квантовых запросов , которая является ограниченной моделью, где нижние границы гораздо проще доказать и не обязательно переводится в ускорение для практических задач.

Другие проблемы, включая моделирование квантовых физических процессов из химии и физики твердого тела, аппроксимацию определенных полиномов Джонса и квантовый алгоритм для линейных систем уравнений, имеют квантовые алгоритмы, которые, по-видимому, дают суперполиномиальное ускорение и являются BQP -полными. Поскольку эти проблемы являются BQP-полными, столь же быстрый классический алгоритм для них подразумевал бы, что никакой квантовый алгоритм не дает суперполиномиального ускорения, что считается маловероятным. ^[60]

Некоторые квантовые алгоритмы, такие как алгоритм Гровера и амплитудное усиление , дают полиномиальное ускорение по сравнению с соответствующими классическими алгоритмами. ^[58] Хотя эти алгоритмы дают сравнительно скромное квадратичное ускорение, они широко применимы и, таким образом, дают ускорение для широкого круга задач. ^[20]

Моделирование квантовых систем

Поскольку химия и нанотехнологии опираются на понимание квантовых систем, а такие системы невозможно эффективно моделировать классически, квантовое моделирование может быть важным применением квантовых вычислений. ^[61] Квантовое моделирование также может использоваться для моделирования поведения атомов и частиц в необычных условиях, таких как реакции внутри коллайдера . ^[62] В июне 2023 года ученые-компьютерщики IBM сообщили, что квантовый компьютер показал лучшие результаты для физической задачи, чем обычный суперкомпьютер. ^{[63] [64]}

Около 2% ежегодного мирового производства энергии используется для фиксации азота с целью производства аммиака для процесса Габера в сельскохозяйственной промышленности удобрений (хотя встречающиеся в природе организмы также производят аммиак). Квантовое моделирование может быть использовано для понимания этого процесса и повышения энергоэффективности производства. ^[65] Ожидается, что ранним применением квантовых вычислений станет моделирование, которое повысит эффективность процесса Габера-Боша ^[66] к середине 2020-х годов ^[67], хотя некоторые предсказывают, что это займет больше времени. ^[68]

Постквантовая криптография

Известное применение квантовых вычислений — атаки на криптографические системы, которые в настоящее время используются. Факторизация целых чисел , которая лежит в основе безопасности криптографических систем с открытым ключом , считается вычислительно невыполнимой с помощью обычного компьютера для больших целых чисел, если они являются произведением нескольких простых чисел (например, произведениями двух 300-значных простых чисел). ^[69] Для сравнения, квантовый компьютер мог бы решить эту задачу экспоненциально быстрее, используя алгоритм Шора для нахождения ее множителей. ^[70] Эта способность позволила бы квантовому компьютеру взломать многие из криптографических систем, используемых сегодня, в том смысле, что существовал бы алгоритм с полиномиальным временем (по количеству цифр целого числа) для решения этой задачи. В частности, большинство популярных шифров с открытым ключом основаны на трудности факторизации целых чисел или задаче дискретного логарифма , обе из которых могут быть решены алгоритмом Шора. В частности, могут быть взломаны алгоритмы RSA , Диффи-Хеллмана и эллиптической кривой Диффи-Хеллмана . Они используются для защиты защищенных веб-страниц, зашифрованной электронной почты и многих других типов данных. Их взлом будет иметь значительные последствия для электронной конфиденциальности и безопасности.

Выявление криптографических систем, которые могут быть защищены от квантовых алгоритмов, является активно исследуемой темой в области постквантовой криптографии . ^{[71] [72]} Некоторые алгоритмы с открытым ключом основаны на проблемах, отличных от задач факторизации целых чисел и дискретного логарифмирования, к которым применяется алгоритм Шора, например, криптосистема Мак-Элиса , основанная на проблеме в теории кодирования . ^{[71] [73]} Также неизвестно, взламываются ли криптосистемы на основе решеток квантовыми компьютерами, и нахождение алгоритма полиномиального времени для решения задачи о скрытой подгруппе диэдра , который взломал бы многие криптосистемы на основе решеток, является хорошо изученной открытой проблемой. ^[74] Было доказано, что применение алгоритма Гровера для взлома симметричного (секретного ключа) алгоритма методом грубой силы требует времени, равного примерно 2 ^{n /2} вызовов базового криптографического алгоритма, по сравнению с примерно 2 ⁿ в классическом случае, ^[75] что означает, что длина симметричного ключа фактически уменьшается вдвое: AES-256 будет иметь такую ​​же защиту от атаки с использованием алгоритма Гровера, как AES-128 имеет от классического поиска методом грубой силы (см. Размер ключа ).

Проблемы поиска

Наиболее известным примером проблемы, допускающей полиномиальное квантовое ускорение, является неструктурированный поиск , который включает в себя поиск отмеченного элемента из списка элементов в базе данных. Это может быть решено алгоритмом Гровера с использованием запросов к базе данных, квадратично меньше, чем запросы, требуемые для классических алгоритмов. В этом случае преимущество не только доказуемо, но и оптимально: было показано, что алгоритм Гровера дает максимально возможную вероятность нахождения нужного элемента для любого количества поисков оракула. ​​Многие примеры доказуемых квантовых ускорений для задач запросов основаны на алгоритме Гровера, включая алгоритм Брассара, Хойера и Таппа для поиска коллизий в функциях два к одному ^[76] и алгоритм Фархи, Голдстоуна и Гутмана для оценки деревьев NAND. ^[77] ${\displaystyle n}$ ${\displaystyle O({\sqrt {n}})}$ ${\displaystyle \Omega (n)}$

Задачи, которые можно эффективно решить с помощью алгоритма Гровера, обладают следующими свойствами: ^{[78] [79]}

1. В коллекции возможных ответов нет структуры поиска,
2. Количество возможных ответов для проверки совпадает с количеством входных данных алгоритма, и
3. Существует булева функция, которая оценивает каждый входной сигнал и определяет, является ли он правильным ответом.

Для задач со всеми этими свойствами время выполнения алгоритма Гровера на квантовом компьютере масштабируется как квадратный корень из числа входов (или элементов в базе данных), в отличие от линейного масштабирования классических алгоритмов. Общий класс задач, к которым может быть применен алгоритм Гровера ^[80], — это задача выполнимости булевых значений , где база данных , по которой проходит алгоритм, содержит все возможные ответы. Примером и возможным применением этого является взломщик паролей , который пытается угадать пароль. Взлом симметричных шифров с помощью этого алгоритма представляет интерес для государственных учреждений. ^[81]

Квантовый отжиг

Квантовый отжиг опирается на адиабатическую теорему для проведения вычислений. Система помещается в основное состояние для простого гамильтониана, который медленно эволюционирует в более сложный гамильтониан, основное состояние которого представляет собой решение рассматриваемой проблемы. Адиабатическая теорема утверждает, что если эволюция достаточно медленная, система будет оставаться в своем основном состоянии в течение всего процесса.Адиабатическая оптимизация может быть полезна для решения задач вычислительной биологии . ^[82]

Машинное обучение

Поскольку квантовые компьютеры могут производить результаты, которые классические компьютеры не могут производить эффективно, и поскольку квантовые вычисления по своей сути являются линейными алгебраическими, некоторые выражают надежду на разработку квантовых алгоритмов, которые могут ускорить задачи машинного обучения . ^{[47] [83]}

Например, алгоритм HHL , названный в честь его первооткрывателей Харроу, Хассидима и Ллойда, как полагают, обеспечивает ускорение по сравнению с классическими аналогами. ^{[47] [84]} Некоторые исследовательские группы недавно исследовали использование оборудования квантового отжига для обучения машин Больцмана и глубоких нейронных сетей . ^{[85] [86] [87]}

Глубокие модели генеративной химии становятся мощными инструментами для ускорения открытия лекарств . Однако огромный размер и сложность структурного пространства всех возможных молекул, подобных лекарствам, создают значительные препятствия, которые в будущем могут быть преодолены квантовыми компьютерами. Квантовые компьютеры, естественно, хороши для решения сложных квантовых многочастичных задач ^[21] и, таким образом, могут быть полезны в приложениях, связанных с квантовой химией. Поэтому можно ожидать, что квантово-усиленные генеративные модели ^[88], включая квантовые GAN ^[89], в конечном итоге могут быть развиты в конечные алгоритмы генеративной химии.

Инженерное дело

Пластина адиабатических квантовых компьютеров

По состоянию на 2023 год ^[update]классические компьютеры превосходят квантовые компьютеры для всех реальных приложений. Хотя современные квантовые компьютеры могут ускорить решения конкретных математических задач, они не дают никаких вычислительных преимуществ для практических задач. Ученые и инженеры изучают множество технологий для аппаратного обеспечения квантовых вычислений и надеются разработать масштабируемую квантовую архитектуру, но остаются серьезные препятствия. ^{[90] [91]}

Вызовы

Существует ряд технических проблем при создании крупномасштабного квантового компьютера. ^[92] Физик Дэвид ДиВинченцо перечислил следующие требования к практическому квантовому компьютеру: ^[93]

• Физически масштабируемо для увеличения количества кубитов
• Кубиты, которые можно инициализировать произвольными значениями
• Квантовые вентили, которые быстрее времени декогеренции
• Универсальный комплект ворот
• Кубиты, которые можно легко прочитать.

Поиск деталей для квантовых компьютеров также очень сложен. Сверхпроводящие квантовые компьютеры , подобные тем, что построены Google и IBM , нуждаются в гелии-3 , побочном продукте ядерных исследований, и в специальных сверхпроводящих кабелях, которые производит только японская компания Coax Co. ^[94]

Управление многокубитными системами требует генерации и координации большого количества электрических сигналов с жестким и детерминированным временным разрешением. Это привело к разработке квантовых контроллеров, которые позволяют взаимодействовать с кубитами. Масштабирование этих систем для поддержки растущего числа кубитов является дополнительной проблемой. ^[95]

Декогеренция

Одной из самых больших проблем, связанных с созданием квантовых компьютеров, является контроль или устранение квантовой декогеренции . Обычно это означает изоляцию системы от ее окружения, поскольку взаимодействие с внешним миром приводит к декогеренции системы. Однако существуют и другие источники декогеренции. Примерами служат квантовые вентили, а также колебания решетки и фоновый термоядерный спин физической системы, используемой для реализации кубитов. Декогеренция необратима, поскольку она фактически неунитарна, и обычно является тем, что следует строго контролировать, если не избегать. Время декогеренции для систем-кандидатов, в частности, время поперечной релаксации _T2 ( для технологий ЯМР и МРТ , также называемое временем дефазировки ), обычно находится в диапазоне от наносекунд до секунд при низкой температуре. ^[96] В настоящее время некоторые квантовые компьютеры требуют охлаждения своих кубитов до 20 милликельвинов (обычно с использованием холодильника растворения ^[97] ), чтобы предотвратить значительную декогеренцию. ^[98] Исследование 2020 года утверждает, что ионизирующее излучение, такое как космические лучи , тем не менее может вызвать декогерентность определенных систем в течение миллисекунд. ^[99]

В результате, трудоемкие задачи могут сделать некоторые квантовые алгоритмы неработоспособными, поскольку попытка поддерживать состояние кубитов в течение достаточно длительного времени в конечном итоге приведет к повреждению суперпозиций. ^[100]

Эти проблемы сложнее для оптических подходов, поскольку временные шкалы на порядки короче, и часто упоминаемый подход к их преодолению — оптическое формирование импульсов . Частота ошибок обычно пропорциональна отношению времени работы ко времени декогеренции, поэтому любая операция должна быть завершена намного быстрее времени декогеренции.

Как описано в пороговой теореме , если частота ошибок достаточно мала, считается возможным использовать квантовую коррекцию ошибок для подавления ошибок и декогеренции. Это позволяет общему времени вычислений быть больше, чем время декогеренции, если схема коррекции ошибок может исправлять ошибки быстрее, чем декогеренция их вносит. Часто цитируемая цифра для требуемой частоты ошибок в каждом вентиле для отказоустойчивых вычислений составляет 10−3 ^, предполагая, что шум является деполяризующим.

Выполнение этого условия масштабируемости возможно для широкого спектра систем. Однако использование коррекции ошибок влечет за собой стоимость значительно возросшего числа требуемых кубитов. Число, необходимое для факторизации целых чисел с использованием алгоритма Шора, по-прежнему является полиномиальным и, как полагают, находится между L и L ² , где L — количество цифр в факторизуемом числе; алгоритмы коррекции ошибок увеличат это число еще на один фактор L . Для 1000-битного числа это подразумевает необходимость около 10 ⁴ бит без коррекции ошибок. ^[101] С коррекцией ошибок это число возрастет до около 10 ⁷ бит. Время вычисления составляет около L ² или около 10 ⁷ шагов, а на частоте 1  МГц — около 10 секунд. Однако накладные расходы на кодирование и коррекцию ошибок увеличивают размер настоящего отказоустойчивого квантового компьютера на несколько порядков. Тщательные оценки ^{[102] [103]} показывают, что по крайней мере 3  миллиона физических кубитов могли бы факторизовать 2048-битное целое число за 5 месяцев на полностью исправленном погрешностях квантовом компьютере с захваченными ионами. С точки зрения количества физических кубитов, на сегодняшний день это остается самой низкой оценкой ^[104] для практически полезной задачи факторизации целых чисел размером 1024 бита или больше.

Другой подход к проблеме стабильности-декогерентности заключается в создании топологического квантового компьютера с анионами , квазичастицами, используемыми в качестве нитей, и опирающегося на теорию кос для формирования стабильных логических вентилей. ^{[105] [106]}

Квантовое превосходство

Физик Джон Прескилл ввел термин «квантовое превосходство» для описания инженерного подвига, демонстрирующего, что программируемое квантовое устройство может решить проблему, выходящую за рамки возможностей современных классических компьютеров. ^{[107] [108] [109]} Проблема не обязательно должна быть полезной, поэтому некоторые рассматривают тест на квантовое превосходство только как потенциальный будущий критерий. ^[110]

В октябре 2019 года Google AI Quantum при поддержке NASA стала первой, кто заявил о достижении квантового превосходства, выполняя вычисления на квантовом компьютере Sycamore более чем в 3 000 000 раз быстрее, чем это можно было бы сделать на Summit , который обычно считается самым быстрым компьютером в мире. ^{[27] [111] [112]} Это утверждение впоследствии было оспорено: IBM заявила, что Summit может выполнять выборки гораздо быстрее, чем заявлено, ^{[113] [114]} и с тех пор исследователи разработали лучшие алгоритмы для задачи выборки, используемой для заявления о квантовом превосходстве, что существенно сократило разрыв между Sycamore и классическими суперкомпьютерами ^{[115] [116] [117]} и даже превзошло его. ^{[118] [119] [120]}

В декабре 2020 года группа в USTC реализовала тип бозонной выборки на 76 фотонах с помощью фотонного квантового компьютера Jiuzhang , чтобы продемонстрировать квантовое превосходство. ^{[121] [122] [123]} Авторы утверждают, что классическому современному суперкомпьютеру потребовалось бы вычислительное время в 600 миллионов лет для генерации того количества выборок, которое их квантовый процессор может сгенерировать за 20 секунд. ^[124]

Заявления о квантовом превосходстве породили шумиху вокруг квантовых вычислений, ^[125] но они основаны на надуманных тестовых задачах, которые напрямую не подразумевают полезных приложений в реальном мире. ^{[90] [126]}

В январе 2024 года исследование, опубликованное в Physical Review Letters , предоставило прямую проверку экспериментов по квантовому превосходству путем вычисления точных амплитуд для экспериментально сгенерированных битовых строк с использованием суперкомпьютера Sunway нового поколения, продемонстрировав значительный скачок в возможностях моделирования, основанных на алгоритме сжатия тензорной сети с несколькими амплитудами. Эта разработка подчеркивает развивающийся ландшафт квантовых вычислений, подчеркивая как прогресс, так и сложности, связанные с проверкой заявлений о квантовом превосходстве. ^[127]

Скептицизм

Несмотря на большие надежды на квантовые вычисления, значительный прогресс в области аппаратного обеспечения и оптимизм относительно будущих приложений, статья в Nature Spotlight 2023 года резюмировала текущие квантовые компьютеры как «на данный момент [ни для чего] не пригодные». ^[90] В статье подробно описывалось, что квантовые компьютеры в любом случае еще не стали более полезными или эффективными, чем обычные компьютеры, хотя также утверждалось, что в долгосрочной перспективе такие компьютеры, вероятно, будут полезны. В статье Communications of the ACM 2023 года ^[91] было обнаружено, что текущие алгоритмы квантовых вычислений «недостаточны для практического квантового преимущества без значительных улучшений в программном/аппаратном стеке». В ней утверждается, что наиболее перспективными кандидатами для достижения ускорения с помощью квантовых компьютеров являются «задачи с малыми данными», например, в химии и материаловедении. Однако в статье также делается вывод о том, что широкий спектр потенциальных приложений, которые она рассматривает, таких как машинное обучение, «не достигнет квантового преимущества с текущими квантовыми алгоритмами в обозримом будущем», и определяются ограничения ввода-вывода, которые делают маловероятным ускорение для «задач больших данных, неструктурированных линейных систем и поиска в базах данных на основе алгоритма Гровера».

Такое положение дел можно объяснить рядом текущих и долгосрочных соображений.

• Традиционное компьютерное оборудование и алгоритмы не только оптимизированы для практических задач, но и продолжают быстро совершенствоваться, особенно ускорители графических процессоров .
• Современное квантовое вычислительное оборудование генерирует лишь ограниченное количество запутанности , прежде чем оно подавляется шумом.
• Квантовые алгоритмы обеспечивают ускорение по сравнению с обычными алгоритмами только для некоторых задач, и сопоставление этих задач с практическими приложениями оказалось сложной задачей. Некоторые перспективные задачи и приложения требуют ресурсов, значительно превосходящих доступные сегодня. ^{[128] [129]} В частности, обработка больших объемов неквантовых данных является проблемой для квантовых компьютеров. ^[91]
• Некоторые перспективные алгоритмы были «деквантованы», т. е. найдены их неквантовые аналоги со схожей сложностью.
• Если квантовая коррекция ошибок используется для масштабирования квантовых компьютеров до практических приложений, ее накладные расходы могут подорвать ускорение, предлагаемое многими квантовыми алгоритмами. ^[91]
• Анализ сложности алгоритмов иногда делает абстрактные предположения, которые не выполняются в приложениях. Например, входные данные могут быть не доступны в кодировке квантовых состояний, а «функции оракула», используемые в алгоритме Гровера, часто имеют внутреннюю структуру, которую можно использовать для более быстрых алгоритмов.

В частности, создание компьютеров с большим количеством кубитов может быть бесполезным, если эти кубиты недостаточно хорошо связаны и не могут поддерживать достаточно высокую степень запутанности в течение длительного времени. Пытаясь превзойти обычные компьютеры, исследователи квантовых вычислений часто ищут новые задачи, которые можно решить на квантовых компьютерах, но это оставляет возможность того, что в ответ будут разработаны эффективные неквантовые методы, как это было показано для демонстраций квантового превосходства . Поэтому желательно доказать нижние границы сложности наилучших возможных неквантовых алгоритмов (которые могут быть неизвестны) и показать, что некоторые квантовые алгоритмы асимптоматически улучшают эти границы.

Некоторые исследователи скептически относятся к возможности создания масштабируемых квантовых компьютеров, как правило, из-за проблемы поддержания когерентности в больших масштабах, но также и по другим причинам.

Билл Унрух усомнился в практичности квантовых компьютеров в статье, опубликованной в 1994 году. ^[130] Пол Дэвис утверждал, что 400-кубитный компьютер даже вступит в противоречие с космологической информационной связью, подразумеваемой голографическим принципом . ^[131] Скептики, такие как Гил Калай, сомневаются, что квантовое превосходство когда-либо будет достигнуто. ^{[132] [133] [134]} Физик Михаил Дьяконов выразил скептицизм относительно квантовых вычислений следующим образом:

«Таким образом, число непрерывных параметров, описывающих состояние такого полезного квантового компьютера в любой момент времени, должно быть... около 10 ³⁰⁰ ... Сможем ли мы когда-нибудь научиться контролировать более 10 ³⁰⁰ непрерывно изменяющихся параметров, определяющих квантовое состояние такой системы? Мой ответ прост. Нет, никогда » . ^{[135] [136]}

Физические реализации

Quantum System One , квантовый компьютер IBM 2019 года с 20 сверхпроводящими кубитами ^[137]

Практический квантовый компьютер должен использовать физическую систему в качестве программируемого квантового регистра. ^[138] Исследователи изучают несколько технологий в качестве кандидатов на надежные реализации кубитов. ^[139] Сверхпроводники и захваченные ионы являются одними из наиболее разработанных предложений, но экспериментаторы рассматривают и другие аппаратные возможности. ^[140]

Первые квантовые логические вентили были реализованы с захваченными ионами , и были реализованы прототипы машин общего назначения с 20 кубитами. Однако технология, лежащая в основе этих устройств, объединяет сложное вакуумное оборудование, лазеры, микроволновое и радиочастотное оборудование, что затрудняет интеграцию полномасштабных процессоров со стандартным вычислительным оборудованием. Более того, сама система захваченных ионов имеет инженерные проблемы, которые необходимо преодолеть. ^[141]

Крупнейшие коммерческие системы основаны на сверхпроводниковых устройствах и масштабируются до 2000 кубитов. Однако частота ошибок для более крупных машин составляет порядка 5%. Технологически все эти устройства являются криогенными, а масштабирование до большого количества кубитов требует интеграции в масштабе пластины, что само по себе является серьезной инженерной задачей. ^[142]

Исследования по созданию более стабильных кубитов для квантовых вычислений включают топологические квантовые компьютерные подходы. Например, Microsoft работает над компьютером, основанным на квантовых свойствах двумерных квазичастиц, называемых анионы . ^{[143] [144] [145]}

Потенциальные приложения

С точки зрения управления бизнесом потенциальные приложения квантовых вычислений можно разделить на четыре основные категории: кибербезопасность, аналитика данных и искусственный интеллект, оптимизация и моделирование, а также управление данными и поиск. ^[146]

Инвестиции в исследования квантовых вычислений возросли в государственном и частном секторах. ^{[147] [148]} Как резюмировала одна консалтинговая фирма, ^[149]

...  инвестиции текут рекой, и стартапы в области квантовых вычислений процветают.  ... Хотя квантовые вычисления обещают помочь компаниям решать проблемы, которые находятся за пределами досягаемости и скорости обычных высокопроизводительных компьютеров , на данном раннем этапе варианты их использования в основном носят экспериментальный и гипотетический характер.

Теория

Вычислимость

Любая вычислительная задача , решаемая классическим компьютером, также решаема квантовым компьютером. ^[150] Интуитивно это происходит потому, что считается, что все физические явления, включая работу классических компьютеров, могут быть описаны с помощью квантовой механики , которая лежит в основе работы квантовых компьютеров.

И наоборот, любая задача, решаемая квантовым компьютером, также решаема классическим компьютером. Можно вручную смоделировать как квантовые, так и классические компьютеры, имея только бумагу и ручку, если дать достаточно времени. Более формально, любой квантовый компьютер может быть смоделирован машиной Тьюринга . Другими словами, квантовые компьютеры не обеспечивают никакой дополнительной мощности по сравнению с классическими компьютерами с точки зрения вычислимости . Это означает, что квантовые компьютеры не могут решать неразрешимые задачи, такие как проблема остановки , и существование квантовых компьютеров не опровергает тезис Чёрча-Тьюринга . ^[151]

Сложность

Хотя квантовые компьютеры не могут решить никаких проблем, которые классические компьютеры уже не могут решить, есть подозрение, что они могут решать некоторые проблемы быстрее, чем классические компьютеры. Например, известно, что квантовые компьютеры могут эффективно факторизовать целые числа , в то время как считается, что это не относится к классическим компьютерам.

Класс задач , которые могут быть эффективно решены квантовым компьютером с ограниченной ошибкой, называется BQP , что означает «ограниченная ошибка, квантовое, полиномиальное время». Более формально, BQP — это класс задач, которые могут быть решены квантовой машиной Тьюринга с полиномиальным временем с вероятностью ошибки не более 1/3. Как класс вероятностных задач, BQP является квантовым аналогом BPP («ограниченная ошибка, вероятностное, полиномиальное время»), класса задач, которые могут быть решены вероятностными машинами Тьюринга с полиномиальным временем с ограниченной ошибкой. ^[152] Известно, что и широко предполагается, что , что интуитивно означало бы, что квантовые компьютеры мощнее классических компьютеров с точки зрения временной сложности . ^[153] ${\displaystyle {\mathsf {BPP\subseteq BQP}}}$ ${\displaystyle {\mathsf {BQP\subsetneq BPP}}}$

Предполагаемая связь BQP с несколькими классическими классами сложности ^[60]

Точная связь BQP с P , NP и PSPACE неизвестна. Однако известно, что ; то есть все проблемы, которые могут быть эффективно решены детерминированным классическим компьютером, могут быть также эффективно решены квантовым компьютером, и все проблемы, которые могут быть эффективно решены квантовым компьютером, могут быть также решены детерминированным классическим компьютером с полиномиальными ресурсами пространства. Далее предполагается, что BQP является строгим надмножеством P, то есть существуют проблемы, которые эффективно решаются квантовыми компьютерами, но не эффективно решаются детерминированными классическими компьютерами. Например, известно, что целочисленная факторизация и задача дискретного логарифма находятся в BQP и, как предполагается, находятся за пределами P. О связи BQP с NP мало что известно, кроме того факта, что некоторые проблемы NP, которые, как считается, не находятся в P, также находятся в BQP (например, целочисленная факторизация и задача дискретного логарифма обе находятся в NP). Предполагается, что ; то есть, считается, что существуют эффективно проверяемые проблемы, которые не могут быть эффективно решены квантовым компьютером. Как прямое следствие этого убеждения, также предполагается, что BQP не пересекается с классом NP-полных проблем (если бы NP-полная проблема была в BQP, то из NP-трудности следовало бы , что все проблемы в NP находятся в BQP). ^[154] ${\displaystyle {\mathsf {P\subseteq BQP\subseteq PSPACE}}}$ ${\displaystyle {\mathsf {NP\nsubseteq BQP}}}$

Смотрите также

• D-Wave Systems  – канадская компания квантовых вычислений
• Электронная квантовая голография  – Технология хранения информации
• Глоссарий квантовых вычислений
• IARPA  – Американское правительственное агентствоPages displaying short descriptions of redirect targets
• IonQ  – американская компания информационных технологий
• Список новых технологий  – Новые технологии, которые активно разрабатываются
• Список квантовых процессоров  – Список компонентов квантового компьютера
• Магическая дистилляция состояния  – Квантовый вычислительный алгоритм
• Метакомпьютинг  – вычисления с целью вычислений
• Естественные вычисления  – терминология, введенная для охвата трех классов методовPages displaying wikidata descriptions as a fallback
• Оптические вычисления  – компьютер, использующий фотоны или световые волны.
• Квантовая шина  – устройство, которое можно использовать для хранения или передачи информации между независимыми кубитами в квантовом компьютере.Pages displaying wikidata descriptions as a fallback
• Квантовое познание  – применение квантовой теории математики к когнитивным явлениям
• Квантовый объем  – метрика возможностей квантового компьютера.
• Квантовая странность  – Неинтуитивные аспекты квантовой механики
• Rigetti Computing  – американская компания квантовых вычислений
• Суперкомпьютер  – тип чрезвычайно мощного компьютера.
• Теоретическая информатика  – Подотрасль информатики и математики
• Нетрадиционные вычисления  – вычисления с использованием новых или необычных методов.
• Valleytronics  – Экспериментальная область полупроводников

Примечания

1. В этой статье «экспоненциально быстрее» имеет точное теоретическое значение сложности . Обычно это означает, что в зависимости от размера входных данных в битах, наиболее известный классический алгоритм для задачи требует экспоненциально растущего числа шагов, в то время как квантовый алгоритм использует только полиномиальное число шагов.
2. Стандартный базис также является вычислительным базисом . ^[35]

Ссылки

1. Ааронсон 2013, стр. 132.
2. Бхатта, Варун С. (10 мая 2020 г.). «Множественность корпускулярно-волнового дуализма» (PDF) . Current Science . 118 (9): 1365. doi :10.18520/cs/v118/i9/1365-1374. ISSN  0011-3891. S2CID  216143449.
3. Ceruzzi, Paul E. (2012). Computing: A Concise History . Кембридж, Массачусетс : MIT Press. стр. 3, 46. ISBN 978-0-262-31038-3. OCLC  796812982.
4. Ходжес, Эндрю (2014). Алан Тьюринг: Энигма . Принстон, Нью-Джерси: Princeton University Press . стр. xviii. ISBN 9780691164724.
5. Mårtensson-Pendrill, Ann-Marie (1 ноября 2006 г.). «Проект Манхэттен — часть истории физики». Physics Education . 41 (6): 493–501. Bibcode : 2006PhyEd..41..493M. doi : 10.1088/0031-9120/41/6/001. ISSN  0031-9120. S2CID  120294023.
6. Benioff, Paul (1980). «Компьютер как физическая система: микроскопическая квантово-механическая гамильтонова модель компьютеров, представленная машинами Тьюринга». Журнал статистической физики . 22 (5): 563–591. Bibcode : 1980JSP....22..563B. doi : 10.1007/bf01011339. S2CID  122949592.
7. Булута, Юлия; Нори, Франко (2 октября 2009 г.). «Квантовые симуляторы». Science . 326 (5949): 108–111. Bibcode :2009Sci...326..108B. doi :10.1126/science.1177838. ISSN  0036-8075. PMID  19797653. S2CID  17187000.
8. Манин, Ю. И. (1980). Вычислимое и невычислимое [ Computable and Noncomputable ] (на русском языке). Советское радио. С. 13–15. Архивировано из оригинала 10 мая 2013 года . Получено 4 марта 2013 года .
9. Фейнман, Ричард (июнь 1982 г.). «Моделирование физики с помощью компьютеров» (PDF) . International Journal of Theoretical Physics . 21 (6/7): 467–488. Bibcode :1982IJTP...21..467F. doi :10.1007/BF02650179. S2CID  124545445. Архивировано из оригинала (PDF) 8 января 2019 г. . Получено 28 февраля 2019 г. .
10. Нильсен и Чуанг 2010, стр. 214.
11. Bennett, Charles H. ; Brassard, Gilles (декабрь 1984 г.). Квантовая криптография: распределение открытого ключа и подбрасывание монеты . Международная конференция IEEE по компьютерам, системам и обработке сигналов. Бангалор, Индия. стр. 175–179. arXiv : 2003.06557 . doi :10.1016/j.tcs.2014.05.025.
12. Brassard, G. (2005). "Краткая история квантовой криптографии: личная точка зрения". IEEE Information Theory Workshop on Theory and Practice in Information-Theoretic Security, 2005. Остров Авадзи, Япония: IEEE. стр. 19–23. arXiv : quant-ph/0604072 . doi : 10.1109/ITWTPI.2005.1543949. ISBN 978-0-7803-9491-9. S2CID  16118245.
13. Deutsch, D. (8 июля 1985 г.). «Квантовая теория, принцип Чёрча–Тьюринга и универсальный квантовый компьютер». Труды Лондонского королевского общества. A. Mathematical and Physical Sciences . 400 (1818): 97–117. Bibcode : 1985RSPSA.400...97D. doi : 10.1098/rspa.1985.0070. ISSN  0080-4630. S2CID  1438116.
14. Бернстайн, Этан; Вазирани, Умеш (1993). «Квантовая теория сложности». Труды двадцать пятого ежегодного симпозиума ACM по теории вычислений – STOC '93 . Сан-Диего, Калифорния, США: ACM Press. стр. 11–20. doi :10.1145/167088.167097. ISBN 978-0-89791-591-5. S2CID  676378.
15. Саймон, DR (1994). «О силе квантовых вычислений». Труды 35-го ежегодного симпозиума по основам компьютерной науки . Санта-Фе, Нью-Мексико, США: IEEE Comput. Soc. Press. стр. 116–123. doi :10.1109/SFCS.1994.365701. ISBN 978-0-8186-6580-6. S2CID  7457814.
16. Нильсен и Чуанг 2010, стр. 30-32.
17. Шор 1994.
18. Громблинг и Горовиц 2019, стр. 15.
19. Гровер, Лов К. (1996). Быстрый квантово-механический алгоритм поиска в базе данных . Симпозиум ACM по теории вычислений. Филадельфия : ACM Press. С. 212–219. arXiv : quant-ph/9605043 . doi : 10.1145/237814.237866. ISBN 978-0-89791-785-8.
20. Nielsen & Chuang 2010, стр. 7.
21. Ллойд, Сет (23 августа 1996 г.). «Универсальные квантовые симуляторы». Science . 273 (5278): 1073–1078. Bibcode :1996Sci...273.1073L. doi :10.1126/science.273.5278.1073. ISSN  0036-8075. PMID  8688088. S2CID  43496899.
22. Цао, Юдонг; Ромеро, Джонатан; Олсон, Джонатан П.; Дегроот, Маттиас; Джонсон, Питер Д.; и др. (9 октября 2019 г.). «Квантовая химия в эпоху квантовых вычислений». Chemical Reviews . 119 (19): 10856–10915. arXiv : 1812.09976 . doi :10.1021/acs.chemrev.8b00803. ISSN  0009-2665. PMID  31469277. S2CID  119417908.
23. Grumbling & Horowitz 2019, стр. 164–169.
24. Чуан, Айзек Л.; Гершенфельд, Нил; Кубинец, Маркдой (апрель 1998 г.). «Экспериментальная реализация быстрого квантового поиска». Physical Review Letters . 80 (15). Американское физическое общество : 3408–3411. Bibcode : 1998PhRvL..80.3408C. doi : 10.1103/PhysRevLett.80.3408.
25. Холтон, Уильям Коффен. «квантовый компьютер». Encyclopedia Britannica . Encyclopaedia Britannica . Получено 4 декабря 2021 г. .
26. Гибни, Элизабет (23 октября 2019 г.). «Привет, квантовый мир! Google публикует знаковое заявление о квантовом превосходстве». Nature . 574 (7779): 461–462. Bibcode :2019Natur.574..461G. doi : 10.1038/d41586-019-03213-z . PMID  31645740.
27. Lay summary: Мартинис, Джон; Бойксо, Серхио (23 октября 2019 г.). «Квантовое превосходство с использованием программируемого сверхпроводящего процессора». Nature . 574 (7779). Google AI : 505–510. arXiv : 1910.11333 . Bibcode :2019Natur.574..505A. doi :10.1038/s41586-019-1666-5. PMID  31645734. S2CID  204836822 . Получено 27 апреля 2022 г. .
     • Журнальная статья: Аруте, Франк; Арья, Кунал; Бэббуш, Райан; Бэкон, Дэйв; Бардин, Джозеф К.; и др. (23 октября 2019 г.). «Квантовое превосходство с помощью программируемого сверхпроводникового процессора». Природа . 574 (7779): 505–510. arXiv : 1910.11333 . Бибкод : 2019Natur.574..505A. дои : 10.1038/s41586-019-1666-5. PMID  31645734. S2CID  204836822.
28. Ааронсон, Скотт (30 октября 2019 г.). «Мнение | Почему важен этап квантового превосходства Google». The New York Times . ISSN  0362-4331 . Получено 25 сентября 2021 г.
29. Педнолт, Эдвин (22 октября 2019 г.). «О квантовом превосходстве». Блог исследований IBM . Получено 9 февраля 2021 г.
30. Пан, Фэн; Чжан, Пан (4 марта 2021 г.). «Моделирование схем квантового превосходства Sycamore». arXiv : 2103.03074 [quant-ph].
31. Сотрудники (7 декабря 2023 г.). «Физики впервые «запутали» отдельные молекулы, ускорив возможности квантовых вычислений». Phys.org . Архивировано из оригинала 8 декабря 2023 г. Получено 8 декабря 2023 г.
32. Беннетт, Чарли (31 июля 2020 г.). Информация квантовая: как физика помогла объяснить природу информации и что с ней можно сделать (видеозапись). Событие происходит в 1:08:22 – через YouTube.
33. Нильсен и Чуанг 2010, стр. 13.
34. Mermin 2007, стр. 17.
35. Mermin 2007, стр. 18.
36. Ааронсон 2013, стр. 110.
37. Нильсен и Чуанг 2010, стр. 30–32.
38. Мермин 2007, стр. 38–39.
39. Кургалин, Сергей; Борзунов, Сергей (2021). Краткое руководство по квантовым вычислениям: алгоритмы, упражнения и реализации . Тексты по информатике. Cham: Springer. ISBN 978-3-030-65054-4.
40. Das, A.; Chakrabarti, BK (2008). «Квантовый отжиг и аналоговые квантовые вычисления». Rev. Mod. Phys. 80 (3): 1061–1081. arXiv : 0801.2193 . Bibcode :2008RvMP...80.1061D. CiteSeerX 10.1.1.563.9990 . doi :10.1103/RevModPhys.80.1061. S2CID  14255125.  
41. Nayak, Chetan; Simon, Steven; Stern, Ady; Das Sarma, Sankar (2008). «Ненабелевские анионы и квантовые вычисления». Reviews of Modern Physics . 80 (3): 1083–1159. arXiv : 0707.1889 . Bibcode :2008RvMP...80.1083N. doi :10.1103/RevModPhys.80.1083. S2CID  119628297.
42. Чи-Чи Яо, А. (1993). "Квантовая сложность цепей". Труды 1993 IEEE 34th Annual Foundations of Computer Science . стр. 352–361. doi :10.1109/SFCS.1993.366852. ISBN 0-8186-4370-6. S2CID  195866146.
43. Рауссендорф, Роберт; Браун, Дэниел Э.; Бригель, Ганс Дж. (25 августа 2003 г.). «Квантовые вычисления на основе измерений в кластерных состояниях». Physical Review A. 68 ( 2): 022312. arXiv : quant-ph/0301052 . Bibcode : 2003PhRvA..68b2312R. doi : 10.1103/PhysRevA.68.022312. S2CID  6197709.
44. Ааронов, Дорит; ван Дам, Вим; Кемпе, Джулия; Ландау, Зеф; Ллойд, Сет; Регев, Одед (1 января 2008 г.). «Адиабатическое квантовое вычисление эквивалентно стандартному квантовому вычислению». SIAM Review . 50 (4): 755–787. arXiv : quant-ph/0405098 . Bibcode : 2008SIAMR..50..755A. doi : 10.1137/080734479. ISSN  0036-1445. S2CID  1503123.
45. Freedman, Michael H.; Larsen, Michael; Wang, Zhenghan (1 июня 2002 г.). «Модулярный функтор, универсальный для квантовых вычислений». Communications in Mathematical Physics . 227 (3): 605–622. arXiv : quant-ph/0001108 . Bibcode :2002CMaPh.227..605F. doi :10.1007/s002200200645. ISSN  0010-3616. S2CID  8990600.
46. Нильсен и Чуанг 2010, стр. 481.
47. Прескилл, Джон (6 августа 2018 г.). «Квантовые вычисления в эпоху NISQ и далее». Quantum . 2 : 79. arXiv : 1801.00862 . Bibcode :2018Quant...2...79P. doi : 10.22331/q-2018-08-06-79 . S2CID  44098998.
48. Блювштейн, Долев; Эверед, Саймон Дж.; Гейм, Александра А.; Ли, Софи Х.; Чжоу, Хэнъюнь; Мановиц, Том; Эбади, Сепер; Каин, Мэделин; Калиновский, Марцин; Ханглейтер, Доминик; Атаидес, Х. Пабло Бонилья; Маскара, Нишад; Конг, Ирис; Гао, Сюнь; Родригес, Педро Сейлс (6 декабря 2023 г.). «Логический квантовый процессор на основе реконфигурируемых массивов атомов». Природа . 626 (7997): 58–65. arXiv : 2312.03982 . дои : 10.1038/s41586-023-06927-3. ISSN  1476-4687. ПМЦ 10830422 . PMID  38056497. S2CID  266052773. 
49. Freedberg Jr., Sydney J. (7 декабря 2023 г.). «'Off to the races': DARPA, Harvard opening makes quantum computing years towards». Breaking Defense . Получено 9 декабря 2023 г.
50. «Исследования, финансируемые DARPA, привели к прорыву в области квантовых вычислений». darpa.mil . 6 декабря 2023 г. Получено 5 января 2024 г.
51. Чоудхури, Ризван (30 декабря 2023 г.). «7 лучших инновационных историй 2023 года – Интересное машиностроение». interestingengineering.com . Получено 6 января 2024 г.
52. Пирандола, С.; Андерсен, UL; Банки, Л.; Берта, М.; Бунандар, Д.; Колбек, Р.; Инглунд, Д.; Геринг, Т.; Лупо, К.; Оттавиани, К.; Перейра, Дж.; Разави, М.; Шамсул Шаари, Дж.; Томамичел, М.; Усенко, В.К.; Валлоне, Г.; Виллорези, П.; Уоллден, П. (2020). «Достижения квантовой криптографии». Достижения оптики и фотоники . 12 (4): 1012–1236. arXiv : 1906.01645 . Бибкод : 2020AdOP...12.1012P. дои : 10.1364/AOP.361502.
53. Пирандола, С.; Андерсен, UL; Банки, Л.; Берта, М.; Бунандар, Д.; Колбек, Р.; Инглунд, Д.; Геринг, Т.; Лупо, К.; Оттавиани, К.; Перейра, JL; Разави, М.; Шамсул Шаари, Дж.; Томамичел, М.; Усенко, ВК (14 декабря 2020 г.). «Достижения квантовой криптографии». Достижения оптики и фотоники . 12 (4): 1017. arXiv : 1906.01645 . Бибкод : 2020AdOP...12.1012P. дои : 10.1364/AOP.361502. ISSN  1943-8206. S2CID  174799187.
54. Сюй, Фэйху; Ма, Сюнфэн; Чжан, Цян; Ло, Хой-Квонг; Пан, Цзянь-Вэй (26 мая 2020 г.). «Безопасное распределение квантовых ключей с помощью реалистичных устройств». Reviews of Modern Physics . 92 (2): 025002-3. arXiv : 1903.09051 . Bibcode : 2020RvMP...92b5002X. doi : 10.1103/RevModPhys.92.025002. S2CID  210942877.
55. Сюй, Гобин; Мао, Цзяньчжоу; Сакк, Эрик; Ван, Шуанбао Пол (22 марта 2023 г.). «Обзор квантово-безопасных подходов: квантовое распределение ключей и постквантовая криптография». 57-я ежегодная конференция по информационным наукам и системам (CISS) 2023 г. IEEE . стр. 3. doi :10.1109/CISS56502.2023.10089619. ISBN 978-1-6654-5181-9.
56. Козловски, Войцех; Венер, Стефани (25 сентября 2019 г.). «К крупномасштабным квантовым сетям». Труды Шестой ежегодной международной конференции ACM по наномасштабным вычислениям и коммуникациям . ACM. стр. 1–7. arXiv : 1909.08396 . doi :10.1145/3345312.3345497. ISBN 978-1-4503-6897-1.
57. Го, Сюеши; Бреум, Каспер Р.; Боррегор, Йоханнес; Идзуми, Сюро; Ларсен, Миккель В.; Геринг, Тобиас; Кристандл, Матиас; Неергаард-Нильсен, Йонас С.; Андерсен, Ульрик Л. (23 декабря 2019 г.). «Распределенное квантовое зондирование в запутанной сети с непрерывными переменными». Физика природы . 16 (3): 281–284. arXiv : 1905.09408 . дои : 10.1038/s41567-019-0743-x. ISSN  1745-2473. S2CID  256703226.
58. Jordan, Stephen (14 октября 2022 г.) [22 апреля 2011 г.]. «Quantum Algorithm Zoo». Архивировано из оригинала 29 апреля 2018 г.
59. Ааронсон, Скотт ; Архипов, Алекс (6 июня 2011 г.). «Вычислительная сложность линейной оптики». Труды сорок третьего ежегодного симпозиума ACM по теории вычислений . Сан-Хосе, Калифорния : Ассоциация вычислительной техники . С. 333–342. arXiv : 1011.3245 . doi : 10.1145/1993636.1993682. ISBN 978-1-4503-0691-1.
60. Nielsen & Chuang 2010, стр. 42.
61. Нортон, Куинн (15 февраля 2007 г.). «Отец квантовых вычислений». Wired .
62. Амбаинис, Андрис (весна 2014 г.). «Что мы можем сделать с квантовым компьютером?». Институт перспективных исследований.
63. Чанг, Кеннет (14 июня 2023 г.). «Прогресс квантовых вычислений начинает новую эру, заявляет IBM – Квантовый компьютер придумал лучшие ответы на физическую проблему, чем обычный суперкомпьютер». The New York Times . Архивировано из оригинала 14 июня 2023 г. . Получено 15 июня 2023 г.
64. Ким, Ёнсок и др. (14 июня 2023 г.). «Доказательства полезности квантовых вычислений до возникновения отказоустойчивости». Nature . 618 (7965): 500–505. Bibcode :2023Natur.618..500K. doi :10.1038/s41586-023-06096-3. PMC 10266970 . PMID  37316724. 
65. Морелло, Андреа (21 ноября 2018 г.). Обед и обучение: квантовые вычисления. Sibos TV . Архивировано из оригинала 15 февраля 2021 г. Получено 4 февраля 2021 г. – через YouTube.{{cite AV media}}: CS1 maint: bot: original URL status unknown (link)
66. Руан, Джонатан; Макафи, Эндрю; Оливер, Уильям Д. (1 января 2022 г.). «Квантовые вычисления для руководителей бизнеса». Harvard Business Review . ISSN  0017-8012 . Получено 12 апреля 2023 г.
67. Бадде, Флориан; Фольц, Дэниел (12 июля 2019 г.). «Квантовые вычисления и химическая промышленность | McKinsey». www.mckinsey.com . McKinsey and Company . Получено 12 апреля 2023 г. .
68. Бурзак, Кэтрин (30 октября 2017 г.). «Химия — это убийственное приложение квантовых вычислений». cen.acs.org . Американское химическое общество . Получено 12 апреля 2023 г. .
69. Lenstra, Arjen K. (2000). "Integer Factoring" (PDF) . Designs, Codes and Cryptography . 19 (2/3): 101–128. doi :10.1023/A:1008397921377. S2CID  9816153. Архивировано из оригинала (PDF) 10 апреля 2015 г.
70. Нильсен и Чуанг 2010, стр. 216.
71. Bernstein, Daniel J. (2009). "Введение в постквантовую криптографию". Постквантовая криптография . Берлин, Гейдельберг: Springer. стр. 1–14. doi :10.1007/978-3-540-88702-7_1. ISBN 978-3-540-88701-0. S2CID  61401925.
72. См. также pqcrypto.org, библиографию, поддерживаемую Дэниелом Дж. Бернстайном и Таней Ланге, по криптографии, которая, как известно, не может быть взломана квантовыми вычислениями.
73. МакЭлис, Р. Дж. (январь 1978 г.). «Криптосистема с открытым ключом, основанная на алгебраической теории кодирования» (PDF) . DSNPR . 44 : 114–116. Bibcode : 1978DSNPR..44..114M.
74. Кобаяши, Х.; Галл, Ф. Л. (2006). «Проблема скрытой подгруппы диэдра: обзор». Информационные и медиатехнологии . 1 (1): 178–185. doi : 10.2197/ipsjdc.1.470 .
75. Беннетт, Чарльз Х.; Бернстайн, Итан; Брассар, Жиль; Вазирани, Умеш (октябрь 1997 г.). «Сильные и слабые стороны квантовых вычислений». Журнал SIAM по вычислениям . 26 (5): 1510–1523. arXiv : quant-ph/9701001 . Bibcode : 1997quant.ph..1001B. doi : 10.1137/s0097539796300933. S2CID  13403194.
76. Брассар, Жиль; Хойер, Питер; Тапп, Ален (2016). «Квантовый алгоритм для проблемы столкновений». В Као, Мин-Ян (ред.). Энциклопедия алгоритмов . Нью-Йорк, Нью-Йорк: Springer. стр. 1662–1664. arXiv : quant-ph/9705002 . doi : 10.1007/978-1-4939-2864-4_304. ISBN 978-1-4939-2864-4. S2CID  3116149.
77. Фархи, Эдвард; Голдстоун, Джеффри; Гутманн, Сэм (23 декабря 2008 г.). «Квантовый алгоритм для гамильтонового дерева NAND». Теория вычислений . 4 (1): 169–190. doi : 10.4086/toc.2008.v004a008 . ISSN  1557-2862. S2CID  8258191.
78. Уильямс, Колин П. (2011). Исследования в области квантовых вычислений . Springer . С. 242–244. ISBN 978-1-84628-887-6.
79. Гровер, Лов (29 мая 1996 г.). "Быстрый квантово-механический алгоритм поиска в базе данных". arXiv : quant-ph/9605043 .
80. Амбаинис, Амбаинис (июнь 2004 г.). «Квантовые алгоритмы поиска». ACM SIGACT News . 35 (2): 22–35. arXiv : quant-ph/0504012 . Bibcode : 2005quant.ph..4012A. doi : 10.1145/992287.992296. S2CID  11326499.
81. Рич, Стивен; Геллман, Бартон (1 февраля 2014 г.). «АНБ стремится создать квантовый компьютер, который мог бы взломать большинство типов шифрования». The Washington Post .
82. Оутейрал, Карлос; Страм, Мартин; Моррис, Гарретт; Бенджамин, Саймон; Дин, Шарлотта; Ши, Джие (2021). «Перспективы квантовых вычислений в вычислительной молекулярной биологии». WIREs Computational Molecular Science . 11. arXiv : 2005.12792 . doi : 10.1002/wcms.1481 . S2CID  218889377.
83. Биамонте, Якоб; Виттек, Питер; Панкотти, Никола; Ребентрост, Патрик; Вибе, Натан; Ллойд, Сет (сентябрь 2017 г.). «Квантовое машинное обучение». Nature . 549 (7671): 195–202. arXiv : 1611.09347 . Bibcode :2017Natur.549..195B. doi :10.1038/nature23474. ISSN  0028-0836. PMID  28905917. S2CID  64536201.
84. Харроу, Арам; Хассидим, Авинатан; Ллойд, Сет (2009). «Квантовый алгоритм решения линейных систем уравнений». Physical Review Letters . 103 (15): 150502. arXiv : 0811.3171 . Bibcode : 2009PhRvL.103o0502H. doi : 10.1103/PhysRevLett.103.150502. PMID  19905613. S2CID  5187993.
85. Бенедетти, Марчелло; Реалпе-Гомес, Джон; Бисвас, Рупак; Пердомо-Ортис, Алехандро (9 августа 2016 г.). «Оценка эффективных температур в квантовых отжигателях для приложений выборки: исследование случая с возможными приложениями в глубоком обучении». Physical Review A. 94 ( 2): 022308. arXiv : 1510.07611 . Bibcode : 2016PhRvA..94b2308B. doi : 10.1103/PhysRevA.94.022308 .
86. Аджагекар, Акшай; Ю, Фэнци (5 декабря 2020 г.). «Квантовые вычисления с помощью глубокого обучения для обнаружения и диагностики неисправностей в промышленных технологических системах». Компьютеры и химическая инженерия . 143 : 107119. arXiv : 2003.00264 . doi : 10.1016/j.compchemeng.2020.107119. ISSN  0098-1354. S2CID  211678230.
87. Аджагекар, Акшай; Ю, Фэнци (1 декабря 2021 г.). «Гибридное глубокое обучение на основе квантовых вычислений для диагностики неисправностей в электроэнергетических системах». Applied Energy . 303 : 117628. Bibcode : 2021ApEn..30317628A. doi : 10.1016/j.apenergy.2021.117628 . ISSN  0306-2619.
88. Гао, Сюнь; Аншуец, Эрик Р.; Ван, Шэн-Тао; Сирак, Дж. Игнасио; Лукин, Михаил Д. (2022). «Улучшение генеративных моделей с помощью квантовых корреляций». Physical Review X. 12 ( 2): 021037. arXiv : 2101.08354 . Bibcode : 2022PhRvX..12b1037G. doi : 10.1103/PhysRevX.12.021037. S2CID  231662294.
89. Ли, Джунде; Топалоглу, Расит; Гош, Сваруп (9 января 2021 г.). «Квантовые генеративные модели для открытия лекарств на основе малых молекул». arXiv : 2101.03438 [cs.ET].
90. Брукс, Майкл (24 мая 2023 г.). «Квантовые компьютеры: для чего они нужны?». Nature . 617 (7962): S1–S3. Bibcode :2023Natur.617S...1B. doi : 10.1038/d41586-023-01692-9 . PMID  37225885. S2CID  258847001.
91. Торстен Хёфлер; Томас Хенер; Маттиас Тройер (май 2023 г.). «Отделение шумихи от практичности: о реалистичном достижении квантового преимущества». Сообщения ACM.
92. Дьяконов, Михаил (15 ноября 2018 г.). «Дело против квантовых вычислений». IEEE Spectrum .
93. ДиВинченцо, Дэвид П. (13 апреля 2000 г.). «Физическая реализация квантовых вычислений». Fortschritte der Physik . 48 (9–11): 771–783. arXiv : Quant-ph/0002077 . Бибкод : 2000ForPh..48..771D. doi :10.1002/1521-3978(200009)48:9/11<771::AID-PROP771>3.0.CO;2-E. S2CID  15439711.
94. Джайлс, Мартин (17 января 2019 г.). «У нас было бы больше квантовых компьютеров, если бы не было так сложно найти эти чертовы кабели». MIT Technology Review . Получено 17 мая 2021 г.
95. Pauka SJ, Das K, Kalra B, Moini A, Yang Y, Trainer M, Bousquet A, Cantaloube C, Dick N, Gardner GC, Manfra MJ, Reilly DJ (2021). «Криогенный CMOS-чип для генерации управляющих сигналов для нескольких кубитов». Nature Electronics . 4 (4): 64–70. arXiv : 1912.01299 . doi :10.1038/s41928-020-00528-y. S2CID  231715555.
96. ДиВинченцо, Дэвид П. (1995). «Квантовые вычисления». Science . 270 (5234): 255–261. Bibcode :1995Sci...270..255D. CiteSeerX 10.1.1.242.2165 . doi :10.1126/science.270.5234.255. S2CID  220110562. 
97. – обзор». Криогеника . 121. doi :10.1016/j.cryogenics.2021.103390. ISSN  0011-2275. S2CID  244005391.
98. Джонс, Никола (19 июня 2013 г.). «Вычислительная техника: квантовая компания». Nature . 498 (7454): 286–288. Bibcode :2013Natur.498..286J. doi : 10.1038/498286a . PMID  23783610.
99. Vepsäläinen, Antti P.; Karamlou, Amir H.; Orrell, John L.; Dogra, Akshunna S.; Loer, Ben; et al. (август 2020 г.). «Влияние ионизирующего излучения на когерентность сверхпроводящего кубита». Nature . 584 (7822): 551–556. arXiv : 2001.09190 . Bibcode :2020Natur.584..551V. doi :10.1038/s41586-020-2619-8. ISSN  1476-4687. PMID  32848227. S2CID  210920566.
100. Эми, Мэтью; Маттео, Оливия; Георгиу, Влад; Моска, Мишель; Пэрент, Алекс; Шанк, Джон (30 ноября 2016 г.). «Оценка стоимости общих квантовых атак на прообразы SHA-2 и SHA-3». arXiv : 1603.09383 [quant-ph].
101. Дьяконов, MI (14 октября 2006 г.). С. Лурий; Сюй, J.; Заславский, A. (ред.). «Действительно ли возможны отказоустойчивые квантовые вычисления?». Будущие тенденции в микроэлектронике. Up the Nano Creek : 4–18. arXiv : quant-ph/0610117 . Bibcode :2006quant.ph.10117D.
102. Ахсан, Мухаммад (2015). Архитектурная структура для квантового компьютера с захваченными ионами на основе инструмента моделирования производительности. OCLC  923881411.
103. Ахсан, Мухаммад; Метер, Родни Ван; Ким, Юнгсанг (28 декабря 2016 г.). «Проектирование квантового компьютера на миллион кубитов с использованием симулятора производительности ресурсов». Журнал ACM о новых технологиях в вычислительных системах . 12 (4): 39:1–39:25. arXiv : 1512.00796 . doi : 10.1145/2830570 . ISSN  1550-4832. S2CID  1258374.
104. Гидни, Крейг; Экера, Мартин (15 апреля 2021 г.). «Как факторизовать 2048-битные целые числа RSA за 8 часов, используя 20 миллионов шумных кубитов». Quantum . 5 : 433. arXiv : 1905.09749 . Bibcode :2021Quant...5..433G. doi :10.22331/q-2021-04-15-433. ISSN  2521-327X. S2CID  162183806.
105. Freedman, Michael H. ; Китаев, Алексей ; Larsen, Michael J. ; Wang, Zhenghan (2003). «Топологические квантовые вычисления». Бюллетень Американского математического общества . 40 (1): 31–38. arXiv : quant-ph/0101025 . doi :10.1090/S0273-0979-02-00964-3. MR  1943131.
106. Монро, Дон (1 октября 2008 г.). «Anyons: в чем прорыв в квантовых вычислениях?». New Scientist .
107. Прескилл, Джон (26 марта 2012 г.). «Квантовые вычисления и граница запутанности». arXiv : 1203.5813 [quant-ph].
108. Прескилл, Джон (6 августа 2018 г.). «Квантовые вычисления в эпоху NISQ и далее». Quantum . 2 : 79. arXiv : 1801.00862 . Bibcode :2018Quant...2...79P. doi : 10.22331/q-2018-08-06-79 .
109. Boixo, Sergio; Isakov, Sergey V.; Smelyanskiy, Vadim N.; Babbush, Ryan; Ding, Nan; et al. (2018). «Характеристика квантового превосходства в ближнесрочных устройствах». Nature Physics . 14 (6): 595–600. arXiv : 1608.00263 . Bibcode :2018NatPh..14..595B. doi :10.1038/s41567-018-0124-x. S2CID  4167494.
110. Сэвидж, Нил (5 июля 2017 г.). «Квантовые компьютеры соревнуются за «превосходство»». Scientific American .
111. Джайлс, Мартин (20 сентября 2019 г.). «Исследователи Google, как сообщается, достигли «квантового превосходства»». MIT Technology Review . Получено 15 мая 2020 г.
112. Таварес, Фрэнк (23 октября 2019 г.). «Google и NASA достигают квантового превосходства». NASA . Получено 16 ноября 2021 г. .
113. Педнолт, Эдвин; Ганнелс, Джон А.; Нанничини, Джакомо; Хореш, Лиор; Висниефф, Роберт (22 октября 2019 г.). «Использование вторичного хранилища для моделирования глубоких 54-кубитных схем Sycamore». arXiv : 1910.09534 [quant-ph].
114. Чо, Адриан (23 октября 2019 г.). «IBM ставит под сомнение заявления Google о квантовом превосходстве». Science . doi :10.1126/science.aaz6080. ISSN  0036-8075. S2CID  211982610.
115. Лю, Юн (Александр); Лю, Синь (Люси); Ли, Фан (Нэнси); Фу, Хаохуань; Ян, Юйлин; и др. (14 ноября 2021 г.). «Закрытие разрыва «квантового превосходства»». Труды Международной конференции по высокопроизводительным вычислениям, сетям, хранению и анализу . SC '21. Нью-Йорк, Нью-Йорк: Ассоциация вычислительной техники. стр. 1–12. arXiv : 2110.14502 . doi :10.1145/3458817.3487399. ISBN 978-1-4503-8442-1. S2CID  239036985.
116. Балмер, Джейкоб ФФ; Белл, Брин А.; Чедвик, Рэйчел С.; Джонс, Алекс Э.; Моис, Диана; и др. (28 января 2022 г.). «Граница квантового преимущества в гауссовой выборке бозонов». Science Advances . 8 (4): eabl9236. arXiv : 2108.01622 . Bibcode :2022SciA....8.9236B. doi :10.1126/sciadv.abl9236. ISSN  2375-2548. PMC 8791606 . PMID  35080972. 
117. Маккормик, Кэти (10 февраля 2022 г.). «Гонка между классическими и квантовыми компьютерами не окончена». Физика . 15 : 19. Bibcode : 2022PhyOJ..15...19M. doi : 10.1103/Physics.15.19 . S2CID  246910085.
118. Пан, Фэн; Чэнь, Кейанг; Чжан, Пан (2022). «Решение проблемы выборки квантовых схем Sycamore». Physical Review Letters . 129 (9): 090502. arXiv : 2111.03011 . Bibcode : 2022PhRvL.129i0502P. doi : 10.1103/PhysRevLett.129.090502. PMID  36083655. S2CID  251755796.
119. Чо, Адриан (2 августа 2022 г.). «Обычные компьютеры все-таки могут превзойти квантовый компьютер Google». Science . 377 . doi :10.1126/science.ade2364.
120. «Исследователи, использующие обычный суперкомпьютер, узурпировали «квантовое превосходство» Google». TechCrunch . 5 августа 2022 г. . Получено 7 августа 2022 г. .
121. Болл, Филип (3 декабря 2020 г.). «Физики в Китае бросают вызов «квантовому преимуществу» Google". Nature . 588 (7838): 380. Bibcode :2020Natur.588..380B. doi :10.1038/d41586-020-03434-7. PMID  33273711. S2CID  227282052.
122. Гаристо, Дэниел. «Квантовый компьютер на основе света превосходит самые быстрые классические суперкомпьютеры». Scientific American . Получено 7 декабря 2020 г.
123. Коновер, Эмили (3 декабря 2020 г.). «Новый квантовый компьютер на основе света Jiuzhang достиг квантового превосходства». Science News . Получено 7 декабря 2020 г. .
124. Чжун, Хан-Сен; Ван, Хуэй; Дэн, Ю-Хао; Чэнь, Мин-Чэн; Пэн, Ли-Чао; и др. (3 декабря 2020 г.). «Квантовое вычислительное преимущество с использованием фотонов». Science . 370 (6523): 1460–1463. arXiv : 2012.01625 . Bibcode :2020Sci...370.1460Z. doi :10.1126/science.abe8770. ISSN  0036-8075. PMID  33273064. S2CID  227254333.
125. Роберсон, Тара М. (21 мая 2020 г.). "{{subst:title case|Может ли шумиха быть силой добра?}}". Общественное понимание науки . 29 (5): 544–552. doi : 10.1177/0963662520923109 . ISSN  0963-6625. PMID  32438851. S2CID  218831653.
126. Кавальери, Фабио; Мэттссон, Джон; Смитс, Бен (сентябрь 2020 г.). «Влияние квантовой криптографии и квантовых вычислений на безопасность». Network Security . 2020 (9): 9–15. doi :10.1016/S1353-4858(20)30105-7. ISSN  1353-4858. S2CID  222349414.
127. Лю, Юн; Чен, Яоцзянь; Го, Чу; Сун, Цзявэй; Ши, Синьминь; Ган, Лин; У, Вэньчжао; Ву, Вэй; Фу, Хаохуань; Лю, Синь; Чен, Дексун; Чжао, Чжифэн; Ян, Гуанвэнь; Гао, Цзянган (16 января 2024 г.). «Проверка экспериментов по квантовому преимуществу с многократным сокращением тензорной сети амплитуды». Письма о физических отзывах . 132 (3): 030601. arXiv : 2212.04749 . Бибкод : 2024PhRvL.132c0601L. doi : 10.1103/PhysRevLett.132.030601. ISSN  0031-9007. PMID  38307065.
128. Монро, Дон (декабрь 2022 г.). «Квантовые компьютеры и Вселенная». Сообщения ACM.
129. Свэйн, Мэтт (20 июня 2023 г.). «PsiQuantum видит 700-кратное сокращение требований к вычислительным ресурсам для взлома эллиптической кривой криптографии с помощью отказоустойчивого квантового компьютера». Quanrum Insider .
130. Унру, Билл (1995). «Поддержание когерентности в квантовых компьютерах». Physical Review A. 51 ( 2): 992–997. arXiv : hep-th/9406058 . Bibcode : 1995PhRvA..51..992U. doi : 10.1103/PhysRevA.51.992. PMID  9911677. S2CID  13980886.
131. Дэвис, Пол (6 марта 2007 г.). «Значение голографической вселенной для квантовой информационной науки и природы физического закона». arXiv : quant-ph/0703041 .
132. Regan, KW (23 апреля 2016 г.). «Квантовое превосходство и сложность». Потерянное письмо Гёделя и P=NP .
133. Калай, Гил (май 2016 г.). «Загадка квантового компьютера» (PDF) . Уведомления AMS . 63 (5): 508–516.
134. Ринотт, Йосеф; Шохам, Томер; Калай, Гил (13 июля 2021 г.). «Статистические аспекты демонстрации квантового превосходства». arXiv : 2008.05177 [quant-ph].
135. Дьяконов, Михаил (15 ноября 2018 г.). «Дело против квантовых вычислений». IEEE Spectrum . Получено 3 декабря 2019 г.
136. Дьяконов, Михаил (24 марта 2020 г.). Будет ли у нас когда-нибудь квантовый компьютер?. Springer. ISBN 9783030420185. Получено 22 мая 2020 г. .^{[ нужна страница ]}
137. Рассел, Джон (10 января 2019 г.). «Обновление IBM Quantum: запуск Q System One, новые сотрудники и планы центра контроля качества». HPCwire . Получено 9 января 2023 г.
138. Таккино, Франческо; Кьеза, Алессандро; Карретта, Стефано; Джераче, Дарио (19 декабря 2019 г.). «Квантовые компьютеры как универсальные квантовые симуляторы: современное состояние и перспективы». Передовые квантовые технологии . 3 (3): 1900052. arXiv : 1907.03505 . дои : 10.1002/qute.201900052. ISSN  2511-9044. S2CID  195833616.
139. Громблинг и Горовиц 2019, стр. 127.
140. Громблинг и Горовиц 2019, стр. 114.
141. Громблинг и Горовиц 2019, стр. 119.
142. Грэмблинг и Горовиц 2019, стр. 126.
143. Mackie, Kurt (8 февраля 2024 г.). «Microsoft Quantum Computing Getting DARPA Funding». rcpmag.com . Получено 9 февраля 2024 г. .
144. Gent, Edd (5 июля 2023 г.). «Microsoft хочет построить квантовый суперкомпьютер в течение десятилетия». Singularity Hub . Получено 18 октября 2024 г.
145. Lucian Armasu (22 ноября 2016 г.). «Microsoft стремится создать первый в мире топологический квантовый компьютер». Tom's Hardware . Получено 18 октября 2024 г.
146. Леонг, Кельвин; Санг, Анна (ноябрь 2022 г.). «Что бизнес-менеджеры должны знать о квантовых вычислениях?» (PDF) . Журнал междисциплинарных наук . Получено 13 августа 2023 г. .
147. Гибни, Элизабет (2 октября 2019 г.). «Квантовая золотая лихорадка: частное финансирование, вливающееся в квантовые стартапы». Nature . 574 (7776): 22–24. Bibcode :2019Natur.574...22G. doi :10.1038/d41586-019-02935-4. PMID  31578480. S2CID  203626236.
148. Родриго, Крис Миллс (12 февраля 2020 г.). «Бюджетное предложение Трампа увеличивает финансирование искусственного интеллекта и квантовых вычислений». The Hill . Получено 11 июля 2021 г.
149. Бионди, Маттео; Хайд, Анна; Хенке, Николаус; Мор, Нико; Паутассо, Лоренцо; и др. (14 декабря 2021 г.). «Варианты использования квантовых вычислений становятся реальностью — что вам нужно знать». McKinsey & Company . Получено 1 апреля 2022 г.
150. Нильсен и Чуанг 2010, стр. 29.
151. Нильсен и Чуанг 2010, стр. 126.
152. Нильсен и Чуанг 2010, стр. 41.
153. Нильсен и Чуанг 2010, стр. 201.
154. Бернстайн, Итан; Вазирани, Умеш (1997). «Квантовая теория сложности». Журнал SIAM по вычислениям . 26 (5): 1411–1473. CiteSeerX 10.1.1.144.7852 . doi :10.1137/S0097539796300921. 

Источники

• Ааронсон, Скотт (2013). Квантовые вычисления со времен Демокрита . Cambridge University Press. doi :10.1017/CBO9780511979309. ISBN 978-0-521-19956-8. OCLC  829706638.
• Громблинг, Эмили; Горовиц, Марк, ред. (2019). Квантовые вычисления: прогресс и перспективы . Вашингтон, округ Колумбия: The National Academies Press. doi : 10.17226/25196. ISBN 978-0-309-47970-7. OCLC  1091904777. S2CID  125635007.
• Мермин, Н. Дэвид (2007). Квантовая информатика: Введение . doi :10.1017/CBO9780511813870. ISBN 978-0-511-34258-5. OCLC  422727925.
• Нильсен, Майкл ; Чуан, Айзек (2010). Квантовые вычисления и квантовая информация (10-е юбилейное издание). doi :10.1017/CBO9780511976667. ISBN 978-0-511-99277-3. OCLC  700706156. S2CID  59717455.
• Shor, Peter W. (1994). Алгоритмы квантовых вычислений: дискретные логарифмы и факторизация . Симпозиум по основам компьютерной науки . Санта-Фе, Нью-Мексико : IEEE . стр. 124–134. doi :10.1109/SFCS.1994.365700. ISBN 978-0-8186-6580-6.

Дальнейшее чтение

Учебники

• Акама, Сейки (2014). Элементы квантовых вычислений: история, теории и инженерные приложения . Springer. doi :10.1007/978-3-319-08284-4. ISBN 978-3-319-08284-4. OCLC  884786739.
• Бененти, Джулиано; Казати, Джулио; Россини, Давиде; Стрини, Джулиано (2019). Принципы квантовых вычислений и информации: комплексный учебник (2-е изд.). дои : 10.1142/10909. ISBN 978-981-3237-23-0. OCLC  1084428655. S2CID  62280636.
• Бернхардт, Крис (2019). Квантовые вычисления для всех . MIT Press. ISBN 978-0-262-35091-4. OCLC  1082867954.
• Хидари, Джек Д. (2021). Квантовые вычисления: прикладной подход (2-е изд.). doi : 10.1007/978-3-030-83274-2. ISBN 978-3-03-083274-2. OCLC  1272953643. S2CID  238223274.
• Хироси, Имаи; Масахито, Хаяси, ред. (2006). Квантовые вычисления и информация: от теории к эксперименту . Темы прикладной физики. Том 102. doi :10.1007/3-540-33133-6. ISBN 978-3-540-33133-9.
• Хьюз, Сиаран; Айзексон, Джошуа; Перри, Анастасия; Сан, Ранбел Ф.; Тернер, Джессика (2021). Квантовые вычисления для квантовых любознательных (PDF) . doi :10.1007/978-3-030-61601-4. ISBN 978-3-03-061601-4. OCLC  1244536372. S2CID  242566636.
• Jaeger, Gregg (2007). Квантовая информация: обзор . doi :10.1007/978-0-387-36944-0. ISBN 978-0-387-36944-0. OCLC  186509710.
• Джонстон, Эрик Р.; Харриган, Ник; Химено-Сеговия, Мерседес (2019). Программирование квантовых компьютеров: основные алгоритмы и примеры кода . O'Reilly Media, Incorporated. ISBN 978-1-4920-3968-6. OCLC  1111634190.
• Кей, Филлип; Лафламм, Рэймонд ; Моска, Мишель (2007). Введение в квантовые вычисления . OUP Oxford. ISBN 978-0-19-857000-4. OCLC  85896383.
• Китаев, Алексей Ю.; Шен, Александр Х.; Вялый, Михаил Н. (2002). Классические и квантовые вычисления . Американское математическое общество. ISBN 978-0-8218-3229-5. OCLC  907358694.
• Кургалин, Сергей; Борзунов, Сергей (2021). Краткое руководство по квантовым вычислениям: алгоритмы, упражнения и реализации. Springer. doi :10.1007/978-3-030-65052-0. ISBN 978-3-030-65052-0.
• Штольце, Иоахим; Сутер, Дитер (2004). Квантовые вычисления: краткий курс от теории к эксперименту . дои : 10.1002/9783527617760. ISBN 978-3-527-61776-0. OCLC  212140089.
• Сасскинд, Леонард ; Фридман, Арт (2014). Квантовая механика: теоретический минимум . Нью-Йорк : Basic Books . ISBN 978-0-465-08061-8.
• Вихерт, Андреас (2020). Принципы квантового искусственного интеллекта: квантовое решение проблем и машинное обучение (2-е изд.). doi : 10.1142/11938. ISBN 978-981-12-2431-7. OCLC  1178715016. S2CID  225498497.
• Вонг, Томас (2022). Введение в классические и квантовые вычисления (PDF) . Rooted Grove. ISBN 979-8-9855931-0-5. OCLC  1308951401. Архивировано из оригинала (PDF) 29 января 2022 г. . Получено 6 февраля 2022 г. .
• Цзэн, Бэй; Чен, Се; Чжоу, Дуань-Лу; Вэнь, Сяо-Ган (2019). Квантовая информация встречается с квантовой материей . arXiv : 1508.02595 . дои : 10.1007/978-1-4939-9084-9. ISBN 978-1-4939-9084-9. OCLC  1091358969. S2CID  118528258.

Научные статьи

• Эббот, Дерек ; Деринг, Чарльз Р .; Кейвс, Карлтон М.; Лидар , Дэниел М.; Брандт , Говард Э .; и др. (2003). «Мечты против реальности: пленарное заседание по квантовым вычислениям». Квантовая обработка информации . 2 (6): 449–472. arXiv : quant-ph/0310130 . Bibcode : 2003QuIP....2..449A. doi : 10.1023/B:QINP.0000042203.24782.9a. hdl : 2027.42/45526. S2CID  34885835.
• Бертиом, Андре (1 декабря 1998 г.). «Квантовые вычисления». Руководство по решению задач квантовой механики . стр. 233–234. doi :10.1142/9789814541893_0016. ISBN 978-981-4541-88-6. S2CID  128255429 – через Semantic Scholar.
• ДиВинченцо, Дэвид П. (2000). «Физическая реализация квантовых вычислений». Fortschritte der Physik . 48 (9–11): 771–783. arXiv : Quant-ph/0002077 . Бибкод : 2000ForPh..48..771D. doi :10.1002/1521-3978(200009)48:9/11<771::AID-PROP771>3.0.CO;2-E. S2CID  15439711.
• ДиВинченцо, Дэвид П. (1995). «Квантовые вычисления». Science . 270 (5234): 255–261. Bibcode :1995Sci...270..255D. CiteSeerX  10.1.1.242.2165 . doi :10.1126/science.270.5234.255. S2CID  220110562.В таблице 1 приведены времена переключения и дефазировки для различных систем.
• Фейнман, Ричард (1982). «Моделирование физики с помощью компьютеров». Международный журнал теоретической физики . 21 (6–7): 467–488. Bibcode :1982IJTP...21..467F. CiteSeerX  10.1.1.45.9310 . doi :10.1007/BF02650179. S2CID  124545445.
• Йетнер, Валентин (2021). «Квантовый императив: решение правового аспекта квантовых компьютеров». Мораль и машины . 1 (1): 52–59. doi : 10.5771/2747-5174-2021-1-52 . S2CID  236664155.
• Krantz, P.; Kjaergaard, M.; Yan, F.; Orlando, TP; Gustavsson, S.; Oliver, WD (17 июня 2019 г.). «Руководство квантового инженера по сверхпроводящим кубитам». Applied Physics Reviews . 6 (2): 021318. arXiv : 1904.06560 . Bibcode :2019ApPRv...6b1318K. doi :10.1063/1.5089550. ISSN  1931-9401. S2CID  119104251.
• Митчелл, Ян (1998). «Вычислительная мощность в 21 веке: закон Мура и далее».
• Саймон, Дэниел Р. (1994). «О силе квантовых вычислений». Издательство компьютерного общества Института инженеров по электротехнике и электронике.

Внешние ссылки

• Медиа, связанные с квантовым компьютером на Wikimedia Commons
• Учебные материалы по квантовым вычислениям в Викиверситете
• Стэнфордская энциклопедия философии : «Квантовые вычисления» Амита Хагара и Майкла Э. Куффаро.
• «Квантовые вычисления, теория», Энциклопедия математики , EMS Press , 2001 [1994]
• Квантовые вычисления для очень любознательных Энди Матущака и Майкла Нильсена

Лекции

• Квантовые вычисления для решительных – 22 видеолекции Майкла Нильсена
• Видеолекции Дэвида Дойча
• Лекции в Институте Анри Пуанкаре (слайды и видео)
• Онлайн-лекция «Введение в квантовые вычисления», Эдвард Герджой (2008)
• Ломонако, Сэм. Четыре лекции по квантовым вычислениям, прочитанные в Оксфордском университете в июле 2006 г.