Математическая константа

Фиксированный номер, получивший имя

Длина окружности с диаметром 1 равна π .

Математическая константа — это число , значение которого зафиксировано однозначным определением, часто обозначаемым специальным символом (например, буквой алфавита ) или именами математиков для облегчения его использования в различных математических задачах . ^[1] Константы возникают во многих областях математики , причем такие константы, как e и π, встречаются в таких разнообразных контекстах, как геометрия , теория чисел , статистика и исчисление .

Некоторые константы возникают естественным образом из фундаментального принципа или внутреннего свойства, например, соотношение между длиной окружности и диаметром круга ( π ). Другие константы примечательны скорее по историческим причинам, чем из-за своих математических свойств. Наиболее популярные константы изучались на протяжении веков и вычислялись с точностью до многих десятичных знаков.

Все именованные математические константы являются определяемыми числами и, как правило, также вычисляемыми числами ( константа Хайтина является существенным исключением).

Основные математические константы

Это константы, с которыми можно столкнуться в ходе довузовского образования во многих странах.

постоянная Пифагора√ 2

Квадратный корень из 2 равен длине гипотенузы прямоугольного треугольника с катетами длиной 1.

Квадратный корень из 2 , часто называемый корнем 2 или постоянной Пифагора и записываемый как √ 2 , является уникальным положительным действительным числом, которое при умножении само на себя дает число 2. Его точнее называть главным квадратным корнем из 2 , чтобы отличать его от отрицательного числа с тем же свойством.

Геометрически квадратный корень из 2 равен длине диагонали квадрата со стороной в одну единицу длины ; это следует из теоремы Пифагора . Это иррациональное число, возможно, первое число, известное как таковое, и алгебраическое число . Его числовое значение, усеченное до 50 знаков после запятой, равно:

1.41421 35623 73095 04880 16887 24209 69807 85696 71875 37694... (последовательность A002193 в OEIS ).

В качестве альтернативы, быстрое приближение 99/70 (≈ 1,41429) для квадратного корня из двух часто использовалось до повсеместного использования электронных калькуляторов и компьютеров . Несмотря на то, что знаменатель равен всего 70, он отличается от правильного значения менее чем на 1/10 000 (приблизительно 7,2 × 10 ⁻⁵ ).

Ее простая цепная дробь является периодической и задается формулой:

${\displaystyle {\sqrt {2}}=1+{\frac {1}{2+{\frac {1}{2+{\frac {1}{2+{\frac {1}{\ddots }}}}}}}}}$

постоянная Архимедаπ

Площадь круга равна π , умноженному на заштрихованную площадь. Площадь единичного круга равна π .

Константа π (пи) имеет естественное определение в евклидовой геометрии как отношение длины окружности к диаметру круга. Ее можно найти во многих других местах математики: например, в гауссовом интеграле , комплексных корнях из единицы и распределениях Коши в вероятности . Однако ее повсеместность не ограничивается чистой математикой. Она появляется во многих формулах в физике, и несколько физических констант наиболее естественно определяются с помощью π или ее обратной величины, вынесенной за скобки. Например, волновая функция основного состояния атома водорода имеет вид

${\displaystyle \psi (\mathbf {r} )={\frac {1}{\sqrt {\pi {a_{0}}^{3}}}}e^{-r/a_{0}},}$

где - радиус Бора . ${\displaystyle a_{0}}$

π — иррациональное число , трансцендентное число и алгебраический период .

Числовое значение числа π приблизительно равно:

3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510... (последовательность A000796 в OEIS ).

Необычайно хорошие приближения дают дроби 22/7 и 355/113 .

Запоминание и вычисление все большего количества цифр числа π является стремлением к мировым рекордам.

Число Эйлерае

Экспоненциальный рост (зеленый) описывает многие физические явления.

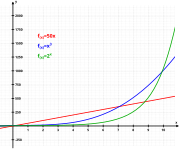
Число Эйлера e , также известное как константа экспоненциального роста , встречается во многих областях математики, и одним из возможных его определений является значение следующего выражения:

${\displaystyle e=\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}}$

Константа e неразрывно связана с экспоненциальной функцией . ${\displaystyle x\mapsto e^{x}}$

Швейцарский математик Якоб Бернулли обнаружил, что e возникает в сложных процентах : если счет начинается с 1 доллара и приносит проценты по годовой ставке R , то по мере того, как количество периодов начисления сложных процентов в году стремится к бесконечности (ситуация, известная как непрерывное начисление сложных процентов ), сумма денег в конце года приблизится к e ^R долларов.

Константа e также имеет приложения к теории вероятностей , где она возникает способом, не связанным с экспоненциальным ростом. В качестве примера предположим, что игровой автомат с вероятностью выигрыша один из n играет n раз, тогда для больших n (например, один миллион) вероятность того, что ничего не будет выиграно, будет стремиться к 1/ e , когда n стремится к бесконечности.

Другое применение e , частично обнаруженное Якобом Бернулли вместе с французским математиком Пьером Раймоном де Монмором , заключается в проблеме расстройств , также известной как проблема проверки шляпы . ^[2] Здесь n гостей приглашаются на вечеринку, и у двери каждый гость сдает свою шляпу дворецкому, который затем кладет их в маркированные коробки. Дворецкий не знает имен гостей и, следовательно, должен положить их в коробки, выбранные случайным образом. Задача де Монмора: какова вероятность того, что ни одна из шляп не будет положена в нужную коробку. Ответ:

${\displaystyle p_{n}=1-{\frac {1}{1!}}+{\frac {1}{2!}}-{\frac {1}{3!}}+\cdots +(-1)^{n}{\frac {1}{n!}}}$

который, когда n стремится к бесконечности, приближается к 1/ e .

е — иррациональное число и трансцендентное число.

Числовое значение e приблизительно равно:

2.71828 18284 59045 23536 02874 71352 66249 77572 47093 69995... (последовательность A001113 в OEIS ).

Мнимая единицая

Мнимая единица i в комплексной плоскости . Действительные числа лежат на горизонтальной оси, а мнимые числа лежат на вертикальной оси

Мнимая единица или единичное мнимое число , обозначаемое как i , является математической концепцией, которая расширяет систему действительных чисел до комплексной системы чисел . Основное свойство мнимой единицы заключается в том, что i ² = −1 . Термин « мнимая » был придуман, потому что не существует ( действительного ) числа, имеющего отрицательный квадрат . ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {C} .}$

На самом деле существует два комплексных квадратных корня из −1, а именно i и − i , так же как существует два комплексных квадратных корня из любого другого действительного числа (за исключением нуля , у которого есть один двойной квадратный корень).

В контекстах, где символ i неоднозначен или проблематичен, иногда используется j или греческая йота ( ι ). Это особенно актуально в электротехнике и инженерии систем управления , где мнимая единица часто обозначается как j , поскольку i обычно используется для обозначения электрического тока .

Константы в высшей математике

Это константы, которые часто встречаются в высшей математике .

Золотое сечениеφ

Золотые прямоугольники в правильном икосаэдре

${\displaystyle F_{n}={\frac {\varphi ^{n}-(1-\varphi )^{n}}{\sqrt {5}}}}$

Явная формула для n- го числа Фибоначчи, включающая золотое сечение φ .

Число φ , также называемое золотым сечением , часто встречается в геометрии , особенно в фигурах с пентагональной симметрией . Действительно, длина диагонали правильного пятиугольника равна φ , умноженному на его сторону. Вершины правильного икосаэдра являются вершинами трех взаимно ортогональных золотых прямоугольников . Кроме того, оно появляется в последовательности Фибоначчи , связанной с ростом посредством рекурсии . ^[3] Кеплер доказал, что это предел отношения последовательных чисел Фибоначчи. ^[4] Золотое сечение имеет самую медленную сходимость среди всех иррациональных чисел. ^[5] По этой причине это один из худших случаев теоремы Лагранжа об аппроксимации и экстремальный случай неравенства Гурвица для диофантовых приближений . Возможно, именно поэтому углы, близкие к золотому сечению, часто появляются в филлотаксисе (росте растений). ^[6] Оно приблизительно равно:

1.61803 39887 49894 84820 45868 34365 63811 77203 09179 80576... (последовательность A001622 в OEIS ).

или, точнее, ${\displaystyle {\frac {1+{\sqrt {5}}}{2}}.}$

Константа Эйлера–Машерони γ

Площадь между двумя кривыми (красная) стремится к пределу, а именно к константе Эйлера-Маскерони.

Постоянная Эйлера или постоянная Эйлера–Маскерони определяется как предельная разность между гармоническим рядом и натуральным логарифмом :

${\displaystyle {\begin{aligned}\gamma &=\lim _{n\to \infty }\left(-\ln n+\sum _{k=1}^{n}{\frac {1}{k}}\right)\\[5px]\end{aligned}}}$

Он часто встречается в математике, особенно в теоретическом контексте чисел, таком как третья теорема Мертенса или скорость роста функции делителей . Он имеет отношение к гамма-функции и ее производным, а также к дзета-функции , и существует много различных интегралов и рядов, включающих . ${\displaystyle \gamma }$

Несмотря на повсеместность константы Эйлера-Маскерони, многие ее свойства остаются неизвестными. Это включает в себя основные открытые вопросы о том, является ли она рациональным или иррациональным числом и является ли она алгебраической или трансцендентной. Фактически, была описана как математическая константа, «затененная только и по важности». ^[7] ${\displaystyle \gamma }$ ${\displaystyle \pi }$ ${\displaystyle e}$

Числовое значение приблизительно равно: ${\displaystyle \gamma }$

0,57721 56649 01532 86060 65120 90082 40243 10421 59335 93992... (последовательность A001620 в OEIS ).

Константа Апери ζ(3)

Константа Апери определяется как сумма обратных величин кубов натуральных чисел: Это особое значение дзета -функции Римана при . Поиск точного значения этой константы через другие известные константы и элементарные функции возник, когда Эйлер знаменитым образом решил Базельскую проблему , дав . На сегодняшний день такое значение не найдено, и предполагается, что его нет. ^[8] Однако существует множество представлений в виде бесконечных рядов. $${\displaystyle \zeta (3)=\sum _{n=1}^{\infty }{\frac {1}{n^{3}}}=1+{\frac {1}{2^{3}}}+{\frac {1}{3^{3}}}+{\frac {1}{4^{3}}}+{\frac {1}{5^{3}}}\cdots }$$ ${\displaystyle \zeta (s)}$ ${\displaystyle s=3}$ ${\displaystyle \zeta (2)={\frac {1}{6}}\pi ^{2}}$ ${\displaystyle \zeta (3)}$

Константа Апери естественным образом возникает в ряде физических задач, в том числе в членах второго и третьего порядка гиромагнитного отношения электрона , вычисляемых с использованием квантовой электродинамики . ^[9]

${\displaystyle \zeta (3)}$Известно, что является иррациональным числом , что было доказано французским математиком Роже Апери в 1979 году. Однако неизвестно, является ли оно алгебраическим или трансцендентным.

Числовое значение постоянной Апери приблизительно равно:

1.20205 69031 59594 28539 97381 61511 44999 07649 86292 34049... (последовательность A002117 в OEIS ).

Постоянная КаталанаГ

Константа Каталана определяется переменной суммой обратных величин нечетных квадратов чисел :

${\displaystyle G=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)^{2}}}={\frac {1}{1^{2}}}-{\frac {1}{3^{2}}}+{\frac {1}{5^{2}}}-{\frac {1}{7^{2}}}+{\frac {1}{9^{2}}}-\cdots }$

Это особое значение бета-функции Дирихле при . Константа Каталана часто появляется в комбинаторике и теории чисел , а также за пределами математики, например, при расчете распределения масс спиральных галактик . ^[10] ${\displaystyle \beta (s)}$ ${\displaystyle s=2}$

Вопросы об арифметической природе этой константы также остаются без ответа, поскольку ее называют «возможно, самой базовой константой, иррациональность и трансцендентность которой (хотя и сильно подозреваемая) остаются недоказанными». ^[11] Существует множество интегральных и рядных представлений константы Каталана. ${\displaystyle G}$

Назван в честь французского и бельгийского математика Шарля Эжена Каталана .

Числовое значение приблизительно равно: ${\displaystyle G}$

0,91596 55941 77219 01505 46035 14932 38411 07741 49374 28167... (последовательность A006752 в OEIS ).

Константы Фейгенбаума α и δ

Диаграмма бифуркации логистической карты.

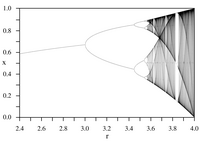
Итерации непрерывных отображений служат простейшими примерами моделей для динамических систем . ^[12] Названные в честь математического физика Митчелла Фейгенбаума , две константы Фейгенбаума появляются в таких итерационных процессах: они являются математическими инвариантами логистических отображений с квадратичными точками максимума ^[7] и их бифуркационных диаграмм . В частности, константа α представляет собой отношение между шириной зубца и шириной одного из двух его подзублатов, а константа δ представляет собой предельное отношение каждого интервала бифуркации к следующему между каждой бифуркацией удвоения периода .

Логистическая карта — это полиномиальное отображение, часто приводимое в качестве архетипического примера того, как хаотическое поведение может возникнуть из очень простых нелинейных динамических уравнений. Карта была популяризирована в основополагающей статье 1976 года австралийского биолога Роберта Мэя [ ^13] отчасти как дискретная временная демографическая модель, аналогичная логистическому уравнению, впервые созданному Пьером Франсуа Верхюльстом . Разностное уравнение предназначено для охвата двух эффектов воспроизводства и голодания.

Константы Фейгенбаума в теории бифуркаций аналогичны π в геометрии и e в исчислении . Ни одна из них не известна как иррациональная или даже трансцендентная. Однако существуют доказательства их универсальности . ^[14]

Соответствующие приблизительные числовые значения δ и α следующие:

4.66920 16091 02990 67185 32038 20466 20161 72581 85577 47576... (последовательность A006890 в OEIS ).

2.50290 78750 95892 82228 39028 73218 21578 63812 71376 72714... (последовательность A006891 в OEIS ).

Математические курьезы

Простые представители множеств чисел

${\displaystyle c=\sum _{j=1}^{\infty }10^{-j!}=0.\underbrace {\overbrace {110001} ^{3!{\text{ digits}}}000000000000000001} _{4!{\text{ digits}}}000\dots }$

Константа Лиувилля — простой пример трансцендентного числа .

Некоторые константы, такие как квадратный корень из 2 , постоянная Лиувилля и постоянная Чамперноуна :

${\displaystyle C_{10}=0.{\color {blue}{1}}2{\color {blue}{3}}4{\color {blue}{5}}6{\color {blue}{7}}8{\color {blue}{9}}10{\color {blue}{11}}12{\color {blue}{13}}14{\color {blue}{15}}16\dots }$

На этой вавилонской глиняной табличке приведено приближенное значение квадратного корня из 2 в виде четырех шестидесятеричных цифр: 1; 24, 51, 10, что соответствует точности около шести десятичных цифр. ^[15]

не являются важными математическими инвариантами, но сохраняют интерес, будучи простыми представителями специальных множеств чисел, иррациональных чисел , ^[16] трансцендентных чисел ^[17] и нормальных чисел (по основанию 10) ^[18] соответственно. Открытие иррациональных чисел обычно приписывается пифагорейцу Гиппасу из Метапонта , который доказал, скорее всего геометрически, иррациональность квадратного корня из 2. Что касается постоянной Лиувилля, названной в честь французского математика Жозефа Лиувилля , то это было первое число, трансцендентность которого была доказана. ^[19]

Постоянная Хайтина Ω

В подразделе компьютерных наук алгоритмической теории информации константа Хайтина — это действительное число, представляющее вероятность остановки случайно выбранной машины Тьюринга , образованное из конструкции аргентинско - американского математика и ученого-компьютерщика Грегори Хайтина . Хотя константа Хайтина и невычислима , было доказано, что она трансцендентна и нормальна . Константа Хайтина не универсальна и сильно зависит от числового кодирования, используемого для машин Тьюринга; однако ее интересные свойства не зависят от кодирования.

Обозначение

Представление констант

Числовое значение константы принято выражать, давая ее десятичное представление (или только первые несколько ее цифр). По двум причинам это представление может вызывать проблемы. Во-первых, хотя все рациональные числа имеют конечное или постоянно повторяющееся десятичное разложение, иррациональные числа не имеют такого выражения, что делает невозможным их полное описание таким образом. Кроме того, десятичное разложение числа не обязательно уникально. Например, два представления 0,999... и 1 эквивалентны ^{[20] [21]} в том смысле, что они представляют одно и то же число.

Вычисление цифр десятичного представления констант было обычным делом на протяжении многих столетий. Например, немецкий математик Людольф ван Кейлен из 16-го века провел большую часть своей жизни, вычисляя первые 35 цифр числа пи. ^[22] С помощью компьютеров и суперкомпьютеров некоторые математические константы, включая π, e и квадратный корень из 2, были вычислены с точностью более ста миллиардов цифр. Были разработаны быстрые алгоритмы , некоторые из которых — как для константы Апери — неожиданно быстры.

${\displaystyle G=\left.{\begin{matrix}3\underbrace {\uparrow \ldots \uparrow } 3\\\underbrace {\vdots } \\3\uparrow \uparrow \uparrow \uparrow 3\end{matrix}}\right\}{\text{64 layers}}}$

Число Грэма, определенное с использованием нотации Кнута со стрелкой вверх .

Некоторые константы настолько отличаются от обычных, что была изобретена новая нотация для их разумного представления. Число Грэма иллюстрирует это, поскольку используется нотация Кнута со стрелкой вверх . ^{[23] [24]}

Может быть интересно представить их с помощью непрерывных дробей для выполнения различных исследований, включая статистический анализ. Многие математические константы имеют аналитическую форму , то есть их можно построить с помощью известных операций, которые легко поддаются вычислениям. Однако не все константы имеют известные аналитические формы; константа Гроссмана ^[25] и константа Фойаса ^[26] являются примерами.

Символизация и наименование констант

Обозначение констант буквами часто используется для того, чтобы сделать запись более краткой. Распространенное соглашение , введенное Рене Декартом в 17 веке и Леонардом Эйлером в 18 веке, заключается в использовании строчных букв из начала латинского или греческого алфавита при работе с константами в целом. ${\displaystyle a,b,c,\dots }$ ${\displaystyle \alpha ,\beta ,\,\gamma ,\dots }$

Однако для более важных констант символы могут быть более сложными и иметь дополнительную букву, звездочку , цифру, лемнискату или использовать другие алфавиты, такие как иврит , кириллица или готика . ^[24]

константа Эрдеша–Борвейна константа Эмбри–Трефетена константа Бруна для простых чисел-близнецов константы Чамперноуна кардинальное число алеф ноль ${\displaystyle E_{B}}$
${\displaystyle \beta ^{*}}$
${\displaystyle B_{2}}$
${\displaystyle C_{b}}$
${\displaystyle \aleph _{0}}$

Примеры различных видов обозначений констант.

Иногда символ, представляющий константу, представляет собой целое слово. Например, 9-летний племянник американского математика Эдварда Каснера придумал названия гугол и гуголплекс . ^{[24] [27]}

${\displaystyle \mathrm {googol} =10^{100}\,\ ,\ \mathrm {googolplex} =10^{\mathrm {googol} }=10^{10^{100}}}$

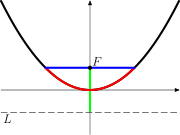
Другие названия связаны либо со значением константы ( универсальная параболическая константа , константа-близнец , ...), либо с конкретным человеком ( константа Серпинского , константа Джозефсона и т. д.).

Универсальная параболическая константа — это отношение длины дуги параболического сегмента (красный), образованного latus rectum (синий), для любой параболы к фокальному параметру (зеленый).

Избранные математические константы

Используемые сокращения:

Gen – Общие сведения , NuT – Теория чисел , ChT – Теория хаоса , Com – Комбинаторика , Ana – Математический анализ

Смотрите также

• Словарь математических символов
• Инвариант (математика)
• Список математических констант
• Список номеров
• Физическая константа
• Список физических констант

Примечания

1. Weisstein, Eric W. "Constant". mathworld.wolfram.com . Получено 2020-08-08 .
2. Гринстед, CM; Снелл, JL "Введение в теорию вероятностей". стр. 85. Архивировано из оригинала 2011-07-27 . Получено 2007-12-09 .
3. Ливио, Марио (2002). Золотое сечение: История Фи, самого удивительного числа в мире. Нью-Йорк: Broadway Books. ISBN 0-7679-0815-5.
4. Тэтерсалл, Джеймс (2005). Элементарная теория чисел в девяти главах (2-е изд. ).
5. "Тайная жизнь непрерывных дробей"
6. Числа Фибоначчи и природа. Часть 2: Почему золотое сечение — «лучшее» расположение?, из книги доктора Рона Нотта «Числа Фибоначчи и золотое сечение», получено 29 ноября 2012 г.
7. Finch, Steven (2003). Математические константы . Cambridge University Press . стр. 67. ISBN 0-521-81805-2.
8. Симосон, Эндрю (2023-03-01). «В погоне за Дзетой-3». The Mathematical Intelligencer . 45 (1): 85–87. doi :10.1007/s00283-022-10184-z. ISSN  1866-7414.
9. Стивен Финч. "Константа Апери". MathWorld .
10. Wyse, AB ; Mayall, NU (январь 1942 г.), «Распределение массы в спиральных туманностях Мессье 31 и Мессье 33», The Astrophysical Journal , 95 : 24–47, Bibcode : 1942ApJ....95...24W, doi : 10.1086/144370
11. Бейли, Дэвид Х.; Борвейн, Джонатан М.; Мэттингли, Эндрю; Уайтвик, Гленн (2013), «Вычисление ранее недоступных цифр и константы Каталана», Notices of the American Mathematical Society , 60 (7): 844–854, doi : 10.1090/noti1015 , MR  3086394 ${\displaystyle \pi ^{2}}$
12. Коллет и Экман (1980). Итерированные отображения на интервале как динамические системы . Биркхаузер. ISBN 3-7643-3026-0.
13. Мэй, Роберт (1976). Теоретическая экология: принципы и приложения . Blackwell Scientific Publishers. ISBN 0-632-00768-0.
14. Ланфорд III, Оскар (1982). «Компьютерное доказательство гипотез Фейгенбаума». Bull. Amer. Math. Soc . 6 (3): 427–434. doi : 10.1090/S0273-0979-1982-15008-X .
15. Фаулер, Дэвид ; Элеанор Робсон (ноябрь 1998 г.). «Приближения квадратного корня в старой вавилонской математике: YBC 7289 в контексте». Historia Mathematica . 25 (4): 368. doi : 10.1006/hmat.1998.2209 .
    Фотография, иллюстрация и описание таблички root(2) из ​​Йельской вавилонской коллекции
    Фотографии высокого разрешения, описания и анализ таблички root(2) (YBC 7289) из Йельской вавилонской коллекции
16. Богомольный, Александр . «Квадратный корень из 2 иррационален».
17. Обри Дж. Кемпнер (октябрь 1916 г.). «О трансцендентных числах». Труды Американского математического общества . 17 (4). Труды Американского математического общества, т. 17, № 4: 476–482. doi : 10.2307/1988833 . JSTOR  1988833.
18. Чамперноун, Дэвид (1933). «Построение нормальных десятичных дробей в десятичной шкале». Журнал Лондонского математического общества . 8 (4): 254–260. doi :10.1112/jlms/s1-8.4.254.
19. Вайсштейн, Эрик В. «Константа Лиувилля». MathWorld .
20. Рудин, Уолтер (1976) [1953]. Принципы математического анализа (3-е изд.). Макгроу-Хилл. Теорема 3.26, стр. 61. ISBN 0-07-054235-X.
21. Стюарт, Джеймс (1999). Исчисление: Ранние трансцендентали (4-е изд.). Брукс/Коул. стр. 706. ISBN 0-534-36298-2.
22. Людольф ван Кейлен. Архивировано 07.07.2015 на Wayback Machine – биография в архиве истории математики MacTutor.
23. Кнут, Дональд (1976). «Математика и компьютерные науки: преодоление конечности. Достижения в нашей способности к вычислениям существенно приближают нас к предельным ограничениям». Science . 194 (4271): 1235–1242. doi :10.1126/science.194.4271.1235. PMID  17797067. S2CID  1690489.
24. "математические константы". Архивировано из оригинала 2012-09-07 . Получено 2007-11-27 .
25. Вайсштейн, Эрик В. "Константа Гроссмана". MathWorld .
26. Вайсштейн, Эрик В. «Константа Фойаса». MathWorld .
27. Эдвард Каснер и Джеймс Р. Ньюман (1989). Математика и воображение . Microsoft Press . стр. 23.
28. "Рекорды, установленные y-cruncher". www.numberworld.org . Получено 2024-08-22 .
29. Weisstein, Eric W. "Константные цифры Глейшера-Кинкелина". mathworld.wolfram.com . Получено 2024-10-05 .
30. Weisstein, Eric W. "Постоянные цифры Хинчина". mathworld.wolfram.com . Получено 2024-10-05 .
31. "A006890 - OEIS". oeis.org . Получено 2024-08-22 .
32. "A006891 - OEIS". oeis.org . Получено 2024-08-22 .

Внешние ссылки

• Константы – из Wolfram MathWorld
• Обратный символьный калькулятор (CECM, ISC) (рассказывает, как заданное число может быть построено из математических констант)
• Онлайновая энциклопедия целочисленных последовательностей (OEIS)
• Инвертор Саймона Плуффа
• Страница Стивена Финча о математических константах (ССЫЛКА НЕ РАБОТАЕТ)
• Стивен Р. Финч, «Математические константы», Энциклопедия математики и ее приложений , Cambridge University Press (2003).
• Страница Ксавье Гурдона и Паскаля Себа о числах, математических константах и ​​алгоритмах