Погружение (математика)

Дифференцируемая функция, производная которой всюду инъективна

Бутылка Клейна , погруженная в трехмерное пространство.

В математике погружение — это дифференцируемая функция между дифференцируемыми многообразиями , дифференциальное выталкивание которых всюду инъективно . ^[1] Явно, f  : M → N является погружением, если

${\displaystyle D_{p}f:T_{p}M\to T_{f(p)}N\,}$

является инъективной функцией в каждой точке p из M (где T _p X обозначает касательное пространство многообразия X в точке p в X ). Эквивалентно, f является погружением, если его производная имеет постоянный ранг , равный размерности M : ^[2]

${\displaystyle \operatorname {rank} \,D_{p}f=\dim M.}$

Сама функция f не обязательно должна быть инъективной, инъективной должна быть только ее производная.

Связанная с этим концепция — это встраивание . Гладкое вложение — это инъективное погружение f :  M → N , которое также является топологическим вложением , так что M диффеоморфно своему образу в N. Погружение - это в точности локальное вложение , то есть для любой точки x ∈ M существует окрестность U ⊆ M точки x такая, что f  : U → N является вложением, и наоборот, локальное вложение является погружением. ^[3] Для бесконечномерных многообразий это иногда считается определением погружения. ^[4]

Инъективно погруженное подмногообразие , не являющееся вложением.

Если M компактно , инъективное погружение является вложением, но если M не компактно, то инъективные погружения не обязательно должны быть вложениями ; сравните с непрерывными биекциями и гомеоморфизмами .

Регулярная гомотопия

Регулярная гомотопия между двумя погружениями f и g из многообразия M в многообразие N определяется как дифференцируемая функция H  : M × [0,1] → N такая, что для всех t в [0, 1] функция H _t  : M → N , определенный формулой H _t ( x ) = H ( x , t ) для всех x ∈ M , является погружением, причем H ₀ = f , H ₁ = g . Таким образом, регулярная гомотопия является гомотопией посредством погружений.

Классификация

Хасслер Уитни инициировал систематическое изучение погружений и регулярных гомотопий в 1940-х годах, доказав, что для 2 m < n + 1 каждое отображение f  : M ^m → N ⁿ m -мерного многообразия в n -мерное многообразие гомотопно погружению. , и фактически к вложению при 2 m < n ; это теорема погружения Уитни и теорема вложения Уитни .

Стивен Смейл выразил регулярные гомотопические классы погружений как гомотопические группы некоторого многообразия Стифеля . Выворот сферы был особенно поразительным последствием. ${\displaystyle f:M^{m}\to \mathbb {R} ^{n}}$

Моррис Хирш обобщил выражение Смейла на описание гомотопической теории регулярных гомотопических классов погружений любого m -мерного многообразия M ^m в любое n -мерное многообразие N ⁿ .

Классификацию погружений Хирша-Смейла обобщил Михаил Громов .

Существование

Лента Мёбиуса не погружается в коразмерность 0, поскольку ее касательное расслоение нетривиально.

Основным препятствием для существования погружения является стабильное нормальное расслоение M , что обнаруживается его характеристическими классами , особенно классами Стифеля-Уитни . То есть, поскольку он распараллеливаем , возврат его касательного расслоения к M тривиален; поскольку этот обратный образ является прямой суммой (внутренне определенного) касательного расслоения на M , TM , которое имеет размерность m , и нормального расслоения ν погружения i , которое имеет размерность n − m , для того, чтобы существовала коразмерность k погружения M , должно существовать векторное расслоение размерности k , ξ ^k , заменяющее нормальное расслоение ν , такое, что оно тривиально. И наоборот, для такого расслоения погружение M в это нормальное расслоение эквивалентно погружению коразмерности 0 всего пространства этого расслоения, которое является открытым многообразием. ${\displaystyle i:M^{m}\to \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle TM\oplus \zeta ^{k}}$

Стабильное нормальное расслоение — это класс нормальных расслоений плюс тривиальные расслоения, и, таким образом, если стабильное нормальное расслоение имеет когомологическую размерность k , оно не может происходить из (нестабильного) нормального расслоения размерности меньше k . Таким образом, когомологическая размерность стабильного нормального расслоения, определяемая его высшим неисчезающим характеристическим классом, является препятствием для погружений.

Поскольку характеристические классы умножаются относительно прямой суммы векторных расслоений, это препятствие можно сформулировать внутренне в терминах пространства M , его касательного расслоения и алгебры когомологий. Это препятствие было сформулировано (в терминах касательного расслоения, а не устойчивого нормального расслоения) Уитни.

Например, лента Мёбиуса имеет нетривиальное касательное расслоение, поэтому она не может погружаться в коразмерность 0 (в ), хотя вкладывается в коразмерность 1 (в ). ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \mathbb {R} ^{3}}$

Уильям С. Мэсси  (1960) показал, что эти характеристические классы (классы Стифеля-Уитни стабильного нормального расслоения) исчезают выше степени n − α ( n ) , где α ( n ) — количество цифр «1», когда n равно записан в двоичном формате; эта граница точна, как это реализуется в реальном проективном пространстве . Это дало подтверждение гипотезе погружения , а именно, что каждое n -многообразие может быть погружено в коразмерность n − α ( n ) , т. е. в Эта гипотеза была доказана Ральфом Коэном  (1985). ${\displaystyle \mathbb {R} ^{2n-\alpha (n)}.}$

Коразмерность 0

Погружения в коразмерности 0 в равной степени являются относительными погружениями в размерности 0 , и их лучше рассматривать как погружения. Погружение замкнутого многообразия коразмерности 0 — это в точности накрывающее отображение , т. е. расслоение с 0-мерным (дискретным) слоем. Согласно теореме Эресмана и теореме Филлипса о субмерсии, правильная субмерсия многообразий представляет собой расслоение, следовательно, погружения/субмерсии коразмерности/относительной размерности 0 ведут себя как субмерсии.

Кроме того, погружения коразмерности 0 ведут себя не так, как другие погружения, которые в значительной степени определяются стабильным нормальным расслоением: в коразмерности 0 возникают проблемы с фундаментальными классами и пространствами покрытий. Например, не существует погружения коразмерности 0, несмотря на то, что круг распараллеливаем, что можно доказать, поскольку линия не имеет фундаментального класса, поэтому невозможно получить требуемое отображение верхних когомологий. Альтернативно, это связано с инвариантностью домена . Аналогично, хотя и 3-тор оба распараллеливаемы, погружения нет – любое такое накрытие должно было бы быть разветвлено в некоторых точках, поскольку сфера односвязна. ${\displaystyle \mathbb {S} ^{1}\to \mathbb {R} ^{1},}$ ${\displaystyle \mathbb {S} ^{3}}$ ${\displaystyle \mathbb {T} ^{3}}$ ${\displaystyle \mathbb {T} ^{3}\to \mathbb {S} ^{3}}$

Другой способ понять это состоит в том, что погружение многообразия коразмерности k соответствует погружению коразмерности 0 k -мерного векторного расслоения, которое является открытым многообразием , если коразмерность больше 0, но замкнутым многообразием коразмерности 0 ( если исходное многообразие закрыто).

Несколько точек

k -кратная точка (двойная, тройная и т. д.) погружения f  : M → N — это неупорядоченное множество { x ₁ , ..., x _k } различных точек x _i ∈ M с одинаковым образом f ( x _я ) ∈ N . Если M — m -мерное многообразие, а N — n - мерное многообразие, то для погружения f  : M → N в общее положение множество k -кортежных точек представляет собой ( n − k ( n − m )) -мерное многообразие. . Каждое вложение — это погружение без кратных точек (где k > 1 ). Однако заметим, что обратное неверно: существуют инъективные погружения, которые не являются вложениями.

Природа множества точек классифицирует погружения; например, погружения окружности в плоскость классифицируются с точностью до регулярной гомотопии по числу двойных точек.

В ключевой момент теории хирургии необходимо решить, является ли погружение m -сферы в 2 m -мерное многообразие регулярным гомотопным вложению, и в этом случае его можно устранить хирургическим путем. Уолл связал с f инвариант µ ( f ) в факторе фундаментального группового кольца , который подсчитывает двойные точки f в универсальном накрытии N. Для m > 2 функция f является регулярной гомотопной вложению тогда и только тогда, когда µ ( f ) = 0 по трюку Уитни . ${\displaystyle f:\mathbb {S} ^{m}\to N^{2m}}$ ${\displaystyle \mathbb {Z} [\pi _{1}(N)]}$

Вложения можно изучать как «погружения без кратных точек», поскольку погружения легче классифицировать. Таким образом, можно начать с погружений и попытаться исключить несколько точек, проверив, можно ли сделать это без введения других особенностей – изучая «множественные дизъюнкции». Впервые это было сделано Андре Хефлигером , и этот подход плодотворен в коразмерности 3 или более — с точки зрения теории хирургии это «высокое (ко)размерность», в отличие от коразмерности 2, которая является измерением завязывания узлов, как в узле . теория . Его категорически изучают с помощью « исчисления функторов » Томаса Гудвилли, Джона Кляйна и Майкла С. Вайса.

Примеры и свойства

Quadrifolium , четырехлепестковая роза .

• Математическая роза с k лепестками — это погружение круга в плоскость с единственной k -кратной точкой; k может быть любым нечетным числом, но если четное должно быть кратно 4, то цифра 8 при k = 2 не является розой.
• Бутылка Клейна и все другие неориентируемые закрытые поверхности могут быть погружены в трехмерное пространство, но не вложены.
• По теореме Уитни-Граустейна регулярные гомотопические классы погружений окружности в плоскость классифицируются по числу обмотки , которое также является числом двойных точек, подсчитанных алгебраически (т.е. со знаками).
• Сферу можно вывернуть наизнанку : стандартное вложение связано с регулярной гомотопией погружений ${\displaystyle f_{0}:\mathbb {S} ^{2}\to \mathbb {R} ^{3}}$ ${\displaystyle f_{1}=-f_{0}:\mathbb {S} ^{2}\to \mathbb {R} ^{3}}$ ${\displaystyle f_{t}:\mathbb {S} ^{2}\to \mathbb {R} ^{3}.}$
• Поверхность Боя представляет собой погружение реальной проективной плоскости в трехмерное пространство; таким образом, также происходит погружение сферы 2 к 1.
• Поверхность Морена представляет собой погружение сферы; и она, и поверхность Боя возникают как промежуточные модели в вывороте сферы.

• Поверхность мальчика
• Поверхность Морена

Погруженные плоские кривые

Эта кривая имеет общую кривизну  6 π и число поворотов  3, хотя число витков  вокруг  p у нее только 2 .

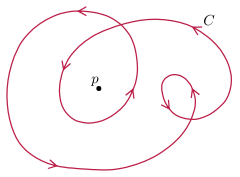
Погруженные плоские кривые имеют четко определенное число поворота , которое можно определить как общую кривизну, деленную на 2 π . Согласно теореме Уитни-Граустейна , это инвариантно относительно регулярной гомотопии - топологически это степень отображения Гаусса или, что то же самое, число обмотки единичного касательного (который не обращается в нуль) относительно начала координат. Далее, это полный набор инвариантов : любые две плоские кривые с одинаковым числом поворота являются регулярными гомотопными.

Каждая погруженная плоская кривая поднимается до встроенной пространственной кривой за счет разделения точек пересечения, что неверно в более высоких измерениях. С добавлением данных (какая нить находится сверху) погруженные плоские кривые дают диаграммы узлов , которые представляют центральный интерес в теории узлов . Если погруженные плоские кривые с точностью до регулярной гомотопии определяются числом их поворотов, то узлы имеют очень богатую и сложную структуру.

Погруженные поверхности в трехмерном пространстве

Исследование погруженных поверхностей в 3-пространстве тесно связано с изучением завязанных (вложенных) поверхностей в 4-пространстве по аналогии с теорией диаграмм узлов (погруженных плоских кривых (2-пространства) как проекций завязанных кривых в 3-мерном пространстве). -пространство): учитывая узловатую поверхность в 4-мерном пространстве, можно спроецировать ее на погруженную поверхность в 3-мерном пространстве, и наоборот, учитывая погруженную поверхность в 3-мерном пространстве, можно спросить, поднимается ли она в 4-мерное пространство - это проекция узловатой поверхности в 4-мерном пространстве? Это позволяет связать вопросы об этих объектах.

Основной результат, в отличие от случая плоских кривых, состоит в том, что не каждая погруженная поверхность поднимается до узловатой поверхности. ^[5] В некоторых случаях препятствием является 2-кручение, например, в примере Кошорке , ^[6] которое представляет собой погруженную поверхность (сформированную из 3 лент Мёбиуса с тройной точкой ), которая не поднимается до узловатой поверхности, но имеет двойную крышку, которая поднимается. Подробный анализ представлен в Carter & Saito (1998a), а более поздний обзор представлен в Carter, Kamada & Saito (2004).

Обобщения

Далеко идущим обобщением теории погружения является принцип гомотопии : можно рассматривать условие погружения (ранг производной всегда k ) как отношение в частных производных (PDR), поскольку его можно сформулировать в терминах частных производных от функция. Тогда теория погружения Смейла-Хирша является результатом того, что это сводится к теории гомотопии, а принцип гомотопии дает общие условия и причины, по которым PDR сводятся к теории гомотопии.

Смотрите также

• Погруженное подмногообразие
• Изометрическое погружение
• Погружение

Примечания

1. Это определение дано Бишопом и Криттенденом, 1964, с. 185, Дарлинг 1994, с. 53, do Carmo 1994, с. 11, Франкель 1997, с. 169, Галло, Хулин и Лафонтен 2004, с. 12, Кобаяши и Номидзу 1963, с. 9, Косински 2007, с. 27, Секерес 2004, с. 429.
2. Это определение дано Крампином и Пирани 1994, стр. 243, Спивак 1999, с. 46.
3. Такое определение, основанное на локальных диффеоморфизмах, дано Бишопом и Голдбергом 1968, с. 40, Ланг 1999, с. 26.
4. Такое бесконечномерное определение дано Лангом 1999, стр. 26.
5. Картер и Сайто 1998; Картер, Камада и Сайто 2004, замечание 1.23, с. 17
6. Кошорке 1979

Рекомендации

• Адачи, Масахиса (1993), Вложения и погружения, перевод Кики Хадсон, ISBN 978-0-8218-4612-4
• Арнольд, VI ; Варченко А.Н.; Гусейн-Заде, С.М. (1985), Особенности дифференцируемых отображений: Том 1 , Биркхойзер, ISBN 0-8176-3187-9
• Бишоп, Ричард Лоуренс ; Криттенден, Ричард Дж. (1964), Геометрия многообразий , Нью-Йорк: Academic Press, ISBN 978-0-8218-2923-3
• Бишоп, РЛ ; Гольдберг, С.И. (1968), Тензорный анализ многообразий (первое изд. Дувра, 1980 г.), The Macmillan Company, ISBN 0-486-64039-6
• Брюс, JW; Гиблин, П.Дж. (1984), Кривые и особенности , издательство Кембриджского университета, ISBN 0-521-42999-4
• Картер, Дж. Скотт; Сайто, Масахико (1998a), «Поверхности в трехмерном пространстве, которые не поднимаются до вложений в четырехмерном пространстве», Теория узлов (Варшава, 1995) , Banach Center Publ., vol. 42, польский акад. Sci., Варшава, стр. 29–47, CiteSeerX  10.1.1.44.1505 , MR  1634445..
• Картер, Дж. Скотт; Сайто, Масахико (1998), Узловатые поверхности и их диаграммы , Математические обзоры и монографии, том. 55, с. 258, ISBN 978-0-8218-0593-0
• Картер, Скотт; Камада, Сейичи; Сайто, Масахико (2004), Поверхности в 4-мерном пространстве , Энциклопедия математических наук, том. 142, Берлин: Springer-Verlag, номер документа : 10.1007/978-3-662-10162-9, ISBN. 3-540-21040-7, МР  2060067.
• Коэн, Ральф Л. (1985), «Гипотеза погружения для дифференцируемых многообразий», Annals of Mathematics , Second Series, 122 (2): 237–328, doi : 10.2307/1971304, JSTOR  1971304, MR  0808220.
• Крампин, Майкл; Пирани, Феликс Арнольд Эдвард (1994), Прикладная дифференциальная геометрия , Кембридж, Англия: Издательство Кембриджского университета, ISBN 978-0-521-23190-9
• Дарлинг, Ричард Уильям Рамзи (1994), Дифференциальные формы и связи , Кембридж, Великобритания: Издательство Кембриджского университета, Бибкод : 1994dfc..book.....D, ISBN 978-0-521-46800-8.
• ду Карму, Манфредо Пердигао (1994), Риманова геометрия , ISBN 978-0-8176-3490-2
• Франкель, Теодор (1997), Геометрия физики , Кембридж: Издательство Кембриджского университета, ISBN 0-521-38753-1
• Галло, Сильвестр; Хулин, Доминик ; Лафонтен, Жак (2004), Риманова геометрия (3-е изд.), Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-3-540-20493-0
• Громов, М. (1986), Частные дифференциальные отношения , Springer, ISBN 3-540-12177-3
• Хирш, Моррис В. (1959), «Погружения многообразий», Труды Американского математического общества , 93 (2): 242–276, doi : 10.2307/1993453 , JSTOR  1993453, MR  0119214.
• Кобаяши, Шошичи; Номидзу, Кацуми (1963), Основы дифференциальной геометрии, Том 1 , Нью-Йорк: Wiley-Interscience
• Кошорке, Ульрих (1979), «Множественные точки погружения и теорема Кана-Придди», Mathematische Zeitschrift , 169 (3): 223–236, doi : 10.1007/BF01214837, MR  0554526, S2CID  121273182.
• Косински, Антони Альберт (2007) [1993], Дифференциальные многообразия , Минеола, Нью-Йорк: Dover Publications, ISBN 978-0-486-46244-8
• Ланг, Серж (1999), Основы дифференциальной геометрии , Тексты для аспирантов по математике, Нью-Йорк: Springer, ISBN 978-0-387-98593-0
• Мэсси, WS (1960), «О классах Стифеля-Уитни многообразия», American Journal of Mathematics , 82 (1): 92–102, doi : 10.2307/2372878, JSTOR  2372878, MR  0111053.
• Смейл, Стивен (1958), «Классификация погружений двухсфер», Труды Американского математического общества , 90 (2): 281–290, doi : 10.2307/1993205 , JSTOR  1993205, MR  0104227.
• Смейл, Стивен (1959), «Классификация погружений сфер в евклидовы пространства», Annals of Mathematics , Second Series, 69 (2): 327–344, doi : 10.2307/1970186, JSTOR  1970186, MR  0105117.
• Спивак, Майкл (1999) [1970], Всестороннее введение в дифференциальную геометрию (Том 1) , Опубликуй или погибни, ISBN 0-914098-70-5
• Спринг, Дэвид (2005), «Золотой век теории погружения в топологии: 1959–1973: математический обзор с исторической точки зрения», Бюллетень Американского математического общества , новая серия, 42 (2): 163–180, CiteSeerX  10.1.1.363.913 , doi : 10.1090/S0273-0979-05-01048-7, MR  2133309, S2CID  9237068.
• Секерес, Питер (2004), Курс современной математической физики: группы, гильбертово пространство и дифференциальная геометрия , Кембридж, Великобритания: Cambridge University Press, ISBN 978-0-521-82960-1
• Уолл, CTC (1999), Хирургия на компактных многообразиях (PDF) , Математические обзоры и монографии, том. 69 (второе изд.), Провиденс, Род-Айленд: Американское математическое общество, номер документа : 10.1090/surv/069, ISBN. 0-8218-0942-3, МР  1687388.

Внешние ссылки

• Погружение в Атлас многообразия
• Погружение многообразия в Математической энциклопедии