Широта

В географии широта — это координата , которая определяет положение точки на поверхности Земли или другого небесного тела с севера на юг . Широта задается как угол, который находится в диапазоне от −90° на южном полюсе до 90° на северном полюсе, с 0° на экваторе . Линии постоянной широты , или параллели , проходят с востока на запад как окружности, параллельные экватору. Широта и долгота используются вместе как пара координат для указания местоположения на поверхности Земли.

Сам по себе термин «широта» обычно относится к геодезической широте , как определено ниже. Вкратце, геодезическая широта точки — это угол, образованный между вектором, перпендикулярным (или нормальным ) к эллипсоидальной поверхности из точки, и плоскостью экватора .

Фон

В определениях широты и долготы используются два уровня абстракции. На первом этапе физическая поверхность моделируется геоидом , поверхностью, которая аппроксимирует средний уровень моря над океанами и его продолжением под сушей. На втором этапе геоид аппроксимируется математически более простой опорной поверхностью. Простейшим выбором для опорной поверхности является сфера , но геоид точнее моделируется эллипсоидом вращения . Определения широты и долготы на таких опорных поверхностях подробно изложены в следующих разделах. Линии постоянной широты и долготы вместе составляют сетку на опорной поверхности. Широта точки на фактической поверхности — это широта соответствующей точки на опорной поверхности, причем соответствие осуществляется вдоль нормали к опорной поверхности, которая проходит через точку на физической поверхности. Широта и долгота вместе с некоторой спецификацией высоты составляют географическую систему координат , как определено в спецификации стандарта ISO 19111. ^[1]

Поскольку существует множество различных референц-эллипсоидов , точная широта объекта на поверхности не является уникальной: это подчеркивается в стандарте ISO, в котором говорится, что «без полной спецификации системы координат координаты (то есть широта и долгота) в лучшем случае неоднозначны, а в худшем — бессмысленны». Это имеет большое значение в точных приложениях, таких как Глобальная система позиционирования (GPS), но в обычном использовании, где высокая точность не требуется, референц-эллипсоид обычно не указывается.

В английских текстах угол широты, определенный ниже, обычно обозначается греческой строчной буквой фи ( $ϕ$ или $φ$ ). Он измеряется в градусах , минутах и секундах или десятичных градусах , к северу или югу от экватора. Для навигационных целей положения указываются в градусах и десятичных минутах. Например, маяк The Needles находится на 50°39.734′ с.ш. 001°35.500′ з.д. ^[2]

В этой статье рассматриваются системы координат для Земли: они могут быть адаптированы для охвата Луны, планет и других небесных объектов ( планетографическая широта ).

Краткую историю см. в разделе История широты .

Определение

В астрономической навигации широта определяется методом высоты меридиана . Более точное измерение широты требует понимания гравитационного поля Земли, либо для установки теодолитов , либо для определения орбит спутников GPS. Изучение фигуры Земли вместе с ее гравитационным полем является наукой геодезии .

Широта на сфере

Сетка на сфере

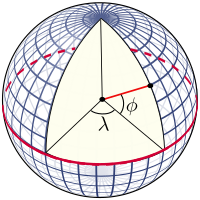
Координатная сетка образована линиями постоянной широты и постоянной долготы, которые построены относительно оси вращения Земли. Основными опорными точками являются полюса , где ось вращения Земли пересекает опорную поверхность. Плоскости, содержащие ось вращения, пересекают поверхность по меридианам ; а угол между любой плоскостью меридиана и плоскостью, проходящей через Гринвич ( начальный меридиан ), определяет долготу: меридианы являются линиями постоянной долготы. Плоскость, проходящая через центр Земли и перпендикулярная оси вращения, пересекает поверхность по большому кругу, называемому экватором . Плоскости, параллельные экваториальной плоскости, пересекают поверхность по кругам постоянной широты; это параллели. Экватор имеет широту 0°, Северный полюс имеет широту 90° северной широты (пишется 90° с.ш. или +90°), а Южный полюс имеет широту 90° южной широты (пишется 90° ю.ш. или −90°). Широта произвольной точки — это угол между экваториальной плоскостью и нормалью к поверхности в этой точке: нормаль к поверхности сферы направлена вдоль радиального вектора.

Широту, определенную таким образом для сферы, часто называют сферической широтой, чтобы избежать двусмысленности с геодезической широтой и вспомогательными широтами, определенными в последующих разделах этой статьи.

Названия широт на Земле

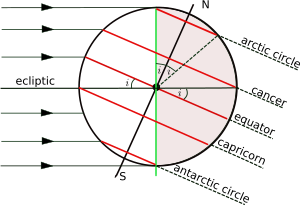
Помимо экватора, имеют значение еще четыре параллели:

Плоскость орбиты Земли вокруг Солнца называется эклиптикой , а плоскость, перпендикулярная оси вращения Земли, — экваториальной плоскостью. Угол между эклиптикой и экваториальной плоскостью по-разному называется наклоном оси, наклоном или наклоном эклиптики и условно обозначается $i$ . Широта тропических кругов равна $i$ , а широта полярных кругов — ее дополнением (90° — i ). Ось вращения медленно меняется со временем, и приведенные здесь значения соответствуют текущей эпохе . Изменение во времени более подробно обсуждается в статье об наклоне оси . ^[a]

На рисунке показана геометрия поперечного сечения плоскости, перпендикулярной эклиптике и проходящей через центры Земли и Солнца в декабрьское солнцестояние , когда Солнце находится в зените в некоторой точке тропика Козерога . Южные полярные широты ниже Южного полярного круга находятся в дневном свете, в то время как северные полярные широты выше Полярного круга находятся в ночном. Ситуация обратная в июньское солнцестояние, когда Солнце находится в зените в тропике Рака. Только на широтах между двумя тропиками Солнце может находиться прямо над головой (в зените ).

В картографических проекциях нет универсального правила, как должны выглядеть меридианы и параллели. Примеры ниже показывают названные параллели (красными линиями) на обычно используемой проекции Меркатора и поперечной проекции Меркатора . На первой параллели горизонтальны, а меридианы вертикальны, тогда как на последней нет точного соотношения параллелей и меридианов с горизонталью и вертикалью: обе являются сложными кривыми.

Широта на эллипсоиде

Эллипсоиды

В 1687 году Исаак Ньютон опубликовал Philosophiæ Naturalis Principia Mathematica , в котором он доказал, что вращающееся самогравитирующее жидкое тело в равновесии принимает форму сплющенного эллипсоида. ^[3] (В этой статье термин «эллипсоид» используется вместо более старого термина «сфероид» .) Результат Ньютона был подтвержден геодезическими измерениями в 18 веке. (См. Дуга меридиана .) Сплющенный эллипсоид — это трехмерная поверхность, образованная вращением эллипса вокруг его более короткой оси (малой оси). «Сплющенный эллипсоид вращения» в оставшейся части этой статьи сокращенно обозначается как «эллипсоид». (Эллипсоиды, не имеющие оси симметрии, называются трехосными .)

В истории геодезии использовалось множество различных референц-эллипсоидов . В доспутниковые времена они были разработаны для того, чтобы дать хорошее соответствие геоиду на ограниченной площади съемки, но с появлением GPS стало естественным использовать референц-эллипсоиды (такие как WGS84 ) с центром в центре масс Земли и малой осью, совмещенной с осью вращения Земли. Эти геоцентрические эллипсоиды обычно находятся в пределах 100 м (330 футов) от геоида. Поскольку широта определяется относительно эллипсоида, положение заданной точки различно на каждом эллипсоиде: невозможно точно указать широту и долготу географического объекта, не указав используемый эллипсоид. Многие карты, поддерживаемые национальными агентствами, основаны на старых эллипсоидах, поэтому необходимо знать, как значения широты и долготы преобразуются из одного эллипсоида в другой. В комплект GPS-устройств входит программное обеспечение для выполнения преобразований координат , связывающих WGS84 с местным референц-эллипсоидом и соответствующей сеткой.

Геометрия эллипсоида

Форма эллипсоида вращения определяется формой эллипса , который вращается вокруг своей малой (короткой) оси. Требуются два параметра. Один из них — это неизменно экваториальный радиус, который является большой полуосью , $a$ . Другой параметр — это обычно (1) полярный радиус или малая полуось , $b$ ; или (2) (первое) сплющивание , $f$ ; или (3) эксцентриситет , $e$ . Эти параметры не являются независимыми: они связаны соотношением

f={\frac {ab}{a}},\qquad e^{2}=2f-f^{2},\qquad b=a(1-f)=a{\sqrt {1-e^{2}}}\,.

Многие другие параметры (см. эллипс , эллипсоид ) появляются в изучении геодезии, геофизики и картографических проекций, но все они могут быть выражены через один или два члена множества $a$ , $b$ , $f$ и $e$ . Оба параметра $f$ и $e$ малы и часто появляются в рядах при вычислениях; они имеют порядок ⁠1/298⁠ и 0,0818 соответственно. Значения для ряда эллипсоидов приведены в Фигуре Земли . Референтные эллипсоиды обычно определяются большой полуосью и обратным сжатием, $⁠$ $1 / ф ⁠$ . Например, определяющие значения для эллипсоида WGS84 , используемые всеми устройствами GPS, следующие^[4]

$а$ (экваториальный радиус):6 378 137 .0 м точно
$⁠ 1 / ф ⁠$ (обратное сглаживание):298.257 223 563 точно

из которых получены

$b$ (полярный радиус):6 356 752 .314 25 м
$e 2$ (квадрат эксцентриситета):0,006 694 379 990 14

Разница между большой и малой полуосью составляет около 21 км (13 миль) и как часть большой полуоси она равна сплющиванию; на мониторе компьютера эллипсоид может иметь размер 300 на 299 пикселей. Это было бы едва отличимо от сферы размером 300 на 300 пикселей, поэтому иллюстрации обычно преувеличивают сплющивание.

Геодезические и геоцентрические широты

Сетка на эллипсоиде строится точно так же, как и на сфере. Нормаль в точке на поверхности эллипсоида не проходит через центр, за исключением точек на экваторе или на полюсах, но определение широты остается неизменным как угол между нормалью и экваториальной плоскостью. Терминология широты должна быть уточнена путем различения:

Геодезическая широта : угол между нормалью и экваториальной плоскостью. Стандартное обозначение в английских публикациях — $ϕ$ . Это определение подразумевается, когда слово широта используется без уточнения. Определение должно сопровождаться спецификацией эллипсоида.
Геоцентрическая широта (также известная как сферическая широта , по названию 3D полярного угла ): угол между радиусом (от центра до точки на поверхности) и экваториальной плоскостью. (Рисунок ниже). Стандартного обозначения нет: примеры из различных текстов включают $θ$ , $ψ$ , $q$ , $ϕ'$ , $ϕ c$ , $ϕ g$ . В этой статье используется $θ$ .

Географическую широту следует использовать с осторожностью, поскольку некоторые авторы используют ее как синоним геодезической широты, в то время как другие используют ее как альтернативу астрономической широте. «Широта» (без уточнений) обычно должна относиться к геодезической широте.

Важность указания опорного датума можно проиллюстрировать на простом примере. На опорном эллипсоиде для WGS84 центр Эйфелевой башни имеет геодезическую широту 48° 51′ 29″ N или 48.8583° N и долготу 2° 17′ 40″ E или 2.2944° E. Те же координаты на датуме ED50 определяют точку на земле, которая находится на расстоянии 140 метров (460 футов) от башни. ^{[ необходима цитата ]} Поиск в Интернете может выдать несколько различных значений широты башни; опорный эллипсоид указывается редко.

Расстояние по меридиану

Длина градуса широты зависит от предполагаемой фигуры Земли .

Меридиональное расстояние на сфере

На сфере нормаль проходит через центр, и широта ( $ϕ$ ) поэтому равна углу, образуемому в центре дугой меридиана от экватора до рассматриваемой точки. Если меридиональное расстояние обозначить как $m (ϕ),$ то

m(\phi)={\frac {\pi }{180^{\circ }}}R\phi _ {\ mathrm {градусы} } = R\phi _ {\ mathrm {радианы} }

где $R$ обозначает средний радиус Земли. $R$ равен 6371 км или 3959 миль. Более высокая точность не подходит для $R,$ поскольку для более точных результатов необходима модель эллипсоида. При таком значении $R$ длина меридиана 1 градуса широты на сфере составляет 111,2 км (69,1 статутных миль) (60,0 морских миль). Длина 1 минуты широты составляет 1,853 км (1,151 статутных миль) (1,00 морских миль), а длина 1 секунды широты составляет 30,8 м или 101 фут (см. морская миля ).

Меридиональное расстояние на эллипсоиде

В текстах по дуге меридиана и стандартным текстам ^[5]^[6]^[7] показано, что расстояние вдоль меридиана от широты $ϕ$ до экватора определяется выражением ( $ϕ$ в радианах)

m(\phi)=\int _{0}^{\phi }M(\phi ')\,d\phi '=a\left(1-e^{2}\right)\int _ {0}^{\phi }\left(1-e^{2}\sin ^{2}\phi '\right)^{-{\frac {3}{2}}}\,d\phi '

где $M (ϕ)$ — меридиональный радиус кривизны .

Расстояние по четверти меридиана от экватора до полюса равно

m_{\mathrm {p} }=m\left({\frac {\pi }{2}}\right)\,

Для WGS84 это расстояние равно10 001 .965 729 км .

Оценка интеграла меридианного расстояния является центральной для многих исследований в области геодезии и картографической проекции. Его можно оценить, разложив интеграл по биномиальному ряду и проинтегрировав член за членом: см. Дуга меридиана для получения подробной информации. Длина дуги меридиана между двумя заданными широтами определяется путем замены пределов интеграла на соответствующие широты. Длина малой дуги меридиана определяется как ^[6]^[7]

\delta m(\phi)=M(\phi)\,\delta \phi =a\left(1-e^{2}\right)\left(1-e^{2}\sin ^ {2}\phi \right)^{-{\frac {3}{2}}}\,\delta \phi

Когда разница широты составляет 1 градус, что соответствует ⁠ $π$ /180⁠ радиан, дуговое расстояние составляет около

\Delta _{\text{lat}}^{1}={\frac {\pi a\left(1-e^{2}\right)}{180^{\circ }\left(1-e^{2}\sin ^{2}\phi \right)^{\frac {3}{2}}}}

Расстояние в метрах (с точностью до 0,01 метра) между широтами −0,5 градуса и +0,5 градуса на сфероиде WGS84 составляет $\фи$ $\фи$

\Delta _{\text{lat}}^{1}=111\,132.954-559.822\cos 2\phi +1.175\cos 4\phi

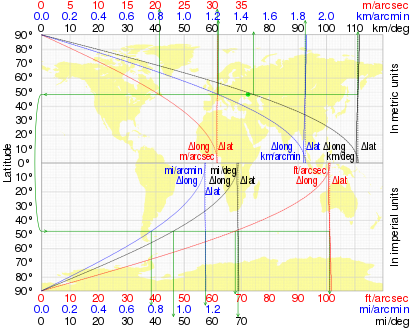
Изменение этого расстояния в зависимости от широты (по системе координат WGS84 ) показано в таблице вместе с длиной градуса долготы (расстояние с востока на запад):

\Delta _{\text{long}}^{1}={\frac {\pi a\cos \phi }{180^{\circ }{\sqrt {1-e^{2}\sin ^{2}\фи }}}}\,

Калькулятор для любой широты предоставлен Национальным агентством геопространственной разведки правительства США (NGA). ^[8]

На следующем графике показано изменение градуса широты и градуса долготы в зависимости от широты.

Вспомогательные широты

Существует шесть вспомогательных широт , которые имеют приложения к специальным задачам геодезии, геофизики и теории картографических проекций:

Геоцентрическая широта
Параметрическая (или редуцированная) широта
Исправление широты
Подлинная широта
Конформная широта
Изометрическая широта

Определения, данные в этом разделе, все относятся к местоположениям на референц-эллипсоиде, но первые две вспомогательные широты, как и геодезическая широта, могут быть расширены для определения трехмерной географической системы координат , как обсуждается ниже. Остальные широты не используются таким образом; они используются только как промежуточные конструкции в картографических проекциях референц-эллипсоида на плоскость или в расчетах геодезических на эллипсоиде. Их числовые значения не представляют интереса. Например, никому не нужно будет вычислять аутентичную широту Эйфелевой башни.

Выражения ниже дают вспомогательные широты в терминах геодезической широты, большой полуоси, $a$ , и эксцентриситета, $e$ . (Обратные величины см. ниже.) Приведенные формы, за исключением вариантов обозначений, являются теми, что содержатся в стандартном справочнике по картографическим проекциям, а именно "Map Projections: a Working Manual" Дж. П. Снайдера. ^[9] Выводы этих выражений можно найти в работе Адамса ^[10] и в онлайн-публикациях Осборна ^[6] и Раппа ^{[7] .}

Геоцентрическая широта

Геоцентрическая широта — это угол между экваториальной плоскостью и радиусом от центра до точки интереса.

Когда точка находится на поверхности эллипсоида, соотношение между геоцентрической широтой ( $θ$ ) и геодезической широтой ( $ϕ$ ) равно:

\theta (\phi )=\tan ^{-1}\left(\left(1-e^{2}\right)\tan \phi \right)=\tan ^{-1}\left((1-f)^{2}\tan \phi \right)\,.

Для точек, не лежащих на поверхности эллипсоида, в соотношение дополнительно включается эллипсоидальная высота h :

\theta (\phi ,h)=\tan ^{-1}\left({\frac {N(1-f)^{2}+h}{N+h}}\tan \phi \right)

где $N$ — это основной вертикальный радиус кривизны. Геодезическая и геоцентрическая широты равны на экваторе и полюсах, но на других широтах они отличаются на несколько минут дуги. Принимая значение квадрата эксцентриситета за 0,0067 (зависит от выбора эллипсоида), можно показать, что максимальная разница составляет около 11,5 минут дуги на геодезической широте приблизительно 45° 6′. ^[b] $\phi {-}\theta$

Параметрическая широта (или редуцированная широта)

Параметрическая широта или приведенная широта , $β$ , определяется радиусом, проведенным из центра эллипсоида в точку $Q$ на окружающей сфере (радиуса $a$ ), которая является проекцией, параллельной земной оси, точки $P$ на эллипсоиде на широте $ϕ$ . Она была введена Лежандром ^[11] и Бесселем ^[12], которые решали задачи для геодезических на эллипсоиде, преобразуя их в эквивалентную задачу для сферических геодезических, используя эту меньшую широту. Обозначение Бесселя, $u (ϕ)$ , также используется в современной литературе. Параметрическая широта связана с геодезической широтой следующим образом: ^[6]^[7]

\beta (\phi )=\tan ^{-1}\left({\sqrt {1-e^{2}}}\tan \phi \right)=\tan ^{-1}\left((1-f)\tan \phi \right)

Альтернативное название возникает из параметризации уравнения эллипса, описывающего меридиональное сечение. В декартовых координатах $p$ , расстояние от малой оси, и $z$ , расстояние над экваториальной плоскостью, уравнение эллипса имеет вид:

{\frac {p^{2}}{a^{2}}}+{\frac {z^{2}}{b^{2}}}=1\,.

Декартовы координаты точки параметризуются следующим образом:

p=a\cos \beta \,,\qquad z=b\sin \beta \,;

Кейли предложил термин «параметрическая широта» из-за формы этих уравнений. ^[13]

Параметрическая широта не используется в теории картографических проекций. Ее наиболее важное применение — в теории эллипсоидальных геодезических ( Винсенти , Карни ^[14] ).

Исправление широты

Выпрямляющая широта , $μ$ , представляет собой меридиональное расстояние, масштабированное таким образом, что его значение на полюсах равно 90 градусам или ⁠ $π$ /2⁠ радианы:

\mu (\phi )={\frac {\pi }{2}}{\frac {m(\phi )}{m_{\mathrm {p} }}}

где меридиональное расстояние от экватора до широты $ϕ$ равно (см. Дуга меридиана )

m(\phi )=a\left(1-e^{2}\right)\int _{0}^{\phi }\left(1-e^{2}\sin ^{2}\phi '\right)^{-{\frac {3}{2}}}\,d\phi '\,,

а длина меридианного квадранта от экватора до полюса ( полярное расстояние ) равна

m_{\mathrm {p} }=m\left({\frac {\pi }{2}}\right)\,.

Использование спрямляющей широты для определения широты на сфере радиуса

R={\frac {2m_{\mathrm {p} }}{\pi }}

определяет проекцию эллипсоида на сферу таким образом, что все меридианы имеют истинную длину и равномерный масштаб. Затем сфера может быть спроецирована на плоскость с помощью равнопромежуточной проекции, чтобы получить двойную проекцию эллипсоида на плоскость таким образом, что все меридианы имеют истинную длину и равномерный масштаб меридиана. Примером использования выпрямляющей широты является равнопромежуточная коническая проекция . (Снайдер, раздел 16). ^[9] Выпрямляющая широта также имеет большое значение при построении поперечной проекции Меркатора .

Подлинная широта

Подлинная широта (от греческого «та же площадь»), $ξ$ , дает равновеликую проекцию на сферу.

\xi (\phi )=\sin ^{-1}\left({\frac {q(\phi )}{q_{\mathrm {p} }}}\right)

где

{\begin{aligned}q(\phi )&={\frac {\left(1-e^{2}\right)\sin \phi }{1-e^{2}\sin ^{2}\phi }}-{\frac {1-e^{2}}{2e}}\ln \left({\frac {1-e\sin \phi }{1+e\sin \phi }}\right)\\[2pt]&={\frac {\left(1-e^{2}\right)\sin \phi }{1-e^{2}\sin ^{2}\phi }}+{\frac {1-e^{2}}{e}}\tanh ^{-1}(e\sin \phi )\end{aligned}}

{\begin{aligned}q_{\mathrm {p} }=q\left({\frac {\pi }{2}}\right)&=1-{\frac {1-e^{2}}{2e}}\ln \left({\frac {1-e}{1+e}}\right)\\&=1+{\frac {1-e^{2}}{e}}\tanh ^{-1}e\end{aligned}}

а радиус сферы принимается равным

R_{q}=a{\sqrt {\frac {q_{\mathrm {p} }}{2}}}\,.

Примером использования подлинной широты является равновеликая коническая проекция Альберса . ^[9]^{: §14}

Конформная широта

Конформная широта , $χ$ , дает сохраняющее угол ( конформное ) преобразование сферы. ^[15]

{\begin{aligned}\chi (\phi )&=2\tan ^{-1}\left[\left({\frac {1+\sin \phi }{1-\sin \phi }}\right)\left({\frac {1-e\sin \phi }{1+e\sin \phi }}\right)^{e}\right]^{\frac {1}{2}}-{\frac {\pi }{2}}\\[2pt]&=2\tan ^{-1}\left[\tan \left({\frac {\phi }{2}}+{\frac {\pi }{4}}\right)\left({\frac {1-e\sin \phi }{1+e\sin \phi }}\right)^{\frac {e}{2}}\right]-{\frac {\pi }{2}}\\[2pt]&=\tan ^{-1}\left[\sinh \left(\sinh ^{-1}(\tan \phi )-e\tanh ^{-1}(e\sin \phi )\right)\right]\\&=\operatorname {gd} \left[\operatorname {gd} ^{-1}(\phi )-e\tanh ^{-1}(e\sin \phi )\right]\end{aligned}}

где $gd(x)$ — функция Гудермана . (См. также Проекция Меркатора .)

Конформная широта определяет преобразование из эллипсоида в сферу произвольного радиуса таким образом, что угол пересечения между любыми двумя линиями на эллипсоиде такой же, как соответствующий угол на сфере (так что форма малых элементов хорошо сохраняется). Дальнейшее конформное преобразование из сферы в плоскость дает конформную двойную проекцию из эллипсоида на плоскость. Это не единственный способ создания такой конформной проекции. Например, «точная» версия поперечной проекции Меркатора на эллипсоиде не является двойной проекцией. (Она, однако, включает обобщение конформной широты на комплексную плоскость).

Изометрическая широта

Изометрическая широта , $ψ$ , используется при разработке эллипсоидальных версий нормальной проекции Меркатора и поперечной проекции Меркатора . Название «изометрическая» возникает из того факта, что в любой точке эллипсоида равные приращения $ψ$ и долготы $λ$ приводят к равным смещениям по меридианам и параллелям соответственно. Сетка, определяемая линиями постоянной $ψ$ и постоянной $λ$ , делит поверхность эллипсоида на сетку квадратов (разного размера). Изометрическая широта равна нулю на экваторе, но быстро расходится с геодезической широтой, стремясь к бесконечности на полюсах. Условные обозначения приведены в работе Снайдера (стр. 15): ^[9]

{\begin{aligned}\psi (\phi )&=\ln \left[\tan \left({\frac {\pi }{4}}+{\frac {\phi }{2}}\right)\right]+{\frac {e}{2}}\ln \left[{\frac {1-e\sin \phi }{1+e\sin \phi }}\right]\\&=\sinh ^{-1}(\tan \phi )-e\tanh ^{-1}(e\sin \phi )\\&=\operatorname {gd} ^{-1}(\phi )-e\tanh ^{-1}(e\sin \phi ).\end{aligned}}

Для нормальной проекции Меркатора (на эллипсоиде) эта функция определяет расстояние между параллелями: если длина экватора на проекции равна $E$ (единицы длины или пиксели), то расстояние $y$ от параллели широты $ϕ$ до экватора равно

y(\phi )={\frac {E}{2\pi }}\psi (\phi )\,.

Изометрическая широта $ψ$ тесно связана с конформной широтой $χ$ :

\psi (\phi )=\operatorname {gd} ^{-1}\chi (\phi )\,.

Обратные формулы и ряды

Формулы в предыдущих разделах дают вспомогательную широту в терминах геодезической широты. Выражения для геоцентрической и параметрической широты могут быть обращены непосредственно, но это невозможно в четырех оставшихся случаях: выпрямляющей, аутентичной, конформной и изометрической широты. Существует два метода действий.

Первый — численная инверсия определяющего уравнения для каждого конкретного значения вспомогательной широты. Доступные методы — итерация с фиксированной точкой и поиск корня Ньютона–Рафсона .
- При преобразовании из изометрической или конформной проекции в геодезическую две итерации Ньютона-Рафсона дают двойную точность . ^[16]
Другой, более полезный подход заключается в выражении вспомогательной широты в виде ряда в терминах геодезической широты, а затем в инвертировании ряда методом обращения Лагранжа . Такие ряды представлены Адамсом, который использует разложения в ряды Тейлора и дает коэффициенты в терминах эксцентриситета. ^[10] Ориуэла ^[17] дает ряды для преобразований между всеми парами вспомогательных широт в терминах третьего сглаживания, $n = (a - b)/(a + b)$ . Карни ^[18] устанавливает, что ошибки усечения для таких рядов последовательно меньше, чем у эквивалентного ряда в терминах эксцентриситета. Метод рядов неприменим к изометрической широте, и необходимо найти конформную широту на промежуточном этапе. ^[6]

Численное сравнение вспомогательных широт

График справа показывает разницу между геодезической широтой и вспомогательными широтами, отличными от изометрической широты (которая расходится до бесконечности на полюсах) для случая эллипсоида WGS84. Различия, показанные на графике, указаны в угловых минутах. В Северном полушарии (положительные широты) θ ≤ χ ≤ μ ≤ ξ ≤ β ≤ ϕ ; в Южном полушарии (отрицательные широты) неравенства обратные, с равенством на экваторе и полюсах. Хотя график кажется симметричным относительно 45°, минимумы кривых на самом деле лежат между 45° 2′ и 45° 6′. Некоторые репрезентативные точки данных приведены в таблице ниже. Конформные и геоцентрические широты почти неразличимы, что использовалось во времена ручных калькуляторов для ускорения построения картографических проекций. ^[9]^{: 108}

В первом порядке по сглаживанию f вспомогательные широты можно выразить как ζ = ϕ − Cf sin 2 ϕ, где постоянная C принимает значения [ 1 ⁄ 2 , 2 ⁄ 3 , 3 ⁄ 4 , 1, 1] для ζ = [ β , ξ , μ , χ , θ ].

Широта и системы координат

Геодезическая широта или любая из вспомогательных широт, определенных на референц-эллипсоиде, вместе с долготой образует двумерную систему координат на этом эллипсоиде. Чтобы определить положение произвольной точки, необходимо расширить такую систему координат до трех измерений. Таким образом, используются три широты: геодезическая, геоцентрическая и параметрическая широты используются в геодезических координатах, сферических полярных координатах и эллипсоидальных координатах соответственно.

Геодезические координаты

В произвольной точке $P$ рассмотрим линию $PN$ , которая нормальна к референц-эллипсоиду. Геодезические координаты $P(ɸ, λ, h)$ — это широта и долгота точки $N$ на эллипсоиде и расстояние $PN$ . Эта высота отличается от высоты над геоидом или отсчетной высоты, такой как высота над средним уровнем моря в указанном месте. Направление $PN$ также будет отличаться от направления вертикальной отвесной линии. Соотношение этих различных высот требует знания формы геоида, а также гравитационного поля Земли.

Сферические полярные координаты

Геоцентрическая широта $θ$ является дополнением полярного угла или кошироты $θ'$ в обычных сферических полярных координатах , в которых координаты точки равны $P(r, θ', λ)$ , где $r$ — расстояние $P$ от центра $O$ , $θ'$ — угол между радиусом-вектором и полярной осью, а $λ$ — долгота. Поскольку нормаль в общей точке эллипсоида не проходит через центр, ясно, что точки $P'$ на нормали, которые все имеют одинаковую геодезическую широту, будут иметь разные геоцентрические широты. Сферические полярные системы координат используются при анализе гравитационного поля.

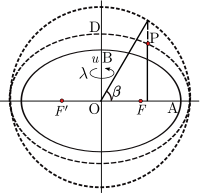
Эллипсоидально-гармонические координаты

Параметрическую широту можно также расширить до трехмерной системы координат. Для точки $P,$ не лежащей на референц-эллипсоиде (полуоси $OA$ и $OB$ ), построим вспомогательный эллипсоид, который является конфокальным (те же фокусы $F$ , $F'$ ) с референц-эллипсоидом: необходимым условием является то, что произведение $ae$ большой полуоси и эксцентриситета одинаково для обоих эллипсоидов. Пусть $u$ будет малой полуосью ( $OD$ ) вспомогательного эллипсоида. Далее пусть $β$ будет параметрической широтой $P$ на вспомогательном эллипсоиде. Набор $(u, β, λ)$ определяет эллипсоидально-гармонические координаты ^[19] или просто эллипсоидальные координаты ^[5]^{: §4.2.2} (хотя этот термин также используется для обозначения геодезической координаты). Эти координаты являются естественным выбором в моделях гравитационного поля для вращающегося эллипсоидального тела. Вышеизложенное относится к двуосному эллипсоиду (сфероиду, как в сплющенных сфероидальных координатах ); для обобщения см. трехосные эллипсоидальные координаты .

Преобразования координат

Отношения между указанными выше системами координат, а также декартовыми координатами здесь не представлены. Преобразование между геодезическими и декартовыми координатами можно найти в преобразовании географических координат . Отношение декартовых и сферических полярных координат дано в сферической системе координат . Отношение декартовых и эллипсоидальных координат обсуждается в Torge. ^[5]

Астрономическая широта

Океан
Эллипсоид
Местный отвес
Континент
Геоид

Астрономическая широта ( $Φ$ ) — это угол между экваториальной плоскостью и истинным вертикальным направлением в точке на поверхности. Истинная вертикаль, направление отвесной линии , также является направлением силы тяжести (результирующей гравитационного ускорения (на основе массы) и центробежного ускорения ) на этой широте. ^[5] Астрономическая широта вычисляется из углов, измеренных между зенитом и звездами, склонение которых точно известно.

В общем случае истинная вертикаль в точке на поверхности не совпадает точно ни с нормалью к референц-эллипсоиду, ни с нормалью к геоиду. Геоид — это идеализированная, теоретическая форма «на среднем уровне моря». Точки на суше не лежат точно на геоиде, а вертикаль в точке в определенное время находится под влиянием приливных сил, которые теоретический геоид усредняет. Угол между астрономической и геодезической нормалями называется вертикальным отклонением и обычно составляет несколько секунд дуги, но он важен в геодезии. ^[5]^[20]

Астрономическую широту не следует путать со склонением — координатой, которую астрономы используют аналогичным образом для указания углового положения звезд к северу-югу от небесного экватора (см. экваториальные координаты ), а также с эклиптической широтой — координатой, которую астрономы используют для указания углового положения звезд к северу-югу от эклиптики (см. эклиптические координаты ).

Смотрите также

Ссылки

Сноски

^ Значение этого угла сегодня составляет 23°26′09.9″ (или 23.43608°). Эта цифра предоставлена Template:Circle of latitude .
^ Элементарный расчет включает дифференцирование для нахождения максимальной разницы геодезической и геоцентрической широт.

Цитаты

^ "ISO 19111 Географическая информация — Ссылки по координатам". ISO . 2021-06-01 . Получено 2022-01-16 .
↑ Корпорация Trinity House (10 января 2020 г.). «1/2020 Needles Lighthouse». Извещения мореплавателям . Получено 24 мая 2020 г.
^ Ньютон, Исаак. «Книга III. Предложение XIX. Проблема III». Philosophiæ Naturalis Principia Mathematica. Перевод Мотта, Эндрю. п. 407.
^ Национальное агентство по картографии и изображениям (23 июня 2004 г.). "Department of Defense World Geodetic System 1984" (PDF) . Национальное агентство по картографии и изображениям. стр. 3-1. TR8350.2 . Получено 25 апреля 2020 г.
^ abcde Торге, В. (2001). Геодезия (3-е изд.). Де Грюйтер. ISBN 3-11-017072-8.
^ abcde Осборн, Питер (2013). "Главы 5,6". Проекции Меркатора . doi :10.5281/zenodo.35392.для кода и рисунков LaTeX.
^ abcd Рапп, Ричард Х. (1991). "Глава 3". Геометрическая геодезия, часть I. Колумбус, Огайо: Кафедра геодезической науки и съемки, Университет штата Огайо. hdl :1811/24333.
^ "Калькулятор длины градуса". Национальное агентство геопространственной разведки. Архивировано из оригинала 2012-12-11 . Получено 2011-02-08 .
^ abcde Снайдер, Джон П. (1987). Картографические проекции: рабочее руководство. Профессиональная статья Геологической службы США 1395. Вашингтон, округ Колумбия: Типография правительства США. Архивировано из оригинала 2008-05-16 . Получено 2017-09-02 .
^ ab Adams, Oscar S. (1921). Широтные разработки, связанные с геодезией и картографией (с таблицами, включая таблицу для равновеликой меридиональной проекции Ламберта (PDF) . Специальная публикация № 67. Береговая и геодезическая служба США.( Примечание : Адамс использует термин изометрическая широта для обозначения конформной широты в этой статье (и во всей современной литературе).)
^ Лежандр, AM (1806). «Анализ следов треугольников на поверхности сфероида». Память Инст. Нат. о . 1 семестр: 130–161.
^ Бессель, FW (1825). «Über die Berechnung der geographischen Langen und Breiten aus geodatischen Vermessungen». Астрон. Нахр . 4 (86): 241–254. arXiv : 0908.1824 . Бибкод : 2010AN....331..852K. дои : 10.1002/asna.201011352. S2CID 118760590.
Перевод: Karney, CFF; Deakin, RE (2010). «Вычисление долготы и широты по геодезическим измерениям». Astron. Nachr . 331 (8): 852–861. arXiv : 0908.1824 . Bibcode : 1825AN......4..241B. doi : 10.1002/asna.18260041601. S2CID 118630614.
↑ Кэли, А. (1870). «О геодезических линиях на сплющенном сфероиде». Phil. Mag . 40 (4-я серия): 329–340. doi :10.1080/14786447008640411.
^ Karney, CFF (2013). «Алгоритмы для геодезических задач». Journal of Geodesy . 87 (1): 43–55. arXiv : 1109.4448 . Bibcode : 2013JGeod..87...43K. doi : 10.1007/s00190-012-0578-z. S2CID 119310141.
^ Лагранж, Жозеф-Луи (1779). «Сюр-ла-Строительство географических карт». Оевр (на французском языке). Том. IV. п. 667.
^ Карни, Чарльз ФФ (август 2011 г.). «Поперечная проекция Меркатора с точностью в несколько нанометров». Журнал геодезии . 85 (8): 475–485. arXiv : 1002.1417 . Bibcode : 2011JGeod..85..475K. doi : 10.1007/s00190-011-0445-3. S2CID 118619524.
^ Ориуэла, Себастьян (2013). «Функции широты».
^ Карни, Чарльз ФФ (2023). «О вспомогательных широтах». Обзор . 56 (395): 165–180. arXiv : 2212.05818 . doi : 10.1080/00396265.2023.2217604.
^ Хольфманн-Велленфор и Мориц (2006) Физическая геодезия , стр. 240, уравнения (6-6) - (6-10).
^ Хофманн-Велленхоф, Б.; Мориц, Х. (2006). Физическая геодезия (2-е изд.). ISBN 3-211-33544-7.

Внешние ссылки

Сервер имен GEONets. Архивировано 09.03.2008 на Wayback Machine . Доступ к базе данных названий иностранных географических объектов Национального агентства геопространственной разведки (NGA).
Ресурсы для определения широты и долготы Архивировано 2008-05-19 на Wayback Machine
Перевод десятичных градусов в градусы, минуты, секунды. Архивировано 2012-11-07 на Wayback Machine – информация о преобразовании десятичных чисел в шестидесятеричные .
Преобразовать десятичные градусы в градусы, минуты, секунды
Расчет расстояния на основе широты и долготы – версия JavaScript
Широтная съемка XVI века
Определение широты Фрэнсисом Дрейком на побережье Калифорнии в 1579 году