stringtranslate.com

Метод Монте-Карло

Аппроксимация нормального распределения методом Монте-Карло

Методы Монте-Карло или эксперименты Монте-Карло — это широкий класс вычислительных алгоритмов , которые опираются на повторную случайную выборку для получения числовых результатов. Основная концепция заключается в использовании случайности для решения задач, которые в принципе могут быть детерминированными . Название происходит от казино Монте-Карло в Монако, где главный разработчик метода, математик Станислав Улам , был вдохновлен азартными привычками своего дяди.

Методы Монте-Карло в основном используются в трех различных классах задач: оптимизация, численное интегрирование и генерация розыгрышей из распределения вероятностей. Их также можно использовать для моделирования явлений со значительной неопределенностью во входных данных, таких как расчет риска отказа атомной электростанции. Методы Монте-Карло часто реализуются с использованием компьютерного моделирования, и они могут предоставлять приблизительные решения проблем, которые в противном случае неразрешимы или слишком сложны для математического анализа.

Методы Монте-Карло широко используются в различных областях науки, техники и математики, таких как физика, химия, биология, статистика, искусственный интеллект, финансы и криптография. Они также применяются в социальных науках, таких как социология, психология и политология. Методы Монте-Карло признаны одной из самых важных и влиятельных идей 20-го века, и они позволили совершить множество научных и технологических прорывов.

Методы Монте-Карло также имеют некоторые ограничения и проблемы, такие как компромисс между точностью и вычислительными затратами, проклятие размерности, надежность генераторов случайных чисел, а также проверка и подтверждение результатов.

Обзор

Методы Монте-Карло различаются, но, как правило, следуют определенному шаблону:

  1. Определить область возможных входных данных
  2. Генерировать входные данные случайным образом из распределения вероятностей по домену
  3. Выполнить детерминированное вычисление выходных данных
  4. Обобщите результаты
Метод Монте-Карло, применяемый для аппроксимации значения π

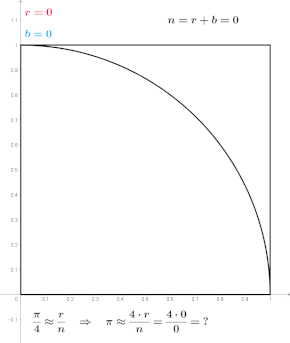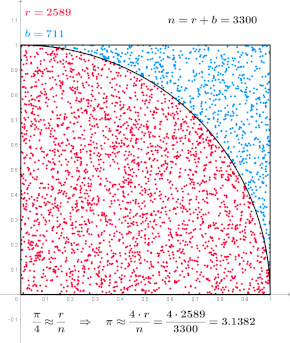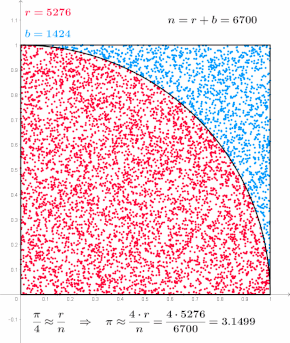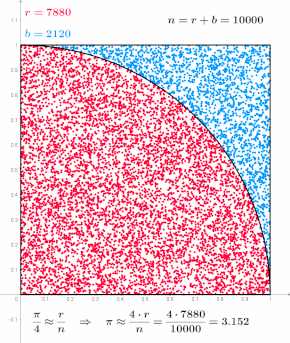
Например, рассмотрим квадрант (круговой сектор), вписанный в единичный квадрат . Учитывая, что отношение их площадей равно ⁠π/4⁠ , значение π можно приблизительно определить с помощью метода Монте-Карло: [1]

  1. Нарисуйте квадрат, затем впишите в него квадрант.
  2. Равномерно распределить заданное количество точек по квадрату
  3. Подсчитайте количество точек внутри квадранта, т.е. имеющих расстояние от начала координат менее 1.
  4. Соотношение внутреннего количества и общего количества образцов представляет собой оценку соотношения двух площадей, ⁠π/4⁠ . Умножьте результат на 4, чтобы оценить π .

В этой процедуре областью входных данных является квадрат, описывающий квадрант. Можно генерировать случайные входные данные, разбрасывая зерна по квадрату, а затем выполнять вычисления для каждого входного данных (проверять, попадает ли он в квадрант). Объединение результатов дает наш конечный результат, приближение π .

Есть два важных соображения:

  1. Если точки распределены неравномерно, то аппроксимация будет плохой.
  2. Аппроксимация обычно плохая, если только несколько точек случайно размещены во всем квадрате. В среднем аппроксимация улучшается по мере размещения большего количества точек.

Использование методов Монте-Карло требует большого количества случайных чисел, и их применение во многом выиграло от использования генераторов псевдослучайных чисел , которые гораздо быстрее в использовании, чем таблицы случайных чисел, которые ранее применялись для статистической выборки.

Приложение

Методы Монте-Карло часто используются в физических и математических задачах и наиболее полезны, когда трудно или невозможно использовать другие подходы. Методы Монте-Карло в основном используются в трех классах задач: [2] оптимизация , численное интегрирование и генерация розыгрышей из распределения вероятностей .

В задачах, связанных с физикой, методы Монте-Карло полезны для моделирования систем со многими связанными степенями свободы , таких как жидкости, неупорядоченные материалы, сильно связанные твердые тела и ячеистые структуры (см. ячеистую модель Поттса , взаимодействующие системы частиц , процессы Маккина–Власова , кинетические модели газов ).

Другие примеры включают моделирование явлений со значительной неопределенностью входных данных, таких как расчет риска в бизнесе и, в математике, оценка многомерных определенных интегралов со сложными граничными условиями . В применении к проблемам системной инженерии (космос, разведка нефти , проектирование самолетов и т. д.) прогнозы отказов, перерасхода средств и срыва графика на основе Монте-Карло обычно лучше, чем человеческая интуиция или альтернативные «мягкие» методы. [3]

В принципе, методы Монте-Карло можно использовать для решения любой проблемы, имеющей вероятностную интерпретацию. По закону больших чисел интегралы, описываемые ожидаемым значением некоторой случайной величины, можно аппроксимировать, взяв эмпирическое среднее ( также известное как «выборочное среднее») независимых выборок переменной. Когда распределение вероятностей переменной параметризовано, математики часто используют выборку Монте-Карло на основе цепи Маркова (MCMC). [4] [5] [6] Основная идея заключается в разработке разумной модели цепи Маркова с заданным стационарным распределением вероятностей . То есть, в пределе выборки, генерируемые методом MCMC, будут выборками из желаемого (целевого) распределения. [7] [8] По эргодической теореме стационарное распределение аппроксимируется эмпирическими мерами случайных состояний выборки MCMC.

В других задачах целью является генерация розыгрышей из последовательности распределений вероятностей, удовлетворяющих нелинейному уравнению эволюции. Эти потоки распределений вероятностей всегда можно интерпретировать как распределения случайных состояний марковского процесса , вероятности переходов которого зависят от распределений текущих случайных состояний (см. процессы Маккина–Власова , уравнение нелинейной фильтрации ). [9] [10] В других случаях возникает поток распределений вероятностей с возрастающим уровнем сложности выборки (модели пространств путей с увеличивающимся временным горизонтом, меры Больцмана–Гиббса, связанные с уменьшающимися температурными параметрами, и многие другие). Эти модели также можно рассматривать как эволюцию закона случайных состояний нелинейной цепи Маркова. [10] [11] Естественным способом моделирования этих сложных нелинейных марковских процессов является выборка нескольких копий процесса, заменяя в уравнении эволюции неизвестные распределения случайных состояний выборочными эмпирическими мерами . В отличие от традиционных методологий Монте-Карло и MCMC, эти методы частиц среднего поля основаны на последовательных взаимодействующих выборках. Терминология среднее поле отражает тот факт, что каждый из образцов ( он же частицы, индивидуумы, ходоки, агенты, существа или фенотипы) взаимодействует с эмпирическими мерами процесса. Когда размер системы стремится к бесконечности, эти случайные эмпирические меры сходятся к детерминированному распределению случайных состояний нелинейной цепи Маркова, так что статистическое взаимодействие между частицами исчезает.

Простой Монте-Карло

Предположим, что кто - то хочет узнать ожидаемое значение μ популяции (и знает, что μ существует), но не имеет формулы для его вычисления. Простой метод Монте-Карло дает оценку для μ , запуская n симуляций и усредняя результаты симуляций. Он не имеет ограничений на распределение вероятностей входных данных для симуляций, требуя только, чтобы входные данные были сгенерированы случайным образом и независимы друг от друга, и чтобы μ существовало. Достаточно большое n даст значение для m , которое будет произвольно близко к μ ; более формально, это будет иметь место, что для любого ε > 0, | μ – m | ≤ ε . [12]

Обычно алгоритм получения m следующий:

s = 0; для  i = 1 до n  запустить симуляцию i-й раз , получив результат r i ;  s = s + r i ; повторить m = s / n ;

Пример

Предположим, мы хотим узнать, сколько раз нам следует бросать три восьмигранных кубика, чтобы общее количество бросков кубиков было не менее T. Мы знаем, что ожидаемое значение существует. Броски кубиков распределены случайным образом и независимы друг от друга. Поэтому применим простой метод Монте-Карло:

s = 0; для  i = 1 до n  бросайте три кубика, пока не будет достигнуто или впервые превышено значение T ; r i = количество бросков ;  s = s + r i ; повторите m = s / n ;

Если n достаточно велико, m будет находиться в пределах ε от μ для любого ε > 0.

Определение достаточно большогон

Общая формула

Пусть ε = | μ – m | > 0. Выберите желаемый уровень достоверности – процентную вероятность того, что после завершения алгоритма Монте-Карло m действительно будет в пределах ε от μ . Пусть z будет z -оценкой, соответствующей этому уровню достоверности.

Пусть s 2 будет оценочной дисперсией, иногда называемой дисперсией «выборки»; это дисперсия результатов, полученных из относительно небольшого числа k «выборочных» симуляций. Выберите a k ; Дриелс и Шин отмечают, что «даже для размеров выборки на порядок меньше требуемого числа, расчет этого числа достаточно стабилен». [13]

Следующий алгоритм вычисляет s2 за один проход, сводя к минимуму вероятность того, что накопленная числовая ошибка приведет к ошибочным результатам: [ 12]

с 1 = 0;запустить симуляцию в первый раз, получив результат r 1 ; m 1 = r 1 ; // m i - среднее значение первых i симуляций для i = 2 до k  запустить  симуляцию в i -й раз, получив результат r i ;  δ i = r i - m i -1 ;  m i = m i-1  + (1/ i ) δ i ;  s i = s i-1  + (( i - 1)/ i )( δ i ) 2 ; повторить s 2 = s k /( k - 1);

Обратите внимание, что после завершения алгоритма m k представляет собой среднее значение k результатов.

n достаточно велико, когда

[12] [13]

Если n ≤ k , то m k = m ; достаточное количество симуляций выборки было сделано для того, чтобы убедиться, что m k находится в пределах ε от μ . Если n > k , то n симуляций можно запустить «с нуля» или, поскольку k симуляций уже были выполнены, можно просто запустить еще n – k симуляций и добавить их результаты к результатам симуляций выборки:

с = м к * к ;для i = k + 1 до n выполнить  симуляцию для i -го раза, получив результат r i ; s = s + r i ; m = s / n ;

Формула, когда результаты моделирования ограничены

Альтернативную формулу можно использовать в особом случае, когда все результаты моделирования ограничены сверху и снизу.

Выберите значение для ε, которое в два раза больше максимально допустимой разницы между μ и m. Пусть 0 < δ < 100 будет желаемым уровнем достоверности, выраженным в процентах. Пусть каждый результат моделирования r 1 , r 2 , … r i , … r n будет таким, что a ≤ r i ≤ b для конечных a и b . Чтобы иметь уверенность по крайней мере δ в том, что | μ – m | < ε /2, используйте значение для n такое, что

Например, если δ = 99%, то n ≥ 2( b – a ) 2 ln(2/0,01)/ ε 2 ≈ 10,6( b – a ) 2 / ε 2 . [12]

Вычислительные затраты

Несмотря на концептуальную и алгоритмическую простоту, вычислительные затраты, связанные с моделированием Монте-Карло, могут быть ошеломляюще высокими. В целом, метод требует много выборок для получения хорошего приближения, что может повлечь за собой произвольно большое общее время выполнения, если время обработки одной выборки велико. [14] Хотя это является серьезным ограничением в очень сложных задачах, смущающе параллельная природа алгоритма позволяет снизить эти большие затраты (возможно, до осуществимого уровня) с помощью стратегий параллельных вычислений в локальных процессорах, кластерах, облачных вычислениях, GPU, FPGA и т. д. [15] [16] [17] [18]

История

До того, как был разработан метод Монте-Карло, симуляции проверяли ранее понятую детерминированную проблему, а статистическая выборка использовалась для оценки неопределенностей в симуляциях. Моделирование Монте-Карло инвертирует этот подход, решая детерминированные проблемы с использованием вероятностной метаэвристики (см. имитацию отжига ).

Ранний вариант метода Монте-Карло был разработан для решения проблемы иглы Бюффона , в которой π можно оценить, бросая иголки на пол, сделанный из параллельных равноудаленных полос. В 1930-х годах Энрико Ферми впервые экспериментировал с методом Монте-Карло, изучая диффузию нейтронов, но он не опубликовал эту работу. [19]

В конце 1940-х годов Станислав Улам изобрел современную версию метода Монте-Карло с цепями Маркова, работая над проектами ядерного оружия в Лос-Аламосской национальной лаборатории . В 1946 году физики-атомщики в Лос-Аламосе исследовали диффузию нейтронов в ядре ядерного оружия. [19] Несмотря на наличие большинства необходимых данных, таких как среднее расстояние, которое нейтрон должен пройти в веществе до столкновения с атомным ядром, и сколько энергии нейтрон, вероятно, выделит после столкновения, физики из Лос-Аламоса не смогли решить эту проблему с помощью обычных, детерминированных математических методов. Улам предложил использовать случайные эксперименты. Он рассказывает о своем вдохновении следующим образом:

Первые мысли и попытки, которые я предпринял для практики [метода Монте-Карло], были навеяны вопросом, который пришел мне в голову в 1946 году, когда я выздоравливал после болезни и раскладывал пасьянсы. Вопрос был в том, каковы шансы того, что пасьянс Кэнфилда, разложенный из 52 карт, сложится успешно? Потратив много времени на попытки оценить их с помощью чисто комбинаторных вычислений, я задался вопросом, не может ли более практичным методом, чем «абстрактное мышление», разложить его, скажем, сто раз и просто наблюдать и подсчитывать количество успешных ходов. Это уже можно было представить с началом новой эры быстрых компьютеров, и я сразу же подумал о проблемах диффузии нейтронов и других вопросах математической физики, и, в более общем плане, как преобразовать процессы, описываемые определенными дифференциальными уравнениями, в эквивалентную форму, интерпретируемую как последовательность случайных операций. Позже [в 1946 году] я рассказал об этой идее Джону фон Нейману , и мы начали планировать реальные вычисления. [20]

Будучи секретной, работа фон Неймана и Улама требовала кодового имени. [21] Коллега фон Неймана и Улама, Николас Метрополис , предложил использовать название Монте-Карло , которое отсылает к казино Монте-Карло в Монако , где дядя Улама занимал деньги у родственников, чтобы играть в азартные игры. [19] Методы Монте-Карло были центральными для моделирования, необходимого для дальнейшей послевоенной разработки ядерного оружия, включая проектирование водородной бомбы, хотя и были сильно ограничены вычислительными инструментами того времени. Фон Нейман, Николас Метрополис и другие запрограммировали компьютер ENIAC для выполнения первых полностью автоматизированных вычислений Монте-Карло для ядра ядерного оружия весной 1948 года. [22] В 1950-х годах методы Монте-Карло использовались в Лос-Аламосе для разработки водородной бомбы и стали популярными в областях физики , физической химии и исследования операций . Корпорация Rand и Военно-воздушные силы США были двумя основными организациями, ответственными за финансирование и распространение информации о методах Монте-Карло в то время, и они начали находить широкое применение во многих различных областях.

Теория более сложных методов Монте-Карло для частиц среднего поля, безусловно, началась в середине 1960-х годов с работы Генри П. Маккина-младшего по марковским интерпретациям класса нелинейных параболических уравнений в частных производных, возникающих в механике жидкости. [23] [24] Более ранняя пионерская статья Теодора Э. Харриса и Германа Кана, опубликованная в 1951 году, использовала методы Монте-Карло среднего поля генетического типа для оценки энергий передачи частиц. [25] Методологии Монте-Карло среднего поля генетического типа также используются в качестве эвристических алгоритмов естественного поиска (также известных как метаэвристические ) в эволюционных вычислениях. Истоки этих вычислительных методов среднего поля можно проследить до 1950 и 1954 годов с работы Алана Тьюринга по машинам обучения мутационного отбора генетического типа [26] и статей Нильса Алла Барричелли в Институте перспективных исследований в Принстоне, штат Нью-Джерси . [27] [28]

Квантовый Монте-Карло , и, более конкретно, диффузионные методы Монте-Карло, также можно интерпретировать как приближение Монте-Карло частиц среднего поля интегралов Фейнмана – Каца по траекториям. [29] [30] [31] [32] [33] [34] [35] Истоки квантовых методов Монте-Карло часто приписывают Энрико Ферми и Роберту Рихтмайеру , которые в 1948 году разработали интерпретацию частиц среднего поля для нейтронных цепных реакций, [36] но первый эвристический и генетический алгоритм частиц (также известный как методы Монте-Карло с повторной выборкой или реконфигурацией) для оценки энергий основного состояния квантовых систем (в моделях с редуцированной матрицей) был создан Джеком Х. Хетерингтоном в 1984 году. [35] В молекулярной химии использование генетических эвристических методологий частиц (также известных как стратегии обрезки и обогащения) можно проследить до 1955 года с основополагающей работой Маршалла Н. Розенблута и Арианны В. Розенблута . [37]

Использование последовательного Монте-Карло в расширенной обработке сигналов и байесовском выводе появилось позднее. В 1993 году Гордон и др. опубликовали в своей основополагающей работе [38] первое применение алгоритма повторной выборки Монте-Карло в байесовском статистическом выводе. Авторы назвали свой алгоритм «бутстрап-фильтром» и продемонстрировали, что по сравнению с другими методами фильтрации их бутстрап-алгоритм не требует никаких предположений о пространстве состояний или шуме системы. Другой пионерской статьей в этой области была статья Генширо Китагавы о связанном «фильтре Монте-Карло» [39] и статьи Пьера Дель Мораля [40] и Химилькона Карвальо, Пьера Дель Мораля, Андре Монена и Жерара Салюта [41] о фильтрах частиц, опубликованные в середине 1990-х годов. Фильтры частиц также были разработаны в обработке сигналов в 1989–1992 годах П. Дель Моралем, Ж. К. Нойером, Г. Ригалом и Г. Салютом в LAAS-CNRS в серии закрытых и секретных исследовательских отчетов с STCAN (Service Technique des Constructions et Armes Navales), ИТ-компанией DIGILOG и LAAS-CNRS (Лабораторией анализа и архитектуры систем) по проблемам обработки сигналов радаров/сонаров и GPS. [42] [43] [44] [45] [46] [47] Эти последовательные методологии Монте-Карло можно интерпретировать как приемочно-отбраковочный сэмплер, оснащенный взаимодействующим механизмом рециркуляции.

С 1950 по 1996 год все публикации по методологиям последовательного Монте-Карло, включая методы Монте-Карло обрезки и повторной выборки, введенные в вычислительную физику и молекулярную химию, представляют естественные и эвристические алгоритмы, применяемые к различным ситуациям без единого доказательства их согласованности, а также без обсуждения смещения оценок и генеалогических и родовых алгоритмов на основе деревьев. Математические основы и первый строгий анализ этих алгоритмов частиц были написаны Пьером Дель Моралем в 1996 году. [40] [48]

Методологии частиц ветвящегося типа с различными размерами популяции были также разработаны в конце 1990-х годов Дэном Крисаном, Джессикой Гейнс и Терри Лайонсом, [49] [50] [51] и Дэном Крисаном, Пьером Дель Моралем и Терри Лайонсом. [52] Дальнейшие разработки в этой области были описаны в 1999–2001 годах П. Дель Моралем, А. Гионне и Л. Микло. [30] [53] [54]

Определения

Нет единого мнения о том, как следует определять Монте-Карло . Например, Рипли [55] определяет большинство вероятностных моделей как стохастическое моделирование , при этом Монте-Карло зарезервировано для интеграции Монте-Карло и статистических тестов Монте-Карло. Савиловски [56] различает моделирование , метод Монте-Карло и моделирование Монте-Карло: моделирование — это фиктивное представление реальности, метод Монте-Карло — это метод, который можно использовать для решения математической или статистической задачи, а моделирование Монте-Карло использует повторную выборку для получения статистических свойств некоторого явления (или поведения).

Вот примеры:

Калос и Уитлок [57] отмечают, что такие различия не всегда легко поддерживать. Например, испускание радиации атомами является естественным стохастическим процессом. Его можно моделировать напрямую, или его среднее поведение можно описать стохастическими уравнениями, которые сами могут быть решены с использованием методов Монте-Карло. «Действительно, один и тот же компьютерный код можно рассматривать одновременно как «естественное моделирование» или как решение уравнений путем естественной выборки».

Сходимость моделирования Монте-Карло можно проверить с помощью статистики Гельмана-Рубина .

Монте-Карло и случайные числа

Основная идея этого метода заключается в том, что результаты вычисляются на основе повторной случайной выборки и статистического анализа. Моделирование Монте-Карло, по сути, является случайным экспериментированием, в том случае, если результаты этих экспериментов недостаточно известны. Моделирование Монте-Карло обычно характеризуется множеством неизвестных параметров, многие из которых трудно получить экспериментально. [58] Методы моделирования Монте-Карло не всегда требуют действительно случайных чисел , чтобы быть полезными (хотя для некоторых приложений, таких как проверка простоты , непредсказуемость имеет жизненно важное значение). [59] Многие из наиболее полезных методов используют детерминированные псевдослучайные последовательности, что упрощает тестирование и повторный запуск моделирования. Единственное качество, обычно необходимое для создания хорошего моделирования , — это чтобы псевдослучайная последовательность казалась «достаточно случайной» в определенном смысле.

Что это значит, зависит от приложения, но обычно они должны пройти ряд статистических тестов. Проверка того, что числа распределены равномерно или следуют другому желаемому распределению, когда рассматривается достаточно большое количество элементов последовательности, является одной из самых простых и распространенных. Слабые корреляции между последовательными выборками также часто желательны/необходимы.

Савиловский перечисляет характеристики высококачественного моделирования Монте-Карло: [56]

Алгоритмы выборки псевдослучайных чисел используются для преобразования равномерно распределенных псевдослучайных чисел в числа, распределенные в соответствии с заданным распределением вероятностей .

Последовательности с низким расхождением часто используются вместо случайной выборки из пространства, поскольку они обеспечивают равномерное покрытие и обычно имеют более быстрый порядок сходимости, чем симуляции Монте-Карло с использованием случайных или псевдослучайных последовательностей. Методы, основанные на их использовании, называются методами квази-Монте-Карло .

В попытке оценить влияние качества случайных чисел на результаты моделирования Монте-Карло, астрофизические исследователи протестировали криптографически безопасные псевдослучайные числа, сгенерированные с помощью набора инструкций Intel RDRAND , по сравнению с числами, полученными с помощью алгоритмов, таких как Mersenne Twister , в моделировании Монте-Карло радиовспышек от коричневых карликов . Не было обнаружено статистически значимой разницы между моделями, сгенерированными с помощью типичных генераторов псевдослучайных чисел и RDRAND для испытаний, состоящих из генерации 10 7 случайных чисел. [60]

Моделирование Монте-Карло против сценариев «что если»

Существуют способы использования вероятностей, которые определенно не являются симуляциями Монте-Карло – например, детерминированное моделирование с использованием одноточечных оценок. Каждой неопределенной переменной в модели назначается оценка «наилучшего предположения». Выбираются сценарии (такие как наилучший, наихудший или наиболее вероятный случай) для каждой входной переменной, и результаты записываются. [61]

Напротив, моделирование Монте-Карло делает выборку из распределения вероятностей для каждой переменной, чтобы получить сотни или тысячи возможных результатов. Результаты анализируются, чтобы получить вероятности возникновения различных результатов. [62] Например, сравнение модели построения стоимости электронной таблицы, запущенной с использованием традиционных сценариев «что если», а затем повторное сравнение с моделированием Монте-Карло и треугольными распределениями вероятностей показывает, что анализ Монте-Карло имеет более узкий диапазон, чем анализ «что если». [ нужен пример ] Это происходит потому, что анализ «что если» дает равный вес всем сценариям (см. количественную оценку неопределенности в корпоративных финансах ), в то время как метод Монте-Карло почти не делает выборки в областях с очень низкой вероятностью. Выборки в таких областях называются «редкими событиями».

Приложения

Методы Монте-Карло особенно полезны для моделирования явлений со значительной неопределенностью во входных данных и систем со многими связанными степенями свободы. Области применения включают:

Физические науки

Методы Монте-Карло очень важны в вычислительной физике , физической химии и смежных прикладных областях и имеют разнообразные приложения от сложных квантовых хромодинамических расчетов до проектирования тепловых экранов и аэродинамических форм, а также для моделирования переноса излучения для расчетов радиационной дозиметрии. [63] [64] [65] В статистической физике молекулярное моделирование Монте-Карло является альтернативой вычислительной молекулярной динамике , и методы Монте-Карло используются для вычисления статистических полевых теорий простых систем частиц и полимеров. [37] [66] Квантовые методы Монте-Карло решают задачу многих тел для квантовых систем. [9] [10] [29] В радиационном материаловедении приближение бинарных столкновений для моделирования ионной имплантации обычно основано на подходе Монте-Карло для выбора следующего сталкивающегося атома. [67] В экспериментальной физике частиц методы Монте-Карло используются для проектирования детекторов , понимания их поведения и сравнения экспериментальных данных с теорией. В астрофизике они используются столь разнообразными способами, как для моделирования как эволюции галактик [68] , так и передачи микроволнового излучения через шероховатую поверхность планеты. [69] Методы Монте-Карло также используются в ансамблевых моделях , которые составляют основу современного прогнозирования погоды .

Инженерное дело

Методы Монте-Карло широко используются в машиностроении для анализа чувствительности и количественного вероятностного анализа в проектировании процессов . Необходимость возникает из-за интерактивного, коллинеарного и нелинейного поведения типичных симуляций процессов. Например,

Изменение климата и радиационное воздействие

Межправительственная группа экспертов по изменению климата использует методы Монте-Карло при анализе функции плотности вероятности радиационного воздействия . [73]

Вычислительная биология

Методы Монте-Карло используются в различных областях вычислительной биологии , например, для байесовского вывода в филогении или для изучения биологических систем, таких как геномы, белки [74] или мембраны. [75] Системы могут изучаться в рамках крупнозернистых или ab initio в зависимости от желаемой точности. Компьютерное моделирование позволяет контролировать локальное окружение конкретной молекулы , чтобы увидеть, происходит ли какая-либо химическая реакция , например. В случаях, когда невозможно провести физический эксперимент, можно проводить мысленные эксперименты (например: разрыв связей, введение примесей в определенных местах, изменение локальной/глобальной структуры или введение внешних полей).

Компьютерная графика

Трассировка пути , иногда называемая трассировкой лучей Монте-Карло, визуализирует 3D-сцену путем случайной трассировки выборок возможных световых путей. Повторная выборка любого заданного пикселя в конечном итоге приведет к тому, что среднее значение выборок сойдется на правильном решении уравнения рендеринга , что делает его одним из самых физически точных методов рендеринга 3D-графики из существующих.

Прикладная статистика

Стандарты для экспериментов Монте-Карло в статистике были установлены Савиловским. [76] В прикладной статистике методы Монте-Карло могут использоваться по крайней мере для четырех целей:

  1. Для сравнения конкурирующих статистик для небольших выборок в условиях реалистичных данных. Хотя ошибка типа I и свойства мощности статистики могут быть рассчитаны для данных, полученных из классических теоретических распределений ( например , нормальная кривая , распределение Коши ) для асимптотических условий ( т. е . бесконечный размер выборки и бесконечно малый эффект обработки), реальные данные часто не имеют таких распределений. [77]
  2. Обеспечить реализацию проверок гипотез , которые более эффективны, чем точные тесты, такие как тесты перестановки (которые часто невозможно вычислить), и в то же время более точны, чем критические значения для асимптотических распределений .
  3. Для предоставления случайной выборки из апостериорного распределения в байесовском выводе . Затем эта выборка аппроксимирует и суммирует все существенные характеристики апостериорного распределения.
  4. Обеспечить эффективные случайные оценки матрицы Гессе отрицательной логарифмической функции правдоподобия, которые могут быть усреднены для формирования оценки информационной матрицы Фишера . [78] [79]

Методы Монте-Карло также являются компромиссом между приблизительными рандомизациями и тестами перестановок. Приблизительный рандомизационный тест основан на указанном подмножестве всех перестановок (что влечет за собой потенциально огромную уборку, в которой перестановки были рассмотрены). Подход Монте-Карло основан на указанном количестве случайно выбранных перестановок (обменивая небольшую потерю точности, если перестановка выбирается дважды — или чаще — на эффективность, заключающуюся в отсутствии необходимости отслеживать, какие перестановки уже были выбраны).

Искусственный интеллект для игр

Методы Монте-Карло были разработаны в технику, называемую поиском по дереву Монте-Карло , которая полезна для поиска лучшего хода в игре. Возможные ходы организованы в дерево поиска , и множество случайных симуляций используются для оценки долгосрочного потенциала каждого хода. Симулятор черного ящика представляет ходы противника. [80]

Метод поиска по дереву Монте-Карло (MCTS) состоит из четырех шагов: [81]

  1. Начиная с корневого узла дерева, выберите оптимальные дочерние узлы, пока не достигнете конечного узла.
  2. Разверните конечный узел и выберите один из его дочерних узлов.
  3. Начните смоделированную игру, начиная с этого узла.
  4. Используйте результаты этой смоделированной игры для обновления узла и его предков.

Конечный эффект в ходе многих моделируемых игр заключается в том, что значение узла, представляющего ход, будет увеличиваться или уменьшаться, что, как мы надеемся, будет соответствовать тому, представляет ли этот узел хороший ход.

Поиск по дереву Монте-Карло успешно использовался в таких играх, как Go , [82] Tantrix , [83] Battleship , [84] Havannah , [85] и Arimaa . [86]

Дизайн и визуальные эффекты

Методы Монте-Карло также эффективны при решении связанных интегрально-дифференциальных уравнений полей излучения и переноса энергии, и поэтому эти методы использовались в вычислениях глобального освещения , которые создают фотореалистичные изображения виртуальных 3D-моделей, с применением в видеоиграх , архитектуре , дизайне , компьютерных фильмах и кинематографических спецэффектах. [87]

Поисково-спасательные работы

Береговая охрана США использует методы Монте-Карло в своей программе компьютерного моделирования SAROPS для расчета вероятного местоположения судов во время поисково-спасательных операций. Каждая симуляция может генерировать до десяти тысяч точек данных, которые случайным образом распределяются на основе предоставленных переменных. [88] Затем шаблоны поиска генерируются на основе экстраполяции этих данных для оптимизации вероятности сдерживания (POC) и вероятности обнаружения (POD), которые вместе будут равняться общей вероятности успеха (POS). В конечном счете, это служит практическим применением распределения вероятностей для обеспечения самого быстрого и целесообразного метода спасения, спасая как жизни, так и ресурсы. [89]

Финансы и бизнес

Моделирование Монте-Карло обычно используется для оценки риска и неопределенности, которые могут повлиять на результат различных вариантов решений. Моделирование Монте-Карло позволяет аналитику бизнес-рисков учитывать общие эффекты неопределенности в таких переменных, как объем продаж, цены на товары и рабочую силу, процентные ставки и обменные курсы, а также влияние отдельных рисковых событий, таких как расторжение контракта или изменение налогового законодательства.

Методы Монте-Карло в финансах часто используются для оценки инвестиций в проекты на уровне бизнес-единицы или корпорации или других финансовых оценок. Их можно использовать для моделирования графиков проектов , где симуляции объединяют оценки для худшего случая, лучшего случая и наиболее вероятной продолжительности для каждой задачи, чтобы определить результаты для всего проекта. [90] Методы Монте-Карло также используются в ценообразовании опционов, анализе риска дефолта. [91] [92] Кроме того, их можно использовать для оценки финансового воздействия медицинских вмешательств. [93]

Закон

Подход Монте-Карло использовался для оценки потенциальной ценности предлагаемой программы, чтобы помочь женщинам-просителям в Висконсине добиться успеха в своих заявлениях на запретительные судебные приказы о преследовании и домашнем насилии . Было предложено помочь женщинам добиться успеха в своих ходатайствах, предоставив им большую защиту, тем самым потенциально снизив риск изнасилования и физического нападения . Однако в игре было много переменных, которые нельзя было оценить идеально, включая эффективность запретительных судебных приказов, показатель успешности просителей как с защитой, так и без нее, и многие другие. В исследовании проводились испытания, которые варьировали эти переменные, чтобы прийти к общей оценке уровня успешности предлагаемой программы в целом. [94]

Библиотечное дело

Подход Монте-Карло также использовался для моделирования количества книжных публикаций на основе книжного жанра в Малайзии. Моделирование Монте-Карло использовало ранее опубликованные данные о национальных книжных публикациях и цену книги в соответствии с книжным жанром на местном рынке. Результаты Монте-Карло использовались для определения того, какой книжный жанр нравится малазийцам, и использовались для сравнения книжных публикаций между Малайзией и Японией . [95]

Другой

Нассим Николас Талеб пишет о генераторах Монте-Карло в своей книге 2001 года «Одураченные случайностью» как о реальном примере обратного теста Тьюринга : человека можно объявить неразумным, если его текст невозможно отличить от сгенерированного текста.

Использование в математике

В целом, методы Монте-Карло используются в математике для решения различных задач путем генерации подходящих случайных чисел (см. также Генерация случайных чисел ) и наблюдения за той долей чисел, которая подчиняется некоторому свойству или свойствам. Метод полезен для получения численных решений задач, слишком сложных для аналитического решения. Наиболее распространенным применением метода Монте-Карло является интегрирование Монте-Карло.

Интеграция

Интеграция Монте-Карло работает путем сравнения случайных точек со значением функции.
Ошибки уменьшаются в .

Детерминированные алгоритмы численного интегрирования хорошо работают в небольшом количестве измерений, но сталкиваются с двумя проблемами, когда функции имеют много переменных. Во-первых, количество необходимых оценок функций быстро увеличивается с количеством измерений. Например, если 10 оценок обеспечивают достаточную точность в одном измерении, то для 100 измерений требуется 10 100 точек — слишком много для вычисления. Это называется проклятием размерности . Во-вторых, граница многомерной области может быть очень сложной, поэтому может оказаться невозможным свести задачу к итеративному интегралу . [96] 100 измерений — это отнюдь не редкость, поскольку во многих физических задачах «измерение» эквивалентно степени свободы .

Методы Монте-Карло предоставляют выход из этого экспоненциального увеличения времени вычислений. Пока рассматриваемая функция ведет себя достаточно хорошо , ее можно оценить, случайным образом выбрав точки в 100-мерном пространстве и взяв некое среднее значение функции в этих точках. Согласно центральной предельной теореме , этот метод демонстрирует сходимость — т. е. учетверение числа точек выборки вдвое уменьшает ошибку, независимо от числа измерений. [96]

Усовершенствование этого метода, известное в статистике как выборка по важности , включает выборку точек случайным образом, но чаще там, где подынтегральное выражение велико. Чтобы сделать это точно, нужно уже знать интеграл, но можно аппроксимировать интеграл интегралом аналогичной функции или использовать адаптивные процедуры, такие как стратифицированная выборка , рекурсивная стратифицированная выборка , адаптивная зонтичная выборка [97] [98] или алгоритм VEGAS .

Похожий подход, метод квази-Монте-Карло , использует последовательности с низким расхождением . Эти последовательности лучше «заполняют» область и чаще выбирают наиболее важные точки, поэтому методы квази-Монте-Карло часто могут сходиться к интегралу быстрее.

Другой класс методов для выборки точек в объеме — это имитация случайных блужданий по нему ( цепь Маркова Монте-Карло ). Такие методы включают алгоритм Метрополиса–Гастингса , выборку Гиббса , алгоритм Ванга и Ландау и методологии MCMC взаимодействующего типа, такие как последовательные выборки Монте-Карло . [99]

Моделирование и оптимизация

Другое мощное и очень популярное применение случайных чисел в численном моделировании — численная оптимизация . Задача состоит в минимизации (или максимизации) функций некоторого вектора, который часто имеет много измерений. Многие проблемы можно сформулировать таким образом: например, компьютерную шахматную программу можно рассматривать как пытающуюся найти набор из, скажем, 10 ходов, который в итоге даст наилучшую оценочную функцию. В задаче коммивояжера цель состоит в минимизации пройденного расстояния. Существуют также приложения к инженерному проектированию, такие как многопрофильная оптимизация проектирования . Она применялась с квазиодномерными моделями для решения задач динамики частиц путем эффективного исследования большого конфигурационного пространства. Ссылка [100] представляет собой всесторонний обзор многих вопросов, связанных с моделированием и оптимизацией.

Задача коммивояжера — это то, что называется обычной задачей оптимизации. То есть все факты (расстояния между каждой точкой назначения), необходимые для определения оптимального пути следования, известны с уверенностью, и цель состоит в том, чтобы перебрать возможные варианты путешествия, чтобы найти тот, у которого общее расстояние наименьшее. Если вместо цели минимизировать общее расстояние, пройденное для посещения каждого желаемого пункта назначения, а вместо этого минимизировать общее время, необходимое для достижения каждого пункта назначения, это выходит за рамки обычной оптимизации, поскольку время в пути по своей сути неопределенно (пробки, время суток и т. д.). В результате для определения оптимального пути требуется другое моделирование: оптимизация для того, чтобы сначала понять диапазон потенциального времени, которое может потребоваться для перехода из одной точки в другую (представленного в данном случае распределением вероятностей, а не определенным расстоянием), а затем оптимизировать решения о путешествии для определения наилучшего пути следования с учетом этой неопределенности.

Обратные задачи

Вероятностная формулировка обратных задач приводит к определению распределения вероятностей в модельном пространстве. Это распределение вероятностей объединяет априорную информацию с новой информацией, полученной путем измерения некоторых наблюдаемых параметров (данных). Поскольку в общем случае теория, связывающая данные с параметрами модели, нелинейна, апостериорную вероятность в модельном пространстве может быть непросто описать (она может быть многомодальной, некоторые моменты могут быть не определены и т. д.).

При анализе обратной задачи получение модели максимального правдоподобия обычно недостаточно, так как обычно требуется информация о разрешающей способности данных. В общем случае моделируется много параметров, и проверка предельных плотностей вероятности, представляющих интерес, может быть непрактичной или даже бесполезной. Но можно псевдослучайно сгенерировать большой набор моделей в соответствии с апостериорным распределением вероятностей и проанализировать и отобразить модели таким образом, чтобы информация об относительных правдоподобиях свойств модели передавалась наблюдателю. Это можно сделать с помощью эффективного метода Монте-Карло, даже в случаях, когда недоступна явная формула для априорного распределения.

Самый известный метод выборки по важности, алгоритм Метрополиса, может быть обобщен, и это дает метод, позволяющий анализировать (возможно, сильно нелинейные) обратные задачи со сложной априорной информацией и данными с произвольным распределением шума. [101] [102]

Философия

Популярное изложение метода Монте-Карло было проведено Мак-Кракеном. [103] Общая философия метода обсуждалась Элишакоффом [104] , а также Грюне-Яноффом и Вейрихом. [105]

Смотрите также

Ссылки

Цитаты

  1. ^ Калос и Уитлок 2008.
  2. ^ Kroese, DP; Brereton, T.; Taimre, T.; Botev, ZI (2014). «Почему метод Монте-Карло так важен сегодня». WIREs Comput Stat . 6 (6): 386–392. doi :10.1002/wics.1314. S2CID  18521840.
  3. ^ Хаббард, Дуглас; Самуэльсон, Дуглас А. (октябрь 2009 г.). «Моделирование без измерений». OR/MS Today : 28–33.
  4. ^ Метрополис, Николас; Розенблут, Арианна В.; Розенблут, Маршалл Н.; Теллер, Августа Х.; Теллер, Эдвард (1 июня 1953 г.). «Вычисления уравнений состояния на быстрых вычислительных машинах». Журнал химической физики . 21 (6): 1087–1092. Bibcode : 1953JChPh..21.1087M. doi : 10.1063/1.1699114. ISSN  0021-9606. OSTI  4390578. S2CID  1046577.
  5. ↑ Hastings, WK (1 апреля 1970 г.). «Методы выборки Монте-Карло с использованием цепей Маркова и их приложения». Biometrika . 57 (1): 97–109. Bibcode :1970Bimka..57...97H. doi :10.1093/biomet/57.1.97. ISSN  0006-3444. S2CID  21204149.
  6. ^ Лю, Цзюнь С.; Лян, Фэминг; Вонг, Винг Хунг (1 марта 2000 г.). «Метод множественных попыток и локальная оптимизация в выборке мегаполисов». Журнал Американской статистической ассоциации . 95 (449): 121–134. doi :10.1080/01621459.2000.10473908. ISSN  0162-1459. S2CID  123468109.
  7. ^ Сполл, Дж. К. (2003). «Оценка с помощью Монте-Карло на основе цепи Маркова». Журнал IEEE Control Systems . 23 (2): 34–45. doi :10.1109/MCS.2003.1188770.
  8. ^ Хилл, Стейси Д.; Сполл, Джеймс К. (2019). «Стационарность и сходимость алгоритма Метрополиса-Гастингса: взгляд на теоретические аспекты». Журнал IEEE Control Systems . 39 : 56–67. doi :10.1109/MCS.2018.2876959. S2CID  58672766.
  9. ^ ab Колокольцев, Василий (2010). Нелинейные марковские процессы . Cambridge University Press . стр. 375.
  10. ^ abc Del Moral, Pierre (2013). Моделирование среднего поля для интегрирования Монте-Карло. Chapman & Hall/ CRC Press . стр. 626. Монографии по статистике и прикладной вероятности
  11. ^ Дель Мораль, П.; Дусе, А.; Ясра, А. (2006). «Последовательные пробоотборники Монте-Карло». Журнал Королевского статистического общества, серия B. 68 (3): 411–436. arXiv : cond-mat/0212648 . дои : 10.1111/j.1467-9868.2006.00553.x. S2CID  12074789.
  12. ^ abcd Оуэн, Арт Б. (2013). Теория Монте-Карло, методы и примеры (PDF) . Работа в процессе. С. 15–36.
  13. ^ ab Driels, Morris R.; Shin, Young S. (апрель 2004 г.). «Определение количества итераций для моделирования эффективности оружия методом Монте-Карло». Технический отчет Военно-морской аспирантуры (март 2003 г. — март 2004 г.): 10–11.
  14. ^ Шонквилер, Р. В.; Мендивил, Ф. (2009). Исследования в области методов Монте-Карло . Springer.
  15. ^ Атанасова, Е.; Гуров, Т.; Караиванова, А.; Ивановска, С.; Дурхова, М.; Димитров, Д. (2016). «О подходах к распараллеливанию для архитектуры Intel MIC». Труды конференции AIP . 1773 (1): 070001. Bibcode : 2016AIPC.1773g0001A. doi : 10.1063/1.4964983.
  16. ^ Кунья младший, А.; Нассер, Р.; Сампайо, Р.; Лопес, Х.; Брейтман, К. (2014). «Количественная оценка неопределенности с помощью метода Монте-Карло в условиях облачных вычислений». Computer Physics Communications . 185 (5): 1355–1363. arXiv : 2105.09512 . Bibcode : 2014CoPhC.185.1355C. doi : 10.1016/j.cpc.2014.01.006. S2CID  32376269.
  17. ^ Wei, J.; Kruis, FE (2013). «Основанный на GPU параллельный метод Монте-Карло для коагуляции частиц с использованием стратегии принятия-отклонения». Chemical Engineering Science . 104 : 451–459. Bibcode :2013ChEnS.104..451W. doi :10.1016/j.ces.2013.08.008.
  18. ^ Линь, И.; Ван, Ф.; Лю, Б. (2018). «Генератор случайных чисел для крупномасштабного параллельного моделирования Монте-Карло на ПЛИС». Журнал вычислительной физики . 360 : 93–103. Bibcode : 2018JCoPh.360...93L. doi : 10.1016/j.jcp.2018.01.029.
  19. ^ abc Метрополис 1987.
  20. ^ Экхардт 1987.
  21. ^ аб Маждраков, Бенов и Валканов 2018, с. 250.
  22. ^ Хейг, Томас; Пристли, Марк; Роуп, Криспин (2014). «Лос-Аламос делает ставку на ENIAC: ядерное моделирование Монте-Карло, 1947-1948». IEEE Annals of the History of Computing . 36 (3): 42–63. doi :10.1109/MAHC.2014.40. S2CID  17470931.
  23. ^ МакКин, Генри П. (1967). «Распространение хаоса для класса нелинейных параболических уравнений». Серия лекций по дифференциальным уравнениям, Католический ун-т . 7 : 41–57.
  24. ^ МакКин, Генри П. (1966). «Класс марковских процессов, связанных с нелинейными параболическими уравнениями». Proc. Natl. Acad. Sci. USA . 56 (6): 1907–1911. Bibcode :1966PNAS...56.1907M. doi : 10.1073/pnas.56.6.1907 . PMC 220210 . PMID  16591437. 
  25. ^ Герман, Кан; Теодор, Харрис Э. (1951). «Оценка передачи частиц методом случайной выборки» (PDF) . Natl. Bur. Stand. Appl. Math. Ser . 12 : 27–30.
  26. ^ Тьюринг, Алан М. (1950). «Вычислительная техника и интеллект». Mind . LIX (238): 433–460. doi :10.1093/mind/LIX.236.433.
  27. ^ Барричелли, Нильс Аалл (1954). «Числовые примеры процесса эволюции». Методы : 45–68.
  28. ^ Барричелли, Нильс Аалл (1957). «Симбиогенетические эволюционные процессы, реализуемые искусственными методами». Методос : 143–182.
  29. ^ ab Del Moral, Pierre (2004). Формулы Фейнмана–Каца. Генеалогические и взаимодействующие приближения частиц. Вероятность и ее приложения. Springer. стр. 575. ISBN 9780387202686. Серия: Вероятность и приложения
  30. ^ ab Del Moral, P.; Miclo, L. (2000). «Аппроксимации ветвящихся и взаимодействующих систем частиц формул Фейнмана–Каца с приложениями к нелинейной фильтрации». Séminaire de Probabilités XXXIV. Lecture Notes in Mathematics. Vol. 1729. Berlin: Springer. pp. 1–145. doi :10.1007/BFb0103798. ISBN 978-3-540-67314-9. МР  1768060.
  31. ^ Del Moral, Pierre; Miclo, Laurent (2000). «Приближение системы частиц Морана для формул Фейнмана–Каца». Стохастические процессы и их приложения . 86 (2): 193–216. doi : 10.1016/S0304-4149(99)00094-0 .
  32. ^ Del Moral, Pierre (2003). «Частичные приближения показателей Ляпунова, связанных с операторами Шредингера и полугруппами Фейнмана–Каца». ESAIM Probability & Statistics . 7 : 171–208. doi : 10.1051/ps:2003001 .
  33. ^ Ассараф, Роланд; Каффарель, Мишель; Хелиф, Анатоль (2000). «Методы диффузионного Монте-Карло с фиксированным числом пешеходов» (PDF) . Phys. Rev. E . 61 (4): 4566–4575. Bibcode :2000PhRvE..61.4566A. doi :10.1103/physreve.61.4566. PMID  11088257. Архивировано из оригинала (PDF) 7 ноября 2014 г.
  34. ^ Каффарель, Мишель; Сеперли, Дэвид; Калос, Малвин (1993). «Комментарий к расчету интегралов по траектории Фейнмана–Каца для энергий основного состояния атомов». Phys. Rev. Lett . 71 (13): 2159. Bibcode : 1993PhRvL..71.2159C. doi : 10.1103/physrevlett.71.2159. PMID  10054598.
  35. ^ ab Hetherington, Jack H. (1984). «Наблюдения за статистической итерацией матриц». Phys. Rev. A. 30 ( 2713): 2713–2719. Bibcode :1984PhRvA..30.2713H. doi :10.1103/PhysRevA.30.2713.
  36. ^ Ферми, Энрике; Рихтмайер, Роберт Д. (1948). «Заметка о проведении переписи в расчетах Монте-Карло» (PDF) . LAM . 805 (A). Рассекреченный отчет Архив Лос-Аламоса
  37. ^ ab Rosenbluth, Marshall N.; Rosenbluth, Arianna W. (1955). «Расчеты Монте-Карло среднего удлинения макромолекулярных цепей». J. Chem. Phys . 23 (2): 356–359. Bibcode :1955JChPh..23..356R. doi : 10.1063/1.1741967 . S2CID  89611599.
  38. ^ Гордон, NJ; Салмонд, DJ; Смит, AFM (апрель 1993 г.). «Новый подход к нелинейной/негауссовой байесовской оценке состояния». Труды IEE F — Радар и обработка сигналов . 140 (2): 107–113. doi :10.1049/ip-f-2.1993.0015. ISSN  0956-375X. S2CID  12644877.
  39. ^ Китагава, Г. (1996). «Фильтр Монте-Карло и сглаживатель для негауссовых нелинейных моделей пространства состояний». Журнал вычислительной и графической статистики . 5 (1): 1–25. doi :10.2307/1390750. JSTOR  1390750.
  40. ^ ab Del Moral, Pierre (1996). "Non Linear Filtering: Interacting Particle Solution" (PDF) . Markov Processes and Related Fields . 2 (4): 555–580. Архивировано из оригинала (PDF) 4 марта 2016 г. . Получено 11 июня 2015 г. .
  41. ^ Carvalho, Himilcon; Del Moral, Pierre; Monin, André; Salut, Gérard (июль 1997 г.). "Optimal Non-linear Filtering in GPS/INS Integration" (PDF) . IEEE Transactions on Aerospace and Electronic Systems . 33 (3): 835–850. Bibcode :1997ITAES..33..835C. doi :10.1109/7.599254. S2CID  27966240. Архивировано из оригинала (PDF) 10 ноября 2022 г. . Получено 11 июня 2015 г. .
  42. ^ П. Дель Мораль, Г. Ригал и Г. Салют. «Оценка и нелинейное оптимальное управление: единая основа для решений частиц». LAAS-CNRS, Тулуза, отчет об исследовании №. 91137, контракт DRET-DIGILOG-LAAS/CNRS, апрель (1991 г.).
  43. ^ P. Del Moral, G. Rigal и G. Salut. «Нелинейные и негауссовские фильтры частиц, применяемые к изменению положения инерциальной платформы». LAAS-CNRS, Тулуза, Исследовательский отчет № 92207, Конвенция STCAN/DIGILOG-LAAS/CNRS STCAN № A.91.77.013, (94 стр.) Сентябрь (1991).
  44. ^ P. Del Moral, G. Rigal и G. Salut. "Оценка и нелинейное оптимальное управление: разрешение частиц при фильтрации и оценке: экспериментальные результаты". Конвенция DRET № 89.34.553.00.470.75.01, Исследовательский отчет № 2 (54 стр.), январь (1992).
  45. ^ P. Del Moral, G. Rigal и G. Salut. "Оценка и нелинейное оптимальное управление: разрешение частиц при фильтрации и оценке: теоретические результаты". Конвенция DRET № 89.34.553.00.470.75.01, Исследовательский отчет № 3 (123 стр.), октябрь (1992).
  46. ^ П. Дель Мораль, Ж.-Ч. Нойер, Г. Ригал и Г. Салют. «Фильтры частиц в обработке радиолокационных сигналов: обнаружение, оценка и распознавание воздушных целей». LAAS-CNRS, Тулуза, Исследовательский отчет № 92495, декабрь (1992).
  47. ^ P. Del Moral, G. Rigal и G. Salut. "Оценка и нелинейное оптимальное управление: разрешение частиц при фильтрации и оценке". Исследования по: Фильтрация, оптимальное управление и оценка максимального правдоподобия. Конвенция DRET № 89.34.553.00.470.75.01. Исследовательский отчет № 4 (210 стр.), январь (1993).
  48. ^ Дель Мораль, Пьер (1998). «Измерительные процессы и взаимодействующие системы частиц. Применение к задачам нелинейной фильтрации». Анналы прикладной теории вероятности . 8 (2) (Publications du Laboratoire de Statistique et Probabilités, 96-15 (1996), изд.): 438–495. CiteSeerX 10.1.1.55.5257 . дои : 10.1214/aoap/1028903535. 
  49. ^ Крисан, Дэн; Гейнс, Джессика; Лайонс, Терри (1998). «Сходимость метода разветвленных частиц к решению задачи Закаи». Журнал SIAM по прикладной математике . 58 (5): 1568–1590. doi :10.1137/s0036139996307371. S2CID  39982562.
  50. ^ Крисэн, Дэн; Лайонс, Терри (1997). «Нелинейная фильтрация и процессы со значениями меры». Теория вероятностей и смежные области . 109 (2): 217–244. doi : 10.1007/s004400050131 . S2CID  119809371.
  51. ^ Крисан, Дэн; Лайонс, Терри (1999). «Частичное приближение решения уравнения Кушнера–Стратоновича». Теория вероятностей и смежные области . 115 (4): 549–578. doi : 10.1007/s004400050249 . S2CID  117725141.
  52. ^ Крисан, Дэн; Дель Морал, Пьер; Лайонс, Терри (1999). «Дискретная фильтрация с использованием разветвленных и взаимодействующих систем частиц» (PDF) . Марковские процессы и смежные области . 5 (3): 293–318.
  53. ^ Дель Мораль, Пьер; Гионне, Элис (1999). «Об устойчивости измеряемых процессов с приложениями к фильтрации». CR Acad. Sci. Paris . 39 (1): 429–434.
  54. ^ Del Moral, Pierre; Guionnet, Alice (2001). «О стабильности взаимодействующих процессов с приложениями к фильтрации и генетическим алгоритмам». Annales de l'Institut Henri Poincaré . 37 (2): 155–194. Bibcode : 2001AIHPB..37..155D. doi : 10.1016/s0246-0203(00)01064-5.
  55. ^ Рипли 1987
  56. ^ ab Sawilowsky 2003
  57. ^ Калос и Уитлок 2008
  58. ^ Shojaeefard, MH; Khalkhali, A.; Yarmohammadisatri, Sadegh (2017). «Эффективный метод анализа чувствительности для модифицированной геометрии подвески Macpherson на основе коэффициента корреляции Пирсона». Vehicle System Dynamics . 55 (6): 827–852. Bibcode : 2017VSD....55..827S. doi : 10.1080/00423114.2017.1283046. S2CID  114260173.
  59. ^ Дэвенпорт 1992
  60. ↑ Route, Matthew (10 августа 2017 г.). «Синтез популяции сверххолодных карликов в радиоизлучении». The Astrophysical Journal . 845 (1): 66. arXiv : 1707.02212 . Bibcode : 2017ApJ...845...66R. doi : 10.3847/1538-4357/aa7ede . S2CID  118895524.
  61. ↑ Восе 2008, стр. 13.
  62. ↑ Восе 2008, стр. 16.
  63. ^ Цзя, Сюнь; Цигенхайн, Питер; Цзян, Стив Б. (2014). «Высокопроизводительные вычисления на базе GPU для лучевой терапии». Физика в медицине и биологии . 59 (4): R151–R182. Bibcode : 2014PMB....59R.151J. doi : 10.1088/0031-9155/59/4/R151. PMC 4003902. PMID  24486639 . 
  64. ^ Хилл, Р.; Хили, Б.; Холлоуэй, Л.; Кунчич, З.; Туэйтс, Д.; Балдок, К. (март 2014 г.). «Достижения в дозиметрии рентгеновского пучка киловольтного напряжения». Физика в медицине и биологии . 59 (6): R183–R231. Bibcode : 2014PMB....59R.183H. doi : 10.1088/0031-9155/59/6/R183. PMID  24584183. S2CID  18082594.
  65. ^ Роджерс, DWO (2006). «Пятьдесят лет моделирования Монте-Карло для медицинской физики». Физика в медицине и биологии . 51 (13): R287–R301. Bibcode : 2006PMB....51R.287R. doi : 10.1088/0031-9155/51/13/R17. PMID  16790908. S2CID  12066026.
  66. ^ Бэрле 2009
  67. ^ Möller, W.; Eckstein, W. (1 марта 1984 г.). "Tridyn — код моделирования TRIM, включающий динамические изменения состава". Ядерные приборы и методы в исследованиях физики, раздел B: Взаимодействие пучков с материалами и атомами . 2 (1): 814–818. Bibcode :1984NIMPB...2..814M. doi :10.1016/0168-583X(84)90321-5.
  68. ^ Макгилливрей и Додд 1982
  69. ^ Золотой 1979
  70. ^ GA Bird, Молекулярная газовая динамика, Кларендон, Оксфорд (1976)
  71. ^ Дитрих, С.; Бойд, И. (1996). «Оптимизированная скалярная параллельная реализация метода DSMC». Журнал вычислительной физики . 126 (2): 328–42. Bibcode : 1996JCoPh.126..328D. doi : 10.1006/jcph.1996.0141 .
  72. ^ Чэнь, Шан-Ин; Сюй, Куо-Чин; Фань, Чиа-Мин (15 марта 2021 г.). «Улучшение обобщенного метода конечных разностей для стохастического моделирования подземных потоков». Журнал вычислительной физики . 429 : 110002. Bibcode : 2021JCoPh.42910002C. doi : 10.1016/J.JCP.2020.110002. S2CID  228828681.
  73. ^ Изменение климата 2013 Физическая научная основа (PDF) . Cambridge University Press . 2013. стр. 697. ISBN 978-1-107-66182-0. Получено 6 июля 2023 г. .
  74. ^ Охеда и др. 2009.
  75. ^ Милик и Сколник 1993.
  76. ^ Кэсси; Смит (2014). «Моделирование уверенности для индекса Эллисона-Глейзера». Журнал городской экономики . 81 : 93. doi :10.1016/j.jue.2014.02.005.
  77. ^ Савиловски и Фахум 2003
  78. ^ Сполл, Джеймс С. (2005). «Вычисление Монте-Карло информационной матрицы Фишера в нестандартных настройках». Журнал вычислительной и графической статистики . 14 (4): 889–909. CiteSeerX 10.1.1.142.738 . doi :10.1198/106186005X78800. S2CID  16090098. 
  79. ^ Das, Sonjoy; Spall, James C.; Ghanem, Roger (2010). «Эффективное вычисление Монте-Карло информационной матрицы Фишера с использованием априорной информации». Computational Statistics & Data Analysis . 54 (2): 272–289. doi :10.1016/j.csda.2009.09.018.
  80. ^ Шасло, Гийом; Баккес, Сандер; Сита, Иштван; Спронк, Питер. «Поиск в дереве Монте-Карло: новая основа для игрового ИИ» (PDF) . Sander.landofsand.com . Проверено 28 октября 2017 г.
  81. ^ "Monte Carlo Tree Search - About". Архивировано из оригинала 29 ноября 2015 г. Получено 15 мая 2013 г.
  82. ^ Шасло, Гийом MJ -B; Винандс, Марк Х.М.; Ван Ден Херик, Х. Яап (2008). «Параллельный поиск в дереве Монте-Карло». Компьютеры и игры . Конспекты лекций по информатике. Том. 5131. стр. 60–71. CiteSeerX 10.1.1.159.4373 . дои : 10.1007/978-3-540-87608-3_6. ISBN  978-3-540-87607-6.
  83. ^ Брунс, Пит. Поиск по дереву Монте-Карло в игре Tantrix: Заключительный отчет Cosc490 (PDF) (Отчет).
  84. ^ Сильвер, Дэвид; Венесс, Джоэл. «Планирование Монте-Карло в крупных POMDP» (PDF) . 0.cs.ucl.ac.uk . Архивировано из оригинала (PDF) 18 июля 2016 г. . Получено 28 октября 2017 г. .
  85. ^ Лоренц, Ричард Дж. (2011). «Улучшение поиска по дереву Монте–Карло в Гаване». Компьютеры и игры . Конспект лекций по информатике. Том 6515. С. 105–115. Bibcode :2011LNCS.6515..105L. doi :10.1007/978-3-642-17928-0_10. ISBN 978-3-642-17927-3.
  86. ^ Якл, Томас. «Arimaa challenge – сравнительное исследование MCTS и альфа-бета методов» (PDF) . Arimaa.com . Получено 28 октября 2017 г. .
  87. ^ Ширмай-Калос 2008.
  88. ^ «Как береговая охрана использует аналитику для поиска пропавших в море». Dice Insights . 3 января 2014 г.
  89. ^ Стоун, Лоуренс Д.; Крацке, Томас М.; Фрост, Джон Р. «Моделирование и оптимизация поиска в системе оптимального планирования поисково-спасательных операций (SAROPS) Береговой охраны США» (PDF) . Ifremer.fr . Получено 28 октября 2017 г. .
  90. ^ "Моделирование рисков проекта (BETA)". risk.octigo.pl . Получено 21 мая 2024 г. .
  91. ^ Кармона, Рене; Дель Морал, Пьер; Ху, Пэн; Уджане, Надя (2012). «Введение в методы частиц с финансовыми приложениями». В Кармона, Рене А.; Морал, Пьер Дель; Ху, Пэн; и др. (ред.). Численные методы в финансах . Springer Proceedings in Mathematics. Том 12. Springer Berlin Heidelberg. стр. 3–49. CiteSeerX 10.1.1.359.7957 . doi :10.1007/978-3-642-25746-9_1. ISBN  978-3-642-25745-2.
  92. ^ Kroese, DP; Taimre, T.; Botev, ZI (2011). Справочник по методам Монте-Карло . John Wiley & Sons.
  93. ^ Аренас, Дэниел Дж.; Летт, Ланэр А.; Клусариц, Хизер; Тейтельман, Энн М. (2017). «Подход Монте-Карло к моделированию для оценки воздействия вмешательств, предоставляемых в студенческой клинике, на здоровье и экономику». PLOS ONE . 12 (12): e0189718. Bibcode : 2017PLoSO..1289718A. doi : 10.1371/journal.pone.0189718 . PMC 5746244. PMID  29284026 . 
  94. ^ Элварт, Лиз; Эмерсон, Нина; Эндерс, Кристина; Фумия, Дани; Мерфи, Кевин (декабрь 2006 г.). «Расширение доступа к запретительным постановлениям для малоимущих жертв домашнего насилия: анализ затрат и выгод предлагаемой программы грантов для жертв домашнего насилия» (PDF) . Государственная коллегия адвокатов Висконсина . Архивировано из оригинала (PDF) 6 ноября 2018 г. . Получено 12 декабря 2016 г. .
  95. ↑ Дахлан, Хади Акбар (29 октября 2021 г.). «Perbandingan Penerbitan dan Harga Buku Mengikut Genre di Malaysia dan Jepun Menggunakan Data Akses Terbuka dan Simulasi Monte Carlo» (PDF) . Каджян Малайзия . 39 (2): 179–202. дои : 10.21315/км2021.39.2.8. S2CID  240435973.
  96. ^ ab Press и др. 1996
  97. ^ MEZEI, M (31 декабря 1986 г.). «Адаптивная зонтичная выборка: Самосогласованное определение небольцмановского смещения». Журнал вычислительной физики . 68 (1): 237–248. Bibcode : 1987JCoPh..68..237M. doi : 10.1016/0021-9991(87)90054-4.
  98. ^ Бартельс, Кристиан; Карплус, Мартин (31 декабря 1997 г.). «Распределения вероятностей для сложных систем: адаптивная зонтичная выборка потенциальной энергии». Журнал физической химии B. 102 ( 5): 865–880. doi :10.1021/jp972280j.
  99. ^ Дель Мораль, Пьер; Дусе, Арно; Ясра, Аджай (2006). «Последовательные пробоотборники Монте-Карло». Журнал Королевского статистического общества, серия B. 68 (3): 411–436. arXiv : cond-mat/0212648 . дои : 10.1111/j.1467-9868.2006.00553.x. S2CID  12074789.
  100. ^ Сполл, Дж. К. (2003), Введение в стохастический поиск и оптимизацию: оценка, моделирование и управление , Wiley, Хобокен, Нью-Джерси. http://www.jhuapl.edu/ISSO
  101. ^ Мосегаард и Тарантола 1995
  102. ^ Тарантола 2005
  103. ^ Маккракен, Д.Д., (1955) Метод Монте-Карло, Scientific American, 192(5), стр. 90-97
  104. ^ Элишакофф, И., (2003) Заметки о философии метода Монте-Карло, Международная прикладная механика, 39(7), стр.753-762
  105. ^ Грюне-Янофф, Т. и Вайрих, П. (2010). Философия и эпистемология симуляции: обзор, Simulation & Gaming, 41(1), стр. 20-50

Источники

Внешние ссылки