Возведение в степень

Arithmetic operation

Графики y = b ^x для различных оснований b :  основание 10,   основание е,   база 2,   база  ⁠1/2⁠ .Каждая кривая проходит через точку(0, 1), поскольку любое ненулевое число, возведенное в степень0,равно1.Приx= 1значениеyравно основанию, поскольку любое число, возведенное в степень1,равно самому числу.

В математике возведение в степень — это операция, включающая два числа : основание и показатель степени или степень . Возведение в степень записывается как b ⁿ , где b — основание , а n — степень ; это произносится как « b (возведенное) в степень n ». ^[1] Когда n — положительное целое число , возведение в степень соответствует повторному умножению основания: то есть b ⁿ — это произведение умножения n оснований: ^[1] $${\displaystyle b^{n}=\underbrace {b\times b\times \dots \times b\times b} _{n{\text{ times}}}.}$$

Экспонента обычно отображается в виде верхнего индекса справа от основания. В этом случае b ⁿ называется « b, возведенное в степень n », « b (возведенное) в степень n », « n -я степень b », « b в n- й степени» ^[2] или, короче, « b в степени n (й)».

Исходя из основного факта, изложенного выше, что для любого положительного целого числа есть вхождения всех умноженных друг на друга, отсюда непосредственно вытекают несколько других свойств возведения в степень. В частности: ^{[nb 1]} ${\displaystyle n}$ ${\displaystyle b^{n}}$ ${\displaystyle n}$ ${\displaystyle b}$

$${\displaystyle {\begin{aligned}b^{n+m}&=\underbrace {b\times \dots \times b} _{n+m{\text{ times}}}\\[1ex]&=\underbrace {b\times \dots \times b} _{n{\text{ times}}}\times \underbrace {b\times \dots \times b} _{m{\text{ times}}}\\[1ex]&=b^{n}\times b^{m}\end{aligned}}}$$

Другими словами, при умножении основания, возведенного в одну степень, на то же основание, возведенное в другую степень, показатели степеней складываются. Из этого основного правила, что показатели степеней складываются, мы можем вывести, что должно быть равно 1 для любого , следующим образом. Для любого , . Разделив обе части на , получаем . ${\displaystyle b^{0}}$ ${\displaystyle b\neq 0}$ ${\displaystyle n}$ ${\displaystyle b^{0}\times b^{n}=b^{0+n}=b^{n}}$ ${\displaystyle b^{n}}$ ${\displaystyle b^{0}=b^{n}/b^{n}=1}$

Тот факт, что можно аналогичным образом вывести из того же правила. Например, . Взяв кубический корень из обеих сторон, получим . ${\displaystyle b^{1}=b}$ ${\displaystyle (b^{1})^{3}=b^{1}\times b^{1}\times b^{1}=b^{1+1+1}=b^{3}}$ ${\displaystyle b^{1}=b}$

Правило, согласно которому умножение заставляет экспоненты складываться, можно использовать и для вывода свойств отрицательных целых экспонент. Рассмотрим вопрос о том, что должно означать. Чтобы соблюсти правило «экспоненты складываются», должно быть так, что . Разделив обе части на , получаем , что можно записать проще как , используя полученный выше результат . Подобным же образом, . ${\displaystyle b^{-1}}$ ${\displaystyle b^{-1}\times b^{1}=b^{-1+1}=b^{0}=1}$ ${\displaystyle b^{1}}$ ${\displaystyle b^{-1}=1/b^{1}}$ ${\displaystyle b^{-1}=1/b}$ ${\displaystyle b^{1}=b}$ ${\displaystyle b^{-n}=1/b^{n}}$

Свойства дробных показателей степени также следуют из того же правила. Например, предположим, что мы рассматриваем и спрашиваем, есть ли некоторая подходящая экспонента, которую мы можем назвать , такая, что . Из определения квадратного корня имеем, что . Следовательно, показатель степени должен быть таким, что . Используя тот факт, что умножение заставляет показатели степени складывать, получаем . С правой стороны можно также записать как , что дает . Приравнивая показатели степени с обеих сторон, имеем . Следовательно, , поэтому . ${\displaystyle {\sqrt {b}}}$ ${\displaystyle r}$ ${\displaystyle b^{r}={\sqrt {b}}}$ ${\displaystyle {\sqrt {b}}\times {\sqrt {b}}=b}$ ${\displaystyle r}$ ${\displaystyle b^{r}\times b^{r}=b}$ ${\displaystyle b^{r+r}=b}$ ${\displaystyle b}$ ${\displaystyle b^{1}}$ ${\displaystyle b^{r+r}=b^{1}}$ ${\displaystyle r+r=1}$ ${\displaystyle r={\tfrac {1}{2}}}$ ${\displaystyle {\sqrt {b}}=b^{1/2}}$

Определение возведения в степень может быть расширено, чтобы разрешить любую действительную или комплексную экспоненту. Возведение в степень целыми экспонентами также может быть определено для широкого спектра алгебраических структур, включая матрицы .

Возведение в степень широко используется во многих областях, включая экономику , биологию , химию , физику и информатику , в таких приложениях, как сложные проценты , рост населения , кинетика химических реакций , волновое поведение и криптография с открытым ключом .

Этимология

Термин exponent происходит от латинского exponentem , настоящего причастия exponere , означающего «выдвигать». ^[3] Термин power ( лат . potentia, potestas, dignitas ) является неправильным переводом ^{[4] [5]} древнегреческого δύναμις ( dúnamis , здесь: «усиление» ^{[4] ), который} греческий математик Евклид использовал для обозначения квадрата прямой, ^[6] следуя Гиппократу Хиосскому . ^[7]

История

Древность

Песчаный счетовод

В «Песочном счетоводе » Архимед доказал закон степеней, 10a · 10b ⁼ 10a ^{+ b ,} необходимый для манипулирования степенями числа 10. ^[8] Затем он использовал степени числа 10 , чтобы оценить количество песчинок, которые могут содержаться во ^{Вселенной} .

Золотой век ислама

МалиКааба(«квадрат» и «куб»)

В IX веке персидский математик Аль-Хорезми использовал термины مَال ( māl , «имущество», «собственность») для квадрата — мусульмане, «как и большинство математиков тех и более ранних времен, думали о квадратном числе как о изображении площади, особенно земли, следовательно, собственности» ^[9] — и كَعْبَة ( Kaʿbah , «куб») для куба , который позднее исламские математики представляли в математической нотации как буквы mīm (m) и kāf (k) соответственно, к XV веку, как видно из работы Абу-ль-Хасана ибн Али аль-Каласади . ^[10]

15–18 век

Введение в экспоненты

Николя Шюке использовал форму экспоненциальной записи в 15 веке, например, 12 ² для представления 12 x ² . ^[11] Позже это использовали Хенрикус Грамматеус и Михаэль Штифель в 16 веке. В конце 16 века Йост Бюрги использовал римские цифры для показателей степени способом, похожим на тот, что использовал Шюке, напримерiii4для 4 x ^{3. [12} ]

«Экспонента»; «квадрат» и «куб»

Слово показатель степени было введено в 1544 году Михаэлем Штифелем. ^{[13] [14]} В XVI веке Роберт Рекорд использовал термины квадрат, куб, зензизензик ( четвертая степень ), сурсолид (пятая), зензикуб (шестая), второй сурсолид (седьмая) и зензизензизензик (восьмая). ^[9] Биквадрат также использовался для обозначения четвертой степени.

Современная экспоненциальная запись

В 1636 году Джеймс Юм использовал по существу современную нотацию, когда в L'algèbre de Viète он записал A ⁱⁱⁱ вместо A ³ . ^[15] В начале 17 века первая форма нашей современной экспоненциальной записи была введена Рене Декартом в его тексте под названием La Géométrie ; там эта нотация введена в Книге I. ^[16]

^{Я обозначаю} ... аа , или 2 ^при умножении а на само себя; и 3 при умножении его еще раз на а , и так до бесконечности.

—  Рене Декарт, «Геометрия».

Некоторые математики (например, Декарт) использовали показатели только для степеней больше двух, предпочитая представлять квадраты как повторное умножение. Таким образом, они записывали многочлены , например, как ax + bxx + cx ³ + d .

"Индексы"

Сэмюэл Джик ввел термин «индексы» в 1696 году. ^[6] Термин «инволюция» использовался как синоним термина « индексы» , но со временем его использование сократилось ^[17] и его не следует путать с его более общим значением .

Переменные показатели, нецелые показатели

В 1748 году Леонард Эйлер ввел переменные показатели степени и, неявно, нецелые показатели, написав:

Рассмотрим показательные функции или степени, в которых показатель степени сам по себе является переменной. Ясно, что величины такого рода не являются алгебраическими функциями , поскольку в них показатели степени должны быть постоянными. ^[18]

Терминология

Выражение b ² = b · b называется « квадрат b » или « b в квадрате», потому что площадь квадрата со стороной b равна b ² . (Правда, его можно было бы также назвать « b во второй степени», но «квадрат b » и « b в квадрате» настолько укоренились в традиции и удобстве, что « b во второй степени» имеет тенденцию звучать необычно или неуклюже.)

Аналогично, выражение b ³ = b · b · b называется « кубом b » или « b в кубе», поскольку объем куба со стороной b равен b ³ .

Когда показатель степени является положительным целым числом , этот показатель указывает, сколько копий основания умножаются вместе. Например, 3 ⁵ = 3 · 3 · 3 · 3 · 3 = 243. Основание 3 появляется 5 раз в умножении, потому что показатель степени равен 5. Здесь 243 — это 5-я степень числа 3 , или 3, возведенная в 5-ю степень .

Слово «raised» обычно опускается, а иногда и «power», так что 3 ⁵ можно просто прочитать «3 в 5-й степени» или «3 в 5-й степени». Таким образом, возведение в степень b ⁿ можно выразить как « b в степени n », « b в n- й степени», « b в n- й степени» или, короче, как « b в n-й степени ».

Целые показатели степеней

Операция возведения в степень с целыми показателями может быть определена непосредственно из элементарных арифметических операций .

Положительные показатели степени

Определение возведения в степень как итеративного умножения можно формализовать с помощью индукции ^[19] , и это определение можно использовать, как только появляется ассоциативное умножение:

Базовый вариант:

${\displaystyle b^{1}=b}$

и повторение есть

${\displaystyle b^{n+1}=b^{n}\cdot b.}$

Ассоциативность умножения подразумевает, что для любых положительных целых чисел m и n ,

${\displaystyle b^{m+n}=b^{m}\cdot b^{n},}$

и

${\displaystyle (b^{m})^{n}=b^{mn}.}$

Нулевой показатель степени

Как упоминалось ранее, (ненулевое) число, возведенное в степень 0 , равно 1 : ^{[20] [1]}

${\displaystyle b^{0}=1.}$

Это значение также получается с помощью соглашения о пустом произведении , которое может использоваться в любой алгебраической структуре с умножением, имеющим тождество . Таким образом, формула

${\displaystyle b^{m+n}=b^{m}\cdot b^{n}}$

также справедливо для . ${\displaystyle n=0}$

Случай 0 ⁰ является спорным. В контекстах, где рассматриваются только целые степени, значение 1 обычно присваивается 0 ^0, но в противном случае выбор того, присваивать ли ему значение и какое значение присваивать, может зависеть от контекста. Для получения более подробной информации см. Ноль в степени нуля .

Отрицательные показатели степени

Возведение в степень с отрицательными показателями определяется следующим тождеством, которое справедливо для любого целого числа n и ненулевого b :

${\displaystyle b^{-n}={\frac {1}{b^{n}}}}$. ^[1]

Возведение 0 в отрицательную степень не определено, но в некоторых обстоятельствах может интерпретироваться как бесконечность ( ). ^[21] ${\displaystyle \infty }$

Это определение возведения в степень с отрицательными показателями является единственным, которое позволяет распространить тождество на отрицательные показатели (рассмотрим случай ). ${\displaystyle b^{m+n}=b^{m}\cdot b^{n}}$ ${\displaystyle m=-n}$

То же самое определение применимо к обратимым элементам в мультипликативном моноиде , то есть алгебраической структуре , с ассоциативным умножением и мультипликативным тождеством, обозначаемым 1 (например, квадратные матрицы заданной размерности). В частности, в такой структуре обратный элемент обратимого элемента x стандартно обозначается ${\displaystyle x^{-1}.}$

Идентичность и свойства

Следующие идентичности , часто называемыеПравила экспоненты справедливы для всех целочисленных экспонент, при условии, что основание не равно нулю:^[1]

${\displaystyle {\begin{aligned}b^{m+n}&=b^{m}\cdot b^{n}\\\left(b^{m}\right)^{n}&=b^{m\cdot n}\\(b\cdot c)^{n}&=b^{n}\cdot c^{n}\end{aligned}}}$

В отличие от сложения и умножения, возведение в степень не является коммутативным . Например, 2 ³ = 8 ≠ 3 ² = 9. Также в отличие от сложения и умножения, возведение в степень не является ассоциативным . Например, (2 ³ ) ² = 8 ² = 64 , тогда как 2 ^{(3 2 )} = 2 ⁹ = 512. Без скобок общепринятый порядок операций для последовательного возведения в степень в надстрочной нотации — сверху вниз (или правоассоциативный ), а не снизу вверх ^{[22] [23] [24]} (или левоассоциативный ). То есть,

${\displaystyle b^{p^{q}}=b^{\left(p^{q}\right)},}$

что, в общем, отличается от

${\displaystyle \left(b^{p}\right)^{q}=b^{pq}.}$

Степени суммы

Степени суммы обычно можно вычислить из степеней слагаемых по биномиальной формуле

${\displaystyle (a+b)^{n}=\sum _{i=0}^{n}{\binom {n}{i}}a^{i}b^{n-i}=\sum _{i=0}^{n}{\frac {n!}{i!(n-i)!}}a^{i}b^{n-i}.}$

Однако эта формула верна только в том случае, если слагаемые коммутируют (т. е. ab = ba ), что подразумевается, если они принадлежат структуре , которая является коммутативной . В противном случае, если a и b являются, скажем, квадратными матрицами одинакового размера, эту формулу использовать нельзя. Из этого следует, что в компьютерной алгебре многие алгоритмы , включающие целочисленные показатели, должны быть изменены, когда основания возведения в степень не коммутируют. Некоторые системы компьютерной алгебры общего назначения используют другую нотацию (иногда ^^ вместо ^ ) для возведения в степень с некоммутирующими основаниями, что тогда называется некоммутативным возведением в степень .

Комбинаторная интерпретация

Для неотрицательных целых чисел n и m значение n ^m равно числу функций из набора из m элементов в набор из n элементов (см. кардинальное возведение в степень ). Такие функции могут быть представлены в виде m - кортежей из набора из n элементов (или в виде m -буквенных слов из n -буквенного алфавита). Некоторые примеры для конкретных значений m и n приведены в следующей таблице:

Конкретные базы

Степени десяти

В десятичной системе счисления целые степени числа 10 записываются как цифра 1 , за которой следует или которой предшествует количество нулей, определяемое знаком и величиной показателя степени. Например,10 ³ =1000 и10 ⁻⁴ =0,0001 .

Возведение в степень с основанием 10 используется в научной записи для обозначения больших или малых чисел. Например,299 792 458  м/с ( скорость света в вакууме, в метрах в секунду ) можно записать как2,997 924 58 × 10 ⁸  м/с и затем аппроксимируется как2,998 × 10 ⁸  м/с .

Префиксы СИ, основанные на степенях числа 10, также используются для описания малых или больших величин. Например, префикс кило означает10 ³ =1000 , поэтому километр равен1000 м .

Степени двойки

Обычно используются первые отрицательные степени числа 2 , которые имеют специальные названия, например: половина и четверть .

Степени числа 2 появляются в теории множеств , поскольку множество с n элементами имеет множество степеней — множество всех его подмножеств , которое имеет 2 ⁿ элементов.

Целые степени числа 2 важны в информатике . Положительные целые степени числа 2 ⁿ дают количество возможных значений для n - битного целого двоичного числа ; например, байт может принимать 2 ⁸ = 256 различных значений. Двоичная система счисления выражает любое число как сумму степеней числа 2 и обозначает его как последовательность 0 и 1 , разделенных двоичной точкой , где 1 указывает на степень числа 2 , которая появляется в сумме; показатель степени определяется местом этой 1 : неотрицательные показатели степени являются рангом 1 слева от точки (начиная с 0 ), а отрицательные показатели степени определяются рангом справа от точки.

Полномочия одного

Каждая степень единицы равна: 1 ⁿ = 1. Это верно, даже если n отрицательно.

Первая степень числа — это само число: n ¹ = n .

Степени нуля

Если показатель степени n положительный ( n > 0 ), то n-я степень нуля равна нулю: 0 ⁿ = 0 .

Если показатель степени n отрицателен ( n < 0 ), то n- я степень нуля 0 ⁿ не определена, поскольку она должна быть равна − n > 0 , и это будет соответствовать вышесказанному. ${\displaystyle 1/0^{-n}}$ ${\displaystyle 1/0}$

Выражение 0 0 либо определяется как 1 , либо остается неопределенным.

Степени отрицательной единицы

Если n — четное целое число, то (−1) ⁿ = 1. Это происходит потому, что отрицательное число, умноженное на другое отрицательное число, отменяет знак и, таким образом, дает положительное число.

Если n — нечетное целое число, то (−1) ⁿ = −1 . Это происходит потому, что после удаления −1 пар останется −1 .

Из-за этого степени −1 полезны для выражения чередующихся последовательностей . Для похожего обсуждения степеней комплексного числа i см. § Корни n-й степени комплексного числа .

Большие показатели степени

Предел последовательности степеней числа, большего единицы, расходится; другими словами, последовательность растет неограниченно:

b ⁿ → ∞ при n → ∞, когда b > 1

Это можно прочитать как « b в степени n стремится к +∞, когда n стремится к бесконечности, когда b больше единицы».

Степени числа, модуль которого меньше единицы, стремятся к нулю:

b ⁿ → 0 при n → ∞, когда | b | < 1

Любая степень единицы всегда равна единице:

b ⁿ = 1 для всех n, если b = 1

Степени –1 чередуются между 1 и –1 , когда n чередуется между четным и нечетным, и, таким образом, не стремятся к какому-либо пределу с ростом n .

Если b < –1 , то b ⁿ чередуется между все большими и большими положительными и отрицательными числами, так как n чередуется между четным и нечетным, и, таким образом, не стремится ни к какому пределу по мере роста n .

Если возведенное в степень число изменяется, стремясь к 1 , когда показатель степени стремится к бесконечности, то предел не обязательно один из приведенных выше. Особенно важным случаем является

(1 + 1/ n ) ⁿ → e при n → ∞

См . § Экспоненциальная функция ниже.

Другие ограничения, в частности, ограничения выражений, принимающих неопределенную форму , описаны в § Ограничения полномочий ниже.

Функции мощности

Степенные функции для n = 1, 3, 5

Степенные функции для n = 2, 4, 6

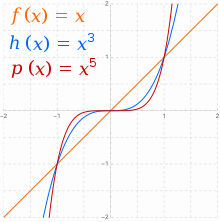
Действительные функции вида , где , иногда называются степенными функциями. ^[25] Когда — целое число и , существуют два основных семейства: для четных и для нечетных. В общем случае для , когда — четное, будет стремиться к положительной бесконечности с увеличением , а также к положительной бесконечности с уменьшением . Все графики из семейства четных степенных функций имеют общую форму , сглаживаясь в середине по мере увеличения. ^[26] Функции с таким видом симметрии ( ) называются четными функциями . ${\displaystyle f(x)=cx^{n}}$ ${\displaystyle c\neq 0}$ ${\displaystyle n}$ ${\displaystyle n\geq 1}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle c>0}$ ${\displaystyle n}$ ${\displaystyle f(x)=cx^{n}}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle y=cx^{2}}$ ${\displaystyle n}$ ${\displaystyle f(-x)=f(x)}$

Когда нечетно, асимптотическое поведение меняется с положительного на отрицательное . Для также будет стремиться к положительной бесконечности с увеличением , но к отрицательной бесконечности с уменьшением . Все графики из семейства нечетных степенных функций имеют общую форму , более уплощаясь в середине по мере увеличения и теряя всю плоскость там на прямой линии для . Функции с таким видом симметрии ( ) называются нечетными функциями . ${\displaystyle n}$ ${\displaystyle f(x)}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle c>0}$ ${\displaystyle f(x)=cx^{n}}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle y=cx^{3}}$ ${\displaystyle n}$ ${\displaystyle n=1}$ ${\displaystyle f(-x)=-f(x)}$

Для в каждом случае справедливо противоположное асимптотическое поведение. ^[26] ${\displaystyle c<0}$

Таблица степеней десятичных цифр

Рациональные показатели степени

Сверху вниз: x ^1/8 , x ^1/4 , x ^1/2 , x ¹ , x ² , x ⁴ , x ⁸ .

Если x — неотрицательное действительное число , а n — положительное целое число, или обозначает единственный положительный действительный корень степени n из x , то есть единственное положительное действительное число y, такое что ${\displaystyle x^{1/n}}$ ${\displaystyle {\sqrt[{n}]{x}}}$ ${\displaystyle y^{n}=x.}$

Если x — положительное действительное число, а также рациональное число , причем p и q > 0 целых чисел, то определяется как ${\displaystyle {\frac {p}{q}}}$ ${\textstyle x^{p/q}}$

${\displaystyle x^{\frac {p}{q}}=\left(x^{p}\right)^{\frac {1}{q}}=(x^{\frac {1}{q}})^{p}.}$

Равенство справа можно вывести, положив и записав ${\displaystyle y=x^{\frac {1}{q}},}$ ${\displaystyle (x^{\frac {1}{q}})^{p}=y^{p}=\left((y^{p})^{q}\right)^{\frac {1}{q}}=\left((y^{q})^{p}\right)^{\frac {1}{q}}=(x^{p})^{\frac {1}{q}}.}$

Если r — положительное рациональное число, то 0 ^r = 0 , по определению.

Все эти определения необходимы для распространения тождества на рациональные показатели степеней. ${\displaystyle (x^{r})^{s}=x^{rs}}$

С другой стороны, существуют проблемы с расширением этих определений на основания, которые не являются положительными действительными числами. Например, отрицательное действительное число имеет действительный корень степени n , который отрицателен, если n нечетно , и не имеет действительного корня, если n четно . В последнем случае, какой бы комплексный корень степени n ни был выбран для тождества, он не может быть удовлетворен. Например, ${\displaystyle x^{\frac {1}{n}},}$ ${\displaystyle (x^{a})^{b}=x^{ab}}$

${\displaystyle \left((-1)^{2}\right)^{\frac {1}{2}}=1^{\frac {1}{2}}=1\neq (-1)^{2\cdot {\frac {1}{2}}}=(-1)^{1}=-1.}$

Подробную информацию о том, как можно решать эти проблемы, см. в разделах § Действительные показатели степени и § Нецелые степени комплексных чисел .

Действительные показатели степени

Для положительных действительных чисел возведение в степень может быть определено двумя эквивалентными способами: либо путем расширения рациональных степеней до действительных чисел по непрерывности ( § Пределы рациональных экспонент , ниже), либо в терминах логарифма основания и показательной функции ( § Степени через логарифмы , ниже). Результатом всегда является положительное действительное число, а тождества и свойства, показанные выше для целых экспонент, остаются верными с этими определениями для действительных экспонент. Второе определение используется чаще, поскольку оно напрямую обобщается на комплексные экспоненты.

С другой стороны, возведение в действительную степень отрицательного действительного числа гораздо сложнее определить последовательно, поскольку оно может быть недействительным и иметь несколько значений. Можно выбрать одно из этих значений, называемое главным значением , но нет выбора главного значения, для которого тождество

${\displaystyle \left(b^{r}\right)^{s}=b^{rs}}$

верно; см. § Несостоятельность тождеств степени и логарифма . Поэтому возведение в степень с основанием, не являющимся положительным действительным числом, обычно рассматривается как многозначная функция .

Пределы рациональных показателей степеней

Предел e ^{1/ n} равен e ⁰ = 1, когда n стремится к бесконечности.

Поскольку любое иррациональное число можно выразить как предел последовательности рациональных чисел, возведение в степень положительного действительного числа b с произвольным действительным показателем степени x можно определить по непрерывности с помощью правила ^[27]

${\displaystyle b^{x}=\lim _{r(\in \mathbb {Q} )\to x}b^{r}\quad (b\in \mathbb {R} ^{+},\,x\in \mathbb {R} ),}$

где предел берется только по рациональным значениям r . Этот предел существует для каждого положительного b и каждого действительного x .

Например, если x = π , то бесконечное десятичное представление π = 3,14159... и монотонность рациональных степеней можно использовать для получения интервалов, ограниченных рациональными степенями, которые сколь угодно малы и должны содержать ${\displaystyle b^{\pi }:}$

${\displaystyle \left[b^{3},b^{4}\right],\left[b^{3.1},b^{3.2}\right],\left[b^{3.14},b^{3.15}\right],\left[b^{3.141},b^{3.142}\right],\left[b^{3.1415},b^{3.1416}\right],\left[b^{3.14159},b^{3.14160}\right],\ldots }$

Итак, верхние и нижние границы интервалов образуют две последовательности , имеющие один и тот же предел, обозначаемый ${\displaystyle b^{\pi }.}$

Это определяет для каждого положительного b и действительного x как непрерывную функцию b и x . См. также Well -defined expression . ^[28] ${\displaystyle b^{x}}$

Экспоненциальная функция

The exponential function is often defined as ${\displaystyle x\mapsto e^{x},}$ where ${\displaystyle e\approx 2.718}$ is Euler's number. To avoid circular reasoning, this definition cannot be used here. So, a definition of the exponential function, denoted ${\displaystyle \exp(x),}$ and of Euler's number are given, which rely only on exponentiation with positive integer exponents. Then a proof is sketched that, if one uses the definition of exponentiation given in preceding sections, one has

${\displaystyle \exp(x)=e^{x}.}$

There are many equivalent ways to define the exponential function, one of them being

${\displaystyle \exp(x)=\lim _{n\rightarrow \infty }\left(1+{\frac {x}{n}}\right)^{n}.}$

One has ${\displaystyle \exp(0)=1,}$ and the exponential identity ${\displaystyle \exp(x+y)=\exp(x)\exp(y)}$ holds as well, since

${\displaystyle \exp(x)\exp(y)=\lim _{n\rightarrow \infty }\left(1+{\frac {x}{n}}\right)^{n}\left(1+{\frac {y}{n}}\right)^{n}=\lim _{n\rightarrow \infty }\left(1+{\frac {x+y}{n}}+{\frac {xy}{n^{2}}}\right)^{n},}$

and the second-order term ${\displaystyle {\frac {xy}{n^{2}}}}$ does not affect the limit, yielding ${\displaystyle \exp(x)\exp(y)=\exp(x+y)}$.

Euler's number can be defined as ${\displaystyle e=\exp(1)}$. It follows from the preceding equations that ${\displaystyle \exp(x)=e^{x}}$ when x is an integer (this results from the repeated-multiplication definition of the exponentiation). If x is real, ${\displaystyle \exp(x)=e^{x}}$ results from the definitions given in preceding sections, by using the exponential identity if x is rational, and the continuity of the exponential function otherwise.

The limit that defines the exponential function converges for every complex value of x, and therefore it can be used to extend the definition of ${\displaystyle \exp(z)}$, and thus ${\displaystyle e^{z},}$ from the real numbers to any complex argument z. This extended exponential function still satisfies the exponential identity, and is commonly used for defining exponentiation for complex base and exponent.

Powers via logarithms

The definition of e^x as the exponential function allows defining b^x for every positive real numbers b, in terms of exponential and logarithm function. Specifically, the fact that the natural logarithm ln(x) is the inverse of the exponential function e^x means that one has

${\displaystyle b=\exp(\ln b)=e^{\ln b}}$

for every b > 0. For preserving the identity ${\displaystyle (e^{x})^{y}=e^{xy},}$ one must have

${\displaystyle b^{x}=\left(e^{\ln b}\right)^{x}=e^{x\ln b}}$

So, ${\displaystyle e^{x\ln b}}$ can be used as an alternative definition of b^x for any positive real b. This agrees with the definition given above using rational exponents and continuity, with the advantage to extend straightforwardly to any complex exponent.

Complex exponents with a positive real base

If b is a positive real number, exponentiation with base b and complex exponent z is defined by means of the exponential function with complex argument (see the end of § Exponential function, above) as

${\displaystyle b^{z}=e^{(z\ln b)},}$

where ${\displaystyle \ln b}$ denotes the natural logarithm of b.

This satisfies the identity

${\displaystyle b^{z+t}=b^{z}b^{t},}$

In general, ${\textstyle \left(b^{z}\right)^{t}}$ is not defined, since b^z is not a real number. If a meaning is given to the exponentiation of a complex number (see § Non-integer powers of complex numbers, below), one has, in general,

${\displaystyle \left(b^{z}\right)^{t}\neq b^{zt},}$

unless z is real or t is an integer.

Euler's formula,

${\displaystyle e^{iy}=\cos y+i\sin y,}$

allows expressing the polar form of ${\displaystyle b^{z}}$ in terms of the real and imaginary parts of z, namely

${\displaystyle b^{x+iy}=b^{x}(\cos(y\ln b)+i\sin(y\ln b)),}$

where the absolute value of the trigonometric factor is one. This results from

${\displaystyle b^{x+iy}=b^{x}b^{iy}=b^{x}e^{iy\ln b}=b^{x}(\cos(y\ln b)+i\sin(y\ln b)).}$

Non-integer powers of complex numbers

In the preceding sections, exponentiation with non-integer exponents has been defined for positive real bases only. For other bases, difficulties appear already with the apparently simple case of nth roots, that is, of exponents ${\displaystyle 1/n,}$ where n is a positive integer. Although the general theory of exponentiation with non-integer exponents applies to nth roots, this case deserves to be considered first, since it does not need to use complex logarithms, and is therefore easier to understand.

nth roots of a complex number

Every nonzero complex number z may be written in polar form as

${\displaystyle z=\rho e^{i\theta }=\rho (\cos \theta +i\sin \theta ),}$

where ${\displaystyle \rho }$ is the absolute value of z, and ${\displaystyle \theta }$ is its argument. The argument is defined up to an integer multiple of 2π; this means that, if ${\displaystyle \theta }$ is the argument of a complex number, then ${\displaystyle \theta +2k\pi }$ is also an argument of the same complex number for every integer ${\displaystyle k}$.

The polar form of the product of two complex numbers is obtained by multiplying the absolute values and adding the arguments. It follows that the polar form of an nth root of a complex number can be obtained by taking the nth root of the absolute value and dividing its argument by n:

${\displaystyle \left(\rho e^{i\theta }\right)^{\frac {1}{n}}={\sqrt[{n}]{\rho }}\,e^{\frac {i\theta }{n}}.}$

If ${\displaystyle 2\pi }$ is added to ${\displaystyle \theta }$, the complex number is not changed, but this adds ${\displaystyle 2i\pi /n}$ to the argument of the nth root, and provides a new nth root. This can be done n times, and provides the n nth roots of the complex number.

It is usual to choose one of the n nth root as the principal root. The common choice is to choose the nth root for which ${\displaystyle -\pi <\theta \leq \pi ,}$ that is, the nth root that has the largest real part, and, if there are two, the one with positive imaginary part. This makes the principal nth root a continuous function in the whole complex plane, except for negative real values of the radicand. This function equals the usual nth root for positive real radicands. For negative real radicands, and odd exponents, the principal nth root is not real, although the usual nth root is real. Analytic continuation shows that the principal nth root is the unique complex differentiable function that extends the usual nth root to the complex plane without the nonpositive real numbers.

If the complex number is moved around zero by increasing its argument, after an increment of ${\displaystyle 2\pi ,}$ the complex number comes back to its initial position, and its nth roots are permuted circularly (they are multiplied by $e^{2i\pi /n}$). This shows that it is not possible to define a nth root function that is continuous in the whole complex plane.

Roots of unity

The three third roots of 1

The nth roots of unity are the n complex numbers such that wⁿ = 1, where n is a positive integer. They arise in various areas of mathematics, such as in discrete Fourier transform or algebraic solutions of algebraic equations (Lagrange resolvent).

The n nth roots of unity are the n first powers of ${\displaystyle \omega =e^{\frac {2\pi i}{n}}}$, that is ${\displaystyle 1=\omega ^{0}=\omega ^{n},\omega =\omega ^{1},\omega ^{2},\omega ^{n-1}.}$ The nth roots of unity that have this generating property are called primitive nth roots of unity; they have the form ${\displaystyle \omega ^{k}=e^{\frac {2k\pi i}{n}},}$ with k coprime with n. The unique primitive square root of unity is ${\displaystyle -1;}$ the primitive fourth roots of unity are ${\displaystyle i}$ and ${\displaystyle -i.}$

The nth roots of unity allow expressing all nth roots of a complex number z as the n products of a given nth roots of z with a nth root of unity.

Geometrically, the nth roots of unity lie on the unit circle of the complex plane at the vertices of a regular n-gon with one vertex on the real number 1.

As the number ${\displaystyle e^{\frac {2k\pi i}{n}}}$ is the primitive nth root of unity with the smallest positive argument, it is called the principal primitive nth root of unity, sometimes shortened as principal nth root of unity, although this terminology can be confused with the principal value of ${\displaystyle 1^{1/n}}$, which is 1.^[29][30][31]

Complex exponentiation

Defining exponentiation with complex bases leads to difficulties that are similar to those described in the preceding section, except that there are, in general, infinitely many possible values for $z^{w}$. So, either a principal value is defined, which is not continuous for the values of z that are real and nonpositive, or $z^{w}$ is defined as a multivalued function.

In all cases, the complex logarithm is used to define complex exponentiation as

${\displaystyle z^{w}=e^{w\log z},}$

where ${\displaystyle \log z}$ is the variant of the complex logarithm that is used, which is, a function or a multivalued function such that

${\displaystyle e^{\log z}=z}$

for every z in its domain of definition.

Principal value

The principal value of the complex logarithm is the unique continuous function, commonly denoted ${\displaystyle \log ,}$ such that, for every nonzero complex number z,

${\displaystyle e^{\log z}=z,}$

and the argument of z satisfies

${\displaystyle -\pi <\operatorname {Arg} z\leq \pi .}$

The principal value of the complex logarithm is not defined for ${\displaystyle z=0,}$ it is discontinuous at negative real values of z, and it is holomorphic (that is, complex differentiable) elsewhere. If z is real and positive, the principal value of the complex logarithm is the natural logarithm: ${\displaystyle \log z=\ln z.}$

The principal value of ${\displaystyle z^{w}}$ is defined as ${\displaystyle z^{w}=e^{w\log z},}$where ${\displaystyle \log z}$ is the principal value of the logarithm.

The function ${\displaystyle (z,w)\to z^{w}}$ is holomorphic except in the neighbourhood of the points where z is real and nonpositive.

If z is real and positive, the principal value of ${\displaystyle z^{w}}$ equals its usual value defined above. If ${\displaystyle w=1/n,}$ where n is an integer, this principal value is the same as the one defined above.

Multivalued function

In some contexts, there is a problem with the discontinuity of the principal values of ${\displaystyle \log z}$ and ${\displaystyle z^{w}}$ at the negative real values of z. In this case, it is useful to consider these functions as multivalued functions.

If ${\displaystyle \log z}$ denotes one of the values of the multivalued logarithm (typically its principal value), the other values are ${\displaystyle 2ik\pi +\log z,}$ where k is any integer. Similarly, if ${\displaystyle z^{w}}$ is one value of the exponentiation, then the other values are given by

${\displaystyle e^{w(2ik\pi +\log z)}=z^{w}e^{2ik\pi w},}$

where k is any integer.

Different values of k give different values of ${\displaystyle z^{w}}$ unless w is a rational number, that is, there is an integer d such that dw is an integer. This results from the periodicity of the exponential function, more specifically, that ${\displaystyle e^{a}=e^{b}}$ if and only if ${\displaystyle a-b}$ is an integer multiple of ${\displaystyle 2\pi i.}$

If ${\displaystyle w={\frac {m}{n}}}$ is a rational number with m and n coprime integers with ${\displaystyle n>0,}$ then ${\displaystyle z^{w}}$ has exactly n values. In the case ${\displaystyle m=1,}$ these values are the same as those described in § nth roots of a complex number. If w is an integer, there is only one value that agrees with that of § Integer exponents.

The multivalued exponentiation is holomorphic for ${\displaystyle z\neq 0,}$ in the sense that its graph consists of several sheets that define each a holomorphic function in the neighborhood of every point. If z varies continuously along a circle around 0, then, after a turn, the value of ${\displaystyle z^{w}}$ has changed of sheet.

Computation

The canonical form ${\displaystyle x+iy}$ of ${\displaystyle z^{w}}$ can be computed from the canonical form of z and w. Although this can be described by a single formula, it is clearer to split the computation in several steps.

• Polar form of z. If ${\displaystyle z=a+ib}$ is the canonical form of z (a and b being real), then its polar form is $${\displaystyle z=\rho e^{i\theta }=\rho (\cos \theta +i\sin \theta ),}$$ where ${\displaystyle \rho ={\sqrt {a^{2}+b^{2}}}}$ and ${\displaystyle \theta =\operatorname {atan2} (a,b)}$ (see atan2 for the definition of this function).
• Logarithm of z. The principal value of this logarithm is ${\displaystyle \log z=\ln \rho +i\theta ,}$ where ${\displaystyle \ln }$ denotes the natural logarithm. The other values of the logarithm are obtained by adding ${\displaystyle 2ik\pi }$ for any integer k.
• Canonical form of ${\displaystyle w\log z.}$ If ${\displaystyle w=c+di}$ with c and d real, the values of ${\displaystyle w\log z}$ are $${\displaystyle w\log z=(c\ln \rho -d\theta -2dk\pi )+i(d\ln \rho +c\theta +2ck\pi ),}$$ the principal value corresponding to ${\displaystyle k=0.}$
• Final result. Using the identities ${\displaystyle e^{x+y}=e^{x}e^{y}}$ and ${\displaystyle e^{y\ln x}=x^{y},}$ one gets $${\displaystyle z^{w}=\rho ^{c}e^{-d(\theta +2k\pi )}\left(\cos(d\ln \rho +c\theta +2ck\pi )+i\sin(d\ln \rho +c\theta +2ck\pi )\right),}$$ with ${\displaystyle k=0}$ for the principal value.

Examples

• ${\displaystyle i^{i}}$
  The polar form of i is ${\displaystyle i=e^{i\pi /2},}$ and the values of ${\displaystyle \log i}$ are thus $${\displaystyle \log i=i\left({\frac {\pi }{2}}+2k\pi \right).}$$ It follows that $${\displaystyle i^{i}=e^{i\log i}=e^{-{\frac {\pi }{2}}}e^{-2k\pi }.}$$So, all values of ${\displaystyle i^{i}}$ are real, the principal one being $${\displaystyle e^{-{\frac {\pi }{2}}}\approx 0.2079.}$$
• ${\displaystyle (-2)^{3+4i}}$
  Similarly, the polar form of −2 is ${\displaystyle -2=2e^{i\pi }.}$ So, the above described method gives the values $${\displaystyle {\begin{aligned}(-2)^{3+4i}&=2^{3}e^{-4(\pi +2k\pi )}(\cos(4\ln 2+3(\pi +2k\pi ))+i\sin(4\ln 2+3(\pi +2k\pi )))\\&=-2^{3}e^{-4(\pi +2k\pi )}(\cos(4\ln 2)+i\sin(4\ln 2)).\end{aligned}}}$$In this case, all the values have the same argument ${\displaystyle 4\ln 2,}$ and different absolute values.

In both examples, all values of ${\displaystyle z^{w}}$ have the same argument. More generally, this is true if and only if the real part of w is an integer.

Failure of power and logarithm identities

Some identities for powers and logarithms for positive real numbers will fail for complex numbers, no matter how complex powers and complex logarithms are defined as single-valued functions. For example:

• The identity log(b^x) = x ⋅ log b holds whenever b is a positive real number and x is a real number. But for the principal branch of the complex logarithm one has

  $${\displaystyle \log((-i)^{2})=\log(-1)=i\pi \neq 2\log(-i)=2\log(e^{-i\pi /2})=2\,{\frac {-i\pi }{2}}=-i\pi }$$

  Regardless of which branch of the logarithm is used, a similar failure of the identity will exist. The best that can be said (if only using this result) is that: $${\displaystyle \log w^{z}\equiv z\log w{\pmod {2\pi i}}}$$

  This identity does not hold even when considering log as a multivalued function. The possible values of log(w^z) contain those of z ⋅ log w as a proper subset. Using Log(w) for the principal value of log(w) and m, n as any integers the possible values of both sides are:

  $${\displaystyle {\begin{aligned}\left\{\log w^{z}\right\}&=\left\{z\cdot \operatorname {Log} w+z\cdot 2\pi in+2\pi im\mid m,n\in \mathbb {Z} \right\}\\\left\{z\log w\right\}&=\left\{z\operatorname {Log} w+z\cdot 2\pi in\mid n\in \mathbb {Z} \right\}\end{aligned}}}$$
• The identities (bc)^x = b^xc^x and (b/c)^x = b^x/c^x are valid when b and c are positive real numbers and x is a real number. But, for the principal values, one has $${\displaystyle (-1\cdot -1)^{\frac {1}{2}}=1\neq (-1)^{\frac {1}{2}}(-1)^{\frac {1}{2}}=-1}$$and $${\displaystyle \left({\frac {1}{-1}}\right)^{\frac {1}{2}}=(-1)^{\frac {1}{2}}=i\neq {\frac {1^{\frac {1}{2}}}{(-1)^{\frac {1}{2}}}}={\frac {1}{i}}=-i}$$On the other hand, when x is an integer, the identities are valid for all nonzero complex numbers. If exponentiation is considered as a multivalued function then the possible values of (−1 ⋅ −1)^1/2 are {1, −1}. The identity holds, but saying {1} = {(−1 ⋅ −1)^1/2} is incorrect.
• The identity (e^x)^y = e^xy holds for real numbers x and y, but assuming its truth for complex numbers leads to the following paradox, discovered in 1827 by Clausen:^[32]For any integer n, we have:
  1. ${\displaystyle e^{1+2\pi in}=e^{1}e^{2\pi in}=e\cdot 1=e}$
  2. ${\displaystyle \left(e^{1+2\pi in}\right)^{1+2\pi in}=e\qquad }$ (taking the ${\displaystyle (1+2\pi in)}$-th power of both sides)
  3. ${\displaystyle e^{1+4\pi in-4\pi ^{2}n^{2}}=e\qquad }$ (using ${\displaystyle \left(e^{x}\right)^{y}=e^{xy}}$ and expanding the exponent)
  4. ${\displaystyle e^{1}e^{4\pi in}e^{-4\pi ^{2}n^{2}}=e\qquad }$ (using ${\displaystyle e^{x+y}=e^{x}e^{y}}$)
  5. ${\displaystyle e^{-4\pi ^{2}n^{2}}=1\qquad }$ (dividing by e)
  but this is false when the integer n is nonzero. The error is the following: by definition, ${\displaystyle e^{y}}$ is a notation for ${\displaystyle \exp(y),}$ a true function, and ${\displaystyle x^{y}}$ is a notation for ${\displaystyle \exp(y\log x),}$ which is a multi-valued function. Thus the notation is ambiguous when x = e. Here, before expanding the exponent, the second line should be $${\displaystyle \exp \left((1+2\pi in)\log \exp(1+2\pi in)\right)=\exp(1+2\pi in).}$$Therefore, when expanding the exponent, one has implicitly supposed that ${\displaystyle \log \exp z=z}$ for complex values of z, which is wrong, as the complex logarithm is multivalued. In other words, the wrong identity (e^x)^y = e^xy must be replaced by the identity $${\displaystyle \left(e^{x}\right)^{y}=e^{y\log e^{x}},}$$which is a true identity between multivalued functions.

Irrationality and transcendence

If b is a positive real algebraic number, and x is a rational number, then b^x is an algebraic number. This results from the theory of algebraic extensions. This remains true if b is any algebraic number, in which case, all values of b^x (as a multivalued function) are algebraic. If x is irrational (that is, not rational), and both b and x are algebraic, Gelfond–Schneider theorem asserts that all values of b^x are transcendental (that is, not algebraic), except if b equals 0 or 1.

In other words, if x is irrational and ${\displaystyle b\not \in \{0,1\},}$ then at least one of b, x and b^x is transcendental.

Integer powers in algebra

The definition of exponentiation with positive integer exponents as repeated multiplication may apply to any associative operation denoted as a multiplication.^{[nb 2]} The definition of x⁰ requires further the existence of a multiplicative identity.^[33]

An algebraic structure consisting of a set together with an associative operation denoted multiplicatively, and a multiplicative identity denoted by 1 is a monoid. In such a monoid, exponentiation of an element x is defined inductively by

• ${\displaystyle x^{0}=1,}$
• ${\displaystyle x^{n+1}=xx^{n}}$ for every nonnegative integer n.

If n is a negative integer, ${\displaystyle x^{n}}$ is defined only if x has a multiplicative inverse.^[34] In this case, the inverse of x is denoted x⁻¹, and xⁿ is defined as ${\displaystyle \left(x^{-1}\right)^{-n}.}$

Exponentiation with integer exponents obeys the following laws, for x and y in the algebraic structure, and m and n integers:

${\displaystyle {\begin{aligned}x^{0}&=1\\x^{m+n}&=x^{m}x^{n}\\(x^{m})^{n}&=x^{mn}\\(xy)^{n}&=x^{n}y^{n}\quad {\text{if }}xy=yx,{\text{and, in particular, if the multiplication is commutative.}}\end{aligned}}}$

These definitions are widely used in many areas of mathematics, notably for groups, rings, fields, square matrices (which form a ring). They apply also to functions from a set to itself, which form a monoid under function composition. This includes, as specific instances, geometric transformations, and endomorphisms of any mathematical structure.

When there are several operations that may be repeated, it is common to indicate the repeated operation by placing its symbol in the superscript, before the exponent. For example, if f is a real function whose valued can be multiplied, ${\displaystyle f^{n}}$ denotes the exponentiation with respect of multiplication, and ${\displaystyle f^{\circ n}}$ may denote exponentiation with respect of function composition. That is,

${\displaystyle (f^{n})(x)=(f(x))^{n}=f(x)\,f(x)\cdots f(x),}$

and

${\displaystyle (f^{\circ n})(x)=f(f(\cdots f(f(x))\cdots )).}$

Commonly, ${\displaystyle (f^{n})(x)}$ is denoted ${\displaystyle f(x)^{n},}$ while ${\displaystyle (f^{\circ n})(x)}$ is denoted ${\displaystyle f^{n}(x).}$

In a group

A multiplicative group is a set with as associative operation denoted as multiplication, that has an identity element, and such that every element has an inverse.

So, if G is a group, ${\displaystyle x^{n}}$ is defined for every ${\displaystyle x\in G}$ and every integer n.

The set of all powers of an element of a group form a subgroup. A group (or subgroup) that consists of all powers of a specific element x is the cyclic group generated by x. If all the powers of x are distinct, the group is isomorphic to the additive group ${\displaystyle \mathbb {Z} }$ of the integers. Otherwise, the cyclic group is finite (it has a finite number of elements), and its number of elements is the order of x. If the order of x is n, then ${\displaystyle x^{n}=x^{0}=1,}$ and the cyclic group generated by x consists of the n first powers of x (starting indifferently from the exponent 0 or 1).

Order of elements play a fundamental role in group theory. For example, the order of an element in a finite group is always a divisor of the number of elements of the group (the order of the group). The possible orders of group elements are important in the study of the structure of a group (see Sylow theorems), and in the classification of finite simple groups.

Superscript notation is also used for conjugation; that is, g^h = h⁻¹gh, where g and h are elements of a group. This notation cannot be confused with exponentiation, since the superscript is not an integer. The motivation of this notation is that conjugation obeys some of the laws of exponentiation, namely ${\displaystyle (g^{h})^{k}=g^{hk}}$ and ${\displaystyle (gh)^{k}=g^{k}h^{k}.}$

In a ring

In a ring, it may occur that some nonzero elements satisfy ${\displaystyle x^{n}=0}$ for some integer n. Such an element is said to be nilpotent. In a commutative ring, the nilpotent elements form an ideal, called the nilradical of the ring.

If the nilradical is reduced to the zero ideal (that is, if ${\displaystyle x\neq 0}$ implies ${\displaystyle x^{n}\neq 0}$ for every positive integer n), the commutative ring is said to be reduced. Reduced rings are important in algebraic geometry, since the coordinate ring of an affine algebraic set is always a reduced ring.

More generally, given an ideal I in a commutative ring R, the set of the elements of R that have a power in I is an ideal, called the radical of I. The nilradical is the radical of the zero ideal. A radical ideal is an ideal that equals its own radical. In a polynomial ring ${\displaystyle k[x_{1},\ldots ,x_{n}]}$ over a field k, an ideal is radical if and only if it is the set of all polynomials that are zero on an affine algebraic set (this is a consequence of Hilbert's Nullstellensatz).

Matrices and linear operators

If A is a square matrix, then the product of A with itself n times is called the matrix power. Also ${\displaystyle A^{0}}$ is defined to be the identity matrix,^[35] and if A is invertible, then ${\displaystyle A^{-n}=\left(A^{-1}\right)^{n}}$.

Matrix powers appear often in the context of discrete dynamical systems, where the matrix A expresses a transition from a state vector x of some system to the next state Ax of the system.^[36] This is the standard interpretation of a Markov chain, for example. Then ${\displaystyle A^{2}x}$ is the state of the system after two time steps, and so forth: ${\displaystyle A^{n}x}$ is the state of the system after n time steps. The matrix power ${\displaystyle A^{n}}$ is the transition matrix between the state now and the state at a time n steps in the future. So computing matrix powers is equivalent to solving the evolution of the dynamical system. In many cases, matrix powers can be expediently computed by using eigenvalues and eigenvectors.

Apart from matrices, more general linear operators can also be exponentiated. An example is the derivative operator of calculus, ${\displaystyle d/dx}$, which is a linear operator acting on functions ${\displaystyle f(x)}$ to give a new function ${\displaystyle (d/dx)f(x)=f'(x)}$. The nth power of the differentiation operator is the nth derivative:

${\displaystyle \left({\frac {d}{dx}}\right)^{n}f(x)={\frac {d^{n}}{dx^{n}}}f(x)=f^{(n)}(x).}$

These examples are for discrete exponents of linear operators, but in many circumstances it is also desirable to define powers of such operators with continuous exponents. This is the starting point of the mathematical theory of semigroups.^[37] Just as computing matrix powers with discrete exponents solves discrete dynamical systems, so does computing matrix powers with continuous exponents solve systems with continuous dynamics. Examples include approaches to solving the heat equation, Schrödinger equation, wave equation, and other partial differential equations including a time evolution. The special case of exponentiating the derivative operator to a non-integer power is called the fractional derivative which, together with the fractional integral, is one of the basic operations of the fractional calculus.

Finite fields

A field is an algebraic structure in which multiplication, addition, subtraction, and division are defined and satisfy the properties that multiplication is associative and every nonzero element has a multiplicative inverse. This implies that exponentiation with integer exponents is well-defined, except for nonpositive powers of 0. Common examples are the field of complex numbers, the real numbers and the rational numbers, considered earlier in this article, which are all infinite.

A finite field is a field with a finite number of elements. This number of elements is either a prime number or a prime power; that is, it has the form ${\displaystyle q=p^{k},}$ where p is a prime number, and k is a positive integer. For every such q, there are fields with q elements. The fields with q elements are all isomorphic, which allows, in general, working as if there were only one field with q elements, denoted ${\displaystyle \mathbb {F} _{q}.}$

One has

${\displaystyle x^{q}=x}$

for every ${\displaystyle x\in \mathbb {F} _{q}.}$

A primitive element in ${\displaystyle \mathbb {F} _{q}}$ is an element g such that the set of the q − 1 first powers of g (that is, ${\displaystyle \{g^{1}=g,g^{2},\ldots ,g^{p-1}=g^{0}=1\}}$) equals the set of the nonzero elements of ${\displaystyle \mathbb {F} _{q}.}$ There are ${\displaystyle \varphi (p-1)}$ primitive elements in ${\displaystyle \mathbb {F} _{q},}$ where ${\displaystyle \varphi }$ is Euler's totient function.

In ${\displaystyle \mathbb {F} _{q},}$ the freshman's dream identity

${\displaystyle (x+y)^{p}=x^{p}+y^{p}}$

is true for the exponent p. As ${\displaystyle x^{p}=x}$ in ${\displaystyle \mathbb {F} _{q},}$ It follows that the map

${\displaystyle {\begin{aligned}F\colon {}&\mathbb {F} _{q}\to \mathbb {F} _{q}\\&x\mapsto x^{p}\end{aligned}}}$

is linear over ${\displaystyle \mathbb {F} _{q},}$ and is a field automorphism, called the Frobenius automorphism. If ${\displaystyle q=p^{k},}$ the field ${\displaystyle \mathbb {F} _{q}}$ has k automorphisms, which are the k first powers (under composition) of F. In other words, the Galois group of ${\displaystyle \mathbb {F} _{q}}$ is cyclic of order k, generated by the Frobenius automorphism.

The Diffie–Hellman key exchange is an application of exponentiation in finite fields that is widely used for secure communications. It uses the fact that exponentiation is computationally inexpensive, whereas the inverse operation, the discrete logarithm, is computationally expensive. More precisely, if g is a primitive element in ${\displaystyle \mathbb {F} _{q},}$ then ${\displaystyle g^{e}}$ can be efficiently computed with exponentiation by squaring for any e, even if q is large, while there is no known computationally practical algorithm that allows retrieving e from ${\displaystyle g^{e}}$ if q is sufficiently large.

Powers of sets

The Cartesian product of two sets S and T is the set of the ordered pairs ${\displaystyle (x,y)}$ such that ${\displaystyle x\in S}$ and ${\displaystyle y\in T.}$ This operation is not properly commutative nor associative, but has these properties up to canonical isomorphisms, that allow identifying, for example, ${\displaystyle (x,(y,z)),}$ ${\displaystyle ((x,y),z),}$ and ${\displaystyle (x,y,z).}$

This allows defining the nth power ${\displaystyle S^{n}}$ of a set S as the set of all n-tuples ${\displaystyle (x_{1},\ldots ,x_{n})}$ of elements of S.

When S is endowed with some structure, it is frequent that ${\displaystyle S^{n}}$ is naturally endowed with a similar structure. In this case, the term "direct product" is generally used instead of "Cartesian product", and exponentiation denotes product structure. For example ${\displaystyle \mathbb {R} ^{n}}$ (where ${\displaystyle \mathbb {R} }$ denotes the real numbers) denotes the Cartesian product of n copies of ${\displaystyle \mathbb {R} ,}$ as well as their direct product as vector space, topological spaces, rings, etc.

Sets as exponents

A n-tuple ${\displaystyle (x_{1},\ldots ,x_{n})}$ of elements of S can be considered as a function from ${\displaystyle \{1,\ldots ,n\}.}$ This generalizes to the following notation.

Given two sets S and T, the set of all functions from T to S is denoted ${\displaystyle S^{T}}$. This exponential notation is justified by the following canonical isomorphisms (for the first one, see Currying):

${\displaystyle (S^{T})^{U}\cong S^{T\times U},}$

${\displaystyle S^{T\sqcup U}\cong S^{T}\times S^{U},}$

where ${\displaystyle \times }$ denotes the Cartesian product, and ${\displaystyle \sqcup }$ the disjoint union.

One can use sets as exponents for other operations on sets, typically for direct sums of abelian groups, vector spaces, or modules. For distinguishing direct sums from direct products, the exponent of a direct sum is placed between parentheses. For example, ${\displaystyle \mathbb {R} ^{\mathbb {N} }}$ denotes the vector space of the infinite sequences of real numbers, and ${\displaystyle \mathbb {R} ^{(\mathbb {N} )}}$ the vector space of those sequences that have a finite number of nonzero elements. The latter has a basis consisting of the sequences with exactly one nonzero element that equals 1, while the Hamel bases of the former cannot be explicitly described (because their existence involves Zorn's lemma).

In this context, 2 can represents the set ${\displaystyle \{0,1\}.}$ So, ${\displaystyle 2^{S}}$ denotes the power set of S, that is the set of the functions from S to ${\displaystyle \{0,1\},}$ which can be identified with the set of the subsets of S, by mapping each function to the inverse image of 1.

This fits in with the exponentiation of cardinal numbers, in the sense that |S^T| = |S|^|T|, where |X| is the cardinality of X.

In category theory

In the category of sets, the morphisms between sets X and Y are the functions from X to Y. It results that the set of the functions from X to Y that is denoted ${\displaystyle Y^{X}}$ in the preceding section can also be denoted ${\displaystyle \hom(X,Y).}$ The isomorphism ${\displaystyle (S^{T})^{U}\cong S^{T\times U}}$ can be rewritten

${\displaystyle \hom(U,S^{T})\cong \hom(T\times U,S).}$

This means the functor "exponentiation to the power T " is a right adjoint to the functor "direct product with T ".

This generalizes to the definition of exponentiation in a category in which finite direct products exist: in such a category, the functor ${\displaystyle X\to X^{T}}$ is, if it exists, a right adjoint to the functor ${\displaystyle Y\to T\times Y.}$ A category is called a Cartesian closed category, if direct products exist, and the functor ${\displaystyle Y\to X\times Y}$ has a right adjoint for every T.

Repeated exponentiation

Just as exponentiation of natural numbers is motivated by repeated multiplication, it is possible to define an operation based on repeated exponentiation; this operation is sometimes called hyper-4 or tetration. Iterating tetration leads to another operation, and so on, a concept named hyperoperation. This sequence of operations is expressed by the Ackermann function and Knuth's up-arrow notation. Just as exponentiation grows faster than multiplication, which is faster-growing than addition, tetration is faster-growing than exponentiation. Evaluated at (3, 3), the functions addition, multiplication, exponentiation, and tetration yield 6, 9, 27, and 7625597484987 (=3²⁷ = 3³³ = ³3) respectively.

Limits of powers

Zero to the power of zero gives a number of examples of limits that are of the indeterminate form 0⁰. The limits in these examples exist, but have different values, showing that the two-variable function x^y has no limit at the point (0, 0). One may consider at what points this function does have a limit.

More precisely, consider the function ${\displaystyle f(x,y)=x^{y}}$ defined on ${\displaystyle D=\{(x,y)\in \mathbf {R} ^{2}:x>0\}}$. Then D can be viewed as a subset of R² (that is, the set of all pairs (x, y) with x, y belonging to the extended real number line R = [−∞, +∞], endowed with the product topology), which will contain the points at which the function f has a limit.

In fact, f has a limit at all accumulation points of D, except for (0, 0), (+∞, 0), (1, +∞) and (1, −∞).^[38] Accordingly, this allows one to define the powers x^y by continuity whenever 0 ≤ x ≤ +∞, −∞ ≤ y ≤ +∞, except for 0⁰, (+∞)⁰, 1^+∞ and 1^−∞, which remain indeterminate forms.

Under this definition by continuity, we obtain:

• x^+∞ = +∞ and x^−∞ = 0, when 1 < x ≤ +∞.
• x^+∞ = 0 and x^−∞ = +∞, when 0 ≤ x < 1.
• 0^y = 0 and (+∞)^y = +∞, when 0 < y ≤ +∞.
• 0^y = +∞ and (+∞)^y = 0, when −∞ ≤ y < 0.

These powers are obtained by taking limits of x^y for positive values of x. This method does not permit a definition of x^y when x < 0, since pairs (x, y) with x < 0 are not accumulation points of D.

On the other hand, when n is an integer, the power xⁿ is already meaningful for all values of x, including negative ones. This may make the definition 0ⁿ = +∞ obtained above for negative n problematic when n is odd, since in this case xⁿ → +∞ as x tends to 0 through positive values, but not negative ones.

Efficient computation with integer exponents

Computing bⁿ using iterated multiplication requires n − 1 multiplication operations, but it can be computed more efficiently than that, as illustrated by the following example. To compute 2¹⁰⁰, apply Horner's rule to the exponent 100 written in binary:

${\displaystyle 100=2^{2}+2^{5}+2^{6}=2^{2}(1+2^{3}(1+2))}$.

Then compute the following terms in order, reading Horner's rule from right to left.

This series of steps only requires 8 multiplications instead of 99.

In general, the number of multiplication operations required to compute bⁿ can be reduced to ${\displaystyle \sharp n+\lfloor \log _{2}n\rfloor -1,}$ by using exponentiation by squaring, where ${\displaystyle \sharp n}$ denotes the number of 1s in the binary representation of n. For some exponents (100 is not among them), the number of multiplications can be further reduced by computing and using the minimal addition-chain exponentiation. Finding the minimal sequence of multiplications (the minimal-length addition chain for the exponent) for bⁿ is a difficult problem, for which no efficient algorithms are currently known (see Subset sum problem), but many reasonably efficient heuristic algorithms are available.^[39] However, in practical computations, exponentiation by squaring is efficient enough, and much more easy to implement.

Iterated functions

Function composition is a binary operation that is defined on functions such that the codomain of the function written on the right is included in the domain of the function written on the left. It is denoted ${\displaystyle g\circ f,}$ and defined as

${\displaystyle (g\circ f)(x)=g(f(x))}$

for every x in the domain of f.

If the domain of a function f equals its codomain, one may compose the function with itself an arbitrary number of time, and this defines the nth power of the function under composition, commonly called the nth iterate of the function. Thus ${\displaystyle f^{n}}$ denotes generally the nth iterate of f; for example, ${\displaystyle f^{3}(x)}$ means ${\displaystyle f(f(f(x))).}$^[40]

When a multiplication is defined on the codomain of the function, this defines a multiplication on functions, the pointwise multiplication, which induces another exponentiation. When using functional notation, the two kinds of exponentiation are generally distinguished by placing the exponent of the functional iteration before the parentheses enclosing the arguments of the function, and placing the exponent of pointwise multiplication after the parentheses. Thus ${\displaystyle f^{2}(x)=f(f(x)),}$ and ${\displaystyle f(x)^{2}=f(x)\cdot f(x).}$ When functional notation is not used, disambiguation is often done by placing the composition symbol before the exponent; for example ${\displaystyle f^{\circ 3}=f\circ f\circ f,}$ and ${\displaystyle f^{3}=f\cdot f\cdot f.}$ For historical reasons, the exponent of a repeated multiplication is placed before the argument for some specific functions, typically the trigonometric functions. So, ${\displaystyle \sin ^{2}x}$ and ${\displaystyle \sin ^{2}(x)}$ both mean ${\displaystyle \sin(x)\cdot \sin(x)}$ and not ${\displaystyle \sin(\sin(x)),}$ which, in any case, is rarely considered. Historically, several variants of these notations were used by different authors.^[41][42][43]

In this context, the exponent ${\displaystyle -1}$ denotes always the inverse function, if it exists. So ${\displaystyle \sin ^{-1}x=\sin ^{-1}(x)=\arcsin x.}$ For the multiplicative inverse fractions are generally used as in ${\displaystyle 1/\sin(x)={\frac {1}{\sin x}}.}$

In programming languages

Programming languages generally express exponentiation either as an infix operator or as a function application, as they do not support superscripts. The most common operator symbol for exponentiation is the caret (^). The original version of ASCII included an uparrow symbol (↑), intended for exponentiation, but this was replaced by the caret in 1967, so the caret became usual in programming languages.^[44]The notations include:

• x ^ y: AWK, BASIC, J, MATLAB, Wolfram Language (Mathematica), R, Microsoft Excel, Analytica, TeX (and its derivatives), TI-BASIC, bc (for integer exponents), Haskell (for nonnegative integer exponents), Lua, and most computer algebra systems.
• x ** y. The Fortran character set did not include lowercase characters or punctuation symbols other than +-*/()&=.,' and so used ** for exponentiation^[45][46] (the initial version used a xx b instead.^[47]). Many other languages followed suit: Ada, Z shell, KornShell, Bash, COBOL, CoffeeScript, Fortran, FoxPro, Gnuplot, Groovy, JavaScript, OCaml, F#, Perl, PHP, PL/I, Python, Rexx, Ruby, SAS, Seed7, Tcl, ABAP, Mercury, Haskell (for floating-point exponents), Turing, and VHDL.
• x ↑ y: Algol Reference language, Commodore BASIC, TRS-80 Level II/III BASIC.^[48][49]
• x ^^ y: Haskell (for fractional base, integer exponents), D.
• x⋆y: APL.

In most programming languages with an infix exponentiation operator, it is right-associative, that is, a^b^c is interpreted as a^(b^c).^[50] This is because (a^b)^c is equal to a^(b*c) and thus not as useful. In some languages, it is left-associative, notably in Algol, MATLAB, and the Microsoft Excel formula language.

Other programming languages use functional notation:

• (expt x y): Common Lisp.
• pown x y: F# (for integer base, integer exponent).

Still others only provide exponentiation as part of standard libraries:

• pow(x, y): C, C++ (in math library).
• Math.Pow(x, y): C#.
• math:pow(X, Y): Erlang.
• Math.pow(x, y): Java.
• [Math]::Pow(x, y): PowerShell.

In some statically typed languages that prioritize type safety such as Rust, exponentiation is performed via a multitude of methods:

• x.pow(y) for x and y as integers
• x.powf(y) for x and y as floating point numbers
• x.powi(y) for x as a float and y as an integer

See also

• Mathematics portal

• Double exponential function
• Exponential decay
• Exponential field
• Exponential growth
• Hyperoperation
• Tetration
• Pentation
• List of exponential topics
• Modular exponentiation
• Scientific notation
• Unicode subscripts and superscripts
• x^y = y^x
• Zero to the power of zero

Notes

1. There are three common notations for multiplication: ${\displaystyle x\times y}$ is most commonly used for explicit numbers and at a very elementary level; ${\displaystyle xy}$ is most common when variables are used; ${\displaystyle x\cdot y}$ is used for emphasizing that one talks of multiplication or when omitting the multiplication sign would be confusing.
2. More generally, power associativity is sufficient for the definition.

References

1. Nykamp, Duane. "Basic rules for exponentiation". Math Insight. Retrieved 2020-08-27.
2. Weisstein, Eric W. "Power". MathWorld. Retrieved 2020-08-27.
3. "Exponent | Etymology of exponent by etymonline".
4. Rotman, Joseph J. (2015). Advanced Modern Algebra, Part 1. Graduate Studies in Mathematics. Vol. 165 (3rd ed.). Providence, RI: American Mathematical Society. p. 130, fn. 4. ISBN 978-1-4704-1554-9.
5. Szabó, Árpád (1978). The Beginnings of Greek Mathematics. Synthese Historical Library. Vol. 17. Translated by A.M. Ungar. Dordrecht: D. Reidel. p. 37. ISBN 90-277-0819-3.
6. O'Connor, John J.; Robertson, Edmund F. "Etymology of some common mathematical terms". MacTutor History of Mathematics Archive. University of St Andrews.
7. Ball, W. W. Rouse (1915). A Short Account of the History of Mathematics (6th ed.). London: Macmillan. p. 38.
8. Archimedes. (2009). THE SAND-RECKONER. In T. Heath (Ed.), The Works of Archimedes: Edited in Modern Notation with Introductory Chapters (Cambridge Library Collection - Mathematics, pp. 229-232). Cambridge: Cambridge University Press. doi:10.1017/CBO9780511695124.017.
9. Quinion, Michael. "Zenzizenzizenzic". World Wide Words. Retrieved 2020-04-16.
10. O'Connor, John J.; Robertson, Edmund F. "Abu'l Hasan ibn Ali al Qalasadi". MacTutor History of Mathematics Archive. University of St Andrews.
11. Cajori, Florian (1928). A History of Mathematical Notations. Vol. 1. The Open Court Company. p. 102.
12. Cajori, Florian (1928). A History of Mathematical Notations. Vol. 1. London: Open Court Publishing Company. p. 344.
13. "Earliest Known Uses of Some of the Words of Mathematics (E)". 2017-06-23.
14. Stifel, Michael (1544). Arithmetica integra. Nuremberg: Johannes Petreius. p. 235v.
15. Cajori, Florian (1928). A History of Mathematical Notations. Vol. 1. The Open Court Company. p. 204.
16. Descartes, René (1637). "La Géométrie". Discourse de la méthode [...]. Leiden: Jan Maire. p. 299. Et aa, ou a², pour multiplier a par soy mesme; Et a³, pour le multiplier encore une fois par a, & ainsi a l'infini (And aa, or a², in order to multiply a by itself; and a³, in order to multiply it once more by a, and thus to infinity).
17. The most recent usage in this sense cited by the OED is from 1806 ("involution". Oxford English Dictionary (Online ed.). Oxford University Press. (Subscription or participating institution membership required.)).
18. Euler, Leonhard (1748). Introductio in analysin infinitorum (in Latin). Vol. I. Lausanne: Marc-Michel Bousquet. pp. 69, 98–99. Primum ergo considerandæ sunt quantitates exponentiales, seu Potestates, quarum Exponens ipse est quantitas variabilis. Perspicuum enim est hujusmodi quantitates ad Functiones algebraicas referri non posse, cum in his Exponentes non nisi constantes locum habeant.
19. Hodge, Jonathan K.; Schlicker, Steven; Sundstorm, Ted (2014). Abstract Algebra: an inquiry based approach. CRC Press. p. 94. ISBN 978-1-4665-6706-1.
20. Achatz, Thomas (2005). Technical Shop Mathematics (3rd ed.). Industrial Press. p. 101. ISBN 978-0-8311-3086-2.
21. Knobloch, Eberhard (1994). "The infinite in Leibniz's mathematics – The historiographical method of comprehension in context". In Kostas Gavroglu; Jean Christianidis; Efthymios Nicolaidis (eds.). Trends in the Historiography of Science. Boston Studies in the Philosophy of Science. Vol. 151. Springer Netherlands. p. 276. doi:10.1007/978-94-017-3596-4_20. ISBN 9789401735964. A positive power of zero is infinitely small, a negative power of zero is infinite.
22. Bronstein, Ilja Nikolaevič; Semendjajew, Konstantin Adolfovič (1987) [1945]. "2.4.1.1. Definition arithmetischer Ausdrücke" [Definition of arithmetic expressions]. Written at Leipzig, Germany. In Grosche, Günter; Ziegler, Viktor; Ziegler, Dorothea (eds.). Taschenbuch der Mathematik [Pocketbook of mathematics] (in German). Vol. 1. Translated by Ziegler, Viktor. Weiß, Jürgen (23 ed.). Thun, Switzerland / Frankfurt am Main, Germany: Verlag Harri Deutsch (and B. G. Teubner Verlagsgesellschaft, Leipzig). pp. 115–120, 802. ISBN 3-87144-492-8.
23. Olver, Frank W. J.; Lozier, Daniel W.; Boisvert, Ronald F.; Clark, Charles W., eds. (2010). NIST Handbook of Mathematical Functions. National Institute of Standards and Technology (NIST), U.S. Department of Commerce, Cambridge University Press. ISBN 978-0-521-19225-5. MR 2723248.[1]
24. Zeidler, Eberhard [in German]; Schwarz, Hans Rudolf; Hackbusch, Wolfgang; Luderer, Bernd [in German]; Blath, Jochen; Schied, Alexander; Dempe, Stephan; Wanka, Gert; Hromkovič, Juraj; Gottwald, Siegfried (2013) [2012]. Zeidler, Eberhard [in German] (ed.). Springer-Handbuch der Mathematik I (in German). Vol. I (1 ed.). Berlin / Heidelberg, Germany: Springer Spektrum, Springer Fachmedien Wiesbaden. p. 590. ISBN 978-3-658-00284-8. (xii+635 pages)
25. Hass, Joel R.; Heil, Christopher E.; Weir, Maurice D.; Thomas, George B. (2018). Thomas' Calculus (14 ed.). Pearson. pp. 7–8. ISBN 9780134439020.
26. Anton, Howard; Bivens, Irl; Davis, Stephen (2012). Calculus: Early Transcendentals (9th ed.). John Wiley & Sons. p. 28. ISBN 9780470647691.
27. Denlinger, Charles G. (2011). Elements of Real Analysis. Jones and Bartlett. pp. 278–283. ISBN 978-0-7637-7947-4.
28. Tao, Terence (2016). "Limits of sequences". Analysis I. Texts and Readings in Mathematics. Vol. 37. pp. 126–154. doi:10.1007/978-981-10-1789-6_6. ISBN 978-981-10-1789-6.
29. Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001). Introduction to Algorithms (second ed.). MIT Press. ISBN 978-0-262-03293-3. Online resource Archived 2007-09-30 at the Wayback Machine.
30. Cull, Paul; Flahive, Mary; Robson, Robby (2005). Difference Equations: From Rabbits to Chaos (Undergraduate Texts in Mathematics ed.). Springer. ISBN 978-0-387-23234-8. Defined on p. 351.
31. Weisstein, Eric W. "Principal root of unity". MathWorld.
32. Steiner, J.; Clausen, T.; Abel, Niels Henrik (1827). "Aufgaben und Lehrsätze, erstere aufzulösen, letztere zu beweisen" [Problems and propositions, the former to solve, the later to prove]. Journal für die reine und angewandte Mathematik. 2: 286–287.
33. Bourbaki, Nicolas (1970). Algèbre. Springer. I.2.
34. Bloom, David M. (1979). Linear Algebra and Geometry. Cambridge University Press. p. 45. ISBN 978-0-521-29324-2.
35. Chapter 1, Elementary Linear Algebra, 8E, Howard Anton.
36. Strang, Gilbert (1988). Linear algebra and its applications (3rd ed.). Brooks-Cole. Chapter 5.
37. E. Hille, R. S. Phillips: Functional Analysis and Semi-Groups. American Mathematical Society, 1975.
38. Nicolas Bourbaki, Topologie générale, V.4.2.
39. Gordon, D. M. (1998). "A Survey of Fast Exponentiation Methods" (PDF). Journal of Algorithms. 27: 129–146. CiteSeerX 10.1.1.17.7076. doi:10.1006/jagm.1997.0913. Archived from the original (PDF) on 2018-07-23. Retrieved 2024-01-11.
40. Peano, Giuseppe (1903). Formulaire mathématique (in French). Vol. IV. p. 229.
41. Herschel, John Frederick William (1813) [1812-11-12]. "On a Remarkable Application of Cotes's Theorem". Philosophical Transactions of the Royal Society of London. 103 (Part 1). London: Royal Society of London, printed by W. Bulmer and Co., Cleveland-Row, St. James's, sold by G. and W. Nicol, Pall-Mall: 8–26 [10]. doi:10.1098/rstl.1813.0005. JSTOR 107384. S2CID 118124706.
42. Herschel, John Frederick William (1820). "Part III. Section I. Examples of the Direct Method of Differences". A Collection of Examples of the Applications of the Calculus of Finite Differences. Cambridge, UK: Printed by J. Smith, sold by J. Deighton & sons. pp. 1–13 [5–6]. Archived from the original on 2020-08-04. Retrieved 2020-08-04. [2] (NB. Inhere, Herschel refers to his 1813 work and mentions Hans Heinrich Bürmann's older work.)
43. Cajori, Florian (1952) [March 1929]. A History of Mathematical Notations. Vol. 2 (3rd ed.). Chicago, USA: Open court publishing company. pp. 108, 176–179, 336, 346. ISBN 978-1-60206-714-1. Retrieved 2016-01-18.
44. Richard Gillam (2003). Unicode Demystified: A Practical Programmer's Guide to the Encoding Standard. Addison-Wesley Professional. p. 33. ISBN 0201700522.
45. Backus, John Warner; Beeber, R. J.; Best, Sheldon F.; Goldberg, Richard; Herrick, Harlan L.; Hughes, R. A.; Mitchell, L. B.; Nelson, Robert A.; Nutt, Roy; Sayre, David; Sheridan, Peter B.; Stern, Harold; Ziller, Irving (1956-10-15). Sayre, David (ed.). The FORTRAN Automatic Coding System for the IBM 704 EDPM: Programmer's Reference Manual (PDF). New York, USA: Applied Science Division and Programming Research Department, International Business Machines Corporation. p. 15. Archived (PDF) from the original on 2022-07-04. Retrieved 2022-07-04. (2+51+1 pages)
46. Brice Carnahan; James O. Wilkes (1968). Introduction to Digital Computing and FORTRAN IV with MTS Applications. pp. 2–2, 2–6.
47. Backus, John Warner; Herrick, Harlan L.; Nelson, Robert A.; Ziller, Irving (1954-11-10). Backus, John Warner (ed.). Specifications for: The IBM Mathematical FORmula TRANSlating System, FORTRAN (PDF) (Preliminary report). New York, USA: Programming Research Group, Applied Science Division, International Business Machines Corporation. pp. 4, 6. Archived (PDF) from the original on 2022-03-29. Retrieved 2022-07-04. (29 pages)
48. Daneliuk, Timothy "Tim" A. (1982-08-09). "BASCOM - A BASIC compiler for TRS-80 I and II". InfoWorld. Software Reviews. Vol. 4, no. 31. Popular Computing, Inc. pp. 41–42. Archived from the original on 2020-02-07. Retrieved 2020-02-06.
49. "80 Contents". 80 Micro (45). 1001001, Inc.: 5. October 1983. ISSN 0744-7868. Retrieved 2020-02-06.
50. Robert W. Sebesta (2010). Concepts of Programming Languages. Addison-Wesley. pp. 130, 324. ISBN 978-0136073475.