В финансах опцион — это контракт , который передает его владельцу, держателю , право, но не обязательство, купить или продать определенное количество базового актива или инструмента по указанной цене исполнения в указанную дату или до нее , в зависимости от стиля опциона.
Опционы обычно приобретаются путем покупки, в качестве формы компенсации или как часть сложной финансовой транзакции. Таким образом, они также являются формой актива (или условного обязательства) и имеют оценку , которая может зависеть от сложной взаимосвязи между ценой базового актива, временем до истечения срока, рыночной волатильностью , безрисковой процентной ставкой и ценой исполнения опциона.
Опционы могут продаваться между частными лицами на внебиржевом рынке (OTC) или могут продаваться на бирже на публичных рынках в форме стандартизированных контрактов.
Опцион — это контракт, который позволяет держателю купить или продать базовый актив или финансовый инструмент по указанной цене исполнения в указанную дату или до нее, в зависимости от формы опциона. Продажа или исполнение опциона до истечения срока действия обычно требует от покупателя выкупа контракта по согласованной цене. Цена исполнения может быть установлена на основе спотовой цены (рыночной цены) базового актива или товара в день выпуска опциона или может быть зафиксирована со скидкой или с премией. Эмитент имеет соответствующее обязательство выполнить сделку (продать или купить), если держатель «использует» опцион. Опцион, который передает держателю право купить по указанной цене, называется колл , в то время как тот, который передает право продать по указанной цене, называется пут .
Эмитент может предоставить опцион покупателю в рамках другой сделки (например, выпуска акций или в рамках программы поощрения сотрудников), или покупатель может заплатить эмитенту премию за опцион. Колл-опцион обычно исполняется только в том случае, если цена исполнения ниже рыночной стоимости базового актива, тогда как пут-опцион обычно исполняется только в том случае, если цена исполнения выше рыночной стоимости. При исполнении опциона стоимость для держателя опциона составляет цену исполнения приобретенного актива плюс премия, если таковая имеется, уплаченная эмитенту. Если дата истечения опциона проходит без исполнения опциона, опцион истекает, и держатель теряет премию, уплаченную эмитенту. В любом случае премия является доходом для эмитента и обычно капитальным убытком для держателя опциона.
Держатель опциона может перепродать опцион третьей стороне на вторичном рынке , либо в рамках внебиржевой сделки, либо на бирже опционов , в зависимости от опциона. Рыночная цена опциона американского типа обычно близко следует за рыночной ценой базовых акций, представляя собой разницу между рыночной ценой акций и ценой исполнения опциона. Фактическая рыночная цена опциона может варьироваться в зависимости от ряда факторов, таких как необходимость крупного держателя опциона продать опцион из-за приближающейся даты истечения срока и отсутствие финансовых ресурсов для исполнения опциона или попытка покупателя на рынке накопить большой пакет опционов. Владение опционом, как правило, не дает держателю никаких прав, связанных с базовым активом, таких как право голоса или какой-либо доход от базового актива, такой как дивиденды .
Контракты, похожие на опционы, использовались с древних времен. [1] Первым известным покупателем опционов был древнегреческий математик и философ Фалес Милетский . В определенном случае было предсказано, что урожай оливок в этом сезоне будет больше обычного, и в межсезонье он приобрел право использовать несколько оливковых прессов следующей весной. Когда наступила весна и урожай оливок оказался больше ожидаемого, он воспользовался своими опционами, а затем сдал прессы в аренду по гораздо более высокой цене, чем он заплатил за свой «опцион». [2] [3]
В книге 1688 года «Путаница путаниц» описывается торговля « опционами » на Амстердамской фондовой бирже (ныне Euronext ), и объясняется, что «для вас будут лишь ограниченные риски, в то время как прибыль может превзойти все ваши представления и надежды». [4]
В Лондоне путы и «отказы» (коллы) впервые стали известными торговыми инструментами в 1690-х годах во время правления Вильгельма и Марии . [5] Привилегии были опционами, продаваемыми вне биржи в Америке девятнадцатого века, причем как путы, так и коллы на акции предлагались специализированными дилерами. Их цена исполнения была зафиксирована на уровне округленной рыночной цены в день или неделю, когда опцион был куплен, а дата истечения срока обычно составляла три месяца после покупки. Они не торговались на вторичных рынках.
На рынке недвижимости колл-опционы уже давно используются для объединения крупных участков земли от отдельных владельцев; например, застройщик платит за право купить несколько смежных участков, но не обязан покупать эти участки и может не покупать их, если не сможет купить все участки на всем участке. Кроме того, покупка недвижимости, например домов, требует от покупателя внесения продавцу на счет условного депонирования задатка , который дает покупателю право купить недвижимость на установленных условиях, включая цену покупки. [ необходима цитата ]
В киноиндустрии продюсеры фильмов и театральных постановок часто покупают опцион, дающий право (но не обязанность) экранизировать определенную книгу или сценарий.
Кредитные линии предоставляют потенциальному заемщику право — но не обязательство — взять кредит в течение определенного периода времени.
Многие варианты выбора или встроенные опционы традиционно включаются в облигационные контракты. Например, многие облигации конвертируются в обыкновенные акции по выбору покупателя или могут быть отозваны (выкуплены) по указанным ценам по выбору эмитента. Ипотечные заемщики уже давно имеют возможность досрочного погашения кредита, что соответствует опциону на отзывную облигацию.
Опционные контракты известны уже несколько десятилетий. Чикагская биржа опционов была основана в 1973 году, что создало режим с использованием стандартизированных форм и условий и торговли через гарантированную клиринговую палату. С тех пор торговая активность и академический интерес возросли.
Сегодня многие опционы создаются в стандартизированной форме и торгуются через клиринговые палаты на регулируемых опционных биржах . Напротив, другие внебиржевые опционы пишутся как двусторонние, индивидуальные контракты между одним покупателем и продавцом, один или оба из которых могут быть дилером или маркет-мейкером. Опционы являются частью более крупного класса финансовых инструментов, известных как производные продукты , или просто производные инструменты. [6] [7]
Финансовый опцион — это контракт между двумя контрагентами, условия которого указаны в перечне условий . Опционные контракты могут быть довольно сложными; однако, как минимум, они обычно содержат следующие спецификации: [8]
Биржевые опционы (также называемые «листинговыми опционами») представляют собой класс биржевых деривативов . Биржевые опционы имеют стандартизированные контракты и урегулируются через клиринговую палату с гарантией исполнения Корпорацией по клирингу опционов (OCC). Поскольку контракты стандартизированы, часто доступны точные модели ценообразования. Биржевые опционы включают: [9] [10]
Внебиржевые опционы (OTC-опционы, также называемые «дилерскими опционами») торгуются между двумя частными сторонами и не котируются на бирже. Условия внебиржевого опциона не ограничены и могут быть индивидуально адаптированы для удовлетворения любых бизнес-потребностей. В целом, автор опциона — это хорошо капитализированное учреждение (для предотвращения кредитного риска). Типы опционов, которые обычно торгуются внебиржевыми опционами, включают:
Избегая обмена, пользователи внебиржевых опционов могут узко подгонять условия опционного контракта под индивидуальные бизнес-требования. Кроме того, внебиржевые опционные сделки, как правило, не требуют рекламы на рынке и не имеют практически никаких нормативных требований. Однако внебиржевые контрагенты должны устанавливать кредитные линии друг с другом и соблюдать процедуры клиринга и расчетов друг друга.
За редкими исключениями, [11] вторичных рынков для опционов на акции сотрудников не существует . Они должны быть либо реализованы первоначальным получателем, либо истечь.
Наиболее распространенный способ торговли опционами — через стандартизированные опционные контракты, котируемые на различных фьючерсных и опционных биржах . [12] Листинги и цены отслеживаются и могут быть найдены по тикерному символу . Публикуя непрерывные, живые рынки для опционных цен, биржа позволяет независимым сторонам участвовать в определении цен и совершать транзакции. Как посредник для обеих сторон транзакции, биржа предоставляет транзакции следующие преимущества:

Эти сделки описаны с точки зрения спекулянта. Если они объединены с другими позициями, их также можно использовать в хеджировании . Опционный контракт на рынках США обычно представляет собой 100 акций базовой ценной бумаги. [13] [14]

Трейдер, ожидающий роста цены акций, может купить опцион колл , чтобы купить акции по фиксированной цене ( страйк-цене ) в более поздний срок, а не покупать акции напрямую. Денежные затраты на опцион являются премией. Трейдер не обязан покупать акции, но имеет право сделать это только в день истечения срока или до него. Риск убытка будет ограничен уплаченной премией, в отличие от возможных убытков, если бы акции были куплены напрямую.
Держатель опциона колл американского типа может продать опцион в любое время до даты истечения срока и рассмотрит возможность сделать это, когда спотовая цена акций превысит цену исполнения, особенно если держатель ожидает, что цена опциона упадет. Продав опцион на ранней стадии в этой ситуации, трейдер может получить немедленную прибыль. В качестве альтернативы трейдер может исполнить опцион — например, если для опционов нет вторичного рынка — и затем продать акции, получив прибыль. Трейдер получит прибыль, если спотовая цена акций вырастет больше, чем премия. Например, если цена исполнения составляет 100, а уплаченная премия составляет 10, то если спотовая цена 100 вырастет всего до 110, сделка будет безубыточной; рост цены акций выше 110 приносит прибыль.
Если цена акций на момент истечения срока действия ниже цены исполнения, держатель опциона на тот момент позволит колл-контракту истечь и потеряет только премию (или цену, уплаченную при переводе).
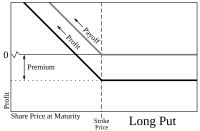
Трейдер, ожидающий снижения цены акций, может купить опцион пут , чтобы продать акции по фиксированной цене (цене исполнения) в более позднюю дату. Трейдер не обязан продавать акции, но имеет право сделать это в день истечения срока или до него. Если цена акций на момент истечения срока ниже цены исполнения более чем на уплаченную премию, трейдер получает прибыль. Если цена акций на момент истечения срока выше цены исполнения, трейдер позволяет контракту пут истечь и теряет только уплаченную премию. В сделке премия также играет роль, поскольку она повышает точку безубыточности. Например, если цена исполнения составляет 100, а уплаченная премия составляет 10, то спотовая цена между 90 и 100 невыгодна. Трейдер получает прибыль, только если спотовая цена ниже 90.
Трейдеру, исполняющему опцион пут на акцию, не обязательно владеть базовым активом, поскольку большинство акций можно продавать в шорт .

Трейдер, ожидающий снижения цены акций, может продать акции в короткую или вместо этого продать, или «написать», колл. Трейдер, продающий колл, обязан продать акции покупателю колл по фиксированной цене («цена исполнения»). Если продавец не владеет акциями на момент исполнения опциона, он обязан купить акции на рынке по преобладающей рыночной цене. Если цена акций падает, продавец колл (автор колл) получает прибыль в размере премии. Если цена акций превышает цену исполнения больше, чем на сумму премии, продавец теряет деньги, причем потенциальные потери неограниченны.

Трейдер, ожидающий роста цены акций, может купить акции или вместо этого продать, или «выписать», пут. Трейдер, продающий пут, обязан купить акции у покупателя пут по фиксированной цене («цена страйка»). Если цена акций на момент истечения срока выше цены страйка, продавец пут (автор пут) получает прибыль в размере премии. Если цена акций на момент истечения срока ниже цены страйка более чем на сумму премии, трейдер теряет деньги, а потенциальный убыток составляет цену страйка за вычетом премии. Эталонным индексом для оценки эффективности позиции по короткому опциону пут, обеспеченному наличными, является индекс CBOE S&P 500 PutWrite (тикер PUT).
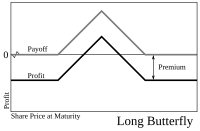


Объединение любого из четырех основных видов опционных сделок (возможно, с различными ценами исполнения и сроками погашения) и двух основных видов акций (длинных и коротких) позволяет использовать различные опционные стратегии . Простые стратегии обычно объединяют только несколько сделок, в то время как более сложные стратегии могут объединять несколько.
Стратегии часто используются для разработки определенного профиля риска для движений базовой ценной бумаги. Например, покупка спреда «бабочка» (длинный один колл X1, короткие два колла X2 и длинный один колл X3) позволяет трейдеру получить прибыль, если цена акций на дату истечения срока близка к средней цене исполнения X2, и не подвергает трейдера большим убыткам.
Кондор — это стратегия , похожая на спред «бабочка», но с разными страйками для коротких опционов, что обеспечивает большую вероятность прибыли, но с меньшим чистым кредитом по сравнению со спредом «бабочка».
Продажа стрэддла (продажа пут-опциона и колл-опциона по одинаковой цене исполнения) принесет трейдеру большую прибыль, чем бабочка, если окончательная цена акций близка к цене исполнения, но может привести к большим убыткам.
Аналогичным опциону стрэддл является опцион стрэнгл , который также формируется из опционов колл и пут, но их страйки различны, что снижает чистый дебет сделки, а также снижает риск убытков в сделке.
Одной из известных стратегий является покрытый колл , при котором трейдер покупает акцию (или удерживает ранее купленную позицию по акциям) и продает колл. (Это можно сравнить с непокрытым колл . См. также непокрытый пут .) Если цена акций поднимется выше цены исполнения, колл будет исполнен, и трейдер получит фиксированную прибыль. Если цена акций упадет, колл не будет исполнен, и любые убытки, понесенные трейдером, будут частично компенсированы премией, полученной от продажи колла. В целом, выплаты соответствуют выплатам от продажи пут. Это соотношение известно как паритет пут-колл и дает представление о финансовой теории. Эталонным индексом для эффективности стратегии покупки-записи является индекс CBOE S&P 500 BuyWrite (тикерный символ BXM).
Другая очень распространенная стратегия — защитный пут , при котором трейдер покупает акцию (или удерживает ранее купленную длинную позицию по акциям) и покупает пут. Эта стратегия действует как страховка при инвестировании в длинную позицию по базовым акциям, хеджируя потенциальные убытки инвестора, но также сокращая иную большую прибыль, если бы он просто купил акции без пут. Максимальная прибыль защитного пут теоретически не ограничена, поскольку стратегия подразумевает длинную позицию по базовым акциям. Максимальный убыток ограничен покупной ценой базовых акций за вычетом цены исполнения опциона пут и уплаченной премии. Защитный пут также известен как супружеский пут.
Варианты можно классифицировать несколькими способами.
Другим важным классом опционов, особенно в США, являются опционы на акции сотрудников , которые компания предоставляет своим сотрудникам в качестве формы поощрительной компенсации. Другие типы опционов существуют во многих финансовых контрактах. Например, опционы на недвижимость часто используются для объединения больших участков земли, а опционы на предоплату обычно включаются в ипотечные кредиты . Однако многие принципы оценки и управления рисками применяются ко всем финансовым опционам.
Варианты подразделяются на несколько стилей, наиболее распространенными из которых являются:
Их часто называют ванильными вариантами. Другие стили включают:
Поскольку стоимость опционных контрактов зависит от ряда различных переменных в дополнение к стоимости базового актива, их сложно оценить. Существует много моделей ценообразования, хотя все они по сути включают концепции рационального ценообразования (т. е. нейтральности к риску ), денежности , временной стоимости опциона и паритета пут-колл .
Сама оценка объединяет модель поведения ( «процесса» ) базовой цены с математическим методом, который возвращает премию как функцию предполагаемого поведения. Модели варьируются от (прототипической) модели Блэка-Шоулза для акций [16] [ ненадежный источник? ] [17] до модели Хита-Джарроу-Мортона для процентных ставок и модели Хестона , где сама волатильность считается стохастической . См. Asset pricing для списка различных моделей здесь.
В самом общем виде стоимость опциона обычно разлагается на две части:
Как и выше, стоимость опциона оценивается с использованием различных количественных методов, все из которых основаны на принципе ценообразования , нейтрального к риску , и используют стохастическое исчисление в своем решении. Самая простая модель — это модель Блэка-Шоулза . Более сложные модели используются для моделирования улыбки волатильности . Эти модели реализуются с использованием различных числовых методов. [18] В целом, стандартные модели оценки опционов зависят от следующих факторов:
Более продвинутые модели могут потребовать дополнительных факторов, таких как оценка того, как волатильность изменяется с течением времени и для различных базовых уровней цен, или динамика стохастических процентных ставок.
Ниже приведены некоторые основные методы оценки, используемые на практике для оценки опционных контрактов.
После ранних работ Луи Башелье и более поздних работ Роберта К. Мертона Фишер Блэк и Майрон Шоулз совершили крупный прорыв, выведя дифференциальное уравнение, которому должна удовлетворять цена любого производного инструмента, зависящего от акций, не приносящих дивиденды. Используя технику построения портфеля с нейтральным риском, который воспроизводит доходность опциона, Блэк и Шоулз создали решение в замкнутой форме для теоретической цены европейского опциона. [19] В то же время модель генерирует параметры хеджирования, необходимые для эффективного управления рисками опционных холдингов.
Хотя идеи, лежащие в основе модели Блэка-Шоулза, были новаторскими и в конечном итоге привели к тому, что Шоулз и Мертон получили премию Шведского центрального банка за достижения в экономике (она же Нобелевская премия по экономике), [20] применение модели в реальной торговле опционами неуклюже из-за предположений о непрерывной торговле, постоянной волатильности и постоянной процентной ставке. Тем не менее, модель Блэка-Шоулза по-прежнему является одним из важнейших методов и основ для существующего финансового рынка, на котором результат находится в разумных пределах. [21]
После биржевого краха 1987 года было замечено, что подразумеваемая рыночная волатильность для опционов с более низкими ценами исполнения, как правило, выше, чем для опционов с более высокими ценами исполнения, что позволяет предположить, что волатильность меняется как во времени, так и в зависимости от уровня цены базовой ценной бумаги — так называемая улыбка волатильности ; а с учетом времени — поверхность волатильности .
Основной подход здесь заключается в том, чтобы рассматривать волатильность как стохастическую , с полученными моделями стохастической волатильности и моделью Хестона в качестве прототипа; [22] см. #Risk-neutral_measure для обсуждения логики. Другие модели включают модели волатильности CEV и SABR . Однако одним из главных преимуществ модели Хестона является то, что ее можно решить в замкнутой форме, в то время как другие модели стохастической волатильности требуют сложных численных методов . [22]
Альтернативный, хотя и связанный, подход заключается в применении модели локальной волатильности , где волатильность рассматривается как детерминированная функция как текущего уровня активов, так и времени . Таким образом, модель локальной волатильности является обобщением модели Блэка-Шоулза , где волатильность является константой. Концепция была разработана, когда Бруно Дюпир [23] и Эмануэль Дерман и Ирадж Кани [24] отметили, что существует уникальный процесс диффузии, соответствующий нейтральным по риску плотностям, полученным из рыночных цен европейских опционов. См. обсуждение #Разработка .
Для оценки опционов на облигации , свопционов (т. е. опционов на свопы ), а также пределов и полов процентной ставки (фактически опционов на процентную ставку) были разработаны различные модели краткосрочных ставок (применимые, по сути, к производным процентных ставок в целом). Наиболее известными из них являются модели Блэка-Дермана-Тоя и Халла-Уайта . [25] Эти модели описывают будущую эволюцию процентных ставок , описывая будущую эволюцию краткосрочной ставки. Другой основной структурой для моделирования процентных ставок является структура Хита-Джарроу-Мортона (HJM). Отличие состоит в том, что HJM дает аналитическое описание всей кривой доходности , а не только краткосрочной ставки. (Структура HJM включает модель Брейса-Гатарека-Мусиелы и рыночные модели. И некоторые из моделей краткосрочных ставок могут быть напрямую выражены в структуре HJM.) Для некоторых целей, например, оценки ценных бумаг, обеспеченных ипотекой , это может быть большим упрощением; тем не менее, структура часто предпочтительна для моделей более высокой размерности. Обратите внимание, что для более простых вариантов, т.е. тех, которые упомянуты изначально, можно использовать модель Блэка с определенными допущениями.
После выбора модели оценки существует ряд различных методов ее реализации.
В некоторых случаях можно взять математическую модель и, используя аналитические методы, разработать решения в замкнутой форме, такие как модель Блэка–Шоулза и модель Блэка . Полученные решения легко вычислимы, как и их «греки» . Хотя модель Ролл–Геске–Уэйли применима к американскому колл-опциону с одним дивидендом, для других случаев американских опционов решения в замкнутой форме недоступны; приближения здесь включают Бароне-Адези и Уэйли , Бьерксунда и Стенсланда и других.
Внимательно следуя выводам Блэка и Шоулза, Джон Кокс , Стивен Росс и Марк Рубинштейн разработали оригинальную версию биномиальной модели ценообразования опционов . [26] [27] Она моделирует динамику теоретической стоимости опциона для дискретных временных интервалов в течение срока действия опциона. Модель начинается с биномиального дерева дискретных будущих возможных базовых цен акций. Создавая безрисковый портфель опциона и акций (как в модели Блэка-Шоулза), можно использовать простую формулу для нахождения цены опциона в каждом узле дерева. Это значение может приближать теоретическое значение, полученное Блэком-Шоулзом, с желаемой степенью точности. Однако биномиальная модель считается более точной, чем модель Блэка-Шоулза, поскольку она более гибкая; например, дискретные будущие выплаты дивидендов могут быть смоделированы правильно на надлежащих временных шагах вперед, и американские опционы могут быть смоделированы так же, как и европейские. Биномиальные модели широко используются профессиональными трейдерами опционов. Триномиальное дерево — это похожая модель, допускающая восходящий, нисходящий или стабильный путь; хотя считается более точным, особенно когда моделируется меньше временных шагов, он используется реже, поскольку его реализация сложнее. Для более общего обсуждения, а также для применения к товарам, процентным ставкам и гибридным инструментам см. Модель Lattice (финансы) .
Для многих классов опционов традиционные методы оценки не поддаются обработке из-за сложности инструмента. В этих случаях часто может быть полезен подход Монте-Карло. Вместо того чтобы пытаться решать дифференциальные уравнения движения, которые описывают стоимость опциона по отношению к цене базовой ценной бумаги, модель Монте-Карло использует моделирование для генерации случайных ценовых траекторий базового актива, каждая из которых приводит к выплате за опцион. Среднее значение этих выплат может быть дисконтировано для получения ожидаемой стоимости опциона. [28] Однако следует отметить, что, несмотря на свою гибкость, использование моделирования для опционов в американском стиле несколько сложнее, чем для моделей на основе решеток.
Уравнения, используемые для моделирования опциона, часто выражаются в виде уравнений с частными производными (см., например, уравнение Блэка-Шоулза ). После выражения в этой форме можно вывести модель конечных разностей и получить оценку. Существует ряд реализаций методов конечных разностей для оценки опционов, включая: явную конечную разность , неявную конечную разность и метод Кранка-Николсона . Можно показать, что модель ценообразования опционов на основе триномиального дерева является упрощенным применением явного метода конечных разностей. Хотя подход с использованием конечных разностей является математически сложным, он особенно полезен, когда предполагаются изменения с течением времени во входных данных модели — например, доходность дивидендов, безрисковая ставка или волатильность или некоторая их комбинация — которые не поддаются обработке в замкнутой форме.
Другие числовые реализации, которые использовались для оценки опционов, включают методы конечных элементов .
Как и все ценные бумаги, торговля опционами влечет за собой риск изменения стоимости опциона с течением времени. Однако, в отличие от традиционных ценных бумаг, доходность от владения опционом нелинейно зависит от стоимости базового актива и других факторов. Поэтому риски, связанные с владением опционами, сложнее понять и предсказать.
В общем случае изменение стоимости опциона можно вывести из леммы Ито следующим образом:
где греки , , и являются стандартными параметрами хеджирования, рассчитанными с помощью модели оценки опционов, такой как модель Блэка-Шоулза , а , и являются единичными изменениями цены базового актива, волатильности базового актива и времени соответственно.
Таким образом, в любой момент времени можно оценить риск, присущий удержанию опциона, вычислив его параметры хеджирования, а затем оценив ожидаемое изменение в исходных данных модели, , и , при условии, что изменения этих значений невелики. Этот метод можно эффективно использовать для понимания и управления рисками, связанными со стандартными опционами. Например, компенсируя удержание опциона количеством акций в базовом активе, трейдер может сформировать дельта-нейтральный портфель, который хеджируется от убытков при небольших изменениях цены базового актива. Соответствующая формула ценовой чувствительности для этого портфеля выглядит следующим образом:
Особая ситуация, называемая риском булавки, может возникнуть, когда базовый актив закрывается на уровне или очень близко к значению страйка опциона в последний день торговли опционом перед истечением срока действия. Продавец опциона (автор) может не знать наверняка, будет ли опцион фактически исполнен или ему будет разрешено истечь. Таким образом, продавец опциона может оказаться с большой нежелательной остаточной позицией в базовом активе, когда рынки откроются на следующий торговый день после истечения срока действия, независимо от его или ее наилучших усилий избежать такого остатка.
Еще один, часто игнорируемый риск в производных инструментах, таких как опционы, — это риск контрагента . В опционном контракте этот риск заключается в том, что продавец не продаст или не купит базовый актив, как было согласовано. Риск можно минимизировать, используя финансово сильного посредника, способного окупить сделку, но в случае крупной паники или краха количество дефолтов может подавить даже самых сильных посредников.
Чтобы ограничить риск, брокеры используют системы контроля доступа , чтобы ограничить трейдеров от выполнения определенных опционных стратегий, которые им не подходят. Брокеры обычно предлагают около четырех или пяти уровней одобрения, причем самый низкий уровень предлагает самый низкий риск, а самый высокий уровень предлагает самый высокий риск. Фактическое количество уровней и конкретные опционные стратегии, разрешенные на каждом уровне, различаются у разных брокеров. Брокеры также могут иметь свои собственные критерии проверки, но они обычно основаны на таких факторах, как годовая зарплата и чистый капитал трейдера, опыт торговли и инвестиционные цели (сохранение капитала, доход, рост или спекуляция). Например, трейдеру с низкой зарплатой и чистым капиталом, небольшим опытом торговли и озабоченному только сохранением капитала, как правило, не будет разрешено выполнять высокорисковые стратегии, такие как непокрытые коллы и непокрытые путы . Трейдеры могут обновить свою информацию, запросив разрешение на повышение до более высокого уровня одобрения. [29]
Чикагская биржа опционов (CBOE) — это биржа опционов, расположенная в Чикаго, штат Иллинойс. Основанная в 1973 году, CBOE является первой биржей опционов в Соединенных Штатах. CBOE предлагает торговлю опционами на различные базовые ценные бумаги, включая рыночные индексы, биржевые фонды (ETF), акции и индексы волатильности. Ее флагманский продукт — опционы на индекс S&P 500 (SPX), один из наиболее активно торгуемых опционов в мире. В дополнение к своей открытой торговле на бирже CBOE также управляет полностью электронной торговой платформой . CBOE регулируется Комиссией по ценным бумагам и биржам США (SEC). [30]
Основанная в 1790 году, NASDAQ OMX PHLX , также известная как Филадельфийская фондовая биржа, является биржей опционов и фьючерсов, расположенной в Филадельфии, штат Пенсильвания. Это старейшая фондовая биржа в Соединенных Штатах. NASDAQ OMX PHLX позволяет торговать опционами на акции, индексы, ETF и иностранные валюты. Это одна из немногих бирж, предназначенных для торговли валютными опционами в США. В 2008 году NASDAQ приобрела Филадельфийскую фондовую биржу и переименовала ее в NASDAQ OMX PHLX. Она работает как дочерняя компания NASDAQ, Inc. [31]
Международная фондовая биржа (ISE) — электронная опционная биржа, расположенная в Нью-Йорке. Запущенная в 2000 году, ISE стала первой полностью электронной опционной биржей США. ISE обеспечивает торговлю опционами на американские акции, индексы и ETF. Ее торговая платформа обеспечивает аукцион максимального улучшения цены, позволяющий маркет-мейкерам конкурировать за заказы. ISE регулируется SEC и принадлежит Nasdaq, Inc. [32]
Eurex Exchange — это биржа деривативов, расположенная во Франкфурте, Германия. Она предлагает торговлю фьючерсами и опционами на процентные ставки, акции, индексы и продукты с фиксированным доходом. Образованная в 1998 году в результате слияния Deutsche Terminbörse (DTB) и Swiss Options and Financial Futures Exchange (SOFFEX), Eurex Exchange управляет электронными и открытыми торговыми платформами. Eurex Exchange принадлежит Eurex Frankfurt AG. [33]
Основанная в 1878 году, Токийская фондовая биржа (TSE) — это фондовая биржа, расположенная в Токио, Япония. Помимо акций, TSE также обеспечивает торговлю фьючерсами и опционами на фондовые индексы. Торговля ведется в электронном виде, а также посредством аукционных торгов компаниями, торгующими ценными бумагами. TSE регулируется Агентством финансовых услуг Японии. Она принадлежит Japan Exchange Group . [34]
{{cite book}}: CS1 maint: location missing publisher (link)