Спиновое квантовое число

Квантовое число, параметризующее спин и угловой момент

В физике и химии квантовое число спина — это квантовое число (обозначаемое s ), которое описывает собственный угловой момент (или угловой момент спина, или просто спин ) электрона или другой частицы . Оно имеет одинаковое значение для всех частиц одного типа, например s = ⁠1/2⁠ для всех электронов. Это целое число для всех бозонов , таких как фотоны , и полунечетное целое число для всех фермионов , таких как электроны и протоны .

Компонента спина вдоль указанной оси задается спиновым магнитным квантовым числом , обычно записываемым как m _s . ^{[1] [2]} Значение m _s является компонентом спинового углового момента в единицах приведенной постоянной Планка ħ , параллельного заданному направлению (обычно обозначаемому как ось z ). Он может принимать значения от + s до − s с целыми приращениями. Для электрона m _s может быть либо ⁠++1/2⁠ или ⁠−+1/2⁠ .

Номенклатура

Квантовая проекция S на z для спиновых половинных частиц

Фраза спиновое квантовое число относится к квантованному спиновому угловому моменту . Символ s используется для спинового квантового числа, а m _s описывается как спиновое магнитное квантовое число ^[3] или как z -компонента спина s _z . ^[4]

Как полный спин, так и z-компонента спина квантуются, что приводит к двум квантовым числам спина и спинового магнитного квантового числа. ^[5] (Полное) спиновое квантовое число имеет только одно значение для каждой элементарной частицы. Некоторые вводные учебники по химии описывают m _s как спиновое квантовое число , ^{[6] [7]} а s не упоминается, поскольку его значение ⁠1/2⁠ — фиксированное свойство электрона; некоторые даже используют переменную s вместо m _s . ^[5]

Два спиновых квантовых числа и являются аналогами спинового углового момента двух орбитальных квантовых чисел углового момента и . ^{[8] : 152} ${\displaystyle s}$ ${\displaystyle m_{s}}$ ${\displaystyle l}$ ${\displaystyle m_{l}}$

Спиновые квантовые числа применяются также к системам связанных спинов, таким как атомы, которые могут содержать более одного электрона. Используются заглавные символы: S для полного электронного спина и m _S или M _S для компонента оси z . Пара электронов в состоянии синглета спина имеет S = 0, а пара в состоянии триплета имеет S = 1, причем m _S = −1, 0 или +1. Ядерно-спиновые квантовые числа обычно записываются как I для спина и m _I или M _I для компонента оси z .

Название «спин» происходит от геометрического вращения электрона вокруг оси, предложенного Уленбеком и Гоудсмитом . Однако эта упрощенная картина быстро оказалась физически нереалистичной, поскольку для этого потребовалось бы, чтобы электроны вращались быстрее скорости света. ^[9] Поэтому ее заменили более абстрактным квантово-механическим описанием.

История

В период между 1916 и 1925 годами был достигнут значительный прогресс в отношении расположения электронов в периодической таблице . Чтобы объяснить эффект Зеемана в атоме Бора, Зоммерфельд предположил, что электроны будут основаны на трех «квантовых числах», n, k и m, которые описывают размер орбиты, форму орбиты и направление, в котором указывает орбита. ^[10] Ирвинг Ленгмюр объяснил в своей статье 1919 года об электронах в их оболочках: «Ридберг указал, что эти числа получаются из ряда . Фактор два предполагает фундаментальную двукратную симметрию для всех стабильных атомов». ^[11] Эта конфигурация была принята Эдмундом Стоунером в октябре 1924 года в его статье «Распределение электронов среди атомных уровней», опубликованной в Philosophical Magazine. ${\displaystyle N=2(1+2^{2}+2^{2}+3^{2}+3^{2}+4^{2})}$ ${\displaystyle 2n^{2}}$

Качественный успех схемы квантовых чисел Зоммерфельда не смог объяснить эффект Зеемана в слабых магнитных полях, аномальный эффект Зеемана . В декабре 1924 года Вольфганг Паули показал, что угловой момент электрона ядра не связан с эффектом, как предполагалось ранее. ^{[12] : 563} Вместо этого он предположил, что только внешние «легкие» электроны определяют угловой момент, и выдвинул гипотезу, что для этого требуется четвертое квантовое число с двузначностью. ^[13] Это четвертое квантовое число стало спиновым магнитным квантовым числом.

Спин электрона

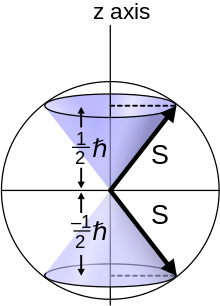
Спин- ⁠ 1 /2⁠ частица характеризуется квантовым числом углового момента для спина s = ⁠ 1 /2⁠ . В решениях уравнения Шредингера-Паули момент импульса квантуется в соответствии с этим числом, так что величина спинового момента импульса равна

$${\displaystyle \|{\mathbf {S}}\|=\hbar {\sqrt {s(s+1)}}={\tfrac {\sqrt {3}}{2}}\ \hbar ~.}$$

Тонкая структура спектра водорода наблюдается в виде дублета, соответствующего двум возможностям для z -компоненты углового момента, где для любого заданного направления z : $${\displaystyle s_{z}=\pm {\tfrac {1}{2}}\hbar ~.}$$

чье решение имеет только две возможные z -компоненты для электрона. В электроне две различные ориентации спина иногда называются «спин-вверх» или «спин-вниз».

Спиновое свойство электрона приводит к возникновению магнитного момента , который является необходимым условием для четвертого квантового числа.

Вектор магнитного момента спина электрона определяется выражением:

$${\displaystyle \ {\boldsymbol {\mu }}_{\text{s}}=-{\frac {e}{\ 2m\ }}\ g_{\text{s}}\ {\mathbf {S}}\ }$$

где — заряд электрона , — масса электрона , — g-фактор спина электрона , который приблизительно равен 2,0023. Его проекция на ось z задается спиновым магнитным квантовым числом в соответствии с: ${\displaystyle -e}$ ${\displaystyle m}$ ${\displaystyle g_{\text{s}}}$ ${\displaystyle m_{\text{s}}}$

$${\displaystyle \mu _{z}=-m_{\text{s}}\ g_{\text{s}}\ \mu _{\mathsf {B}}=\pm {\tfrac {1}{2}}\ g_{\text{s}}\ \mu _{\mathsf {B}}\ }$$

где находится магнетон Бора . ${\displaystyle \ \mu _{\mathsf {B}}\ }$

Когда атомы имеют четное число электронов, спин каждого электрона на каждой орбитали имеет противоположную ориентацию по отношению к спину его ближайшего соседа(ов). Однако многие атомы имеют нечетное число электронов или расположение электронов, в котором существует неравное число ориентаций «спин вверх» и «спин вниз». Говорят, что эти атомы или электроны имеют неспаренные спины, которые обнаруживаются в электронном спиновом резонансе .

Ядерный спин

Атомные ядра также имеют спины. Ядерный спин I является фиксированным свойством каждого ядра и может быть как целым, так и полуцелым числом. Компонент m _I ядерного спина, параллельный оси z , может иметь (2 I + 1) значений I , I –1, ..., –I . Например, ядро ^​​14 N имеет I = 1, так что существует 3 возможных ориентации относительно оси z , соответствующих состояниям m _I = +1, 0 и −1. ^[14]

Спины I различных ядер интерпретируются с помощью модели ядерных оболочек . Четно-четные ядра с четным числом как протонов, так и нейтронов, такие как 12 C и 16 O , имеют нулевой спин. Ядра с нечетным массовым числом имеют полуцелые спины, такие как ⁠3/ 2 ⁠ для 7 Ли , ⁠ 1 /2⁠ для 13 С и ⁠5/ 2 ⁠ для 17 O , обычно соответствующий угловому моменту последнего добавленного нуклона . Нечетно-нечетные ядра с нечетным числом как протонов, так и нейтронов имеют целые спины, например, 3 для 10 B , и 1 для 14 N . ^[15] Значения ядерного спина для данного изотопа находятся в списках изотопов для каждого элемента. (См. изотопы кислорода , изотопы алюминия и т. д. и т. п.)

Обнаружение спина

При исследовании линий спектра водорода с очень высоким разрешением обнаруживается, что они представляют собой близко расположенные дублеты. Это расщепление называется тонкой структурой и было одним из первых экспериментальных доказательств существования электронного спина. Прямое наблюдение собственного углового момента электрона было достигнуто в эксперименте Штерна–Герлаха .

Эксперимент Штерна–Герлаха

Теория пространственного квантования спинового момента импульса электронов атомов, находящихся в магнитном поле, нуждалась в экспериментальном подтверждении. В 1922 году (за два года до создания теоретического описания спина) Отто Штерн и Вальтер Герлах наблюдали это в проведенном ими эксперименте.

Атомы серебра испарялись с помощью электрической печи в вакууме. С помощью тонких щелей атомы направлялись в плоский пучок, который затем направлялся через неоднородное магнитное поле, прежде чем столкнуться с металлической пластиной. Законы классической физики предсказывают, что совокупность конденсированных атомов серебра на пластине должна образовывать тонкую сплошную линию той же формы, что и исходный пучок. Однако неоднородное магнитное поле заставило пучок разделиться в двух отдельных направлениях, создав две линии на металлической пластине.

Феномен можно объяснить пространственным квантованием спинового момента импульса. В атомах электроны спарены таким образом, что один из них вращается вверх, а другой вниз, нейтрализуя влияние их спина на действие атома в целом. Но в валентной оболочке атомов серебра есть один электрон, спин которого остается несбалансированным.

Несбалансированный спин создает спиновый магнитный момент , заставляя электрон действовать как очень маленький магнит. Когда атомы проходят через неоднородное магнитное поле, момент силы в магнитном поле влияет на диполь электрона до тех пор, пока его положение не совпадет с направлением более сильного поля. Затем атом будет притягиваться к более сильному магнитному полю или от него на определенную величину, в зависимости от значения спина валентного электрона. Когда спин электрона равен ⁠++ 1 /2⁠ атом движется от более сильного поля, и когда спин ⁠−+ 1 /2⁠ атом движется к нему. Таким образом, пучок атомов серебра расщепляется при прохождении через неоднородное магнитное поле в соответствии со спином валентного электрона каждого атома.

В 1927 году Фиппс и Тейлор провели аналогичный эксперимент, используя атомы водорода с похожими результатами. Позже ученые провели эксперименты с другими атомами, имеющими только один электрон в своей валентной оболочке: ( медь , золото , натрий , калий ). Каждый раз на металлической пластине образовывались две линии.

Атомное ядро ​​также может иметь спин, но протоны и нейтроны намного тяжелее электронов (примерно в 1836 раз), а магнитный дипольный момент обратно пропорционален массе. Таким образом, ядерный магнитный дипольный момент намного меньше, чем у всего атома. Этот небольшой магнитный диполь позже был измерен Штерном, Фришем и Истерманом.

Электронный парамагнитный резонанс

Для атомов или молекул с неспаренным электроном также могут наблюдаться переходы в магнитном поле, при которых изменяется только спиновое квантовое число, без изменения электронной орбитали или других квантовых чисел. Это метод электронного парамагнитного резонанса (ЭПР) или электронного спинового резонанса (ЭПР), используемый для изучения свободных радикалов . Поскольку изменяется только магнитное взаимодействие спина, изменение энергии намного меньше, чем при переходах между орбиталями, а спектры наблюдаются в микроволновой области.

Отношение к спиновым векторам

Для решения нерелятивистского уравнения Паули или релятивистского уравнения Дирака квантованный угловой момент (см. квантовое число углового момента ) можно записать как: где $${\displaystyle \Vert \mathbf {s} \Vert ={\sqrt {s\,(s+1)\,}}\,\hbar }$$

• ${\displaystyle \mathbf {s} }$квантованный спиновый вектор или спинор
• ${\displaystyle \Vert \mathbf {s} \Vert }$норма вектора спина
• s — спиновое квантовое число, связанное со спиновым угловым моментом
• ${\displaystyle \hbar }$— это приведенная постоянная Планка .

При произвольном направлении z (обычно определяемом внешним магнитным полем) проекция спина z определяется выражением

${\displaystyle s_{z}=m_{s}\,\hbar }$

где m _s — магнитное спиновое квантовое число , варьирующееся от − s до + s с шагом 1. Это генерирует 2  s + 1 различных значений m _s .

Допустимые значения для s — неотрицательные целые числа или полуцелые числа . Фермионы имеют полуцелые значения, включая электрон , протон и нейтрон , которые все имеют s = ⁠+ + 1 /2⁠ . Бозоны, такие как фотон и все мезоны ) имеют целочисленные значения спина.

Алгебра

Алгебраическая теория спина является точной копией углового момента в теории квантовой механики. ^[16] Прежде всего, спин удовлетворяет фундаментальному коммутационному соотношению : где — (антисимметричный) символ Леви-Чивиты . Это означает, что невозможно знать две координаты спина одновременно из-за ограничения принципа неопределенности . $${\displaystyle \ [S_{i},S_{j}]=i\ \hbar \ \epsilon _{ijk}\ S_{k}\ ,}$$ $${\displaystyle \ \left[S_{i},S^{2}\right]=0\ }$$ ${\displaystyle \ \epsilon _{ijk}\ }$

Далее, собственные векторы и удовлетворяют : где — операторы лестницы (или «подъема» и «опускания»). ${\displaystyle \ S^{2}\ }$ ${\displaystyle \ S_{z}\ }$ $${\displaystyle \ S^{2}\ |s,m_{s}\rangle ={\hbar }^{2}\ s(s+1)\ |s,m_{s}\rangle \ }$$ $${\displaystyle \ S_{z}\ |s,m_{s}\rangle =\hbar \ m_{s}\ |s,m_{s}\rangle \ }$$ $${\displaystyle \ S_{\pm }\ |s,m_{s}\rangle =\hbar \ {\sqrt {s(s+1)-m_{s}(m_{s}\pm 1)\ }}\;|s,m_{s}\pm 1\rangle \ }$$ ${\displaystyle \ S_{\pm }=S_{x}\pm iS_{y}\ }$

Уровни энергии из уравнения Дирака

В 1928 году Поль Дирак разработал релятивистское волновое уравнение , теперь называемое уравнением Дирака , которое правильно предсказало спиновый магнитный момент и в то же время рассматривало электрон как точечную частицу. Решая уравнение Дирака для энергетических уровней электрона в атоме водорода, все четыре квантовых числа, включая s, возникли естественным образом и хорошо согласовались с экспериментом.

Полный спин атома или молекулы

Для некоторых атомов спины нескольких неспаренных электронов ( s ₁ , s ₂ , ...) связаны, образуя полное квантовое число спина S . ^{[17] [18]} Это происходит особенно в легких атомах (или в молекулах, образованных только из легких атомов), когда спин-орбитальная связь слаба по сравнению со связью между спинами или связью между орбитальными угловыми моментами , ситуация, известная как связь L S , поскольку L и S являются константами движения . Здесь L - полное квантовое число орбитального углового момента. ^[18]

Для атомов с четко определенным S кратность состояния определяется как 2 S + 1 . Это равно числу различных возможных значений полного (орбитального плюс спинового) углового момента J для данной комбинации ( L , S ), при условии, что S ≤ L (типичный случай). Например, если S = ​​1, то существует три состояния, которые образуют триплет . Собственные значения S z для этих трех состояний равны + 1ħ _, 0 и −1ħ . [ ^17] Термин символ атомного состояния указывает его значения L , S и J .

Например, основные состояния атома кислорода и молекулы дикислорода имеют два неспаренных электрона и, следовательно, являются триплетными состояниями. Атомное состояние описывается символом ³ P, а молекулярное состояние — символом ³ Σ⁻
_г.

Смотрите также

• Квантовое число полного углового момента
• Вращательная спектроскопия
• Основы квантовой механики

Ссылки

1. Полинг, Лайнус (1960). Природа химической связи и структура молекул и кристаллов: введение в современную структурную химию . Итака, Нью-Йорк: Издательство Корнеллского университета. ISBN 0-8014-0333-2. OCLC  545520.
2. "ISO 80000-10:2019". Международная организация по стандартизации . Получено 15 сентября 2019 г.
3. Аткинс, Питер; де Паула, Хулио (2006). Физическая химия Аткинса (8-е изд.). WH Freeman. стр. 308. ISBN 0-7167-8759-8.
4. Банвелл, Колин Н.; Маккэш, Элейн М. (1994). Основы молекулярной спектроскопии . McGraw-Hill. стр. 135. ISBN 0-07-707976-0.
5. Perrino, Charles T.; Peterson, Donald L. (1989). "Другое квантовое число?". J. Chem. Educ . 66 (8): 623. Bibcode :1989JChEd..66..623P. doi :10.1021/ed066p623. ISSN  0021-9584.
6. Петруччи, Ральф Х.; Харвуд, Уильям С.; Херринг, Ф. Джеффри (2002). Общая химия (8-е изд.). Prentice Hall. стр. 333. ISBN 0-13-014329-4.
7. Уиттен, Кеннет В.; Гэлли, Кеннет Д.; Дэвис, Рэймонд Э. (1992). Общая химия (4-е изд.). Saunders College Publishing. стр. 196. ISBN 0-03-072373-6.
8. Карплус, Мартин и Портер, Ричард Нидхэм. Атомы и молекулы. Соединенные Штаты, WA Benjamin, 1970.
9. Халперн, Пол (2017-11-21). «Спин: квантовое свойство, которое должно было быть невозможным». Forbes . Начинается с грохота. Архивировано из оригинала 2018-03-10 . Получено 2018-03-10 .
10. Манджит Кумар, Квант: Эйнштейн, Бор и великий спор о природе реальности, 2008.
11. Ленгмюр, Ирвинг (1919). «Расположение электронов в атомах и молекулах». Журнал Института Франклина . 187 (3): 359–362. doi :10.1016/S0016-0032(19)91097-0.
12. Giulini, Domenico (сентябрь 2008 г.). «Спин электрона или «классически неописуемая двузначность»». Исследования по истории и философии науки Часть B: Исследования по истории и философии современной физики . 39 (3): 557–578. arXiv : 0710.3128 . Bibcode :2008SHPMP..39..557G. doi :10.1016/j.shpsb.2008.03.005. hdl :11858/00-001M-0000-0013-13C8-1. S2CID  15867039.
13. Вольфганг Паули. Принцип исключения и квантовая механика Нобелевская лекция, прочитанная 13 декабря 1946 года по случаю вручения Нобелевской премии по физике 1945 года.
14. Аткинс, Питер; де Паула, Хулио (2006). Физическая химия Аткинса (8-е изд.). WH Freeman. стр. 515. ISBN 0-7167-8759-8.
15. Cottingham, WN; Greenwood, DA (1986). Введение в ядерную физику . Cambridge University Press. стр. 36, 57. ISBN 0-521-31960-9.
16. Дэвид Дж. Гриффитс , Введение в квантовую механику (книга) , Орегон, Рид-колледж, 2018, 166 стр. ISBN 9781107189638 . 
17. Merzbacher, E. (1998). Квантовая механика (3-е изд.). John Wiley. стр. 430–431. ISBN 0-471-88702-1.
18. Atkins, P. ; de Paula, J. (2006). Физическая химия (8-е изд.). WH Freeman. стр. 352. ISBN 0-7167-8759-8.

Внешние ссылки

• Вайс, Майкл (2001). «Полное рассмотрение спина – включая происхождение, эволюцию теории спина и детали уравнений спина». Кафедра математики . Калифорнийский университет в Риверсайде .