Клавдий Птолемей ( / ˈ t ɒ l ə m i / ; греч . : Πτολεμαῖος , Ptolemaios ; лат. : Claudius Ptolemaeus ; ок. 100 – ок. 170 н. э.) [1] был александрийским математиком , астрономом , астрологом , географом и теоретиком музыки [2], который написал около дюжины научных трактатов , три из которых были важны для более поздней византийской , исламской и западноевропейской науки. Первым был его астрономический трактат , ныне известный как Альмагест , первоначально называвшийся Математический трактат ( греч. : Μαθηματικὴ Σύνταξις , Mathēmatikḗ Syntaxis ). Вторая — География , которая представляет собой тщательное обсуждение карт и географических знаний греко-римского мира . Третья — астрологический трактат, в котором он попытался адаптировать гороскопическую астрологию к аристотелевской естественной философии своего времени. Иногда его называют Апотелесматика ( греч . Αποτελεσματικά , букв . « О последствиях » ), но более широко известно как Тетрабиблос , от греческого койне, означающего «четыре книги», или по его латинскому эквиваленту Quadripartite .
Католическая церковь продвигала его работу, которая включала единственную математически обоснованную геоцентрическую модель Солнечной системы , и в отличие от большинства греческих математиков , труды Птолемея (прежде всего Альмагест ) никогда не переставали копироваться или комментироваться, как в поздней античности , так и в Средние века . [3] Однако, вероятно, что лишь немногие действительно овладели математикой, необходимой для понимания его трудов, о чем свидетельствуют, в частности, многочисленные сокращенные и смягченные введения в астрономию Птолемея, которые были популярны среди арабов и византийцев. [4] [5] Его работа об эпициклах стала символом очень сложной теоретической модели, построенной для того, чтобы объяснить ложное предположение.
Дата и место рождения Птолемея неизвестны. Астроном XIV века Феодор Мелитениотис писал, что местом рождения Птолемея была Птолемаида Гермиу , греческий город в регионе Фиваида в Египте (ныне Эль-Манша, провинция Сохаг ). Однако это свидетельство довольно позднее, и нет никаких доказательств, подтверждающих его. [6] [b]
Известно, что Птолемей жил в городе Александрия или его окрестностях , в римской провинции Египет под римским правлением . [8] У него было латинское имя Клавдий, которое, как обычно считается, подразумевает, что он был римским гражданином . [9] Он был знаком с греческими философами и использовал вавилонские наблюдения и вавилонскую лунную теорию. В половине своих сохранившихся работ Птолемей обращается к некоему Сиру, фигуре, о которой почти ничего не известно, но которая, вероятно, разделяла некоторые астрономические интересы Птолемея. [10]
Птолемей умер в Александрии около 168 г. [11] (стр. 311)

Греческое имя Птолемея , Птолемей ( Πτολεμαῖος , Ptolemaîos ), является древнегреческим личным именем . Оно встречается один раз в греческой мифологии и имеет гомеровскую форму . [12] Оно было распространено среди македонского высшего класса во времена Александра Великого , и в армии Александра было несколько носителей этого имени, один из которых сделал себя фараоном в 323 г. до н. э.: Птолемей I Сотер , первый фараон Птолемеевского царства . Почти все последующие фараоны Египта, за несколькими исключениями, носили имя Птолемей , пока Египет не стал римской провинцией в 30 г. до н. э., положив конец правлению македонской семьи. [13]
Имя Клавдий — римское имя, принадлежащее к роду Клавдия ; своеобразная многосоставная форма полного имени Клавдий Птолемей — римский обычай, характерный для римских граждан. Это указывает на то, что Птолемей был римским гражданином . [ 6] Джеральд Тумер, переводчик « Альмагеста» Птолемея на английский язык, предполагает, что гражданство, вероятно, было предоставлено одному из предков Птолемея либо императором Клавдием , либо императором Нероном . [14]
Персидский астроном IX века Абу Машар аль-Балхи ошибочно представляет Птолемея как члена царской линии Птолемеевского Египта , заявляя, что потомки александрийского генерала и фараона Птолемея I Сотера были мудрыми «и включали Птолемея Мудрого, который составил книгу Альмагест » . Абу Машар записал убеждение, что другой член этой царской линии «составил книгу по астрологии и приписал ее Птолемею». Историческая путаница по этому вопросу может быть выведена из последующего замечания Абу Машара: «Иногда говорят, что очень ученый человек, который написал книгу по астрологии, также написал книгу Альмагест . Правильный ответ неизвестен». [15] Не так много положительных свидетельств известно о происхождении Птолемея, помимо того, что можно почерпнуть из деталей его имени, хотя современные ученые пришли к выводу, что рассказ Абу Машара ошибочен. [16] Больше не вызывает сомнений, что астроном, написавший Альмагест , также написал Тетрабиблос как его астрологический аналог. [17] (стр. х ) В более поздних арабских источниках его часто называли « Верхним Египтянином », [18] [19] (стр. 606) предполагая, что он мог иметь происхождение из Южного Египта . [19] (стр. 602, 606) Арабские астрономы , географы и физики называли его имя на арабском языке как Батлумюс ( арабский : بَطْلُمْيوس ). [20]
Птолемей писал на греческом койне [21] и, как можно показать, использовал вавилонские астрономические данные . [22] [23] (стр. 99) Он мог быть римским гражданином, но этнически был либо греком [1] [24] [25] или, по крайней мере, эллинизированным египтянином. [c] [26] [27]
Астрономия была предметом, которому Птолемей посвятил больше всего времени и усилий; около половины всех сохранившихся трудов посвящены астрономическим вопросам, и даже другие, такие как « География» и «Тетрабиблос», содержат значительные ссылки на астрономию. [5]

Mathēmatikē Syntaxis Птолемея ( греч . Μαθηματικὴ Σύνταξις , букв. « Математический систематический трактат » ), более известный как Альмагест , является единственным сохранившимся всеобъемлющим древним трактатом по астрономии. Хотя вавилонские астрономы разработали арифметические методы для расчета и прогнозирования астрономических явлений, они не были основаны на какой-либо базовой модели небес; с другой стороны, ранние греческие астрономы предоставили качественные геометрические модели, чтобы «сохранить видимость» небесных явлений без возможности делать какие-либо прогнозы. [28]
Первым человеком, который попытался объединить эти два подхода, был Гиппарх , создавший геометрические модели , которые не только отражали расположение планет и звезд, но и могли использоваться для расчета небесных движений. [23] Птолемей, следуя Гиппарху, вывел каждую из своих геометрических моделей Солнца, Луны и планет из избранных астрономических наблюдений, проведенных на протяжении более 800 лет; однако многие астрономы на протяжении столетий подозревали, что некоторые параметры его моделей были приняты независимо от наблюдений. [29]
Птолемей представил свои астрономические модели вместе с удобными таблицами, которые можно было использовать для вычисления будущего или прошлого положения планет. [30] Альмагест также содержит звездный каталог , который является версией каталога, созданного Гиппархом . Его список из сорока восьми созвездий является предком современной системы созвездий, но, в отличие от современной системы, они не охватывали все небо (только то, что можно было увидеть невооруженным глазом в северном полушарии). [31] Более тысячи лет Альмагест был авторитетным текстом по астрономии по всей Европе, на Ближнем Востоке и в Северной Африке. [32]
Альмагест , как и многие сохранившиеся греческие научные труды, сохранился в арабских рукописях; современное название, как полагают, является арабским искажением греческого названия Hē Megistē Syntaxis (букв . «Величайший трактат»), под которым работа предположительно была известна в эпоху поздней античности . [33] Благодаря своей репутации, она была широко востребована и дважды переведена на латынь в XII веке , один раз на Сицилии и еще раз в Испании. [34] Планетарные модели Птолемея, как и большинства его предшественников, были геоцентрическими и почти общепринятыми до повторного появления гелиоцентрических моделей во время научной революции .
Под пристальным вниманием современных ученых и перекрестной проверкой наблюдений, содержащихся в Альмагесте, с помощью цифр, полученных путем обратной экстраполяции, в работе были выявлены различные модели ошибок. [35] [36] Значительная ошибка в расчетах заключается в использовании Птолемеем измерений, которые, как он утверждал, проводились в полдень, но которые систематически дают показания, которые, как теперь показано, отличаются на полчаса, как если бы наблюдения проводились в 12:30 дня. [35]
Общее качество наблюдений Птолемея было оспорено несколькими современными учеными, но особенно Робертом Р. Ньютоном в его книге 1977 года «Преступление Клавдия Птолемея» , в которой он утверждал, что Птолемей сфабриковал многие из своих наблюдений, чтобы соответствовать своим теориям. [37] Ньютон обвинил Птолемея в систематическом придумывании данных или фальсификации данных более ранних астрономов и назвал его «самым успешным мошенником в истории науки». [35] Одной из поразительных ошибок, отмеченных Ньютоном, было осеннее равноденствие, которое, как говорят, наблюдал Птолемей и «измерено с величайшей тщательностью» в 14:00 25 сентября 132 года, когда равноденствие должно было наблюдаться около 9:55 утра накануне. [35] Пытаясь опровергнуть Ньютона, Герберт Льюис также согласился с тем, что «Птолемей был возмутительным мошенником» [36] и что «все эти результаты, поддающиеся статистическому анализу, несомненно указывают на мошенничество и исключают случайную ошибку» [36] .
Обвинения, выдвинутые Ньютоном и другими, стали предметом широких дискуссий и получили значительное сопротивление со стороны других ученых против результатов. [35] Оуэн Джинджерич , хотя и согласился, что Альмагест содержит «некоторые удивительно подозрительные числа», [35] в том числе в вопросе о смещенном на 30 часов равноденствии, которое, как он отметил, идеально совпадало с предсказаниями, сделанными Гиппархом 278 лет назад, [38] отверг квалификацию мошенничества. [35] Возражения также выдвинул Бернард Голдштейн , который подверг сомнению результаты Ньютона и предположил, что он неправильно понял вторичную литературу, отметив при этом, что проблемы с точностью наблюдений Птолемея были известны давно. [37] Другие авторы указали, что искривление инструментов или атмосферная рефракция также могут объяснить некоторые наблюдения Птолемея в неправильное время. [39] [40]
В 2022 году в палимпсесте были обнаружены первые греческие фрагменты утерянного звездного каталога Гиппарха , которые опровергли обвинения, выдвинутые французским астрономом Деламбре в начале 1800-х годов, которые были повторены Р. Р. Ньютоном. В частности, это доказало, что Гиппарх не был единственным источником каталога Птолемея, как они оба утверждали, и доказало, что Птолемей не просто скопировал измерения Гиппарха и скорректировал их для учета прецессии равноденствий, как они утверждали. Ученые, проанализировавшие карты, пришли к выводу:
Это также подтверждает, что звездный каталог Птолемея основывался не только на данных каталога Гиппарха.
... Эти наблюдения согласуются с точкой зрения, что Птолемей составил свой звездный каталог, объединив различные источники, включая каталог Гиппарха, свои собственные наблюдения и, возможно, наблюдения других авторов. [41]
Handy Tables ( греч . Πρόχειροι κανόνες ) — это набор астрономических таблиц вместе с канонами для их использования. Чтобы облегчить астрономические вычисления, Птолемей свел в таблицу все данные, необходимые для вычисления положений Солнца, Луны и планет, восхода и захода звезд, а также затмений Солнца и Луны, что сделало их полезным инструментом для астрономов и астрологов. Сами таблицы известны по версии Теона Александрийского . Хотя Handy Tables Птолемея не сохранились как таковые на арабском или латинском языках, они представляют собой прототип большинства арабских и латинских астрономических таблиц или zījes . [42]
Кроме того, введение к « Удобным таблицам» сохранилось отдельно от самих таблиц (очевидно, как часть собрания некоторых более коротких сочинений Птолемея) под названием «Расположение и расчет удобных таблиц» . [43]
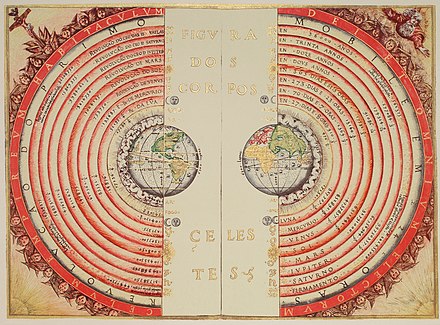
Планетарные гипотезы ( греч . Ὑποθέσεις τῶν πλανωμένων , букв. « Гипотезы планет » ) — космологическая работа, вероятно, одна из последних, написанных Птолемеем, в двух книгах, посвященных структуре Вселенной и законам, управляющим движением небесных тел . [44] Птолемей выходит за рамки математических моделей Альмагеста, чтобы представить физическую реализацию Вселенной как набора вложенных сфер, [45] в которой он использовал эпициклы своей планетарной модели для вычисления размеров Вселенной. Он оценил, что Солнце находится на среднем расстоянии в 1 210 радиусов Земли (теперь известно, что на самом деле это ~23 450 радиусов), в то время как радиус сферы неподвижных звезд был в 20 000 раз больше радиуса Земли. [46]
Работа также примечательна тем, что содержит описания того, как построить инструменты для изображения планет и их движения с геоцентрической точки зрения, во многом подобно тому, как это делала бы планетария для гелиоцентрической точки зрения, предположительно в дидактических целях. [47]
Аналемма — это короткий трактат , в котором Птолемей предлагает метод указания местоположения Солнца в трех парах локально ориентированных дуг координат как функции склонения Солнца, земной широты и часа. Ключ к подходу — представить твердую конфигурацию на плоской диаграмме, которую Птолемей называет аналеммой . [ 48]
В другом труде, « Фазис» ( «Восходы неподвижных звезд »), Птолемей дал парапегму — звездный календарь или альманах , основанный на появлении и исчезновении звезд в течение солнечного года. [49]
Planisphaerium ( греч . Ἅπλωσις ἐπιφανείας σφαίρας , букв. « Уплощение сферы » ) содержит 16 положений, касающихся проекции небесных кругов на плоскость. Текст на греческом языке утерян (за исключением фрагмента) и сохранился только на арабском и латинском языках. [ 50]
Птолемей также воздвиг надпись в храме в Канопусе , около 146–147 гг. н. э., известную как Канобическая надпись . Хотя надпись не сохранилась, кто-то в шестом веке переписал ее, и рукописные копии сохранили ее на протяжении всего Средневековья. Она начинается так: «Богу-спасителю Клавдий Птолемей (посвящает) первые принципы и модели астрономии», за которым следует каталог чисел, определяющих систему небесной механики, управляющую движениями Солнца, Луны, планет и звезд. [51]
В 2023 году археологи смогли прочитать рукопись, в которой даны инструкции по созданию астрономического инструмента, называемого метеороскопом ( μετεωροσκόπιον или μετεωροσκοπεῖον ). Текст, который происходит из рукописи восьмого века, которая также содержит Аналемму Птолемея , был идентифицирован на основе как его содержания, так и лингвистического анализа как принадлежащий Птолемею. [52] [53]

Вторая наиболее известная работа Птолемея — его «Geographike Hyphegesis» ( греч . Γεωγραφικὴ Ὑφήγησις ; букв. « Руководство по рисованию Земли » ), известная как « География» , — руководство по составлению карт с использованием географических координат для частей римского мира, известных в то время. [54] [55] Он опирался на предыдущие работы более раннего географа Марина Тирского , а также на географические справочники Римской и древней Персидской империй . [55] [54] Он также выразил признательность древнему астроному Гиппарху за то, что тот определил высоту северного небесного полюса [56] для нескольких городов. Хотя карты, основанные на научных принципах, создавались еще со времен Эратосфена ( ок. 276 – ок. 195 до н. э. ), Птолемей усовершенствовал картографические проекции .
Первая часть « Географии» представляет собой обсуждение данных и методов, которые он использовал. Птолемей отмечает превосходство астрономических данных над измерениями земли или отчетами путешественников, хотя он обладал этими данными только для нескольких мест. Однако настоящее новшество Птолемея происходит во второй части книги, где он предоставляет каталог из 8000 местностей, которые он собрал у Марина и других, — самую большую подобную базу данных со времен античности. [57] Около 6300 из этих мест и географических объектов имеют назначенные координаты, так что их можно разместить в сетке , охватывающей земной шар. [5] Широта измерялась от экватора , как и сегодня, но Птолемей предпочитал выражать ее как climata , длину самого длинного дня, а не как градусы дуги : длина дня в середине лета увеличивается с 12 до 24 часов по мере продвижения от экватора к полярному кругу . [58] Одним из мест, для которых Птолемей указал конкретные координаты, была ныне утерянная каменная башня , которая обозначала середину древнего Шелкового пути , и которую ученые пытаются найти с тех пор. [59]
В третьей части Географии Птолемей дает инструкции о том, как создавать карты как всего обитаемого мира ( oikoumenē ), так и римских провинций, включая необходимые топографические списки и подписи к картам. Его oikoumenē охватывала 180 градусов долготы от островов Блаженных в Атлантическом океане до середины Китая и около 80 градусов широты от Шетландских островов до Анти-Мероэ (восточное побережье Африки ); Птолемей прекрасно понимал, что он знал только четверть земного шара, и ошибочное расширение Китая на юг предполагает, что его источники не доходили до Тихого океана. [54] [55]
Кажется вероятным, что топографические таблицы во второй части работы (книги 2–7) являются кумулятивными текстами, которые были изменены по мере того, как новые знания становились доступными в веках после Птолемея. [60] Это означает, что информация, содержащаяся в разных частях Географии , вероятно, относится к разным датам, в дополнение к содержанию множества ошибок переписчиков. Однако, хотя региональные и мировые карты в сохранившихся рукописях датируются примерно 1300 годом н. э. (после того, как текст был заново открыт Максимом Планудом ), есть некоторые ученые, которые считают, что такие карты восходят к самому Птолемею. [57]

Птолемей написал астрологический трактат в четырех частях, известный под греческим термином Tetrabiblos (букв. «Четыре книги») или под его латинским эквивалентом Quadripartitum . [61] Его первоначальное название неизвестно, но, возможно, это был термин, встречающийся в некоторых греческих рукописях, Apotelesmatiká ( biblía ), что примерно означает «(книги) о Влиянии» или «Результатах», или «Прогностике». [17] (стр. x ) Как источник справочной информации, Tetrabiblos , как говорят, «пользовался почти авторитетом Библии среди астрологических писателей тысячи лет или более». [17] (стр. xii ) Он был впервые переведен с арабского на латынь Платоном из Тиволи (Тибуртинусом) в 1138 году, когда он был в Испании. [62]
Большая часть содержания Тетрабиблоса была собрана из более ранних источников; достижение Птолемея состояло в том, что он систематически упорядочил свой материал, показав, как, по его мнению, можно было рационализировать предмет. Он, действительно, представлен как вторая часть изучения астрономии, первой из которых был Альмагест , посвященная влиянию небесных тел в подлунной сфере . [4] [16] Таким образом, даются своего рода объяснения астрологических эффектов планет , основанные на их комбинированном воздействии нагревания, охлаждения, увлажнения и высыхания. [63] Птолемей отвергает другие астрологические практики, такие как рассмотрение нумерологического значения имен, которые, по его мнению, не имеют под собой прочной основы, и оставляет популярные темы, такие как элективная астрология (интерпретация астрологических карт для определения курса действий) и медицинская астрология , по аналогичным причинам. [64]
Большое уважение, с которым более поздние астрологи относились к « Тетрабиблосу», проистекало из его природы как изложения теории, а не как руководства. [64]
Сборник из ста афоризмов об астрологии, называемый Centiloquium , приписываемый Птолемею, широко воспроизводился и комментировался арабскими, латинскими и еврейскими учеными, и часто объединялся в средневековых рукописях после Tetrabiblos как своего рода суммирование. [5] Сейчас считается, что это гораздо более позднее псевдоэпиграфическое сочинение. Личность и дата настоящего автора работы, называемой теперь Псевдо-Птолемеем , остаются предметом догадок. [65]

Птолемей написал труд под названием «Гармоникон» ( греч . Ἁρμονικόν , известный как « Гармоника» ) , посвященный теории музыки и математике, лежащей в основе музыкальных гамм, в трех книгах. [66]
Гармоники начинаются с определения гармонической теории, с длинного изложения взаимосвязи между разумом и чувственным восприятием в подкреплении теоретических предположений. После критики подходов своих предшественников, Птолемей выступает за обоснование музыкальных интервалов на математических соотношениях (в отличие от идей, отстаиваемых последователями Аристоксена ), подкрепленных эмпирическими наблюдениями (в отличие от чрезмерно теоретического подхода пифагорейцев ) . [67] [68]
Птолемей вводит гармонический канон (греческое название) или монохорд (латинское название), который является экспериментальным музыкальным аппаратом, который он использовал для измерения относительных высот, и использовал для описания своим читателям того, как продемонстрировать отношения, обсуждаемые в следующих главах, для себя. После раннего изложения того, как построить и использовать монохорд для проверки предлагаемых систем настройки, Птолемей переходит к обсуждению пифагорейской настройки (и того, как продемонстрировать, что их идеализированная музыкальная шкала не работает на практике). Пифагорейцы считали, что математика музыки должна основываться только на одном конкретном соотношении 3:2, чистой квинте , и считали, что настройки, математически точные для их системы, окажутся мелодичными, если только можно будет вычислить (вручную) чрезвычайно большие задействованные числа. Напротив, Птолемей считал, что музыкальные гаммы и настройки должны в целом включать несколько различных соотношений, организованных так, чтобы они равномерно вписывались в меньшие тетрахорды (комбинации четырех соотношений высот, которые вместе составляют чистую кварту ) и октавы . [69] [70] Птолемей рассмотрел стандартную (и древнюю, вышедшую из употребления) музыкальную практику настройки своего времени, которую он затем сравнил со своими собственными подразделениями тетрахорда и октавы , которые он вывел экспериментально, используя монохорд / гармонический канон. Том заканчивается более спекулятивным изложением взаимоотношений между гармонией, душой ( психика ) и планетами ( гармония сфер ). [71]
Хотя «Гармоники» Птолемея никогда не имели влияния его «Альмагеста» или «Географии» , тем не менее, это хорошо структурированный трактат, содержащий больше методологических размышлений, чем любые другие его труды. В частности, это зарождающаяся форма того, что в следующем тысячелетии развилось в научный метод, с конкретными описаниями экспериментального аппарата, который он построил и использовал для проверки музыкальных предположений, и эмпирических музыкальных отношений, которые он определил, проверяя высоты звука друг против друга: он был в состоянии точно измерить относительные высоты звука, основываясь на соотношениях вибрирующих длин двух отдельных сторон одной и той же струны , следовательно, которые были гарантированно под равным натяжением, устраняя один источник ошибки. Он проанализировал эмпирически определенные соотношения «приятных» пар высот звука, а затем синтезировал их все в связное математическое описание, которое сохраняется и поныне как просто интонация – стандарт для сравнения консонанса во многих других, менее точных, но более гибких компромиссных системах настройки. [72] [73]
В эпоху Возрождения идеи Птолемея вдохновляли Кеплера в его собственных размышлениях о гармонии мира ( Harmonice Mundi , Приложение к Книге V). [74]
Optica ( греч. койне : Ὀπτικά ), известная как Оптика, — это труд, сохранившийся только в довольно плохой латинской версии, которая, в свою очередь, была переведена с утерянной арабской версии Евгением Палермским ( ок. 1154 г. ). В нем Птолемей пишет о свойствах зрения (не света), включая отражение , преломление и цвет . Работа является значительной частью ранней истории оптики и повлияла на более известную и превосходную Книгу оптики XI века Ибн аль-Хайтама . [75] Птолемей предложил объяснения многих явлений, касающихся освещения и цвета, размера, формы, движения и бинокулярного зрения. Он также разделил иллюзии на те, которые вызваны физическими или оптическими факторами, и те, которые вызваны факторами суждения. Он предложил неясное объяснение иллюзии Солнца или Луны (увеличенный видимый размер на горизонте), основанное на трудности взгляда вверх. [76] [77]
Работа разделена на три основных раздела. Первый раздел (Книга II) рассматривает прямое зрение с первых принципов и заканчивается обсуждением бинокулярного зрения. Второй раздел (Книги III-IV) рассматривает отражение в плоских, выпуклых, вогнутых и составных зеркалах. [78] Последний раздел (Книга V) рассматривает рефракцию и включает в себя самую раннюю сохранившуюся таблицу рефракции от воздуха к воде, для которой значения (за исключением угла падения 60°) показывают признаки того, что они были получены из арифметической прогрессии. [79] Однако, по словам Марка Смита, таблица Птолемея была частично основана на реальных экспериментах. [80]
Теория зрения Птолемея состояла из лучей (или потока), исходящих из глаза, образующих конус, вершина которого находилась внутри глаза, а основание определяло поле зрения. Лучи были чувствительными и передавали информацию обратно в интеллект наблюдателя о расстоянии и ориентации поверхностей. Размер и форма определялись углом зрения, образуемым глазом, в сочетании с воспринимаемым расстоянием и ориентацией. [75] [81] Это было одно из ранних утверждений об инвариантности размера-расстояния как причине перцептивного постоянства размера и формы, точка зрения, поддержанная стоиками. [82]
Хотя Птолемей в основном известен своим вкладом в астрономию и другие научные дисциплины, он также участвовал в эпистемологических и психологических дискуссиях в своем корпусе. [83] Он написал короткое эссе под названием «О критерии и гегемониконе» ( греч . Περὶ Κριτηρίου καὶ Ἡγεμονικοῡ ), которое, возможно, было одной из его самых ранних работ. Птолемей конкретно рассматривает то, как люди получают научные знания (т. е. «критерий» истины), а также природу и структуру человеческой психики или души, в частности, ее правящую способность (т. е. гегемоникон ). [71] Птолемей утверждает, что для достижения истины следует использовать как разум, так и чувственное восприятие способами, которые дополняют друг друга. «О критерии» также примечательно тем, что это единственное произведение Птолемея, в котором отсутствует математика . [84]
В другом месте Птолемей утверждает превосходство математического знания над другими формами знания. Как и Аристотель до него, Птолемей классифицирует математику как тип теоретической философии; однако Птолемей считает, что математика превосходит теологию или метафизику , потому что последние являются предположительными, в то время как только первая может обеспечить определенное знание. Эта точка зрения противоречит платоновским и аристотелевским традициям , где теология или метафизика занимали высшую позицию. [83] Несмотря на то, что Птолемей был в меньшинстве среди древних философов, его взгляды разделяли и другие математики, такие как Герон Александрийский . [85]
В честь Птолемея названо несколько персонажей и предметов, в том числе:
{{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка ){{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )