Механика жидкости — раздел физики, изучающий механику жидкостей ( жидкостей , газов и плазмы ) и действующие на них силы . [1] : 3 Она применяется в широком спектре дисциплин, включая машиностроение , аэрокосмическую технику , гражданское строительство , химическую и биомедицинскую технику , а также геофизику , океанографию , метеорологию , астрофизику и биологию .
Ее можно разделить на статику жидкости , изучение жидкостей в состоянии покоя, и динамику жидкости , изучение влияния сил на движение жидкости. [1] : 3 Это раздел механики сплошных сред , предмет, который моделирует материю без использования информации о том, что она состоит из атомов; то есть он моделирует материю с макроскопической точки зрения, а не с микроскопической .
Механика жидкости, особенно динамика жидкости, является активной областью исследований, как правило, математически сложной. Многие проблемы частично или полностью не решены и лучше всего решаются численными методами , как правило, с использованием компьютеров. Современная дисциплина, называемая вычислительной гидродинамикой (CFD), посвящена этому подходу. [2] Велосиметрия изображения частиц , экспериментальный метод визуализации и анализа потока жидкости, также использует преимущества высоковизуальной природы потока жидкости.
Изучение механики жидкости восходит, по крайней мере, к временам Древней Греции , когда Архимед исследовал статику жидкости и плавучесть и сформулировал свой знаменитый закон, известный сейчас как принцип Архимеда , который был опубликован в его работе «О плавающих телах» — обычно считающейся первой крупной работой по механике жидкости. Иранский ученый Абу Райхан Бируни , а позже Аль-Хазини применили экспериментальные научные методы к механике жидкости. [3] Быстрое развитие механики жидкости началось с Леонардо да Винчи (наблюдения и эксперименты), Эванджелиста Торричелли (изобрел барометр ), Исаака Ньютона (исследовал вязкость ) и Блеза Паскаля (исследовал гидростатику , сформулировал закон Паскаля ) и было продолжено Даниилом Бернулли с введением математической динамики жидкости в «Гидродинамике» (1739).
Невязкий поток был далее проанализирован различными математиками ( Жан Лерон Д'Аламбер , Жозеф Луи Лагранж , Пьер-Симон Лаплас , Симеон Дени Пуассон ), а вязкий поток исследовался множеством инженеров, включая Жана Леонара Мари Пуазейля и Готхильфа Хагена . Дальнейшее математическое обоснование было предоставлено Клодом-Луи Навье и Джорджем Габриэлем Стоксом в уравнениях Навье-Стокса , и были исследованы пограничные слои ( Людвиг Прандтль , Теодор фон Карман ), в то время как различные ученые, такие как Осборн Рейнольдс , Андрей Колмогоров и Джеффри Ингрэм Тейлор, продвинули понимание вязкости жидкости и турбулентности .
Статика жидкости или гидростатика — это раздел механики жидкости, изучающий жидкости в состоянии покоя. Он охватывает изучение условий, при которых жидкости находятся в состоянии покоя в устойчивом равновесии ; и противопоставляется динамике жидкости , изучению жидкостей в движении. Гидростатика предлагает физические объяснения многих явлений повседневной жизни, например, почему атмосферное давление изменяется с высотой , почему дерево и масло плавают на воде и почему поверхность воды всегда ровная, независимо от формы ее контейнера. Гидростатика имеет основополагающее значение для гидравлики , проектирования оборудования для хранения, транспортировки и использования жидкостей . Она также имеет отношение к некоторым аспектам геофизики и астрофизики (например, к пониманию тектоники плит и аномалий в гравитационном поле Земли ), метеорологии , медицине (в контексте артериального давления ) и многим другим областям.
Гидродинамика — это подраздел механики жидкости, который занимается потоком жидкости — наукой о жидкостях и газах в движении. [4] Гидродинамика предлагает систематическую структуру, которая лежит в основе этих практических дисциплин , которая охватывает эмпирические и полуэмпирические законы, полученные из измерения потока и используемые для решения практических задач. Решение проблемы гидродинамики обычно включает в себя расчет различных свойств жидкости, таких как скорость , давление , плотность и температура , как функций пространства и времени. Она сама по себе имеет несколько подразделов, включая аэродинамику [5] [6] [7] [8] (изучение воздуха и других газов в движении) и гидродинамику [9] [10] (изучение жидкостей в движении). Гидродинамика имеет широкий спектр приложений, включая расчет сил и движений на самолетах, определение массового расхода нефти по трубопроводам , прогнозирование развивающихся погодных условий , понимание туманностей в межзвездномпространстве и моделирование взрывов . Некоторые принципы гидродинамики используются в дорожном движении и динамике толпы.
Механика жидкости является подразделом механики сплошной среды , как показано в следующей таблице.
С механической точки зрения, жидкость — это вещество, которое не выдерживает напряжения сдвига ; поэтому жидкость в состоянии покоя имеет форму содержащего ее сосуда. Жидкость в состоянии покоя не имеет напряжения сдвига.
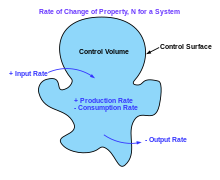
Предположения, присущие механическому лечению жидкости физической системы, могут быть выражены в терминах математических уравнений. По сути, каждая механическая система жидкости должна подчиняться:
Например, предположение о сохранении массы означает, что для любого фиксированного контрольного объема (например, сферического объема) — ограниченного контрольной поверхностью — скорость изменения массы, содержащейся в этом объеме, равна скорости, с которой масса проходит через поверхность снаружи внутрь, за вычетом скорости, с которой масса проходит изнутри наружу . Это можно выразить в виде уравнения в интегральной форме по контрольному объему. [11] : 74
TheПредположение континуума является идеализациеймеханики континуума, при которой жидкости можно рассматривать какнепрерывные, хотя в микроскопическом масштабе они состоят измолекул. В предположении континуума макроскопические (наблюдаемые/измеряемые) свойства, такие как плотность, давление, температура и объемная скорость, считаются хорошо определенными в «бесконечно малых» элементах объема — малых по сравнению с характерным масштабом длины системы, но больших по сравнению с молекулярным масштабом длины. Свойства жидкости могут непрерывно меняться от одного элемента объема к другому и являются средними значениями молекулярных свойств. Гипотеза континуума может приводить к неточным результатам в таких приложениях, как сверхзвуковые скоростные потоки или молекулярные потоки в наномасштабе.[12]Те проблемы, для которых гипотеза континуума не работает, можно решить с помощьюстатистической механики. Чтобы определить, применима ли гипотеза континуума,число Кнудсенасредней длины свободного пробегамолекулк характерномумасштабу. Проблемы с числами Кнудсена ниже 0,1 можно оценить с помощью гипотезы континуума, но для нахождения движения жидкости при больших числах Кнудсена можно применить молекулярный подход (статистическую механику).
Уравнения Навье–Стокса (названные в честь Клода-Луи Навье и Жоржа Габриэля Стокса ) — это дифференциальные уравнения , описывающие баланс сил в заданной точке внутри жидкости. Для несжимаемой жидкости с векторным полем скорости уравнения Навье–Стокса имеют вид [13] [14] [15] [16]
Эти дифференциальные уравнения являются аналогами для деформируемых материалов уравнений движения Ньютона для частиц – уравнения Навье–Стокса описывают изменения импульса ( силы ) в ответ на давление и вязкость, параметризованные кинематической вязкостью . Иногда к уравнениям добавляются объемные силы , такие как сила тяготения или сила Лоренца.
Решения уравнений Навье–Стокса для заданной физической задачи должны быть найдены с помощью исчисления . С практической точки зрения, только самые простые случаи могут быть решены именно таким образом. Эти случаи обычно включают нетурбулентный, стационарный поток, в котором число Рейнольдса мало. Для более сложных случаев, особенно тех, которые включают турбулентность , таких как глобальные погодные системы, аэродинамика, гидродинамика и многие другие, решения уравнений Навье–Стокса в настоящее время могут быть найдены только с помощью компьютеров. Эта отрасль науки называется вычислительной гидродинамикой . [17] [18] [19] [20] [21]
Невязкая жидкость не имеет вязкости , . На практике невязкий поток является идеализацией , которая облегчает математическую обработку. Фактически, чисто невязкие потоки, как известно, реализуются только в случае сверхтекучести . В противном случае жидкости, как правило, вязкие , свойство, которое часто является наиболее важным в пограничном слое вблизи твердой поверхности, [22] где поток должен соответствовать условию отсутствия скольжения на твердом теле. В некоторых случаях математику жидкостной механической системы можно рассматривать, предполагая, что жидкость вне пограничных слоев невязка, а затем сопоставляя ее решение с решением для тонкого ламинарного пограничного слоя.
Для потока жидкости через пористую границу скорость жидкости может быть прерывистой между свободной жидкостью и жидкостью в пористой среде (это связано с условием Биверса и Джозефа). Кроме того, при низких дозвуковых скоростях полезно предположить, что газ несжимаем , то есть плотность газа не меняется, даже если скорость и статическое давление изменяются.
Ньютоновская жидкость (названная в честь Исаака Ньютона ) определяется как жидкость , напряжение сдвига которой линейно пропорционально градиенту скорости в направлении, перпендикулярном плоскости сдвига. Это определение означает, что независимо от сил, действующих на жидкость, она продолжает течь . Например, вода является ньютоновской жидкостью, потому что она продолжает проявлять свойства жидкости независимо от того, насколько сильно ее перемешивают или смешивают. Немного менее строгое определение заключается в том, что сопротивление небольшого объекта, медленно перемещаемого через жидкость, пропорционально силе, приложенной к объекту. (Сравните трение ). Важные жидкости, такие как вода, а также большинство газов, ведут себя — в хорошем приближении — как ньютоновская жидкость в нормальных условиях на Земле. [11] : 145
Напротив, перемешивание неньютоновской жидкости может оставить «дыру». Она будет постепенно заполняться с течением времени — это поведение наблюдается в таких материалах, как пудинг, ооблеки или песок (хотя песок не является строго жидкостью). С другой стороны, перемешивание неньютоновской жидкости может привести к снижению вязкости, поэтому жидкость будет казаться «жиже» (это наблюдается в некапающих красках ). Существует много типов неньютоновских жидкостей, поскольку они определяются как нечто, что не подчиняется определенному свойству — например, большинство жидкостей с длинными молекулярными цепями могут реагировать неньютоновским образом. [11] : 145
Константа пропорциональности между тензором вязкого напряжения и градиентом скорости известна как вязкость . Простое уравнение для описания поведения несжимаемой ньютоновской жидкости:
где
Для ньютоновской жидкости вязкость, по определению, зависит только от температуры , а не от сил, действующих на нее. Если жидкость несжимаема, то уравнение, регулирующее вязкое напряжение (в декартовых координатах ), имеет вид
где
Если жидкость не является несжимаемой, общая форма для вязкого напряжения в ньютоновской жидкости имеет вид
где - второй коэффициент вязкости (или объемная вязкость). Если жидкость не подчиняется этому соотношению, ее называют неньютоновской жидкостью , которая бывает нескольких типов. Неньютоновские жидкости могут быть пластичными, пластичными по Бингаму, псевдопластичными, дилатантными, тиксотропными, реопектическими, вязкоупругими.
В некоторых приложениях проводится еще одно грубое широкое разделение жидкостей: идеальные и неидеальные жидкости. Идеальная жидкость не вязкая и не оказывает никакого сопротивления сдвигающей силе. Идеальной жидкости на самом деле не существует, но в некоторых расчетах это предположение оправдано. Одним из примеров этого является течение вдали от твердых поверхностей. Во многих случаях вязкие эффекты сосредоточены вблизи твердых границ (например, в пограничных слоях), тогда как в областях поля течения вдали от границ вязкими эффектами можно пренебречь, и жидкость там рассматривается как невязкая (идеальное течение). Когда вязкостью пренебрегают, член, содержащий тензор вязких напряжений в уравнении Навье–Стокса, исчезает. Уравнение, приведенное к такому виду, называется уравнением Эйлера .