Треугольник

Форма с тремя сторонами

Треугольник — это многоугольник с тремя углами и тремя сторонами, одна из основных фигур в геометрии . Углы, также называемые вершинами , являются нульмерными точками , в то время как стороны, соединяющие их, также называемые ребрами , являются одномерными отрезками . Треугольник имеет три внутренних угла , каждый из которых ограничен парой смежных ребер; сумма углов треугольника всегда равна развернутому углу (180 градусов или π радиан). Треугольник является плоской фигурой , а его внутренняя часть — плоской областью . Иногда произвольное ребро выбирается в качестве основания , и в этом случае противоположная вершина называется вершиной ; кратчайший отрезок между основанием и вершиной — это высота . Площадь треугольника равна половине произведения высоты на длину основания.

В евклидовой геометрии любые две точки определяют уникальный отрезок, расположенный внутри уникальной прямой линии , а любые три точки, которые не лежат на одной прямой, определяют уникальный треугольник, расположенный внутри уникальной плоскости . В более общем смысле, четыре точки в трехмерном евклидовом пространстве определяют тетраэдр .

В неевклидовых геометриях три «прямых» сегмента (имеющих нулевую кривизну ) также определяют треугольник, например, сферический треугольник или гиперболический треугольник . Геодезический треугольник — это область общей двумерной поверхности, ограниченная тремя сторонами, которые являются прямыми относительно поверхности ( геодезическими ).Криволинейный треугольник— это фигура с тремяизогнутымисторонами, например,круговой треугольниксов виде дуг окружности. Эта статья о прямосторонних треугольниках в евклидовой геометрии, если не указано иное.

Треугольники классифицируются на различные типы в зависимости от их углов и длин сторон. Соотношения между углами и длинами сторон являются основным направлением тригонометрии . В частности, функции синуса, косинуса и тангенса связывают длины сторон и углы в прямоугольных треугольниках .

Определение, терминология и типы

Треугольник — это фигура, состоящая из трех отрезков, конечные точки которых соединены. ^[1] Это образует многоугольник с тремя сторонами и тремя углами. Терминология для классификации треугольников существует более двух тысяч лет и была определена в первой книге « Начал» Евклида . ^[2] Названия, используемые для современной классификации, являются либо прямой транслитерацией греческого слова Евклида, либо их латинскими переводами.

Треугольники имеют много типов, основанных на длине сторон и углах. Треугольник, все стороны которого имеют одинаковую длину, является равносторонним треугольником , ^[3] треугольник с двумя сторонами, имеющими одинаковую длину, является равнобедренным треугольником , ^{[4] [a]} а треугольник с тремя сторонами разной длины является разносторонним треугольником . ^[7] Треугольник, в котором один из углов является прямым углом, является прямоугольным треугольником , треугольник, в котором все его углы меньше этого угла, является остроугольным треугольником , а треугольник, в котором один из его углов больше этого угла, является тупоугольным треугольником . ^[8] Эти определения восходят, по крайней мере, к Евклиду . ^[9]

• 
  Равносторонний треугольник
• 
  Равнобедренный треугольник
• 
  Разносторонний треугольник

• 
  Прямоугольный треугольник
• 
  Остроугольный треугольник
• 
  Тупоугольный треугольник

Появления

Треугольная бипирамида может быть построена путем присоединения двух тетраэдров . Этот многогранник можно назвать симплициальным многогранником, поскольку все его грани являются треугольниками. Более конкретно, когда грани равносторонние, он классифицируется как дельтаэдр .

Треугольники можно найти в трехмерных объектах, например, в многограннике , теле, граница которого покрыта плоскими многоугольниками, известными как грани, острыми углами, известными как вершины, и отрезками прямых, известными как ребра. Многогранники в некоторых случаях можно классифицировать, судя по форме их граней. Например, когда многогранники имеют все равносторонние треугольники в качестве своих граней, они известны как дельтаэдр . ^[10] Антипризмы имеют чередующиеся треугольники на своих сторонах. ^[11] Пирамиды и бипирамиды являются многогранниками с многоугольными основаниями, а их боковые грани являются треугольниками; треугольники являются равнобедренными, когда они являются правильными пирамидами и бипирамидами. Клетоп пяти Платоновых тел — это примеры многогранников с треугольными гранями, полученные путем присоединения пяти Платоновых тел — тетраэдра , октаэдра , икосаэдра , додекаэдра и куба — к пирамидам. ^[12] В более общем смысле, треугольники можно найти в более высоких измерениях, как в обобщенном понятии треугольников, известном как симплекс , и многогранников с треугольными гранями, известных как симплициальные многогранники . ^[13]

Характеристики

Точки, линии и окружности, связанные с треугольником

Каждый треугольник имеет много особых точек внутри себя, на своих ребрах или иным образом связанных с ним. Они строятся путем нахождения трех линий, симметрично связанных с тремя сторонами (или вершинами), а затем доказательства того, что три линии пересекаются в одной точке. Важным инструментом для доказательства существования этих точек является теорема Чевы , которая дает критерий для определения того, когда три такие линии являются конкурирующими . ^[14] Аналогично, линии, связанные с треугольником, часто строятся путем доказательства того, что три симметрично построенные точки являются коллинеарными ; здесь теорема Менелая дает полезный общий критерий. ^[15] В этом разделе объясняются лишь некоторые из наиболее часто встречающихся конструкций.

Центр описанной окружности — центр окружности, проходящей через три вершины треугольника; пересечение высот — ортоцентр . Пересечение биссектрис — центр вписанной окружности .

Перпендикуляр к стороне треугольника — это прямая линия, проходящая через середину стороны и перпендикулярная ей, образующая с ней прямой угол. ^{[16] Три} перпендикулярных серединных линии пересекаются в одной точке, центре описанной окружности треугольника ; эта точка является центром описанной окружности , окружности, проходящей через все три вершины. ^[17] Теорема Фалеса подразумевает, что если центр описанной окружности расположен на стороне треугольника, то угол, противолежащий этой стороне, является прямым углом. ^[18] Если центр описанной окружности расположен внутри треугольника, то треугольник остроугольный; если центр описанной окружности расположен снаружи треугольника, то треугольник тупоугольный. ^[19]

Высота треугольника — это прямая линия, проходящая через вершину и перпендикулярная к противоположной стороне. Эта противоположная сторона называется основанием высоты , а точка, где высота пересекает основание (или его продолжение), называется основанием высоты . ^[20] Длина высоты — это расстояние между основанием и вершиной. Три высоты пересекаются в одной точке, называемой ортоцентром треугольника. ^[21] Ортоцентр лежит внутри треугольника тогда и только тогда, когда треугольник остроугольный. ^[22]

Окружность девяти точек демонстрирует симметрию, где шесть точек лежат на стороне треугольника. Линия Эйлера — это прямая линия, проходящая через ортоцентр (синий), центр окружности девяти точек (красный), центроид (оранжевый) и центр описанной окружности (зеленый).

Биссектриса треугольника — это прямая линия, проходящая через вершину и делящая соответствующий угол пополам. Три биссектрисы пересекаются в одной точке, инцентре , который является центром вписанной окружности треугольника . Вписанная окружность — это окружность, которая лежит внутри треугольника и касается всех трех сторон. Ее радиус называется вписанным радиусом . Существуют еще три важные окружности, вневписанные окружности ; они лежат вне треугольника и касаются одной стороны, а также продолжений двух других. Центры вписанных и вневписанных окружностей образуют ортоцентрическую систему . ^{[23] Середины трех сторон и основания трех высот лежат на одной окружности,} девятиточечной окружности треугольника . ^[24] Остальные три точки, по которым она получила свое название, являются серединами части высоты между вершинами и ортоцентром . Радиус девятиточечной окружности составляет половину радиуса описанной окружности. Он касается вписанной окружности (в точке Фейербаха ) и трех вневписанных окружностей . Ортоцентр (синяя точка), центр окружности с девятью точками (красная), центроид (оранжевый) и центр описанной окружности (зеленый) лежат на одной прямой, известной как линия Эйлера (красная линия). Центр окружности с девятью точками лежит в средней точке между ортоцентром и центром описанной окружности, а расстояние между центроидом и центром описанной окружности составляет половину расстояния между центроидом и ортоцентром. ^[24] Как правило, центр вписанной окружности не находится на прямой Эйлера. ^{[25] [26]}

Вписанная окружность треугольника и пересечение медиан, известное как центроид.

Медиана треугольника — это прямая линия, проходящая через вершину и середину противоположной стороны, и делящая треугольник на две равные области. Три медианы пересекаются в одной точке, центроиде треугольника или геометрическом барицентре. Центроид жесткого треугольного объекта (вырезанного из тонкого листа однородной плотности) также является его центром масс : объект может быть сбалансирован на своем центроиде в однородном гравитационном поле. ^[27] Центроид пересекает каждую медиану в соотношении 2:1, т. е. расстояние между вершиной и центроидом в два раза больше расстояния между центроидом и серединой противоположной стороны. Если отразить медиану в биссектрисе угла, проходящей через ту же вершину, то получится симедиана . Три симедианы пересекаются в одной точке, точке симедианы треугольника. ^[28]

Углы

Сумма внутренних углов треугольника всегда составляет 180 градусов (они выделены одним цветом, чтобы подчеркнуть их равенство).

Сумма мер внутренних углов треугольника в евклидовом пространстве всегда равна 180 градусам. ^[29] Этот факт эквивалентен постулату Евклида о параллельных . Это позволяет определить меру третьего угла любого треугольника, зная меру двух углов. ^[30] Внешний угол треугольника — это угол, который является линейной парой (и, следовательно, дополнительным ) к внутреннему углу. Мера внешнего угла треугольника равна сумме мер двух внутренних углов, которые не являются смежными с ним; это теорема о внешнем угле . ^[31] Сумма мер трех внешних углов (по одному для каждой вершины) любого треугольника равна 360 градусам, и действительно, это верно для любого выпуклого многоугольника, независимо от того, сколько у него сторон. ^[32]

Другое отношение между внутренними углами и треугольниками создает новую концепцию тригонометрических функций . Основными тригонометрическими функциями являются синус и косинус , а также другие функции. Их можно определить как отношение между любыми двумя сторонами прямоугольного треугольника . ^[33] В разностороннем треугольнике тригонометрические функции можно использовать для нахождения неизвестной меры либо стороны, либо внутреннего угла; методы для этого используют закон синусов и закон косинусов . ^[34]

Любые три угла, которые в сумме составляют 180°, могут быть внутренними углами треугольника. Бесконечно много треугольников имеют одинаковые углы, поскольку указание углов треугольника не определяет его размер. ( Вырожденный треугольник , вершины которого лежат на одной прямой , имеет внутренние углы 0° и 180°; считается ли такая фигура треугольником, является вопросом соглашения. ^{[ требуется ссылка ]} ) Условия для трех углов , , и , каждый из которых находится в диапазоне от 0° до 180°, быть углами треугольника также можно сформулировать с помощью тригонометрических функций. Например, треугольник с углами , , и существует тогда и только тогда, когда ^[35] ${\displaystyle \alpha }$ ${\displaystyle \beta }$ ${\displaystyle \gamma }$ ${\displaystyle \alpha }$ ${\displaystyle \beta }$ ${\displaystyle \gamma }$ $${\displaystyle \cos ^{2}\alpha +\cos ^{2}\beta +\cos ^{2}\gamma +2\cos(\alpha )\cos(\beta )\cos(\gamma )=1.}$$

Сходство и соответствие

Эта диаграмма иллюстрирует геометрический принцип равенства треугольников по углу-углу-стороне: даны треугольник ABC и треугольник A'B'C', треугольник ABC равен треугольнику A'B'C' тогда и только тогда, когда: угол CAB равен углу C'A'B', а угол ABC равен углу A'B'C', а BC равен B'C'. Обратите внимание, что штриховка здесь используется для обозначения равенства углов и сторон.

Говорят, что два треугольника подобны , если каждый угол одного треугольника имеет ту же меру, что и соответствующий угол в другом треугольнике. Соответственные стороны подобных треугольников имеют длины, которые находятся в той же пропорции, и это свойство также достаточно для установления подобия. ^[36]

Вот некоторые основные теоремы о подобных треугольниках:

• Тогда и только тогда, когда одна пара внутренних углов двух треугольников имеет одинаковую меру друг с другом, и другая пара также имеет одинаковую меру друг с другом, треугольники подобны. ^[37]
• Тогда и только тогда, когда одна пара соответствующих сторон двух треугольников находится в той же пропорции, что и другая пара соответствующих сторон, и их внутренние углы имеют одинаковую меру, то треугольники подобны. ^[38] ( Внешний угол для любых двух сторон многоугольника — это внутренний угол между этими двумя сторонами.)
• Если и только если три пары соответствующих сторон двух треугольников находятся в одинаковой пропорции, то треугольники подобны. ^[b]

Два конгруэнтных треугольника имеют абсолютно одинаковый размер и форму. Все пары конгруэнтных треугольников также подобны, но не все пары подобных треугольников конгруэнтны. Если даны два конгруэнтных треугольника, все пары соответствующих внутренних углов равны по величине, и все пары соответствующих сторон имеют одинаковую длину. Это в общей сложности шесть равенств, но трех часто достаточно, чтобы доказать конгруэнтность. ^[39]

Некоторые индивидуально необходимые и достаточные условия для того, чтобы пара треугольников была конгруэнтна: ^[40]

• Постулат SAS: Две стороны одного треугольника имеют ту же длину, что и две стороны другого треугольника, а углы, заключенные между ними, имеют ту же величину.
• ASA: Два внутренних угла и сторона между ними в треугольнике имеют ту же меру и длину, что и в другом треугольнике. (Это основа съемки методом триангуляции .)
• SSS: Каждая сторона треугольника имеет ту же длину, что и соответствующая сторона другого треугольника.
• AAS: Два угла и соответствующая (не включенная) сторона в треугольнике имеют ту же меру и длину, что и в другом треугольнике. (Иногда это называется AAcorrS и тогда включает ASA выше.)

Область

Формулу площади треугольника можно доказать, разрезав две копии треугольника на части и сложив их в прямоугольник.

В евклидовой плоскости площадь определяется путем сравнения с квадратом длины стороны ⁠ ⁠ ${\displaystyle 1}$ , площадь которого равна 1. Существует несколько способов вычисления площади произвольного треугольника. Один из самых старых и простых — взять половину произведения длины одной стороны ⁠ ⁠ ${\displaystyle b}$ (основания) на соответствующую высоту ⁠ ⁠ ${\displaystyle h}$ : ^[41] $${\displaystyle T={\tfrac {1}{2}}bh.}$$

Эту формулу можно доказать, разрезав треугольник и его идентичную копию на части и переставив части в форму прямоугольника с основанием ⁠ ⁠ ${\displaystyle b}$ и высотой ⁠ ⁠ ${\displaystyle h}$ .

Применяем тригонометрию для нахождения высоты h

Если известны две стороны ⁠ ⁠ ${\displaystyle a}$ и ⁠ ⁠ ${\displaystyle b}$ и их угол между ними , то высоту можно вычислить с помощью тригонометрии, ⁠ ⁠ , поэтому площадь треугольника равна: ${\displaystyle \gamma }$ ${\displaystyle h=a\sin(\gamma )}$ $${\displaystyle T={\tfrac {1}{2}}ab\sin \gamma .}$$

Формула Герона , названная в честь Герона Александрийского , — это формула для нахождения площади треугольника по длинам его сторон , , . Пусть — полупериметр , ^[42] ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle s={\tfrac {1}{2}}(a+b+c)}$ $${\displaystyle T={\sqrt {s(s-a)(s-b)(s-c)}}.}$$

Оранжевые треугольники △ ABC имеют общее основание AB и площадь. Геометрическое место их вершин C — это прямая (штриховая зеленая), параллельная основанию. Это евклидова версия теоремы Лекселла .

Поскольку соотношения между площадями фигур в одной и той же плоскости сохраняются при аффинных преобразованиях , относительные площади треугольников в любой аффинной плоскости могут быть определены без ссылки на понятие расстояния или квадратов. В любом аффинном пространстве (включая евклидовы плоскости) каждый треугольник с тем же основанием и ориентированной площадью имеет свою вершину (третью вершину) на прямой, параллельной основанию, и их общая площадь составляет половину площади параллелограмма с тем же основанием, противолежащая сторона которого лежит на параллельной прямой. Этот аффинный подход был разработан в Книге 1 «Начал» Евклида . ^[43]

Если заданы аффинные координаты (например, декартовы координаты ) ⁠ ⁠ ${\displaystyle (x_{A},y_{A})}$ , ⁠ ⁠ ${\displaystyle (x_{B},y_{B})}$ , ⁠ ⁠ ${\displaystyle (x_{C},y_{C})}$ для вершин треугольника, его относительная ориентированная площадь может быть вычислена с помощью формулы шнуровки ,

$${\displaystyle {\begin{aligned}T&={\tfrac {1}{2}}{\begin{vmatrix}x_{A}&x_{B}&x_{C}\\y_{A}&y_{B}&y_{C}\\1&1&1\end{vmatrix}}={\tfrac {1}{2}}{\begin{vmatrix}x_{A}&x_{B}\\y_{A}&y_{B}\end{vmatrix}}+{\tfrac {1}{2}}{\begin{vmatrix}x_{B}&x_{C}\\y_{B}&y_{C}\end{vmatrix}}+{\tfrac {1}{2}}{\begin{vmatrix}x_{C}&x_{A}\\y_{C}&y_{A}\end{vmatrix}}\\&={\tfrac {1}{2}}(x_{A}y_{B}-x_{B}y_{A}+x_{B}y_{C}-x_{C}y_{B}+x_{C}y_{A}-x_{A}y_{C}),\end{aligned}}}$$

где — определитель матрицы . ${\displaystyle |\cdot |}$

Неравенство

Неравенство треугольника гласит , что сумма длин любых двух сторон треугольника должна быть больше или равна длине третьей стороны. ^[44] Треугольник с тремя заданными положительными длинами сторон существует тогда и только тогда, когда эти длины сторон удовлетворяют неравенству треугольника. ^[45] Сумма длин двух сторон может быть равна длине третьей стороны только в случае вырожденного треугольника, вершины которого лежат на одной прямой.

Жесткость

Жесткость треугольника и квадрата

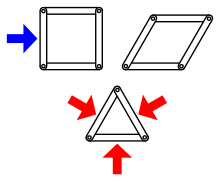
В отличие от прямоугольника, который может сжаться в параллелограмм при давлении на одну из своих точек, ^[46] треугольники прочны, потому что указание длин всех трех сторон определяет углы. ^[47] Таким образом, треугольник не изменит форму, если его стороны не согнутся, не вытянутся или не сломаются, или если его соединения не сломаются; по сути, каждая из трех сторон поддерживает две другие. Прямоугольник, напротив, больше зависит от прочности своих соединений в структурном смысле.

Треугольники прочны с точки зрения жесткости, но будучи упакованными в мозаичное расположение, треугольники не так прочны, как шестиугольники при сжатии (отсюда преобладание шестиугольных форм в природе ). Однако мозаичные треугольники все еще сохраняют превосходную прочность для консольной конструкции , поэтому в инженерии используются тетраэдрические фермы . ^{[ требуется цитата ]}

Триангуляция

Триангуляция в простом многоугольнике

Триангуляция означает разбиение любого плоского объекта на набор треугольников. Например, в триангуляции полигона полигон подразделяется на несколько треугольников, которые прикреплены ребром к ребру, со свойством, что их вершины совпадают с набором вершин полигона. ^[48] В случае простого полигона со сторонами существуют треугольники, которые разделены диагоналями. Триангуляция простого полигона имеет отношение к уху , вершине, соединенной двумя другими вершинами, диагональ между которыми полностью лежит внутри полигона. Теорема о двух ушах гласит, что каждый простой полигон, который сам по себе не является треугольником, имеет по крайней мере два уха. ^[49] ${\displaystyle n}$ ${\displaystyle n-2}$ ${\displaystyle n-3}$

Местоположение точки

Один из способов определения местоположений точек в треугольнике (или за его пределами) — поместить треугольник в произвольное место и ориентацию в декартовой плоскости и использовать декартовы координаты. Хотя этот подход удобен для многих целей, его недостаток заключается в том, что все значения координат точек зависят от произвольного расположения в плоскости. ^[50]

Две системы избегают этой особенности, так что координаты точки не изменяются при перемещении треугольника, его вращении или отражении его как в зеркале, что в любом случае дает конгруэнтный треугольник, или даже при изменении его масштаба до подобного треугольника: ^[51]

• Трилинейные координаты определяют относительные расстояния точки от сторон, так что координаты указывают, что отношение расстояния точки от первой стороны к ее расстоянию от второй стороны равно и т. д. ${\displaystyle x:y:z}$ ${\displaystyle x:y}$
• Барицентрические координаты формы определяют местоположение точки с помощью относительных весов, которые необходимо приложить к трем вершинам, чтобы уравновесить невесомый треугольник в данной точке. ${\displaystyle \alpha :\beta :\gamma }$

Связанные цифры

Фигуры, вписанные в треугольник

Как обсуждалось выше, каждый треугольник имеет уникальную вписанную окружность (incircle), которая является внутренней по отношению к треугольнику и касается всех трех сторон. Каждый треугольник имеет уникальный вписанный круг Штейнера , который является внутренней по отношению к треугольнику и касается в серединах сторон. Теорема Мардена показывает, как найти фокусы этого эллипса . ^[52] Этот эллипс имеет наибольшую площадь среди всех эллипсов, касающихся всех трех сторон треугольника. Вписанный круг Мандарта треугольника — это эллипс, вписанный в треугольник и касающийся его сторон в точках соприкосновения его вневписанных окружностей. Для любого эллипса, вписанного в треугольник , пусть фокусы будут и , тогда: ^[53] ${\displaystyle ABC}$ ${\displaystyle P}$ ${\displaystyle Q}$ $${\displaystyle {\frac {{\overline {PA}}\cdot {\overline {QA}}}{{\overline {CA}}\cdot {\overline {AB}}}}+{\frac {{\overline {PB}}\cdot {\overline {QB}}}{{\overline {AB}}\cdot {\overline {BC}}}}+{\frac {{\overline {PC}}\cdot {\overline {QC}}}{{\overline {BC}}\cdot {\overline {CA}}}}=1.}$$

Педальный треугольник и треугольник Жергонна

Из внутренней точки в референтном треугольнике ближайшие точки на трех сторонах служат вершинами педального треугольника этой точки. Если внутренняя точка является центром описанной окружности референтного треугольника, вершины педального треугольника являются серединами сторон референтного треугольника, и поэтому педальный треугольник называется треугольником средней точки или срединным треугольником. Треугольник средней точки подразделяет референтный треугольник на четыре конгруэнтных треугольника, которые подобны референтному треугольнику. ^[54]

Треугольник , входящий в исходный треугольник, имеет свои вершины в трех точках касания сторон исходного треугольника с его вписанной окружностью. ^[55] Треугольник , входящий в исходный треугольник, имеет свои вершины в точках касания вневписанных окружностей исходного треугольника с его сторонами (не продолженными). ^[56]

Каждый остроугольный треугольник имеет три вписанных квадрата (квадраты внутри него, такие, что все четыре вершины квадрата лежат на стороне треугольника, так что две из них лежат на одной стороне, и, следовательно, одна сторона квадрата совпадает с частью стороны треугольника). В прямоугольном треугольнике два квадрата совпадают и имеют вершину в прямом углу треугольника, так что прямоугольный треугольник имеет только два различных вписанных квадрата. Тупоугольный треугольник имеет только один вписанный квадрат, со стороной, совпадающей с частью самой длинной стороны треугольника. Внутри данного треугольника более длинная общая сторона связана с меньшим вписанным квадратом. Если вписанный квадрат имеет сторону длины , а треугольник имеет сторону длины , часть которой совпадает со стороной квадрата, то , , от стороны , и площадь треугольника связаны согласно ^[57] Наибольшее возможное отношение площади вписанного квадрата к площади треугольника равно 1/2, что имеет место, когда , , а высота треугольника от основания длины равна . Наименьшее возможное отношение стороны одного вписанного квадрата к стороне другого в том же нетупоугольном треугольнике равно . ^[58] Оба этих крайних случая имеют место для равнобедренного прямоугольного треугольника. ^{[ необходима ссылка ]} ${\displaystyle q_{a}}$ ${\displaystyle a}$ ${\displaystyle q_{a}}$ ${\displaystyle a}$ ${\displaystyle h_{a}}$ ${\displaystyle a}$ ${\displaystyle T}$ $${\displaystyle q_{a}={\frac {2Ta}{a^{2}+2T}}={\frac {ah_{a}}{a+h_{a}}}.}$$ ${\displaystyle a^{2}=2T}$ ${\displaystyle q=a/2}$ ${\displaystyle a}$ ${\displaystyle a}$ ${\displaystyle 2{\sqrt {2}}/3}$

Шестиугольник Лемуана, вписанный в треугольник

Шестиугольник Лемуана — это циклический шестиугольник с вершинами, заданными шестью пересечениями сторон треугольника с тремя прямыми, параллельными сторонам и проходящими через его точку симедианы . В своей простой форме или в самопересекающейся форме шестиугольник Лемуана является внутренним по отношению к треугольнику с двумя вершинами на каждой стороне треугольника. ^{[ необходима цитата ]}

Каждый выпуклый многоугольник с площадью может быть вписан в треугольник с площадью, не превышающей . Равенство имеет место только в том случае, если многоугольник является параллелограммом . ^[59] ${\displaystyle T}$ ${\displaystyle 2T}$

Фигуры, описанные около треугольника

Описанная окружность, касающаяся треугольника и описанного эллипса Штейнера

Тангенциальный треугольник исходного треугольника (кроме прямоугольного треугольника) — это треугольник, стороны которого лежат на касательных линиях к описанной окружности исходного треугольника в его вершинах. ^[60]

Как упоминалось выше, каждый треугольник имеет уникальную описанную окружность, окружность, проходящую через все три вершины, центр которой является пересечением перпендикуляров, проведенных к серединам сторон треугольника. Кроме того, каждый треугольник имеет уникальный окружность Штейнера , которая проходит через вершины треугольника и имеет свой центр в центроиде треугольника. Из всех эллипсов, проходящих через вершины треугольника, он имеет наименьшую площадь. ^[61]

Гипербола Киперта — это уникальная коническая кривая , проходящая через три вершины треугольника, его центроид и центр описанной окружности. ^[62]

Из всех треугольников, содержащихся в данном выпуклом многоугольнике , один с максимальной площадью может быть найден за линейное время; его вершины могут быть выбраны как три вершины данного многоугольника. ^[63]

Разные треугольники

Круглые треугольники

Круглые треугольники с комбинацией выпуклых и вогнутых краев.

Круговой треугольник — это треугольник с дугообразными ребрами . Ребра кругового треугольника могут быть как выпуклыми (изгибающимися наружу), так и вогнутыми (изгибающимися внутрь). ^[c] Пересечение трех дисков образует круговой треугольник, все стороны которого выпуклые. Примером кругового треугольника с тремя выпуклыми ребрами является треугольник Рело , который можно получить путем пересечения трех окружностей одинакового размера. Построение можно выполнить с помощью одного циркуля, без использования линейки, по теореме Мора–Маскерони . В качестве альтернативы его можно построить, округлив стороны равностороннего треугольника. ^[64]

Частный случай вогнутого кругового треугольника можно увидеть в псевдотреугольнике . ^[65] Псевдотреугольник — это односвязное подмножество плоскости, лежащее между тремя взаимно касательными выпуклыми областями. Эти стороны представляют собой три сглаженные кривые линии, соединяющие их конечные точки, называемые точками возврата . Любой псевдотреугольник можно разбить на множество псевдотреугольников с границами выпуклых дисков и двухкасательных линий , этот процесс известен как псевдотриангуляция. Для дисков в псевдотреугольнике разбиение дает псевдотреугольники и двухкасательные линии. ^[66] Выпуклая оболочка любого псевдотреугольника — треугольник. ^[67] ${\displaystyle n}$ ${\displaystyle 2n-2}$ ${\displaystyle 3n-3}$

Треугольник в неплоском пространстве

Гиперболический треугольник и сферический треугольник

Неплоский треугольник — это треугольник, не входящий в евклидово пространство , грубо говоря, плоское пространство. Это означает, что треугольники могут быть обнаружены также в нескольких пространствах, как в гиперболическом пространстве и сферической геометрии . Треугольник в гиперболическом пространстве называется гиперболическим треугольником , и его можно получить, рисуя на отрицательно искривленной поверхности, такой как седловая поверхность . Аналогично, треугольник в сферической геометрии называется сферическим треугольником , и его можно получить, рисуя на положительно искривленной поверхности, такой как сфера . ^[68]

Треугольники в обоих пространствах обладают свойствами, отличными от треугольников в евклидовом пространстве. Например, как упоминалось выше, внутренние углы треугольника в евклидовом пространстве всегда составляют в сумме 180°. Однако сумма внутренних углов гиперболического треугольника меньше 180°, а для любого сферического треугольника эта сумма больше 180°. ^[68] В частности, можно нарисовать треугольник на сфере так, чтобы мера каждого из его внутренних углов равнялась 90°, что в сумме составляет 270°. По теореме Жирара сумма углов треугольника на сфере равна , где — доля площади сферы, заключенная в треугольнике. ^{[69] [70]} ${\displaystyle 180^{\circ }\times (1+4f)}$ ${\displaystyle f}$

В более общих пространствах существуют теоремы сравнения, связывающие свойства треугольника в пространстве со свойствами соответствующего треугольника в модельном пространстве, таком как гиперболическое или эллиптическое пространство. ^[71] Например, пространство CAT(k) характеризуется такими сравнениями. ^[72]

Фрактальная геометрия

Фрактальные формы, основанные на треугольниках, включают в себя салфетку Серпинского и снежинку Коха . ^[73]

Ссылки

Примечания

1. Определение Евклида гласит, что равнобедренный треугольник — это треугольник, у которого ровно две равные стороны. ^[5] Согласно современному определению, он имеет по крайней мере две равные стороны, что подразумевает, что равносторонний треугольник является частным случаем равнобедренного треугольника. ^[6]
2. Опять же, во всех случаях «зеркальные отражения» также схожи.
3. Подмножество плоскости является выпуклым , если для любых двух точек этого подмножества весь отрезок прямой, соединяющий их, также лежит внутри этого подмножества.

Сноски

1. Лэнг и Мэрроу 1988, стр. 4.
2. Бирн 2013, стр. xx–xxi.
3. • Лэнг и Мэрроу 1988, стр. 4
   • Хит 1926, Определение 20
4. • Лэнг и Мэрроу 1988, стр. 4
   • Райан 2008, стр. 91
5. Хит 1926, стр. 187, Определение 20.
6. Шталь 2003, стр. 37.
7. • Райан 2008, стр. 91
   • Усискин и Гриффин 2008, стр. 4
8. • Лэнг и Мэрроу 1988, стр. 44
   • Райан 2008, стр. 96
9. Хит 1926, Определение 20, Определение 21.
10. Канди (1952).
11. Монтролл (2009), стр. 4.
12. • Ларднер (1840), стр. 46
    • Монтролл (2009), стр. 6
13. Кромвель (1997), стр. 341.
14. Холм 2010, стр. 210.
15. Холм 2010, стр. 143.
16. Лэнг и Мэрроу 1988, стр. 126–127.
17. Лэнг и Мэрроу 1988, стр. 128.
18. Англин и Ламбек 1995, с. 30.
19. Райан 2008, стр. 105.
20. • Лэнг и Мэрроу 1988, стр. 84
    • Кинг 2021, стр. 78
21. Кинг 2021, стр. 153.
22. Райан 2008, стр. 106.
23. Райан 2008, стр. 104.
24. King 2021, стр. 155.
25. Шаттшнайдер, Дорис; Кинг, Джеймс (1997). Геометрия включена: динамическое программное обеспечение в обучении, преподавании и исследованиях. Математическая ассоциация Америки. стр. 3–4. ISBN 978-0883850992.
26. Эдмондс, Аллан Л.; Хаджа, Моваффак; Мартини, Хорст (2008). «Ортоцентрические симплексы и бирегулярность». Результаты в Mathematics . 52 (1–2): 41–50. doi :10.1007/s00025-008-0294-4. MR  2430410. Хорошо известно, что инцентр евклидова треугольника лежит на его прямой Эйлера, соединяющей центроид и центр описанной окружности, тогда и только тогда, когда треугольник равнобедренный.
27. Райан 2008, стр. 102.
28. Холм 2010, стр. 240.
29. Хит 1926, Предложение 32.
30. Гоник 2024, стр. 107–109.
31. Рэмси и Рихтмайер 1995, стр. 38.
32. Гоник 2024, стр. 224–225.
33. Янг 2017, стр. 27.
34. Акслер 2012, стр. 634.
35. • Вердиян и Салас 2007
    • Лонге-Хиггинс 2003
36. Гоник 2024, стр. 157–167.
37. Гоник 2024, стр. 167.
38. Гоник 2024, стр. 171.
39. Гоник 2024, стр. 64.
40. Гоник 2024, стр. 65, 72–73, 111.
41. Райан 2008, стр. 98.
42. О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Герон Александрийский», Архив истории математики Мактьютора , Университет Сент-Эндрюс
43. Хит 1926, Предложения 36–41.
44. • Гоник 2024, стр. 80
    • Апостол 1997, стр. 34–35
45. Смит 2000, стр. 86–87.
46. Джордан и Смит 2010, стр. 834.
47. Гоник 2024, стр. 125.
48. Берг и др. 2000.
49. Мейстерс 1975.
50. Олдноу 1995.
51. • Олдноу 1995
    • Эриксон 2005, стр. 46–47
52. Калман 2008.
53. Аллер, Чжоу и Яо 2012.
54. Коксетер и Грейтцер 1967, стр. 18, 23–25.
55. Кимберлинг, Кларк (март 2008 г.). «Двадцать одна точка на окружности из девяти точек». The Mathematical Gazette . 92 (523): 29–38. doi :10.1017/S002555720018249X. ISSN  0025-5572.
56. Моисей, Питер; Кимберлинг, Чарльз (2009). «Перспективы, вызванные отражением среди треугольников» (PDF) . Журнал геометрии и графики . 13 (1): 15–24.
57. • Бейли и Детемпл 1998
    • Оксман и Ступель 2013
58. Оксман и Ступель 2013.
59. Эгглстон 2007, стр. 149–160.
60. Смит, Джефф; Леверша, Джерри (ноябрь 2007 г.). «Эйлер и геометрия треугольника». Mathematical Gazette . 91 (522): 436–452. doi :10.1017/S0025557200182087. JSTOR  40378417.
61. Сильвестр, Джон Р. (март 2017 г.). «Экстремальные площади эллипсов выпуклого четырехугольника». The Mathematical Gazette . 101 (550): 11–26. doi :10.1017/mag.2017.2.
62. Эдди, Р. Х.; Фрич, Р. (1994). «Конические сечения Людвига Киперта: всеобъемлющий урок геометрии треугольника». Mathematics Magazine . 67 (3): 188–205. doi :10.1080/0025570X.1994.11996212.
63. Чандра и Маунт 1992.
64. • Ханн 2014, стр. 34
    • Хунгербюлер 1994
65. Вахеди и ван дер Стаппен 2008, с. 73.
66. Поччиола и Вегтер 1999, стр. 259.
67. Девадосс и О'Рурк 2011, стр. 93.
68. Nielsen 2021, стр. 154.
69. Полкинг, Джон К. (25 апреля 1999 г.). "Площадь сферического треугольника. Теорема Жирара". Геометрия сферы . Получено 19 августа 2024 г.
70. Вуд, Джон. "LAS 100 — Семинар первокурсников — Осень 1996: Рассуждения с формой и количеством" . Получено 19 августа 2024 г. .
71. Бергер 2002, стр. 134–139.
72. Баллманн 1995, стр. viii+112.
73. Фрейм, Майкл; Урри, Амелия (21 июня 2016 г.). Фрактальные миры: выращенные, построенные и воображаемые. Yale University Press. стр. 21. ISBN 978-0-300-22070-4.

Цитируемые работы

• Аллер, Патрисия Р.; Чжоу, Цзюньминь; Яо, Хайшэнь (2012). «Доказательство тождества эллипса девятнадцатого века»". Математическая газета . 96 : 161–165. doi :10.1017/S0025557200004277.
• Anglin, WS; Lambek, J. (1995). Наследие Фалеса . Springer. doi :10.1007/978-1-4612-0803-7. ISBN 978-1-4612-0803-7.
• Апостол, Том М. (1997). Линейная алгебра . Wiley. ISBN 0-471-17421-1.
• Акслер, Шелдон (2012). Алгебра и тригонометрия. John Wiley & Sons . ISBN 978-0470-58579-5.
• Бейли, Герберт; Детемпл, Дуэйн (1998). «Квадраты, вписанные в углы и треугольники». Mathematics Magazine . 71 (4): 278–284. doi :10.1080/0025570X.1998.11996652.
• Баллманн, Вернер (1995). Лекции о пространствах неположительной кривизны . Семинар DMV 25. Базель: Birkhäuser Verlag. С. viii+112. ISBN 3-7643-5242-6. МР  1377265.
• Бергер, Марсель (2002). Панорамный вид римановой геометрии . Springer. doi :10.1007/978-3-642-18245-7. ISBN 978-3-642-18245-7.
• Берг, Марк Теодор де; Кревелд, Марк ван; Овермарс, Марк Х.; Шварцкопф, Отфрид (2000). Вычислительная геометрия: алгоритмы и приложения (2-е изд.). Берлин Гейдельберг: Springer. стр. 45–61. ISBN 978-3-540-65620-3.
• Бирн, Оливер (2013) [1847]. Первые шесть книг «Начал» Евклида (факсимильное издание). TASCHEN GmbH. ISBN 978-3-8365-4471-9.
• Кромвель, Питер Р. (1997). Многогранники. Cambridge University Press . ISBN 978-0-521-55432-9.
• Канди, Х. Мартин (1952). «Дельтаэдры». Mathematical Gazette . 36 : 263–266. doi :10.2307/3608204. JSTOR  3608204.
• Эгглстон, Х. Г. (2007) [1957]. Проблемы в евклидовом пространстве: приложения выпуклости . Dover Publications. стр. 149–160. ISBN 978-0-486-45846-5.
• Чандран, Шарат; Маунт, Дэвид М. (1992). «Параллельный алгоритм для вложенных и вложенных треугольников». Международный журнал вычислительной геометрии и приложений . 2 (2): 191–214. doi :10.1142/S0218195992000123. MR  1168956.
• Coxeter, HSM ; Greitzer, SL (1967). Geometry Revisited . Anneli Lax New Mathematical Library . Vol. 19. Mathematical Association of America. ISBN 978-0-88385-619-2.
• Девадосс, Сатьян Л.; О'Рурк, Джозеф (2011). Дискретная и вычислительная геометрия. Princeton University Press . ISBN 978-0-691-14553-2.
• Эриксон, Кристер (2005). Обнаружение столкновений в реальном времени. CRC Press . ISBN 978-1-55860-732-3.
• Гоник, Ларри (2024). Мультипликационное руководство по геометрии . Уильям Морроу. ISBN 978-0-06-315757-6.
• Ханн, Майкл (2014). Структура и форма в дизайне: критические идеи для творческой практики. A&C Black. ISBN 978-1-4725-8431-1.
• Хит, Томас Л. (1926). Тринадцать книг «Начал Евклида». Т. 1 (2-е изд.). Cambridge University Press. hdl :2027/uva.x001426155.Переиздание Дувра, 1956. SBN 486-60088-2 . 
• Холм, А. (2010). Геометрия: наше культурное наследие. Springer . doi :10.1007/978-3-642-14441-7. ISBN 978-3-642-14441-7.
• Хунгербюлер, Норберт (1994). «Короткое элементарное доказательство теоремы Мора-Маскерони». American Mathematical Monthly . 101 (8): 784–787. CiteSeerX  10.1.1.45.9902 . doi :10.2307/2974536. JSTOR  2974536. MR  1299166.
• Jordan, DW; Smith, P. (2010). Математические методы: Введение в инженерные, физические и математические науки (4-е изд.). Oxford University Press . ISBN 978-0-19-928201-2.
• Калман, Дэн (2008). «Элементарное доказательство теоремы Мардена». American Mathematical Monthly . 115 (4): 330–338. doi :10.1080/00029890.2008.11920532.
• Кинг, Джеймс Р. (2021). Преобразованная геометрия: геометрия евклидовой плоскости, основанная на жестких движениях. Американское математическое общество . ISBN 9781470464431.
• Ланг, Серж ; Марроу, Джин (1988). Геометрия: курс средней школы (2-е изд.). Springer. doi :10.1007/978-1-4757-2022-8. ISBN 978-1-4757-2022-8.
• Ларднер, Дионисий (1840). Трактат о геометрии и ее применении в искусствах. The Cabinet Cyclopædia. Лондон.
• Лонге-Хиггинс, Майкл С. (2003). «О соотношении радиуса вписанной окружности к радиусу описанной окружности треугольника». Mathematical Gazette . 87 : 119–120. doi :10.1017/S0025557200172249.
• Мейстерс, ГХ (1975). «У многоугольников есть уши». The American Mathematical Monthly . 82 (6): 648–651. doi :10.2307/2319703. JSTOR  2319703. MR  0367792.
• Монтролл, Джон (2009). Проектирование оригами-многогранников . AK Peters. ISBN 9781439871065.
• Нильсен, Франк (2021). «О геодезических треугольниках с прямыми углами в дуально плоском пространстве». В Нильсен, Франк (ред.). Прогресс в информационной геометрии: теория и приложения . Сигналы и коммуникационные технологии. Springer. doi : 10.1007/978-3-030-65459-7. ISBN 978-3-030-65458-0.
• Oldknow, Adrian (1995). «Computer Aided Research into Triangle Geometry». The Mathematical Gazette . 79 (485 =): 263–274. doi :10.2307/3618298. JSTOR  3618298.
• Оксман, Виктор; Ступель, Моше (2013). «Почему длины сторон квадратов, вписанных в треугольник, так близки друг к другу?». Forum Geometricorum . 13 : 113–115.
• Pocchiola, Michel; Vegter, Gert (1999). "On Polygonal Covers". В Chazelle, Bernard; Goodman, Jacob E.; Pollack, Richard (ред.). Advances in Discrete and Computational Geometry: Proceedings of the 1996 AMS-IMS-SIAM Joint Summer Research Conference, Discrete and Computational Geometry—Ten Years Later, 14-18 июля 1996 г., Mount Holyoke College. Американское математическое общество. ISBN 978-0-8218-0674-6.
• Рамсей, Арлан; Рихтмайер, Роберт Д. (1995). Введение в гиперболическую геометрию . Springer. doi :10.1007/978-1-4757-5585-5. ISBN 978-1-4757-5585-5.
• Райан, Марк (2008). Геометрия для чайников. John Wiley & Sons . ISBN 978-0-470-08946-0.
• Смит, Джеймс Т. (2000). Методы геометрии . Wiley. ISBN 0-471-25183-6.
• Шталь, Саул (2003). Геометрия от Евклида до узлов . Prentice-Hall. ISBN 0-13-032927-4.
• Usiskin, Zalman ; Griffin, Jennifer (2008). Классификация четырехугольников: исследование определения . Исследования в области математического образования. Information Age Publishing. ISBN 9781607526001.
• Vahedi, Mostafa; van der Stappen, A. Frank (2008). "Caging Polygons with Two and Three Fingers". В Akella, Srinivas; Amato, Nancy M.; Huang, Wesley; Mishra, Bud (ред.). Algorithmic Foundation of Robotics VII: Selected Contributions of the Seventh International Workshop on the Algorithmic Foundations of Robotics . doi :10.1007/978-3-540-68405-3. ISBN 978-3-540-68405-3.
• Вердиян, Вардан; Салас, Даниэль Кампос (2007). «Простые тригонометрические подстановки с широкими результатами». Математические размышления (6).
• Янг, Синтия (2017). Тригонометрия (4-е изд.). John Wiley & Sons. ISBN 978-1-119-32113-2.

Внешние ссылки

• Иванов, А. Б. (2001) [1994]. «Треугольник». Энциклопедия математики . Издательство EMS .
• Кларк Кимберлинг: Энциклопедия центров треугольников. Перечисляет около 5200 интересных точек, связанных с любым треугольником.