Белый шум

Тип сигнала при обработке сигнала

Форма сигнала гауссовского белого шума, отображенная на графике

В обработке сигналов белый шум — это случайный сигнал , имеющий одинаковую интенсивность на разных частотах , что дает ему постоянную спектральную плотность мощности . ^[1] Термин используется с этим или похожими значениями во многих научных и технических дисциплинах, включая физику , акустическую инженерию , телекоммуникации и статистическое прогнозирование . Белый шум относится к статистической модели сигналов и источников сигналов, а не к какому-либо конкретному сигналу. Белый шум получил свое название от белого света , ^[2] хотя свет, который кажется белым, обычно не имеет плоской спектральной плотности мощности в видимом диапазоне .

Изображение шума «соль и перец»

В дискретном времени белый шум — это дискретный сигнал , выборки которого рассматриваются как последовательность последовательно некоррелированных случайных величин с нулевым средним значением и конечной дисперсией ; единичная реализация белого шума — это случайный шок . В некоторых контекстах также требуется, чтобы выборки были независимыми и имели одинаковое распределение вероятностей (другими словами, независимые и одинаково распределенные случайные величины являются простейшим представлением белого шума). ^[3] В частности, если каждая выборка имеет нормальное распределение с нулевым средним значением, сигнал называется аддитивным белым гауссовым шумом . ^[4]

Образцы сигнала белого шума могут быть последовательными во времени или располагаться вдоль одного или нескольких пространственных измерений. В цифровой обработке изображений пиксели изображения белого шума обычно располагаются в прямоугольной сетке и считаются независимыми случайными величинами с равномерным распределением вероятностей на некотором интервале. Понятие может быть определено также для сигналов, распределенных по более сложным областям, таким как сфера или тор .

Звук белого шума

АнСигнал белого шума с бесконечной полосой пропускания является чисто теоретической конструкцией. Полоса пропускания белого шума ограничена на практике механизмом генерации шума, средой передачи и конечными возможностями наблюдения. Таким образом, случайные сигналы считаются белым шумом, если они наблюдаются с плоским спектром в диапазоне частот, которые имеют отношение к контексту. Для аудиосигналасоответствующимдиапазоном является полоса слышимых звуковых частот (от 20 до 20 000Гц). Такой сигнал воспринимается человеческим ухом как шипящий звук, напоминающий звук /h/ в устойчивом придыхании. С другой стороны, звукsh/ʃ/вслове ashявляется цветным шумом, поскольку имеетформантнуюструктуру. Вмузыкеиакустикетерминбелый шумможет использоваться для любого сигнала, который имеет похожий шипящий звук.

В контексте филогенетических статистических методов термин « белый шум » может относиться к отсутствию филогенетической модели в сравнительных данных. ^[5] В нетехническом контексте он иногда используется для обозначения «беспорядочных разговоров без значимого содержания». ^{[6] [7]}

Статистические свойства

Спектрограмма розового шума (слева) и белого шума (справа), показанная с линейной осью частоты (вертикальной) в зависимости от оси времени (горизонтальной)

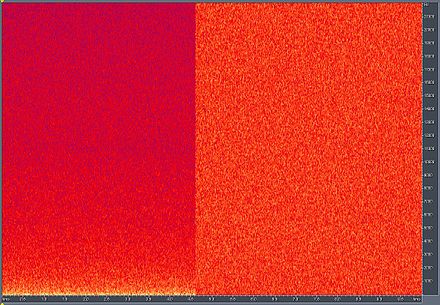
Любое распределение значений возможно (хотя оно должно иметь нулевую DC-компоненту ). Даже двоичный сигнал, который может принимать только значения 1 или -1, будет белым, если последовательность статистически некоррелирована. Шум, имеющий непрерывное распределение, например, нормальное распределение , конечно, может быть белым.

Часто ошибочно полагают, что гауссовский шум (т. е. шум с гауссовым распределением амплитуды – см. нормальное распределение ) обязательно относится к белому шуму, однако ни одно из свойств не подразумевает другое. Гауссовость относится к распределению вероятности относительно значения, в данном контексте к вероятности попадания сигнала в какой-либо определенный диапазон амплитуд, тогда как термин «белый» относится к способу распределения мощности сигнала (т. е. независимо) во времени или между частотами.

Одной из форм белого шума является обобщенная среднеквадратичная производная винеровского процесса или броуновского движения .

Обобщением для случайных элементов в бесконечномерных пространствах, таких как случайные поля , является мера белого шума .

Практические применения

Музыка

Белый шум обычно используется в производстве электронной музыки , обычно либо напрямую, либо в качестве входного сигнала для фильтра для создания других типов шумового сигнала. Он широко используется в аудиосинтезе , как правило, для воссоздания ударных инструментов, таких как тарелки или малые барабаны , которые имеют высокое содержание шума в своей частотной области. ^[8] Простым примером белого шума является несуществующая радиостанция (статическая).

Электронная инженерия

Белый шум также используется для получения импульсной характеристики электрической цепи, в частности усилителей и другого аудиооборудования. Он не используется для тестирования громкоговорителей, поскольку его спектр содержит слишком большое количество высокочастотного контента. Розовый шум , который отличается от белого шума тем, что имеет одинаковую энергию в каждой октаве, используется для тестирования преобразователей, таких как громкоговорители и микрофоны.

Вычислительная техника

Белый шум используется в качестве основы некоторых генераторов случайных чисел . Например, Random.org использует систему атмосферных антенн для генерации случайных цифровых шаблонов из источников, которые могут быть хорошо смоделированы белым шумом. ^[9]

Лечение звона в ушах

Белый шум — это распространенный источник синтетического шума, используемый для маскировки звука тиннитус-маскером . ^[10] Машины с белым шумом и другие источники белого шума продаются как усилители конфиденциальности и средства для сна (см. Музыка и сон ), а также для маскировки тиннитуса . ^[11] Marpac Sleep-Mate был первым бытовым генератором белого шума, созданным в 1962 году коммивояжером Джимом Баквалтером. ^[12] В качестве альтернативы, использование AM-радио, настроенного на неиспользуемые частоты («статика»), является более простым и экономически эффективным источником белого шума. ^[13] Однако белый шум, генерируемый обычным коммерческим радиоприемником, настроенным на неиспользуемую частоту, чрезвычайно уязвим для загрязнения паразитными сигналами, такими как соседние радиостанции, гармоники от несмежных радиостанций, электрооборудование в непосредственной близости от приемной антенны, вызывающее помехи, или даже атмосферные явления, такие как солнечные вспышки и особенно молнии.

Рабочая среда

Влияние белого шума на когнитивные функции неоднозначно. Недавно небольшое исследование показало, что фоновая стимуляция белым шумом улучшает когнитивные функции среди учащихся средних школ с синдромом дефицита внимания и гиперактивности (СДВГ), в то время как у учащихся без СДВГ производительность снижается. ^{[14] [15]} Другие исследования показывают, что он эффективен для улучшения настроения и производительности работников, маскируя фоновый шум офиса, ^[16] но снижает когнитивные способности при выполнении сложных задач по сортировке карточек. ^[17]

Аналогичным образом был проведен эксперимент на шестидесяти шести здоровых участниках, чтобы наблюдать преимущества использования белого шума в учебной среде. В ходе эксперимента участники идентифицировали различные изображения, имея на заднем плане различные звуки. В целом эксперимент показал, что белый шум действительно имеет преимущества в отношении обучения. Эксперименты показали, что белый шум немного улучшил способности участников к обучению и их память распознавания. ^[18]

Математические определения

Вектор белого шума

Случайный вектор (то есть случайная величина со значениями в R ⁿ ) называется вектором белого шума или белым случайным вектором, если каждый из его компонентов имеет ^{распределение} вероятностей с нулевым средним и конечной дисперсией [ ^{необходимо разъяснение ]} и является статистически независимым : то есть их совместное распределение вероятностей должно быть произведением распределений отдельных компонентов. ^[19]

Необходимым (но, в общем случае, недостаточным ) условием статистической независимости двух переменных является их статистическая некоррелированность ; то есть их ковариация равна нулю. Следовательно, ковариационная матрица R компонентов вектора белого шума w с n элементами должна быть диагональной матрицей размером n на n , где каждый диагональный элемент R _ii является дисперсией компонента w _i ; а корреляционная матрица должна быть единичной матрицей размером n на n .

Если, в дополнение к независимости, каждая переменная в w также имеет нормальное распределение с нулевым средним значением и той же дисперсией , w называется гауссовым вектором белого шума. В этом случае совместное распределение w является многомерным нормальным распределением ; независимость между переменными тогда подразумевает, что распределение имеет сферическую симметрию в n -мерном пространстве. Следовательно, любое ортогональное преобразование вектора приведет к гауссовскому белому случайному вектору. В частности, при большинстве типов дискретного преобразования Фурье , таких как БПФ и Хартли , преобразование W вектора w также будет гауссовым вектором белого шума; то есть n коэффициентов Фурье вектора w будут независимыми гауссовыми переменными с нулевым средним значением и той же дисперсией . ${\displaystyle \sigma ^{2}}$ ${\displaystyle \sigma ^{2}}$

Спектр мощности P случайного вектора w можно определить как ожидаемое значение квадрата модуля каждого коэффициента его преобразования Фурье W , то есть P _i = E(| W _i | ² ). Согласно этому определению, вектор гауссовского белого шума будет иметь идеально плоский спектр мощности, при этом P _i  =  σ ² для всех  i .

Если w — белый случайный вектор, но не гауссовский, его коэффициенты Фурье W _i не будут полностью независимы друг от друга; хотя для больших n и общих распределений вероятностей зависимости очень тонкие, и их попарные корреляции можно считать равными нулю.

Часто в определении белого шума используется более слабое условие статистически некоррелируемого, а не статистически независимого. Однако некоторые из обычно ожидаемых свойств белого шума (такие как плоский спектр мощности) могут не выполняться для этой более слабой версии. При этом предположении более строгая версия может быть явно названа независимым вектором белого шума. ^{[20] : стр. 60} Другие авторы используют вместо этого строго белый и слабо белый. ^[21]

Примером случайного вектора, который является гауссовым белым шумом в слабом, но не в сильном смысле, является , где — нормальная случайная величина с нулевым средним и равна или с равной вероятностью. Эти две переменные некоррелированы и по отдельности нормально распределены, но они не распределены совместно нормально и не являются независимыми. Если повернуть на 45 градусов, его два компонента по-прежнему будут некоррелированными, но их распределение больше не будет нормальным. ${\displaystyle x=[x_{1},x_{2}]}$ ${\displaystyle x_{1}}$ ${\displaystyle x_{2}}$ ${\displaystyle +x_{1}}$ ${\displaystyle -x_{1}}$ ${\displaystyle x}$

В некоторых ситуациях можно смягчить определение, разрешив каждому компоненту белого случайного вектора иметь ненулевое ожидаемое значение . В обработке изображений, особенно, где выборки обычно ограничены положительными значениями, часто принимают за половину максимального значения выборки. В этом случае коэффициент Фурье, соответствующий компоненту нулевой частоты (по сути, среднее значение ), также будет иметь ненулевое ожидаемое значение ; и спектр мощности будет плоским только на ненулевых частотах. ${\displaystyle w}$ ${\displaystyle \mu }$ ${\displaystyle \mu }$ ${\displaystyle W_{0}}$ ${\displaystyle w_{i}}$ ${\displaystyle \mu {\sqrt {n}}}$ ${\displaystyle P}$

Дискретный по времени белый шум

Стохастический процесс с дискретным временем — это обобщение случайного вектора с конечным числом компонент до бесконечного числа компонент. Стохастический процесс с дискретным временем называется белым шумом, если его среднее значение равно нулю для всех , то есть и если функция автокорреляции имеет ненулевое значение только для , то есть . ^{[ требуется цитата ] [ требуется пояснение ]} ${\displaystyle W(n)}$ ${\displaystyle W(n)}$ ${\displaystyle n}$ ${\displaystyle \operatorname {E} [W(n)]=0}$ ${\displaystyle R_{W}(n)=\operatorname {E} [W(k+n)W(k)]}$ ${\displaystyle n=0}$ ${\displaystyle R_{W}(n)=\sigma ^{2}\delta (n)}$

Непрерывный белый шум

Чтобы определить понятие белого шума в теории непрерывных во времени сигналов, необходимо заменить понятие случайного вектора на непрерывный во времени случайный сигнал, то есть случайный процесс, который генерирует функцию действительного параметра . ${\displaystyle w}$ ${\displaystyle t}$

Такой процесс называется белым шумом в самом сильном смысле, если значение для любого времени является случайной величиной, которая статистически независима от всей своей истории до . Более слабое определение требует независимости только между значениями и в каждой паре различных моментов времени и . Еще более слабое определение требует только того, чтобы такие пары и были некоррелированными. ^[22] Как и в дискретном случае, некоторые авторы принимают более слабое определение для белого шума и используют квалификатор независимый для обозначения любого из более сильных определений. Другие используют слабо белый и сильно белый, чтобы различать их. ${\displaystyle w(t)}$ ${\displaystyle t}$ ${\displaystyle t}$ ${\displaystyle w(t_{1})}$ ${\displaystyle w(t_{2})}$ ${\displaystyle t_{1}}$ ${\displaystyle t_{2}}$ ${\displaystyle w(t_{1})}$ ${\displaystyle w(t_{2})}$

Однако точное определение этих понятий не является тривиальным, поскольку некоторые величины, которые являются конечными суммами в конечном дискретном случае, должны быть заменены интегралами, которые могут не сходиться. Действительно, множество всех возможных случаев сигнала больше не является конечномерным пространством , а является бесконечномерным функциональным пространством . Более того, по любому определению сигнал белого шума должен был бы быть по существу прерывистым в каждой точке; поэтому даже самые простые операции над , такие как интегрирование по конечному интервалу, требуют продвинутого математического аппарата. ${\displaystyle w}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle w}$ ${\displaystyle w}$

Некоторые авторы ^{[ требуется цитирование ] [ требуется разъяснение ]} требуют, чтобы каждое значение было действительной случайной величиной с ожиданием и некоторой конечной дисперсией . Тогда ковариация между значениями в два момента времени и хорошо определена: она равна нулю, если моменты времени различны, и если они равны. Однако, согласно этому определению, интеграл ${\displaystyle w(t)}$ ${\displaystyle \mu }$ ${\displaystyle \sigma ^{2}}$ ${\displaystyle \mathrm {E} (w(t_{1})\cdot w(t_{2}))}$ ${\displaystyle t_{1}}$ ${\displaystyle t_{2}}$ ${\displaystyle \sigma ^{2}}$

${\displaystyle W_{[a,a+r]}=\int _{a}^{a+r}w(t)\,dt}$

на любом интервале с положительной шириной будет просто ширина, умноженная на ожидание: . ^{[ необходимо разъяснение ]} Это свойство делает концепцию неадекватной как модель сигналов белого шума ни в физическом, ни в математическом смысле. ^{[ необходимо разъяснение ]} ${\displaystyle r}$ ${\displaystyle r\mu }$

Поэтому большинство авторов определяют сигнал косвенно, указывая случайные значения для интегралов и по каждому интервалу . Однако при таком подходе значение в изолированном времени не может быть определено как действительная случайная величина ^{[ требуется цитирование ]} . Также ковариация становится бесконечной, когда ; и автокорреляционная функция должна быть определена как , где — некоторая действительная константа, а — дельта-функция Дирака . ^{[ требуется разъяснение ]} ${\displaystyle w}$ ${\displaystyle w(t)}$ ${\displaystyle |w(t)|^{2}}$ ${\displaystyle [a,a+r]}$ ${\displaystyle w(t)}$ ${\displaystyle \mathrm {E} (w(t_{1})\cdot w(t_{2}))}$ ${\displaystyle t_{1}=t_{2}}$ ${\displaystyle \mathrm {R} (t_{1},t_{2})}$ ${\displaystyle N\delta (t_{1}-t_{2})}$ ${\displaystyle N}$ ${\displaystyle \delta }$

При таком подходе обычно указывается, что интеграл по интервалу является действительной случайной величиной с нормальным распределением, нулевым средним значением и дисперсией ; а также, что ковариация интегралов , равна , где — ширина пересечения двух интервалов . Эта модель называется гауссовым белым шумовым сигналом (или процессом). ${\displaystyle W_{I}}$ ${\displaystyle w(t)}$ ${\displaystyle I=[a,b]}$ ${\displaystyle (b-a)\sigma ^{2}}$ ${\displaystyle \mathrm {E} (W_{I}\cdot W_{J})}$ ${\displaystyle W_{I}}$ ${\displaystyle W_{J}}$ ${\displaystyle r\sigma ^{2}}$ ${\displaystyle r}$ ${\displaystyle I\cap J}$ ${\displaystyle I,J}$

В математической области, известной как анализ белого шума , гауссовский белый шум определяется как стохастическое темперированное распределение, т.е. случайная величина со значениями в пространстве темперированных распределений . Аналогично случаю конечномерных случайных векторов, вероятностный закон на бесконечномерном пространстве может быть определен через его характеристическую функцию (существование и единственность гарантируются расширением теоремы Бохнера–Минлоса, которая известна под названием теоремы Бохнера–Минлоса–Сазанова); аналогично случаю многомерного нормального распределения , которое имеет характеристическую функцию ${\displaystyle w}$ ${\displaystyle {\mathcal {S}}'(\mathbb {R} )}$ ${\displaystyle {\mathcal {S}}'(\mathbb {R} )}$ ${\displaystyle X\sim {\mathcal {N}}_{n}(\mu ,\Sigma )}$

${\displaystyle \forall k\in \mathbb {R} ^{n}:\quad \mathrm {E} (\mathrm {e} ^{\mathrm {i} \langle k,X\rangle })=\mathrm {e} ^{\mathrm {i} \langle k,\mu \rangle -{\frac {1}{2}}\langle k,\Sigma k\rangle },}$

белый шум должен удовлетворять ${\displaystyle w:\Omega \to {\mathcal {S}}'(\mathbb {R} )}$

${\displaystyle \forall \varphi \in {\mathcal {S}}(\mathbb {R} ):\quad \mathrm {E} (\mathrm {e} ^{\mathrm {i} \langle w,\varphi \rangle })=\mathrm {e} ^{-{\frac {1}{2}}\|\varphi \|_{2}^{2}},}$

где — естественное сопряжение смягченного распределения с функцией Шварца , взятое по сценарию для , и . ${\displaystyle \langle w,\varphi \rangle }$ ${\displaystyle w(\omega )}$ ${\displaystyle \varphi }$ ${\displaystyle \omega \in \Omega }$ ${\displaystyle \|\varphi \|_{2}^{2}=\int _{\mathbb {R} }\vert \varphi (x)\vert ^{2}\,\mathrm {d} x}$

Математические приложения

Анализ временных рядов и регрессия

В статистике и эконометрике часто предполагается, что наблюдаемый ряд значений данных представляет собой сумму значений, сгенерированных детерминированным линейным процессом , зависящим от определенных независимых (объяснительных) переменных , и от ряда случайных шумовых значений. Затем регрессионный анализ используется для вывода параметров модельного процесса из наблюдаемых данных, например, с помощью обычного метода наименьших квадратов , и для проверки нулевой гипотезы о том, что каждый из параметров равен нулю, против альтернативной гипотезы о том, что он не равен нулю. Проверка гипотез обычно предполагает, что шумовые значения взаимно некоррелированы с нулевым средним и имеют одинаковое гауссовское распределение вероятностей — другими словами, что шум является гауссовым белым (а не просто белым). Если между шумовыми значениями, лежащими в основе различных наблюдений, существует ненулевая корреляция, то оцененные параметры модели по-прежнему являются несмещенными , но оценки их неопределенностей (такие как доверительные интервалы ) будут смещенными (не точными в среднем). Это также верно, если шум гетероскедастичен  , то есть имеет разные дисперсии для разных точек данных.

В качестве альтернативы, в подмножестве регрессионного анализа, известном как анализ временных рядов, часто нет никаких объясняющих переменных, кроме прошлых значений моделируемой переменной ( зависимой переменной ). В этом случае шумовой процесс часто моделируется как процесс скользящего среднего , в котором текущее значение зависимой переменной зависит от текущих и прошлых значений последовательного процесса белого шума.

Случайные векторные преобразования

Эти две идеи имеют решающее значение в таких приложениях, как оценка канала и выравнивание канала в коммуникациях и аудио . Эти концепции также используются в сжатии данных .

В частности, с помощью подходящего линейного преобразования (преобразования раскрашивания) белый случайный вектор может быть использован для создания небелого случайного вектора (то есть списка случайных величин), элементы которого имеют заданную ковариационную матрицу . И наоборот, случайный вектор с известной ковариационной матрицей может быть преобразован в белый случайный вектор с помощью подходящего отбеливающего преобразования .

Поколение

Белый шум может быть сгенерирован в цифровом виде с помощью цифрового сигнального процессора , микропроцессора или микроконтроллера . Генерация белого шума обычно подразумевает подачу соответствующего потока случайных чисел на цифро-аналоговый преобразователь . Качество белого шума будет зависеть от качества используемого алгоритма. ^[23]

Неформальное использование

Термин иногда используется как разговорное выражение для описания фона окружающего звука, создающего нечеткое или бесшовное волнение. Ниже приведены некоторые примеры:

• Шум от многочисленных разговоров в акустике замкнутого пространства.
• Плеонастический жаргон , используемый политиками для маскировки того, что они не хотят замечать. ^[24]
• Неприятная, резкая, диссонирующая или диссонирующая музыка , не имеющая мелодии .

Термин также может использоваться метафорически, как в романе Дона Делилло «Белый шум» (1985) , в котором исследуются симптомы современной культуры , которые объединились таким образом, чтобы затруднить для человека реализацию своих идей и личности.

Смотрите также

• Теорема Бохнера–Минлоса
• броуновский шум
• Дельта-функция Дирака
• Независимый компонентный анализ
• МойШум
• Шум (электроника)
• Шум (видео)
• Обонятельный белый
• Розовый шум
• Анализ главных компонент
• Звуковая маскировка

Ссылки

1. Картер, Манчини, Брюс, Рон (2009). Операционные усилители для всех . Texas Instruments. стр. 10–11. ISBN 978-0-08-094948-2.{{cite book}}: CS1 maint: multiple names: authors list (link)
2. Stein, Michael L. (1999). Интерполяция пространственных данных: некоторая теория для кригинга . Springer Series in Statistics. Springer. стр. 40. doi :10.1007/978-1-4612-1494-6. ISBN 978-1-4612-7166-6. Белый свет представляет собой приблизительно равную смесь всех видимых частот света, что было продемонстрировано Исааком Ньютоном.
3. Stein, Michael L. (1999). Интерполяция пространственных данных: некоторая теория для кригинга . Springer Series in Statistics. Springer. стр. 40. doi :10.1007/978-1-4612-1494-6. ISBN 978-1-4612-7166-6. Наиболее известным обобщенным процессом является белый шум, который можно рассматривать как непрерывный во времени аналог последовательности независимых и одинаково распределенных наблюдений.
4. Диболд, Франк (2007). Элементы прогнозирования (Четвертое издание).
5. Fusco, G; Garland, T. Jr; Hunt, G; Hughes, NC (2011). «Эволюция признаков развития у трилобитов». Evolution . 66 (2): 314–329. doi : 10.1111/j.1558-5646.2011.01447.x . PMID  22276531. S2CID  14726662.
6. Клэр Шипман (2005), Good Morning America : «Политическая риторика о социальном обеспечении — это белый шум». Сказано в телешоу Good Morning America на канале ABC 11 января 2005 г.
7. Дон Делилло (1985), Белый шум
8. Кларк, Декстер. «Знаете ли вы все эти секреты белого шума? (советы по созданию музыки)». www.learnhowtoproducemusic.com . Получено 25.07.2022 .
9. О'Коннелл, Памела ЛиКалзи (8 апреля 2004 г.). «Лотерейные номера и книги с голосом». The New York Times . Архивировано из оригинала 26 июля 2009 г. Получено 25 июля 2022 г.
10. Jastreboff, PJ (2000). «Терапия привыкания к тиннитусу (THT) и терапия переподготовки к тиннитусу (TRT)». Справочник по тиннитусу . Сан-Диего: Singular. С. 357–376.
11. Лопес, ХХ; Браха, А.С.; Браха, Х.С. (сентябрь 2002 г.). «Доказательно обоснованное дополнительное вмешательство при бессоннице» (PDF) . Hawaii Med J. 61 ( 9): 192, 213. PMID  12422383.
12. Грин, Пенелопа (2018-12-27). «Звук тишины». The New York Times . ISSN  0362-4331 . Получено 20 мая 2021 г.
13. Ноэлл, Кортни А.; Уильям Л. Мейерхофф (февраль 2003 г.). «Тиннитус. Диагностика и лечение этого неуловимого симптома». Гериатрия . 58 (2): 28–34. ISSN  0016-867X. PMID  12596495.
14. Содерлунд, Горан; Сверкер Сикстром; Ян Лофтеснес; Эдмунд Сонуга Барке (2010). «Влияние фонового белого шума на производительность памяти у невнимательных школьников». Поведенческие и мозговые функции . 6 (1): 55. doi : 10.1186/1744-9081-6-55 . PMC 2955636. PMID  20920224 . 
15. Сёдерлунд, Йоран; Сверкер Сикстрём; Эндрю Смарт (2007). «Слушайте шум: шум полезен для когнитивных способностей при СДВГ». Журнал детской психологии и психиатрии . 48 (8): 840–847. CiteSeerX 10.1.1.452.530 . doi :10.1111/j.1469-7610.2007.01749.x. ISSN  0021-9630. PMID  17683456. 
16. Лоуэн, Лора Дж.; Питер Сьюдфельд (1992-05-01). «Когнитивные и возбуждающие эффекты маскировки офисного шума». Окружающая среда и поведение . 24 (3): 381–395. doi :10.1177/0013916592243006. S2CID  144443528.
17. Бейкер, Мэри Энн; Деннис Х. Холдинг (июль 1993 г.). «Влияние шума и речи на выполнение когнитивных задач». Журнал общей психологии . 120 (3): 339–355. doi :10.1080/00221309.1993.9711152. ISSN  0022-1309. PMID  8138798.
18. Рауш, В. Х. (2014). Белый шум улучшает обучение, модулируя активность в дофаминергических областях среднего мозга и правой верхней височной борозде. Журнал когнитивной нейронауки, 1469-1480
19. Джеффри А. Фесслер (1998), О преобразованиях случайных векторов. Технический отчет 314, Кафедра электротехники и компьютерных наук, Мичиганский университет. ( PDF )
20. Эрик Зивот и Цзяхуэй Ванг (2006), Моделирование финансовых временных рядов с помощью S-PLUS. Второе издание. ( PDF )
21. Фрэнсис X. Диболд (2007), Элементы прогнозирования, 4-е издание. ( PDF )
22. Процесс белого шума Архивировано 11.09.2016 в Wayback Machine . Автор Econterms через About.com. Доступ 12.02.2013.
23. Мэтт Донадио. "Как генерировать белый гауссовский шум" (PDF) . Архивировано из оригинала (PDF) 2021-02-24 . Получено 2012-09-19 .
24. белый шум, Merriam-Webster , получено 2022-05-06

Внешние ссылки