Основная группа

Математическая группа гомотопических классов петель в топологическом пространстве

В математической области алгебраической топологии фундаментальная группа топологического пространства — это группа классов эквивалентности относительно гомотопии петель, содержащихся в пространстве. Она записывает информацию о базовой форме или дырках топологического пространства. Фундаментальная группа — это первая и простейшая гомотопическая группа . Фундаментальная группа — это гомотопический инвариант — топологические пространства, которые гомотопически эквивалентны (или более сильный случай гомеоморфны ), имеют изоморфные фундаментальные группы. Фундаментальная группа топологического пространства обозначается как . ${\displaystyle X}$ ${\displaystyle \pi _{1}(X)}$

Интуиция

Начните с пространства (например, поверхности ), некоторой точки в ней и всех петель, начинающихся и заканчивающихся в этой точке — пути , которые начинаются в этой точке, блуждают и в конечном итоге возвращаются в исходную точку. Две петли можно объединить очевидным образом: пройти по первой петле, затем по второй. Две петли считаются эквивалентными, если одну можно деформировать в другую, не разрывая ее. Множество всех таких петель с этим методом объединения и этой эквивалентностью между ними является фундаментальной группой для этого конкретного пространства.

История

Анри Пуанкаре определил фундаментальную группу в 1895 году в своей статье « Анализ Situs ». ^[1] Эта концепция возникла в теории римановых поверхностей , в работах Бернхарда Римана , Пуанкаре и Феликса Клейна . Она описывает свойства монодромии комплекснозначных функций, а также обеспечивает полную топологическую классификацию замкнутых поверхностей .

Определение

В этой статье X — топологическое пространство. Типичным примером является поверхность, изображенная справа. Более того, — это точка в X, называемая базовой точкой . (Как объясняется ниже, ее роль скорее вспомогательная.) Идея определения гомотопической группы состоит в том, чтобы измерить, сколько (в широком смысле) кривых на X можно деформировать друг в друга. Точное определение зависит от понятия гомотопии петель, которое объясняется в первую очередь. ${\displaystyle x_{0}}$

Гомотопия петель

Для топологического пространства X цикл ${\displaystyle x_{0}}$ , основанный на , определяется как непрерывная функция (также известная как непрерывное отображение)

${\displaystyle \gamma \colon [0,1]\to X}$

таким образом, что начальная и конечная точки равны . ${\displaystyle \gamma (0)}$ ${\displaystyle \gamma (1)}$ ${\displaystyle x_{0}}$

Гомотопия петель

Гомотопия — это непрерывная интерполяция между двумя петлями. Точнее, гомотопия между двумя петлями (базирующаяся в одной точке ) — это непрерывное отображение ${\displaystyle \gamma ,\gamma '\colon [0,1]\to X}$ ${\displaystyle x_{0}}$

${\displaystyle h\colon [0,1]\times [0,1]\to X,}$

такой что

• ${\displaystyle h(0,t)=x_{0}}$при этом начальная точка гомотопии равна для всех t (что часто рассматривается как временной параметр). ${\displaystyle t\in [0,1],}$ ${\displaystyle x_{0}}$
• ${\displaystyle h(1,t)=x_{0}}$при всем при этом конечная точка аналогично остается в для всех t . ${\displaystyle t\in [0,1],}$ ${\displaystyle x_{0}}$
• ${\displaystyle h(r,0)=\gamma (r),\,h(r,1)=\gamma '(r)}$для всех . ${\displaystyle r\in [0,1]}$

Если такая гомотопия h существует, и называются гомотопными . Отношение « гомотопно » является отношением эквивалентности , так что множество классов эквивалентности можно рассматривать: ${\displaystyle \gamma }$ ${\displaystyle \gamma '}$ ${\displaystyle \gamma }$ ${\displaystyle \gamma '}$

${\displaystyle \pi _{1}(X,x_{0}):=\{{\text{all loops }}\gamma {\text{ based at }}x_{0}\}/{\text{homotopy}}}$.

Это множество (с описанной ниже структурой группы) называется фундаментальной группой топологического пространства X в базовой точке . Целью рассмотрения классов эквивалентности петель с точностью до гомотопии, в отличие от множества всех петель (так называемого пространства петель X ) , является то, что последнее, хотя и полезно для различных целей, является довольно большим и громоздким объектом. Напротив, указанное выше частное во многих случаях более управляемо и вычислимо. ${\displaystyle x_{0}}$

Структура группы

Добавление петель

Согласно данному выше определению, это просто набор. Он становится группой (и поэтому заслуживает названия фундаментальная группа ) с помощью конкатенации циклов. Точнее, если даны два цикла , их произведение определяется как цикл ${\displaystyle \pi _{1}(X,x_{0})}$ ${\displaystyle \gamma _{0},\gamma _{1}}$

${\displaystyle \gamma _{0}\cdot \gamma _{1}\colon [0,1]\to X}$

${\displaystyle (\gamma _{0}\cdot \gamma _{1})(t)={\begin{cases}\gamma _{0}(2t)&0\leq t\leq {\tfrac {1}{2}}\\\gamma _{1}(2t-1)&{\tfrac {1}{2}}\leq t\leq 1.\end{cases}}}$

Таким образом, сначала цикл следует за циклом с «удвоенной скоростью», а затем следует с «удвоенной скоростью». ${\displaystyle \gamma _{0}\cdot \gamma _{1}}$ ${\displaystyle \gamma _{0}}$ ${\displaystyle \gamma _{1}}$

Произведение двух гомотопических классов петель и тогда определяется как . Можно показать, что это произведение не зависит от выбора представителей и, следовательно, дает хорошо определенную операцию на множестве . Эта операция превращается в группу. Ее нейтральным элементом является постоянная петля, которая остается в для всех времен t . Обратной петлей (гомотопическим классом петли) является та же петля, но пройденная в противоположном направлении. Более формально, ${\displaystyle [\gamma _{0}]}$ ${\displaystyle [\gamma _{1}]}$ ${\displaystyle [\gamma _{0}\cdot \gamma _{1}]}$ ${\displaystyle \pi _{1}(X,x_{0})}$ ${\displaystyle \pi _{1}(X,x_{0})}$ ${\displaystyle x_{0}}$

${\displaystyle \gamma ^{-1}(t):=\gamma (1-t)}$.

Учитывая три базовых цикла, произведение ${\displaystyle \gamma _{0},\gamma _{1},\gamma _{2},}$

${\displaystyle (\gamma _{0}\cdot \gamma _{1})\cdot \gamma _{2}}$

является конкатенацией этих циклов, проходящих и затем с учетверенной скоростью, и затем с удвоенной скоростью. Для сравнения, ${\displaystyle \gamma _{0}}$ ${\displaystyle \gamma _{1}}$ ${\displaystyle \gamma _{2}}$

${\displaystyle \gamma _{0}\cdot (\gamma _{1}\cdot \gamma _{2})}$

проходит те же пути (в том же порядке), но с удвоенной скоростью и с учетверенной скоростью. Таким образом, из-за разной скорости два пути не идентичны. Аксиома ассоциативности ${\displaystyle \gamma _{0}}$ ${\displaystyle \gamma _{1},\gamma _{2}}$

${\displaystyle [\gamma _{0}]\cdot \left([\gamma _{1}]\cdot [\gamma _{2}]\right)=\left([\gamma _{0}]\cdot [\gamma _{1}]\right)\cdot [\gamma _{2}]}$

поэтому решающим образом зависит от того, что пути рассматриваются с точностью до гомотопии. Действительно, оба приведенных выше композита гомотопны, например, петле, которая проходит все три петли с утроенной скоростью. Множество базовых петель с точностью до гомотопии, снабженное приведенной выше операцией, таким образом, превращается в группу. ${\displaystyle \gamma _{0},\gamma _{1},\gamma _{2}}$ ${\displaystyle \pi _{1}(X,x_{0})}$

Зависимость от базовой точки

Хотя фундаментальная группа в общем случае зависит от выбора базовой точки, оказывается, что с точностью до изоморфизма (на самом деле, даже с точностью до внутреннего изоморфизма) этот выбор не имеет значения, пока пространство X линейно связно . Поэтому для линейно связных пространств многие авторы пишут вместо ${\displaystyle \pi _{1}(X)}$ ${\displaystyle \pi _{1}(X,x_{0}).}$

Конкретные примеры

Звездообразный домен является односвязным, поскольку любую петлю можно стянуть к центру домена, обозначенному . ${\displaystyle x_{0}}$

В этом разделе перечислены некоторые основные примеры фундаментальных групп. Для начала, в евклидовом пространстве ( ) или любом выпуклом подмножестве есть только один гомотопический класс петель, и фундаментальная группа, следовательно, является тривиальной группой с одним элементом. В более общем смысле, любая звездная область – и еще более общем смысле, любое стягиваемое пространство – имеет тривиальную фундаментальную группу. Таким образом, фундаментальная группа не различает такие пространства. ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {R} ^{n},}$

2-сфера

Петля на 2-сфере (поверхность шара), стягивающаяся в точку

Путевое связное пространство, фундаментальная группа которого тривиальна, называется просто связным . Например, 2-сфера, изображенная справа, а также все многомерные сферы , являются односвязными. Рисунок иллюстрирует гомотопию, стягивающую одну конкретную петлю к постоянной петле. Эту идею можно адаптировать ко всем петлям таким образом, что есть точка , которая не находится в изображении Однако, поскольку существуют петли такие, что (построенные из кривой Пеано , например), полное доказательство требует более тщательного анализа с использованием инструментов алгебраической топологии, таких как теорема Зейферта–ван Кампена или теорема о клеточной аппроксимации . ${\displaystyle S^{2}=\left\{(x,y,z)\in \mathbb {R} ^{3}\mid x^{2}+y^{2}+z^{2}=1\right\}}$ ${\displaystyle \gamma }$ ${\displaystyle (x,y,z)\in S^{2}}$ ${\displaystyle \gamma .}$ ${\displaystyle \gamma ([0,1])=S^{2}}$

Круг

Элементы гомотопической группы окружности

Круг ( также известный как 1-сфера)

${\displaystyle S^{1}=\left\{(x,y)\in \mathbb {R} ^{2}\mid x^{2}+y^{2}=1\right\}}$

не является просто связным. Вместо этого каждый гомотопический класс состоит из всех петель, которые обвивают окружность заданное число раз (которое может быть положительным или отрицательным, в зависимости от направления обвивания). Произведение петли, которая обвивает m раз, и другой петли, которая обвивает n раз, является петлей, которая обвивает m + n раз. Следовательно, фундаментальная группа окружности изоморфна аддитивной группе целых чисел . Этот факт можно использовать для доказательства теоремы Брауэра о неподвижной точке ^[2] и теоремы Борсука–Улама в размерности 2. ^[3] ${\displaystyle (\mathbb {Z} ,+),}$

Восьмерка

Фундаментальная группа восьмерки — это свободная группа с двумя образующими a и b .

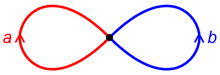
Фундаментальная группа восьмерки — это свободная группа на двух буквах. Идея доказательства заключается в следующем: выбрав базовую точку в точке пересечения двух окружностей (отмечена черным на рисунке справа), любую петлю можно разложить как ${\displaystyle \gamma }$

${\displaystyle \gamma =a^{n_{1}}b^{m_{1}}\cdots a^{n_{k}}b^{m_{k}}}$

где a и b — две петли, обвивающие каждую половину фигуры, как показано, а показатели степени — целые числа. В отличие от фундаментальной группы фигуры восьмерка не абелева : два способа составления a и b не гомотопны друг другу: ${\displaystyle n_{1},\dots ,n_{k},m_{1},\dots ,m_{k}}$ ${\displaystyle \pi _{1}(S^{1}),}$

${\displaystyle [a]\cdot [b]\neq [b]\cdot [a].}$

В более общем смысле фундаментальная группа букета из r окружностей — это свободная группа из r букв.

Фундаментальная группа клиновой суммы двух линейно связных пространств X и Y может быть вычислена как свободное произведение отдельных фундаментальных групп:

${\displaystyle \pi _{1}(X\vee Y)\cong \pi _{1}(X)*\pi _{1}(Y).}$

Это обобщает приведенные выше наблюдения, поскольку восьмерка представляет собой клиновидную сумму двух окружностей.

Фундаментальная группа плоскости, проколотой в n точках, также является свободной группой с n образующими. i -я образующая является классом петли, которая обходит i -ю проколотую точку, не обходя никаких других проколов.

Графики

Фундаментальная группа может быть определена и для дискретных структур. В частности, рассмотрим связный граф G = ( V , E ) с обозначенной вершиной v ₀ в V . Петли в G являются циклами , которые начинаются и заканчиваются в v ₀ . ^[4] Пусть T будет остовным деревом G . Каждая простая петля в G содержит ровно одно ребро в E \ T ; каждая петля в G является конкатенацией таких простых петель. Следовательно, фундаментальная группа графа является свободной группой , в которой число генераторов в точности равно числу ребер в E \ T . Это число равно | E | − | V | + 1 . ^[5]

Например, предположим, что G имеет 16 вершин, расположенных в 4 ряда по 4 вершины в каждом, с ребрами, соединяющими вершины, которые являются смежными по горизонтали или вертикали. Тогда G имеет 24 ребра в целом, и число ребер в каждом остовном дереве равно 16 − 1 = 15 , поэтому фундаментальная группа G является свободной группой с 9 генераторами. ^[6] Обратите внимание, что G имеет 9 «дырок», аналогично букету из 9 кругов, который имеет ту же фундаментальную группу.

Группы узлов

Узел -трилистник .

Группы узлов по определению являются фундаментальной группой дополнения узла , вложенного вНапример,известно, что группа узлов узла трилистника является группой кос , которая дает еще один пример неабелевой фундаментальной группы. Презентация Виртингера явно описывает группы узлов в терминах генераторов и отношений, основанных на диаграмме узла. Следовательно, группы узлов имеют некоторое применение в теории узлов для различения узлов: еслине изоморфна некоторой другой группе узловдругого узла, тоне может быть преобразована в. Таким образом, узел трилистника не может быть непрерывно преобразован в круг (также известный как неразвязный узел ), поскольку последний имеет группу узлов. Однако существуют узлы, которые не могут быть деформированы друг в друга, но имеют изоморфные группы узлов. ${\displaystyle K}$ ${\displaystyle \mathbb {R} ^{3}.}$ ${\displaystyle B_{3},}$ ${\displaystyle \pi _{1}(\mathbb {R} ^{3}\setminus K)}$ ${\displaystyle \pi _{1}(\mathbb {R} ^{3}\setminus K')}$ ${\displaystyle K'}$ ${\displaystyle K}$ ${\displaystyle K'}$ ${\displaystyle \mathbb {Z} }$

Ориентированные поверхности

Фундаментальная группа ориентируемой поверхности рода n может быть вычислена в терминах образующих и соотношений следующим образом:

${\displaystyle \left\langle A_{1},B_{1},\ldots ,A_{n},B_{n}\left|A_{1}B_{1}A_{1}^{-1}B_{1}^{-1}\cdots A_{n}B_{n}A_{n}^{-1}B_{n}^{-1}\right.\right\rangle .}$

Это включает в себя тор , относящийся к роду 1, фундаментальная группа которого

${\displaystyle \left\langle A_{1},B_{1}\left|A_{1}B_{1}A_{1}^{-1}B_{1}^{-1}\right.\right\rangle \cong \mathbb {Z} ^{2}.}$

Топологические группы

Фундаментальная группа топологической группы X (относительно базовой точки, являющейся нейтральным элементом) всегда коммутативна. В частности, фундаментальная группа группы Ли коммутативна. Фактически, структура группы на X наделяет другой структурой группы: если заданы две петли и в X , то другая петля может быть определена с помощью группового умножения в X : ${\displaystyle \pi _{1}(X)}$ ${\displaystyle \gamma }$ ${\displaystyle \gamma '}$ ${\displaystyle \gamma \star \gamma '}$

${\displaystyle (\gamma \star \gamma ')(x)=\gamma (x)\cdot \gamma '(x).}$

Эта бинарная операция на множестве всех циклов априори независима от описанной выше. Однако аргумент Экмана–Хилтона показывает, что она фактически согласуется с приведенной выше конкатенацией циклов, и, более того, что результирующая структура группы является абелевой. ^{[7] [8]} ${\displaystyle \star }$

Проверка доказательства показывает, что, в более общем случае, является абелевой для любого H-пространства X , т. е. умножение не обязательно должно иметь обратную и не обязательно быть ассоциативным. Например, это показывает, что фундаментальная группа пространства петель другого топологического пространства Y , является абелевой. Связанные с этим идеи приводят к вычислению Хайнцем Хопфом когомологий группы Ли . ${\displaystyle \pi _{1}(X)}$ ${\displaystyle X=\Omega (Y),}$

Функториальность

Если — непрерывное отображение , и с то каждая петля в с базовой точкой может быть составлена ​​с для получения петли в с базовой точкой Эта операция совместима с отношением гомотопической эквивалентности и с композицией петель. Результирующий гомоморфизм группы , называемый индуцированным гомоморфизмом , записывается как или, чаще, ${\displaystyle f\colon X\to Y}$ ${\displaystyle x_{0}\in X}$ ${\displaystyle y_{0}\in Y}$ ${\displaystyle f(x_{0})=y_{0},}$ ${\displaystyle X}$ ${\displaystyle x_{0}}$ ${\displaystyle f}$ ${\displaystyle Y}$ ${\displaystyle y_{0}.}$ ${\displaystyle \pi (f)}$

${\displaystyle f_{*}\colon \pi _{1}(X,x_{0})\to \pi _{1}(Y,y_{0}).}$

Это отображение непрерывных отображений в групповые гомоморфизмы совместимо с композицией отображений и тождественных морфизмов . На языке теории категорий формирование сопоставления топологическому пространству его фундаментальной группы является, следовательно, функтором

${\displaystyle {\begin{aligned}\pi _{1}\colon \mathbf {Top} _{*}&\to \mathbf {Grp} \\(X,x_{0})&\mapsto \pi _{1}(X,x_{0})\end{aligned}}}$

из категории топологических пространств вместе с базовой точкой в ​​категорию групп . Оказывается, этот функтор не различает отображения, гомотопные относительно базовой точки: если — непрерывные отображения с , а f и g гомотопны относительно { x ₀ }, то f _∗ = g _∗ . Как следствие, два гомотопически эквивалентных линейно связных пространства имеют изоморфные фундаментальные группы: ${\displaystyle f,g:X\to Y}$ ${\displaystyle f(x_{0})=g(x_{0})=y_{0}}$

${\displaystyle X\simeq Y\implies \pi _{1}(X,x_{0})\cong \pi _{1}(Y,y_{0}).}$

Например, включение окружности в проколотую плоскость

${\displaystyle S^{1}\subset \mathbb {R} ^{2}\setminus \{0\}}$

является гомотопической эквивалентностью и, следовательно, даёт изоморфизм их фундаментальных групп.

Фундаментальный групповой функтор переводит продукты в продукты и копроизведения в копроизведения . То есть, если X и Y связаны путями, то

${\displaystyle \pi _{1}(X\times Y,(x_{0},y_{0}))\cong \pi _{1}(X,x_{0})\times \pi _{1}(Y,y_{0})}$

и если они также локально стягиваемы , то

${\displaystyle \pi _{1}(X\vee Y)\cong \pi _{1}(X)*\pi _{1}(Y).}$

(В последней формуле обозначает клиновидную сумму выделенных топологических пространств и свободное произведение групп.) Последняя формула является частным случаем теоремы Зейферта–ван Кампена , которая утверждает, что фундаментальный групповой функтор переводит выталкивания вдоль включений в выталкивания. ${\displaystyle \vee }$ ${\displaystyle *}$

Абстрактные результаты

Как было упомянуто выше, вычисление фундаментальной группы даже относительно простых топологических пространств, как правило, не является полностью тривиальной задачей, а требует некоторых методов алгебраической топологии .

Связь с первой группой гомологии

Абелианизацию фундаментальной группы можно отождествить с первой группой гомологий пространства.

Частный случай теоремы Гуревича утверждает, что первая сингулярная группа гомологий является, говоря простым языком, ближайшим приближением к фундаментальной группе посредством абелевой группы. Более подробно, отображение гомотопического класса каждой петли в гомологический класс петли дает гомоморфизм групп ${\displaystyle H_{1}(X)}$

${\displaystyle \pi _{1}(X)\to H_{1}(X)}$

из фундаментальной группы топологического пространства X в его первую сингулярную группу гомологий Этот гомоморфизм в общем случае не является изоморфизмом, поскольку фундаментальная группа может быть неабелевой, но группа гомологий по определению всегда абелева. Однако это различие единственное: если X линейно связно, этот гомоморфизм сюръективен , а его ядром является коммутант фундаментальной группы, так что он изоморфен абелианизации фундаментальной группы. ^[9] ${\displaystyle H_{1}(X).}$ ${\displaystyle H_{1}(X)}$

Склеивание топологических пространств

Обобщая вышеприведенное утверждение, для семейства линейно связных пространств фундаментальная группа является свободным произведением фундаментальных групп ^[10] Этот факт является частным случаем теоремы Зейферта–ван Кампена , которая позволяет вычислять, в более общем виде, фундаментальные группы пространств, склеенных из других пространств. Например, 2-сфера может быть получена путем склеивания двух копий слегка перекрывающихся полусфер вдоль окрестности экватора . В этом случае теорема дает тривиальное утверждение, поскольку две полусферы стягиваемы и, следовательно, имеют тривиальную фундаментальную группу. Фундаментальные группы поверхностей, как упоминалось выше, также могут быть вычислены с помощью этой теоремы . ${\displaystyle X_{i},}$ ${\textstyle \pi _{1}\left(\bigvee _{i\in I}X_{i}\right)}$ ${\displaystyle X_{i}.}$ ${\displaystyle S^{2}}$ ${\displaystyle \pi _{1}(S^{2})}$

На языке теории категорий теорему можно кратко сформулировать, сказав, что фундаментальный групповой функтор переводит выталкивания (в категории топологических пространств) вдоль включений в выталкивания (в категории групп). ^[11]

Покрытия

Карта является покрытием: прообраз U (выделен серым цветом) является несвязным объединением копий U. Более того, это универсальное покрытие, поскольку оно стягиваемо и, следовательно, односвязно. ${\displaystyle \mathbb {R} \times [0,1]\to S^{1}\times [0,1]}$ ${\displaystyle \mathbb {R} \times [0,1]}$

Дано топологическое пространство B , непрерывное отображение

${\displaystyle f:E\to B}$

называется покрытием или E называется покрывающим пространством B , если каждая точка b в B допускает открытую окрестность U такую, что существует гомеоморфизм между прообразом U и несвязным объединением копий U (индексированным некоторым множеством I ),

${\displaystyle \varphi :\bigsqcup _{i\in I}U\to f^{-1}(U)}$

таким образом, что это стандартная проекционная карта ^[12] ${\displaystyle \pi \circ \varphi }$ ${\displaystyle \bigsqcup _{i\in I}U\to U.}$

Универсальное покрытие

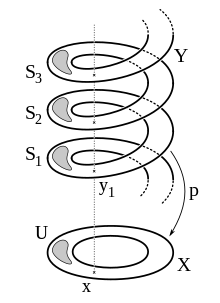
Покрытие называется универсальным, если E , в дополнение к предыдущему условию, односвязно. ^[13] Оно универсально в том смысле, что все другие покрытия могут быть построены путем подходящего определения точек в E. Зная универсальное покрытие

${\displaystyle p:{\widetilde {X}}\to X}$

топологического пространства X полезно для понимания его фундаментальной группы несколькими способами: во-первых, отождествляется с группой преобразований палубы , т. е. группой гомеоморфизмов , которые коммутируют с отображением в X , т. е. Другое отношение к фундаментальной группе заключается в том, что его можно отождествить со слоем Например, отображение ${\displaystyle \pi _{1}(X)}$ ${\displaystyle \varphi :{\widetilde {X}}\to {\widetilde {X}}}$ ${\displaystyle p\circ \varphi =p.}$ ${\displaystyle \pi _{1}(X,x)}$ ${\displaystyle p^{-1}(x).}$

${\displaystyle p:\mathbb {R} \to S^{1},\,t\mapsto \exp(2\pi it)}$

(или, что то же самое, ) является универсальным покрытием. Преобразования колоды являются картами для Это соответствует идентификации, в частности, это доказывает приведенное выше утверждение ${\displaystyle \pi :\mathbb {R} \to \mathbb {R} /\mathbb {Z} ,\ t\mapsto [t]}$ ${\displaystyle t\mapsto t+n}$ ${\displaystyle n\in \mathbb {Z} .}$ ${\displaystyle p^{-1}(1)=\mathbb {Z} ,}$ ${\displaystyle \pi _{1}(S^{1})\cong \mathbb {Z} .}$

Любое путе-связное, локально путе-связное и локально односвязное топологическое пространство X допускает универсальное покрытие. ^[14] Абстрактное построение осуществляется аналогично фундаментальной группе, взяв пары ( x , γ), где x — точка в X , а γ — гомотопический класс путей из x ₀ в x . Переход от топологического пространства к его универсальному покрытию может быть использован для понимания геометрии X . Например, теорема об униформизации показывает, что любая односвязная риманова поверхность (изоморфна) либо , либо верхней полуплоскости . ^[15] Общие римановы поверхности затем возникают как факторы групповых действий на этих трех поверхностях. ${\displaystyle S^{2},}$ ${\displaystyle \mathbb {C} ,}$

Фактор свободного действия дискретной группы G на односвязном пространстве Y имеет фундаментальную группу

${\displaystyle \pi _{1}(Y/G)\cong G.}$

Например, вещественное n -мерное вещественное проективное пространство получается как фактор n -мерной единичной сферы по антиподальному действию группы, отправляющей в Поскольку является односвязным при n ≥ 2, оно является универсальным покрытием в этих случаях, что влечет для n ≥ 2. ${\displaystyle \mathbb {R} \mathrm {P} ^{n}}$ ${\displaystyle S^{n}}$ ${\displaystyle \mathbb {Z} /2}$ ${\displaystyle x\in S^{n}}$ ${\displaystyle -x.}$ ${\displaystyle S^{n}}$ ${\displaystyle \mathbb {R} \mathrm {P} ^{n}}$ ${\displaystyle \pi _{1}(\mathbb {R} \mathrm {P} ^{n})\cong \mathbb {Z} /2}$

Группы Ли

Пусть G — связная, односвязная компактная группа Ли , например, специальная унитарная группа SU( n ), и пусть Γ — конечная подгруппа группы G . Тогда однородное пространство X  =  G / Γ имеет фундаментальную группу Γ, которая действует правым умножением на универсальном накрывающем пространстве G . Среди множества вариантов этой конструкции один из наиболее важных задается локально симметричными пространствами X  = Γ \ G / K , где

• G — некомпактная односвязная, связная группа Ли (часто полупростая ),
• K — максимальная компактная подгруппа группы G
• Γ — дискретная счетная подгруппа без кручения группы G.

В этом случае фундаментальной группой является Γ, а универсальное накрывающее пространство G / K фактически стягиваемо (по разложению Картана для групп Ли).

В качестве примера возьмем G  = SL(2, R ), K = SO(2) и Γ — любую конгруэнц-подгруппу  без кручения модулярной группы SL(2, Z ).

Из явной реализации также следует, что универсальное накрывающее пространство топологической группы линейной связности H снова является топологической группой линейной связности G. Более того, накрывающее отображение является непрерывным открытым гомоморфизмом G на H с ядром Γ, замкнутой дискретной нормальной подгруппой G :

${\displaystyle 1\to \Gamma \to G\to H\to 1.}$

Так как G — связная группа с непрерывным действием сопряжения на дискретной группе Γ, она должна действовать тривиально, так что Γ должна быть подгруппой центра G. В частности , π ₁ ( H ) = Γ — абелева группа ; это также легко увидеть напрямую, без использования покрывающих пространств. Группа G называется универсальной покрывающей группой H  .

Как предполагает универсальная накрывающая группа, существует аналогия между фундаментальной группой топологической группы и центром группы; это подробно рассматривается в Решетке накрывающих групп .

Фибрации

Расслоения предоставляют очень мощное средство для вычисления гомотопических групп. Расслоение так называемого тотального пространства и базового пространства B имеет, в частности, то свойство, что все его слоигомотопически эквивалентны и, следовательно, не могут быть различены с помощью фундаментальных групп (и высших гомотопических групп), при условии, что B линейно связно. ^[16] Поэтому пространство E можно рассматривать как « скрученное произведение» базового пространства B и слоя Большое значение расслоений для вычисления гомотопических групп вытекает из длинной точной последовательности ${\displaystyle f^{-1}(b)}$ ${\displaystyle F=f^{-1}(b).}$

${\displaystyle \dots \to \pi _{2}(B)\to \pi _{1}(F)\to \pi _{1}(E)\to \pi _{1}(B)\to \pi _{0}(F)\to \pi _{0}(E)}$

при условии, что B является линейно связным. ^[17] Термин является второй гомотопической группой B , которая определяется как множество гомотопических классов отображений из в B , по прямой аналогии с определением ${\displaystyle \pi _{2}(B)}$ ${\displaystyle S^{2}}$ ${\displaystyle \pi _{1}.}$

Если E является линейно связным и односвязным, эта последовательность сводится к изоморфизму

${\displaystyle \pi _{1}(B)\cong \pi _{0}(F)}$

что обобщает вышеприведенный факт об универсальном покрытии (что равносильно случаю, когда волокно F также дискретно). Если вместо этого F оказывается связным и односвязным, это сводится к изоморфизму

${\displaystyle \pi _{1}(E)\cong \pi _{1}(B).}$

Более того, последовательность может быть продолжена слева с помощью высших гомотопических групп трех пространств, что дает некоторый доступ к вычислению таких групп в том же ключе. ${\displaystyle \pi _{n}}$

Классические группы Ли

Такие последовательности волокон можно использовать для индуктивного вычисления фундаментальных групп компактных классических групп Ли, таких как специальная унитарная группа с Эта группа действует транзитивно на единичной сфере внутри Стабилизатор точки в сфере изоморфен Тогда можно показать ^[18], что это дает последовательность волокон ${\displaystyle \mathrm {SU} (n),}$ ${\displaystyle n\geq 2.}$ ${\displaystyle S^{2n-1}}$ ${\displaystyle \mathbb {C} ^{n}=\mathbb {R} ^{2n}.}$ ${\displaystyle \mathrm {SU} (n-1).}$

${\displaystyle \mathrm {SU} (n-1)\to \mathrm {SU} (n)\to S^{2n-1}.}$

Так как сфера имеет размерность не менее 3, это означает, ${\displaystyle n\geq 2,}$ ${\displaystyle S^{2n-1}}$

${\displaystyle \pi _{1}(S^{2n-1})\cong \pi _{2}(S^{2n-1})=1.}$

Длинная точная последовательность затем показывает изоморфизм

${\displaystyle \pi _{1}(\mathrm {SU} (n))\cong \pi _{1}(\mathrm {SU} (n-1)).}$

Так как это одна точка, то это тривиально, это показывает, что является односвязным для всех ${\displaystyle \mathrm {SU} (1)}$ ${\displaystyle \pi _{1}(\mathrm {SU} (1))}$ ${\displaystyle \mathrm {SU} (n)}$ ${\displaystyle n.}$

Фундаментальная группа некомпактных групп Ли может быть сведена к компактному случаю, поскольку такая группа гомотопна своей максимальной компактной подгруппе. ^[19] Эти методы дают следующие результаты: ^[20]

Второй метод вычисления фундаментальных групп применим ко всем связным компактным группам Ли и использует аппарат максимального тора и ассоциированную корневую систему . В частности, пусть будет максимальным тором в связной компактной группе Ли и пусть будет алгеброй Ли Экспоненциальное отображение ${\displaystyle T}$ ${\displaystyle K,}$ ${\displaystyle {\mathfrak {t}}}$ ${\displaystyle T.}$

${\displaystyle \exp :{\mathfrak {t}}\to T}$

является расслоением и, следовательно, его ядро ​​отождествляется с отображением ${\displaystyle \Gamma \subset {\mathfrak {t}}}$ ${\displaystyle \pi _{1}(T).}$

${\displaystyle \pi _{1}(T)\to \pi _{1}(K)}$

можно показать, что он сюръективен ^[21] с ядром, заданным множеством I целочисленной линейной комбинации кокорней . Это приводит к вычислению

${\displaystyle \pi _{1}(K)\cong \Gamma /I.}$^[22]

Этот метод показывает, например, что любая связная компактная группа Ли, для которой ассоциированная корневая система имеет тип ${\displaystyle G_{2}}$ , является односвязной. ^[23] Таким образом, существует (с точностью до изоморфизма) только одна связная компактная группа Ли, имеющая алгебру Ли типа ; эта группа односвязна и имеет тривиальный центр. ${\displaystyle G_{2}}$

Группа ребер-путей симплициального комплекса

Когда топологическое пространство гомеоморфно симплициальному комплексу , его фундаментальная группа может быть явно описана в терминах образующих и соотношений .

Если X — связный симплициальный комплекс, то реберный путь в X определяется как цепочка вершин, соединенных ребрами в X. Два реберных пути называются реберно эквивалентными , если один может быть получен из другого путем последовательного переключения между ребром и двумя противоположными ребрами треугольника в X. Если v — фиксированная вершина в X , реберная петля в v является реберным путем, начинающимся и заканчивающимся в v . Группа реберных путей E ( X ,  v ) определяется как множество классов реберной эквивалентности реберных петель в v , с произведением и обратным значением, определяемым конкатенацией и обращением реберных петель.

Группа реберных путей естественно изоморфна π ₁ (| X  |,  v ), фундаментальной группе геометрической реализации | X  | многообразия X . ^[24] Поскольку она зависит только от 2-скелета X ² многообразия X (то есть вершин, ребер и треугольников многообразия X ), группы π ₁ (| X  |, v ) и π ₁ (| X ² |,  v ) изоморфны.

Группа реберных путей может быть явно описана в терминах генераторов и отношений . Если T — максимальное остовное дерево в 1-скелете X , то E ( X ,  v ) канонически изоморфна группе с генераторами (ориентированными ребрами-путями X , не встречающимися в T ) и отношениями (эквивалентностями ребер, соответствующими треугольникам в X ). Похожий результат имеет место, если T заменить любым односвязным — в частности, стягиваемым — подкомплексом X . Это часто дает практический способ вычисления фундаментальных групп и может быть использовано для того, чтобы показать, что каждая конечно представленная группа возникает как фундаментальная группа конечного симплициального комплекса. Это также один из классических методов, используемых для топологических поверхностей , которые классифицируются по своим фундаментальным группам.

Универсальное покрывающее пространство конечного связного симплициального комплекса X также может быть описано непосредственно как симплициальный комплекс с использованием реберных путей. Его вершинами являются пары ( w ,γ), где w — вершина X , а γ — класс реберной эквивалентности путей из v в w . K -симплексы, содержащие ( w ,γ), естественным образом соответствуют k -симплексам, содержащим w . Каждая новая вершина u k - симплекса дает ребро wu и, следовательно, путем конкатенации, новый путь γ _u из v в u . Точки ( w ,γ) и ( u , γ _u ) являются вершинами « перенесенного» симплекса в универсальном покрывающем пространстве. Группа реберных путей действует естественным образом путем конкатенации, сохраняя симплициальную структуру, а факторпространство — это просто X.

Хорошо известно, что этот метод также может быть использован для вычисления фундаментальной группы произвольного топологического пространства. Это, несомненно, было известно Эдуарду Чеху и Жану Лере и явно появилось как замечание в статье Андре Вейля ; ^[25] различные другие авторы, такие как Лоренцо Калаби, У Вэнь-цунь и Нодар Берикашвили, также опубликовали доказательства. В простейшем случае компактного пространства X с конечным открытым покрытием, в котором все непустые конечные пересечения открытых множеств в покрытии стягиваемы, фундаментальную группу можно отождествить с группой ребер-путей симплициального комплекса, соответствующего нерву покрытия .

Реализуемость

• Каждая группа может быть реализована как фундаментальная группа связного CW-комплекса размерности 2 (или выше). Однако, как отмечено выше, только свободные группы могут встречаться как фундаментальные группы одномерных CW-комплексов (то есть графов).
• Каждая конечно представленная группа может быть реализована как фундаментальная группа компактного , связного, гладкого многообразия размерности 4 (или выше). Но существуют строгие ограничения на то, какие группы встречаются как фундаментальные группы низкоразмерных многообразий. Например, никакая свободная абелева группа ранга 4 или выше не может быть реализована как фундаментальная группа многообразия размерности 3 или ниже. Можно доказать, что каждая группа может быть реализована как фундаментальная группа компактного хаусдорфова пространства тогда и только тогда, когда не существует измеримого кардинала . ^[26]

Связанные концепции

Высшие гомотопические группы

Грубо говоря, фундаментальная группа обнаруживает одномерную дырочную структуру пространства, но не более многомерные дыры, такие как для 2-сферы. Такие "более многомерные дыры" можно обнаружить с помощью более высоких гомотопических групп , которые определяются как состоящие из гомотопических классов (сохраняющих базовую точку) отображений из в X . Например, теорема Гуревича подразумевает, что для всех n -й гомотопической группы n -сферы ${\displaystyle \pi _{n}(X)}$ ${\displaystyle S^{n}}$ ${\displaystyle n\geq 1}$

${\displaystyle \pi _{n}(S^{n})=\mathbb {Z} .}$^[27]

Как было упомянуто выше в вычислении классических групп Ли, высшие гомотопические группы могут быть актуальны даже для вычисления фундаментальных групп. ${\displaystyle \pi _{1}}$

Пространство петли

Множество базовых петель (как есть, т.е. не доведенных до гомотопии) в выделенном пространстве X , снабженном компактной открытой топологией , известно как пространство петель и обозначается как Фундаментальная группа X находится во взаимно однозначном соответствии с множеством компонент путей его пространства петель: ^[28] ${\displaystyle \Omega X.}$

${\displaystyle \pi _{1}(X)\cong \pi _{0}(\Omega X).}$

Фундаментальный группоид

Фундаментальный группоид — это вариант фундаментальной группы, который полезен в ситуациях, когда выбор базовой точки нежелателен . Он определяется путем предварительного рассмотрения категории путей в т.е. непрерывных функций ${\displaystyle x_{0}\in X}$ ${\displaystyle X,}$

${\displaystyle \gamma \colon [0,r]\to X}$,

где r — произвольное неотрицательное действительное число. Поскольку длина r является переменной в этом подходе, такие пути могут быть объединены как есть (т.е. не с точностью до гомотопии) и, следовательно, дать категорию. ^[29] Два таких пути с одинаковыми конечными точками и длиной r , соответственно r' считаются эквивалентными, если существуют действительные числа, такие что и гомотопны относительно своих конечных точек, где ^{[30] [31]} ${\displaystyle \gamma ,\gamma '}$ ${\displaystyle u,v\geqslant 0}$ ${\displaystyle r+u=r'+v}$ ${\displaystyle \gamma _{u},\gamma '_{v}\colon [0,r+u]\to X}$ ${\displaystyle \gamma _{u}(t)={\begin{cases}\gamma (t),&t\in [0,r]\\\gamma (r),&t\in [r,r+u].\end{cases}}}$

Категория путей до этого отношения эквивалентности обозначается Каждый морфизм в является изоморфизмом , обратный которому задается тем же путем, пройденным в противоположном направлении. Такая категория называется группоидом . Она воспроизводит фундаментальную группу, поскольку ${\displaystyle \Pi (X).}$ ${\displaystyle \Pi (X)}$

${\displaystyle \pi _{1}(X,x_{0})=\mathrm {Hom} _{\Pi (X)}(x_{0},x_{0})}$.

В более общем смысле можно рассмотреть фундаментальный группоид на множестве A базовых точек, выбранных в соответствии с геометрией ситуации; например, в случае окружности, которая может быть представлена ​​как объединение двух соединенных открытых множеств, пересечение которых имеет два компонента, можно выбрать одну базовую точку в каждом компоненте. Теорема ван Кампена допускает версию для фундаментальных группоидов, которая дает, например, другой способ вычисления фундаментальной группы (оида) ^[32] ${\displaystyle S^{1}.}$

Локальные системы

Вообще говоря, представления могут служить для демонстрации особенностей группы посредством ее действий на других математических объектах, часто векторных пространствах . Представления фундаментальной группы имеют очень геометрическое значение: любая локальная система (т. е. пучок на X со свойством, что локально в достаточно малой окрестности U любой точки на X ограничение F является постоянным пучком вида ) порождает так называемое представление монодромии, представление фундаментальной группы на n -мерном -векторном пространстве. Наоборот , любое такое представление на линейно связном пространстве X возникает таким образом. ^[33] Эта эквивалентность категорий между представлениями и локальными системами используется, например, при изучении дифференциальных уравнений , таких как уравнения Книжника–Замолодчикова . ${\displaystyle {\mathcal {F}}}$ ${\displaystyle {\mathcal {F}}|_{U}=\mathbb {Q} ^{n}}$ ${\displaystyle \mathbb {Q} }$ ${\displaystyle \pi _{1}(X)}$

Этальная фундаментальная группа

В алгебраической геометрии в качестве замены фундаментальной группы используется так называемая этальная фундаментальная группа. ^[34] Поскольку топология Зарисского на алгебраическом многообразии или схеме X намного грубее , чем, скажем, топология открытых подмножеств в , то больше не имеет смысла рассматривать непрерывные отображения из интервала в X. Вместо этого подход, разработанный Гротендиком, состоит в построении, рассматривая все конечные этальные покрытия X. Они служат алгебро - геометрическим аналогом покрытий с конечными слоями. ${\displaystyle \mathbb {R} ^{n},}$ ${\displaystyle \pi _{1}^{\text{et}}}$

Это дает теорию, применимую в ситуациях, когда недоступна никакая классическая топологическая интуиция большой общности, например, для многообразий, определенных над конечным полем . Кроме того, этальная фундаментальная группа поля является его ( абсолютной ) группой Галуа . С другой стороны, для гладких многообразий X над комплексными числами этальная фундаментальная группа сохраняет большую часть информации, присущей классической фундаментальной группе: первая является проконечным пополнением второй. ^[35]

Фундаментальная группа алгебраических групп

Фундаментальная группа корневой системы определяется по аналогии с вычислением для групп Ли. ^[36] Это позволяет определить и использовать фундаментальную группу полупростой линейной алгебраической группы G , которая является полезным базовым инструментом в классификации линейных алгебраических групп. ^[37]

Фундаментальная группа симплициальных множеств

Гомотопическое отношение между 1-симплексами симплициального множества X является отношением эквивалентности, если X является комплексом Кана , но не обязательно таковым в общем случае. ^[38] Таким образом, комплекс Кана может быть определен как множество гомотопических классов 1-симплексов. Фундаментальная группа произвольного симплициального множества X определяется как гомотопическая группа его топологической реализации, т. е . топологическое пространство, полученное путем склеивания топологических симплексов, как предписано структурой симплициального множества X. ^[39] ${\displaystyle \pi _{1}}$ ${\displaystyle |X|,}$

Смотрите также

• Орбифолдная фундаментальная группа
• Фундаментальная групповая схема

Примечания

1. Пуанкаре, Анри (1895). «Анализ места». Журнал Политехнической школы . (2) (на французском языке). 1 :1–123.Перевод в Poincaré, Henri (2009). "Analysis situs" (PDF) . Статьи по топологии: Analysis Situs и его пять дополнений . Перевод Джона Стиллвелла . стр. 18–99. Архивировано (PDF) из оригинала 2012-03-27.
2. Май (1999, Гл. 1, §6)
3. Мэсси (1991, гл. V, §9)
4. "Значение фундаментальной группы графа". Mathematics Stack Exchange . Получено 28.07.2020 .
5. Simon, J (2008). "Пример вычисления фундаментальной группы графа G" (PDF) . Архивировано из оригинала (PDF) 2020-07-28 . Получено 2020-07-28 .
6. "Фундаментальные группы связных графов - Mathonline". mathonline.wikidot.com . Получено 28.07.2020 .
7. Strom (2011, Задача 9.30, 9.31), Hall (2015, Упражнение 13.7)
8. Доказательство: Даны две петли в определяют отображение на умноженное поточечно в Рассмотрим гомотопическое семейство путей в прямоугольнике от до , которое начинается с горизонтального, затем вертикального пути, проходит через различные диагональные пути и заканчивается вертикальным, затем горизонтальным путем. Составление этого семейства с дает гомотопию , которая показывает, что фундаментальная группа абелева. ${\displaystyle \alpha ,\beta :[0,1]\to G}$ ${\displaystyle \pi _{1}(G),}$ ${\displaystyle A\colon [0,1]\times [0,1]\to G}$ ${\displaystyle A(s,t)=\alpha (s)\cdot \beta (t),}$ ${\displaystyle G.}$ ${\displaystyle (s,t)=(0,0)}$ ${\displaystyle (1,1)}$ ${\displaystyle A}$ ${\displaystyle \alpha *\beta \sim \beta *\alpha ,}$
9. Фултон (1995, Предложение 12.22)
10. Мэй (1999, Гл. 2, §8, Предложение)
11. Май (1999, гл. 2, §7)
12. Хэтчер (2002, §1.3)
13. Хэтчер (2002, стр. 65)
14. Хэтчер (2002, Предложение 1.36)
15. Форстер (1981, Теорема 27.9)
16. Хэтчер (2002, Предложение 4.61)
17. Хэтчер (2002, Теорема 4.41)
18. Холл (2015, Предложение 13.8)
19. Холл (2015, Раздел 13.3)
20. Холл (2015, Предложение 13.10)
21. Bump (2013, Предложение 23.7)
22. Холл (2015, Следствие 13.18)
23. Холл (2015, Пример 13.45)
24. Сингер, Изадор ; Торп, Джон А. (1967). Конспект лекций по элементарной топологии и геометрии . Springer-Verlag. стр. 98. ISBN 0-387-90202-3.
25. Андре Вейль , О дискретных подгруппах групп Ли , Annals of Mathematics 72 (1960), 369-384.
26. Адам Пшездзецкий, Измеримые кардиналы и фундаментальные группы компактных пространств, Fundamenta Mathematicae 192 (2006), 87-92 [1]
27. Хэтчер (2002, §4.1)
28. Адамс (1978, стр. 5)
29. Браун (2006, §6.1)
30. Браун (2006, §6.2)
31. Кроуэлл и Фокс (1963) используют другое определение, перепараметризируя пути до длины 1 .
32. Браун (2006, §6.7)
33. Эль Зейн и др. (2010, стр. 117, п. 1.7)
34. Гротендик и Рейно (2003).
35. Гротендик и Рейно (2003, Exposé XII, Cor. 5.2).
36. Хамфрис (1972, §13.1)
37. Хамфрис (2004, §31.1)
38. Goerss & Jardine (1999, §I.7)
39. Goerss & Jardine (1999, §I.11)

Ссылки

• Адамс, Джон Франк (1978), Бесконечные циклические пространства , Annals of Mathematics Studies, т. 90, Princeton University Press , ISBN 978-0-691-08207-3, МР  0505692
• Браун, Рональд (2006), Топология и группоиды, Booksurge, ISBN 1-4196-2722-8
• Бамп, Дэниел (2013), Группы Ли , Graduate Texts in Mathematics, т. 225 (2-е изд.), Springer, doi : 10.1007/978-1-4614-8024-2, ISBN 978-1-4614-8023-5
• Кроуэлл, Ричард Х.; Фокс, Ральф (1963), Введение в теорию узлов , Springer
• El Zein, Fouad; Suciu, Alexander I.; Tosun, Meral; Uludağ, Muhammed; Yuzvinsky, Sergey (2010), Arrangements, Local Systems and Singularities: CIMPA Summer School, Galatasaray University, Istanbul, 2007 , ISBN 978-3-0346-0208-2
• Форстер, Отто (1981), Лекции по римановым поверхностям , ISBN 0-387-90617-7
• Фултон, Уильям (1995), Алгебраическая топология: Первый курс , Springer, ISBN 9780387943275
• Goerss, Paul G.; Jardine, John F. (1999), Simplicial Homotopy Theory , Progress in Mathematics, т. 174, Базель, Бостон, Берлин: Birkhäuser, ISBN 978-3-7643-6064-1
• Гротендик, Александр ; Рейно, Мишель (2003) [1971], Séminaire de Géométrie Algébrique du Bois Marie - 1960-61 - Revêtements étales et groupe Fondamental - (SGA 1) (Documents Mathématiques 3 ) , Париж: Société Mathématique de France , стр. xviii+327 , см. Эксп. V, IX, X, arXiv : math.AG/0206203 , ISBN 978-2-85629-141-2
• Холл, Брайан С. (2015), Группы Ли, алгебры Ли и представления: элементарное введение , Graduate Texts in Mathematics, т. 222 (2-е изд.), Springer, ISBN 978-3319134666
• Хэтчер, Аллен (2002), Алгебраическая топология, Cambridge University Press, ISBN 0-521-79540-0
• Питер Хилтон и Шон Уайли , Теория гомологии , Cambridge University Press (1967) [предупреждение: эти авторы используют контрагомологию вместо когомологии ]
• Хамфрис, Джеймс Э. (2004), Линейные алгебраические группы , Graduate Texts in Mathematics, Springer, ISBN 9780387901084
• Хамфрис, Джеймс Э. (1972), Введение в алгебры Ли и теорию представлений , ISBN 0-387-90052-7
• Маундер, CRF (январь 1996 г.), Алгебраическая топология , Dover Publications , ISBN 0-486-69131-4
• Мэсси, Уильям С. (1991), Базовый курс алгебраической топологии , Springer, ISBN 038797430X
• Мэй, Дж. Питер (1999), Краткий курс алгебраической топологии , ISBN 9780226511832
• Дин Монтгомери и Лео Зиппин, Топологические группы преобразований , Interscience Publishers (1955)
• Манкрес, Джеймс Р. (2000), Топология , Prentice Hall , ISBN 0-13-181629-2
• Ротман, Джозеф (1998-07-22), Введение в алгебраическую топологию , Springer-Verlag , ISBN 0-387-96678-1
• Рубей, Елена (2014), Алгебраическая геометрия, краткий словарь , Берлин/Бостон: Вальтер Де Грюйтер, ISBN 978-3-11-031622-3
• Сейферт, Герберт ; Трелфолл, Уильям (1980), Учебник топологии , перевод Хайля, Вольфганга, Academic Press , ISBN 0-12-634850-2
• Сингер, Изадор. М.; Торп, Дж. А. (1976-12-10), Конспект лекций по элементарной топологии и геометрии , ISBN 0-387-90202-3
• Спаниер, Эдвин Х. (1989), Алгебраическая топология , Springer, ISBN 0-387-94426-5
• Штром, Джеффри (2011), Современная классическая теория гомотопии , AMS, ISBN 9780821852866

Внешние ссылки

• Вайсштейн, Эрик В. «Фундаментальная группа». Математический мир .
• Дилан Г. Л. Аллегретти, Симплициальные множества и теорема Ван Кампена: обсуждение фундаментального группоида топологического пространства и фундаментального группоида симплициального множества
• Анимации для ознакомления с фундаментальной группой Николя Делану
• Множества базовых точек и фундаментальные группоиды: обсуждение на mathoverflow
• Группоиды в математике