Дилемма заключенного

Стандартный пример в теории игр

Дилемма заключенного — это мысленный эксперимент теории игр с участием двух рациональных агентов , каждый из которых может либо сотрудничать ради взаимной выгоды, либо предать своего партнера («предать») ради индивидуальной выгоды. Дилемма возникает из того факта, что, хотя предательство рационально для каждого агента, сотрудничество приносит более высокую выгоду для каждого. Головоломка была разработана Мерриллом Флудом и Мелвином Дрешером в 1950 году во время их работы в корпорации RAND . ^[1] Они пригласили экономиста Армена Алчиана и математика Джона Уильямса сыграть сто раундов игры, заметив, что Алчиан и Уильямс часто выбирали сотрудничество. Когда его спросили о результатах, Джон Нэш заметил, что рациональное поведение в итеративной версии игры может отличаться от поведения в версии с одним раундом. Это понимание предвосхитило ключевой результат в теории игр : сотрудничество может возникать в повторяющихся взаимодействиях, даже в ситуациях, когда оно нерационально в одноразовом взаимодействии.

Альберт В. Такер позже назвал игру «дилеммой заключенного», сформулировав награды в виде тюремных сроков. ^[2] Дилемма заключенного моделирует множество реальных ситуаций, связанных со стратегическим поведением. В повседневном использовании термин «дилемма заключенного» применяется к любой ситуации, в которой два субъекта могут получить важные преимущества, сотрудничая, или пострадать, не сделав этого, но считают сложным или дорогостоящим координировать свой выбор.

Помещение

Пример матрицы выигрышей в дилемме заключенного

Уильям Паундстоун описал эту «типичную современную версию» игры в своей книге « Дилемма заключенного» 1993 года :

Два члена преступной банды арестованы и заключены в тюрьму. Каждый заключенный находится в одиночной камере без возможности поговорить или обменяться сообщениями с другим. Полиция признает, что у них недостаточно доказательств, чтобы осудить пару по основному обвинению. Они планируют приговорить обоих к году тюрьмы по менее серьезному обвинению. Одновременно полиция предлагает каждому заключенному сделку Фауста . Если он даст показания против своего партнера, он выйдет на свободу, а партнер получит три года тюрьмы по основному обвинению. О, да, есть подвох... Если оба заключенных дадут показания друг против друга, оба будут приговорены к двум годам тюрьмы. Заключенным дается немного времени, чтобы все обдумать, но ни в коем случае никто из них не может узнать, что решил другой, пока он окончательно не примет свое решение. Каждому сообщают, что другому заключенному предлагают ту же самую сделку. Каждый заключенный озабочен только своим собственным благополучием — минимизацией своего тюремного срока. ^[3]

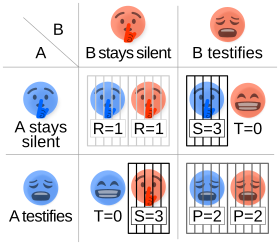
Это приводит к четырем различным возможным результатам для заключенных А и Б:

1. Если А и Б оба будут молчать, каждый из них проведет по одному году в тюрьме.
2. Если А даст показания против Б, но Б будет молчать, то А будет освобожден, а Б отсидит три года в тюрьме.
3. Если А будет молчать, а Б даст показания против А, то А проведет три года в тюрьме, а Б будет освобожден.
4. Если А и Б дадут показания друг против друга, каждый из них будет отбывать наказание в виде двух лет.

Стратегия дилеммы заключенного

Два заключенных находятся в отдельных комнатах и ​​не могут общаться друг с другом. Предполагается, что оба заключенных понимают суть игры, не имеют лояльности друг к другу и не будут иметь возможности для возмездия или вознаграждения вне игры. Нормальная игра показана ниже: ^[4]

Независимо от того, что решит другой, каждый заключенный получает более высокую награду, предав другого («предательство»). Рассуждение включает анализ лучших ответов обоих игроков : B будет либо сотрудничать, либо предать. Если B будет сотрудничать, A должен предать, потому что выйти на свободу лучше, чем отсидеть 1 год. Если B предаст, A также должен предать, потому что отсидеть 2 года лучше, чем отсидеть 3. Так что, в любом случае, A должен предать, поскольку предательство — лучший ответ A независимо от стратегии B. Параллельное рассуждение покажет, что B должен предать.

Дезертирство всегда приводит к лучшему выигрышу, чем сотрудничество, поэтому это строго доминирующая стратегия для обоих игроков. Взаимное дезертирство является единственным сильным равновесием Нэша в игре. Поскольку коллективно идеальный результат взаимного сотрудничества иррационален с точки зрения эгоизма, это равновесие Нэша не является эффективным по Парето .

Обобщенная форма

Структура традиционной дилеммы заключенного может быть обобщена из ее первоначальной установки заключенного. Предположим, что два игрока представлены цветами красный и синий, и что каждый игрок выбирает либо «сотрудничать», либо «предать».

Если оба игрока сотрудничают, они оба получают вознаграждение за сотрудничество. Если оба игрока предают, они оба получают выплату наказания . Если Синий предает, а Красный сотрудничает, то Синий получает выплату искушения , в то время как Красный получает выплату «лоха», . Аналогично, если Синий сотрудничает, а Красный предает, то Синий получает выплату искушения , в то время как Красный получает выплату искушения . ${\displaystyle R}$ ${\displaystyle P}$ ${\displaystyle T}$ ${\displaystyle S}$ ${\displaystyle S}$ ${\displaystyle T}$

Это можно выразить в нормальной форме :

и чтобы игра была игрой «дилемма заключенного» в строгом смысле, для выигрышей должно выполняться следующее условие:

⁠ ⁠ ${\displaystyle T>R>P>S}$

Платежное отношение ⁠ ⁠ ${\displaystyle R>P}$ подразумевает, что взаимное сотрудничество превосходит взаимное предательство, в то время как платежные отношения ⁠ ⁠ ${\displaystyle T>R}$ и ⁠ ⁠ ${\displaystyle P>S}$ подразумевают, что предательство является доминирующей стратегией для обоих агентов.

Повторяющаяся дилемма заключенного

Если два игрока разыгрывают дилемму заключенного более одного раза подряд, помнят предыдущие действия своего противника и имеют право соответствующим образом менять свою стратегию, то игра называется итерированной дилеммой заключенного.

В дополнение к общей форме, описанной выше, итеративная версия также требует, чтобы ⁠ ⁠ ${\displaystyle 2R>T+S}$ не допускалось попеременное сотрудничество и предательство, дающее большую выгоду, чем взаимное сотрудничество.

Итерированная дилемма заключенного является основополагающей для некоторых теорий человеческого сотрудничества и доверия. Предполагая, что игра эффективно моделирует транзакции между двумя людьми, требующие доверия, кооперативное поведение в популяциях может быть смоделировано многопользовательской итерированной версией игры. В 1975 году Грофман и Пул оценили количество научных статей, посвященных ей, в более чем 2000. Итерированную дилемму заключенного также называют « игрой мир-война ». ^{[5] [6]}

Общая стратегия

Если итерированная дилемма заключенного разыгрывается конечное число раз и оба игрока знают это, то доминирующая стратегия и равновесие Нэша — предать во всех раундах. Доказательство индуктивное : один может предать на последнем ходу, так как у противника не будет возможности позже отомстить. Поэтому оба предают на последнем ходу. Таким образом, игрок может предать на предпоследнем ходу, так как противник предаст на последнем, независимо от того, что будет сделано, и так далее. То же самое применимо, если длина игры неизвестна, но имеет известный верхний предел. ^{[ необходима цитата ]}

Для возникновения сотрудничества между рациональными игроками число раундов должно быть неизвестным или бесконечным. В этом случае «всегда предавай» может уже не быть доминирующей стратегией. Как показал Роберт Ауманн в статье 1959 года, ^[7] рациональные игроки, многократно взаимодействующие в течение неопределенно длинных игр, могут поддерживать сотрудничество. В частности, игрок может быть менее склонен к сотрудничеству, если его оппонент не сотрудничал много раз, что вызывает разочарование. И наоборот, с течением времени вероятность сотрудничества имеет тенденцию расти из-за установления «молчаливого соглашения» между участвующими игроками. В экспериментальных ситуациях сотрудничество может происходить даже тогда, когда оба участника знают, сколько итераций будет сыграно. ^[8]

Согласно экспериментальному исследованию 2019 года в American Economic Review , в котором проверялось, какие стратегии использовали реальные субъекты в повторяющихся ситуациях дилеммы заключенного с идеальным мониторингом, большинство выбранных стратегий всегда были предать, зуб за зуб и мрачный триггер . Какую стратегию выбирали субъекты, зависело от параметров игры. ^[9]

Турнир Аксельрода и условия успешной стратегии

Интерес к итерируемой дилемме заключенного был подогрет Робертом Аксельродом в его книге 1984 года «Эволюция сотрудничества» , в которой он сообщает о турнире, который он организовал по N -шаговой дилемме заключенного (с фиксированным N ), в котором участники должны были многократно выбирать свою стратегию и помнить свои предыдущие встречи. Аксельрод пригласил коллег-ученых со всего мира разработать компьютерные стратегии для участия в турнире по итерируемой дилемме заключенного. Программы, которые были представлены, сильно различались по алгоритмической сложности, начальной враждебности, способности к прощению и т. д.

Аксельрод обнаружил, что когда эти встречи повторялись в течение длительного периода времени со многими игроками, каждый из которых имел разные стратегии, жадные стратегии, как правило, давали очень плохие результаты в долгосрочной перспективе, в то время как более альтруистичные стратегии давали лучшие результаты, если судить исключительно по личной заинтересованности. Он использовал это, чтобы показать возможный механизм эволюции альтруистического поведения из механизмов, которые изначально были чисто эгоистичными, путем естественного отбора .

Победившей детерминированной стратегией была t-to-tat , разработанная и представленная на турнире Анатолем Рапопортом . Это была самая простая из всех представленных программ, содержащая всего четыре строки BASIC [ ^10] и выигравшая соревнование. Стратегия заключается в том, чтобы просто сотрудничать на первой итерации игры; после этого игрок делает то, что сделал его или ее противник на предыдущем ходу. ^[11] В зависимости от ситуации, немного лучшей стратегией может быть «t-to-tat с прощением»: когда противник предает, на следующем ходу игрок иногда все равно сотрудничает, с небольшой вероятностью (около 1–5%, в зависимости от состава противников). Это позволяет время от времени восстанавливаться после попадания в цикл предательств.

Проанализировав наиболее результативные стратегии, Аксельрод сформулировал несколько условий, необходимых для успеха стратегии: ^[12]

• Nice : Стратегия не будет первой, кто предаст (иногда это называют "оптимистичным" алгоритмом ^{[ кем? ]} ), т.е. она не будет "обманывать" своего противника по чисто личным причинам первой. Почти все стратегии с наивысшими результатами были хорошими. ^[a]
• Возмездие : Стратегия должна иногда возмездия. Примером невозмездной стратегии является Always Cooperate, очень плохой выбор, который часто будет использоваться «плохими» стратегиями.
• Прощающий : Успешные стратегии должны быть прощающими. Хотя игроки будут мстить, они снова будут сотрудничать, если противник не продолжит предательство. Это может остановить длинные серии мести и контр-мести, максимизируя очки. ^[b]
• Независтливый : Стратегия не должна стремиться набрать больше очков, чем соперник.

В отличие от игры «дилемма заключенного», оптимальная стратегия в итерированной дилемме заключенного зависит от стратегий вероятных противников и того, как они будут реагировать на предательства и сотрудничество. Например, если популяция полностью состоит из игроков, которые всегда предают, за исключением одного, который следует стратегии «око за око», этот человек находится в небольшом невыгодном положении из-за проигрыша на первом ходу. В такой популяции оптимальной стратегией является предательство каждый раз. В более общем смысле, учитывая популяцию с определенным процентом всегда предающих, а остальные игроки являются игроками «око за око», оптимальная стратегия зависит от процента и количества сыгранных итераций. ^{[ необходима цитата ]}

Другие стратегии

Вывод оптимальной стратегии обычно осуществляется двумя способами:

• Байесовское равновесие Нэша : если можно определить статистическое распределение противоположных стратегий, то оптимальную контрстратегию можно вывести аналитически. ^[c]
• Были проведены симуляции популяций методом Монте-Карло , в которых особи с низкими показателями вымирают, а особи с высокими показателями размножаются ( генетический алгоритм для поиска оптимальной стратегии). Смесь алгоритмов в конечной популяции обычно зависит от смеси в исходной популяции. Введение мутации (случайное изменение во время размножения) уменьшает зависимость от исходной популяции; эмпирические эксперименты с такими системами, как правило, приводят к игрокам, действующим по принципу «око за око», ^{[ необходимо разъяснение ],} но не существует аналитических доказательств того, что это будет происходить всегда. ^[16]

В стратегии, называемой « выиграть-остаться, проиграть-переключиться» , столкнувшись с неспособностью сотрудничать, игрок меняет стратегию на следующем ходу. ^[17] При определенных обстоятельствах ^{[ уточнить ]} Павлов превосходит все другие стратегии, предоставляя преимущественное право игрокам, использующим похожую стратегию.

Хотя око за око считается самой надежной базовой стратегией, команда из Университета Саутгемптона в Англии представила более успешную стратегию на 20-летнем юбилейном соревновании по итерационной дилемме заключенного. Она основывалась на сговоре между программами для достижения наибольшего количества очков для одной программы. Университет представил на соревнование 60 программ, которые были разработаны для распознавания друг друга с помощью серии из пяти-десяти ходов в начале. ^[18] После того, как это распознавание было сделано, одна программа всегда сотрудничала, а другая всегда предавалась, гарантируя максимальное количество очков для предателя. Если программа понимала, что играет с игроком не из Саутгемптона, она постоянно предавалась, пытаясь минимизировать счет конкурирующей программы. В результате результаты турнира по дилемме заключенных 2004 года показывают стратегии Университета Саутгемптона на первых трех местах (и ряде позиций ближе к концу), несмотря на то, что у них было меньше побед и гораздо больше поражений, чем у стратегии GRIM. Стратегия «Саутгемптона» использует тот факт, что в этом конкретном соревновании допускалось несколько заявок, и что результативность команды оценивалась по результативности игрока, набравшего наибольшее количество очков (это означает, что использование игроков, готовых на самопожертвование, было формой минимакса ).

Из-за этого нового правила это соревнование также имеет мало теоретического значения при анализе одноагентных стратегий по сравнению с основополагающим турниром Аксельрода. Но оно дало основу для анализа того, как достичь кооперативных стратегий в многоагентных фреймворках, особенно при наличии шума.

Задолго до того, как был сыгран этот турнир по новым правилам, Докинз в своей книге «Эгоистичный ген » указал на возможность выигрыша таких стратегий, если бы допускались множественные заявки, но заметил, что Аксельрод, скорее всего, не допустил бы их, если бы они были поданы. Он также опирается на обход правила, согласно которому между игроками не допускается никакое общение, что, возможно, и сделали программы Саутгемптона с их запрограммированным «танцем из десяти ходов» для узнавания друг друга, что подтверждает, насколько ценным может быть общение в изменении баланса игры.

Даже без неявного сговора между стратегиями программного обеспечения , t-for-tat не всегда является абсолютным победителем любого турнира; точнее, его долгосрочные результаты в серии турниров превосходят его конкурентов, но это не означает, что он является самым успешным в краткосрочной перспективе. То же самое относится к t-for-tat с прощением и другим оптимальным стратегиям.

Это также можно проиллюстрировать с помощью дарвиновской симуляции ESS . В такой симуляции «зуб за зуб» почти всегда будет доминировать, хотя отвратительные стратегии будут то появляться, то исчезать из популяции, поскольку популяция «зуб за зуб» проницаема для невозмещающих хороших стратегий, которые, в свою очередь, являются легкой добычей для отвратительных стратегий. Докинз показал, что здесь никакая статическая смесь стратегий не образует устойчивого равновесия, и система всегда будет колебаться между границами. ^{[ требуется цитата ]}

Стохастическая итеративная дилемма заключенного

В стохастической итерационной игре дилемма заключенного стратегии определяются в терминах «вероятностей сотрудничества». ^[19] В столкновении между игроком X и игроком Y стратегия X определяется набором вероятностей P сотрудничества с Y. P является функцией результатов их предыдущих столкновений или некоторого их подмножества. Если P является функцией только их последних n столкновений, это называется стратегией «памяти-n». Стратегия памяти-1 определяется четырьмя вероятностями сотрудничества: , где P _cd — вероятность того, что X будет сотрудничать в текущем столкновении, учитывая, что предыдущее столкновение характеризовалось сотрудничеством X и предательством Y. Если каждая из вероятностей равна 1 или 0, стратегия называется детерминированной. Примером детерминированной стратегии является стратегия «око за око», записанная как , в которой X отвечает так же, как Y в предыдущем столкновении. Другой — стратегия «выиграл-остался, проиграл», записанная как . Было показано, что для любой стратегии памяти-n существует соответствующая стратегия памяти-1, которая дает те же статистические результаты, поэтому необходимо рассматривать только стратегии памяти-1. ^[19] ${\displaystyle P=\{P_{cc},P_{cd},P_{dc},P_{dd}\}}$ ${\displaystyle P=\{1,0,1,0\}}$ ${\displaystyle P=\{1,0,0,1\}}$

Если определяется как указанный выше 4-элементный вектор стратегии X и как 4-элементный вектор стратегии Y (где индексы взяты с точки зрения Y), то для X может быть определена матрица перехода M , чей ij -й элемент представляет собой вероятность того, что исход конкретной встречи между X и Y будет j, учитывая, что предыдущая встреча была i , где i и j являются одними из четырех индексов результата: cc , cd , dc или dd . Например, с точки зрения X вероятность того, что исход текущей встречи будет cd, учитывая, что предыдущая встреча была cd, равна . Согласно этим определениям, итерированная дилемма заключенного квалифицируется как стохастический процесс , а M является стохастической матрицей , что позволяет применять всю теорию стохастических процессов. ^[19] ${\displaystyle P}$ ${\displaystyle Q=\{Q_{cc},Q_{cd},Q_{dc},Q_{dd}\}}$ ${\displaystyle M_{cd,cd}=P_{cd}(1-Q_{dc})}$

Одним из результатов стохастической теории является то, что существует стационарный вектор v для матрицы v такой, что . Без потери общности можно указать, что v нормализован так, что сумма его четырех компонентов равна единице. ij -й элемент в даст вероятность того, что исход столкновения между X и Y будет j , учитывая, что столкновение n шагов назад было i . В пределе, когда n стремится к бесконечности, M будет сходиться к матрице с фиксированными значениями, давая долгосрочные вероятности столкновения, производящего j , независимо от i . Другими словами, строки будут идентичны, давая долгосрочные равновесные вероятности результата итерированной дилеммы заключенного без необходимости явной оценки большого количества взаимодействий. Можно видеть, что v является стационарным вектором для и в частности , так что каждая строка будет равна v . Таким образом, стационарный вектор определяет равновесные вероятности исхода для X . Определив и как краткосрочные векторы выплат для исходов { cc,cd,dc,dd } (с точки зрения X), равновесные выплаты для X и Y теперь можно указать как и , что позволяет сравнить две стратегии P и Q на предмет их долгосрочных выплат. ${\displaystyle v\cdot M=v}$ ${\displaystyle M^{n}}$ ${\displaystyle M^{\infty }}$ ${\displaystyle M^{n}}$ ${\displaystyle M^{\infty }}$ ${\displaystyle M^{\infty }}$ ${\displaystyle S_{x}=\{R,S,T,P\}}$ ${\displaystyle S_{y}=\{R,T,S,P\}}$ ${\displaystyle s_{x}=v\cdot S_{x}}$ ${\displaystyle s_{y}=v\cdot S_{y}}$

Стратегии с нулевым детерминантом

Взаимосвязь между стратегиями нулевого детерминанта (ZD), сотрудничества и отказа в итерируемой дилемме заключенного (итерируемая дилемма заключенного)

В 2012 году Уильям Х. Пресс и Фримен Дайсон опубликовали новый класс стратегий для стохастической итерированной дилеммы заключенного, названных стратегиями «нулевого детерминанта» (ZD). ^[19] Долгосрочные выигрыши для встреч между X и Y можно выразить как определитель матрицы, которая является функцией двух стратегий и краткосрочных векторов выигрышей: и , которые не включают стационарный вектор v . Поскольку функция определителя линейна по , отсюда следует, что (где ). Любые стратегии, для которых по определению являются стратегией ZD, и долгосрочные выигрыши подчиняются соотношению . ${\displaystyle s_{x}=D(P,Q,S_{x})}$ ${\displaystyle s_{y}=D(P,Q,S_{y})}$ ${\displaystyle s_{y}=D(P,Q,f)}$ ${\displaystyle f}$ ${\displaystyle \alpha s_{x}+\beta s_{y}+\gamma =D(P,Q,\alpha S_{x}+\beta S_{y}+\gamma U)}$ ${\displaystyle U=\{1,1,1,1\}}$ ${\displaystyle D(P,Q,\alpha S_{x}+\beta S_{y}+\gamma U)=0}$ ${\displaystyle \alpha s_{x}+\beta s_{y}+\gamma =0}$

Око за око — это стратегия ZD, которая является «честной» в том смысле, что не получает преимущества над другим игроком. Но пространство ZD также содержит стратегии, которые в случае двух игроков могут позволить одному игроку в одностороннем порядке установить счет другого игрока или, в качестве альтернативы, заставить эволюционного игрока достичь выигрыша на некоторый процент ниже, чем его собственный. Вымогаемый игрок может предать, но тем самым навредить себе, получив более низкий выигрыш. Таким образом, решения вымогательства превращают итеративную дилемму заключенного в своего рода ультимативную игру . В частности, X может выбрать стратегию, для которой , в одностороннем порядке устанавливая s _y на определенное значение в определенном диапазоне значений, независимо от стратегии Y , предлагая возможность для X «вымогать» игрока Y ( и наоборот). Но если X пытается установить s _x на определенное значение, диапазон возможностей намного меньше, состоящий только из полного сотрудничества или полного предательства. ^[19] ${\displaystyle D(P,Q,\beta S_{y}+\gamma U)=0}$

Расширением итерированной дилеммы заключенного является эволюционная стохастическая итерированная дилемма заключенного, в которой относительное обилие конкретных стратегий может меняться, при этом более успешные стратегии относительно увеличиваются. Этот процесс может быть осуществлен путем имитации менее успешными игроками более успешных стратегий или путем исключения менее успешных игроков из игры, при этом умножая более успешных. Было показано, что несправедливые стратегии ZD не являются эволюционно стабильными . Ключевая интуиция заключается в том, что эволюционно стабильная стратегия должна не только иметь возможность вторгаться в другую популяцию (что могут делать вымогательские стратегии ZD), но и должна хорошо работать против других игроков того же типа (что вымогательские игроки ZD делают плохо, потому что они уменьшают излишек друг друга). ^[20]

Теория и моделирование подтверждают, что за пределами критического размера популяции вымогательство ZD проигрывает в эволюционной конкуренции более кооперативным стратегиям, и в результате средний выигрыш в популяции увеличивается, когда популяция больше. Кроме того, есть некоторые случаи, в которых вымогатели могут даже катализировать сотрудничество, помогая вырваться из противостояния между единообразными перебежчиками и агентами «выиграл-остался, проиграл-переключился» . ^[21]

В то время как вымогательские стратегии ZD нестабильны в больших популяциях, другой класс стратегий ZD, называемый «щедрыми», является и стабильным, и надежным. Когда популяция не слишком мала, эти стратегии могут вытеснить любую другую стратегию ZD и даже хорошо работать против широкого спектра общих стратегий для итерированной дилеммы заключенного, включая «выиграть-остаться», «проиграть-переключиться». Это было доказано специально для игры в пожертвования Александром Стюартом и Джошуа Плоткиным в 2013 году. ^[22] Щедрые стратегии будут сотрудничать с другими кооперативными игроками, и в случае предательства щедрый игрок теряет больше полезности, чем его соперник. Щедрые стратегии являются пересечением стратегий ZD и так называемых «хороших» стратегий, которые были определены Итаном Эйкином как те, для которых игрок отвечает на прошлое взаимное сотрудничество будущим сотрудничеством и делит ожидаемые выигрыши поровну, если он получает по крайней мере кооперативный ожидаемый выигрыш. ^[23] Среди хороших стратегий подмножество щедрых (ZD) работает хорошо, когда популяция не слишком мала. Если популяция очень мала, то, как правило, доминируют стратегии дезертирства. ^[22]

Непрерывно повторяющаяся дилемма заключенного

Большая часть работы по итерируемой дилемме заключенного была сосредоточена на дискретном случае, в котором игроки либо сотрудничают, либо предают, поскольку эта модель относительно проста для анализа. Однако некоторые исследователи рассматривали модели непрерывной итерируемой дилеммы заключенного, в которых игроки могут вносить переменный вклад в другого игрока. Ле и Бойд ^[24] обнаружили, что в таких ситуациях сотрудничество гораздо сложнее развить, чем в дискретной итерируемой дилемме заключенного. В непрерывной дилемме заключенного, если популяция начинает в некооперативном равновесии, игроки, которые лишь незначительно более кооперативны, чем некооператоры, получают небольшую выгоду от сортировки друг с другом. Напротив, в дискретной дилемме заключенного кооператоры, работающие по принципу «око за око», получают большой выигрыш от сортировки друг с другом в некооперативном равновесии по сравнению с некооператорами. Поскольку природа, по-видимому, предлагает больше возможностей для разнообразного сотрудничества, чем строгую дихотомию сотрудничества или предательства, непрерывная дилемма заключенного может помочь объяснить, почему реальные примеры сотрудничества по принципу «око за око» чрезвычайно редки ^[25], хотя принцип «око за око» кажется надежным в теоретических моделях.

Примеры из реальной жизни

Многие примеры человеческого взаимодействия и природных процессов имеют матрицы выплат, подобные дилемме заключенного. Поэтому она представляет интерес для социальных наук , таких как экономика , политика и социология , а также для биологических наук, таких как этология и эволюционная биология . Многие природные процессы были абстрагированы в модели, в которых живые существа вовлечены в бесконечные игры дилеммы заключенного.

Экологические исследования

В экологических исследованиях дилемма очевидна в таких кризисах, как глобальное изменение климата . Утверждается, что все страны выиграют от стабильного климата, но любая отдельная страна часто не решается ограничить _{выбросы} CO2 . Немедленная выгода для любой страны от сохранения текущего поведения воспринимается как большая, чем предполагаемая конечная выгода для этой страны, если поведение всех стран изменится, что объясняет тупиковую ситуацию с изменением климата в 2007 году. ^[26]

Важное различие между политикой изменения климата и дилеммой заключенного заключается в неопределенности; степень и скорость, с которой загрязнение может изменить климат, неизвестны. Дилемма, с которой сталкиваются правительства, поэтому отличается от дилеммы заключенного тем, что выигрыши от сотрудничества неизвестны. Это различие предполагает, что государства будут сотрудничать гораздо меньше, чем в реальной итерированной дилемме заключенного, так что вероятность избежать возможной климатической катастрофы намного меньше, чем та, которая предлагается теоретико-игровым анализом ситуации с использованием реальной итерированной дилеммы заключенного. ^[27]

Томас Осанг и Арундати Нанди предлагают теоретическое объяснение с доказательствами беспроигрышной ситуации, основанной на регулировании, в соответствии с гипотезой Майкла Портера , в которой государственное регулирование конкурирующих фирм является существенным. ^[28]

Животные

Кооперативное поведение многих животных можно рассматривать как пример повторяющейся дилеммы заключенного. Часто животные вступают в долгосрочные партнерства; например, гуппи кооперативно проверяют хищников группами, и считается, что они наказывают несотрудничающих инспекторов. ^[29]

Летучие мыши-вампиры — социальные животные, которые участвуют в взаимном обмене пищей. Применение выигрышей из дилеммы заключенного может помочь объяснить это поведение. ^[30]

Психология

В исследовании зависимости и поведенческой экономике Джордж Эйнсли указывает, что зависимость можно рассматривать как проблему дилеммы заключенного между настоящим и будущим «я» наркомана. В этом случае «отказ» означает рецидив, где отсутствие рецидива и сегодня, и в будущем — это, безусловно, лучший результат. Случай, когда человек воздерживается сегодня, но срывается в будущем, — это худший результат: в некотором смысле дисциплина и самопожертвование, необходимые для воздержания сегодня, были «потрачены впустую», потому что будущий рецидив означает, что наркоман снова там, где он начал, и ему придется начинать все заново. Рецидив сегодня и завтра — это немного «лучший» результат, потому что, хотя наркоман все еще зависим, он не приложил усилий, чтобы попытаться остановиться. Последний случай, когда человек сегодня проявляет аддиктивное поведение, а завтра воздерживается от него, имеет ту же проблему (как и в других дилеммах заключенного), что существует очевидная выгода от отказа «сегодня», но завтра человек столкнется с той же дилеммой заключенного, и та же очевидная выгода будет иметь место, что в конечном итоге приведет к бесконечной череде отказов. ^[31]

В своей книге «Наука доверия » Джон Готтман определяет хорошие отношения как такие, в которых партнеры знают, что не следует вступать во взаимное предательское поведение или, по крайней мере, не следует динамически застревать в этом цикле. В когнитивной нейробиологии быстрая мозговая сигнализация, связанная с обработкой различных раундов, может указывать на выбор в следующем раунде. Результаты взаимного сотрудничества влекут за собой изменения мозговой активности, предсказывающие, как быстро человек будет сотрудничать в натуральной форме при следующей возможности; ^[32] эта активность может быть связана с основными гомеостатическими и мотивационными процессами, возможно, увеличивая вероятность сокращения пути к взаимному сотрудничеству.

Экономика

Дилемму заключенного называют кишечной палочкой социальной психологии, и она широко используется для исследования различных тем, таких как олигополистическая конкуренция и коллективные действия по созданию коллективного блага. ^[33]

Рекламу иногда приводят как реальный пример дилеммы заключенного. Когда реклама сигарет была легальна в Соединенных Штатах, конкурирующие производители сигарет должны были решить, сколько денег потратить на рекламу. Эффективность рекламы фирмы A частично определялась рекламой, проводимой фирмой B. Аналогично, прибыль, получаемая фирмой B от рекламы, зависит от рекламы, проводимой фирмой A. Если и фирма A, и фирма B решили рекламироваться в течение определенного периода, то реклама каждой фирмы сводит на нет рекламу другой, выручка остается постоянной, а расходы увеличиваются из-за стоимости рекламы. Обе фирмы выиграют от сокращения рекламы. Однако, если фирма B решит не рекламироваться, фирма A может получить большую выгоду от рекламы. Тем не менее, оптимальный объем рекламы одной фирмы зависит от того, сколько рекламы берет на себя другая. Поскольку лучшая стратегия зависит от того, что выбирает другая фирма, доминирующей стратегии не существует, что делает ее немного отличной от дилеммы заключенного. Однако результат схож в том, что обе фирмы были бы в выигрыше, если бы они рекламировали меньше, чем в равновесии.

Иногда кооперативное поведение действительно возникает в деловых ситуациях. Например, производители сигарет одобрили принятие законов, запрещающих рекламу сигарет, понимая, что это снизит издержки и увеличит прибыль во всей отрасли. ^{[34] [d]}

Без подлежащих исполнению соглашений члены картеля также вовлечены в (многопользовательскую) дилемму заключенного. ^[35] «Сотрудничество» обычно означает согласие на минимальный уровень цен , в то время как «дезертирство» означает продажу ниже этого минимального уровня, мгновенно отнимая бизнес у других членов картеля. Антимонопольные органы хотят, чтобы потенциальные члены картеля взаимно дезертировали, обеспечивая максимально низкие цены для потребителей.

Спорт

Допинг в спорте был приведен в качестве примера дилеммы заключенного. Два соревнующихся спортсмена имеют возможность использовать нелегальный и/или опасный препарат для повышения своих результатов. Если ни один из спортсменов не принимает препарат, то ни один не получает преимущества. Если это делает только один, то этот спортсмен получает значительное преимущество перед конкурентом, уменьшенное на юридические и/или медицинские опасности приема препарата. Но если оба спортсмена принимают препарат, преимущества сводятся на нет, и остаются только опасности, что ставит их обоих в худшее положение, чем если бы ни один из них не принимал допинг. ^[36]

Международная политика

В теории международных отношений дилемма заключенного часто используется для демонстрации того, почему сотрудничество терпит неудачу в ситуациях, когда сотрудничество между государствами является коллективно оптимальным, но индивидуально неоптимальным. ^{[37] [38]} Классическим примером является дилемма безопасности , когда увеличение безопасности одного государства (например, увеличение его военной мощи) приводит к тому, что другие государства начинают опасаться за свою собственную безопасность из-за страха наступательных действий. ^[39] Следовательно, меры по повышению безопасности могут привести к напряженности, эскалации или конфликту с одной или несколькими другими сторонами, что приводит к результату, которого на самом деле не желает ни одна из сторон. ^{[40] [39] [41] [42] [43]} Дилемма безопасности особенно остро стоит в ситуациях, когда трудно отличить наступательное оружие от оборонительного, а наступление имеет преимущество в любом конфликте над обороной. ^[39]

Дилемма заключенного часто использовалась реалистами -теоретиками международных отношений, чтобы продемонстрировать, почему все государства (независимо от их внутренней политики или провозглашаемой идеологии) в условиях международной анархии будут испытывать трудности при сотрудничестве друг с другом, даже если все выигрывают от такого сотрудничества.

Критики реализма утверждают, что итерация и расширение тени будущего являются решениями дилеммы заключенного. Когда актеры разыгрывают дилемму заключенного один раз, у них есть стимулы к отказу, но когда они ожидают, что будут разыгрывать ее неоднократно, у них есть большие стимулы к сотрудничеству. ^[44]

Многопользовательские дилеммы

Многие реальные дилеммы включают в себя несколько игроков. ^{[45] Хотя} трагедия общин Гаррета Хардина является метафорической, ее можно рассматривать как пример многопользовательского обобщения дилеммы заключенного: каждый житель деревни делает выбор в пользу личной выгоды или ограничения. Коллективная награда за единодушное или частое предательство — очень низкие выплаты и разрушение общин.

Общее не всегда эксплуатируется: Уильям Паундстоун в книге о дилемме заключенного описывает ситуацию в Новой Зеландии, где газетные ящики остаются незапертыми. Люди могут взять газету, не заплатив (перебежчик), но очень немногие это делают, чувствуя, что если они не заплатят, то и другие не заплатят, разрушая систему. ^[46] Последующие исследования Элинор Остром , лауреата Нобелевской премии по экономике 2009 года , выдвинули гипотезу, что трагедия общего слишком упрощена, а негативный результат обусловлен внешними влияниями. Не усложняя давления, группы общаются и управляют общими ресурсами между собой для своей взаимной выгоды, применяя социальные нормы для сохранения ресурса и достижения максимального блага для группы, пример осуществления наилучшего исхода для дилеммы заключенного. ^{[47] [48]}

Академические настройки

Дилемма заключенного использовалась в различных академических условиях для иллюстрации сложностей сотрудничества и конкуренции. Одним из примечательных примеров является эксперимент в классе, проведенный профессором социологии Дэном Чамблиссом в колледже Гамильтона в 1980-х годах. Начиная с 1981 года Чамблисс предложил, что если ни один студент не сдаст выпускной экзамен, все получат оценку A, но если хотя бы один студент сдаст его, те, кто не сдаст, получат ноль. В 1988 году Джон Вернер , студент первого курса, успешно организовал своих однокурсников, чтобы бойкотировать экзамен, продемонстрировав практическое применение теории игр и концепции дилеммы заключенного. ^[49]

Почти 25 лет спустя, похожий инцидент произошел в Университете Джонса Хопкинса в 2013 году. Политика оценивания профессора Петера Фрёлиха масштабировала выпускные экзамены в соответствии с наивысшим баллом, что означало, что если бы все получили одинаковый балл, они все получили бы оценку A. Студенты в классах Фрёлиха организовали бойкот выпускного экзамена, гарантируя, что никто его не сдаст. В результате каждый студент получил оценку A, успешно решив дилемму заключенного взаимно оптимальным способом без итерации. ^{[50] [51]} Эти примеры показывают, как дилемму заключенного можно использовать для изучения кооперативного поведения и принятия стратегических решений в образовательных контекстах.

Похожие игры

Закрытый обмен

Дилемма заключенного как обмен портфелями

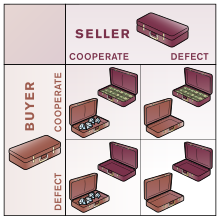
Дуглас Хофштадтер ^[52] предположил, что люди часто находят такие проблемы, как дилемма заключенного, более понятными, когда они проиллюстрированы в форме простой игры или обмена. Одним из нескольких примеров, которые он использовал, был «закрытый обмен сумками»:

Два человека встречаются и обмениваются закрытыми сумками, при этом предполагается, что в одной из них находятся деньги, а в другой — покупка. Любой игрок может выбрать, соблюдать ли сделку, положив в сумку то, что он или она согласились, или он или она может отказаться, передав пустую сумку.

Друг или враг?

Друг или враг? — игровое шоу, которое транслировалось с 2002 по 2003 год на Game Show Network в США. В игровом шоу соревнуются три пары людей. Когда пара выбывает, они играют в игру, похожую на дилемму заключенного, чтобы определить, как делится выигрыш. Если они оба сотрудничают (друг), они делят выигрыш 50 на 50. Если один сотрудничает, а другой предает (враг), предатель получает весь выигрыш, а сотрудничающий не получает ничего. Если оба предают, оба уходят ни с чем. Обратите внимание, что матрица вознаграждения немного отличается от стандартной, приведенной выше, поскольку вознаграждения для случаев «оба предают» и «сотрудничают, а противник предает» идентичны. Это делает случай «оба предают» слабым равновесием по сравнению со строгим равновесием в стандартной дилемме заключенного. Если участник знает, что его противник собирается проголосовать за «враг», то его собственный выбор не влияет на его собственный выигрыш. В определенном смысле в игре « Друг или враг» используется модель вознаграждения, которая находится между дилеммой заключенного и игрой «Цыпленок» .

Вот матрица вознаграждений:

Эта матрица выплат также использовалась в британских телевизионных программах Trust Me , Shafted , The Bank Job и Golden Balls , а также в американских игровых шоу Take It All , а также для победившей пары в реалити-шоу Bachelor Pad и Love Island . Игровые данные из серии Golden Balls были проанализированы группой экономистов, которые обнаружили, что сотрудничество было «удивительно высоким» для сумм денег, которые казались бы значительными в реальном мире, но были сравнительно низкими в контексте игры. ^[53]

Повторяющийся сугроб

Исследователи из Университета Лозанны и Эдинбургского университета предположили, что «Итерированная игра в сугроб» может точнее отражать реальные социальные ситуации, хотя эта модель на самом деле является игрой в курицу . В этой модели риск быть эксплуатируемым через предательство ниже, и люди всегда выигрывают от принятия совместного выбора. Игра в сугроб представляет двух водителей, которые застряли по разные стороны сугроба , каждому из которых предоставляется возможность расчистить снег, чтобы расчистить путь, или остаться в своей машине. Самый высокий выигрыш игрока получается, если он оставляет противника расчищать весь снег самостоятельно, но противник все равно номинально вознаграждается за свою работу.

Это может лучше отражать реальные сценарии, исследователи приводят пример двух ученых, сотрудничающих над отчетом, и оба из них выиграют, если другой будет работать усерднее. «Но когда ваш коллега не выполняет никакой работы, вам, вероятно, лучше сделать всю работу самостоятельно. Вы все равно получите завершенный проект». ^{[54] [55]}

Игры на координацию

В координационных играх игроки должны координировать свои стратегии для хорошего результата. Примером может служить две машины, которые внезапно встречаются в метель; каждая должна выбрать, свернуть ли ей налево или направо. Если обе свернут налево или обе направо, машины не столкнутся. Местная конвенция о левостороннем и правостороннем движении помогает координировать их действия.

Симметричные координационные игры включают «Охоту на оленя» и «Бах или Стравинский» .

Асимметричные дилеммы заключенного

Более общий набор игр асимметричен. Как и в дилемме заключенного, лучшим результатом является сотрудничество, и есть мотивы для предательства. Однако, в отличие от симметричной дилеммы заключенного, один игрок может потерять больше и/или получить больше, чем другой. Некоторые такие игры были описаны как дилемма заключенного, в которой у одного заключенного есть алиби , отсюда и термин «игра алиби». ^[56]

В экспериментах игроки, получающие неравные выплаты в повторяющихся играх, могут стремиться максимизировать прибыль, но только при условии, что оба игрока получают равные выплаты; это может привести к устойчивой равновесной стратегии, в которой находящийся в невыгодном положении игрок предает каждую игру X, в то время как другой всегда сотрудничает. Такое поведение может зависеть от социальных норм эксперимента относительно справедливости. ^[57]

Программное обеспечение

Для проведения симуляций и турниров по «дилемме заключенного» было создано несколько программных пакетов, некоторые из которых имеют доступ к исходному коду:

• Исходный код второго турнира, организованного Робертом Аксельродом (написанный Аксельродом и многими участниками на языке Fortran ), доступен онлайн.
• Prison, библиотека, написанная на Java , последний раз обновленная в 1998 году.
• Axelrod-Python, написанный на Python
• Evoplex — быстрая программа агентного моделирования, выпущенная в 2018 году Маркосом Кардино.

В художественной литературе

Ханну Раджаниеми поместил начальную сцену своей трилогии «Квантовый вор » в «тюрьму дилеммы». Основная тема серии была описана как «неадекватность бинарной вселенной», а конечным антагонистом является персонаж, называемый Всеотступником. Первая книга серии была опубликована в 2010 году, с двумя продолжениями, « Фрактальный принц» и «Причинный ангел» , опубликованными в 2012 и 2014 годах соответственно.

Игра, смоделированная по мотивам повторяющейся дилеммы заключенного, является центральной темой видеоигры 2012 года Zero Escape: Virtue's Last Reward и второстепенной частью ее продолжения 2016 года Zero Escape: Zero Time Dilemma .

В книге «Таинственное общество Бенедикта и дилемма заключенного» Трентона Ли Стюарта главные герои начинают с игры в версию игры и побега из «тюрьмы» в целом. Позже они становятся настоящими заключенными и снова совершают побег.

В «Зоне приключений : Баланс» во время подарки «Игра страданий » персонажи игроков дважды сталкиваются с дилеммой заключенного во время своего пребывания во владениях двух личей: один раз они сотрудничают, а другой раз дезертируют.

В 8-м романе автора Джеймса С. А. Кори « Гнев Тиамата» Уинстон Дуарте объясняет дилемму заключенного своей 14-летней дочери Терезе, чтобы научить ее стратегическому мышлению. ^{[ необходима цитата ]}

В фильме 2008 года «Темный рыцарь» есть сцена, в общих чертах основанная на этой проблеме, в которой Джокер оснащает два парома, один с заключенными, а другой с гражданскими лицами, вооружая обе группы средствами для подрыва бомбы на паромах друг друга, угрожая взорвать их оба, если они будут колебаться. ^{[58] [59]}

В моральной философии

Дилемма заключенного обычно используется как инструмент мышления в моральной философии для иллюстрации потенциального напряжения между выгодой отдельного человека и выгодой общества.

И одноразовая, и итеративная дилемма заключенного имеют приложения в моральной философии. Действительно, многие моральные ситуации, такие как геноцид , нелегко повторить больше одного раза. Более того, во многих ситуациях результаты предыдущих раундов неизвестны игрокам, поскольку они не обязательно одинаковы (например, взаимодействие с попрошайкой на улице). ^[60]

Философ Дэвид Готье использует дилемму заключенного, чтобы показать, как мораль и рациональность могут конфликтовать. ^[61]

Некоторые теоретики игр критиковали использование дилеммы заключенного как инструмента мышления в моральной философии. ^[61] Кеннет Бинмор утверждал, что дилемма заключенного неточно описывает игру, в которую играет человечество, которая, по его мнению, ближе к игре координации . Брайан Скирмс разделяет эту точку зрения.

Стивен Кун предполагает, что эти взгляды можно примирить, если учесть, что моральное поведение может изменить матрицу выигрышей игры, трансформируя ее из дилеммы заключенного в другие игры. ^[61]

Дилемма чистого и нечистого заключенного

Дилемма заключенного считается «нечистой», если смешанная стратегия может дать лучшие ожидаемые выигрыши, чем чистая стратегия. Это создает интересную возможность того, что моральное действие с утилитарной точки зрения (т. е. направленное на максимизацию пользы действия) может потребовать рандомизации стратегии, например, сотрудничества с вероятностью 80% и предательства с вероятностью 20%. ^[62]

Смотрите также

• Абилинский парадокс
• Игра «Сороконожки»
• Проблема коллективных действий
• Внешние эффекты
• Народная теорема (теория игр)
• Проблема безбилетника
• Игра в обмен подарками
• ловушка Гоббса
• Дилемма невиновного заключенного
• Игра в лжеца
• Метагейм
• Необязательная дилемма заключенного
• Дилемма заключенного и сотрудничество
• Игра в общественные блага
• Взаимный альтруизм
• Поиск ренты
• Социальные предпочтения
• Сверхрациональность
• Теория быстрого доверия
• Трагедия общин
• Дилемма путешественника
• Дилемма недобросовестного закусочного

Примечания

1. Турнир состоит из двух раундов. В первом раунде каждая из восьми лучших стратегий была хороша, и ни одна из семи худших не была хороша. Во втором раунде (разработчики стратегий могли принять во внимание результаты первого раунда) все, кроме одной, из пятнадцати лучших стратегий были хороши (и она заняла восьмое место). Из пятнадцати худших стратегий все, кроме одной, не были хороши. ^[13]
2. В отличие от стратегий типа «Grim Trigger» (также называемых «Friedman»), которые никогда не предают первыми, но как только другой предает хотя бы один раз, «Grim Trigger» предает и дальше. ^[14]
3. Например, см. исследование 2003 года ^[15] , где обсуждается концепция и то, можно ли ее применять в реальных экономических или стратегических ситуациях.
4. Этот аргумент в пользу развития сотрудничества через доверие приводится в «Мудрости толпы» , где утверждается, что капитализм на расстоянии смог сформироваться вокруг ядра квакеров , которые всегда вели себя честно со своими деловыми партнерами (вместо того, чтобы дезертировать и нарушать обещания — явление, которое препятствовало более ранним долгосрочным невыполнимым зарубежным контрактам). Утверждается, что сделки с надежными торговцами позволили мему о сотрудничестве распространиться на других торговцев, которые распространили его дальше, пока высокая степень сотрудничества не стала прибыльной стратегией в общей торговле .

Ссылки

1. «Дилемма заключенного». Стэнфордская энциклопедия философии . Получено 10 марта 2024 г.
2. Паундстоун 1993, стр. 8, 117.
3. Паундстоун 1993, стр. 118: «Типичная современная версия истории выглядит так: два члена преступной банды арестованы и заключены в тюрьму. Каждый заключенный находится в одиночной камере без возможности поговорить или обменяться сообщениями с другим. Полиция признает, что у них недостаточно доказательств, чтобы осудить пару по основному обвинению. Они планируют приговорить обоих к году тюрьмы по менее серьезному обвинению. Одновременно полиция предлагает каждому заключенному сделку Фауста. Если он даст показания против своего партнера, он выйдет на свободу, а партнер получит три года тюрьмы по основному обвинению. О, да, есть подвох... Если оба заключенных дадут показания друг против друга, оба будут приговорены к двум годам тюрьмы. Заключенным дается немного времени, чтобы все обдумать, но ни в коем случае никто из них не может узнать, что решил другой, пока он не примет окончательное решение. Каждому сообщают, что другому заключенному предлагают ту же самую сделку. Каждый заключенный озабочен только своим собственным благополучием — минимизацией своего тюремного срока».
4. Паундстоун 1993, стр. 118.
5. Грофман, Бернард; Пул, Джонатан (январь 1977). «Как сделать сотрудничество оптимизирующей стратегией в игре двух человек». Журнал математической социологии . 5 (2): 173–186. doi :10.1080/0022250x.1977.9989871. ISSN  0022-250X.
6. Шай, Оз (1995). Промышленная организация: теория и применение. Издательство Массачусетского технологического института. ISBN 978-0262193665. Получено 27 февраля 2013 г. .
7. Ауманн, Роберт Дж. (2016-03-02), «16. Приемлемые точки в общих кооперативных играх n-человек», Вклад в теорию игр (AM-40), том IV , Princeton University Press, стр. 287–324, doi :10.1515/9781400882168-018, ISBN 978-1-4008-8216-8, получено 2024-05-14
8. Купер, Рассел; ДеДжонг, Дуглас В.; Форсайт, Роберт; Росс, Томас В. (1996). «Сотрудничество без репутации: экспериментальные данные игр «Дилемма заключенного». Игры и экономическое поведение . 12 (2): 187–218. doi :10.1006/game.1996.0013.
9. Даль Бо, Педро; Фрешетт, Гийом Р. (2019). «Выбор стратегии в бесконечно повторяющейся дилемме заключенного». American Economic Review . 109 (11): 3929–3952. doi :10.1257/aer.20181480. ISSN  0002-8282. S2CID  216726890.
10. Аксельрод (2006), стр. 193
11. Аксельрод (2006), стр. 31
12. Аксельрод (2006), гл. 6
13. Аксельрод (2006), стр. 113–114.
14. Аксельрод (2006), стр. 36
15. Ландсбергер, Майкл; Цирельсон, Борис (2003). "Байесовское равновесие Нэша; статистическая проверка гипотезы" (PDF) . Тель-Авивский университет . Архивировано из оригинала (PDF) 2005-10-02.
16. У, Цзядун; Чжао, Чэнье (2019), Сан, Сяомин; Хэ, Кунь; Чэнь, Сяоюнь (ред.), «Сотрудничество по правилу Монте-Карло: игра «Дилемма заключенного» в сетке», Теоретическая информатика , Коммуникации в области компьютерных и информационных наук, т. 1069, Springer Singapore, стр. 3–15, doi : 10.1007/978-981-15-0105-0_1, ISBN 978-981-15-0104-3, S2CID  118687103
17. Ведекинд, К.; Милински, М. (2 апреля 1996 г.). «Человеческое сотрудничество в одновременной и чередующейся дилемме заключенного: Павлов против щедрого «око за око». Труды Национальной академии наук . 93 (7): 2686–2689. Bibcode : 1996PNAS...93.2686W. doi : 10.1073 /pnas.93.7.2686 . PMC 39691. PMID  11607644. 
18. "Команда Университета Саутгемптона выигрывает соревнование по дилемме заключенного" (пресс-релиз). Университет Саутгемптона. 7 октября 2004 г. Архивировано из оригинала 21.04.2014.
19. Press, WH; Dyson, FJ (26 июня 2012 г.). «Повторяющаяся дилемма заключенного содержит стратегии, которые доминируют над любым эволюционным оппонентом». Труды Национальной академии наук Соединенных Штатов Америки . 109 (26): 10409–13. Bibcode : 2012PNAS..10910409P. doi : 10.1073/pnas.1206569109 . PMC 3387070. PMID  22615375 . 
20. Адами, Кристоф; Аренд Хинтце (2013). «Эволюционная нестабильность стратегий с нулевым детерминантом демонстрирует, что победа — это еще не все». Nature Communications . 4 : 3. arXiv : 1208.2666 . Bibcode : 2013NatCo...4.2193A. doi : 10.1038/ncomms3193. PMC 3741637 . PMID  23903782. 
21. Хильбе, Кристиан; Мартин А. Новак; Карл Зигмунд (апрель 2013 г.). «Эволюция вымогательства в играх с итерированной дилеммой заключенного». PNAS . 110 (17): 6913–18. arXiv : 1212.1067 . Bibcode : 2013PNAS..110.6913H . doi : 10.1073/pnas.1214834110 . PMC 3637695. PMID  23572576. 
22. Stewart, Alexander J.; Joshua B. Plotkin (2013). «От вымогательства к щедрости, эволюция в итерированной дилемме заключенного». Труды Национальной академии наук Соединенных Штатов Америки . 110 (38): 15348–53. Bibcode : 2013PNAS..11015348S. doi : 10.1073 / pnas.1306246110 . PMC 3780848. PMID  24003115. 
23. Акин, Итан (2013). «Стабильные кооперативные решения для итерированной дилеммы заключенного». стр. 9. arXiv : 1211.0969 [math.DS]. Библиотечный код : 2012arXiv1211.0969A
24. Le S, Boyd R (2007). «Эволюционная динамика непрерывной итерируемой дилеммы заключенного». Журнал теоретической биологии . 245 (2): 258–67. Bibcode : 2007JThBi.245..258L. doi : 10.1016/j.jtbi.2006.09.016. PMID  17125798.
25. Хаммерштейн, П. (2003). Почему взаимность так редка у социальных животных? Протестантский призыв. В: П. Хаммерштейн, редактор, Genetic and Cultural Evolution of Cooperation, MIT Press. стр. 83–94.
26. "Рынки и данные". The Economist . 2007-09-27.
27. Ремейер, Джули (29.10.2012). «Теория игр предполагает, что текущие переговоры по климату не предотвратят катастрофу». Science News . Society for Science & the Public.
28. Осанг, Томас; Нандийз, Арундати (август 2003 г.). Экологическое регулирование загрязняющих фирм: пересмотр гипотезы Портера (PDF) (статья). Архивировано (PDF) из оригинала 2010-07-02.
29. Броснан, Сара Ф.; Эрли, Райан Л.; Дугаткин, Ли А. (октябрь 2003 г.). «Наблюдательное обучение и осмотр хищников у гуппи (Poecilia reticulata): социальное обучение у гуппи». Этология . 109 (10): 823–833. doi : 10.1046/j.0179-1613.2003.00928.x .
30. Докинз, Ричард (1976). Эгоистичный ген . Oxford University Press.
31. Эйнсли, Джордж (2001). Разрушение воли . Cambridge University Press. ISBN 978-0-521-59694-7.
32. Сервантес Константино, Гарат, Николаисен, Пас, Мартинес-Монтес, Кессель, Кабана и Градин (2020). «Нейронная обработка результатов итерированной дилеммы заключенного указывает на выбор следующего раунда и скорость взаимного сотрудничества». Социальная нейронаука . 16 (2): 103–120. doi :10.1080/17470919.2020.1859410. PMID  33297873. S2CID  228087900.{{cite journal}}: CS1 maint: multiple names: authors list (link)
33. Аксельрод, Роберт (1980). «Эффективный выбор в дилемме заключенного». Журнал разрешения конфликтов . 24 (1): 3–25. doi :10.1177/002200278002400101. ISSN  0022-0027. JSTOR  173932. S2CID  143112198.
34. Хенриксен, Лиза (март 2012 г.). «Комплексные ограничения табачного маркетинга: продвижение, упаковка, цена и место». Tobacco Control . 21 (2): 147–153. doi :10.1136/ tobaccocontrol -2011-050416. PMC 4256379. PMID  22345238. 
35. Николсон, Уолтер (2000). Промежуточная микроэкономика и ее применение (8-е изд.). Форт-Уорт, Техас: Dryden Press: Harcourt College Publishers. ISBN 978-0-030-25916-6.
36. Шнайер, Брюс (26.10.2012). «Лэнс Армстронг и дилемма заключенных допинга в профессиональном спорте». Wired . Wired.com . Получено 29.10.2012 .
37. Снайдер, Гленн Х. (1971). ««Дилемма заключенного» и модели «цыпленка» в международной политике». International Studies Quarterly . 15 (1): 66–103. doi :10.2307/3013593. ISSN  0020-8833. JSTOR  3013593.
38. Джервис, Роберт (1978). «Сотрудничество в условиях дилеммы безопасности». World Politics . 30 (2): 167–214. doi : 10.2307/2009958. hdl : 2027/uc1.31158011478350 . ISSN  1086-3338. JSTOR  2009958. S2CID  154923423.
39. Джервис, Роберт (1978). «Сотрудничество в условиях дилеммы безопасности». Мировая политика . 30 (2): 167–214. doi : 10.2307/2009958. hdl : 2027/uc1.31158011478350 . ISSN  0043-8871. JSTOR  2009958. S2CID  154923423.
40. Херц, Джон Х. (1950). Идеалистический интернационализм и дилемма безопасности . С. 157–180.
41. Снайдер, Гленн Х. (1984). «Дилемма безопасности в политике альянсов». World Politics . 36 (4): 461–495. doi :10.2307/2010183. ISSN  0043-8871. JSTOR  2010183. S2CID  154759602.
42. Джервис, Роберт (1976). Восприятие и заблуждение в международной политике. Princeton University Press. С. 58–113. ISBN 978-0-691-10049-4.
43. Глейзер, Чарльз Л. (2010). Рациональная теория международной политики. Princeton University Press. ISBN 9780691143729.
44. Аксельрод, Роберт; Гамильтон, Уильям Д. (1981). «Эволюция сотрудничества». Science . 211 (4489): 1390–1396. Bibcode :1981Sci...211.1390A. doi :10.1126/science.7466396. ISSN  0036-8075. PMID  7466396.
45. Gokhale CS, Traulsen A. Эволюционные игры в мультивселенной. Труды Национальной академии наук. 2010 г. 23 марта. 107(12):5500–04.
46. Паундстоун 1993, стр. 126–127.
47. "Заговор Волоха" Элинор Остром и трагедия общин". Volokh.com. 2009-10-12 . Получено 2011-12-17 .
48. Остром, Элинор (2015) [1990]. Управление общими ресурсами: эволюция институтов коллективного действия . Cambridge University Press. doi : 10.1017/CBO9781316423936. ISBN 978-1-107-56978-2.
49. Ривард, Рай (21.02.2013). «Взгляд назад на еще один успешный бойкот выпускного экзамена». Inside Higher Ed . Получено 12.07.2024 .
50. Вольферс, Джастин (2013-02-14). «Игра в систему». The New York Times . Получено 2024-07-12 .
51. «Студенты Университета Джонса Хопкинса бойкотируют выпускной экзамен — так что все получат оценку «отлично»». Baltimore Fishbowl. 2013-02-25 . Получено 2024-07-12 .
52. Хофштадтер, Дуглас Р. (1985). "Гл. 29 Дилемма заключенного. Компьютерные турниры и эволюция сотрудничества .". Метамагические темы: поиски сущности разума и модели . Bantam Dell Pub Group. ISBN 978-0-465-04566-2.
53. Ван ден Ассем, Мартейн Дж. (январь 2012 г.). «Разделить или украсть? Кооперативное поведение, когда ставки велики». Наука управления . 58 (1): 2–20. doi :10.1287/mnsc.1110.1413. hdl : 1765/31292 . S2CID  1371739. SSRN  1592456.
54. Zyga, Lisa (2007-10-09). «Игра «Снежный дрейф» превосходит «Дилемму заключенного» в объяснении сотрудничества». Phys.org . Архивировано из оригинала 2024-04-11.
55. Кюммерли, Рольф; Коллиард, Каролина; Фихтер, Николя; Петипьер, Блез; Руссье, Флавиен; Келлер, Лоран (25.09.2007). «Человеческое сотрудничество в социальных дилеммах: сравнение игры «Сугроб» с дилеммой заключенного». Труды Королевского общества B: Биологические науки . 274 (1628). Королевское общество: 2965–2970. doi :10.1098/rspb.2007.0793. ISSN  1471–2954. PMC 2291152. PMID 17895227  . 
56. Робинсон, DR; Гофорт, DJ (5 мая 2004 г.). Игры алиби: асимметричные дилеммы заключенного (PDF) . Заседания Канадской экономической ассоциации, Торонто, 4–6 июня 2004 г. Архивировано (PDF) из оригинала 2004-12-06.
57. Бекенкамп, Мартин; Хенниг-Шмидт, Хайке; Майер-Риго, Франк П. (4 марта 2007 г.). «Сотрудничество в симметричных и асимметричных играх «Дилемма заключенного»» (PDF) . Институт исследований коллективных благ Общества Макса Планка . Архивировано (PDF) из оригинала 02.09.2019.
58. Ромейн, Линдси (2018-07-18). «Единственный искупительный персонаж Темного рыцаря — преступник, который спасает паромы». Polygon . Получено 2024-01-06 .
59. "Темный рыцарь: Теория игр: Блог курса по сетям для INFO 2040/CS 2850/Econ 2040/SOC 2090" . Получено 06.01.2024 .
60. Кун, Стивен Т. (2004-07-01). «Размышления об этике и теории игр». Synthese . 141 (1): 1–44. doi :10.1023/B:SYNT.0000035846.91195.cb. ISSN  1573-0964.
61. Kuhn, Steven (декабрь 2016 г.). «Готье и дилемма заключенного». Диалог . 55 (4): 659–676. doi :10.1017/S0012217316000603. ISSN  0012-2173.
62. Кун, Стивен Т.; Морези, Серж (октябрь 1995 г.). «Чистые и утилитарные дилеммы заключенного». Экономика и философия . 11 (2): 333–343. doi :10.1017/S0266267100003424. ISSN  0266-2671.

Библиография

• Паундстоун, Уильям (1993). Дилемма заключенного (1-е изд. Anchor Books). Нью-Йорк: Anchor. ISBN 0-385-41580-X.

Дальнейшее чтение

• Амаде, С. (2016). «Дилемма заключенного», Узники разума . Cambridge University Press , Нью-Йорк, стр. 24–61.
• Ауманн, Роберт (1959). «Приемлемые точки в общих кооперативных играх с n лицами». В Luce, RD; Tucker, AW (ред.). Вклад в теорию 23 игр IV . Annals of Mathematics Study. Том 40. Princeton NJ: Princeton University Press. С. 287–324. MR  0104521.
• Аксельрод, Роберт (2006). Эволюция сотрудничества (пересмотренное издание). Basic Books. ISBN 0-465-00564-0.
• Биккьери, Кристина (1993). Рациональность и координация. Cambridge University Press .
• Шахматы, Дэвид М. (декабрь 1988 г.). «Моделирование эволюции поведения: проблема итерированной дилеммы заключенных» (PDF) . Complex Systems . 2 (6): 663–70. Архивировано (PDF) из оригинала 2015-05-30.
• Коллинз, Рори В. (март 2022 г.). «Парадокс дилеммы заключенного: рациональность, мораль и взаимность». Think: Philosophy for Everyone . 21 (61): 45–55. doi : 10.1017/S1477175621000464 .
• Дрешер, М. (1961). Математика стратегических игр: теория и приложения Prentice-Hall , Энглвуд Клиффс, Нью-Джерси.
• Грейф, А. (2006). Институты и путь к современной экономике: уроки средневековой торговли. Cambridge University Press, Кембридж , Великобритания.
• Копельман, Ширли (февраль 2020 г.). «Око за око и дальше: легендарная работа Анатоля Рапопорта». Исследования по переговорам и управлению конфликтами . 13 (1): 60–84. doi : 10.1111/ncmr.12172 . hdl : 2027.42/153763 .
• Рапопорт, Анатоль и Альберт М. Чамма (1965). Дилемма заключенного . Издательство Мичиганского университета .
• Шнайдер, Марк; Шилдс, Тимоти У. (июнь 2022 г.). «Мотивы сотрудничества в дилемме заключенного с одним выстрелом». Журнал поведенческих финансов . 23 (4): 438–456. doi : 10.1080/15427560.2022.2081974. S2CID  249903572.

Внешние ссылки

• Медиа, связанные с «Дилеммой заключенного» на Wikimedia Commons
• Дилемма шалашника. Дилемма заключенного в орнитологии — математическая карикатура Ларри Гоника.
• Диксит, Авинаш ; Налбафф, Барри (2008). «Дилемма заключенного». В Дэвиде Р. Хендерсоне (ред.). Краткая энциклопедия экономики (2-е изд.). Индианаполис: Библиотека экономики и свободы . ISBN 978-0865976658. OCLC  237794267.
• Докинз: Хорошие парни приходят к финишу первыми
• Библиотека Python для итерированной дилеммы заключенного Аксельрода
• Играйте в «Дилемму заключенного» на oTree (N/A 11-5-17)
• «Эволюция доверия» Ники Кейса, пример игры с пожертвованиями
• Итерированная онлайн-игра «Дилемма заключенного» Уэйна Дэвиса
• Что «Дилемма заключенного» открывает о жизни, вселенной и всем таком от Veritasium