Распределение вероятностей

Математическая функция вероятности наступления определенного результата в эксперименте.

В теории вероятностей и статистике распределение вероятностей — это математическая функция , которая определяет вероятности наступления возможных результатов эксперимента . ^{[1] [2]} Это математическое описание случайного явления с точки зрения его выборочного пространства и вероятностей событий ( подмножеств выборочного пространства). ^[3]

Например, если X используется для обозначения результата подбрасывания монеты («эксперимент»), то распределение вероятностей X будет иметь значение 0,5 (1 из 2 или 1/2) для X = орла и 0,5 для X = решки (предполагая, что монета честная ). Чаще всего распределения вероятностей используются для сравнения относительной встречаемости многих различных случайных значений.

Распределения вероятностей могут быть определены различными способами и для дискретных или для непрерывных величин. Распределениям со специальными свойствами или для особо важных приложений даются специальные названия.

Введение

Распределение вероятностей — это математическое описание вероятностей событий, подмножеств выборочного пространства . Выборочное пространство, часто представленное в нотации как , представляет собой множество всех возможных результатов случайного наблюдаемого явления. Выборочное пространство может быть любым множеством: множеством действительных чисел , множеством описательных меток, множеством векторов , множеством произвольных нечисловых значений и т. д. Например, выборочное пространство подбрасывания монеты может быть  Ω = { "орел", "решка" } . ${\displaystyle \ \Omega \ ,}$

Чтобы определить распределения вероятностей для конкретного случая случайных величин (чтобы пространство выборки можно было рассматривать как числовой набор), обычно различают дискретные и абсолютно непрерывные случайные величины . В дискретном случае достаточно указать функцию массы вероятности, присваивающую вероятность каждому возможному результату (например, при бросании честной игральной кости каждая из шести цифр от «1» до «6» , соответствующих числу точек на игральной кости, имеет вероятность Вероятность события затем определяется как сумма вероятностей всех результатов, которые удовлетворяют событию; например, вероятность события «на игральной кости выпадает четное значение» равна ${\displaystyle \ p\ }$ ${\displaystyle \ {\tfrac {1}{6}}~).}$ $${\displaystyle \ p({\text{“}}2{\text{”}})+p({\text{“}}4{\text{”}})+p({\text{“}}6{\text{”}})={\tfrac {1}{6}}+{\tfrac {1}{6}}+{\tfrac {1}{6}}={\tfrac {1}{2}}~.}$$

Напротив, когда случайная величина принимает значения из континуума, то по соглашению любому индивидуальному результату присваивается вероятность ноль. Для таких непрерывных случайных величин только события, которые включают бесконечно много результатов, таких как интервалы, имеют вероятность больше 0.

Например, рассмотрим измерение веса куска ветчины в супермаркете и предположим, что весы могут обеспечить произвольное количество цифр точности. Тогда вероятность того, что он весит ровно 500 г, должна быть равна нулю, поскольку независимо от выбранного уровня точности нельзя предположить, что в оставшихся пропущенных цифрах, игнорируемых уровнем точности, нет ненулевых десятичных цифр.

Однако для того же варианта использования можно выполнить требования контроля качества, например, чтобы упаковка ветчины весом "500 г" весила от 490 г до 510 г с вероятностью не менее 98%. Это возможно, поскольку это измерение не требует такой высокой точности от базового оборудования.

Рисунок 1: Левый график показывает функцию плотности вероятности. Правый график показывает кумулятивную функцию распределения. Значение в точке a в кумулятивном распределении равно площади под кривой плотности вероятности до точки a .

Абсолютно непрерывные распределения вероятностей можно описать несколькими способами. Функция плотности вероятности описывает бесконечно малую вероятность любого заданного значения, а вероятность того, что результат лежит в заданном интервале, можно вычислить путем интегрирования функции плотности вероятности по этому интервалу. ^[4] Альтернативное описание распределения — с помощью кумулятивной функции распределения , которая описывает вероятность того, что случайная величина не больше заданного значения (т. е. для некоторых ). Кумулятивная функция распределения — это область под функцией плотности вероятности от до , как показано на рисунке 1. ^[5] ${\displaystyle \ {\boldsymbol {\mathcal {P}}}(X<x)\ }$ ${\displaystyle \ x\ }$ ${\displaystyle \ -\infty \ }$ ${\displaystyle \ x\ ,}$

Общее определение вероятности

Распределение вероятностей может быть описано в различных формах, например, с помощью функции массы вероятности или кумулятивной функции распределения. Одно из наиболее общих описаний, которое применяется для абсолютно непрерывных и дискретных переменных, осуществляется с помощью функции вероятности, входное пространство которой является σ-алгеброй , и дает в качестве выходного значения вероятность действительного числа , в частности, число в . ${\displaystyle P\colon {\mathcal {A}}\to \mathbb {R} }$ ${\displaystyle {\mathcal {A}}}$ ${\displaystyle [0,1]\subseteq \mathbb {R} }$

Функция вероятности может принимать в качестве аргумента подмножества самого пространства выборки, как в примере с подбрасыванием монеты, где функция была определена так, что P (орел) = 0,5 и P (решка) = 0,5 . Однако из-за широкого использования случайных величин , которые преобразуют пространство выборки в набор чисел (например, , ), более распространено изучать распределения вероятностей, аргументом которых являются подмножества этих конкретных видов множеств (множеств чисел), ^[6] и все распределения вероятностей, обсуждаемые в этой статье, относятся к этому типу. Обычно обозначается как вероятность того, что определенное значение переменной принадлежит определенному событию . ^{[7] [8]} ${\displaystyle P}$ ${\displaystyle P}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {N} }$ ${\displaystyle P(X\in E)}$ ${\displaystyle X}$ ${\displaystyle E}$

Вышеуказанная функция вероятности характеризует распределение вероятностей только в том случае, если она удовлетворяет всем аксиомам Колмогорова , то есть:

1. ${\displaystyle P(X\in E)\geq 0\;\forall E\in {\mathcal {A}}}$, поэтому вероятность неотрицательна
2. ${\displaystyle P(X\in E)\leq 1\;\forall E\in {\mathcal {A}}}$, поэтому никакая вероятность не превышает ${\displaystyle 1}$
3. ${\displaystyle P(X\in \bigcup _{i}E_{i})=\sum _{i}P(X\in E_{i})}$для любого счетного непересекающегося семейства множеств ${\displaystyle \{E_{i}\}}$

Понятие функции вероятности становится более строгим, если определить его как элемент вероятностного пространства , где — множество возможных результатов, — множество всех подмножеств , вероятность которых может быть измерена, а — функция вероятности или мера вероятности , которая присваивает вероятность каждому из этих измеримых подмножеств . ^[9] ${\displaystyle (X,{\mathcal {A}},P)}$ ${\displaystyle X}$ ${\displaystyle {\mathcal {A}}}$ ${\displaystyle E\subset X}$ ${\displaystyle P}$ ${\displaystyle E\in {\mathcal {A}}}$

Распределения вероятностей обычно принадлежат к одному из двух классов. Дискретное распределение вероятностей применимо к сценариям, где набор возможных результатов дискретен (например, подбрасывание монеты, бросок игральной кости), а вероятности кодируются дискретным списком вероятностей результатов; в этом случае дискретное распределение вероятностей известно как функция массы вероятности . С другой стороны, абсолютно непрерывные распределения вероятностей применимы к сценариям, где набор возможных результатов может принимать значения в непрерывном диапазоне (например, действительные числа), такие как температура в данный день. В абсолютно непрерывном случае вероятности описываются функцией плотности вероятности , а распределение вероятностей по определению является интегралом функции плотности вероятности. ^{[7] [4] [8]} Нормальное распределение является часто встречающимся абсолютно непрерывным распределением вероятностей. Более сложные эксперименты, такие как эксперименты со стохастическими процессами , определенными в непрерывном времени , могут потребовать использования более общих мер вероятности .

Распределение вероятностей, выборочное пространство которого является одномерным (например, действительные числа, список меток, упорядоченные метки или двоичное), называется одномерным , в то время как распределение, выборочное пространство которого является векторным пространством размерности 2 или более, называется многомерным . Одномерное распределение дает вероятности того, что одна случайная величина принимает различные значения; многомерное распределение ( совместное распределение вероятностей ) дает вероятности того, что случайный вектор — список из двух или более случайных величин — принимает различные комбинации значений. Важные и часто встречающиеся одномерные распределения вероятностей включают биномиальное распределение , гипергеометрическое распределение и нормальное распределение . Часто встречающееся многомерное распределение — это многомерное нормальное распределение .

Помимо функции вероятности, кумулятивная функция распределения, функция массы вероятности и функция плотности вероятности, функция генерации момента и характеристическая функция также служат для определения распределения вероятности, поскольку они однозначно определяют базовую кумулятивную функцию распределения. ^[10]

Рисунок 2: Функция плотности вероятности (pdf) нормального распределения , также называемого гауссовым или "колоколом", наиболее важным абсолютно непрерывным случайным распределением. Как отмечено на рисунке, вероятности интервалов значений соответствуют площади под кривой.

Терминология

Ниже перечислены некоторые ключевые понятия и термины, широко используемые в литературе по теме распределений вероятностей. ^[1]

Основные термины

• Случайная величина : принимает значения из выборочного пространства; вероятности описывают, какие значения и наборы значений принимаются с большей вероятностью.
• Событие : набор возможных значений (результатов) случайной величины, возникающий с определенной вероятностью.
• Функция вероятности или мера вероятности : описывает вероятностьтого, что событиепроизойдет. ^[11] ${\displaystyle P(X\in E)}$ ${\displaystyle E,}$
• Кумулятивная функция распределения : функция, оценивающая вероятность того, чтопримет значение, меньшее или равное(только для действительных случайных величин). ${\displaystyle X}$ ${\displaystyle x}$
• Функция квантиля : обратная функция кумулятивной функции распределения. Даеттакое, что с вероятностьюнепревысит. ${\displaystyle x}$ ${\displaystyle q}$ ${\displaystyle X}$ ${\displaystyle x}$

Дискретные распределения вероятностей

• Дискретное распределение вероятностей : для многих случайных величин с конечным или счетно бесконечным числом значений.
• Функция массы вероятности ( pmf ): функция, которая определяет вероятность того, что дискретная случайная величина равна некоторому значению.
• Распределение частот : таблица, отображающая частоту различных результатов в выборке .
• Относительное частотное распределение : частотное распределение , где каждое значение разделено (нормализовано) на количество результатов в выборке (т. е. размер выборки).
• Категориальное распределение : для дискретных случайных величин с конечным набором значений.

Абсолютно непрерывные распределения вероятностей

• Абсолютно непрерывное распределение вероятностей : для многих случайных величин с несчетным числом значений.
• Функция плотности вероятности ( pdf ) или плотность вероятности : функция, значение которой в любой заданной выборке (или точке) в пространстве выборок (набор возможных значений, принимаемых случайной величиной) можно интерпретировать как обеспечивающую относительную вероятность того, что значение случайной величины будет равно этому образцу.

Связанные термины

• Поддержка : множество значений, которые могут быть приняты с ненулевой вероятностью (или плотностью вероятности в случае непрерывного распределения) случайной величиной. Для случайной величиныэто иногда обозначается как. ${\displaystyle X}$ ${\displaystyle R_{X}}$
• Хвост : ^[12] области, близкие к границам случайной величины, если pmf или pdf относительно низки в них. Обычно имеет форму , или их объединение. ${\displaystyle X>a}$ ${\displaystyle X<b}$
• Голова : ^[12] область, где pmf или pdf относительно высоки. Обычно имеет вид . ${\displaystyle a<X<b}$
• Ожидаемое значение или среднее значение : средневзвешенное значение возможных значений, использующее их вероятности в качестве весов; или его непрерывный аналог.
• Медиана : значение, при котором набор значений, меньших медианы, и набор значений, больших медианы, имеют вероятности не более половины.
• Мода : для дискретной случайной величины — значение с наибольшей вероятностью; для абсолютно непрерывной случайной величины — местоположение, в котором функция плотности вероятности имеет локальный пик.
• Квантиль : q-квантиль — это значение,такое что. ${\displaystyle x}$ ${\displaystyle P(X<x)=q}$
• Дисперсия : второй момент pmf или pdf относительно среднего значения; важная мера дисперсии распределения .
• Стандартное отклонение : квадратный корень из дисперсии и, следовательно, еще одна мера дисперсии.
• Симметрия : свойство некоторых распределений, при котором часть распределения слева от определенного значения (обычно медианы) является зеркальным отражением части справа.
• Асимметрия : мера степени, в которой pmf или pdf «наклоняется» в одну сторону от своего среднего значения. Третий стандартизованный момент распределения.
• Эксцесс : мера «жирности» хвостов pmf или pdf. Четвертый стандартизованный момент распределения.

Кумулятивная функция распределения

В частном случае действительной случайной величины распределение вероятностей может быть эквивалентно представлено кумулятивной функцией распределения вместо вероятностной меры. Кумулятивная функция распределения случайной величины относительно распределения вероятностей определяется как ${\displaystyle X}$ ${\displaystyle p}$ $${\displaystyle F(x)=P(X\leq x).}$$

Кумулятивная функция распределения любой действительной случайной величины обладает свойствами:

• ${\displaystyle F(x)}$не убывает;
• ${\displaystyle F(x)}$непрерывен справа ;
• ${\displaystyle 0\leq F(x)\leq 1}$;
• ${\displaystyle \lim _{x\to -\infty }F(x)=0}$и ; и ${\displaystyle \lim _{x\to \infty }F(x)=1}$
• ${\displaystyle \Pr(a<X\leq b)=F(b)-F(a)}$.

И наоборот, любая функция , которая удовлетворяет первым четырем из приведенных выше свойств, является кумулятивной функцией распределения некоторого распределения вероятностей действительных чисел. ^[13] ${\displaystyle F:\mathbb {R} \to \mathbb {R} }$

Любое распределение вероятностей можно разложить в виде смеси дискретного , абсолютно непрерывного и сингулярного непрерывного распределений ^[14], и , таким образом , любая кумулятивная функция распределения допускает разложение в виде выпуклой суммы трех соответствующих кумулятивных функций распределения.

Дискретное распределение вероятностей

Рисунок 3: Функция массы вероятности (pmf) определяет распределение вероятностей для суммы результатов двух игральных костей . Например, на рисунке показано, что . pmf позволяет вычислять вероятности таких событий, как , и все другие вероятности в распределении. ${\displaystyle p(S)}$ ${\displaystyle S}$ ${\displaystyle p(11)=2/36=1/18}$ ${\displaystyle P(X>9)=1/12+1/18+1/36=1/6}$

Рисунок 4: Функция массы вероятности дискретного распределения вероятностей. Вероятности синглтонов {1} , {3} и {7} соответственно равны 0,2, 0,5, 0,3. Набор, не содержащий ни одной из этих точек, имеет нулевую вероятность.

Рисунок 5: CDF дискретного распределения вероятностей, ...

Рисунок 6: ... непрерывного распределения вероятностей, ...

Рисунок 7: ... распределения, имеющего как непрерывную, так и дискретную часть

Дискретное распределение вероятностей — это распределение вероятностей случайной величины, которая может принимать только счетное число значений ^[15] ( почти наверняка ) ^[16] , что означает, что вероятность любого события может быть выражена в виде (конечной или счетно бесконечной ) суммы: где — счетное множество с . Таким образом, дискретные случайные величины (т. е. случайные величины, распределение вероятностей которых дискретно) — это в точности те, у которых функция массы вероятности . В случае, когда диапазон значений счетно бесконечен, эти значения должны уменьшаться до нуля достаточно быстро, чтобы вероятности в сумме дали 1. Например, если для , сумма вероятностей будет . ${\displaystyle E}$ $${\displaystyle P(X\in E)=\sum _{\omega \in A\cap E}P(X=\omega ),}$$ ${\displaystyle A}$ ${\displaystyle P(X\in A)=1}$ ${\displaystyle p(x)=P(X=x)}$ ${\displaystyle p(n)={\tfrac {1}{2^{n}}}}$ ${\displaystyle n=1,2,...}$ ${\displaystyle 1/2+1/4+1/8+\dots =1}$

Известные дискретные распределения вероятностей, используемые в статистическом моделировании, включают распределение Пуассона , распределение Бернулли , биномиальное распределение , геометрическое распределение , отрицательное биномиальное распределение и категориальное распределение . ^[3] Когда выборка (набор наблюдений) извлекается из более крупной популяции, точки выборки имеют эмпирическое распределение , которое является дискретным и которое предоставляет информацию о распределении популяции. Кроме того, дискретное равномерное распределение обычно используется в компьютерных программах, которые делают равновероятные случайные выборки между несколькими вариантами.

Кумулятивная функция распределения

Действительная дискретная случайная величина может быть эквивалентно определена как случайная величина, кумулятивная функция распределения которой увеличивается только за счет скачков — то есть ее cdf увеличивается только там, где она «прыгает» к более высокому значению, и постоянна в интервалах без скачков. Точки, где происходят скачки, — это как раз те значения, которые может принимать случайная величина. Таким образом, кумулятивная функция распределения имеет вид $${\displaystyle F(x)=P(X\leq x)=\sum _{\omega \leq x}p(\omega ).}$$

Точки, в которых функция cdf совершает скачки, всегда образуют счетное множество; это может быть любое счетное множество, и, таким образом, оно может быть даже плотным по действительным числам.

Дирак дельта представление

Дискретное распределение вероятностей часто представляется мерами Дирака , распределениями вероятностей детерминированных случайных величин . Для любого результата пусть будет мерой Дирака, сосредоточенной в . При наличии дискретного распределения вероятностей существует счетное множество с и функцией массы вероятности . Если - любое событие, то или, короче говоря, ${\displaystyle \omega }$ ${\displaystyle \delta _{\omega }}$ ${\displaystyle \omega }$ ${\displaystyle A}$ ${\displaystyle P(X\in A)=1}$ ${\displaystyle p}$ ${\displaystyle E}$ $${\displaystyle P(X\in E)=\sum _{\omega \in A}p(\omega )\delta _{\omega }(E),}$$ $${\displaystyle P_{X}=\sum _{\omega \in A}p(\omega )\delta _{\omega }.}$$

Аналогично, дискретные распределения могут быть представлены с помощью дельта-функции Дирака как обобщенной функции плотности вероятности , где что означает для любого события ^[17] ${\displaystyle f}$ $${\displaystyle f(x)=\sum _{\omega \in A}p(\omega )\delta (x-\omega ),}$$ $${\displaystyle P(X\in E)=\int _{E}f(x)\,dx=\sum _{\omega \in A}p(\omega )\int _{E}\delta (x-\omega )=\sum _{\omega \in A\cap E}p(\omega )}$$ ${\displaystyle E.}$

Индикаторно-функциональное представление

Для дискретной случайной величины пусть будут значения, которые она может принимать с ненулевой вероятностью. Обозначим ${\displaystyle X}$ ${\displaystyle u_{0},u_{1},\dots }$

$${\displaystyle \Omega _{i}=X^{-1}(u_{i})=\{\omega :X(\omega )=u_{i}\},\,i=0,1,2,\dots }$$

Это непересекающиеся множества , и для таких множеств

$${\displaystyle P\left(\bigcup _{i}\Omega _{i}\right)=\sum _{i}P(\Omega _{i})=\sum _{i}P(X=u_{i})=1.}$$

Отсюда следует, что вероятность того, что принимает любое значение, кроме , равна нулю, и поэтому можно записать как ${\displaystyle X}$ ${\displaystyle u_{0},u_{1},\dots }$ ${\displaystyle X}$

$${\displaystyle X(\omega )=\sum _{i}u_{i}1_{\Omega _{i}}(\omega )}$$

за исключением множества с нулевой вероятностью, где — индикаторная функция . Это может служить альтернативным определением дискретных случайных величин. ${\displaystyle 1_{A}}$ ${\displaystyle A}$

Одноточечное распределение

Особым случаем является дискретное распределение случайной величины, которая может принимать только одно фиксированное значение; другими словами, это детерминированное распределение . Выражаясь формально, случайная величина имеет одноточечное распределение, если она имеет возможный результат такой, что ^[18] Все другие возможные результаты тогда имеют вероятность 0. Ее кумулятивная функция распределения немедленно прыгает от 0 до 1. ${\displaystyle X}$ ${\displaystyle x}$ ${\displaystyle P(X{=}x)=1.}$

Абсолютно непрерывное распределение вероятностей

Абсолютно непрерывное распределение вероятностей — это распределение вероятностей на действительных числах с несчетным количеством возможных значений, таких как целый интервал на действительной прямой, и где вероятность любого события может быть выражена в виде интеграла. ^[19] Точнее, действительная случайная величина имеет абсолютно непрерывное распределение вероятностей, если существует функция такая, что для каждого интервала вероятность принадлежности к задается интегралом от по : [ ^{20] [21]} Это определение функции плотности вероятности , так что абсолютно непрерывные распределения вероятностей — это в точности те, у которых есть функция плотности вероятности. В частности, вероятность для принять любое единственное значение (то есть ) равна нулю, потому что интеграл с совпадающими верхним и нижним пределами всегда равен нулю. Если интервал заменить любым измеримым множеством , соответствующее равенство по-прежнему будет иметь место: ${\displaystyle X}$ ${\displaystyle f:\mathbb {R} \to [0,\infty ]}$ ${\displaystyle I=[a,b]\subset \mathbb {R} }$ ${\displaystyle X}$ ${\displaystyle I}$ ${\displaystyle f}$ ${\displaystyle I}$ $${\displaystyle P\left(a\leq X\leq b\right)=\int _{a}^{b}f(x)\,dx.}$$ ${\displaystyle X}$ ${\displaystyle a}$ ${\displaystyle a\leq X\leq a}$ ${\displaystyle [a,b]}$ ${\displaystyle A}$ $${\displaystyle P(X\in A)=\int _{A}f(x)\,dx.}$$

Абсолютно непрерывная случайная величина — это случайная величина, распределение вероятностей которой абсолютно непрерывно.

Существует множество примеров абсолютно непрерывных распределений вероятностей: нормальное , равномерное , хи-квадрат и другие .

Кумулятивная функция распределения

Абсолютно непрерывные распределения вероятностей, как определено выше, — это именно те, у которых есть абсолютно непрерывная кумулятивная функция распределения. В этом случае кумулятивная функция распределения имеет вид где — плотность случайной величины относительно распределения . ${\displaystyle F}$ $${\displaystyle F(x)=P(X\leq x)=\int _{-\infty }^{x}f(t)\,dt}$$ ${\displaystyle f}$ ${\displaystyle X}$ ${\displaystyle P}$

Примечание по терминологии: Абсолютно непрерывные распределения следует отличать от непрерывных распределений , которые имеют непрерывную кумулятивную функцию распределения. Каждое абсолютно непрерывное распределение является непрерывным распределением, но обратное неверно, существуют сингулярные распределения , которые не являются ни абсолютно непрерывными, ни дискретными, ни смесью тех и других, и не имеют плотности. Примером может служить распределение Кантора . Однако некоторые авторы используют термин «непрерывное распределение» для обозначения всех распределений, кумулятивная функция распределения которых абсолютно непрерывна , т. е. называют абсолютно непрерывные распределения непрерывными распределениями. ^[7]

Более общее определение функций плотности и эквивалентных им абсолютно непрерывных мер см. в статье Абсолютно непрерывная мера .

Определение Колмогорова

В меро-теоретической формализации теории вероятностей случайная величина определяется как измеримая функция из вероятностного пространства в измеримое пространство . Учитывая, что вероятности событий вида удовлетворяют вероятностным аксиомам Колмогорова , распределение вероятностей является мерой изображения , которая является вероятностной мерой при удовлетворении . ^{[22] [23] [24]} ${\displaystyle X}$ ${\displaystyle (\Omega ,{\mathcal {F}},\mathbb {P} )}$ ${\displaystyle ({\mathcal {X}},{\mathcal {A}})}$ ${\displaystyle \{\omega \in \Omega \mid X(\omega )\in A\}}$ ${\displaystyle X}$ ${\displaystyle X_{*}\mathbb {P} }$ ${\displaystyle X}$ ${\displaystyle ({\mathcal {X}},{\mathcal {A}})}$ ${\displaystyle X_{*}\mathbb {P} =\mathbb {P} X^{-1}}$

Другие виды дистрибуции

Рисунок 8: Одно из решений уравнений Рабиновича–Фабриканта . Какова вероятность наблюдения состояния на определенном месте носителя (т.е. красном подмножестве)?

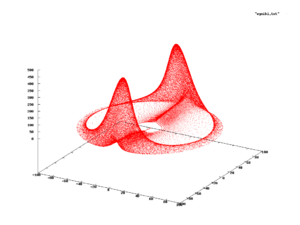
Абсолютно непрерывные и дискретные распределения с поддержкой на или чрезвычайно полезны для моделирования множества явлений, ^{[7] [5],} поскольку большинство практических распределений поддерживаются на относительно простых подмножествах, таких как гиперкубы или шары . Однако это не всегда так, и существуют явления с поддержкой, которые на самом деле являются сложными кривыми в некотором пространстве или подобном. В этих случаях распределение вероятностей поддерживается на изображении такой кривой и, скорее всего, будет определено эмпирически, а не найдена замкнутая формула для него. ^[25] ${\displaystyle \mathbb {R} ^{k}}$ ${\displaystyle \mathbb {N} ^{k}}$ ${\displaystyle \gamma :[a,b]\rightarrow \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {R} ^{n}}$

Один из примеров показан на рисунке справа, который отображает эволюцию системы дифференциальных уравнений (обычно известных как уравнения Рабиновича–Фабриканта ), которые можно использовать для моделирования поведения волн Ленгмюра в плазме . ^[26] При изучении этого явления наблюдаемые состояния из подмножества показаны красным. Поэтому можно спросить, какова вероятность наблюдения состояния в определенном положении красного подмножества; если такая вероятность существует, она называется вероятностной мерой системы. ^{[27] [25]}

Этот вид сложной поддержки довольно часто встречается в динамических системах . Непросто установить, что система имеет вероятностную меру, и основная проблема заключается в следующем. Пусть будут моментами времени и подмножеством поддержки; если вероятностная мера существует для системы, можно было бы ожидать, что частота наблюдения состояний внутри множества будет равна в интервале и , чего может и не произойти; например, она может колебаться подобно синусу, , предел которого при не сходится. Формально мера существует только в том случае, если предел относительной частоты сходится, когда система наблюдается в бесконечном будущем. ^[28] Раздел динамических систем, который изучает существование вероятностной меры, — это эргодическая теория . ${\displaystyle t_{1}\ll t_{2}\ll t_{3}}$ ${\displaystyle O}$ ${\displaystyle O}$ ${\displaystyle [t_{1},t_{2}]}$ ${\displaystyle [t_{2},t_{3}]}$ ${\displaystyle \sin(t)}$ ${\displaystyle t\rightarrow \infty }$

Обратите внимание, что даже в этих случаях распределение вероятностей, если оно существует, все равно можно назвать «абсолютно непрерывным» или «дискретным» в зависимости от того, является ли носитель несчетным или счетным соответственно.

Генерация случайных чисел

Большинство алгоритмов основаны на генераторе псевдослучайных чисел , который производит числа , равномерно распределенные в полуоткрытом интервале [0, 1) . Эти случайные переменные затем преобразуются с помощью некоторого алгоритма для создания новой случайной переменной, имеющей требуемое распределение вероятностей. С этим источником равномерной псевдослучайности можно сгенерировать реализации любой случайной величины. ^[29] ${\displaystyle X}$ ${\displaystyle X}$

Например, предположим, что имеет равномерное распределение между 0 и 1. Чтобы построить случайную переменную Бернулли для некоторого , мы определяем так, что ${\displaystyle U}$ ${\displaystyle 0<p<1}$ $${\displaystyle X={\begin{cases}1,&{\text{if }}U<p\\0,&{\text{if }}U\geq p\end{cases}}}$$ $${\displaystyle \Pr(X=1)=\Pr(U<p)=p,\quad \Pr(X=0)=\Pr(U\geq p)=1-p.}$$

Эта случайная величина X имеет распределение Бернулли с параметром . ^[29] Это преобразование дискретной случайной величины. ${\displaystyle p}$

Для функции распределения абсолютно непрерывной случайной величины необходимо построить абсолютно непрерывную случайную величину. , обратная функция , относится к равномерной величине : ${\displaystyle F}$ ${\displaystyle F^{\mathit {inv}}}$ ${\displaystyle F}$ ${\displaystyle U}$ $${\displaystyle {U\leq F(x)}={F^{\mathit {inv}}(U)\leq x}.}$$

Например, предположим, что необходимо построить случайную величину, имеющую экспоненциальное распределение. ${\displaystyle F(x)=1-e^{-\lambda x}}$

$${\displaystyle {\begin{aligned}F(x)=u&\Leftrightarrow 1-e^{-\lambda x}=u\\[2pt]&\Leftrightarrow e^{-\lambda x}=1-u\\[2pt]&\Leftrightarrow -\lambda x=\ln(1-u)\\[2pt]&\Leftrightarrow x={\frac {-1}{\lambda }}\ln(1-u)\end{aligned}}}$$так и если имеет распределение, то случайная величина определяется как . Это имеет экспоненциальное распределение . ^[29] ${\displaystyle F^{\mathit {inv}}(u)={\frac {-1}{\lambda }}\ln(1-u)}$ ${\displaystyle U}$ ${\displaystyle U(0,1)}$ ${\displaystyle X}$ ${\displaystyle X=F^{\mathit {inv}}(U)={\frac {-1}{\lambda }}\ln(1-U)}$ ${\displaystyle \lambda }$

Частой проблемой статистического моделирования ( метод Монте-Карло ) является генерация псевдослучайных чисел , распределенных заданным образом.

Распространенные распределения вероятностей и их применение

Концепция распределения вероятностей и случайных величин, которые они описывают, лежит в основе математической дисциплины теории вероятностей и науки статистики. Существует разброс или изменчивость почти любой величины, которая может быть измерена в популяции (например, рост людей, прочность металла, рост продаж, транспортный поток и т. д.); почти все измерения производятся с некоторой внутренней ошибкой; в физике многие процессы описываются вероятностно, от кинетических свойств газов до квантово-механического описания фундаментальных частиц . По этим и многим другим причинам простые числа часто неадекватны для описания величины, в то время как распределения вероятностей часто более уместны.

Ниже приведен список некоторых наиболее распространенных распределений вероятностей, сгруппированных по типу процесса, с которым они связаны. Для более полного списка см. список распределений вероятностей , который группируется по характеру рассматриваемого результата (дискретный, абсолютно непрерывный, многомерный и т. д.)

Все одномерные распределения ниже имеют один пик; то есть предполагается, что значения группируются вокруг одной точки. На практике фактически наблюдаемые величины могут группироваться вокруг нескольких значений. Такие величины можно моделировать с помощью смешанного распределения .

Линейный рост (например, ошибки, смещения)

• Нормальное распределение (распределение Гаусса) для одной такой величины; наиболее часто используемое абсолютно непрерывное распределение

Экспоненциальный рост (например, цен, доходов, населения)

• Логарифмически нормальное распределение для одной такой величины, логарифм которой распределен нормально
• Распределение Парето для одной такой величины, логарифм которой распределен экспоненциально ; прототипическое распределение степенного закона

Равномерно распределенные количества

• Дискретное равномерное распределение для конечного набора значений (например, результат честного бросания игральной кости)
• Непрерывное равномерное распределение , для абсолютно непрерывно распределенных значений

Испытания Бернулли (события да/нет, с заданной вероятностью)

• Базовые дистрибутивы:
  • Распределение Бернулли , для результата одного испытания Бернулли (например, успех/неудача, да/нет)
  • Биномиальное распределение для числа «положительных событий» (например, успехов, голосов «за» и т. д.) при фиксированном общем числе независимых событий.
  • Отрицательное биномиальное распределение для наблюдений биномиального типа, но где величина интереса — это число неудач до наступления заданного числа успехов.
  • Геометрическое распределение для наблюдений биномиального типа, но где величина интереса — это число неудач до первого успеха; частный случай отрицательного биномиального распределения.
• Относится к схемам выборки из конечной совокупности:
  • Гипергеометрическое распределение для числа «положительных событий» (например, успехов, голосов «за» и т. д.) при фиксированном общем числе событий, с использованием выборки без возвращения
  • Бета-биномиальное распределение для числа «положительных событий» (например, успехов, голосов «за» и т. д.) при фиксированном общем числе событий, выборка с использованием модели урн Полиа (в некотором смысле «противоположность» выборке без возвращения )

Категориальные результаты (события сКвозможные результаты)

• Категориальное распределение , для одного категориального результата (например, да/нет/может быть в опросе); обобщение распределения Бернулли
• Мультиномиальное распределение для числа каждого типа категориального результата при фиксированном числе общих результатов; обобщение биномиального распределения
• Многомерное гипергеометрическое распределение , похожее на полиномиальное распределение , но использующее выборку без возвращения ; обобщение гипергеометрического распределения.

Процесс Пуассона (события, происходящие независимо с заданной скоростью)

• Распределение Пуассона , для числа появлений события пуассоновского типа за заданный период времени.
• Экспоненциальное распределение , для времени до наступления следующего события пуассоновского типа
• Гамма-распределение , для времени до наступления следующих k событий пуассоновского типа

Абсолютные значения векторов с нормально распределенными компонентами

• Распределение Рэлея , для распределения векторных величин с гауссовыми распределенными ортогональными компонентами. Распределения Рэлея встречаются в радиочастотных сигналах с гауссовыми действительными и мнимыми компонентами.
• Распределение Райса , обобщение распределений Рэлея для случая, когда есть стационарная фоновая компонента сигнала. Найдено в затухании Райса радиосигналов из-за многолучевого распространения и в изображениях МР с шумовым искажением ненулевых сигналов ЯМР.

Нормально распределенные величины, оперируемые суммой квадратов

• Распределение хи-квадрат , распределение суммы квадратов стандартных нормальных переменных; полезно, например, для вывода относительно выборочной дисперсии нормально распределенных выборок (см. критерий хи-квадрат )
• Распределение Стьюдента t , распределение отношения стандартной нормальной переменной и квадратного корня масштабированной переменной хи-квадрат ; полезно для вывода относительно среднего значения нормально распределенных выборок с неизвестной дисперсией (см. t-критерий Стьюдента )
• F-распределение , распределение отношения двух масштабированных переменных хи-квадрат ; полезно, например, для выводов, которые включают сравнение дисперсий или включают R-квадрат (квадрат коэффициента корреляции )

Как сопряженные априорные распределения в байесовском выводе

• Бета-распределение для единичной вероятности (действительное число от 0 до 1); сопряжено с распределением Бернулли и биномиальным распределением
• Гамма-распределение , для неотрицательного параметра масштабирования; сопряжено с параметром скорости распределения Пуассона или экспоненциального распределения , точностью (обратной дисперсией ) нормального распределения и т. д.
• Распределение Дирихле для вектора вероятностей, которые в сумме должны давать 1; сопряжено с категориальным распределением и полиномиальным распределением ; обобщение бета-распределения
• Распределение Уишарта для симметричной неотрицательно определенной матрицы; сопряжено с обратной матрицей ковариации многомерного нормального распределения ; обобщение гамма-распределения ^[30]

Некоторые специализированные приложения вероятностных распределений

• Модели кэшированного языка и другие статистические языковые модели, используемые при обработке естественного языка для назначения вероятностей появления определенных слов и последовательностей слов, делают это с помощью распределений вероятностей.
• В квантовой механике плотность вероятности нахождения частицы в заданной точке пропорциональна квадрату величины волновой функции частицы в этой точке (см. правило Борна ). Таким образом, функция распределения вероятности положения частицы описывается как , вероятность того, что положение частицы x будет находиться в интервале a ≤ x ≤ b в измерении один, и аналогичный тройной интеграл в измерении три. Это ключевой принцип квантовой механики. ^[31] ${\textstyle P_{a\leq x\leq b}(t)=\int _{a}^{b}dx\,|\Psi (x,t)|^{2}}$
• Вероятностный поток нагрузки в исследовании потоков мощности объясняет неопределенности входных переменных как распределение вероятностей и обеспечивает расчет потока мощности также в терминах распределения вероятностей. ^[32]
• Прогнозирование возникновения природных явлений на основе предыдущих распределений частот, таких как тропические циклоны , град, время между событиями и т. д. ^[33]

Подгонка

Подгонка распределения вероятностей или просто подгонка распределения — это подгонка распределения вероятностей к ряду данных, касающихся повторных измерений переменного явления. Цель подгонки распределения — предсказать вероятность или прогнозировать частоту появления величины явления в определенном интервале.

Существует множество распределений вероятностей (см. список распределений вероятностей ), некоторые из которых могут быть более точно подобраны к наблюдаемой частоте данных, чем другие, в зависимости от характеристик явления и распределения. Распределение, дающее близкое соответствие, должно приводить к хорошим прогнозам.

Поэтому при подгонке распределения необходимо выбрать распределение, которое хорошо соответствует данным.

Смотрите также

• Математический портал

• Условное распределение вероятностей
• Эмпирическое распределение вероятностей
• Гистограмма
• Совместное распределение вероятностей
• Мера вероятности
• Распределение квазивероятности
• Применение интеграла Римана–Стилтьеса к теории вероятностей

Списки

• Список вероятностных распределений
• Список статистических тем

Ссылки

Цитаты

1. Everitt, Brian (2006). Кембриджский словарь статистики (3-е изд.). Кембридж, Великобритания: Cambridge University Press. ISBN 978-0-511-24688-3. OCLC  161828328.
2. Эш, Роберт Б. (2008). Основы теории вероятностей (ред. Довер). Минеола, Нью-Йорк: Dover Publications. стр. 66–69. ISBN 978-0-486-46628-6. OCLC  190785258.
3. Эванс, Майкл; Розенталь, Джеффри С. (2010). Вероятность и статистика: наука о неопределенности (2-е изд.). Нью-Йорк: WH Freeman and Co. стр. 38. ISBN 978-1-4292-2462-8. OCLC  473463742.
4. "1.3.6.1. Что такое распределение вероятностей". www.itl.nist.gov . Получено 10.09.2020 .
5. Dekking, Michel (1946–) (2005). Современное введение в теорию вероятностей и статистику: понимание того, почему и как . Лондон, Великобритания: Springer. ISBN 978-1-85233-896-1. OCLC  262680588.{{cite book}}: CS1 maint: numeric names: authors list (link)
6. Уолпол, Р. Э.; Майерс, Р. Х.; Майерс, С. Л.; Йе, К. (1999). Вероятность и статистика для инженеров . Prentice Hall.
7. Росс, Шелдон М. (2010). Первый курс по вероятности . Пирсон.
8. ДеГрут, Моррис Х.; Шервиш, Марк Дж. (2002). Вероятность и статистика . Аддисон-Уэсли.
9. Биллингсли, П. (1986). Вероятность и мера . Wiley. ISBN 9780471804789.
10. Шепард, Н. Г. (1991). «От характеристической функции к функции распределения: простая структура теории». Эконометрическая теория . 7 (4): 519–529. doi :10.1017/S0266466600004746. S2CID  14668369.
11. Главы 1 и 2 Вапника (1998)
12. Более подробную информацию и примеры можно найти в статьях Распределение с тяжелым хвостом , Распределение с длинным хвостом , Распределение с толстым хвостом
13. Эрхан, Чынлар (2011). Вероятность и стохастика . Нью-Йорк: Springer. С. 57. ISBN 9780387878584.
14. см. теорему Лебега о разложении
15. Эрхан, Чынлар (2011). Вероятность и стохастика . Нью-Йорк: Springer. С. 51. ISBN 9780387878591. OCLC  710149819.
16. Кон, Дональд Л. (1993). Теория меры . Биркхойзер.
17. Khuri, André I. (март 2004 г.). «Применение дельта-функции Дирака в статистике». Международный журнал математического образования в науке и технике . 35 (2): 185–195. doi :10.1080/00207390310001638313. ISSN  0020-739X. S2CID  122501973.
18. Фиц, Марек (1963). Теория вероятностей и математическая статистика (3-е изд.). John Wiley & Sons. стр. 129. ISBN 0-471-26250-1.
19. Джеффри Сет Розенталь (2000). Первый взгляд на строгую теорию вероятностей . World Scientific.
20. Глава 3.2 ДеГрута и Шервиша (2002)
21. Борн, Мюррей. "11. Распределения вероятностей - Концепции". www.intmath.com . Получено 10 сентября 2020 г.
22. W., Stroock, Daniel (1999). Теория вероятностей: аналитический взгляд (Rev. ed.). Кембридж [Англия]: Cambridge University Press. стр. 11. ISBN 978-0521663496. OCLC  43953136.{{cite book}}: CS1 maint: multiple names: authors list (link)
23. Колмогоров, Андрей (1950) [1933]. Основы теории вероятностей . Нью-Йорк, США: Chelsea Publishing Company. С. 21–24.
24. Джойс, Дэвид (2014). "Аксиомы вероятности" (PDF) . Университет Кларка . Получено 5 декабря 2019 г. .
25. Alligood, KT; Sauer, TD; Yorke, JA (1996). Хаос: введение в динамические системы . Springer.
26. Рабинович, МИ; Фабрикант, АЛ (1979). «Стохастическая самомодуляция волн в неравновесных средах». J. Exp. Theor. Phys . 77 : 617–629. Bibcode :1979JETP...50..311R.
27. Раздел 1.9 Росс, SM; Пекоз, EA (2007). Второй курс по вероятности (PDF) .
28. Уолтерс, Питер (2000). Введение в эргодическую теорию . Springer.
29. Деккинг, Фредерик Михель; Краайкамп, Корнелис; Лопухаа, Хендрик Пол; Мистер, Людольф Эрвин (2005), «Почему вероятность и статистика?», Современное введение в вероятность и статистику , Springer London, стр. 1–11, doi :10.1007/1-84628-168-7_1, ISBN 978-1-85233-896-1
30. Бишоп, Кристофер М. (2006). Распознавание образов и машинное обучение . Нью-Йорк: Springer. ISBN 0-387-31073-8. OCLC  71008143.
31. Чанг, Рэймонд. (2014). Физическая химия для химических наук . Томан, Джон У., младший, 1960-. [Милл-Вэлли, Калифорния]. стр. 403–406. ISBN 978-1-68015-835-9. OCLC  927509011.{{cite book}}: CS1 maint: location missing publisher (link)
32. Чен, П.; Чен, З.; Бак-Дженсен, Б. (апрель 2008 г.). «Вероятностный поток нагрузки: обзор». Третья международная конференция 2008 г. по дерегулированию и реструктуризации электроэнергетических компаний и энергетическим технологиям . стр. 1586–1591. doi :10.1109/drpt.2008.4523658. ISBN 978-7-900714-13-8. S2CID  18669309.
33. Maity, Rajib (2018-04-30). Статистические методы в гидрологии и гидроклиматологии . Сингапур. ISBN 978-981-10-8779-0. OCLC  1038418263.{{cite book}}: CS1 maint: location missing publisher (link)

Источники

• den Dekker, AJ; Sijbers, J. (2014). «Распределение данных в магнитно-резонансных изображениях: обзор». Physica Medica . 30 (7): 725–741. doi :10.1016/j.ejmp.2014.05.002. PMID  25059432.
• Вапник, Владимир Наумович (1998). Статистическая теория обучения . John Wiley and Sons.

Внешние ссылки

• «Распределение вероятностей», Энциклопедия математики , EMS Press , 2001 [1994]
• Полевое руководство по непрерывным распределениям вероятностей, Гэвин Э. Крукс.
• Различение вероятностной меры, функции и распределения, Math Stack Exchange