Добавление

Арифметическая операция

3 + 2 = 5 с яблоками , популярный выбор в учебниках ^[1]

Сложение (обычно обозначается знаком плюс + ) является одной из четырех основных операций арифметики , остальные три — вычитание , умножение и деление . ^[2] Сложение двух целых чисел дает общую сумму этих значений. Пример на соседнем изображении показывает два столбца по три яблока и два яблока в каждом, что в сумме дает пять яблок. Это наблюдение эквивалентно математическому выражению «3 + 2 = 5» (то есть «3 плюс 2 равно 5»).

Помимо подсчета элементов, сложение также может быть определено и выполнено без ссылки на конкретные объекты , используя вместо этого абстракции, называемые числами , такие как целые числа , действительные числа и комплексные числа . Сложение относится к арифметике, разделу математики . В алгебре , другой области математики, сложение также может быть выполнено на абстрактных объектах, таких как векторы , матрицы , подпространства и подгруппы .

Сложение имеет несколько важных свойств. Оно коммутативно , что означает, что порядок операндов не имеет значения, и ассоциативно , что означает, что при сложении более двух чисел порядок, в котором выполняется сложение, не имеет значения. Повторное сложение 1 равнозначно подсчету (см. Функция Successor ). Сложение не изменяет число. Сложение также подчиняется предсказуемым правилам, касающимся связанных операций, таких как вычитание и умножение.

Выполнение сложения является одной из самых простых числовых задач. Сложение очень маленьких чисел доступно для малышей; самая простая задача, 1 + 1 , может быть выполнена младенцами в возрасте от пяти месяцев и даже некоторыми представителями других видов животных. В начальной школе учеников учат складывать числа в десятичной системе, начиная с однозначных цифр и постепенно решая более сложные задачи. Механические вспомогательные средства варьируются от древних счетов до современных компьютеров , где исследования наиболее эффективных реализаций сложения продолжаются и по сей день.

Обозначения и терминология

Знак плюс

Сложение записывается с использованием знака плюс "+" между членами; ^[3] то есть в инфиксной записи . Результат выражается знаком равенства . Например,

${\displaystyle 1+2=3}$(«один плюс два равно трем»)

${\displaystyle 5+4+2=11}$(см. «ассоциативность» ниже)

${\displaystyle 3+3+3+3=12}$(см. «умножение» ниже)

Сложение столбиков – числа в столбце нужно сложить, а сумму записать под подчеркнутым числом.

Бывают также ситуации, когда сложение «понимается», даже если не появляется никакого символа:

• Целое число, за которым сразу следует дробь , указывает на сумму двух чисел, называемую смешанным числом . ^[4] Например, эта запись может вызвать путаницу, поскольку в большинстве других контекстов сопоставление обозначает умножение . ^[5] $${\displaystyle 3{\frac {1}{2}}=3+{\frac {1}{2}}=3.5.}$$

Сумма ряда связанных чисел может быть выражена с помощью заглавной сигма-обозначения , которая компактно обозначает итерацию . Например,

${\displaystyle \sum _{k=1}^{5}k^{2}=1^{2}+2^{2}+3^{2}+4^{2}+5^{2}=55.}$

Условия

Числа или объекты, которые должны быть сложены в общем сложении, совместно называются членами , [ ^6] слагаемыми [ ^{7] [8] [9]} или слагаемыми ; ^[10] эта терминология переносится на суммирование нескольких членов. Это следует отличать от множителей , которые умножаются . Некоторые авторы называют первое слагаемое слагаемым . [ ^{7] [8] [9]} Фактически, в эпоху Возрождения многие авторы вообще не считали первое слагаемое «слагаемым». Сегодня из-за коммутативного свойства сложения «слагаемое» используется редко, и оба термина обычно называются слагаемыми. ^[11]

Вся вышеприведенная терминология происходит от латинского . «Addition» и «add» — английские слова, произошедшие от латинского глагола addere , который в свою очередь является соединением ad « to» и dare «to give», от протоиндоевропейского корня *deh₃- «to give»; таким образом, to add означает «to give to » . ^[11] Использование суффикса герундия -nd приводит к «addend», «вещь, которая будет добавлена». ^[a] Аналогично от augere «to increase» получается «augend», «вещь, которая будет увеличена».

Перерисованная иллюстрация из «Искусства Номбринга» , одного из первых английских арифметических текстов, написанного в XV веке. ^[12]

«Sum» и «summand» происходят от латинского существительного summa «самый высокий, вершина» и связанного с ним глагола summare . Это уместно не только потому, что сумма двух положительных чисел больше любого из них, но и потому, что для древних греков и римлян было обычным складывать вверх, в отличие от современной практики сложения вниз, так что сумма была буквально больше слагаемых. ^[13] Addere и summare восходят по крайней мере к Боэцию , если не к более ранним римским писателям, таким как Витрувий и Фронтин ; Боэций также использовал несколько других терминов для операции сложения. Более поздние среднеанглийские термины «adden» и «adding» были популяризированы Чосером . ^[14]

Знак плюс «+» ( Unicode :U+002B; ASCII :) +— это сокращение от латинского слова et , означающего «и». ^[15] Он появляется в математических работах, датируемых как минимум 1489 годом. ^[16]

Интерпретации

Сложение используется для моделирования многих физических процессов. Даже для простого случая сложения натуральных чисел существует множество возможных интерпретаций и еще больше визуальных представлений.

Объединение наборов

В одном наборе 3 фигуры, а в другом — 2. Общее количество фигур равно 5, что является следствием сложения объектов из двух наборов (3 + 2 = 5).

Возможно, самая простая интерпретация сложения заключается в объединении множеств :

• Когда две или более непересекающихся коллекции объединяются в одну коллекцию, количество объектов в одной коллекции равно сумме количеств объектов в исходных коллекциях.

Эту интерпретацию легко визуализировать, с небольшой опасностью двусмысленности. Она также полезна в высшей математике (строгое определение, которое она вдохновляет, см. ниже в разделе Натуральные числа). Однако не очевидно, как следует расширить эту версию сложения, чтобы включить дробные числа или отрицательные числа. ^[17]

Одним из возможных решений является рассмотрение наборов объектов, которые можно легко разделить, например, пирогов или, что еще лучше, сегментированных стержней. ^[18] Вместо того, чтобы просто объединять наборы сегментов, стержни можно соединять концом к концу, что иллюстрирует другую концепцию сложения: сложение не стержней, а их длин.

Увеличение длины

Визуализация алгебраического сложения 2 + 4 = 6 на числовой прямой. «Прыжок» на расстояние 2, за которым следует другой, длиной 4, равен переносу на 6.

Визуализация унарного сложения на числовой оси 2 + 4 = 6. Сдвиг на 4 эквивалентен четырем сдвигам на 1.

Вторая интерпретация сложения происходит от увеличения исходной длины на заданную длину:

• Когда исходная длина увеличивается на заданную величину, конечная длина представляет собой сумму исходной длины и длины расширения. ^[19]

Сумма a + b может быть интерпретирована как бинарная операция , которая объединяет a и b , в алгебраическом смысле, или она может быть интерпретирована как добавление b дополнительных единиц к a . Согласно последней интерпретации, части суммы a + b играют асимметричные роли, и операция a + b рассматривается как применение унарной операции + b к a . ^[20] Вместо того, чтобы называть a и b слагаемыми, в этом случае более уместно называть a слагаемым , поскольку a играет пассивную роль. Унарное представление также полезно при обсуждении вычитания , потому что каждая унарная операция сложения имеет обратную унарную операцию вычитания, и наоборот .

Характеристики

Коммутативность

4 + 2 = 2 + 4 с блоками

Сложение коммутативно , то есть можно менять порядок членов в сумме, но все равно получить тот же результат. Символически, если a и b — любые два числа, то

а + б = б + а .

Тот факт, что сложение коммутативно, известен как «коммутативный закон сложения» или «коммутативное свойство сложения». Некоторые другие бинарные операции являются коммутативными, например умножение, но многие другие, например вычитание и деление, таковыми не являются.

Ассоциативность

2 + (1 + 3) = (2 + 1) + 3 с сегментированными стержнями

Сложение является ассоциативным , то есть при сложении трех и более чисел порядок операций не меняет результат.

Например, следует ли выражение a + b + c определить как ( a + b ) + c или a + ( b + c )? Учитывая, что сложение ассоциативно, выбор определения не имеет значения. Для любых трех чисел a , b , и c верно, что ( a + b ) + c = a + ( b + c ) . Например, (1 + 2) + 3 = 3 + 3 = 6 = 1 + 5 = 1 + (2 + 3) .

Когда сложение используется вместе с другими операциями, порядок операций становится важным. В стандартном порядке операций сложение имеет меньший приоритет, чем возведение в степень , корни n-й степени , умножение и деление, но имеет такой же приоритет, как вычитание. ^[21]

Элемент идентичности

5 + 0 = 5 с мешочками точек

Добавление нуля к любому числу не меняет число; это означает, что ноль является элементом тождества для сложения, и также известен как аддитивное тождество . В символах для каждого a есть

а + 0 = 0 + а = а .

Этот закон был впервые выявлен в «Брахмаспхутасиддханте » Брахмагупты в 628 году нашей эры, хотя он записал его как три отдельных закона, в зависимости от того, является ли a отрицательным, положительным или самим нулем, и он использовал слова, а не алгебраические символы. Позднее индийские математики усовершенствовали эту концепцию; около 830 года Махавира написал: «ноль становится тем же самым, что и то, что к нему прибавлено», что соответствует унарному утверждению 0 + a = a . В 12 веке Бхаскара написал: «При сложении нуля или вычитании его количество, положительное или отрицательное, остается тем же самым», что соответствует унарному утверждению a + 0 = a . ^[22]

Преемник

В контексте целых чисел сложение единицы также играет особую роль: для любого целого числа a целое число ( a + 1) является наименьшим целым числом, большим a , также известным как последующее число a . ^[23] Например, 3 является последующим числом 2, а 7 является последующим числом 6. Из-за этой последовательности значение a + b также можно рассматривать как b -е последующее число a , делая сложение итеративным последовательным. Например, 6 + 2 равно 8, потому что 8 является последующим числом 7, которое является последующим числом 6, делая 8 вторым последующим числом 6.

Единицы

Чтобы численно сложить физические величины с единицами , они должны быть выражены в общих единицах. ^[24] Например, добавление 50 миллилитров к 150 миллилитрам дает 200 миллилитров. Однако, если мера 5 футов продлена на 2 дюйма, сумма составит 62 дюйма, поскольку 60 дюймов являются синонимом 5 футов. С другой стороны, обычно бессмысленно пытаться сложить 3 метра и 4 квадратных метра, поскольку эти единицы несопоставимы; такого рода соображения являются основополагающими в размерном анализе . ^[25]

Выполнение сложения

Врожденная способность

Исследования математического развития, начавшиеся примерно в 1980-х годах, использовали явление привыкания : младенцы дольше смотрят на неожиданные ситуации. ^[26] Основополагающий эксперимент Карен Уинн в 1992 году с куклами Микки Мауса , которыми манипулировали за экраном, показал, что пятимесячные младенцы ожидают, что 1 + 1 будет 2, и они сравнительно удивлены, когда физическая ситуация, как им кажется, подразумевает, что 1 + 1 будет либо 1, либо 3. Это открытие с тех пор было подтверждено различными лабораториями, использующими различные методологии. ^[27] Другой эксперимент 1992 года с более старшими малышами , в возрасте от 18 до 35 месяцев, использовал их развитие моторного контроля, позволяя им доставать шарики для пинг-понга из коробки; самые младшие хорошо реагировали на небольшие числа, в то время как более старшие испытуемые могли вычислять суммы до 5. ^[28]

Даже некоторые нечеловеческие животные демонстрируют ограниченную способность к сложению, особенно приматы . В эксперименте 1995 года, имитирующем результат Уинна 1992 года (но с использованием баклажанов вместо кукол), макаки-резусы и хлопковые тамарины показали результаты, схожие с человеческими младенцами. Более драматично, после того, как их научили значениям арабских цифр от 0 до 4, один шимпанзе смог вычислить сумму двух цифр без дальнейшего обучения. ^[29] Совсем недавно азиатские слоны продемонстрировали способность выполнять базовые арифметические действия. ^[30]

Обучение в детстве

Обычно дети сначала осваивают счет . Когда им дают задачу, требующую объединения двух и трех предметов, маленькие дети моделируют ситуацию с помощью физических объектов, часто пальцев или рисунка, а затем подсчитывают общую сумму. По мере накопления опыта они изучают или открывают для себя стратегию «подсчета»: когда их просят найти два плюс три, дети считают три после двух, говоря «три, четыре, пять » (обычно загибая пальцы), и приходят к пяти. Эта стратегия кажется почти универсальной; дети могут легко перенять ее у сверстников или учителей. ^[31] Большинство открывают ее самостоятельно. С дополнительным опытом дети учатся складывать быстрее, используя коммутативность сложения, считая от большего числа, в данном случае, начиная с трех и считая «четыре, пять ». В конце концов дети начинают вспоминать определенные факты сложения (« числовые связи ») либо через опыт, либо через механическое запоминание. Как только некоторые факты запечатлеваются в памяти, дети начинают выводить неизвестные факты из известных. Например, ребенок, которого просят сложить шесть и семь, может знать, что 6 + 6 = 12 , а затем рассуждать, что 6 + 7 — это еще один, или 13. ^[32] Такие производные факты можно найти очень быстро, и большинство учеников начальной школы в конечном итоге полагаются на смесь запомненных и производных фактов, чтобы бегло складывать. ^[33]

В разных странах целые числа и арифметика вводятся в разном возрасте, во многих странах сложение преподается в дошкольных учреждениях. ^[34] Однако во всем мире сложение преподается к концу первого года начальной школы. ^[35]

Стол

Детям часто предлагают запомнить таблицу сложения пар чисел от 0 до 9. Зная ее, дети могут выполнить любое сложение.

Десятичная система счисления

Предпосылкой для сложения в десятичной системе является беглое припоминание или вывод 100 однозначных «фактов сложения». Можно было бы запомнить все факты наизусть , но стратегии, основанные на шаблонах, более познавательны и, для большинства людей, более эффективны: ^[36]

• Коммутативное свойство : упомянутое выше использование шаблона a + b = b + a сокращает количество «фактов сложения» со 100 до 55.
• Еще один или два : Добавление 1 или 2 является базовой задачей, и ее можно выполнить с помощью подсчета или, в конечном счете, интуиции . ^[36]
• Ноль : Поскольку ноль является аддитивным тождеством, добавление нуля тривиально. Тем не менее, при обучении арифметике некоторые студенты знакомятся со сложением как с процессом, который всегда увеличивает слагаемые; текстовые задачи могут помочь рационализировать «исключение» нуля. ^[36]
• Двойники : Сложение числа с самим собой связано со счетом на два и умножением . Факты о двойниках составляют основу многих связанных фактов, и учащиеся считают их относительно простыми для понимания. ^[36]
• Почти двойные суммы : такие суммы, как 6 + 7 = 13, можно быстро вывести из факта двойных чисел 6 + 6 = 12, прибавив еще один, или из 7 + 7 = 14, но вычтя один. ^[36]
• Пять и десять : суммы вида 5 + x и 10 + x обычно запоминаются рано и могут быть использованы для вывода других фактов. Например, 6 + 7 = 13 можно получить из 5 + 7 = 12, добавив еще один. ^[36]
• Получение десяти : продвинутая стратегия использует 10 в качестве промежуточного значения для сумм, включающих 8 или 9; например, 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14. [ ^36]

По мере взросления студенты запоминают больше фактов и учатся быстро и бегло выводить другие факты. Многие студенты никогда не запоминают все факты, но все равно могут быстро найти любой базовый факт. ^[33]

Нести

Стандартный алгоритм сложения многозначных чисел заключается в выравнивании слагаемых по вертикали и сложении столбцов, начиная с столбца единиц справа. Если столбец превышает девять, то лишняя цифра "переносится " в следующий столбец. Например, в сложении 27 + 59

 ¹ 27+ 59———— 86

7 + 9 = 16, а цифра 1 — это перенос. ^[b] Альтернативная стратегия начинается с самой значимой цифры слева; этот путь делает перенос немного более неуклюжим, но он быстрее для получения приблизительной оценки суммы. Существует много альтернативных методов.

С конца 20-го века некоторые программы США, включая TERC, решили исключить традиционный метод перевода из своей учебной программы. ^[37] Это решение подверглось критике, ^[38] поэтому некоторые штаты и округа не поддержали этот эксперимент.

Десятичные дроби

Десятичные дроби можно складывать с помощью простой модификации вышеописанного процесса. ^[39] Две десятичные дроби выравниваются друг над другом, с десятичной точкой в ​​том же месте. При необходимости можно добавить конечные нули к более короткой десятичной дроби, чтобы сделать ее такой же длины, как и более длинная десятичная дробь. Наконец, выполняется тот же процесс сложения, что и выше, за исключением того, что десятичная точка помещается в ответ, точно там, где она была помещена в слагаемых.

Например, 45,1 + 4,34 можно решить следующим образом:

 4 5 . 1 0+ 0 4 . 3 4———————————— 4 9 . 4 4

Научная нотация

В научной нотации числа записываются в форме , где — мантисса, а — показательная часть. Сложение требует, чтобы два числа в научной нотации были представлены с использованием одной и той же показательной части, так что две мантиссы можно просто сложить. ${\displaystyle x=a\times 10^{b}}$ ${\displaystyle a}$ ${\displaystyle 10^{b}}$

Например:

${\displaystyle 2.34\times 10^{-5}+5.67\times 10^{-6}=2.34\times 10^{-5}+0.567\times 10^{-5}=2.907\times 10^{-5}}$

Недесятичные

Сложение в других основаниях очень похоже на десятичное сложение. В качестве примера можно рассмотреть сложение в двоичной системе. ^[40] Сложение двух однозначных двоичных чисел относительно просто, с использованием формы переноса:

0 + 0 → 0

0 + 1 → 1

1 + 0 → 1

1 + 1 → 0, переносим 1 (так как 1 + 1 = 2 = 0 + (1 × 2 ¹ ))

Сложение двух цифр "1" дает цифру "0", а 1 необходимо добавить к следующему столбцу. Это похоже на то, что происходит в десятичной системе счисления, когда складываются определенные однозначные числа; если результат равен или превышает значение основания (10), цифра слева увеличивается:

5 + 5 → 0, переносим 1 (так как 5 + 5 = 10 = 0 + (1 × 10 ¹ ))

7 + 9 → 6, переносим 1 (так как 7 + 9 = 16 = 6 + (1 × 10 ¹ ))

Это известно как перенос . ^[41] Когда результат сложения превышает значение цифры, процедура заключается в «переносе» избыточной суммы, деленной на основание (то есть 10/10), влево, добавляя ее к следующему позиционному значению. Это правильно, поскольку следующая позиция имеет вес, который выше на коэффициент, равный основанию. Перенос работает таким же образом в двоичной системе счисления:

 1 1 1 1 1 (переносимые цифры) 0 1 1 0 1+ 1 0 1 1 1————————————— 1 0 0 1 0 0 = 36

В этом примере складываются две цифры: 01101 ₂ (13 ₁₀ ) и 10111 ₂ (23 ₁₀ ). Верхняя строка показывает используемые биты переноса. Начиная с самого правого столбца, 1 + 1 = 10 ₂ . 1 переносится влево, а 0 записывается внизу самого правого столбца. Добавляется второй столбец справа: 1 + 0 + 1 = 10 ₂ снова; 1 переносится, а 0 записывается внизу. Третий столбец: 1 + 1 + 1 = 11 ₂ . На этот раз переносится 1, и 1 записывается в нижней строке. Продолжая таким образом, получаем окончательный ответ 100100 ₂ (36 ₁₀ ).

Компьютеры

Сложение с операционным усилителем. Подробности см. в разделе Суммирующий усилитель .

Аналоговые компьютеры работают напрямую с физическими величинами, поэтому их механизмы сложения зависят от формы слагаемых. Механический сумматор может представлять два слагаемых как положения скользящих блоков, в этом случае их можно сложить с помощью усредняющего рычага . Если слагаемые являются скоростями вращения двух валов , их можно сложить с помощью дифференциала . Гидравлический сумматор может складывать давления в двух камерах, используя второй закон Ньютона для уравновешивания сил на сборке поршней . Наиболее распространенной ситуацией для аналогового компьютера общего назначения является сложение двух напряжений (относительно земли ); это можно сделать грубо с помощью резисторной сети , но лучшая конструкция использует операционный усилитель . ^[42]

Сложение также имеет основополагающее значение для работы цифровых компьютеров , где эффективность сложения, в частности механизма переноса , является важным ограничением общей производительности.

Часть разностной машины Чарльза Бэббиджа, включая механизмы сложения и переноса.

Абак , также называемый счетной рамкой, является счетным инструментом , который использовался за столетия до принятия современной письменной системы счисления и до сих пор широко используется торговцами, купцами и клерками в Азии , Африке и других местах; он датируется по крайней мере 2700–2300 годами до нашей эры, когда он использовался в Шумере . ^[43]

Блез Паскаль изобрел механический калькулятор в 1642 году; ^[44] это была первая действующая арифмометрическая машина . Он использовал механизм переноса с помощью гравитации. Это был единственный действующий механический калькулятор в 17 веке ^[45] и самый ранний автоматический цифровой компьютер. Калькулятор Паскаля был ограничен своим механизмом переноса, который заставлял его колеса вращаться только в одну сторону, чтобы он мог складывать. Чтобы вычитать, оператор должен был использовать дополнение калькулятора Паскаля , которое требовало столько же шагов, сколько и сложение. Джованни Полени последовал за Паскалем, построив второй функциональный механический калькулятор в 1709 году, вычислительные часы из дерева, которые после настройки могли автоматически умножать два числа.

Логическая схема « полного сумматора », которая складывает две двоичные цифры, A и B , вместе с входным сигналом переноса C _in , создавая бит суммы, S , и выходной сигнал переноса, C _out .

Сумматоры выполняют целочисленное сложение в электронных цифровых компьютерах, обычно используя двоичную арифметику . Простейшая архитектура — это сумматор с волновым переносом, который следует стандартному многоразрядному алгоритму. Одно небольшое улучшение — это конструкция с пропуском переноса , снова следуя человеческой интуиции; не выполняются все переносы при вычислении 999 + 1 , а обходится группа девяток и осуществляется переход к ответу. ^[46]

На практике вычислительное сложение может быть достигнуто с помощью побитовых логических операций XOR и AND в сочетании с операциями сдвига битов, как показано в псевдокоде ниже. Как XOR, так и AND-вентили просты в реализации в цифровой логике, что позволяет реализовать полные схемы сумматора , которые, в свою очередь, могут быть объединены в более сложные логические операции. В современных цифровых компьютерах целочисленное сложение, как правило, является самой быстрой арифметической инструкцией, однако оно оказывает наибольшее влияние на производительность, поскольку лежит в основе всех операций с плавающей точкой , а также таких базовых задач, как генерация адреса во время доступа к памяти и выборка инструкций во время ветвления . Для увеличения скорости современные разработки вычисляют цифры параллельно ; эти схемы носят такие названия, как выбор переноса, опережающий перенос и псевдоперенос Линга . Многие реализации, по сути, являются гибридами этих последних трех разработок. ^{[47] [48]} В отличие от сложения на бумаге, сложение на компьютере часто изменяет слагаемые. На древних счетах и ​​арифмометрической доске оба слагаемых уничтожаются, оставляя только сумму. Влияние абака на математическое мышление было настолько сильным, что в ранних латинских текстах часто утверждалось, что в процессе сложения «числа с числом» оба числа исчезают. ^[49] В наше время инструкция ADD микропроцессора часто заменяет слагаемое на сумму, но сохраняет слагаемое. ^[50] В языке программирования высокого уровня оценка a + b не изменяет ни a, ни b ; если цель состоит в том, чтобы заменить a на сумму, это должно быть явно запрошено, как правило, с помощью оператора a = a + b . Некоторые языки, такие как C или C++, позволяют сокращать это до a += b .

// Итеративный алгоритм int add ( int x , int y ) { int carry = 0 ; while ( y != 0 ) { carry = AND ( x , y ); // Логическое AND x = XOR ( x , y ); // Логическое XOR y = carry << 1 ; // сдвиг бита влево с переносом на единицу } return x ; }                                   // Рекурсивный алгоритм int add ( int x , int y ) { return x if ( y == 0 ) else add ( XOR ( x , y ), AND ( x , y ) << 1 ); }                  

На компьютере, если результат сложения слишком велик для хранения, происходит арифметическое переполнение , что приводит к неправильному ответу. Непредвиденное арифметическое переполнение является довольно распространенной причиной ошибок программы . Такие ошибки переполнения может быть трудно обнаружить и диагностировать, поскольку они могут проявляться только для очень больших наборов входных данных, которые с меньшей вероятностью будут использоваться в проверочных тестах. ^[51] Проблема 2000 года представляла собой серию ошибок, в которых ошибки переполнения возникали из-за использования 2-значного формата для лет. ^[52]

Сложение чисел

Чтобы доказать обычные свойства сложения, нужно сначала определить сложение для рассматриваемого контекста. Сложение сначала определяется для натуральных чисел . В теории множеств сложение затем распространяется на все большие множества, которые включают натуральные числа: целые числа , рациональные числа и действительные числа . ^[53] (В математическом образовании ^[54] положительные дроби складываются до того, как отрицательные числа вообще рассматриваются ; это также исторический путь. ^[55] )

Натуральные числа

Существует два популярных способа определения суммы двух натуральных чисел a и b . Если определить натуральные числа как мощности конечных множеств (мощность множества — это количество элементов в множестве), то уместно определить их сумму следующим образом:

• Пусть N( S ) — мощность множества S . Возьмем два непересекающихся множества A и B , причем N( A ) = a и N( B ) = b . Тогда a + b определяется как . ^[56] ${\displaystyle N(A\cup B)}$

Здесь A ∪ B — это объединение A и B. Альтернативная версия этого определения допускает возможность перекрытия A и B, а затем берет их непересекающееся объединение — механизм , который позволяет разделять общие элементы и, следовательно, учитывать их дважды .

Другое популярное определение — рекурсивное:

• Пусть n ⁺ будет последующим числом n , то есть числом, следующим за n в натуральном ряду, так что 0 ⁺ = 1 , 1 ⁺ = 2 . Определим a + 0 = a . Определим общую сумму рекурсивно как a + ( b ⁺ ) = ( a + b ) ⁺ . Следовательно, 1 + 1 = 1 + 0 ⁺ = (1 + 0) ⁺ = 1 ⁺ = 2 . ^[57]

Опять же, в литературе есть небольшие вариации этого определения. Взятое буквально, вышеприведенное определение является применением теоремы рекурсии к частично упорядоченному множеству N ² . ^[58] С другой стороны, некоторые источники предпочитают использовать ограниченную теорему рекурсии, которая применяется только к множеству натуральных чисел. Затем a рассматривается как временно «фиксированное», применяется рекурсия к b для определения функции « a  +» и вставляется эти унарные операции для всех a вместе, чтобы сформировать полную бинарную операцию. ^[59]

Эта рекурсивная формулировка сложения была разработана Дедекиндом еще в 1854 году, и он расширил ее в последующие десятилетия. ^[60] Он доказал ассоциативные и коммутативные свойства, среди прочего, с помощью математической индукции .

Целые числа

Простейшая концепция целого числа заключается в том, что оно состоит из абсолютного значения (которое является натуральным числом) и знака (обычно либо положительного , либо отрицательного ). Целое число ноль является особым третьим случаем, не являясь ни положительным, ни отрицательным. Соответствующее определение сложения должно осуществляться по случаям:

• Для целого числа n пусть | n | будет его абсолютным значением. Пусть a и b будут целыми числами. Если a или b равны нулю, рассматривать это как тождество. Если a и b оба положительны, определить a + b = | a | + | b | . Если a и b оба отрицательны, определить a + b = −(| a | + | b |) . Если a и b имеют разные знаки, определить a + b как разность между | a | и | b |, со знаком того члена, абсолютная величина которого больше. ^[61] Например, −6 + 4 = −2 ; поскольку −6 и 4 имеют разные знаки, их абсолютные величины вычитаются, и поскольку абсолютная величина отрицательного члена больше, ответ отрицательный.

Хотя это определение может быть полезным для конкретных задач, количество рассматриваемых случаев излишне усложняет доказательства. Поэтому для определения целых чисел обычно используется следующий метод. Он основан на замечании, что каждое целое число является разностью двух натуральных целых чисел и что две такие разности, a – b и c – d, равны тогда и только тогда, когда a + d = b + c . Таким образом, можно формально определить целые числа как классы эквивалентности упорядоченных пар натуральных чисел при отношении эквивалентности

( a , b ) ~ ( c , d ) тогда и только тогда, когда a + d = b + c .

Класс эквивалентности ( a , b ) содержит либо ( a – b , 0) , если a ≥ b , либо (0, b – a ) в противном случае. Если n – натуральное число, можно обозначить + n класс эквивалентности ( n , 0) , а через – n класс эквивалентности (0, n ) . Это позволяет отождествить натуральное число n с классом эквивалентности + n .

Сложение упорядоченных пар выполняется покомпонентно:

${\displaystyle (a,b)+(c,d)=(a+c,b+d).}$

Прямое вычисление показывает, что класс эквивалентности результата зависит только от классов эквивалентности слагаемых, и, таким образом, это определяет сложение классов эквивалентности, то есть целых чисел. ^[62] Другое прямое вычисление показывает, что это сложение совпадает с приведенным выше определением случая.

Этот способ определения целых чисел как классов эквивалентности пар натуральных чисел может быть использован для вложения в группу любой коммутативной полугруппы со свойством сокращения . Здесь полугруппа образована натуральными числами, а группа является аддитивной группой целых чисел. Рациональные числа строятся аналогично, путем взятия в качестве полугруппы ненулевых целых чисел с умножением.

Эта конструкция была также обобщена под названием группы Гротендика на случай любой коммутативной полугруппы. Без свойства сокращения гомоморфизм полугруппы из полугруппы в группу может быть неинъективным. Первоначально группа Гротендика была, более конкретно, результатом этой конструкции, примененной к классам эквивалентностей относительно изоморфизмов объектов абелевой категории , с прямой суммой в качестве операции полугруппы.

Рациональные числа (дроби)

Сложение рациональных чисел можно вычислить с помощью наименьшего общего знаменателя , но концептуально более простое определение включает только сложение и умножение целых чисел:

• Определять ${\displaystyle {\frac {a}{b}}+{\frac {c}{d}}={\frac {ad+bc}{bd}}.}$

В качестве примера можно привести сумму . ${\displaystyle {\frac {3}{4}}+{\frac {1}{8}}={\frac {3\times 8+4\times 1}{4\times 8}}={\frac {24+4}{32}}={\frac {28}{32}}={\frac {7}{8}}}$

Сложение дробей намного проще, когда знаменатели одинаковы; в этом случае можно просто сложить числители, оставив знаменатель прежним: , поэтому . ^[63] ${\displaystyle {\frac {a}{c}}+{\frac {b}{c}}={\frac {a+b}{c}}}$ ${\displaystyle {\frac {1}{4}}+{\frac {2}{4}}={\frac {1+2}{4}}={\frac {3}{4}}}$

Коммутативность и ассоциативность рационального сложения являются простым следствием законов целочисленной арифметики. ^[64] Более строгое и общее обсуждение см. в разделе поле дробей .

Реальные цифры

Распространенной конструкцией множества действительных чисел является дедекиндово пополнение множества рациональных чисел. Действительное число определяется как дедекиндово сечение рациональных чисел: непустое множество рациональных чисел, замкнутое сверху вниз и не имеющее наибольшего элемента . Сумма действительных чисел a и b определяется поэлементно:

• Определить ^[65] ${\displaystyle a+b=\{q+r\mid q\in a,r\in b\}.}$

Это определение было впервые опубликовано в слегка измененном виде Ричардом Дедекиндом в 1872 году. ^[66] Коммутативность и ассоциативность вещественного сложения очевидны; определяя вещественное число 0 как множество отрицательных рациональных чисел, легко увидеть, что оно является аддитивным тождеством. Вероятно, самая сложная часть этой конструкции, относящаяся к сложению, — это определение аддитивных обратных чисел. ^[67]

Сложение π ² /6 и e с использованием последовательностей Коши рациональных чисел.

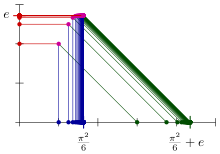
К сожалению, работа с умножением разрезов Дедекинда — это трудоемкий индивидуальный процесс, аналогичный сложению целых чисел со знаком. ^[68] Другой подход — метрическое завершение рациональных чисел. Действительное число по сути определяется как предел последовательности Коши рациональных чисел, lim  a _n . Сложение определяется почленно:

• Определить ^[69] ${\displaystyle \lim _{n}a_{n}+\lim _{n}b_{n}=\lim _{n}(a_{n}+b_{n}).}$

Это определение было впервые опубликовано Георгом Кантором также в 1872 году, хотя его формализм был немного иным. ^[70] Нужно доказать, что эта операция хорошо определена, имея дело с ко-последовательностями Коши. Как только эта задача выполнена, все свойства действительного сложения немедленно следуют из свойств рациональных чисел. Более того, другие арифметические операции, включая умножение, имеют простые, аналогичные определения. ^[71]

Комплексные числа

Сложение двух комплексных чисел можно выполнить геометрически, построив параллелограмм.

Комплексные числа складываются путем сложения действительных и мнимых частей слагаемых. ^{[72] [73]} То есть:

${\displaystyle (a+bi)+(c+di)=(a+c)+(b+d)i.}$

Используя визуализацию комплексных чисел на комплексной плоскости, сложение имеет следующую геометрическую интерпретацию: сумма двух комплексных чисел A и B , интерпретируемых как точки комплексной плоскости, есть точка X, полученная путем построения параллелограмма, три вершины которого O , A и B. Эквивалентно, X есть точка такая, что треугольники с вершинами O , A , B и X , B , A равны .

Обобщения

Существует много бинарных операций, которые можно рассматривать как обобщения операции сложения действительных чисел. Область абстрактной алгебры в основном занимается такими обобщенными операциями, и они также появляются в теории множеств и теории категорий .

Абстрактная алгебра

Векторы

В линейной алгебре векторное пространство — это алгебраическая структура, которая позволяет складывать любые два вектора и масштабировать векторы. Знакомое векторное пространство — это множество всех упорядоченных пар действительных чисел; упорядоченная пара ( a , b ) интерпретируется как вектор из начала координат в евклидовой плоскости в точку ( a , b ) на этой плоскости. Сумма двух векторов получается путем сложения их индивидуальных координат:

${\displaystyle (a,b)+(c,d)=(a+c,b+d).}$

Эта операция сложения является центральной в классической механике , в которой скорости , ускорения и силы представлены векторами. ^[74]

Матрицы

Сложение матриц определяется для двух матриц одинакового размера. Сумма двух матриц A и B размером m × n (произносится как «m на n») , обозначаемая как A + B , снова является матрицей размером m × n, вычисленной путем сложения соответствующих элементов: ^{[75] [76]}

${\displaystyle {\begin{aligned}\mathbf {A} +\mathbf {B} &={\begin{bmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\\\end{bmatrix}}+{\begin{bmatrix}b_{11}&b_{12}&\cdots &b_{1n}\\b_{21}&b_{22}&\cdots &b_{2n}\\\vdots &\vdots &\ddots &\vdots \\b_{m1}&b_{m2}&\cdots &b_{mn}\\\end{bmatrix}}\\&={\begin{bmatrix}a_{11}+b_{11}&a_{12}+b_{12}&\cdots &a_{1n}+b_{1n}\\a_{21}+b_{21}&a_{22}+b_{22}&\cdots &a_{2n}+b_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}+b_{m1}&a_{m2}+b_{m2}&\cdots &a_{mn}+b_{mn}\\\end{bmatrix}}\\\end{aligned}}}$

Например:

${\displaystyle {\begin{bmatrix}1&3\\1&0\\1&2\end{bmatrix}}+{\begin{bmatrix}0&0\\7&5\\2&1\end{bmatrix}}={\begin{bmatrix}1+0&3+0\\1+7&0+5\\1+2&2+1\end{bmatrix}}={\begin{bmatrix}1&3\\8&5\\3&3\end{bmatrix}}}$

Модульная арифметика

В модульной арифметике набор доступных чисел ограничен конечным подмножеством целых чисел, и сложение «оборачивает» при достижении определенного значения, называемого модулем. Например, множество целых чисел по модулю 12 имеет двенадцать элементов; оно наследует операцию сложения от целых чисел, которая является центральной в музыкальной теории множеств . Множество целых чисел по модулю 2 имеет всего два элемента; операция сложения, которую оно наследует, известна в булевой логике как функция « исключающее или ». Похожая операция «оборачивает» возникает в геометрии , где сумма двух угловых мер часто принимается равной их сумме как действительных чисел по модулю 2π. Это равносильно операции сложения на окружности , которая, в свою очередь, обобщается до операций сложения на многомерных торах .

Общая теория

Общая теория абстрактной алгебры допускает, что операция «сложения» может быть любой ассоциативной и коммутативной операцией на множестве. Базовые алгебраические структуры с такой операцией сложения включают коммутативные моноиды и абелевы группы .

Теория множеств и теория категорий

Далеко идущее обобщение сложения натуральных чисел — это сложение порядковых и кардинальных чисел в теории множеств. Они дают два различных обобщения сложения натуральных чисел к трансфинитному . В отличие от большинства операций сложения, сложение порядковых чисел не является коммутативным. ^[77] Однако сложение кардинальных чисел является коммутативной операцией, тесно связанной с операцией дизъюнктного объединения .

В теории категорий непересекающееся объединение рассматривается как частный случай операции копроизведения , ^[78] а общие копроизведения, возможно, являются наиболее абстрактными из всех обобщений сложения. Некоторые копроизведения, такие как прямая сумма и клиновидная сумма , названы так, чтобы подчеркнуть их связь со сложением.

Связанные операции

Сложение, наряду с вычитанием, умножением и делением, считается одной из основных операций и используется в элементарной арифметике .

Арифметика

Вычитание можно рассматривать как своего рода сложение, то есть сложение аддитивной обратной функции . Вычитание само по себе является своего рода обратной функцией сложения, в том смысле, что сложение x и вычитание x являются обратными функциями .

При наличии множества с операцией сложения не всегда можно определить соответствующую операцию вычитания на этом множестве; множество натуральных чисел является простым примером. С другой стороны, операция вычитания однозначно определяет операцию сложения, аддитивную обратную операцию и аддитивную идентичность; по этой причине аддитивную группу можно описать как множество, замкнутое относительно вычитания. ^[79]

Умножение можно рассматривать как повторяющееся сложение . Если один член x появляется в сумме n раз, то сумма является произведением n и x . Если n не является натуральным числом , произведение все равно может иметь смысл; например, умножение на −1 дает аддитивную инверсию числа.

Круглая логарифмическая линейка

В действительных и комплексных числах сложение и умножение можно заменить показательной функцией : ^[80]

${\displaystyle e^{a+b}=e^{a}e^{b}.}$

Это тождество позволяет выполнять умножение, сверяясь с таблицей логарифмов и вычисляя сложение вручную; оно также позволяет умножать на логарифмической линейке . Формула по-прежнему является хорошим приближением первого порядка в широком контексте групп Ли , где она связывает умножение бесконечно малых элементов группы со сложением векторов в связанной алгебре Ли . ^[81]

Существует даже больше обобщений умножения, чем сложения. ^[82] В общем, операции умножения всегда распределяются по сложению; это требование формализовано в определении кольца . В некоторых контекстах, таких как целые числа, дистрибутивность по сложению и существование мультипликативного тождества достаточно, чтобы однозначно определить операцию умножения. Свойство дистрибутивности также предоставляет информацию о сложении; расширяя произведение (1 + 1)( a + b ) в обоих направлениях, можно прийти к выводу, что сложение вынуждено быть коммутативным. По этой причине кольцевое сложение в целом коммутативно. ^[83]

Деление — арифметическая операция, отдаленно связанная со сложением. Поскольку a / b = a ( b ⁻¹ ) , деление дистрибутивно справа относительно сложения: ( a + b ) / c = a / c + b / c . ^[84] Однако деление не дистрибутивно слева относительно сложения; 1 / (2 + 2) — это не то же самое, что 1/2 + 1/2 .

Заказ

Логарифмический график x + 1 и max ( x , 1) от x = 0,001 до 1000 ^[85]

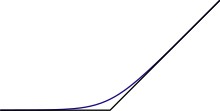
Операция максимума "max ( a , b )" является бинарным действием, аналогичным сложению. Фактически, если два неотрицательных числа a и b имеют разные порядки величины , то их сумма приблизительно равна их максимуму. Это приближение чрезвычайно полезно в приложениях математики, например, при усечении ряда Тейлора . Однако оно представляет собой постоянную трудность в численном анализе , по сути, поскольку "max" необратимо. Если b намного больше a , то прямое вычисление ( a + b ) − b может накапливать неприемлемую ошибку округления , возможно, даже возвращая ноль. См. также Потеря значимости .

Приближение становится точным в своего рода бесконечном пределе; если a или b являются бесконечным кардинальным числом , их кардинальная сумма в точности равна большему из двух. ^[86] Соответственно, для бесконечных кардинальных чисел не существует операции вычитания. ^[87]

Максимизация коммутативна и ассоциативна, как и сложение. Более того, поскольку сложение сохраняет порядок действительных чисел, сложение распределяется по "max" таким же образом, как умножение распределяется по сложению:

${\displaystyle a+\max(b,c)=\max(a+b,a+c).}$

По этим причинам в тропической геометрии умножение заменяют сложением, а сложение — максимизацией. В этом контексте сложение называется «тропическим умножением», максимизация — «тропическим сложением», а тропическое «аддитивное тождество» — это отрицательная бесконечность . ^[88] Некоторые авторы предпочитают заменять сложение минимизацией; тогда аддитивное тождество — это положительная бесконечность. ^[89]

Объединяя эти наблюдения, можно сказать, что тропическое сложение приблизительно связано с обычным сложением через логарифм :

${\displaystyle \log(a+b)\approx \max(\log a,\log b),}$

которая становится более точной по мере увеличения основания логарифма. ^[90] Приближение можно сделать точным, извлекая константу h , названную по аналогии с постоянной Планка из квантовой механики , ^[91] и принимая « классический предел » при h, стремящемся к нулю:

${\displaystyle \max(a,b)=\lim _{h\to 0}h\log(e^{a/h}+e^{b/h}).}$

В этом смысле операция максимума представляет собой деквантованную версию сложения. ^[92]

Другие способы добавления

Инкрементация, также известная как операция наследования , представляет собой прибавление 1 к числу.

Суммирование описывает сложение произвольного количества чисел, обычно больше двух. Оно включает в себя идею суммы одного числа, которое является им самим, и пустой суммы , которая является нулем . ^[93] Бесконечное суммирование — это тонкая процедура, известная как ряд . ^[94]

Подсчет конечного множества эквивалентен суммированию 1 по всему множеству.

Интеграция — это своего рода «суммирование» по континууму , или, точнее и общо, по дифференцируемому многообразию . Интегрирование по нульмерному многообразию сводится к суммированию.

Линейные комбинации объединяют умножение и суммирование ; это суммы, в которых каждый член имеет множитель, обычно действительное или комплексное число. Линейные комбинации особенно полезны в контекстах , где простое сложение нарушило бы некоторое правило нормализации, например смешивание стратегий в теории игр или суперпозиция состояний в квантовой механике . ^[95]

Свертка используется для сложения двух независимых случайных величин, определяемых функциями распределения . Ее обычное определение объединяет интегрирование, вычитание и умножение. ^[96] В общем, свертка полезна как своего рода сложение на стороне домена; в отличие от этого, векторное сложение является своего рода сложением на стороне диапазона.

Смотрите также

• Лунная арифметика
• Ментальная арифметика
• Параллельное сложение (математика)
• Устная арифметика (также известная как криптарифмы), головоломки, включающие сложение

Примечания

1. «Addend» — не латинское слово; в латинском языке оно требует дальнейшего спряжения, например, numerus addendus — «число, которое нужно прибавить».
2. Некоторые авторы считают, что «carry» может быть неподходящим для образования; Ван де Валле (стр. 211) называет его «устаревшим и концептуально вводящим в заблуждение», предпочитая слово «trade». Однако «carry» остается стандартным термином.

Сноски

1. Из Эндертона (стр. 138): «...выберите два набора K и L с картой K = 2 и картой L = 3. Наборы пальцев удобны; наборы яблок предпочтительны в учебниках».
2. Льюис, Рис (1974). «Арифметика». Математика для технических специалистов первого года обучения. Palgrave, Лондон: The MacMillan Press Ltd. стр. 1. doi :10.1007/978-1-349-02405-6_1. ISBN 978-1-349-02405-6.
3. "Дополнение". www.mathsisfun.com . Получено 2020-08-25 .
4. Девайн и др., стр. 263
5. Мазур, Джозеф. Просветляющие символы: краткая история математической нотации и ее скрытых сил . Princeton University Press, 2014. стр. 161
6. Министерство армии (1961) Техническое руководство армии TM 11-684: Принципы и применение математики для связи и электроники. Раздел 5.1
7. Шмерко, вице-президент; Янушкевич [Âнушкевич], Светлана Н. [Свитлана Н.]; Лышевский, С.Е. (2009). Компьютерная арифметика для наноэлектроники . ЦРК Пресс . п. 80.
8. Schmid, Hermann (1974). Десятичные вычисления (1-е изд.). Бингемтон, Нью-Йорк: John Wiley & Sons . ISBN 0-471-76180-X.и Шмид, Герман (1983) [1974]. Десятичные вычисления (переиздание 1-го изд.). Малабар, Флорида: Robert E. Krieger Publishing Company. ISBN 978-0-89874-318-0.
9. Вайсштейн, Эрик В. «Дополнение». mathworld.wolfram.com . Проверено 25 августа 2020 г.
10. Hosch, WL (ред.). (2010). Руководство по числам и измерениям Britannica. Издательская группа Rosen. стр. 38
11. Шварцман стр. 19
12. Карпински, стр. 56–57, воспроизведено на стр. 104.
13. Шварцман (стр. 212) приписывает сложение снизу вверх грекам и римлянам , говоря, что оно было примерно таким же распространенным, как сложение сверху вниз. С другой стороны, Карпински (стр. 103) пишет, что Леонард Пизанский «вводит новизну записи суммы над слагаемыми»; неясно, утверждает ли Карпински это как оригинальное изобретение или просто введение практики в Европу.
14. Карпински стр. 150–153
15. Каджори, Флориан (1928). «Происхождение и значение знаков + и -». История математических обозначений, т. 1. The Open Court Company, Publishers.
16. "plus" . Оксфордский словарь английского языка (Электронная правка). Oxford University Press . (Требуется подписка или членство в участвующем учреждении.)
17. Пример сложности, связанной с сложением множеств «дробной мощности», см. в Viro 2001.
18. В книге «Сложение» (стр. 73) добавление измерительных линеек сравнивается с добавлением наборов кошек: «Например, дюймы можно разделить на части, которые трудно отличить от целых, за исключением того, что они короче; тогда как кошкам больно делить их на части, и это серьезно меняет их природу».
19. Mosley, F (2001). Использование числовых линий с детьми 5–8 лет . Нельсон Торнес. стр. 8
20. Ли, И. и Лаппан, Г. (2014). Программа обучения математике в школьном образовании . Springer. стр. 204
21. Бронштейн, Илья Николаевич; Семендяев, Константин Адольфович (1987) [1945]. «2.4.1.1.». В Гроше, Гюнтер; Зиглер, Виктор; Зиглер, Доротея (ред.). Taschenbuch der Mathematik (на немецком языке). Том. 1. Перевод Циглера Виктора. Вайс, Юрген (23-е изд.). Тун и Франкфурт-на-Майне: Verlag Harri Deutsch (и BG Teubner Verlagsgesellschaft , Лейпциг). стр. 115–120. ISBN 978-3-87144-492-0.
22. Каплан, стр. 69–71.
23. Хемпель, К. Г. (2001). Философия Карла Г. Хемпеля: исследования в области науки, объяснения и рациональности. стр. 7
24. Р. Фиерро (2012) Математика для учителей начальной школы . Cengage Learning. Раздел 2.3
25. Мёбс, Уильям и др. (2022). "1.4 Анализ размерностей". Университетская физика, том 1. OpenStax . ISBN 978-1-947172-20-3.
26. Уинн стр. 5
27. Уинн стр. 15
28. Уинн стр. 17
29. Уинн стр. 19
30. Randerson, James (21 августа 2008 г.). «У слонов голова на цифры». The Guardian . Архивировано из оригинала 2 апреля 2015 г. Получено 29 марта 2015 г.
31. Ф. Смит стр. 130
32. Карпентер, Томас; Феннема, Элизабет ; Франке, Меган Лоэф; Леви, Линда; Эмпсон, Сьюзен (1999). Детская математика: Когнитивно направленное обучение . Портсмут, Нью-Гэмпшир: Heinemann. ISBN 978-0-325-00137-1.
33. Henry, Valerie J.; Brown, Richard S. (2008). «Основные факты для учащихся первого класса: исследование преподавания и изучения ускоренного стандарта запоминания с высокими требованиями». Журнал исследований в области математического образования . 39 (2): 153–183. doi : 10.2307/30034895 . JSTOR  30034895.
34. Бекманн, С. (2014). Двадцать третье исследование ICMI: первичное математическое исследование целых чисел. Международный журнал STEM-образования, 1(1), 1-8. Чикаго
35. Шмидт, В., Хуанг, Р. и Коган, Л. (2002). «Последовательная учебная программа». American Educator , 26(2), 1–18.
36. Фоснот и Долк стр. 99
37. "Стратегия вертикального сложения и вычитания". primarylearning.org . Получено 20 апреля 2022 г. .
38. «Обзоры TERC: Исследования в области чисел, данных и пространства». nychold.com . Получено 20 апреля 2022 г. .
39. Ребекка Вингард-Нельсон (2014) Десятичные дроби и обыкновенные дроби: это просто Enslow Publishers, Inc.
40. Дейл Р. Патрик, Стивен В. Фардо, Виджян Чандра (2008) Основы электронных цифровых систем Fairmont Press, Inc. стр. 155
41. П. Э. Бейтс Ботман (1837) Общая школьная арифметика . Генри Бентон. стр. 31
42. Труитт и Роджерс, стр. 1;44–49 и стр. 2;77–78.
43. Ифра, Жорж (2001). Всеобщая история вычислений: от счетов до квантового компьютера. Нью-Йорк: John Wiley & Sons, Inc. ISBN 978-0-471-39671-0.стр. 11
44. Жан Марген, с. 48 (1994); Цитируя Рене Татона (1963)
45. См . статью « Конкурирующие проекты в калькуляторе Паскаля».
46. Флинн и Оверман, стр. 2, 8.
47. Флинн и Оверман, стр. 1–9.
48. Йео, Сан-Су и др., ред. Алгоритмы и архитектуры для параллельной обработки: 10-я международная конференция, ICA3PP 2010, Пусан, Корея, 21–23 мая 2010 г. Труды. Том 1. Springer, 2010. стр. 194
49. Карпински стр. 102–103
50. Идентичность слагаемого и прибавляемого зависит от архитектуры. Для ADD в x86 см . Horowitz и Hill, стр. 679; для ADD в 68k см . стр. 767.
51. Джошуа Блох, «Extra, Extra – Read All About It: Almosty All Binary Searches and Mergesorts are Broken» Архивировано 01.04.2016 на Wayback Machine . Официальный блог Google Research, 2 июня 2006 г.
52. Neumann, Peter G. (2 февраля 1987 г.). "The Risks Digest Volume 4: Issue 45". The Risks Digest . 4 (45). Архивировано из оригинала 2014-12-28 . Получено 2015-03-30 .
53. Например, главы 4 и 5 Эндертона следуют этому развитию событий.
54. Согласно исследованию стран с самыми высокими результатами теста TIMSS по математике; см. Schmidt, W., Houang, R., & Cogan, L. (2002). Последовательная учебная программа . Американский педагог, 26(2), стр. 4.
55. Баэз (стр. 37) объясняет историческое развитие, «резко контрастирующее» с представлением теории множеств: «Очевидно, половину яблока легче понять, чем отрицательное яблоко!»
56. Бегл с. 49, Джонсон с. 120, Дивайн и др. п. 75
57. Эндертон стр. 79
58. Для версии, которая применима к любому частично упорядоченному множеству с условием нисходящей цепи , см. Бергман, стр. 100.
59. Эндертон (стр. 79) замечает: «Но нам нужна одна бинарная операция +, а не все эти маленькие одноместные функции».
60. Феррейрос стр. 223
61. К. Смит стр. 234, Спаркс и Риз стр. 66
62. Эндертон стр. 92
63. Ширлет Кэмерон и Кэролин Крейг (2013) Сложение и вычитание дробей, классы 5–8 Mark Twain, Inc.
64. Проверки выполнены в работе Эндертона на стр. 104 и схематично изложены для общего поля дробей над коммутативным кольцом в работе Даммита и Фута на стр. 263.
65. Эндертон стр. 114
66. Феррейрос с. 135; см. раздел 6 книги Stetigkeit und irrationale Zahlen. Архивировано 31 октября 2005 г. в Wayback Machine .
67. Интуитивный подход, инвертирующий каждый элемент разреза и берущий его дополнение, работает только для иррациональных чисел; подробности см. в работе Эндертона на стр. 117.
68. Шуберт, Э. Томас, Филлип Дж. Уиндли и Джеймс Алвес-Фосс. «Доказательство теорем логики высшего порядка и его приложения: Труды 8-го международного семинара, том 971». Заметки лекций по информатике (1995).
69. Учебные конструкции обычно не столь бесцеремонны с символом «lim»; см. Беррилл (стр. 138) для более тщательного и развернутого описания сложения с последовательностями Коши.
70. Феррейрос стр. 128
71. Беррилл стр. 140
72. Конвей, Джон Б. (1986), Функции одной комплексной переменной I , Springer, ISBN 978-0-387-90328-6
73. Джоши, Капил Д. (1989), Основы дискретной математики , Нью-Йорк: John Wiley & Sons , ISBN 978-0-470-21152-6
74. Гбур, стр. 1
75. Липшуц, С. и Липсон, М. (2001). Очерк Шаума по теории и проблемам линейной алгебры. Erlangga.
76. Райли, К. Ф.; Хобсон, М. П.; Бенс, С. Дж. (2010). Математические методы для физики и техники . Cambridge University Press. ISBN 978-0-521-86153-3.
77. Чэн, стр. 124–132.
78. Риль, стр. 100
79. Множество все еще должно быть непустым. Даммит и Фут (стр. 48) обсуждают этот критерий, записанный мультипликативно.
80. Рудин стр. 178
81. Ли, стр. 526, Предложение 20.9
82. Линдерхольм (стр. 49) замечает: «Под умножением , собственно говоря, математик может подразумевать практически все, что угодно. Под сложением он может подразумевать большое разнообразие вещей, но не такое большое разнообразие, как под „умножением“».
83. Даммит и Фут, стр. 224. Чтобы этот аргумент работал, все равно нужно предположить, что сложение является групповой операцией, а умножение имеет тождество.
84. Пример левой и правой дистрибутивности см. в Loday, особенно на стр. 15.
85. Сравните Viro Figure 1 (стр. 2)
86. Эндертон называет это утверждение «Законом поглощения кардинальной арифметики»; оно зависит от сравнимости кардинальных чисел и, следовательно, от аксиомы выбора .
87. Эндертон стр. 164
88. Михалкин стр. 1
89. Акиан и др., стр. 4
90. Михалкин стр. 2
91. Литвинов и др. стр. 3
92. Виро стр. 4
93. Мартин стр. 49
94. Стюарт стр. 8
95. Риффель и Полак, стр. 16
96. Гбур, стр. 300

Ссылки

История

• Феррейрос, Хосе (1999). Лабиринт мысли: история теории множеств и ее роль в современной математике . Биркхойзер. ISBN 978-0-8176-5749-9.
• Карпински, Луис (1925). История арифметики . Рэнд Макналли. LCC  QA21.K3.
• Шварцман, Стивен (1994). Слова математики: Этимологический словарь математических терминов, используемых в английском языке . MAA . ISBN 978-0-88385-511-9.
• Уильямс, Майкл (1985). История вычислительной техники . Prentice-Hall. ISBN 978-0-13-389917-7.

Элементарная математика

• Спаркс, Ф.; Риз К. (1979). Обзор базовой математики . McGraw-Hill. ISBN 978-0-07-059902-4.

Образование

• Бегл, Эдвард (1975). Математика начальной школы. McGraw-Hill . ISBN 978-0-07-004325-1.
• Стандарты содержания математики Совета по образованию штата Калифорния. Приняты в декабре 1997 г., дата обращения декабрь 2005 г.
• Devine, D.; Olson, J.; Olson, M. (1991). Элементарная математика для учителей (2-е изд.). Wiley . ISBN 978-0-471-85947-5.
• Национальный исследовательский совет (2001). Adding It Up: Helping Children Learning Mathematics. National Academy Press . doi : 10.17226/9822. ISBN 978-0-309-06995-3.
• Ван де Валле, Джон (2004). Математика начальной и средней школы: развивающее обучение (5-е изд.). Пирсон. ISBN 978-0-205-38689-5.

Когнитивная наука

• Fosnot, Catherine T.; Dolk, Maarten (2001). Молодые математики за работой: построение числового смысла, сложения и вычитания . Heinemann. ISBN 978-0-325-00353-5.
• Уинн, Карен (1998). «Числовая компетентность у младенцев». Развитие математических навыков . Тейлор и Фрэнсис. ISBN 0-86377-816-X.

Математическое изложение

• Богомольный, Александр (1996). "Сложение". Interactive Mathematics Miscellany and Puzzles (cut-the-knot.org) . Архивировано из оригинала 26 апреля 2006 г. . Получено 3 февраля 2006 г.
• Ченг, Евгения (2017). Beyond Infinity: An Expedition to the Outer Limits of Mathematics . Базовые книги. ISBN 978-1-541-64413-7.
• Данэм, Уильям (1994). Математическая вселенная . Wiley. ISBN 978-0-471-53656-7.
• Джонсон, Пол (1975). Из книги «Палки и камни: личные приключения в математике» . Science Research Associates. ISBN 978-0-574-19115-1.
• Линдерхольм, Карл (1971). Математика, ставшая трудной . Вулф. ISBN 978-0-7234-0415-6.
• Смит, Фрэнк (2002). Стеклянная стена: почему математика может показаться сложной . Teachers College Press. ISBN 978-0-8077-4242-6.
• Смит, Карл (1980). Природа современной математики (3-е изд.). Уодсворт. ISBN 978-0-8185-0352-8.

Высшая математика

• Бергман, Джордж (2005). Приглашение к общей алгебре и универсальным конструкциям (2.3 ред.). Общая печать. ISBN 978-0-9655211-4-7.
• Беррилл, Клод (1967). Основы теории действительных чисел . McGraw-Hill. LCC  QA248.B95.
• Даммит, Д.; Фут, Р. (1999). Абстрактная алгебра (2-е изд.). Wiley. ISBN 978-0-471-36857-1.
• Gbur, Greg (2011). Математические методы для оптической физики и техники. Cambridge University Press. ISBN 978-0-511-91510-9. OCLC  704518582.
• Эндертон, Герберт (1977). Элементы теории множеств . Academic Press . ISBN 978-0-12-238440-0.
• Ли, Джон (2003). Введение в гладкие многообразия . Springer. ISBN 978-0-387-95448-6.
• Мартин, Джон (2003). Введение в языки и теорию вычислений (3-е изд.). McGraw-Hill. ISBN 978-0-07-232200-2.
• Риль, Эмили (2016). Теория категорий в контексте. Дувр. ISBN 978-0-486-80903-8.
• Рудин, Уолтер (1976). Принципы математического анализа (3-е изд.). McGraw-Hill. ISBN 978-0-07-054235-8.
• Стюарт, Джеймс (1999). Исчисление: Ранние трансцендентали (4-е изд.). Брукс/Коул. ISBN 978-0-534-36298-0.

Математическое исследование

• Akian, Marianne; Bapat, Ravindra; Gaubert, Stephane (2005). "Метод min-plus в теории возмущений собственных значений и обобщенная теорема Лидского-Вишика-Люстерника". INRIA Reports . arXiv : math.SP/0402090 . Bibcode : 2004math......2090A.
• Baez, J. ; Dolan, J. (2001). Mathematics Unlimited – 2001 и далее. От конечных множеств к диаграммам Фейнмана . стр. 29. arXiv : math.QA/0004133 . ISBN 3-540-66913-2.
• Литвинов, Григорий; Маслов, Виктор; Соболевский, Андрей (1999). Идемпотентная математика и интервальный анализ. Надежные вычисления , Kluwer.
• Лодей, Жан-Луи (2002). «Арифметика». Журнал алгебры . 258 : 275. arXiv : math/0112034 . doi :10.1016/S0021-8693(02)00510-0.
• Михалкин, Григорий (2006). Санс-Соле, Марта (ред.). Труды Международного конгресса математиков (ICM), Мадрид, Испания, 22–30 августа 2006 г. Том II: Приглашенные лекции. Тропическая геометрия и ее приложения . Цюрих: Европейское математическое общество . стр. 827–852. arXiv : math.AG/0601041 . ISBN 978-3-03719-022-7. Збл  1103.14034.
• Виро, Олег (2001). Каскуберта, Карлес; Миро-Роч, Роза Мария; Вердера, Джоан; Ксамбо-Декамп, Себастья (ред.). Европейский конгресс математики: Барселона, 10–14 июля 2000 г., Том I. Деквантование действительной алгебраической геометрии на логарифмической бумаге. Прогресс в математике. Том. 201. Базель: Биркхойзер. стр. 135–146. arXiv : math/0005163 . Бибкод : 2000math......5163V. ISBN 978-3-7643-6417-5. Збл  1024.14026.

Вычислительная техника

• Флинн, М.; Оберман, С. (2001). Advanced Computer Arithmetic Design . Wiley. ISBN 978-0-471-41209-0.
• Хоровиц, П.; Хилл, В. (2001). Искусство электроники (2-е изд.). Cambridge UP. ISBN 978-0-521-37095-0.
• Джексон, Альберт (1960). Аналоговые вычисления . McGraw-Hill. LCC  QA76.4 J3.
• Риффель, Элеанор Г.; Полак, Вольфганг Х. (4 марта 2011 г.). Квантовые вычисления: легкое введение . MIT Press. ISBN 978-0-262-01506-6.
• Труитт, Т.; Роджерс, А. (1960). Основы аналоговых компьютеров . Джон Ф. Райдер. LCC  QA76.4 T7.
• Марген, Жан (1994). Histoire des Instruments et Machines à Calculer, Trois Siècles de Mécanique Pensante 1642–1942 (на французском языке). Герман. ISBN 978-2-7056-6166-3.
• Татон, Рене (1963). Механический расчет. Que Sais-Je? № 367 (на французском языке). Прессы университетов Франции. стр. 20–28.

Дальнейшее чтение

• Баруди, Артур; Тииликайнен, Сирпа (2003). Развитие арифметических понятий и навыков. Две точки зрения на развитие сложения. Routledge. стр. 75. ISBN 0-8058-3155-X.
• Дэвисон, Дэвид М.; Ландау, Марша С.; МакКракен, Лия; Томпсон, Линда (1999). Математика: Исследования и приложения (редактор TE). Prentice Hall. ISBN 978-0-13-435817-8.
• Bunt, Lucas NH; Jones, Phillip S.; Bedient, Jack D. (1976). Исторические корни элементарной математики . Prentice-Hall. ISBN 978-0-13-389015-0.
• Пунен, Бьорн (2010). «Дополнение». Girls' Angle Bulletin . 3 (3–5). ISSN  2151-5743.
• Weaver, J. Fred (1982). "Сложение и вычитание: когнитивная перспектива". Сложение и вычитание: когнитивная перспектива. Интерпретации числовых операций и символические представления сложения и вычитания . Taylor & Francis. стр. 60. ISBN 0-89859-171-6.