Генетический дрейф , также известный как случайный генетический дрейф , аллельный дрейф или эффект Райта , [1] представляет собой изменение частоты существующего варианта гена ( аллеля ) в популяции из-за случайного совпадения. [2]
Генетический дрейф может привести к полному исчезновению вариантов генов и, таким образом, снижению генетической изменчивости . [3] Он также может привести к тому, что изначально редкие аллели станут гораздо более частыми и даже фиксированными.
Когда существует несколько копий аллеля, эффект генетического дрейфа более заметен, а когда существует много копий, эффект менее заметен (из-за закона больших чисел ). В середине 20-го века произошли энергичные дебаты по поводу относительной важности естественного отбора по сравнению с нейтральными процессами, включая генетический дрейф. Рональд Фишер , который объяснил естественный отбор с помощью менделевской генетики , [4] придерживался мнения, что генетический дрейф играет в лучшем случае незначительную роль в эволюции , и это мнение оставалось доминирующим в течение нескольких десятилетий. В 1968 году популяционный генетик Моту Кимура возродил дебаты своей нейтральной теорией молекулярной эволюции , которая утверждает, что большинство случаев, когда генетическое изменение распространяется по популяции (хотя не обязательно изменения в фенотипах ), вызваны генетическим дрейфом, действующим на нейтральные мутации . [5] [6] В 1990-х годах была предложена конструктивная нейтральная эволюция , которая стремится объяснить, как сложные системы возникают посредством нейтральных переходов. [7] [8]
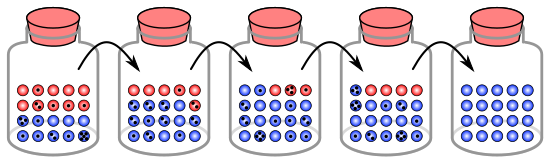
Процесс генетического дрейфа можно проиллюстрировать, используя 20 шариков в банке, чтобы представить 20 организмов в популяции. [9] Рассмотрим эту банку с шариками как начальную популяцию. Половина шариков в банке красные, а половина — синие, причем каждый цвет соответствует разному аллелю одного гена в популяции. В каждом новом поколении организмы размножаются случайным образом. Чтобы представить это размножение, случайным образом выберите шарик из исходной банки и поместите новый шарик того же цвета в новую банку. Это «потомство» исходного шарика, что означает, что исходный шарик остается в своей банке. Повторяйте этот процесс до тех пор, пока во второй банке не окажется 20 новых шариков. Теперь во второй банке будет 20 «потомков» или шариков разных цветов. Если только во второй банке не содержится ровно 10 красных шариков и 10 синих шариков, произошел случайный сдвиг в частотах аллелей.
Если этот процесс повторяется несколько раз, количество красных и синих шариков, выбранных в каждом поколении, колеблется. Иногда в банке больше красных шариков, чем в ее «родительской» банке, а иногда больше синих. Это колебание аналогично генетическому дрейфу — изменению частоты аллелей в популяции в результате случайного изменения распределения аллелей от одного поколения к другому.
В любом поколении не может быть выбран ни один шарик определенного цвета, что означает, что у них нет потомства. В этом примере, если не выбран ни один красный шарик, банка, представляющая новое поколение, содержит только синее потомство. Если это происходит, красный аллель навсегда теряется в популяции, в то время как оставшийся синий аллель становится фиксированным: все будущие поколения полностью синие. В небольших популяциях фиксация может произойти всего за несколько поколений.
Механизмы генетического дрейфа можно проиллюстрировать на очень простом примере. Рассмотрим очень большую колонию бактерий , изолированную в капле раствора. Бактерии генетически идентичны, за исключением одного гена с двумя аллелями, обозначенными как A и B , которые являются нейтральными аллелями, что означает, что они не влияют на способность бактерий выживать и размножаться; все бактерии в этой колонии имеют одинаковую вероятность выжить и размножаться. Предположим, что у половины бактерий есть аллель A , а у другой половины — аллель B. Таким образом, A и B имеют частоту аллеля 1/2.
Затем капля раствора сжимается до тех пор, пока в ней не останется еды, достаточной только для поддержания четырех бактерий. Все остальные бактерии погибают, не размножаясь. Среди четырех выживших существует 16 возможных комбинаций аллелей A и B :
(AAAA), (BAAA), (ABAA),
(BBAA), (AABA), (BABA), (ABBA), (BBBA),
( АААБ), (БААБ), (АБАБ), (ББАВ),
(ААББ), (БАББ), (АБББ), (ББББ).
Поскольку все бактерии в исходном растворе имеют одинаковую вероятность выжить, когда раствор сжимается, четыре выживших представляют собой случайную выборку из исходной колонии. Вероятность того , что каждый из четырех выживших имеет заданный аллель, равна 1/2, и поэтому вероятность того, что любая конкретная комбинация аллелей возникнет, когда раствор сжимается, равна
(Исходный размер популяции настолько велик, что выборка фактически происходит с заменой.) Другими словами, каждая из 16 возможных комбинаций аллелей имеет одинаковую вероятность возникновения с вероятностью 1/16.
Подсчет комбинаций с одинаковым количеством букв A и B дает следующую таблицу:
Как показано в таблице, общее количество комбинаций, которые имеют одинаковое количество аллелей A и аллелей B , равно шести, а вероятность этой комбинации равна 6/16. Общее количество других комбинаций равно десяти, поэтому вероятность неравного количества аллелей A и B составляет 10/16. Таким образом, хотя исходная колония началась с равного количества аллелей A и B , вполне возможно, что количество аллелей в оставшейся популяции из четырех членов не будет равным. Ситуация с равными количествами на самом деле менее вероятна, чем с неравными количествами. В последнем случае произошел генетический дрейф, поскольку частоты аллелей популяции изменились из-за случайной выборки. В этом примере популяция сократилась всего до четырех случайных выживших, явление, известное как бутылочное горлышко популяции .
Вероятности количества выживших копий аллеля A (или B ) (приведенные в последнем столбце приведенной выше таблицы) можно рассчитать непосредственно из биномиального распределения , где вероятность «успеха» (вероятность присутствия данного аллеля) равна 1/2 (т. е. вероятность того, что в комбинации имеется k копий аллеля A (или B )), определяется по формуле:
где n=4 — количество выживших бактерий.
Математические модели генетического дрейфа могут быть разработаны с использованием либо ветвящихся процессов , либо уравнения диффузии, описывающего изменения частоты аллелей в идеализированной популяции . [10]
Рассмотрим ген с двумя аллелями, A или B. При диплоидии популяции, состоящие из N особей, имеют 2 N копий каждого гена. Особь может иметь две копии одного и того же аллеля или два разных аллеля. Частота одного аллеля обозначается как p , а другого — как q . Модель Райта–Фишера (названная в честь Сьюэлла Райта и Рональда Фишера ) предполагает, что поколения не перекрываются (например, однолетние растения имеют ровно одно поколение в год) и что каждая копия гена, обнаруженная в новом поколении, выбирается независимо случайным образом из всех копий гена в старом поколении. Формула для расчета вероятности получения k копий аллеля, имевшего частоту p в последнем поколении, выглядит следующим образом [11] [12]
где символ " ! " обозначает факториальную функцию. Это выражение можно также сформулировать с использованием биномиального коэффициента ,
Модель Морана предполагает перекрывающиеся поколения. На каждом временном шаге выбирается одна особь для размножения, а другая — для смерти. Таким образом, на каждом временном шаге количество копий данного аллеля может увеличиваться на единицу, уменьшаться на единицу или оставаться неизменным. Это означает, что матрица перехода является трехдиагональной , что означает, что математические решения проще для модели Морана, чем для модели Райта–Фишера. С другой стороны, компьютерное моделирование обычно проще выполнять с использованием модели Райта–Фишера, поскольку необходимо вычислить меньше временных шагов. В модели Морана требуется N временных шагов, чтобы пройти через одно поколение, где N — эффективный размер популяции . В модели Райта–Фишера требуется всего один. [13]
На практике модели Морана и Райта–Фишера дают качественно схожие результаты, но генетический дрейф происходит в два раза быстрее в модели Морана.
Если дисперсия в числе потомков намного больше, чем та, которая дается биномиальным распределением, предполагаемым моделью Райта-Фишера, то при той же общей скорости генетического дрейфа (дисперсии эффективного размера популяции) генетический дрейф является менее мощной силой по сравнению с отбором. [14] Даже для той же дисперсии, если более высокие моменты распределения числа потомков превышают моменты биномиального распределения, то снова сила генетического дрейфа существенно ослабевает. [15]
Случайные изменения частот аллелей могут быть вызваны и другими эффектами, помимо ошибки выборки , например, случайными изменениями давления отбора. [16]
Одним из важных альтернативных источников стохастичности , возможно, более важным, чем генетический дрейф, является генетический тяготение . [17] Генетический тяготение — это воздействие на локус отбора на связанных локусах. Математические свойства генетического тяготения отличаются от свойств генетического дрейфа. [18] Направление случайного изменения частоты аллелей автокоррелируется между поколениями. [2]
Принцип Харди-Вайнберга гласит, что в достаточно больших популяциях частоты аллелей остаются постоянными от поколения к поколению, если равновесие не нарушается миграцией , генетическими мутациями или отбором . [19]
Однако в конечных популяциях новые аллели не появляются из случайной выборки аллелей, переданных следующему поколению, но выборка может привести к исчезновению существующего аллеля. Поскольку случайная выборка может удалить, но не заменить аллель, и поскольку случайные снижения или увеличения частоты аллелей влияют на ожидаемые распределения аллелей для следующего поколения, генетический дрейф со временем приводит популяцию к генетической однородности. Когда аллель достигает частоты 1 (100%), говорят, что он «фиксируется» в популяции, а когда аллель достигает частоты 0 (0%), он теряется. Меньшие популяции достигают фиксации быстрее, тогда как в пределе бесконечной популяции фиксация не достигается. Как только аллель фиксируется, генетический дрейф останавливается, и частота аллеля не может измениться, если в популяцию не вводится новый аллель посредством мутации или потока генов . Таким образом, даже если генетический дрейф является случайным, бесцельным процессом, он действует для устранения генетической изменчивости с течением времени. [20]

Предполагая, что генетический дрейф является единственной эволюционной силой, действующей на аллель, после t поколений во многих реплицированных популяциях, начиная с частот аллелей p и q , дисперсия частоты аллелей в этих популяциях составит
Если предположить, что генетический дрейф является единственной эволюционной силой, действующей на аллель, то в любой момент времени вероятность того, что аллель в конечном итоге зафиксируется в популяции, равна просто его частоте в популяции в это время. [22] Например, если частота p для аллеля A составляет 75%, а частота q для аллеля B составляет 25%, то при неограниченном времени вероятность того, что A в конечном итоге зафиксируется в популяции, составляет 75%, а вероятность того, что B зафиксируется, составляет 25%.
Ожидаемое число поколений для фиксации пропорционально размеру популяции, так что фиксация, как предсказывают, будет происходить гораздо быстрее в меньших популяциях. [23] Обычно для определения этих вероятностей используется эффективный размер популяции, который меньше общей численности популяции. Эффективная популяция ( N e ) учитывает такие факторы, как уровень инбридинга , стадия жизненного цикла, на которой популяция является наименьшей, и тот факт, что некоторые нейтральные гены генетически связаны с другими, которые находятся под отбором. [14] Эффективный размер популяции может быть разным для каждого гена в одной и той же популяции. [24]
Одна из перспективных формул, используемых для приблизительной оценки ожидаемого времени до того, как нейтральный аллель зафиксируется посредством генетического дрейфа, согласно модели Райта-Фишера, выглядит следующим образом:
где T — число поколений, N e — эффективный размер популяции, а p — начальная частота для данного аллеля. Результат — число поколений, которые, как ожидается , пройдут, прежде чем произойдет фиксация для данного аллеля в популяции с данным размером ( N e ) и частотой аллеля ( p ). [25]
Ожидаемое время потери нейтрального аллеля в результате генетического дрейфа можно рассчитать как [11]
Когда мутация появляется только один раз в популяции, достаточно большой для того, чтобы начальная частота была незначительной, формулы можно упростить до [26]
для среднего числа поколений, ожидаемых до фиксации нейтральной мутации, и
для среднего числа поколений, ожидаемых до потери нейтральной мутации в популяции фактического размера N. [27]
Формулы выше применяются к аллелю, который уже присутствует в популяции и не подвержен ни мутации, ни естественному отбору. Если аллель теряется в результате мутации гораздо чаще, чем приобретается в результате мутации, то мутация, а также дрейф, могут влиять на время потери. Если аллель, склонный к мутационной потере, изначально зафиксирован в популяции и теряется в результате мутации со скоростью m на репликацию, то ожидаемое время в поколениях до его потери в гаплоидной популяции определяется как
где — постоянная Эйлера . [28] Первое приближение представляет собой время ожидания до первого мутанта, обреченного на потерю, причем потеря затем происходит относительно быстро из-за генетического дрейфа, занимая время 1/м ≫ N e . Второе приближение представляет время, необходимое для детерминированной потери из-за накопления мутаций. В обоих случаях время фиксации определяется мутацией через член 1/м , и в меньшей степени зависит от эффективной численности популяции .
В естественных популяциях генетический дрейф и естественный отбор не действуют изолированно; оба явления всегда присутствуют вместе с мутацией и миграцией. Нейтральная эволюция является продуктом как мутации, так и дрейфа, а не только дрейфа. Аналогично, даже когда отбор подавляет генетический дрейф, он может действовать только на вариации, которые обеспечивает мутация.
В то время как естественный отбор имеет направление, направляя эволюцию к наследуемым адаптациям к текущей среде, генетический дрейф не имеет направления и направляется только математикой случая . [29] В результате дрейф действует на генотипические частоты в популяции без учета их фенотипических эффектов. Напротив, отбор благоприятствует распространению аллелей, фенотипические эффекты которых увеличивают выживаемость и/или воспроизводство их носителей, снижает частоты аллелей, вызывающих неблагоприятные черты, и игнорирует те, которые нейтральны. [30]
Закон больших чисел предсказывает, что когда абсолютное число копий аллеля невелико (например, в небольших популяциях ), величина дрейфа частот аллелей на поколение больше. Величина дрейфа достаточно велика, чтобы подавить отбор при любой частоте аллелей, когда коэффициент отбора меньше 1, деленного на эффективный размер популяции. Поэтому неадаптивная эволюция, являющаяся результатом продукта мутации и генетического дрейфа, считается косвенным механизмом эволюционных изменений, в первую очередь в небольших изолированных популяциях. [31] Математика генетического дрейфа зависит от эффективного размера популяции, но неясно, как это связано с фактическим числом особей в популяции. [17] Генетическая связь с другими генами, находящимися под отбором, может уменьшить эффективный размер популяции, испытываемый нейтральным аллелем. При более высокой скорости рекомбинации сцепление уменьшается, а вместе с ним и этот локальный эффект на эффективный размер популяции. [32] [33] Этот эффект виден в молекулярных данных как корреляция между локальной скоростью рекомбинации и генетическим разнообразием , [34] и отрицательная корреляция между плотностью генов и разнообразием в некодирующих областях ДНК. [35] Стохастичность, связанная со сцеплением с другими генами, которые находятся под отбором, не является тем же самым, что и ошибка выборки, и иногда известна как генетический проект , чтобы отличить его от генетического дрейфа. [17]
Низкая частота аллелей делает аллели более уязвимыми для случайного исключения, даже перекрывая влияние естественного отбора. Например, в то время как неблагоприятные мутации обычно быстро устраняются в популяции, новые выгодные мутации почти так же уязвимы для потери через генетический дрейф, как и нейтральные мутации. Только когда частота аллелей для выгодной мутации достигнет определенного порога, генетический дрейф не будет иметь никакого эффекта. [30]

Бутылочное горлышко популяции — это когда популяция сокращается до значительно меньших размеров за короткий промежуток времени из-за какого-то случайного события в окружающей среде. В настоящем бутылочном горлышке популяции шансы на выживание любого члена популяции являются чисто случайными и не улучшаются каким-либо конкретным врожденным генетическим преимуществом. Бутылочное горлышко может привести к радикальным изменениям в частотах аллелей, совершенно независимым от отбора. [36]
Влияние бутылочного горлышка популяции может быть устойчивым, даже если бутылочное горлышко вызвано одноразовым событием, таким как природная катастрофа. Интересным примером бутылочного горлышка, вызывающего необычное генетическое распределение, является относительно высокая доля особей с полной палочковой клеточной слепотой ( ахроматопсия ) на атолле Пингелап в Микронезии . [37] После бутылочного горлышка инбридинг увеличивается. Это увеличивает ущерб, наносимый рецессивными вредными мутациями, в процессе, известном как инбридинговая депрессия . Худшие из этих мутаций отбираются против, что приводит к потере других аллелей, которые генетически связаны с ними, в процессе фонового отбора . [2] Для рецессивных вредных мутаций этот отбор может быть усилен вследствие бутылочного горлышка из-за генетической чистки . Это приводит к дальнейшей потере генетического разнообразия. Кроме того, устойчивое сокращение размера популяции увеличивает вероятность дальнейших колебаний аллелей из-за дрейфа в будущих поколениях.
Генетическая изменчивость популяции может быть значительно снижена из-за бутылочного горлышка, и даже полезные адаптации могут быть навсегда устранены. [38] Потеря изменчивости делает выжившую популяцию уязвимой к любым новым давлениям отбора, таким как болезни, климатические изменения или сдвиг в доступном источнике пищи, поскольку адаптация в ответ на изменения окружающей среды требует достаточной генетической изменчивости в популяции для того, чтобы естественный отбор имел место. [39] [40]
В недавнем прошлом было известно много случаев «бутылочного горлышка» популяции. До прибытия европейцев североамериканские прерии были средой обитания миллионов больших луговых куропаток . Только в Иллинойсе их численность резко упала с примерно 100 миллионов птиц в 1900 году до примерно 50 птиц в 1990-х годах. Сокращение популяции произошло из-за охоты и разрушения среды обитания , но следствием этого стала потеря большей части генетического разнообразия вида. Анализ ДНК , сравнивающий птиц середины века с птицами 1990-х годов, документирует резкое снижение генетической изменчивости всего за последние несколько десятилетий. В настоящее время большие луговые куропатки испытывают низкий репродуктивный успех . [41]
Однако генетическая потеря, вызванная «бутылочным горлышком» и генетическим дрейфом, может повысить приспособленность, как в случае с Ehrlichia . [42]
Чрезмерная охота также вызвала серьезное бутылочное горлышко популяции северного морского слона в 19 веке. Их последующее снижение генетической изменчивости можно вывести, сравнив его с южным морским слоном , на которого не так агрессивно охотились. [43]

Эффект основателя — это особый случай бутылочного горлышка популяции, возникающий, когда небольшая группа в популяции откалывается от исходной популяции и формирует новую. Ожидается, что случайная выборка аллелей в только что сформированной новой колонии будет грубо искажать исходную популяцию по крайней мере в некоторых отношениях. [44] Возможно даже, что число аллелей для некоторых генов в исходной популяции больше, чем число копий генов у основателей, что делает полное представление невозможным. Когда вновь сформированная колония мала, ее основатели могут сильно влиять на генетический состав популяции в далеком будущем.
Хорошо документированный пример можно найти в миграции амишей в Пенсильванию в 1744 году. Двое членов новой колонии разделяли рецессивный аллель синдрома Эллиса-Ван Кревельда . Члены колонии и их потомки, как правило, являются религиозными изолятами и остаются относительно изолированными. В результате многих поколений инбридинга синдром Эллиса-Ван Кревельда теперь гораздо более распространен среди амишей, чем среди населения в целом. [30] [45]
Разница в частотах генов между исходной популяцией и колонией также может привести к значительному расхождению двух групп в течение многих поколений. По мере увеличения разницы или генетического расстояния две разделенные популяции могут стать различными как генетически, так и фенетически , хотя не только генетический дрейф, но и естественный отбор, поток генов и мутации способствуют этому расхождению. Этот потенциал относительно быстрых изменений в частоте генов колонии заставил большинство ученых считать эффект основателя (и, как следствие, генетический дрейф) значительной движущей силой в эволюции новых видов . Сьюэлл Райт был первым, кто придал это значение случайному дрейфу и небольшим, недавно изолированным популяциям с его теорией смещающегося баланса видообразования. [46] Вслед за Райтом Эрнст Майр создал множество убедительных моделей, чтобы показать, что снижение генетической изменчивости и небольшой размер популяции после эффекта основателя были критически важны для развития новых видов. [47] Однако сегодня эта точка зрения имеет гораздо меньше поддержки, поскольку гипотеза неоднократно проверялась в ходе экспериментальных исследований, и результаты были в лучшем случае двусмысленными. [48]
Роль случайности в эволюции впервые была описана Арендом Л. Хагедорном и Анной Корнелией Хагедорн-Форстейвель Ла Бранд в 1921 году. [49] Они подчеркнули, что случайное выживание играет ключевую роль в потере изменчивости популяций. Фишер (1922) ответил на это первой, хотя и незначительно неверной, математической трактовкой «эффекта Хагедорна». [50] Примечательно, что он ожидал, что многие естественные популяции были слишком велики (N ~10 000) для того, чтобы эффекты дрейфа были существенными, и считал, что дрейф будет иметь незначительное влияние на эволюционный процесс. Исправленная математическая трактовка и термин «генетический дрейф» были позже придуманы основателем популяционной генетики Сьюэллом Райтом . Он впервые использовал термин «дрейф» в 1929 году, [51] хотя в то время он использовал его в смысле направленного процесса изменения или естественного отбора. Случайный дрейф посредством ошибки выборки стал известен как «эффект Сьюэлла–Райта», хотя он никогда не был полностью уверен в том, что ему дали его имя. Райт называл все изменения частоты аллелей либо «устойчивым дрейфом» (например, селекцией), либо «случайным дрейфом» (например, ошибкой выборки). [52] «Дрейф» был принят как технический термин исключительно в стохастическом смысле. [53] Сегодня его обычно определяют еще более узко, в терминах ошибки выборки, [54] хотя это узкое определение не является универсальным. [55] [56] Райт писал, что «ограничение «случайного дрейфа» или даже «дрейфа» только одним компонентом, эффектами случайностей выборки, имеет тенденцию приводить к путанице». [52] Сьюэлл Райт считал процесс случайного генетического дрейфа посредством ошибки выборки эквивалентным процессу посредством инбридинга, но более поздние работы показали, что они различны. [57]
На заре современного эволюционного синтеза ученые начали смешивать новую науку популяционной генетики с теорией естественного отбора Чарльза Дарвина . В рамках этой структуры Райт сосредоточился на эффектах инбридинга на небольших относительно изолированных популяциях. Он ввел концепцию адаптивного ландшафта , в котором такие явления, как скрещивание и генетический дрейф в небольших популяциях, могли отталкивать их от адаптивных пиков, что, в свою очередь, позволяло естественному отбору подталкивать их к новым адаптивным пикам. [58] Райт считал, что меньшие популяции больше подходят для естественного отбора, потому что «инбридинг был достаточно интенсивным, чтобы создавать новые системы взаимодействия посредством случайного дрейфа, но недостаточно интенсивным, чтобы вызывать случайную неадаптивную фиксацию генов». [59]
Взгляды Райта на роль генетического дрейфа в эволюционной схеме были спорными почти с самого начала. Одним из самых громких и влиятельных критиков был коллега Рональд Фишер. Фишер признал, что генетический дрейф играет некоторую роль в эволюции, но незначительную. Фишера обвиняли в непонимании взглядов Райта, поскольку в своих критических замечаниях Фишер, по-видимому, утверждал, что Райт почти полностью отверг отбор. Для Фишера рассмотрение процесса эволюции как долгого, устойчивого, адаптивного прогресса было единственным способом объяснить постоянно растущую сложность от более простых форм. Но дебаты продолжались между «градуалистами» и теми, кто больше склонялся к модели эволюции Райта, где отбор и дрейф вместе играют важную роль. [60]
В 1968 году Мотоо Кимура возобновил дебаты своей нейтральной теорией молекулярной эволюции , которая утверждает, что большинство генетических изменений вызвано генетическим дрейфом, действующим на нейтральные мутации. [5] [6]
Роль генетического дрейфа посредством ошибки выборки в эволюции подверглась критике со стороны Джона Х. Гиллеспи [61] и Уильяма Б. Провайна , которые утверждают, что отбор на связанных участках является более важной стохастической силой.