Трехмерное пространство

В геометрии трехмерное пространство ( 3D-пространство , 3-пространство или, реже, трехмерное пространство ) — это математическое пространство , в котором для определения положения точки требуются три значения ( координаты ) . Чаще всего это трехмерное евклидово пространство , то есть евклидово пространство размерности три, которое моделирует физическое пространство . Более общие трехмерные пространства называются 3-многообразиями . Этот термин может также в разговорной речи относиться к подмножеству пространства, трехмерной области (или 3D- домену ), ^[1] объемной фигуре .

Технически, кортеж из $n$ чисел можно понимать как декартовы координаты местоположения в $n$ -мерном евклидовом пространстве. Набор этих $n$ -кортежей обычно обозначается и может быть идентифицирован как пара, образованная $n$ -мерным евклидовым пространством и декартовой системой координат . Когда $n$ $= 3$ , это пространство называется $\mathbb {R} ^{n},$ трехмерное евклидово пространство (или просто «евклидово пространство», когда контекст ясен). ^[2] В классической физике оно служит моделью физической вселенной , в которой существует вся известная материя . Когда рассматривается теория относительности , его можно считать локальным подпространством пространства-времени . ^[3] Хотя это пространство остается наиболее убедительным и полезным способом моделирования мира, как он воспринимается, ^[4] оно является лишь одним примером большого разнообразия пространств в трех измерениях, называемых 3-многообразиями . В этом классическом примере, когда три значения относятся к измерениям в разных направлениях ( координаты ), могут быть выбраны любые три направления, при условии, что эти направления не лежат в одной плоскости . Кроме того, если эти направления попарно перпендикулярны , три значения часто обозначаются терминами ширина /ширина , высота /глубина и длина .

История

Книги XI–XIII «Начал» Евклида посвящены трехмерной геометрии. В книге XI развиваются понятия ортогональности и параллельности линий и плоскостей, а также определяются тела, включая параллелепипеды, пирамиды, призмы, сферы, октаэдры, икосаэдры и додекаэдры. В книге XII развиваются понятия подобия тел. В книге XIII описывается построение пяти правильных Платоновых тел в сфере.

В XVII веке трехмерное пространство описывалось с помощью декартовых координат , с появлением аналитической геометрии, разработанной Рене Декартом в его работе La Géométrie и Пьером де Ферма в рукописи Ad locos planos et solidos isagoge (Введение в плоские и твердые места), которая не была опубликована при жизни Ферма. Однако только работа Ферма имела дело с трехмерным пространством.

В 19 веке развитие геометрии трехмерного пространства пришло с разработкой кватернионов Уильямом Роуэном Гамильтоном . Фактически, именно Гамильтон ввел термины скаляр и вектор , и они были впервые определены в его геометрической структуре для кватернионов . Затем трехмерное пространство можно было описать кватернионами, имеющими исчезающую скалярную составляющую, то есть . Хотя Гамильтон явно не изучал это, это косвенно ввело понятия базиса, здесь заданного элементами кватерниона , а также скалярным произведением и векторным произведением , которые соответствуют (отрицательной) скалярной части и векторной части произведения двух векторных кватернионов. $q=a+ui+vj+wk$ $а=0$ $я,j,k$

Только Джозайя Уиллард Гиббс самостоятельно определил эти два произведения, а современные обозначения для скалярного и векторного произведений были введены в его методических записях для преподавания в классе, которые также можно найти в учебнике 1901 года «Векторный анализ», написанном Эдвином Бидвеллом Уилсоном на основе лекций Гиббса.

Также в XIX веке появились разработки в области абстрактного формализма векторных пространств благодаря работам Германа Грассмана и Джузеппе Пеано , последний из которых впервые дал современное определение векторных пространств как алгебраической структуры.

В евклидовой геометрии

Системы координат

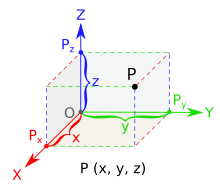
В математике аналитическая геометрия (также называемая декартовой геометрией) описывает каждую точку в трехмерном пространстве с помощью трех координат. Даны три оси координат , каждая из которых перпендикулярна двум другим в начале координат , точке, в которой они пересекаются. Они обычно обозначаются как $x, y$ и $z$ . Относительно этих осей положение любой точки в трехмерном пространстве задается упорядоченной тройкой действительных чисел , каждое число дает расстояние этой точки от начала координат , измеренное вдоль данной оси, которое равно расстоянию этой точки от плоскости, определяемой двумя другими осями. ^[5]

Другие популярные методы описания местоположения точки в трехмерном пространстве включают цилиндрические координаты и сферические координаты , хотя существует бесконечное число возможных методов. Подробнее см. Евклидово пространство .

Ниже приведены изображения вышеупомянутых систем.

Линии и плоскости

Две различные точки всегда определяют (прямую) линию . Три различные точки либо коллинеарны , либо определяют уникальную плоскость . С другой стороны, четыре различные точки могут быть либо коллинеарны, либо компланарны , либо определять все пространство.

Две различные прямые могут пересекаться, быть параллельными или скрещиваться . Две параллельные прямые или две пересекающиеся прямые лежат в одной плоскости, поэтому скрещивающиеся прямые — это прямые, которые не пересекаются и не лежат в общей плоскости.

Две различные плоскости могут либо пересекаться на одной прямой, либо быть параллельными (т. е. не пересекаться). Три различные плоскости, ни одна пара которых не является параллельной, могут либо пересекаться на одной прямой, либо пересекаться в единственной общей точке, либо не иметь общей точки. В последнем случае три линии пересечения каждой пары плоскостей взаимно параллельны.

Прямая может лежать в данной плоскости, пересекать эту плоскость в единственной точке или быть параллельной плоскости. В последнем случае в плоскости будут существовать прямые, параллельные данной прямой.

Гиперплоскость — это подпространство на одну размерность меньше размерности полного пространства. Гиперплоскости трехмерного пространства — это двумерные подпространства, то есть плоскости. В декартовых координатах точки гиперплоскости удовлетворяют одному линейному уравнению , поэтому плоскости в этом трехмерном пространстве описываются линейными уравнениями. Прямая может быть описана парой независимых линейных уравнений, каждое из которых представляет плоскость, имеющую эту прямую в качестве общего пересечения.

Теорема Вариньона утверждает, что середины любого четырехугольника образуют параллелограмм и, следовательно, лежат в одной плоскости. $\mathbb {R} ^{3}$

Сферы и шары

Сфера в 3-пространстве (также называемая 2-сферой , поскольку это 2-мерный объект) состоит из множества всех точек в 3-пространстве, находящихся на фиксированном расстоянии $r$ от центральной точки $P.$ Тело, заключенное в сферу, называется шаром ( или, точнее, 3-шаром ).

Объем шара определяется по формуле

$V={\frac {4}{3}}\pi r^{3},$ и площадь поверхности сферы равна Другой тип сферы возникает из 4-шара, чья трехмерная поверхность является 3-сферой : точки, равноудаленные от начала координат евклидова пространства $R$ $4$ . Если точка имеет координаты $P$ $($ $x$ $,$ $y$ $,$ $z$ $,$ $w$ $)$ , то $x$ $2$ $+$ $y$ $2$ $+$ $z$ $2$ $+$ $w$ $2$ $= 1$ характеризует те точки на единичной 3-сфере с центром в начале координат. $A=4\pi r^{2}.$

Эта 3-сфера является примером 3-многообразия: пространства, которое «локально выглядит» как 3-мерное пространство. В точных топологических терминах каждая точка 3-сферы имеет окрестность, гомеоморфную открытому подмножеству 3-мерного пространства.

Многогранники

В трех измерениях существует девять правильных многогранников: пять выпуклых Платоновых тел и четыре невыпуклых многогранника Кеплера-Пуансо .

Поверхности вращения

Поверхность , образованная вращением плоской кривой вокруг фиксированной линии в ее плоскости как оси, называется поверхностью вращения . Плоская кривая называется образующей поверхности. Сечение поверхности, образованное пересечением поверхности с плоскостью, перпендикулярной (ортогональной) оси, является окружностью.

Простые примеры возникают, когда образующая является прямой. Если образующая пересекает осевую линию, поверхность вращения является прямым круговым конусом с вершиной (апексом) в точке пересечения. Однако, если образующая и ось параллельны, то поверхность вращения является круговым цилиндром .

Квадрические поверхности

По аналогии с коническими сечениями , множество точек, декартовы координаты которых удовлетворяют общему уравнению второй степени, а именно, где $A$ $,$ $B$ $,$ $C$ $,$ $F$ $,$ $G$ $,$ $H$ $,$ $J$ $,$ $K$ $,$ $L$ и $M$ — действительные числа и не все из $A$ $,$ $B$ $,$ $C$ $,$ $F$ $,$ $G$ и $H$ равны нулю, называется квадратичной поверхностью . ^[6] $Ax^{2}+By^{2}+Cz^{2}+Fxy+Gyz+Hxz+Jx+Ky+Lz+M=0,$

Существует шесть типов невырожденных квадратных поверхностей:

Вырожденные квадратичные поверхности — это пустое множество, одна точка, одна прямая, одна плоскость, пара плоскостей или квадратный цилиндр (поверхность, состоящая из невырожденного конического сечения в плоскости $π$ и всех прямых $R 3 ,$ проходящих через эту конику и перпендикулярных к $π$ ). ^[6] Эллиптические конусы иногда также считаются вырожденными квадратичными поверхностями.

И гиперболоид с одной полосой, и гиперболический параболоид являются линейчатыми поверхностями , что означает, что они могут быть составлены из семейства прямых линий. Фактически, каждый из них имеет два семейства образующих линий, члены каждого семейства не пересекаются, и каждый член одного семейства пересекает, за одним исключением, каждого члена другого семейства. ^[7] Каждое семейство называется регулусом .

В линейной алгебре

Другой способ рассмотрения трехмерного пространства можно найти в линейной алгебре , где идея независимости имеет решающее значение. Пространство имеет три измерения, поскольку длина коробки не зависит от ее ширины или ширины. На техническом языке линейной алгебры пространство является трехмерным, поскольку каждая точка в пространстве может быть описана линейной комбинацией трех независимых векторов .

Скалярное произведение, угол и длина

Вектор можно изобразить в виде стрелки. Величина вектора — это его длина, а его направление — это направление, на которое указывает стрелка. Вектор в можно представить упорядоченной тройкой действительных чисел. Эти числа называются компонентами вектора. $\mathbb {R} ^{3}$

Скалярное произведение двух векторов $A = [A 1, A 2, A 3]$ и $B = [B 1, B 2, B 3]$ определяется как: ^[8]

\mathbf {A} \cdot \mathbf {B} =A_{1}B_{1}+A_{2}B_{2}+A_{3}B_{3}=\sum _{i=1}^{3}A_{i}B_{i}.

Величина вектора $A$ обозначается как $|| A ||$ . Скалярное произведение вектора $A = [A 1, A 2, A 3]$ на самого себя равно

\mathbf {A} \cdot \mathbf {A} =\|\mathbf {A} \|^{2}=A_{1}^{2}+A_{2}^{2}+A_{3}^{2},

что дает

\|\mathbf {A} \|={\sqrt {\mathbf {A} \cdot \mathbf {A} }}={\sqrt {A_{1}^{2}+A_{2}^{2}+A_{3}^{2}}},

формула для евклидовой длины вектора.

Без ссылки на компоненты векторов скалярное произведение двух ненулевых евклидовых векторов $A$ и $B$ определяется как ^[9]

\mathbf {A} \cdot \mathbf {B} =\|\mathbf {A} \|\,\|\mathbf {B} \|\cos \theta ,

где $θ$ — угол между $A$ и $B.$

Перекрестное произведение

Перекрестное произведение или векторное произведение — это бинарная операция над двумя векторами в трехмерном пространстве , которая обозначается символом ×. Перекрестное произведение A × B векторов A и B — это вектор, перпендикулярный обоим и, следовательно, нормальный к плоскости, их содержащей. Он имеет множество приложений в математике, физике и технике .

На языке функций векторное произведение — это функция . $\times :\mathbb {R} ^{3}\times \mathbb {R} ^{3}\rightarrow \mathbb {R} ^{3}$

Компоненты векторного произведения — это , и их также можно записать в компонентах, используя соглашение Эйнштейна о суммировании как , где — символ Леви-Чивиты . Он обладает тем свойством, что . $\mathbf {A} \times \mathbf {B} =[A_{2}B_{3}-B_{2}A_{3},A_{3}B_{1}-B_{3}A_{1},A_{1}B_{2}-B_{1}A_{2}]$ $(\mathbf {A} \times \mathbf {B} )_{i}=\varepsilon _{ijk}A_{j}B_{k}$ $\varepsilon _{ijk}$ $\mathbf {A} \times \mathbf {B} =-\mathbf {B} \times \mathbf {A}$

Его величина связана с углом между и соотношением $\theta$ $\mathbf {A}$ $\mathbf {B}$ $\left\|\mathbf {A} \times \mathbf {B} \right\|=\left\|\mathbf {A} \right\|\cdot \left\|\mathbf {B} \right\|\cdot \left|\sin \theta \right|.$

Пространство и произведение образуют алгебру над полем , которая не является ни коммутативной , ни ассоциативной , но является алгеброй Ли с перекрестным произведением, являющимся скобкой Ли. В частности, пространство вместе с произведением изоморфно алгебре Ли трехмерных вращений, обозначаемой . Для того чтобы удовлетворить аксиомам алгебры Ли, вместо ассоциативности перекрестное произведение удовлетворяет тождеству Якоби . Для любых трех векторов и $(\mathbb {R} ^{3},\times )$ ${\mathfrak {so}}(3)$ $\mathbf {A} ,\mathbf {B}$ $\mathbf {C}$

$\mathbf {A} \times (\mathbf {B} \times \mathbf {C} )+\mathbf {B} \times (\mathbf {C} \times \mathbf {A} )+\mathbf {C} \times (\mathbf {A} \times \mathbf {B} )=0$

Можно в n измерениях взять произведение n − 1 векторов, чтобы получить вектор, перпендикулярный всем им. Но если произведение ограничено нетривиальными бинарными произведениями с векторными результатами, оно существует только в трех и семи измерениях . ^[10]

Абстрактное описание

Может быть полезно описывать трехмерное пространство как трехмерное векторное пространство над действительными числами. Это отличается от тонким образом. По определению, существует базис для . Это соответствует изоморфизму между и : конструкция для изоморфизма находится здесь . Однако не существует «предпочтительного» или «канонического базиса» для . $V$ $\mathbb {R} ^{3}$ ${\mathcal {B}}=\{e_{1},e_{2},e_{3}\}$ $V$ $V$ $\mathbb {R} ^{3}$ $V$

С другой стороны, существует предпочтительный базис для , который обусловлен его описанием как декартова произведения копий , то есть . Это позволяет определить канонические проекции, , где . Например, . Затем это позволяет определить стандартный базис, определяемый как , где — дельта Кронекера . Записанный полностью, стандартный базис имеет вид $\mathbb {R} ^{3}$ $\mathbb {R}$ $\mathbb {R} ^{3}=\mathbb {R} \times \mathbb {R} \times \mathbb {R}$ $\pi _{i}:\mathbb {R} ^{3}\rightarrow \mathbb {R}$ $1\leq i\leq 3$ $\pi _{1}(x_{1},x_{2},x_{3})=x$ ${\mathcal {B}}_{\text{Standard}}=\{E_{1},E_{2},E_{3}\}$ $\pi _{i}(E_{j})=\delta _{ij}$ $\delta _{ij}$ $E_{1}={\begin{pmatrix}1\\0\\0\end{pmatrix}},E_{2}={\begin{pmatrix}0\\1\\0\end{pmatrix}},E_{3}={\begin{pmatrix}0\\0\\1\end{pmatrix}}.$

Следовательно, можно рассматривать как абстрактное векторное пространство вместе с дополнительной структурой выбора базиса. Наоборот, можно получить, начав с и «забыв» декартову структуру произведения, или, что эквивалентно, стандартный выбор базиса. $\mathbb {R} ^{3}$ $V$ $\mathbb {R} ^{3}$

В отличие от общего векторного пространства , это пространство иногда называют координатным пространством. ^[11] $V$ $\mathbb {R} ^{3}$

Физически, концептуально желательно использовать абстрактный формализм, чтобы предполагать как можно меньше структуры, если она не задана параметрами конкретной задачи. Например, в задаче с вращательной симметрией работа с более конкретным описанием трехмерного пространства предполагает выбор базиса, соответствующего набору осей. Но в вращательной симметрии нет причин, по которым один набор осей предпочтительнее, скажем, тот же набор осей, который был повернут произвольно. Другими словами, предпочтительный выбор осей нарушает вращательную симметрию физического пространства. $\mathbb {R} ^{3}$

С вычислительной точки зрения необходимо работать с более конкретным описанием , чтобы выполнять конкретные вычисления. $\mathbb {R} ^{3}$

Аффинное описание

Более абстрактное описание все еще заключается в моделировании физического пространства как трехмерного аффинного пространства над действительными числами. Это уникально с точностью до аффинного изоморфизма. Иногда его называют трехмерным евклидовым пространством. Так же, как описание векторного пространства произошло из «забывания предпочтительного базиса» , описание аффинного пространства происходит из «забывания начала» векторного пространства. Евклидовы пространства иногда называют евклидовыми аффинными пространствами для отличия их от евклидовых векторных пространств. ^[12] $E(3)$ $\mathbb {R} ^{3}$

Это физически привлекательно, поскольку делает трансляционную инвариантность физического пространства очевидной. Предпочтительное начало координат нарушает трансляционную инвариантность.

Внутреннее пространство продукта

Приведенное выше обсуждение не включает скалярное произведение . Скалярное произведение является примером скалярного произведения . Физическое пространство может быть смоделировано как векторное пространство, которое дополнительно имеет структуру скалярного произведения. Скалярное произведение определяет понятия длины и угла (и, следовательно, в частности, понятие ортогональности). Для любого скалярного произведения существуют основания, при которых скалярное произведение согласуется со скалярным произведением, но, опять же, существует много различных возможных оснований, ни одно из которых не является предпочтительным. Они отличаются друг от друга поворотом, элементом группы поворотов SO(3) .

В исчислении

Градиент, расхождение и завиток

В прямоугольной системе координат градиент (дифференцируемой) функции определяется выражением $f:\mathbb {R} ^{3}\rightarrow \mathbb {R}$

\nabla f={\frac {\partial f}{\partial x}}\mathbf {i} +{\frac {\partial f}{\partial y}}\mathbf {j} +{\frac {\partial f}{\partial z}}\mathbf {k}

и в индексной нотации пишется

$(\nabla f)_{i}=\partial _{i}f.$

Дивергенция (дифференцируемого) векторного поля F = U i + V j + W k , то есть функции , равна скалярной функции: $\mathbf {F} :\mathbb {R} ^{3}\rightarrow \mathbb {R} ^{3}$

\operatorname {div} \,\mathbf {F} =\nabla \cdot \mathbf {F} ={\frac {\partial U}{\partial x}}+{\frac {\partial V}{\partial y}}+{\frac {\partial W}{\partial z}}.

В индексной записи, с соглашением Эйнштейна о суммировании, это выглядит так: $\nabla \cdot \mathbf {F} =\partial _{i}F_{i}.$

Разложенный в декартовых координатах (см. Del в цилиндрических и сферических координатах для сферических и цилиндрических координатных представлений), ротор ∇ × F равен, для F, составленного из [ F _x , F _y , F _z ]:

{\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\\\{\frac {\partial }{\partial x}}&{\frac {\partial }{\partial y}}&{\frac {\partial }{\partial z}}\\\\F_{x}&F_{y}&F_{z}\end{vmatrix}}

где i , j , и k являются единичными векторами для осей x -, y - и z соответственно. Это расширяется следующим образом: ^[13]

\left({\frac {\partial F_{z}}{\partial y}}-{\frac {\partial F_{y}}{\partial z}}\right)\mathbf {i} +\left({\frac {\partial F_{x}}{\partial z}}-{\frac {\partial F_{z}}{\partial x}}\right)\mathbf {j} +\left({\frac {\partial F_{y}}{\partial x}}-{\frac {\partial F_{x}}{\partial y}}\right)\mathbf {k} .

В индексной нотации, с соглашением Эйнштейна о суммировании, это будет выглядеть так, где — полностью антисимметричный символ, символ Леви-Чивиты . $(\nabla \times \mathbf {F} )_{i}=\epsilon _{ijk}\partial _{j}F_{k},$ $\epsilon _{ijk}$

Линейные, поверхностные и объемные интегралы

Для некоторого скалярного поля f : U ⊆ R ⁿ → R , линейный интеграл вдоль кусочно-гладкой кривой C ⊂ U определяется как

\int \limits _{C}f\,ds=\int _{a}^{b}f(\mathbf {r} (t))|\mathbf {r} '(t)|\,dt.

где r : [a, b] → C — произвольная биективная параметризация кривой C, такая, что r ( a ) и r ( b ) задают конечные точки C и . $a<b$

Для векторного поля F : U ⊆ Rn → Rn интеграл по кусочно-гладкой кривой C ⊂ U ^в^{направлении} r определяется как

\int \limits _{C}\mathbf {F} (\mathbf {r} )\cdot \,d\mathbf {r} =\int _{a}^{b}\mathbf {F} (\mathbf {r} (t))\cdot \mathbf {r} '(t)\,dt.

где · — скалярное произведение , а r : [a, b] → C — биективная параметризация кривой C, такая, что r ( a ) и r ( b ) задают конечные точки C .

Поверхностный интеграл является обобщением множественных интегралов на интегрирование по поверхностям . Его можно рассматривать как двойной интегральный аналог линейного интеграла. Чтобы найти явную формулу для поверхностного интеграла, нам нужно параметризовать интересующую поверхность S , рассмотрев систему криволинейных координат на S , например, широту и долготу на сфере . Пусть такая параметризация будет x ( s , t ), где ( s , t ) изменяется в некоторой области T на плоскости . Тогда поверхностный интеграл задается как

\iint _{S}f\,\mathrm {d} S=\iint _{T}f(\mathbf {x} (s,t))\left\|{\partial \mathbf {x} \over \partial s}\times {\partial \mathbf {x} \over \partial t}\right\|\mathrm {d} s\,\mathrm {d} t

где выражение между чертами с правой стороны является величиной векторного произведения частных производных x ( s , t ) и известно как элемент поверхности . Если задано векторное поле v на S , то есть функция, которая присваивает каждому x в S вектор v ( x ), поверхностный интеграл может быть определен покомпонентно в соответствии с определением поверхностного интеграла скалярного поля; результатом является вектор.

Объемный интеграл — это интеграл по трехмерной области или региону. Когда подынтегральное выражение тривиально (единично), объемный интеграл — это просто объем региона . ^[14][ ^1] Он также может означать тройной интеграл в пределах области D в R ³ функции и обычно записывается как: $f(x,y,z),$

\iiint \limits _{D}f(x,y,z)\,dx\,dy\,dz.

Основная теорема о линейных интегралах

Основная теорема о линейных интегралах гласит, что линейный интеграл через градиентное поле можно вычислить, вычислив исходное скалярное поле в конечных точках кривой.

Пусть . Тогда $\varphi :U\subseteq \mathbb {R} ^{n}\to \mathbb {R}$

\varphi \left(\mathbf {q} \right)-\varphi \left(\mathbf {p} \right)=\int _{\gamma [\mathbf {p} ,\,\mathbf {q} ]}\nabla \varphi (\mathbf {r} )\cdot d\mathbf {r} .

Теорема Стокса

Теорема Стокса связывает поверхностный интеграл ротора векторного поля F по поверхности Σ в евклидовом трехмерном пространстве с линейным интегралом векторного поля по его границе ∂Σ:

\iint _{\Sigma }\nabla \times \mathbf {F} \cdot \mathrm {d} \mathbf {\Sigma } =\oint _{\partial \Sigma }\mathbf {F} \cdot \mathrm {d} \mathbf {r} .

Теорема о дивергенции

Предположим, что $V$ — подмножество (в случае $n$ $= 3$ $V$ представляет собой объем в трехмерном пространстве), которое компактно и имеет кусочно- гладкую границу $S$ (также обозначенную как $\partial$ $V$ $=$ $S$ ). Если $F$ — непрерывно дифференцируемое векторное поле, определенное в окрестности $V$ , то теорема о расходимости гласит: ^[15] $\mathbb {R} ^{n}$

\iiint _{V}\left(\mathbf {\nabla } \cdot \mathbf {F} \right)\,dV=

$\oiint$

\scriptstyle S

(\mathbf {F} \cdot \mathbf {n} )\,dS.

Левая сторона — это интеграл объема по объему $V$ , правая сторона — интеграл поверхности по границе объема $V.$ Замкнутое многообразие $\partial V$ в общем случае является границей $V,$ ориентированной направленными наружу нормалями , а $n$ — это направленное наружу единичное нормальное поле границы $\partial V.$ ( $d S$ можно использовать как сокращение для $n dS$ .)

В топологии

Трехмерное пространство имеет ряд топологических свойств, которые отличают его от пространств с другими размерностями. Например, для того, чтобы завязать узел на веревке, требуется не менее трех измерений. ^[16]

В дифференциальной геометрии общие трехмерные пространства представляют собой 3-многообразия , которые локально напоминают . ${\mathbb {R} }^{3}$

В конечной геометрии

Многие идеи размерности можно проверить с помощью конечной геометрии . Простейшим примером является PG(3,2) , в котором плоскости Фано являются двумерными подпространствами. Это пример геометрии Галуа , изучения проективной геометрии с использованием конечных полей . Таким образом, для любого поля Галуа GF( q ) существует проективное пространство PG(3, q ) трех измерений. Например, любые три скрещивающиеся прямые в PG(3, q ) содержатся ровно в одном регуле . ^[17]

Смотрите также

Примечания

^ ab "IEC 60050 — Подробности для номера IEV 102-04-39: "трехмерная область"". Международный электротехнический словарь (на японском языке) . Получено 19 сентября 2023 г.
^ "Евклидово пространство - Энциклопедия математики". encyclopediaofmath.org . Получено 2020-08-12 .
^ "Подробности для номера IEV 113-01-02: "space"". Международный электротехнический словарь (на японском языке) . Получено 2023-11-07 .
^ "Евклидово пространство | геометрия". Encyclopedia Britannica . Получено 2020-08-12 .
^ Хьюз-Халлетт, Дебора ; МакКаллум, Уильям Г .; Глисон, Эндрю М. (2013). Исчисление: одно- и многомерное (6-е изд.). Джон Уайли. ISBN 978-0470-88861-2.
^ аб Браннан, Эсплен и Грей, 1999, стр. 34–35.
^ Браннан, Эсплен и Грей 1999, стр. 41–42.
^ Антон 1994, стр. 133
^ Антон 1994, стр. 131
^ Massey, WS (1983). «Перекрестные произведения векторов в многомерных евклидовых пространствах». The American Mathematical Monthly . 90 (10): 697–701. doi :10.2307/2323537. JSTOR 2323537. Если требуются только три основных свойства перекрестного произведения... то оказывается, что перекрестное произведение векторов существует только в 3-мерном и 7-мерном евклидовом пространстве.
^ Ланг 1987, гл. I.1
↑ Бергер 1987, Глава 9.
↑ Арфкен, стр. 43.
^ "IEC 60050 — Подробности для номера IEV 102-04-40: "volume"". Международный электротехнический словарь (на японском языке) . Получено 2023-09-19 .
^ Г-н Шпигель; С. Липшуц; Д. Спеллман (2009). Векторный анализ . Очерки Шаума (2-е изд.). США: Макгроу Хилл. ISBN 978-0-07-161545-7.
^ Рольфсен, Дейл (1976). Узлы и связи . Беркли, Калифорния: Опубликуй или погибни. ISBN 0-914098-16-0.
^ Альбрехт Бойтельспахер и Уте Розенбаум (1998) Проективная геометрия , стр. 72, Cambridge University Press ISBN 0-521-48277-1

Ссылки

Антон, Говард (1994), Элементарная линейная алгебра (7-е изд.), John Wiley & Sons, ISBN 978-0-471-58742-2
Арфкен, Джордж Б. и Ханс Дж. Вебер. Математические методы для физиков , Academic Press; 6-е издание (21 июня 2005 г.). ISBN 978-0-12-059876-2 .
Бергер, Марсель (1987), Геометрия I , Берлин: Springer, ISBN 3-540-11658-3
Бреннан, Дэвид А.; Эсплен, Мэтью Ф.; Грей, Джереми Дж. (1999), Геометрия , Cambridge University Press, ISBN 978-0-521-59787-6
Ланг, Серж (1987), Линейная алгебра (3-е изд.), Springer, doi :10.1007/978-1-4757-1949-9, ISBN 978-1-4757-1949-9

Внешние ссылки

В Викицитатнике есть цитаты, связанные с трехмерным пространством .

На Викискладе есть медиафайлы по теме 3D .

Словарное определение термина трехмерный в Викисловаре
Вайсштейн, Эрик В. «Четырехмерная геометрия». MathWorld .
Элементарная линейная алгебра - Глава 8: Трёхмерная геометрия Кит Мэтьюз из Университета Квинсленда , 1991