3 ( три ) — число , цифра и число . Это натуральное число , следующее за 2 и предшествующее 4 , и является наименьшим нечетным простым числом и единственным простым числом, предшествующим квадратному числу. Оно имеет религиозное и культурное значение во многих обществах.
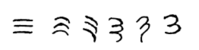
Использование трех линий для обозначения числа 3 встречалось во многих системах письма, включая некоторые (например, римские и китайские цифры ), которые все еще используются. Это было также первоначальное представление числа 3 в брахмической (индийской) числовой нотации, ее самые ранние формы были выровнены по вертикали. [1] Однако во времена империи Гупта знак был изменен путем добавления кривой на каждой строке. Письмо нагари вращало линии по часовой стрелке, поэтому они отображались горизонтально, и заканчивало каждую строку коротким нисходящим штрихом справа. В курсивном письме три штриха в конечном итоге были соединены, образуя глиф, напоминающий ⟨3⟩ с дополнительным штрихом внизу: ३ .
Индийские цифры распространились в Халифате в IX веке. Нижний штрих был убран около X века в западных частях Халифата, таких как Магриб и Аль -Андалус , когда развился особый вариант («западноарабский») цифровых символов, включая современную западную 3. Напротив, восточные арабы сохранили и увеличили этот штрих, повернув цифру еще раз, чтобы получить современную («восточную») арабскую цифру « ٣ ». [2]
В большинстве современных западных шрифтов цифра 3, как и другие десятичные цифры , имеет высоту заглавной буквы и располагается на базовой линии . В шрифтах с текстовыми цифрами , с другой стороны, глиф обычно имеет высоту строчной буквы "x" и выносного элемента : "
". Однако в некоторых французских текстово-цифровых шрифтах вместо подстрочного элемента используется выносной элемент .
Распространенный графический вариант цифры три имеет плоскую вершину, похожую на букву Ʒ (ezh). Эта форма иногда используется для предотвращения фальсификации цифры 3 как 8. Она встречается в штрих-кодах UPC-A и стандартных колодах из 52 карт .
По мнению Пифагора и пифагорейской школы, число 3, которое они называли триадой , является единственным числом, равным сумме всех членов, находящихся ниже него, и единственным числом, сумма которого с членами, находящимися ниже, равна их произведению на себя. [3]
Натуральное число делится на три, если сумма его цифр в десятичной системе счисления делится на 3. Например, число 21 делится на три (3 раза по 7), а сумма его цифр равна 2 + 1 = 3. Из-за этого обратное число любого числа, делящегося на три (или, конечно, любая перестановка его цифр), также делится на три. Например, 1368 и его обратное число 8631 оба делятся на три (как и 1386, 3168, 3186, 3618 и т. д.). См. также Правило делимости . Это работает в десятичной системе счисления и в любой позиционной системе счисления , основание которой делится на три, оставляя остаток один (основания 4, 7, 10 и т. д.).
3 — второе наименьшее простое число и первое нечетное простое число. Это первое уникальное простое число , такое, что значение длины периода 1 десятичного разложения его обратной величины , 0,333..., уникально. 3 — простое число-близнец с 5 и двоюродное простое число с 7 , и единственное известное число, такое что ! − 1 и ! + 1 являются простыми, а также единственное простое число, такое что − 1 дает другое простое число, 2 Это в значительной степени составное число , [4], поскольку оно (как и все простые числа) имеет 2 делителя , и ни одно меньшее число не имеет более 2 делителей (так как нет составного числа меньше 3). Треугольник состоит из трех сторон . Это наименьший несамопересекающийся многоугольник и единственный многоугольник, не имеющий собственных диагоналей . При быстрых оценках 3 является грубым приближением числа π , 3,1415..., и очень грубым приближением числа e , 2,71828...
3 является первым простым числом Мерсенна , а также вторым показателем простого числа Мерсенна и вторым показателем двойного простого числа Мерсенна для 7 и 127 соответственно. 3 также является первым из пяти известных простых чисел Ферма , которые включают 5, 17 , 257 и 65537. Это второе простое число Фибоначчи (и второе простое число Люка ), второе простое число Софи Жермен , третье число Харшада в десятичной системе счисления и второе простое факториал , поскольку оно равно 2! + 1.
3 — второе и единственное простое треугольное число , и Гаусс доказал, что каждое целое число является суммой не более 3 треугольных чисел .
Три — единственное простое число, которое на единицу меньше полного квадрата . Любое другое число, которое равно − 1 для некоторого целого числа, не является простым, так как оно равно ( − 1)( + 1). Это верно и для 3 (с = 2), но в этом случае меньший множитель равен 1. Если больше 2, то и − 1, и + 1 больше 1, поэтому их произведение не является простым.
Трисекция угла была одной из трех знаменитых задач древности.
3 — количество неколлинеарных точек, необходимое для определения плоскости , окружности и параболы .
Существует только три различных панмагических квадрата 4×4 .
Три из пяти Платоновых тел имеют треугольные грани – тетраэдр , октаэдр и икосаэдр . Кроме того, три из пяти Платоновых тел имеют вершины , где встречаются три грани – тетраэдр , гексаэдр ( куб ) и додекаэдр . Кроме того, только три различных типа многоугольников составляют грани пяти Платоновых тел – треугольник , квадрат и пентагон .
Существуют три конечные выпуклые однородные группы многогранников в трех измерениях, помимо бесконечных семейств призм и антипризм : тетраэдральная группа , октаэдральная группа и икосаэдральная группа . В размерностях ⩾ 5 существуют только три правильных многогранника: -симплексы , -кубы и -ортоплексы . В размерностях ⩾ 9 единственными тремя однородными семействами многогранников, помимо многочисленных бесконечных пропризматических семейств, являются симплексные , кубические и полугиперкубические семейства. Для паракомпактных гиперболических сот существуют три группы в размерностях 6 и 9 , или, что эквивалентно, рангов 7 и 10, без других форм в более высоких размерностях. Из последних трех групп самой большой и важной является , которая связана с важной алгеброй Ли Каца–Муди . [5]
Есть некоторые свидетельства, позволяющие предположить, что ранний человек мог использовать системы счета, которые состояли из «Один, Два, Три» и затем «Много» для описания пределов счета. У ранних людей было слово для описания количества одного, двух и трех, но любое количество сверх этого обозначалось просто как «Много». Это, скорее всего, основано на распространенности этого явления среди людей в таких разрозненных регионах, как глубокие джунгли Амазонки и Борнео, где исследователи западной цивилизации имеют исторические записи о своих первых встречах с этими коренными народами. [6]
.svg/1280px-Salt_symbol_(alchemical).svg.png){kind=small}
), сера (.svg/1280px-Sulphur_symbol_(fixed_width).svg.png){kind=small}
) и ртуть (.svg/1280px-Mercury_symbol_(fixed_width).svg.png){kind=small}
). [13] [14]
Во многих мировых религиях присутствуют тройственные божества или концепции троицы, включая индуистских Тримурти и Тридеви , Триглава ( буквально «Трехглавый»), главного бога славян , три Драгоценности буддизма , трех Чистых даосизма , христианскую Святую Троицу и Тройственную Богиню Викки .
Число три является очень значимым в скандинавской мифологии , наряду с его степенями 9 и 27.
Число три (三, официальное написание:叁, пиньинь sān , кантонский диалект : saam 1 ) считается хорошим числом в китайской культуре , поскольку оно звучит как слово «живой» (生pinyin shēng , кантонский диалект: saang 1 ), по сравнению с числом четыре (四, пиньинь sì , кантонский диалект: sei 1 ), которое звучит как слово «смерть» (死pinyin sǐ , кантонский диалект: sei 2 ).
Счет до трех распространен в ситуациях, когда группа людей хочет выполнить действие синхронно : Теперь , на счет три, все тянут! Предполагая, что счетчик идет с одинаковой скоростью, первые два счета необходимы для установления скорости, а счет «три» прогнозируется на основе времени «один» и «два» перед ним. Три, вероятно, используется вместо какого-то другого числа, потому что для этого требуется минимальное количество счетов при установлении скорости.
Есть еще одно суеверие, что не повезло взять третью зажигалку , то есть быть третьим человеком, который зажигает сигарету от той же спички или зажигалки. Иногда утверждается, что это суеверие возникло среди солдат в окопах Первой мировой войны, когда снайпер мог увидеть первую зажигалку, прицелиться во вторую и выстрелить в третью. [ необходима цитата ]
Фраза «Третий раз — это очарование» относится к суеверию, что после двух неудач в любом начинании третья попытка имеет больше шансов на успех. Это также иногда встречается в обратном порядке, как в «третий человек [что-то сделать, предположительно запрещенное] попадает». [ необходима цитата ]
Удача , особенно невезение, часто говорят, что «приходит по трое» [28] .
