
В физике , акустике и телекоммуникациях гармоника — это синусоидальная волна с частотой , которая является положительным целым кратным основной частоты периодического сигнала . Основная частота также называется 1-й гармоникой ; другие гармоники известны как высшие гармоники . Поскольку все гармоники являются периодическими на основной частоте, сумма гармоник также является периодической на этой частоте. Набор гармоник образует гармонический ряд .
Термин используется в различных дисциплинах, включая музыку, физику, акустику , электронную передачу энергии, радиотехнику и другие области. Например, если основная частота составляет 50 Гц , распространенную частоту источника переменного тока , частоты первых трех высших гармоник составляют 100 Гц (2-я гармоника), 150 Гц (3-я гармоника), 200 Гц (4-я гармоника), и любое добавление волн с этими частотами является периодическим с частотой 50 Гц.
n - я характеристическая мода, для n > 1, будет иметь узлы, которые не вибрируют. Например, 3-я характеристическая мода будет иметь узлы в L и L , где L - длина струны. Фактически, каждая n- я характеристическая мода, для n, не кратного 3, не будет иметь узлов в этих точках. Эти другие характеристические моды будут вибрировать в позициях L и L . Если исполнитель слегка касается одной из этих позиций, то эти другие характеристические моды будут подавлены. Тональные гармоники из этих других характеристических мод затем также будут подавлены. Следовательно, тональные гармоники из n- й характеристической моды, где n кратно 3, будут сделаны относительно более заметными. [1]
В музыке гармоники используются на струнных и духовых инструментах как способ создания звука на инструменте, в частности, для игры более высоких нот и, со струнными, для получения нот, которые имеют уникальное качество звука или «тональную окраску». На струнных смычковые гармоники имеют «стеклянный», чистый тон. На струнных инструментах гармоники играются путем прикосновения (но не полного нажатия на струну) к определенной точке на струне во время звучания струны (щипка, смычка и т. д.); это позволяет гармонике звучать, высота тона которой всегда выше основной частоты струны.
Гармоники могут называться «обертонами», «частицами» или «верхними частичками», а в некоторых музыкальных контекстах термины «гармоника», «обертон» и «частица» используются как взаимозаменяемые. Но, если говорить точнее, термин «гармоника» включает в себя все высоты тона в гармоническом ряду (включая основную частоту), тогда как термин «обертон» включает только высоты выше основной.
Свистящий, свистящий тональный характер отличает все гармоники, как естественные, так и искусственные, от жестко остановленных интервалов; поэтому их применение в связи с последними всегда должно быть тщательно продумано. [ необходима цитата ]
— Ричард Шольц ( ок. 1888-1912 ) [2]
Большинство акустических инструментов издают сложные тоны, содержащие множество отдельных частичных тонов (компонентные простые тона или синусоидальные волны), но нетренированное человеческое ухо обычно не воспринимает эти частичные тоны как отдельные явления. Скорее, музыкальная нота воспринимается как один звук, качество или тембр этого звука являются результатом относительной силы отдельных частичных тонов. Многие акустические осцилляторы , такие как человеческий голос или струна смычковой скрипки , производят сложные тоны, которые являются более или менее периодическими , и, таким образом, состоят из частичных тонов, которые почти соответствуют целым кратным основной частоты и, следовательно, напоминают идеальные гармоники и называются «гармоническими частичными» или просто «гармониками» для удобства (хотя не совсем точно называть частичный тон гармоникой , первое является фактическим, а второе — теоретическим).
Осцилляторы, которые производят гармонические обертоны, ведут себя как одномерные резонаторы и часто бывают длинными и тонкими, например, гитарная струна или столб воздуха, открытый с обоих концов (как в случае с металлической современной оркестровой поперечной флейтой ). Духовые инструменты, чей столб воздуха открыт только с одного конца, например, трубы и кларнеты , также производят обертоны, напоминающие гармоники. Однако они производят только обертоны, соответствующие нечетным гармоникам — по крайней мере, в теории. На практике ни один реальный акустический инструмент не ведет себя так идеально, как предсказывают упрощенные физические модели; например, инструменты, сделанные из нелинейно- эластичного дерева вместо металла или натянутые на кишки вместо латунных или стальных струн , как правило, имеют не совсем целые обертоны.
Парциалы, частоты которых не являются целыми кратными основной частоты, называются негармоническими парциалами . Некоторые акустические инструменты издают смесь гармонических и негармонических парциалов, но все равно производят на ухо эффект наличия определенной основной высоты тона, например, фортепиано , струнные щипковые пиццикато , вибрафоны, маримбы и некоторые чисто звучащие колокольчики или куранты. Антикварные поющие чаши известны тем, что производят множественные гармонические парциалы или мультифоники . [3] [4] Другие осцилляторы, такие как тарелки , барабанные пластики и большинство ударных инструментов, естественным образом производят множество негармонических парциалов и не подразумевают какой-либо определенной высоты тона, и поэтому не могут использоваться мелодически или гармонически так же, как другие инструменты.
Основываясь на Sethares (2004), [5] динамическая тональность вводит понятие псевдогармонических обертонов, в которых частота каждого обертона выравнивается так, чтобы соответствовать высоте тона соответствующей ноты в псевдоточной настройке, тем самым максимизируя созвучие этого псевдогармонического тембра с нотами этой псевдоточной настройки. [6] [7] [8] [9]
Обертон — это любой частичный тон выше самого низкого частичного в сложном тоне. Относительные силы и частотные соотношения составляющих частичных тонов определяют тембр инструмента. Сходство между терминами обертон и частичный тон иногда приводит к тому, что их свободно используют как взаимозаменяемые в музыкальном контексте, но они подсчитываются по-разному, что приводит к некоторой возможной путанице. В особом случае инструментальных тембров, чьи составляющие частичные тональные тонали тесно соответствуют гармоническому ряду (например, у большинства струнных и духовых инструментов), а не являются негармоническими частичными тонами (например, у большинства ударных инструментов с высокой высотой тона ), также удобно называть составляющие частичные тональные тонали «гармониками», но это не совсем правильно, потому что гармоники нумеруются одинаково, даже если отсутствуют, в то время как частичные тональные тонали и обертоны подсчитываются только при их наличии. Эта таблица демонстрирует, как подсчитываются три типа названий (частичные, обертональные и гармонические) (при условии, что гармоники присутствуют):
На многих музыкальных инструментах можно играть верхние гармоники без присутствия основной ноты. В простом случае (например, блокфлейта ) это приводит к повышению высоты тона ноты на октаву , но в более сложных случаях получается много других вариаций высоты тона. В некоторых случаях это также изменяет тембр ноты. Это часть обычного метода получения более высоких нот на духовых инструментах , где это называется передуванием . Расширенная техника игры на мультифониках также создает гармоники. На струнных инструментах можно создавать очень чисто звучащие ноты, называемые гармониками или флажолетами струнниками, которые имеют жуткое качество, а также являются высокими по высоте. Гармоники могут использоваться для проверки в унисон настройки струн, которые не настроены в унисон. Например, легкое нажатие пальцами узла, расположенного на полпути вниз по самой высокой струне виолончели, дает ту же высоту тона, что и легкое нажатие пальцами узла 1 /3 пути вниз по второй самой высокой струне. Для человеческого голоса см. Обертонное пение , которое использует гармоники.
Хотя верно, что электронно-сгенерированные периодические тоны (например, квадратные волны или другие несинусоидальные волны) имеют «гармоники», которые являются целыми числами, кратными основной частоте, не все практические инструменты обладают этой характеристикой. Например, более высокие «гармоники» фортепианных нот не являются истинными гармониками, а являются «обертонами» и могут быть очень резкими, то есть иметь более высокую частоту, чем заданная чистым гармоническим рядом . Это особенно верно для инструментов, отличных от струнных , медных или деревянных духовых инструментов . Примерами этих «других» инструментов являются ксилофоны, барабаны, колокольчики, куранты и т. д.; не все их частоты обертонов составляют простое целочисленное отношение с основной частотой. ( Основная частота является обратной величиной самого длительного периода времени совокупности колебаний в некотором единичном периодическом явлении. [10] )

Гармоники могут быть получены по отдельности [на струнных инструментах] (1) путем изменения точки контакта со смычком, или (2) путем легкого нажатия на струну в узлах или разделах ее аликвотных частей ( , , , и т. д.). (1) В первом случае, продвигая смычок от обычного места, где производится основная нота, к подставке, можно последовательно произвести всю гамму гармоник на старом и высоко резонирующем инструменте. Использование этого средства дает эффект, называемый « sul ponticello ». (2) Создание гармоник легким нажатием пальца на открытую струну более полезно. Когда они производятся легким нажатием на различные узлы открытых струн, они называются «натуральными гармониками». ... Скрипачи хорошо знают, что чем длиннее струна по отношению к ее толщине, тем большее количество верхних гармоник она может выдать.
— Словарь музыки и музыкантов Гроува (1879) [11]
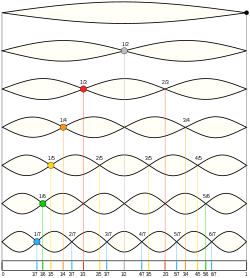
В следующей таблице показаны точки остановки на струнном инструменте, в которых легкое прикосновение к струне заставит ее перейти в гармонический режим при вибрации. Гармоники струн (тоны флажолета) описываются как имеющие «флейтоподобное, серебристое качество», которое может быть очень эффективным как особый цвет или тоновая окраска ( тембр ) при использовании и прослушивании в оркестровке . [12] Необычно встретить натуральные гармоники выше пятой партитуры на любом струнном инструменте, за исключением контрабаса, из-за его гораздо более длинных струн. [12]
Иногда партитура требует искусственной гармоники , создаваемой путем игры обертона на уже остановленной струне. Как исполнительская техника, это достигается использованием двух пальцев на грифе, первый из которых укорачивает струну до желаемого основного тона, а второй касается узла, соответствующего соответствующей гармонике.
Гармоники могут использоваться или рассматриваться как основа только интонационных систем. Композитор Арнольд Дрейблатт способен извлекать различные гармоники на одной струне своего модифицированного контрабаса , слегка изменяя свою уникальную технику смычка на полпути между ударом и смычком по струнам. Композитор Лоуренс Болл использует гармоники для электронного создания музыки.
много способов ухудшить ситуацию, но очень мало — улучшить.— Минимально техническое резюме исследований акустики струнных инструментов, представленных на конференции; обсуждается восприятие слушателями негармонических обертонов фортепиано.