Ориентируемость

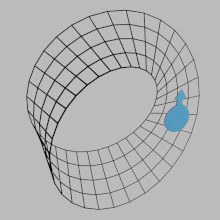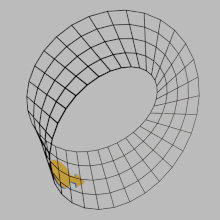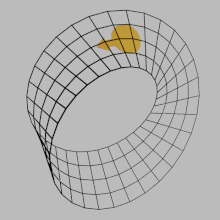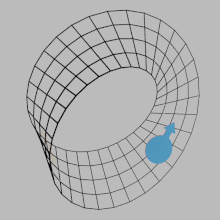
В математике ориентируемость — это свойство некоторых топологических пространств , таких как вещественные векторные пространства , евклидовы пространства , поверхности и, в более общем смысле, многообразия , которое допускает непротиворечивое определение «по часовой стрелке» и «против часовой стрелки». ^[1] Пространство ориентируемо, если существует такое непротиворечивое определение. В этом случае существует два возможных определения, и выбор между ними является ориентацией пространства . Вещественные векторные пространства, евклидовы пространства и сферы ориентируемы. Пространство неориентируемо, если «по часовой стрелке» меняется на «против часовой стрелки» после прохождения в нем некоторых циклов и возвращения в исходную точку. Это означает, что геометрическая фигура , такая как, который непрерывно движется по такой петле, превращается в свое собственное зеркальное отражение . Лента Мёбиуса — пример неориентируемого пространства.

Могут быть даны различные эквивалентные формулировки ориентируемости в зависимости от желаемого применения и уровня общности. Формулировки, применимые к общим топологическим многообразиям, часто используют методы теории гомологии , тогда как для дифференцируемых многообразий присутствует больше структуры, что позволяет формулировать в терминах дифференциальных форм . Обобщением понятия ориентируемости пространства является ориентируемость семейства пространств, параметризованных некоторым другим пространством ( расслоением волокон ), для которого в каждом из пространств должна быть выбрана ориентация, которая непрерывно меняется относительно изменений значений параметров.

Ориентируемые поверхности

Поверхность S в евклидовом пространстве R3 является ориентируемой^, если киральная двумерная фигура (например,) нельзя перемещать по поверхности и возвращаться в исходное положение, чтобы оно выглядело как его собственное зеркальное отражение (). В противном случае поверхность неориентируема . Абстрактная поверхность (т. е. двумерное многообразие ) ориентируема, если на поверхности можно определить непротиворечивую концепцию вращения по часовой стрелке непрерывным образом. То есть петля, проходящая по поверхности в одну сторону, никогда не может быть непрерывно деформирована (без перекрытия самой себя) в петлю, проходящую в противоположную сторону. Это оказывается эквивалентным вопросу о том, содержит ли поверхность подмножество, гомеоморфное ленте Мёбиуса . Таким образом, для поверхностей ленту Мёбиуса можно считать источником всей неориентируемости.

Для ориентируемой поверхности последовательный выбор «по часовой стрелке» (в отличие от против часовой стрелки) называется ориентацией , а поверхность называется ориентированной . Для поверхностей, вложенных в евклидово пространство, ориентация задается выбором непрерывно изменяющейся нормали поверхности n в каждой точке. Если такая нормаль вообще существует, то всегда есть два способа ее выбрать: n или − n . В более общем смысле, ориентируемая поверхность допускает ровно две ориентации, и различие между ориентированной поверхностью и ориентируемой поверхностью тонкое и часто размытое. Ориентируемая поверхность — это абстрактная поверхность, которая допускает ориентацию, в то время как ориентированная поверхность — это поверхность, которая абстрактно ориентируема и имеет дополнительную базу данных выбора одной из двух возможных ориентаций.

Примеры

Большинство поверхностей, встречающихся в физическом мире, являются ориентируемыми. Например, сферы , плоскости и торы являются ориентируемыми. Но ленты Мёбиуса , реальные проективные плоскости и бутылки Клейна неориентируемы. Они, как визуализируются в 3-х измерениях, все имеют только одну сторону. Реальная проективная плоскость и бутылка Клейна не могут быть вложены в R ³ , а только погружены с хорошими пересечениями.

Обратите внимание, что локально у вложенной поверхности всегда есть две стороны, поэтому близорукий муравей, ползущий по односторонней поверхности, будет думать, что есть «другая сторона». Суть односторонности в том, что муравей может переползти с одной стороны поверхности на «другую», не проходя сквозь поверхность и не переворачиваясь через край, а просто проползая достаточно далеко.

В общем случае свойство быть ориентируемым не эквивалентно свойству быть двусторонним; однако это имеет место, когда окружающее пространство (такое как R ³ выше) является ориентируемым. Например, тор, вложенный в

K^{2}\times S^{1}

может быть односторонней, а бутылка Клейна в том же пространстве может быть двусторонней; здесь имеется в виду бутылка Клейна. $К^{2}$

Ориентация по триангуляции

Любая поверхность имеет триангуляцию : разложение на треугольники, при котором каждое ребро треугольника склеивается не более чем с одним другим ребром. Каждый треугольник ориентируется выбором направления по периметру треугольника, связывая направление с каждым ребром треугольника. Если это делается таким образом, что при склеивании соседние ребра указывают в противоположном направлении, то это определяет ориентацию поверхности. Такой выбор возможен только в том случае, если поверхность ориентируема, и в этом случае существует ровно две различные ориентации.

Если цифраможно последовательно расположить во всех точках поверхности, не превращаясь в ее зеркальное отражение, то это вызовет ориентацию в указанном выше смысле на каждом из треугольников триангуляции путем выбора направления каждого из треугольников на основе порядка красный-зеленый-синий цветов любой из фигур внутри треугольника.

Этот подход обобщается на любое n -многообразие, имеющее триангуляцию. Однако некоторые 4-многообразия не имеют триангуляции, и в общем случае для n > 4 некоторые n -многообразия имеют триангуляции, которые неэквивалентны.

Ориентируемость и гомология

Если H ₁ ( S ) обозначает первую группу гомологий замкнутой поверхности S , то S ориентируема тогда и только тогда, когда H ₁ ( S ) имеет тривиальную подгруппу кручения . Точнее, если S ориентируема, то H ₁ ( S ) является свободной абелевой группой , а если нет, то H ₁ ( S ) = F + Z /2 Z , где F является свободной абелевой группой, а фактор Z /2 Z порождается средней кривой в ленте Мёбиуса , вложенной в S .

Ориентируемость многообразий

Пусть M — связное топологическое n - многообразие . Существует несколько возможных определений того, что означает для M быть ориентируемым. Некоторые из этих определений требуют, чтобы M имело дополнительную структуру, например, дифференцируемость. Иногда $n = 0 должно быть превращено в особый случай. Когда к$ M применимо более одного из этих определений , то M ориентируемо при одном определении тогда и только тогда, когда оно ориентируемо при других. ^[2]^[3]

Ориентируемость дифференцируемых многообразий

Наиболее интуитивные определения требуют, чтобы M было дифференцируемым многообразием. Это означает, что функции перехода в атласе M являются C ¹ -функциями. Такая функция допускает определитель Якоби . Когда определитель Якоби положителен, говорят, что функция перехода сохраняет ориентацию . Ориентированный атлас на M — это атлас, для которого все функции перехода сохраняют ориентацию. M является ориентируемым, если он допускает ориентированный атлас. Когда n $> 0$ , ориентация M является максимальным ориентированным атласом. (Когда $n$ $= 0$ , ориентация M является функцией $M$ $\to {\pm1}$ .)

Ориентируемость и ориентации также могут быть выражены в терминах касательного расслоения. Касательное расслоение является векторным расслоением , поэтому оно является расслоением со структурной группой $GL(n, R)$ . То есть, функции перехода многообразия индуцируют функции перехода на касательном расслоении, которые являются послойными линейными преобразованиями. Если структурную группу можно свести к группе $GL + (n, R)$ положительно детерминантных матриц или, что эквивалентно, если существует атлас, функции перехода которого определяют линейное преобразование, сохраняющее ориентацию, на каждом касательном пространстве, то многообразие M ориентируемо. Наоборот, M ориентируемо тогда и только тогда, когда структурная группа касательного расслоения может быть сведена таким образом. Аналогичные наблюдения можно сделать для расслоения рамок.

Другой способ определения ориентаций на дифференцируемом многообразии — через формы объема . Форма объема — это нигде не исчезающее сечение ω многообразия $⋀ n T * M$ , верхней внешней степени кокасательного расслоения M . Например, R ⁿ имеет стандартную форму объема, заданную как $dx 1 \land \dots \land dx n$ . Если задана форма объема на M , то совокупность всех карт $U \to R n ,$ для которых стандартная форма объема возвращается к положительному кратному ω, является ориентированным атласом. Следовательно, существование формы объема эквивалентно ориентируемости многообразия.

Формы объема и касательные векторы можно объединить, чтобы дать еще одно описание ориентируемости. Если $X 1, \dots, X n$ является базисом касательных векторов в точке p , то базис называется правым, если $ω(X 1, \dots, X n) > 0$ . Функция перехода сохраняет ориентацию тогда и только тогда, когда она переводит правые базисы в правые базисы. Существование формы объема подразумевает редукцию структурной группы касательного расслоения или расслоения фрейма к $GL + (n, R)$ . Как и прежде, это подразумевает ориентируемость M . И наоборот, если M ориентируемо, то локальные формы объема можно склеить вместе, чтобы создать глобальную форму объема, причем ориентируемость необходима для того, чтобы глобальная форма нигде не обращалась в нуль.

Гомологии и ориентируемость общих многообразий

В основе всех приведенных выше определений ориентируемости дифференцируемого многообразия лежит понятие функции перехода, сохраняющей ориентацию. Это поднимает вопрос о том, что именно сохраняют такие функции перехода. Они не могут сохранять ориентацию многообразия, поскольку ориентация многообразия является атласом, и нет смысла говорить, что функция перехода сохраняет или не сохраняет атлас, членом которого она является.

Этот вопрос можно решить, определив локальные ориентации. На одномерном многообразии локальная ориентация вокруг точки p соответствует выбору левого и правого направления вблизи этой точки. На двумерном многообразии она соответствует выбору направления по часовой стрелке и против часовой стрелки. Эти две ситуации имеют общую черту: они описываются в терминах поведения верхнего измерения вблизи p, но не в p . В общем случае пусть M будет топологическим n -многообразием. Локальная ориентация M вокруг точки p является выбором генератора группы

H_{n}\left(M,M\setminus \{p\};\mathbf {Z} \right).

Чтобы увидеть геометрическое значение этой группы, выберите карту вокруг p . На этой карте есть окрестность p , которая является открытым шаром B вокруг начала координат O . По теореме об вырезании , изоморфно . Шар B стягиваем, поэтому его группы гомологии исчезают, за исключением степени ноль, а пространство $B$ $\$ $O$ является $($ $n$ $- 1)$ -сферой, поэтому его группы гомологии исчезают, за исключением степеней $n$ $- 1$ и $0$ . Вычисление с длинной точной последовательностью в относительной гомологии показывает, что указанная выше группа гомологии изоморфна . Поэтому выбор генератора соответствует решению о том, является ли в данной карте сфера вокруг p положительной или отрицательной. Отражение $R$ $n$ относительно начала координат действует отрицанием на , поэтому геометрическое значение выбора генератора состоит в том, что он отличает карты от их отражений. $H_{n}\left(M,M\setminus \{p\};\mathbf {Z} \right)$ $H_{n}\left(B,B\setminus \{O\};\mathbf {Z} \right)$ $H_{n-1}\left(S^{n-1};\mathbf {Z} \right)\cong \mathbf {Z}$ $H_{n-1}\left(S^{n-1};\mathbf {Z} \right)$

На топологическом многообразии функция перехода сохраняет ориентацию , если в каждой точке p своей области она фиксирует генераторы . Отсюда соответствующие определения те же, что и в дифференцируемом случае. Ориентированный атлас — это атлас, для которого все функции перехода сохраняют ориентацию, M ориентируем , если он допускает ориентированный атлас, и когда n $>$ $0$ , ориентация M является максимальным ориентированным атласом. $H_{n}\left(M,M\setminus \{p\};\mathbf {Z} \right)$

Интуитивно, ориентация M должна определять уникальную локальную ориентацию M в каждой точке. Это уточняется, если отметить, что любая карта в ориентированном атласе вокруг p может быть использована для определения сферы вокруг p , и эта сфера определяет генератор . Более того, любая другая карта вокруг p связана с первой картой функцией перехода, сохраняющей ориентацию, и это подразумевает, что две карты дают один и тот же генератор, откуда следует, что генератор уникален. $H_{n}\left(M,M\setminus \{p\};\mathbf {Z} \right)$

Чисто гомологические определения также возможны. Предполагая, что M замкнуто и связно, M ориентируемо тогда и только тогда, когда n -я группа гомологии изоморфна целым числам Z. Ориентация M — это выбор генератора $α$ этой группы. Этот генератор определяет ориентированный атлас, фиксируя генератор бесконечной циклической группы и принимая ориентированные карты за те, для которых $α$ продвигается вперед к фиксированному генератору. Наоборот, ориентированный атлас определяет такой генератор, поскольку совместимые локальные ориентации могут быть склеены вместе, чтобы получить генератор для группы гомологии . ^[4] $H_{n}(M;\mathbf {Z} )$ $H_{n}(M;\mathbf {Z} )$ $H_{n}(M;\mathbf {Z} )$

Ориентация и когомологии

Многообразие M ориентируемо тогда и только тогда, когда первый класс Штифеля–Уитни равен нулю. В частности, если первая группа когомологий с коэффициентами Z /2 равна нулю, то многообразие ориентируемо. Более того, если M ориентируемо и w ₁ равен нулю, то параметризует выбор ориентаций. ^[5] Эта характеристика ориентируемости распространяется на ориентируемость общих векторных расслоений над M , а не только касательного расслоения. $w_{1}(M)\in H^{1}(M;\mathbf {Z} /2)$ $H^{0}(M;\mathbf {Z} /2)$

Двойная ориентация крышки

Вокруг каждой точки M есть две локальные ориентации. Интуитивно, есть способ перейти от локальной ориентации в точке $p$ к локальной ориентации в близлежащей точке $p'$ : когда две точки лежат в одной и той же координатной карте $U \to R n$ , эта координатная карта определяет совместимые локальные ориентации в $p$ и $p'$ . Таким образом, набору локальных ориентаций можно задать топологию, и эта топология превращает его в многообразие.

Точнее, пусть O будет множеством всех локальных ориентаций M . Чтобы топологизировать O , мы укажем предбазу для его топологии. Пусть U будет открытым подмножеством M , выбранным таким образом, что оно изоморфно Z . Предположим, что α является генератором этой группы. Для каждого p в U существует функция pushforward . Область значений этой группы имеет два генератора, и α отображается на один из них. Топология на O определяется так, что $H_{n}(M,M\setminus U;\mathbf {Z} )$ $H_{n}(M,M\setminus U;\mathbf {Z} )\to H_{n}\left(M,M\setminus \{p\};\mathbf {Z} \right)$

\{{\text{Изображение }}\alpha {\text{ в }}H_{n}\left(M,M\setminus \{p\};\mathbf {Z} \right)\colon p\in U\}

открыто.

Существует каноническое отображение $π : O \to M$ , которое переводит локальную ориентацию в точке p в точку p . Ясно, что каждая точка M имеет ровно два прообраза относительно $π$ . Фактически, $π$ даже является локальным гомеоморфизмом, поскольку прообразы открытых множеств U , упомянутых выше, гомеоморфны несвязному объединению двух копий U . Если M ориентируемо, то само M является одним из этих открытых множеств, поэтому O является несвязным объединением двух копий M . Однако если M неориентируемо, то O связно и ориентируемо. Многообразие O называется ориентационным двойным покрытием .

Многообразия с границей

Если M — многообразие с границей, то ориентация M определяется как ориентация его внутренней части. Такая ориентация индуцирует ориентацию ∂ M . Действительно, предположим, что ориентация M фиксирована. Пусть $U \to R n +$ — карта в граничной точке M , которая при ограничении внутренней частью M , находится в выбранном ориентированном атласе. Ограничение этой карты на ∂ M является картой ∂ M . Такие карты образуют ориентированный атлас для ∂ M .

Когда M является гладким, в каждой точке p из ∂ M ограничение касательного расслоения M на ∂ M изоморфно $T p \partial M \oplus R$ , где фактор R описывается вектором внутренней нормали. Ориентация T _p ∂ M определяется условием, что базис T _p ∂ M положительно ориентирован тогда и только тогда, когда он, в сочетании с вектором внутренней нормали, определяет положительно ориентированный базис T _p M .

Двойная крышка с возможностью ориентации

Анимация ориентируемой двойной оболочки ленты Мёбиуса .

Близкое понятие использует идею покрывающего пространства . Для связного многообразия M возьмем M ^∗ , множество пар ( x , o), где x — точка M , а o — ориентация в x ; здесь мы предполагаем, что M либо гладкое, поэтому мы можем выбрать ориентацию на касательном пространстве в точке, либо используем сингулярную гомологию для определения ориентации. Затем для каждого открытого ориентированного подмножества M мы рассматриваем соответствующее множество пар и определяем его как открытое множество M ^∗ . Это дает M ^∗ топологию, а проекция, отправляющая ( x , o) в x , тогда является отображением покрытия 2 к 1. Это покрывающее пространство называется ориентируемым двойным покрытием , поскольку оно ориентируемо. M ^∗ связно тогда и только тогда, когда M не ориентируемо.

Другой способ построения этого покрытия — разделить петли, основанные на базовой точке, на петли, сохраняющие ориентацию, или петли, меняющие ориентацию. Петли, сохраняющие ориентацию, порождают подгруппу фундаментальной группы, которая является либо всей группой, либо имеет индекс два. В последнем случае (что означает, что существует путь, меняющий ориентацию), подгруппа соответствует связному двойному покрытию; это покрытие ориентируемо по построению. В первом случае можно просто взять две копии M , каждая из которых соответствует другой ориентации.

Ориентация векторных пучков

Действительное векторное расслоение , которое априори имеет структурную группу GL(n) , называется ориентируемым , когда структурная группа может быть сведена к , группе матриц с положительным определителем . Для касательного расслоения это сведение всегда возможно, если базовое многообразие является ориентируемым, и фактически это обеспечивает удобный способ определения ориентируемости гладкого действительного многообразия : гладкое многообразие определяется как ориентируемое, если его касательное расслоение является ориентируемым (как векторное расслоение). Обратите внимание, что как многообразие само по себе касательное расслоение всегда ориентируемо, даже над неориентируемыми многообразиями. $GL^{+}(n)$

Связанные концепции

Геометрия Лоренца

В лоренцевской геометрии существует два вида ориентируемости: пространственная ориентируемость и временная ориентируемость. Они играют роль в причинной структуре пространства-времени. ^[6] В контексте общей теории относительности пространственно-временное многообразие является пространственно-ориентируемым, если, когда два правых наблюдателя отправляются в ракетных кораблях, стартуя из одной и той же точки пространства-времени, а затем встречаются снова в другой точке, они остаются правыми по отношению друг к другу. Если пространство-время является ориентируемым во времени, то два наблюдателя всегда будут соглашаться относительно направления времени в обеих точках их встречи. Фактически, пространство-время является ориентируемым во времени тогда и только тогда, когда любые два наблюдателя могут договориться, какая из двух встреч предшествовала другой. ^[7]

Формально псевдоортогональная группа O( p , q ) имеет пару символов : символ пространственной ориентации σ ₊ и символ временной ориентации σ ₋ ,

\sigma _{\pm }:\operatorname {O} (p,q)\to \{-1,+1\}.

Их произведение σ = σ ₊ σ ₋ является определителем, который дает характер ориентации. Пространственная ориентация псевдориманова многообразия отождествляется с сечением ассоциированного расслоения

\operatorname {O} (M)\times _{\sigma _{+}}\{-1,+1\}

где O( M ) — это пучок псевдоортогональных фреймов. Аналогично, временная ориентация — это сечение соответствующего пучка

\operatorname {O} (M)\times _{\sigma _{-}}\{-1,+1\}.

Смотрите также

Ссылки

^ Манро, Маршалл Эванс (1963). Современное многомерное исчисление. Эддисон-Уэсли. стр. 263.
^ Спивак, Майкл (1965). Исчисление на многообразиях . HarperCollins . ISBN 978-0-8053-9021-6.
^ Хэтчер, Аллен (2001). Алгебраическая топология . Cambridge University Press . ISBN 978-0521795401.
^ Хэтчер 2001, стр. 236 Теорема 3.26(a)
^ Лоусон, Х. Блейн ; Михельсон, Мари-Луиз (1989). Геометрия спина . Princeton University Press . стр. 79 Теорема 1.2. ISBN 0-691-08542-0.
^ Хокинг, SW ; Эллис, GFR (1973). Крупномасштабная структура пространства-времени . Cambridge University Press. ISBN 0-521-20016-4.
^ Хэдли, Марк Дж. (2002). «Ориентируемость пространства-времени» (PDF) . Классическая и квантовая гравитация . 19 (17): 4565–71. arXiv : gr-qc/0202031v4 . CiteSeerX 10.1.1.340.8125 . doi :10.1088/0264-9381/19/17/308.

Внешние ссылки

Ориентация коллекторов в Атласе коллекторов.
Ориентационная информация в Атласе Манифолда.
Ориентация многообразий в обобщенных теориях когомологий в Атласе многообразий.
Статья в энциклопедии математики об ориентации.