
В физике специальная теория относительности , или сокращенно специальная теория относительности , является научной теорией взаимосвязи пространства и времени . В статье Альберта Эйнштейна 1905 года « Об электродинамике движущихся тел » теория представлена как основанная всего на двух постулатах : [стр. 1] [1] [2]
Первый постулат впервые сформулировал Галилео Галилей (см. Галилеевская инвариантность ).
Специальная теория относительности была описана Альбертом Эйнштейном в статье, опубликованной 26 сентября 1905 года под названием «Об электродинамике движущихся тел». [стр. 1] Уравнения электромагнетизма Максвелла оказались несовместимыми с механикой Ньютона , и эксперимент Майкельсона-Морли не смог обнаружить движение Земли относительно гипотетического светоносного эфира . Это привело к разработке преобразований Лоренца Хендриком Лоренцом , которые корректируют расстояния и время для движущихся объектов. Специальная теория относительности исправляет существующие до сих пор законы механики, чтобы обрабатывать ситуации, включающие все движения, и особенно те, которые происходят со скоростью, близкой к скорости света (известной какрелятивистские скорости ). Сегодня доказано, что специальная теория относительности является наиболее точной моделью движения при любой скорости, когда гравитационные и квантовые эффекты пренебрежимо малы.[3][4]Тем не менее, ньютоновская модель по-прежнему верна как простое и точное приближение при низких скоростях (относительно скорости света), например, при повседневных движениях на Земле.
Специальная теория относительности имеет широкий спектр следствий, которые были экспериментально подтверждены. [5] Они включают в себя относительность одновременности , сокращение длины , замедление времени , релятивистскую формулу сложения скоростей, релятивистский эффект Доплера , релятивистскую массу , универсальный предел скорости , эквивалентность массы и энергии , скорость причинности и прецессию Томаса . [1] [2] Например, она заменила традиционное понятие абсолютного универсального времени на понятие времени, которое зависит от системы отсчета и пространственного положения. Вместо инвариантного временного интервала между двумя событиями существует инвариантный пространственно-временной интервал . В сочетании с другими законами физики два постулата специальной теории относительности предсказывают эквивалентность массы и энергии , как выражено в формуле эквивалентности массы и энергии , где - скорость света в вакууме. [6] [7] Она также объясняет, как связаны явления электричества и магнетизма. [1] [2]
Определяющей чертой специальной теории относительности является замена преобразований Галилея механики Ньютона на преобразования Лоренца . Время и пространство не могут быть определены отдельно друг от друга (как считалось ранее). Скорее, пространство и время переплетены в единый континуум, известный как «пространство-время» . События, которые происходят в одно и то же время для одного наблюдателя, могут происходить в разное время для другого.
До тех пор, пока несколько лет спустя Эйнштейн не разработал общую теорию относительности , которая ввела искривленное пространство-время для включения гравитации, фраза «специальная теория относительности» не использовалась. Иногда используется перевод «ограниченная относительность»; «специальная» на самом деле означает «особый случай». [стр. 2] [стр. 3] [стр. 4] [примечание 1] Некоторые работы Альберта Эйнштейна в области специальной теории относительности основаны на более ранних работах Хендрика Лоренца и Анри Пуанкаре . Теория стала по существу завершенной в 1907 году с работами Германа Минковского о пространстве-времени. [4]
Теория является «специальной» в том смысле, что она применима только в особом случае , когда пространство-время является «плоским», то есть, когда кривизна пространства-времени (следствие тензора энергии-импульса и представляющая гравитацию ) пренебрежимо мала. [8] [примечание 2] Чтобы правильно учесть гравитацию, Эйнштейн сформулировал общую теорию относительности в 1915 году. Специальная теория относительности, вопреки некоторым историческим описаниям, учитывает ускорения , а также ускоряющиеся системы отсчета . [9] [10]
Так же, как теория относительности Галилея теперь считается приближением специальной теории относительности, справедливым для низких скоростей, специальная теория относительности считается приближением общей теории относительности, справедливым для слабых гравитационных полей , то есть в достаточно малых масштабах (например, когда приливные силы пренебрежимо малы) и в условиях свободного падения . Но общая теория относительности включает неевклидову геометрию для представления гравитационных эффектов как геометрической кривизны пространства-времени. Специальная теория относительности ограничена плоским пространством-временем, известным как пространство Минковского . Пока Вселенную можно моделировать как псевдориманово многообразие , лоренц-инвариантная система отсчета, которая подчиняется специальной теории относительности, может быть определена для достаточно малой окрестности каждой точки в этом искривленном пространстве-времени .
Галилео Галилей уже постулировал, что не существует абсолютного и четко определенного состояния покоя (никаких привилегированных систем отсчета ), принцип, который теперь называется принципом относительности Галилея . Эйнштейн расширил этот принцип так, чтобы он учитывал постоянную скорость света, [11] явление, которое наблюдалось в эксперименте Майкельсона-Морли. Он также постулировал, что он справедлив для всех законов физики , включая как законы механики, так и электродинамики . [12]
«Размышления такого рода дали мне ясно понять еще вскоре после 1900 года, т. е. вскоре после новаторской работы Планка, что ни механика, ни электродинамика не могут (за исключением предельных случаев) претендовать на точную обоснованность. Постепенно я отчаялся в возможности открытия истинных законов посредством конструктивных усилий, основанных на известных фактах. Чем дольше и отчаяннее я пытался, тем больше приходил к убеждению, что только открытие универсального формального принципа может привести нас к гарантированным результатам... Как же тогда можно найти такой универсальный принцип?»
Альберт Эйнштейн: Автобиографические заметки [стр. 5]
Эйнштейн выделил два фундаментальных положения, которые казались наиболее достоверными, независимо от точной справедливости (тогда) известных законов механики или электродинамики. Эти положения заключались в постоянстве скорости света в вакууме и независимости физических законов (особенно постоянства скорости света) от выбора инерциальной системы. В своем первоначальном изложении специальной теории относительности в 1905 году он выразил эти постулаты следующим образом: [стр. 1]
Постоянство скорости света было мотивировано теорией электромагнетизма Максвелла [13] и отсутствием доказательств существования светоносного эфира . [14] Существуют противоречивые данные о степени влияния на Эйнштейна нулевого результата эксперимента Майкельсона-Морли. [15] [16] В любом случае, нулевой результат эксперимента Майкельсона-Морли помог представлению о постоянстве скорости света получить широкое и быстрое признание.
Вывод специальной теории относительности зависит не только от этих двух явных постулатов, но и от нескольких неявных предположений ( принимаемых почти во всех теориях физики ), включая изотропность и однородность пространства и независимость измерительных стержней и часов от их прошлой истории. [стр. 6]
После первоначального представления Эйнштейном специальной теории относительности в 1905 году было предложено много различных наборов постулатов в различных альтернативных выводах. [17] Но наиболее распространенным набором постулатов остаются те, которые использовались Эйнштейном в его оригинальной статье. Более математическое изложение принципа относительности, сделанное позже Эйнштейном, которое вводит концепцию простоты, не упомянутую выше, выглядит следующим образом:
Специальный принцип относительности : Если система координат K выбрана так, что по отношению к ней физические законы справедливы в их простейшей форме, то те же законы справедливы по отношению к любой другой системе координат K ′ , движущейся равномерно и поступательно относительно K. [18]
Анри Пуанкаре предоставил математическую основу для теории относительности, доказав, что преобразования Лоренца являются подмножеством его группы преобразований симметрии Пуанкаре . Позднее Эйнштейн вывел эти преобразования из своих аксиом.
Во многих работах Эйнштейна представлены выводы преобразования Лоренца, основанные на этих двух принципах. [стр. 7]

Системы отсчета играют решающую роль в теории относительности. Термин «система отсчета», используемый здесь, представляет собой перспективу наблюдения в пространстве, которое не претерпевает никаких изменений в движении (ускорении), из которой можно измерить положение по 3 пространственным осям (то есть в состоянии покоя или постоянной скорости). Кроме того, система отсчета имеет возможность определять измерения времени событий с помощью «часов» (любого устройства отсчета с равномерной периодичностью).
Событие — это явление, которому можно приписать единственный уникальный момент и местоположение в пространстве относительно системы отсчета: это «точка» в пространстве-времени . Поскольку скорость света постоянна в теории относительности независимо от системы отсчета, импульсы света можно использовать для однозначного измерения расстояний и отсылки к времени, когда события произошли, по часам, даже несмотря на то, что свету требуется время, чтобы достичь часов после того, как событие произошло.
Например, взрыв петарды можно считать «событием». Мы можем полностью определить событие по его четырем пространственно-временным координатам: время возникновения и его трехмерное пространственное положение определяют точку отсчета. Назовем эту систему отсчета S.
В теории относительности мы часто хотим вычислить координаты события из разных систем отсчета. Уравнения, связывающие измерения, сделанные в разных системах отсчета, называются уравнениями преобразования .
Чтобы получить представление о том, как пространственно-временные координаты, измеренные наблюдателями в разных системах отсчета, сравниваются друг с другом, полезно работать с упрощенной установкой с системами в стандартной конфигурации . [19] : 107 При осторожности это позволяет упростить математику без потери общности в полученных выводах. На рис. 2-1 две галилеевы системы отсчета (т. е. обычные трехмерные системы отсчета) показаны в относительном движении. Система S принадлежит первому наблюдателю O , а система S ′ (произносится как «S штрих» или «S тире») принадлежит второму наблюдателю O ′ .
Поскольку в теории относительности нет абсолютной системы отсчета, понятие «движение» строго не существует, поскольку все может двигаться относительно какой-то другой системы отсчета. Вместо этого любые две системы, которые движутся с одинаковой скоростью в одном направлении, называются сопутствующими . Следовательно, S и S ′ не сопутствуют .
Принцип относительности , который гласит, что физические законы имеют одинаковую форму в каждой инерциальной системе отсчета , восходит к Галилею и был включен в ньютоновскую физику. Но в конце 19 века существование электромагнитных волн привело некоторых физиков к предположению, что вселенная заполнена веществом, которое они назвали « эфиром », которое, как они постулировали, будет действовать как среда, через которую распространяются эти волны или вибрации (во многих отношениях аналогично тому, как звук распространяется по воздуху). Считалось, что эфир является абсолютной системой отсчета , относительно которой можно измерить все скорости, и его можно считать фиксированным и неподвижным относительно Земли или какой-либо другой фиксированной точки отсчета. Предполагалось, что эфир достаточно упруг, чтобы поддерживать электромагнитные волны, в то время как эти волны могут взаимодействовать с материей, не оказывая при этом никакого сопротивления проходящим через него телам (его единственным свойством было то, что он позволял электромагнитным волнам распространяться). Результаты различных экспериментов, включая эксперимент Майкельсона-Морли в 1887 году (впоследствии подтвержденный более точными и новаторскими экспериментами), привели к появлению специальной теории относительности, показав, что эфира не существует. [20] Решение Эйнштейна состояло в том, чтобы отказаться от понятия эфира и абсолютного состояния покоя. В теории относительности любая система отсчета, движущаяся равномерно, будет соблюдать одни и те же законы физики. В частности, скорость света в вакууме всегда измеряется как c , даже если она измеряется несколькими системами, движущимися с разными (но постоянными) скоростями.
Из принципа относительности, без предположения о постоянстве скорости света (т. е. используя изотропию пространства и симметрию, подразумеваемую принципом специальной теории относительности), можно показать , что преобразования пространства-времени между инерциальными системами являются либо евклидовыми, либо галилеевыми, либо лоренцевскими. В лоренцевом случае можно получить релятивистское сохранение интервала и определенную конечную предельную скорость. Эксперименты показывают, что эта скорость является скоростью света в вакууме. [стр. 8] [21]
Эйнштейн последовательно основывал вывод инвариантности Лоренца (сущностного ядра специальной теории относительности) всего на двух основных принципах относительности и инвариантности скорости света. Он писал:
Фундаментальное понимание специальной теории относительности заключается в следующем: Допущения относительности и инвариантности скорости света совместимы, если постулируются соотношения нового типа («преобразования Лоренца») для преобразования координат и времени событий... Универсальный принцип специальной теории относительности содержится в постулате: Законы физики инвариантны относительно преобразований Лоренца (для перехода от одной инерциальной системы к любой другой произвольно выбранной инерциальной системе). Это ограничивающий принцип для законов природы... [стр. 5]
Таким образом, многие современные трактовки специальной теории относительности основывают ее на единственном постулате универсальной лоренц-ковариантности или, что эквивалентно, на единственном постулате пространства-времени Минковского . [стр. 9] [стр. 10]
Вместо того чтобы считать универсальную лоренц-ковариантность производным принципом, в этой статье она рассматривается как фундаментальный постулат специальной теории относительности. Традиционный двухпостулатный подход к специальной теории относительности представлен в бесчисленных учебниках для колледжей и популярных презентациях. [22] Учебники, начинающиеся с единственного постулата пространства-времени Минковского, включают учебники Тейлора и Уиллера [11] и Каллахана. [23] Этот подход также используется в статьях Википедии Пространство-время и Диаграмма Минковского .
Определим событие , имеющее пространственно-временные координаты ( t , x , y , z ) в системе S и ( t ′ , x ′ , y ′ , z ′ ) в системе отсчета, движущейся со скоростью v по оси x относительно этой системы S ′ . Тогда преобразование Лоренца указывает, что эти координаты связаны следующим образом: где — фактор Лоренца , а c — скорость света в вакууме, а скорость v системы S ′ относительно S параллельна оси x . Для простоты координаты y и z не затрагиваются; преобразуются только координаты x и t . Эти преобразования Лоренца образуют однопараметрическую группу линейных отображений , причем этот параметр называется быстротой .
Решение четырех уравнений преобразования, приведенных выше, для нештрихованных координат дает обратное преобразование Лоренца:
Это показывает, что нештрихованная система отсчета движется со скоростью − v , измеренной в штрихованной системе отсчета. [24]
Ничего особенного в оси x нет . Преобразование может применяться к оси y или z , или в любом направлении, параллельном движению (которое искривляется фактором γ ) и перпендикулярном; подробности см. в статье Преобразование Лоренца .
Величина, инвариантная относительно преобразований Лоренца, называется скаляром Лоренца .
Записывая преобразование Лоренца и его обратное в терминах разностей координат, где одно событие имеет координаты ( x 1 , t 1 ) и ( x ′ 1 , t ′ 1 ) , другое событие имеет координаты ( x 2 , t 2 ) и ( x ′ 2 , t ′ 2 ) , а разности определяются как
мы получаем
Если вместо разностей взять дифференциалы, то получим
Пространственно-временные диаграммы ( диаграммы Минковского ) являются чрезвычайно полезным средством визуализации того, как координаты преобразуются между различными системами отсчета. Хотя с их помощью не так просто выполнять точные вычисления, как напрямую используя преобразования Лоренца, их главная сила заключается в их способности обеспечивать интуитивное понимание результатов релятивистского сценария. [21]
Чтобы нарисовать пространственно-временную диаграмму, начнем с рассмотрения двух галилеевых систем отсчета, S и S', в стандартной конфигурации, как показано на рис. 2-1. [21] [25] : 155–199
Рис. 3-1a . Нарисуйте оси и кадра S. Ось горизонтальна, а (фактически ) ось вертикальна, что противоположно обычному соглашению в кинематике. Ось масштабируется с коэффициентом , так что обе оси имеют общие единицы длины. На показанной схеме линии сетки отстоят друг от друга на одну единицу расстояния. Диагональные линии под углом 45° представляют мировые линии двух фотонов, проходящих через начало координат в момент времени Наклон этих мировых линий равен 1, поскольку фотоны продвигаются на одну единицу в пространстве за единицу времени. Два события и были нанесены на этот график, так что их координаты можно сравнить в кадрах S и S'.
Рис. 3-1b . Нарисуйте оси и кадра S'. Ось представляет собой мировую линию начала системы координат S', измеренную в кадре S. На этом рисунке обе оси и наклонены относительно нештрихованных осей на угол , где Штрихованная и нештрихованная оси имеют общее начало, поскольку кадры S и S' были настроены в стандартной конфигурации, так что когда
Рис. 3-1c . Единицы в штрихованных осях имеют другой масштаб, чем единицы в нештрихованных осях. Из преобразований Лоренца мы видим, что координаты в штрихованной системе координат преобразуются в в нештрихованной системе координат. Аналогично, координаты в штрихованной системе координат преобразуются в в нештрихованной системе. Проведите линии сетки параллельно оси через точки , измеренные в нештрихованной системе отсчета, где — целое число. Аналогично, проведите линии сетки параллельно оси через , измеренные в нештрихованной системе отсчета. Используя теорему Пифагора, мы видим, что расстояние между единицами равно расстоянию между единицами, умноженному на расстояние между единицами, измеренное в системе отсчета S. Это отношение всегда больше 1 и в конечном итоге стремится к бесконечности, поскольку
Рис. 3-1d . Поскольку скорость света является инвариантом, мировые линии двух фотонов, проходящих через начало координат в момент времени, по-прежнему отображаются в виде диагональных линий под углом 45°. Штрихованные координаты и связаны с нештрихованными координатами посредством преобразований Лоренца и могут быть приблизительно измерены по графику (предполагая, что он был построен достаточно точно), но настоящее достоинство диаграммы Минковского заключается в том, что она предоставляет нам геометрическое представление сценария. Например, на этом рисунке мы видим, что два времениподобно разделенных события, которые имели разные x-координаты в нештрихованной системе отсчета, теперь находятся в одном и том же положении в пространстве.
В то время как нештрихованная рамка нарисована с пространственными и временными осями, которые встречаются под прямым углом, заштрихованная рамка нарисована с осями, которые встречаются под острым или тупым углом. Эта асимметрия вызвана неизбежными искажениями в том, как пространственно-временные координаты отображаются на декартовой плоскости , но рамки на самом деле эквивалентны.
Следствия специальной теории относительности можно вывести из уравнений преобразования Лоренца . [26] Эти преобразования, а следовательно, и специальная теория относительности, приводят к иным физическим предсказаниям, чем предсказания ньютоновской механики при всех относительных скоростях, и наиболее выражены, когда относительные скорости становятся сравнимыми со скоростью света. Скорость света настолько больше всего, с чем сталкивается большинство людей, что некоторые эффекты, предсказываемые теорией относительности, изначально противоречат здравому смыслу .
В теории относительности Галилея длина объекта ( ) [примечание 3] и временное разделение между двумя событиями ( ) являются независимыми инвариантами, значения которых не меняются при наблюдении из разных систем отсчета. [примечание 4] [примечание 5]
Однако в специальной теории относительности переплетение пространственных и временных координат порождает концепцию инвариантного интервала , обозначаемого как : [примечание 6]
Переплетение пространства и времени отменяет неявно предполагаемые концепции абсолютной одновременности и синхронизации в несопутствующих системах отсчета.
Форма, представляющая собой разницу квадрата промежутка времени и квадрата пространственного расстояния, демонстрирует фундаментальное расхождение между евклидовыми и пространственно-временными расстояниями. [примечание 7] Инвариантность этого интервала является свойством общего преобразования Лоренца (также называемого преобразованием Пуанкаре ), что делает его изометрией пространства-времени. Общее преобразование Лоренца расширяет стандартное преобразование Лоренца (которое имеет дело с переносами без вращения, то есть с прибавками Лоренца в направлении x) на все другие переносы , отражения и вращения между любой декартовой инерциальной системой отсчета. [30] : 33–34
При анализе упрощенных сценариев, таких как пространственно-временные диаграммы, часто используется форма инвариантного интервала с уменьшенной размерностью:
Демонстрация того, что интервал является инвариантным, проста для случая пониженной размерности и с рамками в стандартной конфигурации: [21]
Следовательно, значение не зависит от системы отсчета, в которой оно измеряется.
При рассмотрении физического значения следует отметить три случая: [21] [31] : 25–39

Рассмотрим два события, происходящие в двух разных местах, которые происходят одновременно в системе отсчета одного инерциального наблюдателя. Они могут происходить неодновременно в системе отсчета другого инерциального наблюдателя (отсутствие абсолютной одновременности ).
Из уравнения 3 (прямое преобразование Лоренца в терминах разностей координат)
Ясно, что два события, которые являются одновременными в системе S (удовлетворяющей Δ t = 0 ), не обязательно являются одновременными в другой инерциальной системе S ′ (удовлетворяющей Δ t ′ = 0 ). Только если эти события дополнительно колокальны в системе S (удовлетворяющей Δ x = 0 ), они будут одновременными в другой системе S ′ .
Эффект Саньяка можно считать проявлением относительности одновременности. [32] Поскольку относительность одновременности является эффектом первого порядка в , [21] приборы, работающие на основе эффекта Саньяка, такие как кольцевые лазерные гироскопы и волоконно-оптические гироскопы , способны достигать экстремальных уровней чувствительности. [стр. 14]
Промежуток времени между двумя событиями не является постоянным для разных наблюдателей, а зависит от относительных скоростей систем отсчета наблюдателей.
Предположим, что часы находятся в состоянии покоя в нештрихованной системе S. Положение часов в двух разных тиках тогда характеризуется Δ x = 0. Чтобы найти соотношение между временами между этими тиками, измеренными в обеих системах, можно использовать уравнение 3 для нахождения:
Это показывает, что время (Δ t ′ ) между двумя тиками, как видно в кадре, в котором движутся часы ( S ′ ), больше , чем время (Δ t ) между этими тиками, измеренное в неподвижной системе часов ( S ). Замедление времени объясняет ряд физических явлений; например, время жизни высокоскоростных мюонов, созданных столкновением космических лучей с частицами во внешней атмосфере Земли и движущихся к поверхности, больше, чем время жизни медленно движущихся мюонов, созданных и распадающихся в лаборатории. [33]

Всякий раз, когда слышишь утверждение о том, что «движущиеся часы идут медленно», следует представить себе инерциальную систему отсчета, густо заполненную идентичными, синхронизированными часами. Когда движущиеся часы проходят через этот массив, их показания в любой конкретной точке сравниваются с показаниями неподвижных часов в той же точке. [34] : 149–152
Измерения, которые мы получили бы, если бы мы действительно смотрели на движущиеся часы, в общем случае были бы совсем не тем же самым, потому что время, которое мы увидели бы, было бы задержано из-за конечной скорости света, т. е. время, которое мы видим, было бы искажено эффектом Доплера . Измерения релятивистских эффектов всегда следует понимать как сделанные после того, как эффекты конечной скорости света были вынесены за скобки. [34] : 149–152

Поль Ланжевен , один из первых сторонников теории относительности, сделал многое для популяризации теории, несмотря на сопротивление многих физиков революционным концепциям Эйнштейна. Среди его многочисленных вкладов в основы специальной теории относительности были независимые работы по соотношению массы и энергии, тщательное изучение парадокса близнецов и исследования вращающихся систем координат. Его имя часто связывают с гипотетической конструкцией, называемой «световыми часами» (первоначально разработанной Льюисом и Толменом в 1909 году [35] ), которую он использовал для выполнения нового вывода преобразования Лоренца. [36]
Световые часы представляются как ящик с идеально отражающими стенками, в котором световой сигнал отражается вперед и назад от противоположных сторон. Концепция замедления времени часто преподается с использованием световых часов, которые движутся равномерно инерционно перпендикулярно линии, соединяющей два зеркала. [37] [38] [39] [40] (Сам Ланжевен использовал световые часы, ориентированные параллельно своей линии движения. [36] )
Рассмотрим сценарий, показанный на рис. 4-3A. Наблюдатель A держит световые часы длины , а также электронный таймер, с помощью которого он измеряет, сколько времени требуется импульсу, чтобы совершить круговое путешествие вверх и вниз по световым часам. Хотя наблюдатель A быстро движется по поезду, с его точки зрения излучение и получение импульса происходят в одном и том же месте, и он измеряет интервал, используя одни часы, расположенные в точном месте этих двух событий. Для интервала между этими двумя событиями наблюдатель A находит Интервал времени, измеренный с помощью одних часов, которые неподвижны в определенной системе отсчета, называется собственным интервалом времени . [41]
Рис. 4-3B иллюстрирует эти же два события с точки зрения наблюдателя B, который стоит у путей, пока поезд проезжает со скоростью Вместо того, чтобы совершать прямые движения вверх-вниз, наблюдатель B видит, что импульсы движутся по зигзагообразной линии. Однако из-за постулата постоянства скорости света скорость импульсов вдоль этих диагональных линий та же самая, которую наблюдатель A видел для своих импульсов вверх-вниз. B измеряет скорость вертикальной составляющей этих импульсов как так что общее время прохождения импульсов туда и обратно составляет Обратите внимание, что для наблюдателя B излучение и получение светового импульса происходили в разных местах, и он измерял интервал, используя два неподвижных и синхронизированных часа, расположенных в двух разных положениях в его системе отсчета. Интервал, который измерял B, поэтому не был надлежащим временным интервалом, потому что он измерял его не с помощью одних покоящихся часов. [41]
В приведенном выше описании световых часов Ланжевена обозначение одного наблюдателя как неподвижного, а другого как движущегося было совершенно произвольным. Можно было бы с тем же успехом иметь наблюдателя B, несущего световые часы и движущегося со скоростью влево, в этом случае наблюдатель A воспринимал бы часы B как идущие медленнее, чем его локальные часы.
Здесь нет парадокса, потому что нет независимого наблюдателя C, который согласится и с A, и с B. Наблюдатель C обязательно производит свои измерения из своей собственной системы отсчета. Если эта система отсчета совпадает с системой отсчета A, то C согласится с измерением времени A. Если система отсчета C совпадает с системой отсчета B, то C согласится с измерением времени B. Если система отсчета C не совпадает ни с системой отсчета A, ни с системой отсчета B, то измерение времени C будет противоречить как измерению времени A , так и измерению времени B. [42]
Взаимность замедления времени между двумя наблюдателями в отдельных инерциальных системах отсчета приводит к так называемому парадоксу близнецов , сформулированному в его нынешней форме Ланжевеном в 1911 году. [43] Ланжевен представил себе авантюриста, желающего исследовать будущее Земли. Этот путешественник садится в снаряд, способный двигаться со скоростью 99,995% скорости света. Совершив путешествие туда и обратно к ближайшей звезде, длящееся всего два года его собственной жизни, он возвращается на Землю, которая на двести лет старше.
Этот результат кажется загадочным, поскольку и путешественник, и земной наблюдатель будут видеть друг друга движущимися, и поэтому, из-за взаимности замедления времени, можно было бы изначально ожидать, что каждый должен был бы обнаружить, что другой постарел меньше. На самом деле, нет никакого парадокса вообще, потому что для того, чтобы два наблюдателя могли сравнить свое собственное время, симметрия ситуации должна быть нарушена: по крайней мере один из двух наблюдателей должен изменить свое состояние движения, чтобы соответствовать состоянию другого. [44]

Однако знание общего решения парадокса не дает немедленной возможности вычислять правильные количественные результаты. Многие решения этой головоломки были предоставлены в литературе и рассмотрены в статье о парадоксе близнецов . Далее мы рассмотрим одно такое решение парадокса.
Наша основная цель — продемонстрировать, что после путешествия оба близнеца находятся в полном согласии относительно того, кто и на сколько постарел, независимо от их разного опыта. Рис. 4-4 иллюстрирует сценарий, в котором путешествующий близнец летит со скоростью 0,6 с к звезде, удаленной на 3 световых года , и обратно. Во время путешествия каждый близнец посылает друг другу ежегодные сигналы времени (измеренные в их собственном времени). После путешествия сравниваются накопленные подсчеты. На внешней фазе путешествия каждый близнец получает сигналы другого с пониженной частотой Первоначально ситуация совершенно симметрична: обратите внимание, что каждый близнец получает годовой сигнал другого через два года, измеренных по его собственным часам. Симметрия нарушается, когда путешествующий близнец оборачивается на четырехлетней отметке, измеренной по его часам. В течение оставшихся четырех лет своего путешествия она получает сигналы с повышенной частотой Ситуация совершенно иная с неподвижным близнецом. Из-за задержки, связанной со скоростью света, он не видит, как его сестра оборачивается, пока не пройдет восемь лет по его собственным часам. Таким образом, он получает сигналы повышенной частоты от своей сестры только в течение относительно короткого периода. Хотя близнецы расходятся в своих соответствующих измерениях общего времени, мы видим в следующей таблице, а также путем простого наблюдения за диаграммой Минковского, что каждый близнец находится в полном согласии с другим относительно общего числа сигналов, отправленных от одного к другому. Следовательно, нет никакого парадокса. [34] : 152–159
Размеры (например, длина) объекта, измеренные одним наблюдателем, могут быть меньше результатов измерений того же объекта, сделанных другим наблюдателем (например, парадокс лестницы подразумевает, что длинная лестница движется со скоростью, близкой к скорости света, и находится в меньшем гараже).
Аналогично, предположим, что измерительный стержень находится в состоянии покоя и выровнен вдоль оси x в нештрихованной системе S. В этой системе длина этого стержня записывается как Δ x . Чтобы измерить длину этого стержня в системе S ′ , в которой стержень движется, расстояния x ′ до конечных точек стержня должны быть измерены одновременно в этой системе S ′ . Другими словами, измерение характеризуется Δ t ′ = 0 , что можно объединить с уравнением 4, чтобы найти соотношение между длинами Δ x и Δ x ′ :
Это показывает, что длина (Δ x ′ ) стержня, измеренная в системе, в которой он движется ( S ′ ), короче его длины (Δ x ) в его собственной системе покоя ( S ).
Замедление времени и сокращение длины — это не просто видимости. Замедление времени явно связано с нашим способом измерения временных интервалов между событиями, которые происходят в одном и том же месте в данной системе координат (называемые «колокальными» событиями). Эти временные интервалы (которые могут быть и фактически измеряются экспериментально соответствующими наблюдателями) отличаются в другой системе координат, движущейся относительно первой, если только события, в дополнение к тому, что они колокальны, также не являются одновременными. Аналогично, сокращение длины связано с нашими измеренными расстояниями между разделенными, но одновременными событиями в данной выбранной системе координат. Если эти события не колокальны, а разделены расстоянием (пространством), они не будут происходить на одном и том же пространственном расстоянии друг от друга, если смотреть из другой движущейся системы координат.
Рассмотрим две системы отсчета S и S ′ в стандартной конфигурации. Частица в системе отсчета S движется в направлении x со скоростью вектора. Какова ее скорость в системе отсчета S ′ ?
Мы можем написать
Подстановка выражений для и из уравнения 5 в уравнение 8 , а затем простые математические преобразования и обратная подстановка из уравнения 7 дают преобразование Лоренца скорости :
Обратное отношение получается путем перестановки штрихованных и нештрихованных символов и замены на
Для невыровненных по оси x точек запишем: [12] : 47–49
Прямые и обратные преобразования для этого случая следующие:
Уравнение 10 и уравнение 14 можно интерпретировать как дающие результирующую двух скоростей и и они заменяют формулу , которая действительна в теории относительности Галилея. Интерпретируемые таким образом, они обычно называются формулами сложения (или композиции) релятивистских скоростей , действительными для трех осей S и S ′, выровненных друг с другом (хотя не обязательно в стандартной конфигурации). [12] : 47–49
Отметим следующие моменты:
В стандартной конфигурации нет ничего особенного в направлении x . Вышеуказанный формализм применим к любому направлению; и три ортогональных направления позволяют иметь дело со всеми направлениями в пространстве, разлагая векторы скорости на их компоненты в этих направлениях. Подробности см. в формуле сложения скоростей .
Композиция двух неколлинеарных усилений Лоренца (т. е. двух неколлинеарных преобразований Лоренца, ни одно из которых не включает вращение) приводит к преобразованию Лоренца, которое не является чистым усилением, а представляет собой композицию усиления и вращения.
Вращение Томаса является результатом относительности одновременности. На рис. 4-5а стержень длиной в своей системе покоя (т.е. имеющий собственную длину ) поднимается вертикально вдоль оси y в наземной системе отсчета.
На рис. 4-5b тот же стержень наблюдается из рамы ракеты, движущейся со скоростью вправо. Если мы представим себе двое часов, расположенных на левом и правом концах стержня, которые синхронизированы в раме стержня , относительность одновременности заставляет наблюдателя в раме ракеты наблюдать (не видеть) часы на правом конце стержня как опережающие во времени на , а стержень соответственно наблюдается наклонным. [31] : 98–99
В отличие от релятивистских эффектов второго порядка, таких как сокращение длины или замедление времени, этот эффект становится весьма существенным даже при довольно низких скоростях. Например, это можно увидеть в спине движущихся частиц , где прецессия Томаса является релятивистской поправкой, которая применяется к спину элементарной частицы или вращению макроскопического гироскопа , связывая угловую скорость спина частицы, следующей по криволинейной орбите, с угловой скоростью орбитального движения. [31] : 169–174
Вращение Томаса дает решение известного «парадокса линейки и отверстия». [стр. 15] [31] : 98–99

На рис. 4-6 временной интервал между событиями A («причина») и B («следствие») является «временеподобным»; то есть существует система отсчета, в которой события A и B происходят в одном и том же месте пространства , разделенные только тем, что происходят в разное время. Если A предшествует B в этой системе, то A предшествует B во всех системах, доступных преобразованию Лоренца. Материя (или информация) может перемещаться (со скоростью ниже скорости света) из местоположения A, начиная с момента A, в местоположение B, прибывая во время B, поэтому может существовать причинно-следственная связь (где A является причиной, а B — следствием).
Интервал AC на диаграмме является «пространственно-подобным»; то есть, есть система отсчета, в которой события A и C происходят одновременно, разделенные только пространством. Есть также системы, в которых A предшествует C (как показано) и системы, в которых C предшествует A. Но ни одна система не доступна преобразованию Лоренца, в которой события A и C происходят в одном и том же месте. Если бы между событиями A и C могла существовать причинно-следственная связь, возникли бы парадоксы причинности.
Например, если бы сигналы можно было посылать быстрее света, то сигналы можно было бы посылать в прошлое отправителя (наблюдатель B на диаграммах). [45] [стр. 16] Тогда можно было бы сконструировать множество причинных парадоксов.
Рассмотрим пространственно-временные диаграммы на рис. 4-7. A и B стоят вдоль железнодорожных путей, когда мимо проезжает скоростной поезд, причем C едет в последнем вагоне поезда, а D едет в головном вагоне. Мировые линии A и B вертикальны ( ct ), что указывает на неподвижное положение этих наблюдателей на земле, в то время как мировые линии C и D наклонены вперед ( ct ′ ), отражая быстрое движение наблюдателей C и D, неподвижных в своем поезде, как это наблюдается с земли.
Сигналам не обязательно быть мгновенными, чтобы нарушить причинность. Даже если бы сигнал от D до C был немного мельче оси (а сигнал от A до B немного круче оси ), B все равно мог бы получить свое сообщение до того, как он его отправил. Увеличивая скорость поезда до скоростей, близких к световым, оси и можно сжать очень близко к пунктирной линии, представляющей скорость света. С помощью этой измененной установки можно продемонстрировать, что даже сигналы, лишь немного превышающие скорость света, приведут к нарушению причинности. [47]
Таким образом, если необходимо сохранить причинность , одним из следствий специальной теории относительности является то, что никакой информационный сигнал или материальный объект не может перемещаться быстрее света в вакууме.
Это не означает, что все скорости, превышающие скорость света, невозможны. Можно описать различные тривиальные ситуации, в которых некоторые «вещи» (не материя и не энергия) движутся быстрее света. [48] Например, место, где луч прожектора попадает на дно облака, может двигаться быстрее света, если прожектор быстро поворачивается (хотя это не нарушает причинность или любое другое релятивистское явление). [49] [50]

В 1850 году Ипполит Физо и Леон Фуко независимо друг от друга установили, что свет распространяется в воде медленнее, чем в воздухе, тем самым подтвердив предсказание волновой теории света Френеля и опровергнув соответствующее предсказание корпускулярной теории Ньютона . [51] Скорость света была измерена в стоячей воде. Какова будет скорость света в текущей воде?
В 1851 году Физо провел эксперимент, чтобы ответить на этот вопрос, упрощенное представление которого показано на рис. 5-1. Луч света разделяется расщепителем луча, и разделенные лучи пропускаются в противоположных направлениях через трубку с текущей водой. Они рекомбинируются, образуя интерференционные полосы, указывающие на разницу в оптической длине пути, которую может видеть наблюдатель. Эксперимент продемонстрировал, что увлечение света текущей водой вызывает смещение полос, показывая, что движение воды повлияло на скорость света.
Согласно теориям, господствовавшим в то время, свет, проходящий через движущуюся среду, будет простой суммой его скорости через среду плюс скорость среды . Вопреки ожиданиям, Физо обнаружил, что хотя свет, казалось бы, увлекается водой, величина увлечения была намного ниже ожидаемой. Если — скорость света в стоячей воде, — скорость воды, — скорость света в воде в лабораторной системе отсчета, при этом поток воды добавляется или вычитается из скорости света, то
Результаты Физо, хотя и согласуются с более ранней гипотезой Френеля о частичном увлечении эфира , были крайне обескураживающими для физиков того времени. Среди прочего, наличие члена показателя преломления означало, что, поскольку зависит от длины волны, эфир должен быть способен поддерживать различные движения одновременно . [примечание 8] Было предложено множество теоретических объяснений для объяснения коэффициента увлечения Френеля , которые полностью противоречили друг другу. Еще до эксперимента Майкельсона-Морли экспериментальные результаты Физо были среди ряда наблюдений, которые создали критическую ситуацию в объяснении оптики движущихся тел. [52]
С точки зрения специальной теории относительности результат Физо есть не что иное, как приближение к уравнению 10 , релятивистской формуле для сложения скоростей. [30]

Из-за конечной скорости света, если относительные движения источника и приемника включают поперечную составляющую, то направление, из которого свет достигает приемника, будет смещено от геометрического положения в пространстве источника относительно приемника. Классический расчет смещения имеет две формы и делает разные предсказания в зависимости от того, приемник, источник или оба находятся в движении относительно среды. (1) Если приемник находится в движении, смещение будет следствием аберрации света . Угол падения луча относительно приемника можно вычислить из векторной суммы движений приемника и скорости падающего света. [53] (2) Если источник находится в движении, смещение будет следствием коррекции светового времени . Смещение видимого положения источника от его геометрического положения будет результатом движения источника в течение времени, которое требуется его свету, чтобы достичь приемника. [54]
Классическое объяснение не прошло экспериментальную проверку. Поскольку угол аберрации зависит от соотношения между скоростью приемника и скоростью падающего света, прохождение падающего света через преломляющую среду должно изменить угол аберрации. В 1810 году Араго использовал это ожидаемое явление в неудачной попытке измерить скорость света, [55] а в 1870 году Джордж Эйри проверил гипотезу, используя заполненный водой телескоп, обнаружив, что, вопреки ожиданиям, измеренная аберрация была идентична аберрации, измеренной с помощью заполненного воздухом телескопа. [56] «Громоздкая» попытка объяснить эти результаты использовала гипотезу частичного увлечения эфиром, [57], но была несовместима с результатами эксперимента Майкельсона–Морли, который, по-видимому, требовал полного увлечения эфиром. [58]
Предполагая инерциальные системы отсчета, релятивистское выражение для аберрации света применимо как к случаям перемещения приемника, так и к случаям перемещения источника. Было опубликовано множество тригонометрически эквивалентных формул. Выраженные через переменные на рис. 5-2, они включают [30] : 57–60
Классический эффект Доплера зависит от того, движутся ли источник, приемник или оба относительно среды. Релятивистский эффект Доплера не зависит от какой-либо среды. Тем не менее, релятивистский доплеровский сдвиг для продольного случая, когда источник и приемник движутся прямо друг к другу или друг от друга, может быть получен так, как если бы это было классическое явление, но модифицированное добавлением члена замедления времени , и это описанная здесь обработка. [59] [60]
Предположим, что приемник и источник удаляются друг от друга с относительной скоростью , измеренной наблюдателем на приемнике или источнике (принятое здесь соглашение о знаках является отрицательным , если приемник и источник движутся навстречу друг другу). Предположим, что источник неподвижен в среде. Тогда где скорость звука.
Для света, и с приемником, движущимся с релятивистской скоростью, часы на приемнике растянуты по времени относительно часов на источнике. Приемник будет измерять полученную частоту, чтобы быть там, где
Идентичное выражение для релятивистского доплеровского сдвига получается при выполнении анализа в системе отсчета приемника с движущимся источником. [61] [21]

Поперечный эффект Доплера — одно из главных новых предсказаний специальной теории относительности.
Классически можно было бы ожидать, что если источник и приемник движутся поперечно друг другу без продольной составляющей в их относительном движении, то не должно быть доплеровского сдвига в свете, достигающем приемника.
Специальная теория относительности предсказывает иное. Рис. 5-3 иллюстрирует два распространенных варианта этого сценария. Оба варианта можно проанализировать с использованием простых аргументов замедления времени. [21] На рис. 5-3a приемник наблюдает свет от источника как смещенный в синюю сторону на коэффициент . На рис. 5-3b свет смещен в красную сторону на тот же коэффициент.

Замедление времени и сокращение длины — это не оптические иллюзии, а реальные эффекты. Измерения этих эффектов не являются артефактом доплеровского сдвига и не являются результатом пренебрежения временем, которое требуется свету для прохождения от события до наблюдателя.
Ученые проводят фундаментальное различие между измерением или наблюдением , с одной стороны, и визуальным видом , или тем, что человек видит . Измеренная форма объекта — это гипотетический снимок всех точек объекта, которые существуют в один момент времени. Но визуальный вид объекта зависит от разной продолжительности времени, которое требуется свету, чтобы пройти от разных точек объекта до глаза.

В течение многих лет различие между ними не было общепризнанным, и обычно считалось, что объект с сокращенной длиной, проходящий мимо наблюдателя, на самом деле будет фактически виден как сокращенный по длине. В 1959 году Джеймс Террелл и Роджер Пенроуз независимо друг от друга указали, что дифференциальные эффекты задержки во времени в сигналах, достигающих наблюдателя от разных частей движущегося объекта, приводят к тому, что визуальный вид быстро движущегося объекта сильно отличается от его измеренной формы. Например, удаляющийся объект будет казаться сокращенным, приближающийся объект будет казаться удлиненным, а проходящий объект будет иметь перекошенный вид, который можно сравнить с вращением. [стр. 19] [стр. 20] [62] [63] Движущаяся сфера сохраняет круговой контур для всех скоростей, для любого расстояния и для всех углов обзора, хотя поверхность сферы и изображения на ней будут казаться искаженными. [64] [65]
.jpg/440px-M87_jet_(1).jpg)
На обоих рисунках, рис. 5-4 и рис. 5-5, изображены объекты, движущиеся поперек линии зрения. На рис. 5-4 куб рассматривается с расстояния, в четыре раза превышающего длину его сторон. На высоких скоростях стороны куба, перпендикулярные направлению движения, кажутся гиперболическими по форме. Куб на самом деле не вращается. Скорее, свету с задней стороны куба требуется больше времени, чтобы достичь глаз, по сравнению со светом с передней стороны, за это время куб перемещается вправо. На высоких скоростях сфера на рис. 5-5 приобретает вид сплющенного диска, наклоненного до 45° от линии зрения. Если движения объектов не строго поперечные, а вместо этого включают продольную составляющую, могут быть видны преувеличенные искажения в перспективе. [66] Эта иллюзия стала известна как вращение Террелла или эффект Террелла-Пенроуза . [примечание 9]
Другой пример, когда визуальный вид не соответствует измерению, получен из наблюдения кажущегося сверхсветового движения в различных радиогалактиках , объектах BL Lac , квазарах и других астрономических объектах, которые выбрасывают струи материи с релятивистской скоростью под узкими углами по отношению к наблюдателю. Возникает кажущаяся оптическая иллюзия, создающая видимость движения со скоростью, превышающей скорость света. [67] [68] [69] На рис. 5-6 галактика M87 выбрасывает высокоскоростную струю субатомных частиц почти прямо к нам, но вращение Пенроуза-Террелла заставляет струю казаться движущейся вбок таким же образом, как был вытянут вид куба на рис. 5-4. [70]
Раздел Следствия, полученные из преобразования Лоренца, посвящен исключительно кинематике , изучению движения точек, тел и систем тел без учета сил, вызвавших движение. В этом разделе обсуждаются массы, силы, энергия и т. д., и, как таковой, требуется рассмотрение физических эффектов, выходящих за рамки тех, которые охватываются самим преобразованием Лоренца.
По мере того, как скорость объекта приближается к скорости света с точки зрения наблюдателя, его релятивистская масса увеличивается, тем самым затрудняя его ускорение из системы отсчета наблюдателя.
Содержание энергии в покоящемся объекте с массой m равно mc 2 . Сохранение энергии подразумевает, что в любой реакции уменьшение суммы масс частиц должно сопровождаться увеличением кинетической энергии частиц после реакции. Аналогично, масса объекта может быть увеличена за счет поглощения кинетической энергии.
В дополнение к статьям, упомянутым выше, в которых приводятся выводы преобразований Лоренца и описываются основы специальной теории относительности, Эйнштейн также написал по крайней мере четыре статьи, в которых приводятся эвристические аргументы в пользу эквивалентности (и превращаемости) массы и энергии, поскольку E = mc2 .
Эквивалентность массы и энергии является следствием специальной теории относительности. Энергия и импульс, которые разделены в ньютоновской механике, образуют четырехвектор в теории относительности, и это связывает временную компоненту (энергию) с пространственными компонентами (импульсом) нетривиальным образом. Для покоящегося объекта четырехвектор энергии-импульса равен ( E / c , 0, 0, 0) : он имеет временную компоненту, которая является энергией, и три пространственных компонента, которые равны нулю. При смене систем отсчета с помощью преобразования Лоренца в направлении x с малым значением скорости v четырехвектор энергии-импульса становится равным ( E / c , Ev / c2 , 0, 0) . Импульс равен энергии, умноженной на скорость, деленную на c2 . Таким образом, ньютоновская масса объекта, которая является отношением импульса к скорости для медленных скоростей , равна E / c2 .
Энергия и импульс являются свойствами материи и излучения, и невозможно вывести, что они образуют четырехвектор, только из двух основных постулатов специальной теории относительности, потому что они не говорят о материи или излучении, они говорят только о пространстве и времени. Поэтому вывод требует некоторых дополнительных физических рассуждений. В своей статье 1905 года Эйнштейн использовал дополнительные принципы, которые ньютоновская механика должна соблюдать для медленных скоростей, так что существует один скаляр энергии и один трехвекторный импульс на медленных скоростях, и что закон сохранения энергии и импульса в точности верен в теории относительности. Более того, он предположил, что энергия света преобразуется тем же фактором доплеровского сдвига, что и его частота, что он ранее показал на основе уравнений Максвелла. [стр. 1] Первой из статей Эйнштейна на эту тему была «Зависит ли инерция тела от его энергетического содержания?» в 1905 году. [стр. 21] Хотя аргумент Эйнштейна в этой статье почти повсеместно принят физиками как правильный, даже самоочевидный, многие авторы на протяжении многих лет предполагали, что он неверен. [71] Другие авторы предполагают, что аргумент был просто неубедительным, поскольку он опирался на некоторые неявные предположения. [72]
Эйнштейн признал противоречия по поводу своего вывода в своей обзорной статье 1907 года по специальной теории относительности. Там он отмечает, что проблематично полагаться на уравнения Максвелла для эвристического аргумента массы-энергии. Аргумент в его статье 1905 года может быть реализован с излучением любых безмассовых частиц, но уравнения Максвелла неявно используются, чтобы сделать очевидным, что излучение света в частности может быть достигнуто только путем совершения работы. Чтобы испустить электромагнитные волны, все, что вам нужно сделать, это встряхнуть заряженную частицу, и это, очевидно, является выполнением работы, так что излучение является энергией. [стр. 22] [примечание 10]
В четвертой из своих статей Annus mirabilis 1905 года [ стр . 21] Эйнштейн представил эвристический аргумент в пользу эквивалентности массы и энергии. Хотя, как обсуждалось выше, последующая наука установила, что его аргументы не дотягивают до общеопределенного доказательства, выводы, к которым он пришел в этой статье, выдержали испытание временем.
В качестве исходных предположений Эйнштейн взял недавно открытую им формулу для релятивистского доплеровского сдвига , законы сохранения энергии и сохранения импульса , а также соотношение между частотой света и его энергией, вытекающее из уравнений Максвелла .
Рис. 6-1 (вверху). Рассмотрим систему плоских волн света, имеющих частоту , распространяющуюся в направлении относительно оси x системы отсчета S. Частота (и, следовательно, энергия) волн, измеренная в системе S ′ , движущейся вдоль оси x со скоростью, определяется релятивистской формулой доплеровского сдвига, которую Эйнштейн вывел в своей статье 1905 года по специальной теории относительности: [стр. 1]
Рис. 6-1 (внизу). Рассмотрим произвольное тело, неподвижное в системе отсчета S. Пусть это тело испускает пару световых импульсов равной энергии в противоположных направлениях под углом к оси x. Каждый импульс имеет энергию . Из-за сохранения импульса тело остается неподвижным в S после испускания двух импульсов. Пусть будет энергией тела до испускания двух импульсов и после их испускания.
Далее рассмотрим ту же систему, наблюдаемую из системы S ′ , которая движется вдоль оси x со скоростью относительно системы S . В этой системе свет от прямого и обратного импульсов будет релятивистски смещен Доплером. Пусть будет энергией тела, измеренной в системе отсчета S ′ до испускания двух импульсов и после их испускания. Получаем следующие соотношения: [стр. 21]
Из приведенных выше уравнений получаем следующее:
Два различия формы, которые можно увидеть в приведенном выше уравнении, имеют простую физическую интерпретацию. Поскольку и являются энергиями произвольного тела в движущейся и неподвижной системах отсчета, а представляет собой кинетическую энергию тел до и после испускания света (за исключением аддитивной константы, которая фиксирует нулевую точку энергии и традиционно принимается равной нулю). Следовательно,
Используя разложение в ряд Тейлора и пренебрегая членами более высокого порядка, он получил
Сравнивая приведенное выше выражение с классическим выражением для кинетической энергии, KE = 1/2 mv 2 , Эйнштейн затем заметил: «Если тело выделяет энергию L в виде излучения, его масса уменьшается на L / c 2 ».
Риндлер заметил, что эвристический аргумент Эйнштейна предполагал лишь то, что энергия вносит вклад в массу. В 1905 году осторожное выражение Эйнштейном соотношения массы и энергии допускало возможность существования «спящей» массы, которая останется после того, как вся энергия тела будет удалена. Однако к 1907 году Эйнштейн был готов утверждать, что вся инертная масса представляет собой запас энергии. «Чтобы приравнять всю массу к энергии, требовался акт эстетической веры, очень характерный для Эйнштейна». [12] : 81–84 Смелая гипотеза Эйнштейна была полностью подтверждена в годы, последовавшие за его первоначальным предложением.
По разным причинам оригинальный вывод Эйнштейна в настоящее время редко преподается. Помимо бурных дебатов, которые продолжаются и по сей день относительно формальной правильности его оригинального вывода, признание специальной теории относительности тем, что Эйнштейн называл «принципиальной теорией», привело к переходу от опоры на электромагнитные явления к чисто динамическим методам доказательства. [73]
Поскольку ничто не может двигаться быстрее света, можно сделать вывод, что человек никогда не сможет путешествовать дальше от Земли, чем на ~100 световых лет. Вы могли бы легко подумать, что путешественник никогда не сможет достичь более нескольких солнечных систем, которые существуют в пределах 100 световых лет от Земли. Однако из-за замедления времени гипотетический космический корабль может пролететь тысячи световых лет за время жизни пассажира. Если бы можно было построить космический корабль, который ускоряется с постоянным ускорением 1 g , через год он будет двигаться почти со скоростью света, наблюдаемой с Земли. Это описывается следующим образом: где v ( t ) — скорость в момент времени t , a — ускорение космического корабля, а t — координатное время, измеренное людьми на Земле. [стр. 23] Таким образом, после одного года ускорения со скоростью 9,81 м/с 2 космический корабль будет двигаться со скоростью v = 0,712 c и 0,946 c через три года относительно Земли. После трех лет этого ускорения, когда космический корабль достигнет скорости 94,6% от скорости света относительно Земли, замедление времени приведет к тому, что каждая секунда, испытываемая на космическом корабле, будет соответствовать 3,1 секунде на Земле. Во время своего путешествия люди на Земле будут ощущать больше времени, чем они испытывают, поскольку их часы (все физические явления) будут действительно идти в 3,1 раза быстрее, чем часы космического корабля. 5-летнее путешествие туда и обратно для путешественника займет 6,5 земных лет и покроет расстояние более 6 световых лет. 20-летнее путешествие туда и обратно для них (5 лет ускорения, 5 замедления, дважды каждое) вернет их на Землю, проделав путь в 335 земных лет и пройдя расстояние в 331 световой год. [74] Полное 40-летнее путешествие при 1 g покажется на Земле продолжительностью 58 000 лет и покроет расстояние в 55 000 световых лет. 40-летнее путешествие при 1,1 g займет 148 000 земных лет и охватит около 140 000 световых лет. Одностороннее 28-летнее (14 лет ускорения, 14 лет замедления, как измеряется по часам астронавта) путешествие при ускорении 1 g может достичь 2 000 000 световых лет до галактики Андромеды. [74] Это же самое замедление времени является причиной того, что мюон, движущийся близко к c , как наблюдается, движется намного дальше, чем c, умноженное на его период полураспада (в состоянии покоя). [75]
Изучение продуктов столкновений, полученных с помощью ускорителей частиц по всему миру, дает ученым доказательства структуры субатомного мира и законов природы, управляющих им. Анализ продуктов столкновений, сумма масс которых может значительно превышать массы падающих частиц, требует специальной теории относительности. [76]
В ньютоновской механике анализ столкновений включает использование законов сохранения массы , импульса и энергии . В релятивистской механике масса не сохраняется независимо, поскольку она включена в общую релятивистскую энергию. Мы иллюстрируем различия, возникающие между ньютоновской и релятивистской трактовками столкновений частиц, рассматривая простой случай двух абсолютно упругих сталкивающихся частиц одинаковой массы. ( Неупругие столкновения обсуждаются в разделе Пространство-время#Законы сохранения . Радиоактивный распад можно рассматривать как своего рода неупругое столкновение, обращенное во времени. [76] )
Упругое рассеяние заряженных элементарных частиц отклоняется от идеальности из-за возникновения тормозного излучения. [77] [78]

Рис. 6-2 демонстрирует результат, знакомый игрокам в бильярд, что если неподвижный шар упруго ударяется другим шаром той же массы (предполагая отсутствие бокового вращения, или «английского»), то после столкновения расходящиеся траектории двух шаров будут стягивать прямой угол. (a) В неподвижной системе отсчета падающая сфера, движущаяся со скоростью 2 v, ударяется о неподвижную сферу. (b) В системе отсчета центра импульса две сферы сближаются симметрично со скоростью ± v . После упругого столкновения две сферы отскакивают друг от друга с равными и противоположными скоростями ± u . Закон сохранения энергии требует, чтобы | u | = | v |. (c) Возвращаясь к неподвижной системе отсчета, скорости отскока равны v ± u . Скалярное произведение ( v + u ) ⋅ ( v − u ) = v 2 − u 2 = 0 , что указывает на то, что векторы ортогональны. [12] : 26–27

Рассмотрим сценарий упругого столкновения на рис. 6-3 между движущейся частицей, сталкивающейся с неподвижной частицей равной массы. В отличие от ньютоновского случая, угол между двумя частицами после столкновения меньше 90°, зависит от угла рассеяния и становится все меньше и меньше по мере того, как скорость падающей частицы приближается к скорости света:
Релятивистский импульс и полная релятивистская энергия частицы определяются как
Закон сохранения импульса гласит, что сумма импульсов входящей частицы и неподвижной частицы (которая изначально имеет импульс = 0) равна сумме импульсов вылетевших частиц:
Аналогично, сумма полных релятивистских энергий входящей частицы и неподвижной частицы (которая изначально имеет полную энергию mc2 ) равна сумме полных энергий вылетевших частиц:
Разложение ( 6-5 ) на составляющие, замена на безразмерные и вынесение за скобки общих членов из ( 6-5 ) и ( 6-6 ) дает следующее: [стр. 24]
Из них мы получаем следующие соотношения: [стр. 24]
Для симметричного случая, в котором и ( 6-12 ) принимает более простую форму: [стр. 24]
Преобразования Лоренца связывают координаты событий в одной системе отсчета с координатами событий в другой системе отсчета. Релятивистское сложение скоростей используется для сложения двух скоростей. Формулы для выполнения последних вычислений нелинейны, что делает их более сложными, чем соответствующие формулы Галилея.
Эта нелинейность является артефактом нашего выбора параметров. [11] : 47–59 Ранее мы отмечали, что в пространственно-временной диаграмме x–ct точки на некотором постоянном пространственно-временном интервале от начала координат образуют инвариантную гиперболу. Мы также отмечали, что системы координат двух пространственно-временных систем отсчета в стандартной конфигурации гиперболически повернуты относительно друг друга.
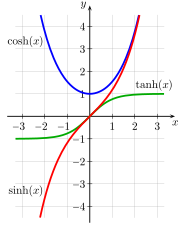
Естественными функциями для выражения этих отношений являются гиперболические аналоги тригонометрических функций . На рис. 7-1a показана единичная окружность с sin( a ) и cos( a ), единственное отличие этой диаграммы от знакомой единичной окружности элементарной тригонометрии заключается в том, что a интерпретируется не как угол между лучом и осью x , а как удвоенная площадь сектора, выметаемого лучом из оси x . Численно угол и 2 × меры площади для единичной окружности идентичны. На рис. 7-1b показана единичная гипербола с sinh( a ) и cosh( a ), где a также интерпретируется как удвоенная окрашенная площадь. [79] На рис. 7-2 представлены графики функций sinh, cosh и tanh.
Для единичной окружности наклон луча определяется выражением
В декартовой плоскости поворот точки ( x , y ) в точку ( x ' , y ' ) на угол θ задается формулой
В пространственно-временной диаграмме параметр скорости является аналогом наклона. Быстрота , φ , определяется как [21] : 96–99
где
Быстрота, определенная выше, очень полезна в специальной теории относительности, поскольку многие выражения принимают значительно более простую форму, когда выражаются через нее. Например, быстрота просто аддитивна в формуле коллинеарного сложения скоростей; [11] : 47–59
или другими словами,
Преобразования Лоренца принимают простую форму, если их выразить через быстроту. Фактор γ можно записать как
Преобразования, описывающие относительное движение с постоянной скоростью и без поворота осей пространственных координат, называются бустингами .
Подставляя γ и γβ в преобразования, представленные ранее, и переписывая в матричной форме, усиление Лоренца в направлении x можно записать как
и обратный Лоренц-буст в направлении x может быть записан как
Другими словами, лоренцевские усиления представляют собой гиперболические вращения в пространстве-времени Минковского. [21] : 96–99
Преимущества использования гиперболических функций таковы, что некоторые учебники, такие как классические учебники Тейлора и Уиллера, вводят их использование на очень раннем этапе. [11] [примечание 11]
Четырехвекторы были упомянуты выше в контексте 4-вектора энергии-импульса , но без особого акцента. Действительно, ни один из элементарных выводов специальной теории относительности не требует их. Но как только они поняты, 4-векторы и, в более общем смысле , тензоры значительно упрощают математику и концептуальное понимание специальной теории относительности. Работа исключительно с такими объектами приводит к формулам, которые явно релятивистски инвариантны, что является значительным преимуществом в нетривиальных контекстах. Например, демонстрация релятивистской инвариантности уравнений Максвелла в их обычной форме не является тривиальной, в то время как это всего лишь рутинное вычисление, на самом деле не более чем наблюдение, использующее формулировку тензора напряженности поля . [80]
С другой стороны, общая теория относительности с самого начала в значительной степени опирается на 4-векторы и, в более общем смысле, тензоры, представляющие физически значимые сущности. Связывание их посредством уравнений, которые не опираются на конкретные координаты, требует тензоров, способных связывать такие 4-векторы даже в искривленном пространстве-времени, а не только в плоском , как в специальной теории относительности. Изучение тензоров выходит за рамки этой статьи, которая дает только базовое обсуждение пространства-времени.
Четверка, является «4-вектором», если ее компонент A i преобразуется между кадрами в соответствии с преобразованием Лоренца.
При использовании координат A является 4-вектором , если он преобразуется (в направлении x ) согласно
что получается простой заменой ct на A 0 и x на A 1 в более раннем представлении преобразования Лоренца.
Как обычно, когда мы пишем x , t и т. д., мы обычно подразумеваем Δx , Δt и т. д.
Последние три компонента 4-вектора должны быть стандартным вектором в трехмерном пространстве. Поэтому 4-вектор должен преобразовываться как при преобразованиях Лоренца, а также при вращениях. [81] : 36–59
Как и ожидалось, конечные компоненты вышеуказанных 4-векторов являются стандартными 3-векторами, соответствующими пространственному 3-импульсу , 3-силе и т. д. [21] : 178–181 [81] : 36–59
Первый постулат специальной теории относительности провозглашает эквивалентность всех инерциальных систем отсчета. Физический закон, действующий в одной системе отсчета, должен применяться во всех системах отсчета, поскольку в противном случае можно было бы различать системы отсчета. Ньютоновские импульсы не ведут себя должным образом при преобразованиях Лоренца, и Эйнштейн предпочел изменить определение импульса на определение, включающее 4-векторы , чем отказаться от сохранения импульса.
Физические законы должны быть основаны на конструкциях, которые не зависят от системы отсчета. Это означает, что физические законы могут принимать форму уравнений, связывающих скаляры, которые всегда независимы от системы отсчета. Однако уравнения, включающие 4-векторы, требуют использования тензоров с соответствующим рангом, которые сами по себе могут рассматриваться как построенные из 4-векторов . [21] : 186
Распространено заблуждение, что специальная теория относительности применима только к инерциальным системам и что она не может справиться с ускоряющимися объектами или ускоряющимися системами отсчета. На самом деле, ускоряющиеся объекты можно анализировать, не имея дела с ускоряющимися системами отсчета вообще. Общая теория относительности требуется только тогда, когда гравитация существенна. [82]
Однако правильная работа с ускоряющимися системами отсчета требует некоторой осторожности. Разница между специальной и общей теорией относительности заключается в том, что (1) в специальной теории относительности все скорости относительны, но ускорение абсолютно. (2) в общей теории относительности все движения относительны, будь то инерционные, ускоряющиеся или вращательные. Чтобы учесть это различие, общая теория относительности использует искривленное пространство-время. [82]
В этом разделе мы анализируем несколько сценариев с участием ускоренных систем отсчета.
Парадокс космического корабля Дьюана–Берана–Белла ( парадокс космического корабля Белла ) является хорошим примером проблемы, в которой интуитивные рассуждения без помощи геометрического понимания пространственно-временного подхода могут привести к проблемам.

На рис. 7-4 два одинаковых космических корабля плавают в пространстве и находятся в состоянии покоя относительно друг друга. Они соединены струной, которая способна растягиваться лишь на ограниченное количество единиц, прежде чем разорваться. В заданный момент в нашей системе отсчета, системе отсчета наблюдателя, оба космических корабля ускоряются в одном и том же направлении вдоль линии между ними с одинаковым постоянным собственным ускорением. [примечание 12] Оборвется ли струна?
Когда парадокс был новым и относительно неизвестным, даже профессиональные физики испытывали трудности с решением. Две линии рассуждений приводят к противоположным выводам. Оба аргумента, представленные ниже, ошибочны, хотя один из них дает правильный ответ. [21] : 106, 120–122
Проблема с первым аргументом в том, что не существует «системы отсчета космических кораблей». Не может быть, потому что два космических корабля измеряют растущее расстояние между собой. Поскольку нет общей системы отсчета космических кораблей, длина струны определена неточно. Тем не менее, вывод правильный, и аргумент в основном правильный. Однако второй аргумент полностью игнорирует относительность одновременности. [21] : 106, 120–122
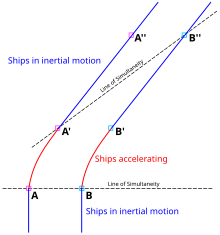
Пространственно-временная диаграмма (рис. 7-5) делает правильное решение этого парадокса почти сразу очевидным. Два наблюдателя в пространстве-времени Минковского ускоряются с постоянной величиной ускорения в течение собственного времени (ускорение и прошедшее время измеряются самими наблюдателями, а не каким-то инерциальным наблюдателем). Они сопутствующие и инерциальные до и после этой фазы. В геометрии Минковского длина вдоль линии одновременности оказывается больше длины вдоль линии одновременности .
Увеличение длины можно рассчитать с помощью преобразования Лоренца. Если, как показано на рис. 7-5, ускорение закончится, то корабли останутся на постоянном смещении в некоторой системе отсчета Если и — положения кораблей в позициях в системе отсчета : [83]
«Парадокс», так сказать, исходит из способа, которым Белл построил свой пример. В обычном обсуждении сокращения Лоренца длина покоя фиксирована, а движущаяся длина сокращается, измеряемая в системе отсчета . Как показано на рис. 7-5, пример Белла утверждает, что движущиеся длины и измеряемые в системе отсчета фиксированы, тем самым заставляя длину покоящейся системы отсчета увеличиваться.
Определенные постановки задач специальной теории относительности могут привести к пониманию явлений, обычно связанных с общей теорией относительности, таких как горизонты событий . В тексте, сопровождающем раздел «Инвариантная гипербола» статьи Пространство-время , пурпурные гиперболы представляли реальные пути, которые отслеживает постоянно ускоряющийся путешественник в пространстве-времени. В периоды положительного ускорения скорость путешественника лишь приближается к скорости света, в то время как, измеренное в нашей системе отсчета, ускорение путешественника постоянно уменьшается.
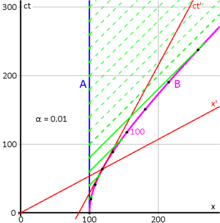
Рис. 7-6 более подробно описывает различные особенности движения путешественника. В любой момент времени ее пространственная ось образована линией, проходящей через начало координат и ее текущее положение на гиперболе, тогда как ее ось времени является касательной к гиперболе в ее положении. Параметр скорости приближается к пределу единицы по мере увеличения. Аналогично, приближается к бесконечности.
Форма инвариантной гиперболы соответствует траектории постоянного собственного ускорения. Это можно продемонстрировать следующим образом:
Рис. 7-6 иллюстрирует конкретный расчетный сценарий. Теренс (A) и Стелла (B) изначально находятся вместе в 100 световых часах от начала координат. Стелла стартует в момент времени 0, ее космический корабль ускоряется со скоростью 0,01 с в час. Каждые двадцать часов Теренс передает Стелле радиосообщения о ситуации дома (сплошные зеленые линии). Стелла получает эти регулярные передачи, но увеличивающееся расстояние (отчасти компенсированное замедлением времени) заставляет ее получать сообщения Теренса все позже и позже, как измерено по ее часам, и она никогда не получает никаких сообщений от Теренса после 100 часов по его часам (пунктирные зеленые линии). [84] : 110–113
Через 100 часов по часам Теренса Стелла попадает в темную область. Она вышла за пределы временного будущего Теренса. С другой стороны, Теренс может продолжать получать сообщения Стеллы к себе бесконечно. Ему просто нужно подождать достаточно долго. Пространство-время разделено на отдельные области, разделенные видимым горизонтом событий. Пока Стелла продолжает ускоряться, она никогда не узнает, что происходит за этим горизонтом. [84] : 110–113
Теоретическое исследование классического электромагнетизма привело к открытию распространения волн. Уравнения, обобщающие электромагнитные эффекты, обнаружили, что конечная скорость распространения полей E и B требует определенного поведения заряженных частиц. Общее изучение движущихся зарядов формирует потенциал Льенара–Вихерта , который является шагом к специальной теории относительности.
Преобразование Лоренца электрического поля движущегося заряда в систему отсчета неподвижного наблюдателя приводит к появлению математического термина, обычно называемого магнитным полем . Наоборот, магнитное поле, создаваемое движущимся зарядом, исчезает и становится чисто электростатическим полем в сопутствующей системе отсчета. Уравнения Максвелла, таким образом, являются просто эмпирической подгонкой к специальным релятивистским эффектам в классической модели Вселенной. Поскольку электрические и магнитные поля зависят от системы отсчета и, таким образом, переплетены, говорят об электромагнитных полях. Специальная теория относительности предоставляет правила преобразования для того, как электромагнитное поле в одной инерциальной системе появляется в другой инерциальной системе.
Уравнения Максвелла в трехмерной форме уже согласуются с физическим содержанием специальной теории относительности, хотя ими легче манипулировать в явно ковариантной форме, то есть на языке тензорного исчисления. [80]
Специальная теория относительности может быть объединена с квантовой механикой для формирования релятивистской квантовой механики и квантовой электродинамики . То, как общая теория относительности и квантовая механика могут быть объединены, является одной из нерешенных проблем в физике ; квантовая гравитация и « теория всего », которые требуют объединения, включающего также общую теорию относительности, являются активными и продолжающимися областями теоретических исследований.
Ранняя атомная модель Бора-Зоммерфельда объясняла тонкую структуру атомов щелочных металлов, используя как специальную теорию относительности, так и предварительные знания квантовой механики того времени. [85]
В 1928 году Поль Дирак построил влиятельное релятивистское волновое уравнение , теперь известное как уравнение Дирака в его честь, [стр. 25], которое полностью совместимо как со специальной теорией относительности, так и с окончательной версией квантовой теории, существовавшей после 1926 года. Это уравнение не только описывало собственный угловой момент электронов, называемый спином , но и привело к предсказанию античастицы электрона ( позитрона ), [стр. 25] [стр. 26] и тонкая структура могла быть полностью объяснена только с помощью специальной теории относительности. Это было первым основанием релятивистской квантовой механики .
С другой стороны, существование античастиц приводит к выводу, что релятивистской квантовой механики недостаточно для более точной и полной теории взаимодействия частиц. Вместо этого становится необходимой теория частиц, интерпретируемых как квантованные поля, называемая квантовой теорией поля ; в которой частицы могут создаваться и уничтожаться в пространстве и времени.
Специальная теория относительности в ее пространстве-времени Минковского точна только тогда, когда абсолютное значение гравитационного потенциала намного меньше c 2 в интересующей области. [86] В сильном гравитационном поле необходимо использовать общую теорию относительности . Общая теория относительности становится специальной теорией относительности на пределе слабого поля. В очень малых масштабах, таких как длина Планка и ниже, необходимо учитывать квантовые эффекты, приводящие к квантовой гравитации . Но в макроскопических масштабах и при отсутствии сильных гравитационных полей специальная теория относительности экспериментально проверена с чрезвычайно высокой степенью точности (10 −20 ) [87] и, таким образом, принята физическим сообществом. Экспериментальные результаты, которые кажутся противоречащими ей, не воспроизводимы и, таким образом, широко считаются вызванными экспериментальными ошибками. [88]
Специальная теория относительности математически самосогласована и является органической частью всех современных физических теорий, в первую очередь квантовой теории поля , теории струн и общей теории относительности (в предельном случае пренебрежимо малых гравитационных полей).
Ньютоновская механика математически следует из специальной теории относительности при малых скоростях (по сравнению со скоростью света) – таким образом, ньютоновскую механику можно рассматривать как специальную теорию относительности медленно движущихся тел. Более подробное обсуждение см. в классической механике .
Несколько экспериментов, предшествовавших статье Эйнштейна 1905 года, теперь интерпретируются как доказательства относительности. Из них известно, что Эйнштейн знал об эксперименте Физо до 1905 года, [89] и историки пришли к выводу, что Эйнштейн, по крайней мере, знал об эксперименте Майкельсона-Морли еще в 1899 году, несмотря на заявления, которые он делал в последние годы, что эксперимент не играл никакой роли в развитии его теории. [16]
Ускорители частиц ускоряют и измеряют свойства частиц, движущихся со скоростью, близкой к скорости света, где их поведение согласуется с теорией относительности и не согласуется с более ранней ньютоновской механикой . Эти машины просто не работали бы, если бы они не были спроектированы в соответствии с релятивистскими принципами. Кроме того, было проведено значительное количество современных экспериментов для проверки специальной теории относительности. Вот несколько примеров:

Специальная теория относительности использует «плоское» 4-мерное пространство Минковского – пример пространства- времени . Пространство-время Минковского, по-видимому, очень похоже на стандартное 3-мерное евклидово пространство , но есть принципиальное различие в отношении времени.
В трехмерном пространстве дифференциал расстояния (линейный элемент) ds определяется как где d x = ( dx 1 , dx 2 , dx 3 ) — дифференциалы трех пространственных измерений. В геометрии Минковского существует дополнительное измерение с координатой X 0 , полученное из времени, так что дифференциал расстояния удовлетворяет где d X = ( dX 0 , dX 1 , dX 2 , dX 3 ) — дифференциалы четырех измерений пространства-времени. Это предполагает глубокое теоретическое понимание: специальная теория относительности — это просто вращательная симметрия нашего пространства-времени, аналогичная вращательной симметрии евклидова пространства (см. рис. 10-1). [91] Так же, как евклидово пространство использует евклидову метрику , так и пространство-время использует метрику Минковского .По сути, специальная теория относительности может быть сформулирована как инвариантность любого интервала пространства-времени (то есть 4-мерного расстояния между любыми двумя событиями) при наблюдении из любой инерциальной системы отсчета . Все уравнения и эффекты специальной теории относительности могут быть выведены из этой вращательной симметрии ( группы Пуанкаре ) пространства-времени Минковского.
Фактическая форма ds выше зависит от метрики и от выбора координаты X 0 . Чтобы временная координата выглядела как пространственные координаты, ее можно рассматривать как мнимую : X 0 = ict (это называется вращением Вика ). Согласно Мизнеру, Торну и Уилеру (1971, §2.3), в конечном счете более глубокое понимание как специальной, так и общей теории относительности придет из изучения метрики Минковского (описанной ниже) и взятия X 0 = ct , а не «замаскированной» евклидовой метрики, использующей ict в качестве временной координаты.
Некоторые авторы используют X 0 = t , с множителями c в других местах для компенсации; например, пространственные координаты делятся на c или множители c ±2 включаются в метрический тензор. [92] Эти многочисленные соглашения могут быть заменены использованием естественных единиц , где c = 1 . Тогда пространство и время имеют эквивалентные единицы, и множители c нигде не появляются.

Если мы уменьшим пространственные измерения до 2, так чтобы мы могли представить физику в трехмерном пространстве, мы увидим, что нулевые геодезические лежат вдоль двойного конуса (см. рис. 10-2), определяемого уравнением; или, проще говоря , которое является уравнением окружности радиуса c dt .
Если мы расширим это до трех пространственных измерений, то нулевые геодезические будут четырехмерным конусом: так что

Как показано на рис. 10-3, нулевые геодезические можно визуализировать как набор непрерывных концентрических сфер с радиусами = c dt .
Этот нулевой двойной конус представляет собой «линию видимости» точки в пространстве. То есть, когда мы смотрим на звезды и говорим «Свет от этой звезды, который я получаю, имеет возраст X лет», мы смотрим вдоль этой линии видимости: нулевой геодезической. Мы смотрим на событие, находящееся на расстоянии и во времени d/c в прошлом. По этой причине нулевой двойной конус также известен как «световой конус». (Точка в левом нижнем углу рис. 10-2 представляет собой звезду, начало координат представляет собой наблюдателя, а линия представляет собой нулевую геодезическую «линию видимости».)
Конус в области −t — это информация, которую точка «принимает», тогда как конус в области + t — это информация, которую точка «отправляет».
Геометрию пространства Минковского можно изобразить с помощью диаграмм Минковского , которые также полезны для понимания многих мысленных экспериментов в специальной теории относительности.
Выше, преобразование Лоренца для временной координаты и трех пространственных координат иллюстрирует, что они переплетены. Это верно в более общем смысле: определенные пары «временеподобных» и «пространственноподобных» величин естественным образом объединяются на равных основаниях под одним и тем же преобразованием Лоренца.
Преобразование Лоренца в стандартной конфигурации, представленное выше, то есть для усиления в направлении x , можно преобразовать в матричную форму следующим образом:
В ньютоновской механике величины, имеющие величину и направление, математически описываются как 3d-векторы в евклидовом пространстве, и в общем случае они параметризуются временем. В специальной теории относительности это понятие расширяется путем добавления соответствующей времениподобной величины к пространственноподобной векторной величине, и мы имеем 4d-векторы или « четырехмерные векторы » в пространстве-времени Минковского. Компоненты векторов записываются с использованием индексной нотации тензора , поскольку это имеет многочисленные преимущества. Эта нотация ясно показывает, что уравнения явно ковариантны относительно группы Пуанкаре , тем самым обходя утомительные вычисления для проверки этого факта. При построении таких уравнений мы часто обнаруживаем, что уравнения, которые ранее считались не связанными, на самом деле тесно связаны, являясь частью одного и того же тензорного уравнения. Распознавание других физических величин как тензоров упрощает их законы преобразования. Везде верхние индексы (надстрочные индексы) являются контравариантными индексами, а не показателями степени, за исключением случаев, когда они указывают на квадрат (это должно быть ясно из контекста), а нижние индексы (подстрочные индексы) являются ковариантными индексами. Для простоты и согласованности с предыдущими уравнениями будут использоваться декартовы координаты.
Простейшим примером 4-вектора является положение события в пространстве-времени, которое составляет времениподобную компоненту ct и пространственноподобную компоненту x = ( x , y , z ) , в контравариантном позиционном 4-векторе с компонентами: где мы определяем X 0 = ct так, чтобы временная координата имела ту же размерность расстояния, что и другие пространственные измерения; так что пространство и время рассматриваются одинаково. [93] [94] [95] Теперь преобразование контравариантных компонент позиционного 4-вектора можно компактно записать как: где подразумевается суммирование от 0 до 3, а является матрицей .
В более общем случае все контравариантные компоненты четырехвектора преобразуются из одной системы отсчета в другую с помощью преобразования Лоренца :
Примерами других 4-векторов являются 4-скорость, определяемая как производная 4-вектора положения по собственному времени : где фактор Лоренца равен:
Релятивистская энергия и релятивистский импульс объекта являются соответственно времениподобной и пространственноподобной компонентами контравариантного вектора четырехимпульса : где m — инвариантная масса .
Четырехкратное ускорение является собственной производной по времени от четырехкратной скорости:
Правила преобразования для трехмерных скоростей и ускорений очень неуклюжи; даже выше в стандартной конфигурации уравнения скорости довольно сложны из-за их нелинейности. С другой стороны, преобразование четырех -скорости и четырех -ускорения проще с помощью матрицы преобразования Лоренца.
Четырехградиентное скалярное поле φ преобразуется ковариантно, а не контравариантно: что является транспонированием: только в декартовых координатах. Это ковариантная производная , которая преобразуется в явной ковариантности, в декартовых координатах это происходит , сводясь к частным производным, но не в других координатах.
В более общем случае ковариантные компоненты 4-векторного преобразования в соответствии с обратным преобразованием Лоренца: где — обратная матрица .
Постулаты специальной теории относительности ограничивают точную форму матриц преобразования Лоренца.
В более общем смысле большинство физических величин лучше всего описывать как (компоненты) тензоров . Поэтому для преобразования из одной системы отсчета в другую мы используем известный закон преобразования тензора [96] , где — обратная матрица . Все тензоры преобразуются по этому правилу.
Примером четырехмерного антисимметричного тензора второго порядка является релятивистский момент импульса , который имеет шесть компонент: три из них являются классическим моментом импульса , а остальные три связаны с усилением центра масс системы. Производная релятивистского момента импульса по собственному времени — релятивистский момент силы, также антисимметричный тензор второго порядка .
Тензор электромагнитного поля — это еще одно антисимметричное тензорное поле второго порядка с шестью компонентами: три для электрического поля и еще три для магнитного поля . Существует также тензор энергии-импульса для электромагнитного поля, а именно тензор энергии-импульса электромагнитного поля .
Метрический тензор позволяет определить внутреннее произведение двух векторов, что в свою очередь позволяет присвоить вектору величину. Учитывая четырехмерную природу пространства-времени, метрика Минковского η имеет компоненты (действительные с соответствующим образом выбранными координатами), которые можно расположить в матрице 4 × 4 : которая равна своей обратной величине, , в этих системах отсчета. Везде мы используем знаки, как указано выше, разные авторы используют разные соглашения – см. альтернативные знаки метрики Минковского .
Группа Пуанкаре — это наиболее общая группа преобразований, которая сохраняет метрику Минковского: это физическая симметрия, лежащая в основе специальной теории относительности.
Метрика может быть использована для повышения и понижения индексов векторов и тензоров. Инварианты могут быть построены с использованием метрики, скалярное произведение 4-вектора T с другим 4-вектором S равно:
Инвариант означает, что он принимает одно и то же значение во всех инерциальных системах отсчета, поскольку является скаляром (тензором ранга 0), и поэтому в его тривиальном преобразовании не появляется Λ . Величина 4-вектора T является положительным квадратным корнем внутреннего произведения с самим собой:
Эту идею можно распространить на тензоры более высокого порядка, для тензора второго порядка мы можем сформировать инварианты: аналогично для тензоров более высокого порядка. Инвариантные выражения, в частности, внутренние произведения 4-векторов с самими собой, дают уравнения, которые полезны для вычислений, поскольку для определения инвариантов не требуется выполнять преобразования Лоренца.
Координатные дифференциалы преобразуются также контравариантно: так что квадрат длины дифференциала позиционного четырехвектора dX μ, построенного с использованием, является инвариантом. Обратите внимание, что когда элемент линии d X 2 отрицателен, то √ − d X 2 является дифференциалом собственного времени , тогда как когда d X 2 положителен, то √ d X 2 является дифференциалом собственного расстояния .
4-скорость U μ имеет инвариантную форму: что означает, что все 4-векторы скорости имеют величину c . Это выражение того факта, что в теории относительности не существует такого понятия, как нахождение в координатном покое: по крайней мере, вы всегда движетесь вперед во времени. Дифференцирование приведенного выше уравнения по τ дает: Таким образом, в специальной теории относительности 4-вектор ускорения и 4-вектор скорости ортогональны.
Инвариантная величина 4-вектора импульса порождает соотношение энергия-импульс :
Мы можем выяснить, что представляет собой этот инвариант, сначала предположив, что, поскольку он является скаляром, не имеет значения, в какой системе отсчета мы его вычисляем, а затем выполнив преобразование в систему, в которой полный импульс равен нулю.
Мы видим, что энергия покоя является независимым инвариантом. Энергию покоя можно вычислить даже для частиц и систем в движении, переведя ее в систему отсчета, в которой импульс равен нулю.
Энергия покоя связана с массой согласно знаменитому уравнению, рассмотренному выше:
Масса систем, измеренная в их системе отсчета центра импульса (где полный импульс равен нулю), определяется полной энергией системы в этой системе отсчета. Она может не быть равна сумме масс отдельных систем, измеренных в других системах отсчета.
Чтобы использовать третий закон движения Ньютона , обе силы должны быть определены как скорость изменения импульса относительно одной и той же временной координаты. То есть, требуется 3D-сила, определенная выше. К сожалению, в 4D нет тензора, который содержал бы компоненты 3D-вектора силы среди своих компонентов.
Если частица не движется со скоростью c , можно преобразовать 3D-силу из сопутствующей системе отсчета частицы в систему отсчета наблюдателя. Это дает 4-вектор, называемый 4-силой . Это скорость изменения вышеуказанного 4-вектора энергии-импульса относительно собственного времени. Ковариантная версия 4-силы:
В системе покоя объекта временная составляющая 4-силы равна нулю, если только не изменяется « инвариантная масса » объекта (для этого требуется незамкнутая система, в которой энергия/масса напрямую добавляется или удаляется из объекта), в этом случае она равна отрицательной скорости изменения массы, умноженной на c . Однако в общем случае компоненты 4-силы не равны компонентам 3-силы, поскольку 3-сила определяется скоростью изменения импульса относительно координатного времени, то есть dp / dt , в то время как 4-сила определяется скоростью изменения импульса относительно собственного времени, то есть dp / dτ .
В непрерывной среде 3D- плотность силы объединяется с плотностью мощности , образуя ковариантный 4-вектор. Пространственная часть является результатом деления силы на небольшой ячейке (в 3-пространстве) на объем этой ячейки. Временная составляющая равна −1/ c , умноженной на мощность, переданную этой ячейке, деленную на объем ячейки. Это будет использовано ниже в разделе об электромагнетизме.
{{cite book}}: CS1 maint: multiple names: authors list (link)