
В развлекательной математике квадратный массив чисел, обычно положительных целых чисел , называется магическим квадратом , если суммы чисел в каждой строке, каждом столбце и обеих главных диагоналях одинаковы. [1] [2] «Порядок» магического квадрата — это количество целых чисел вдоль одной стороны ( n ), а постоянная сумма называется « магической константой ». Если массив включает только положительные целые числа , магический квадрат называется «нормальным». Некоторые авторы считают, что магический квадрат означает обычный магический квадрат. [3]
Магические квадраты, включающие повторяющиеся записи, не подпадают под это определение и называются «тривиальными». Некоторые известные примеры, в том числе магический квадрат Саграда Фамилия и площадь Паркера, в этом смысле тривиальны. Когда все строки и столбцы, но не обе диагонали, суммируются с магической константой, это дает полумагический квадрат (иногда называемый ортомагическим квадратом ).
Математическое исследование магических квадратов обычно связано с их построением, классификацией и перечислением. Хотя совершенно общих методов создания всех магических квадратов всех порядков не существует, исторически были открыты три общих метода: метод окантовки, создание составных магических квадратов и добавление двух предварительных квадратов. Существуют также более конкретные стратегии, такие как метод непрерывного подсчета, который воспроизводит определенные закономерности. Магические квадраты обычно классифицируются в соответствии с их порядком n : нечетные, если n нечетное, четно-четные (также называемые «дважды четными»), если n кратно 4, нечетно-четные (также известные как «единственно-четные»), если n — любое другое четное число. Эта классификация основана на различных методах, необходимых для построения нечетных, четных и нечетных квадратов. Кроме того, в зависимости от дополнительных свойств магические квадраты также классифицируются на ассоциативные магические квадраты , пандиагональные магические квадраты , наиболее совершенные магические квадраты и так далее. Еще сложнее то, что были также предприняты попытки классифицировать все магические квадраты данного порядка как преобразования меньшего набора квадратов. За исключением n ≤ 5, перечисление магических квадратов более высокого порядка все еще остается открытой проблемой. Перечисление наиболее совершенных магических квадратов любого порядка было осуществлено только в конце 20 века.
Магические квадраты имеют долгую историю, начиная с 190 г. до н.э. в Китае. В разное время они приобретали оккультное или мифическое значение и выступали в качестве символов в произведениях искусства. В наше время они были обобщены несколькими способами, включая использование дополнительных или других ограничений, умножение вместо добавления ячеек, использование альтернативных форм или более двух измерений, а также замену чисел фигурами и сложение геометрическими операциями.

.jpg/440px-Albrecht_Dürer_-_Melencolia_I_(detail).jpg)

Магический квадрат третьего порядка был известен китайским математикам еще в 190 г. до н.э. и явно определен в первом веке нашей эры. Первый датируемый случай магического квадрата четвертого порядка произошел в 587 году нашей эры в Индии. Образцы магических квадратов от 3 до 9 появляются в энциклопедии из Багдада ок. 983 , Энциклопедия Братьев Чистоты ( Расаил Ихван ас-Сафа ). К концу XII века были хорошо известны общие методы построения магических квадратов. Примерно в это же время некоторые из этих квадратов все чаще использовались в сочетании с магическими буквами, как в Шамс Аль-Маариф , в оккультных целях. [4] В Индии все пандиагональные магические квадраты четвертого порядка были перечислены Нараяной в 1356 году. Магические квадраты стали известны Европе благодаря переводу арабских источников как оккультные объекты в эпоху Возрождения, и общую теорию пришлось открыть заново. независимо от предшествующих событий в Китае, Индии и на Ближнем Востоке. Также примечательны древние культуры с традициями математики и нумерологии, которые не открыли магические квадраты: греки, вавилоняне, египтяне и американцы доколумбовой эпохи.

В то время как древние упоминания о порядке четных и нечетных чисел в магическом квадрате 3×3 появляются в « И Цзин» , первый недвусмысленный пример этого магического квадрата появляется в главе под названием Минтан (Светлый зал) книги Да Дай I века. Лицзи («Запись обрядов Старейшины Дая»), в которой якобы описываются древние китайские обряды династии Чжоу. [5] [6] [7] [8] Эти числа также встречаются, возможно, в более раннем математическом тексте под названием Шушу джии («Воспоминания о некоторых традициях математического искусства»), который, как говорят, был написан в 190 году до нашей эры. Это самое раннее зарегистрированное появление магического квадрата; и в основном его использовали для гадания и астрологии. [5] Магический квадрат 3×3 ранние китайские математики называли «Девять залов». [7] Идентификация магического квадрата 3×3 с легендарной картой Луошу была сделана только в 12 веке, после чего его стали называть квадратом Луошу. [5] [7] Самый старый сохранившийся китайский трактат, в котором показаны магические квадраты порядка больше 3, - это « Сюгу чжэци суаньфа » Ян Хуэя ( «Продолжение древних математических методов объяснения странного»), написанный в 1275 году. [5] [ 7] содержание трактата Ян Хуэя было собрано из более старых работ, как отечественных, так и зарубежных; и он лишь объясняет построение магических квадратов третьего и четвертого порядка, просто передавая готовые диаграммы более крупных квадратов. [7] Он дает магический квадрат третьего порядка, два квадрата на каждый порядок от 4 до 8, один девятого порядка и один полумагический квадрат 10-го порядка. Он также дает шесть магических кругов различной сложности. [9]
Приведенные выше магические квадраты порядков с 3 по 9 взяты из трактата Ян Хуэя, в котором отчетливо проявляется принцип Ло Шу. [7] [8] Квадрат 5-го порядка представляет собой магический квадрат с окантовкой, центральный квадрат 3×3 сформирован в соответствии с принципом Ло Шу. Квадрат 9-го порядка представляет собой составной магический квадрат, в котором девять дополнительных квадратов 3×3 также являются магическими. [7] После Ян Хуэя магические квадраты часто встречаются в китайской математике, например, в «Даян суойинь» Дин Идуна ( ок . 1300 г. ), «Суаньфа тунцзонг » Чэн Давэя (1593 г.), « Шудуянь » Фан Чжунтуна (1661 г.), в которой содержатся магические круги, кубы и сферы, « Синьчжай дзазу » Чжан Чао ( ок. 1650 г. ), опубликовавший первый в Китае магический квадрат десятого порядка, и, наконец, « Бинайшаньфан цзи » Бао Цишоу ( ок. 1880 г. ), который дал различные трехмерные магические конфигурации. [5] [8] Однако, несмотря на то, что Китай первым открыл магические квадраты и получил фору на несколько столетий, китайское развитие магических квадратов намного уступает развитию Индии, Ближнего Востока или Европы. Высшая точка китайской математики, связанная с магическими квадратами, по-видимому, заключена в работах Ян Хуэя; но даже будучи собранием более старых методов, эта работа гораздо более примитивна, лишена общих методов построения магических квадратов любого порядка, по сравнению с аналогичным сборником, написанным примерно в то же время византийским учёным Мануэлем Мосхопулосом . [7] Возможно, это связано с увлечением китайских ученых принципом Ло Шу, который они пытались адаптировать для решения более высоких квадратов; и после Ян Хуэя и падения династии Юань , их систематическое очищение от иностранного влияния в китайской математике. [7]
Япония и Китай имеют схожие математические традиции и неоднократно влияли друг на друга в истории магических квадратов. [10] Интерес японцев к магическим квадратам начался после распространения китайских работ — « Суаньфа » Ян Хуэя и «Суанфа тунцзун » Чэна Давэя — в 17 веке, и в результате почти все васаны посвятили свое время его изучению.
В издании «Кецуги-сё» 1660 года Исомура Киттоку представил как нечетные, так и четные магические квадраты с границами, а также магические круги; в то время как издание той же книги 1684 года содержало большой раздел, посвященный магическим квадратам, демонстрирующий, что у него был общий метод построения магических квадратов с рамкой. [11] В «Дзинко-ки» (1665) Мурамацу Кудаю Мосея показаны как магические квадраты, так и магические круги. Самая большая квадратная конструкция Моисея относится к 19-му порядку. Различные магические квадраты и магические круги были также опубликованы Нодзава Тейчо в «Докай-сё» (1666 г.), Сато Сэйко в «Конгенки» (1666 г.) и Хосино Санэнобу в « Ко-ко-ген сё» (1673 г.). [12] Одна из семи книг Сэки Такакадзу ( Ходзин Йенсан ) (1683) полностью посвящена магическим квадратам и кругам. Это первая японская книга, в которой дается общее описание магических квадратов, в которой четко описаны алгоритмы построения нечетных, однократно-четных и дважды-четных магических квадратов. [13] В 1694 и 1695 годах Юэки Андо предложил различные методы создания магических квадратов и отобразил квадраты от 3 до 30. Магический куб четвертого порядка был построен Ёсидзанэ Танакой (1651–1719) в Ракусё-кикан (1683). . Изучение магических квадратов было продолжено учениками Секи, в частности Катахиро Такэбе, чьи квадраты были показаны в четвертом томе « Ичиген Каппо» Сюкеем Ирие, Ёсисуке Мацунага в «Ходзин-Син-дзюцу» , Ёсихиро Курушима в «Кюси Ико» , который заново открыл метод создайте нечетные квадраты, данные Агриппой [14] и Наонобу Адзимой . [15] [16] Таким образом, к началу 18 века японские математики владели методами построения магических квадратов произвольного порядка. После этого попытки подсчета магических квадратов были предприняты Нусидзуми Ямаджи. [16]

Магический квадрат 3х3 впервые появляется в Индии в «Гаргасамхите » Гарги, который рекомендует использовать его для умиротворения девяти планет ( наваграха ). Самая старая версия этого текста датируется 100 г. н.э., но отрывок о планетах не мог быть написан ранее 400 г. н.э. Первый датируемый случай магического квадрата 3×3 в Индии встречается в медицинском тексте « Сиддхайог» ( ок. 900 г. н.э. ) Вринды, который прописывался роженицам для облегчения родов. [17]
Самый старый датируемый магический квадрат четвертого порядка в мире найден в энциклопедическом труде, написанном Варахамихирой около 587 года нашей эры, под названием «Брихат Самхита» . Магический квадрат создан для создания духов с использованием 4 веществ, выбранных из 16 различных веществ. Каждая ячейка квадрата представляет определенный ингредиент, а число в ячейке представляет пропорцию соответствующего ингредиента, так что смесь любых четырех комбинаций ингредиентов по столбцам, строкам, диагоналям и т. д. дает общий объем. смеси — 18. Хотя книга в основном посвящена гаданию, магический квадрат дан в результате комбинаторного замысла, и ему не приписываются никакие магические свойства. Особенности этого магического квадрата были прокомментированы Бхаттотпалой ( ок. 966 г. н. э. ) [18] [17]
Сумма квадрата Варахамихиры, как указано выше, равна 18. Здесь числа от 1 до 8 встречаются в квадрате дважды. Это пандиагональный магический квадрат . Четыре разных магических квадрата можно получить, добавив 8 к одному из двух наборов последовательностей от 1 до 8. Последовательность выбрана такая, чтобы число 8 добавлялось ровно два раза в каждой строке, каждом столбце и каждой из главных диагоналей. Один из возможных магических квадратов показан справа. Этот магический квадрат примечателен тем, что представляет собой поворот на 90 градусов магического квадрата, который в исламском мире 13 века является одним из самых популярных магических квадратов. [19]
Построение магического квадрата 4-го порядка подробно описано в работе под названием « Какшапута» , написанной алхимиком Нагарджуной около 10 века нашей эры. Все квадраты, данные Нагарджуной, представляют собой магические квадраты 4×4, и один из них назван в его честь Нагарджуной . Нагарджуна предложил метод построения магического квадрата 4×4 с использованием основного скелетного квадрата по нечетной или четной магической сумме. [18] Ниже приведен квадрат Нагарджуния, его общая сумма равна 100.
Квадрат Нагарджуния представляет собой пандиагональный магический квадрат . Квадрат Нагарджунии состоит из двух арифметических прогрессий, начинающихся с 6 и 16, по восемь членов в каждой, с общей разницей между последовательными членами, равной 4. Когда эти две прогрессии сводятся к нормальной прогрессии от 1 до 8, получается соседний квадрат. .
Примерно в 12 веке на стене храма Паршванатх в Кхаджурахо , Индия , был начертан магический квадрат 4×4 . Несколько джайнских гимнов учат, как составлять магические квадраты, хотя датировать их невозможно. [17]
Насколько известно, первое систематическое исследование магических квадратов в Индии было проведено Тхаккаром Феру , джайнским ученым, в его работе «Ганитасара Каумуди» (ок. 1315 г.). Эта работа содержит небольшой раздел о магических квадратах, состоящий из девяти стихов. Здесь он дает квадрат четвертого порядка и намекает на его перестановку; классифицирует магические квадраты на три (нечетные, четные и нечетные) в соответствии с их порядком; дает квадрат шестого порядка; и предписывает по одному методу построения четных и нечетных квадратов. Для четных квадратов Феру делит квадрат на составляющие квадраты четвертого порядка и помещает числа в ячейки по образцу стандартного квадрата четвертого порядка. Для нечетных полей Феру предлагает метод, использующий ход коня или ход коня . Хотя алгоритмически он отличается, он дает тот же квадрат, что и метод Де ла Лубера. [17]
Следующий всеобъемлющий труд о магических квадратах был предпринят Нараяной Пандитом , который в четырнадцатой главе своей «Ганиты Каумуди» (1356 г.) дает общие методы их построения, а также принципы, управляющие такими построениями. Он состоит из 55 стихов правил и 17 стихов примеров. Нараяна дает метод построения всех панмагических квадратов четвертого порядка с помощью хода коня; перечисляет количество пандиагональных магических квадратов четвертого порядка, 384, включая все вариации, созданные вращением и отражением; три общих метода для квадратов любого порядка и постоянной суммы, когда известен стандартный квадрат того же порядка; по два метода построения четно-четных, нечетно-четных и квадратов при заданной сумме. Хотя Нараяна описывает один более старый метод для каждого вида квадратов, он утверждает, что метод суперпозиции для четных и нечетных квадратов и метод перестановки нечетно-четных квадратов являются его собственным изобретением. Позднее метод суперпозиции был вновь открыт Де ла Гиром в Европе. В последнем разделе он представляет себе другие фигуры, такие как круги, прямоугольники и шестиугольники, в которых числа можно расположить так, чтобы они обладали свойствами, подобными свойствам магических квадратов. [18] [17] Ниже приведены некоторые магические квадраты, построенные Нараяной: [18]
Квадрат восьмого порядка интересен сам по себе, поскольку является примером наиболее совершенного магического квадрата. Между прочим, Нараяна утверждает, что цель изучения магических квадратов — построить янтру , разрушить эго плохих математиков и доставить удовольствие хорошим математикам. Тема магических квадратов называется бхадраганита , и Нараяна утверждает, что впервые этому человеку научил бог Шива . [17]

Хотя ранняя история магических квадратов в Персии и Аравии неизвестна, предполагается, что они были известны еще в доисламские времена. [20] Однако ясно, что изучение магических квадратов было обычным явлением в средневековом исламе , и считалось, что оно началось после появления шахмат в регионе. [21] [22] [23] Первое датируемое появление магического квадрата 3-го порядка встречается в книге Джабира ибн Хайяна (ок. 721 – ок. 815) «Китаб аль-мавазин ас-Сагир» («Маленькая книга Balances), где магический квадрат и связанная с ним нумерология связаны с алхимией. [8] Хотя известно, что трактаты о магических квадратах были написаны в 9 веке, самые ранние из сохранившихся договоров датируются 10 веком: один Абуль -Вафа аль-Бузджани ( ок. 998 г. ), а другой Али б. . Ахмад аль-Антаки ( ок. 987 ). [22] [24] [25] Эти ранние трактаты были чисто математическими, а арабское обозначение используемых магических квадратов - вафк аль-адад , что переводится как гармоничное расположение чисел . [23] К концу X века в двух трактатах Бузджани и Антаки становится ясно, что математики Ближнего Востока поняли, как строить квадраты с рамкой любого порядка, а также простые магические квадраты малых порядков ( n ≤ 6), которые использовались для составления составных магических квадратов. [22] [24] Образец магических квадратов 3-9 порядков, разработанных ближневосточными математиками, появляется в энциклопедии из Багдада ок. 983 , Расаил Ихван ас-Сафа ( Энциклопедия Братьев Чистоты ). [26] Ниже приведены квадраты порядка 3–7 от Расаила: [26]
В 11 веке было обнаружено несколько способов построения простых магических квадратов нечетного и четно-четного порядков; более сложный случай равномерно-нечетного случая ( n = 4k + 2 ) был решен Ибн аль-Хайсамом с k четным (ок. 1040 г.) и полностью к началу 12 века, если не уже во второй половине 11 век. [22] Примерно в то же время строились пандиагональные площади. Договоры о магических квадратах были многочисленными в 11 и 12 веках. Эти более поздние разработки, как правило, представляли собой улучшения или упрощения существующих методов. Начиная с 13 века, магические квадраты все чаще использовались в оккультных целях. [22] Однако большая часть этих более поздних текстов, написанных для оккультных целей, просто изображают определенные магические квадраты и упоминают их атрибуты, не описывая принцип их построения, и лишь некоторые авторы поддерживают общую теорию. [22] Одним из таких оккультистов был алжирец Ахмад аль-Буни (ок. 1225 г.), который дал общие методы построения магических квадратов с границами; некоторыми другими были египтянин Шабрамаллиси 17 века и нигериец аль-Кишнави 18 века. [27]
Магический квадрат третьего порядка описывался как амулет для деторождения [28] [29] с момента его первого литературного появления в алхимических трудах Джабира ибн Хайяна (ок. 721 – ок. 815) [29] [30] и аль-Газали (1058–1111) [31] и сохранилось в традиции планетарных таблиц. Самое раннее упоминание о связи семи магических квадратов с достоинствами семи небесных тел встречается в книге андалузского ученого Ибн Заркали (известного в Европе как Азаркиэль) (1029–1087) «Китаб тадбират аль-кавакиб» ( «Книга о влиянии небесных тел»). Планеты ). [32] Столетие спустя алжирский учёный Ахмад аль-Буни приписал мистические свойства магическим квадратам в своей весьма влиятельной книге Шамс аль-Маариф ( «Книга Солнца гнозиса и тонкости возвышенных вещей »), в которой также описывается их строительство. Эта традиция о серии магических квадратов от третьего до девятого порядка, связанных с семью планетами, сохранилась в греческой, арабской и латинской версиях. [33] Есть также упоминания об использовании магических квадратов в астрологических расчетах, практика, которая, по-видимому, возникла у арабов. [34] [35]

В отличие от Персии и Аравии, существует более подробная документация о том, как магические квадраты были переданы в Европу. Около 1315 года под влиянием арабских источников греческий византийский ученый Мануэль Мосхопулос написал математический трактат на тему магических квадратов, оставив без внимания мистицизм своих ближневосточных предшественников, где он предложил два метода для нечетных квадратов и два метода для четных квадратов. . Мосхопулос был практически неизвестен в Латинской Европе до конца 17 века, когда Филипп де ла Гир заново открыл свой трактат в Королевской библиотеке Парижа. [36] Однако он не был первым европейцем, писавшим на магических квадратах; а магические квадраты распространились по остальной Европе через Испанию и Италию как оккультные предметы. Ранние оккультные договоры, в которых были изображены квадраты, не описывали, как они были построены. Таким образом, всю теорию пришлось открыть заново.
Магические квадраты впервые появились в Европе в Китаб тадбират аль-кавакиб ( «Книга о влиянии планет »), написанной Ибн Заркали из Толедо, Аль-Андалус, как планетарные квадраты к 11 веку. [32] Магический квадрат трёх обсуждался в нумерологической манере в начале 12 века еврейским учёным Авраамом ибн Эзрой из Толедо, оказавшим влияние на более поздних каббалистов. [37] Работа Ибн Заркали была переведена как «Libro de Astromagia» в 1280-х годах, [38] благодаря Альфонсо X Кастильскому. [39] [32] В тексте Альфонсина магические квадраты разных порядков присвоены соответствующим планетам, как и в исламской литературе; к сожалению, из всех обсуждаемых квадратов магический квадрат Марса пятого порядка — единственный квадрат, представленный в рукописи. [40] [32]
Магические квадраты снова появляются во Флоренции, Италия, в 14 веке. Квадраты 6×6 и 9×9 представлены в рукописи « Траттато д'Аббако» (Трактат о счетах) Паоло Дагомари . [41] [42] Интересно отметить, что Паоло Дагомари, как и Пачоли после него, называет квадраты полезной основой для изобретения математических вопросов и игр и не упоминает о каком-либо магическом использовании. Между прочим, однако, он также называет их квадратами Солнца и Луны соответственно и упоминает, что они входят в астрологические расчеты, которые не являются более точными. Как уже говорилось, та же точка зрения, по-видимому, мотивирует флорентийца Луку Пачоли , который в конце 15 века описывает квадраты от 3×3 до 9×9 в своей работе De Viribus Quantitatis . [43] [44]

К концу 15 века планетарные квадраты распространились по Северной Европе. Например, в краковской рукописи Пикатрикса из Польши показаны магические квадраты порядков с 3 по 9. Тот же набор квадратов, что и в краковской рукописи, позже появляется в трудах Парацельса в Archidoxa Magica (1567), хотя и в сильно искаженной форме. В 1514 году Альбрехт Дюрер увековечил квадрат 4×4 на своей знаменитой гравюре «Меланхолия I» . Современник Парацельса Генрих Корнелиус Агриппа фон Неттесгейм опубликовал в 1531 году свою знаменитую трехтомную книгу «Оккультная философия» , где посвятил главу 22 книги II квадратам планет, показанным ниже. [37] Тот же набор квадратов, данный Агриппой, снова появляется в 1539 году в « Практике арифметики» Джироламо Кардано , где он объясняет построение нечетно упорядоченных квадратов с использованием «метода ромба», который позже был воспроизведен Баше. [45] Традиция планетарных квадратов была продолжена в 17 веке Афанасием Кирхером в «Эдипах Египта» (1653). В Германии математические трактаты о магических квадратах были написаны в 1544 году Михаэлем Стифелем в «Арифметике Интегра» , который заново открыл квадраты с рамкой, и Адамом Ризе , который заново открыл метод непрерывной нумерации для построения нечетных упорядоченных квадратов, опубликованный Агриппой. Однако из-за религиозных потрясений того времени эти работы были неизвестны остальной Европе. [37]
В 1624 году во Франции Клод Гаспар Баше описал «алмазный метод» построения нечетных упорядоченных квадратов Агриппы в своей книге « Problèmes Plaisants» . В 1640 году Бернар Френикль де Бесси и Пьер Ферма обменялись буквами о магических квадратах и кубах, и в одном из писем Ферма хвастается, что смог построить своим методом 1 004 144 995 344 магических квадрата восьмого порядка. [45] Ранний отчет о строительстве квадратов с границами был дан Антуаном Арно в его «Новых элементах геометрии» (1667). [46] В двух трактатах «Des Quarrez ou Tables magiques» и «Table générale des Quarrez magiques de Quatre de Côté », опубликованных посмертно в 1693 году, через двадцать лет после его смерти, Бернар Френикль де Бесси продемонстрировал, что существует ровно 880 различных магических квадратов четвертого порядка. . Френикл дал методы построения магических квадратов любого нечетного и четного порядка, при этом четные квадраты строились с использованием границ. Он также показал, что перестановка строк и столбцов магического квадрата приводит к появлению новых магических квадратов. [45] В 1691 году Симон де ла Лубер описал индийский непрерывный метод построения нечетно упорядоченных магических квадратов в своей книге Du Royaume de Siam , которому он научился, возвращаясь из дипломатической миссии в Сиам, который был быстрее, чем метод Баше. Пытаясь объяснить его работу, де ла Лубер использовал первичные числа и корневые числа, а также заново открыл метод сложения двух предварительных квадратов. Этот метод был дополнительно исследован аббатом Пуаньяром в «Трактате о возвышенных камнях» (1704 г.), Филиппом де Ла Гиром в «Записках Академии наук для Королевской академии» (1705 г.) и Жозефом Совером в « Строительство магических камней» (1710 г.). . Квадраты с концентрическими границами также изучались Де ла Гиром в 1705 году, в то время как Совер представил магические кубы и квадраты с буквами, которые позже были подхвачены Эйлером в 1776 году, которому часто приписывают их изобретение. В 1750 д'Он-ле-Брэ заново открыл метод построения двояко-четных и одинарно-четных квадратов с использованием техники окантовки; а в 1767 году Бенджамин Франклин опубликовал полумагический квадрат, имевший свойства одноименного квадрата Франклина. [47] К этому времени прежний мистицизм, связанный с магическими квадратами, полностью исчез, и этот предмет стал рассматриваться как часть развлекательной математики. [37] [48]
В XIX веке Бернар Виоль подробно изложил магические квадраты в своем трехтомном « Трактате о магических квадратах» (1837–1838), в котором также описывались магические кубы, параллелограммы, параллелепипеды и круги. Пандиагональные квадраты были тщательно изучены Эндрю Холлингвортом Фростом, который изучил его в городе Насик, Индия (назвав их таким образом квадратами Насика) в серии статей: « На пути рыцаря » (1877 г.), «Об общих свойствах квадратов Насика». (1878 г.), « Об общих свойствах кубов Насика» (1878 г.), «О построении квадратов Насика любого порядка» (1896 г.). Он показал, что невозможно иметь нормальные одно-четные пандиагональные магические квадраты. Фредерик А. П. Барнард построил инкрустированные магические квадраты и другие трехмерные магические фигуры, такие как магические сферы и магические цилиндры, в « Теории магических квадратов и магических кубов» (1888). [48] В 1897 году Эмрой МакКлинток опубликовал « О самой совершенной форме магических квадратов» , введя слова пандиагональный квадрат и самый совершенный квадрат , который ранее назывался совершенным, или дьявольским, или Насиком.

Легенды, датируемые 650 годом до нашей эры, рассказывают историю Ло Шу (洛書) или «свитка реки Ло». [8] Согласно легенде, однажды в древнем Китае произошло огромное наводнение. Пока великий царь Юй пытался направить воду в море, из нее вышла черепаха с любопытным узором на панцире: сеткой 3×3, в которой были расположены круглые точки чисел, так что сумма чисел в каждая строка, столбец и диагональ были одинаковыми: 15. По преданию, в дальнейшем люди смогли использовать этот узор определенным образом, чтобы управлять рекой и защищаться от наводнений. Квадрат Ло Шу , как называется магический квадрат на панцире черепахи, представляет собой уникальный нормальный магический квадрат третьего порядка, в котором 1 находится внизу, а 2 — в правом верхнем углу. Каждый нормальный магический квадрат третьего порядка получается из Ло Шу путем вращения или отражения.

На стене храма Паршванатх в Кхаджурахо , Индия , начертан известный обычный магический квадрат 4х4 XII века . [18] [17] [49]
Это известно как Чаутиша Янтра ( Чаутиша , 34; Янтра , букв. «устройство»), поскольку ее магическая сумма равна 34. Это один из трех пандиагональных магических квадратов 4×4 , а также пример наиболее совершенного магический квадрат . Изучение этого квадрата привело к пониманию пандиагональных квадратов европейскими математиками в конце 19 века. Пандиагональные квадраты в старой английской литературе назывались квадратами Насика или джайнскими квадратами.
.jpg/440px-Albrecht_Dürer_-_Melencolia_I_(detail).jpg)
Нормальный магический квадрат четвертого порядка, увековеченный Альбрехтом Дюрером на гравюре «Меленхолия I» 1514 года , упомянутой выше, считается первым, увиденным в европейском искусстве. Квадрат, связанный с Юпитером, является талисманом, отгоняющим меланхолию. Он очень похож на квадрат Ян Хуэя , который был создан в Китае примерно за 250 лет до времен Дюрера. Как и в каждом нормальном магическом квадрате 4-го порядка, магическая сумма равна 34. Но в квадрате Дюрера эта сумма также находится в каждом из квадрантов, в четырех центральных квадратах и в угловых квадратах (также в квадрате 4 × 4). поскольку четыре содержали сетки 3×3). Эту сумму также можно найти в четырех внешних числах по часовой стрелке от углов (3+8+14+9), а также в четырех против часовой стрелки (расположение четырех ферзей в двух решениях головоломки о 4 ферзях [50] ). , два набора из четырех симметричных чисел (2+8+9+15 и 3+5+12+14), сумма двух средних записей двух внешних столбцов и строк (5+9+8+12 и 3 +2+15+14), а также в четырёх квартетах в форме змея или креста (3+5+11+15, 2+10+8+14, 3+9+7+15 и 2+6+12+14) . Две цифры в середине нижнего ряда обозначают дату гравюры: 1514 год. Было высказано предположение, что цифры 4,1, граничащие с датой публикации, соответствуют инициалам Дюрера D,A. Но если бы это было его намерением, он мог бы поменять порядок столбцов 1 и 4, чтобы получить «A1514D», не ставя под угрозу свойства квадрата.
Магический квадрат Дюрера также можно расширить до магического куба. [51]

Фасад Страстей церкви Саграда Фамилия в Барселоне , задуманный Антонио Гауди и спроектированный скульптором Хосепом Субираксом , представляет собой тривиальный магический квадрат четвертого порядка: магическая константа квадрата равна 33 годам, возрасту Иисуса во время Страстей . [52] Структурно он очень похож на магический квадрат Меланхолии , но в нем числа в четырех ячейках уменьшены на 1.
Тривиальные квадраты, подобные этому, обычно не представляют интереса с математической точки зрения и имеют лишь историческое значение. Ли Саллоуз отметил, что из-за незнания Субираксом теории магических квадратов известный скульптор допустил ненужную ошибку, и подкрепил это утверждение, приведя несколько примеров нетривиальных магических квадратов 4×4, показывающих желаемую магическую константу 33. [ 53]
Подобно магическому квадрату Дюрера, магический квадрат Саграда Фамилия также можно расширить до магического куба. [54]
Квадрат Паркера , названный в честь математика-любителя Мэтта Паркера , [55] представляет собой попытку создать магический квадрат квадратов 3 × 3 — ценную нерешенную задачу со времен Эйлера . [56] Квадрат Паркера — это тривиальный полумагический квадрат, поскольку в нем некоторые числа используются более одного раза, а сумма диагонали 23 2 + 37 2 + 47 2 равна4107 , нет3051 , как и для всех остальных строк, столбцов или диагонали. Паркер-сквер стал популярен в математической культуре. [55] [57]
Квадрат Гарднера, названный в честь математика-любителя Мартина Гарднера , похож на квадрат Паркера и задан как задача на определение a, b, c и d .
Это решение для a=74, b=113, c=94 и d=97 дает полумагический квадрат; диагональ 127 2 + b 2 + d 2 равна38 307 , нет21 609 , как и для всех остальных строк, столбцов и диагонали. [58] [59] [60]
Константа, которая является суммой любой строки, столбца или диагонали, называется магической константой или магической суммой M. Каждый нормальный магический квадрат имеет константу, зависящую от порядка n , вычисляемую по формуле . Это можно продемонстрировать, заметив, что сумма равна . Поскольку сумма каждой строки равна , сумма строк равна , что при делении на порядок n дает магическую константу. Для обычных магических квадратов порядков n = 3, 4, 5, 6, 7 и 8 магическими константами являются соответственно: 15, 34, 65, 111, 175 и 260 (последовательность A006003 в OEIS ) .
Магический квадрат 1×1, в котором только одна ячейка содержит число 1, называется тривиальным , поскольку он обычно не рассматривается при обсуждении магических квадратов; но это действительно магический квадрат по определению, если одну ячейку рассматривать как квадрат первого порядка.
Можно построить обычные магические квадраты любого размера, кроме 2×2 (то есть порядка n = 2). [61]
Если числа в магическом квадрате рассматривать как массы, расположенные в различных ячейках, то центр масс магического квадрата совпадает с его геометрическим центром.
Момент инерции магического квадрата определяется как сумма по всем ячейкам числа в ячейке, умноженная на квадрат расстояния от центра ячейки до центра квадрата; здесь единицей измерения является ширина одной ячейки. [62] (Так, например, расстояние до угловой ячейки квадрата 3×3 равно 1, а до центральной ячейки — 0.) Тогда все магические квадраты данного порядка имеют одинаковые моменты инерции друг друга. Для случая 3-го порядка момент инерции всегда равен 60, а для случая 4-го порядка момент инерции всегда равен 340. В общем, для случая n × n момент инерции равен [62]
Разделив каждое число магического квадрата на магическую константу, получим дважды стохастическую матрицу , суммы строк и суммы столбцов которой равны единице. Однако, в отличие от дважды стохастической матрицы, диагональные суммы таких матриц также будут равны единице. Таким образом, такие матрицы составляют подмножество дважды стохастической матрицы. Теорема Биркгофа – фон Неймана утверждает, что для любой дважды стохастической матрицы существуют действительные числа , где и матрицы перестановок такие, что
Это представление вообще не может быть уникальным. Однако по теореме Маркуса-Ри в любом разложении не должно быть больше членов. [63] Очевидно, что это разложение распространяется и на магические квадраты, поскольку магический квадрат можно восстановить из дважды стохастической матрицы, умножив ее на магическую константу.

Классифицировать магические квадраты можно разными способами, но ниже приведены некоторые полезные категории. Квадратный массив n × n целых чисел 1, 2, ..., n 2 называется :
Сколько существует магических торов и магических квадратов порядка n для и соответственно?
Существует только один (тривиальный) магический квадрат первого порядка и нет магического квадрата второго порядка. Как упоминалось выше, набор нормальных квадратов третьего порядка образует единый класс эквивалентности - все они эквивалентны квадрату Ло Шу. Таким образом, по сути, существует только один нормальный магический квадрат третьего порядка.
Количество различных магических квадратов n × n для n от 1 до 6, не считая вращений и отражений, равно:
Число для n = 6 ранее оценивалось как (1,7745 ± 0,0016) × 10 19 . [64] [65] [62]
Ссылаясь на приведенную выше последовательность, новая классификация перечисляет магические торы, отображающие эти магические квадраты. Количество магических торов порядка n от 1 до 5 равно:
Количество различных нормальных магических квадратов быстро увеличивается для более высоких порядков. [66]
880 магических квадратов 4-го порядка отображаются на 255 магических торах 4-го порядка, а 275 305 224 квадрата 5-го порядка отображаются на 251 449 712 магических торах 5-го порядка. Число магических торов и отдельных нормальных квадратов для порядков выше 5 пока неизвестно. и 6 соответственно. [67] [ нужна ссылка ]
Алгоритмы имеют тенденцию генерировать магические квадраты только определенного типа или классификации, что затрудняет подсчет всех возможных магических квадратов. Поскольку традиционные методы подсчета оказались безуспешными, был применен статистический анализ с использованием метода Монте-Карло . Основной принцип, применяемый к магическим квадратам, заключается в случайной генерации матриц размера n × n из элементов от 1 до n 2 и проверке того, является ли результат магическим квадратом. Вероятность того, что случайно сгенерированная матрица чисел является магическим квадратом, затем используется для аппроксимации количества магических квадратов. [68]
Более сложные версии метода Монте-Карло, такие как обмен Монте-Карло и возврат Монте-Карло, дали еще более точные оценки. С помощью этих методов было показано, что вероятность магических квадратов быстро уменьшается с увеличением n. Используя функции подгонки, дайте кривые, показанные справа.
За тысячелетие было открыто множество способов построения магических квадратов. Эти методы можно разделить на общие и специальные в том смысле, что общие методы позволяют нам построить более одного магического квадрата заданного порядка, тогда как специальные методы позволяют нам построить только один магический квадрат заданного порядка. Специальные методы представляют собой конкретные алгоритмы, тогда как общие методы могут потребовать некоторого метода проб и ошибок.
Специальные методы — это стандартные и наиболее простые способы построения магического квадрата. Он следует определенным конфигурациям/формулам/алгоритму, который генерирует регулярные шаблоны чисел в квадрате. Корректность этих специальных методов можно доказать, используя один из общих методов, приведенных в последующих разделах. После того как магический квадрат построен с использованием специального метода, можно применить преобразования, описанные в предыдущем разделе, для получения дополнительных магических квадратов. Специальные методы обычно упоминаются по имени автора(ов) (если известно), описавшего метод, например, метод Де ла Лубера, метод Старчи, метод Баше и т. д.
Магические квадраты существуют для всех значений n , кроме порядка 2. Магические квадраты можно классифицировать в зависимости от их порядка как нечетные, дважды четные ( n делится на четыре) и одинарно четные ( n четное, но не делится на четыре). Эта классификация основана на том факте, что для построения этих разных типов квадратов необходимо использовать совершенно разные методы. Нечетные и дважды четные магические квадраты легко создать; построение одиночных четных магических квадратов сложнее, но существует несколько методов, включая метод LUX для магических квадратов (благодаря Джону Хортону Конвею ) и метод Стрейчи для магических квадратов .
В 19 веке Эдуард Лукас разработал общую формулу магических квадратов третьего порядка. Рассмотрим следующую таблицу, состоящую из положительных целых чисел a , b и c :
Эти девять чисел будут различными целыми положительными числами, образующими магический квадрат с магической константой 3 c , если 0 < a < b < c − a и b ≠ 2 a . Более того, каждый магический квадрат 3 × 3 различных положительных целых чисел имеет такой вид.
В 1997 году Ли Саллоуз обнаружил, что если оставить в стороне вращения и отражения, то каждый отдельный параллелограмм , нарисованный на диаграмме Аргана, определяет уникальный магический квадрат 3×3, и наоборот, результат, который ранее никогда не отмечался. [70]
Метод построения магических квадратов нечетного порядка был опубликован французским дипломатом де ла Лубером в его книге « Новые исторические отношения Сиамского королевства» (Du Royaume de Siam, 1693), в главе, озаглавленной «Проблема магического квадрата». по мнению индейцев . [73] Способ работает следующим образом:
Методика предписывает начинать в центральном столбце первой строки с цифры 1. После этого основное движение по заполнению квадратов – по диагонали вверх и вправо, по одному шагу. Если квадрат заполнен числами, кратными порядку n , вместо этого происходит перемещение вертикально вниз на один квадрат, а затем продолжается, как и раньше. Когда ход «вверх и вправо» выходит за пределы квадрата, он переносится на последнюю строку или первый столбец соответственно.
Можно начинать с других квадратов, а не с центрального столбца первой строки, но тогда только суммы строк и столбцов будут одинаковыми и приведут к магической сумме, тогда как суммы по диагонали будут различаться. Таким образом, результатом будет полумагический квадрат, а не настоящий магический квадрат. Движение в направлениях, отличных от северо-востока, также может привести к образованию магических квадратов.
Дважды четное означает, что n кратно четному целому числу; или 4 p (например, 4, 8, 12), где p представляет собой целое число.
Общий шаблон Все числа записываются по порядку слева направо в каждой строке, начиная с верхнего левого угла. Числа затем либо сохраняются на том же месте, либо меняются местами с диаметрально противоположными числами по определенной закономерности. В магическом квадрате четвертого порядка числа в четырех центральных квадратах и по одному квадрату в каждом углу сохраняются на прежнем месте, а остальные меняются местами с диаметрально противоположными числами.
Построение магического квадрата 4-го порядка. Начиная сверху слева, идите слева направо по каждой строке квадрата, считая каждую клетку от 1 до 16 и заполняя ячейки по диагоналям соответствующим ей числом. Как только нижняя правая ячейка будет достигнута, продолжайте двигаться справа налево, начиная с нижнего правого угла таблицы через каждую строку, и заполняйте недиагональные ячейки, считая от 1 до 16, соответствующим номером. Как показано ниже:
Расширение приведенного выше примера для заказов 8 и 12. Сначала создайте таблицу шаблонов, где «1» указывает на выбор из квадрата, где числа записаны в порядке от 1 до n 2 (слева направо, сверху вниз). ), а «0» указывает на выбор из квадрата, где числа записаны в обратном порядке от n 2 до 1. Для M = 4 таблица шаблонов выглядит так, как показано ниже (третья матрица слева). Если неизмененные ячейки (ячейки с «1») заштриховать, получается узор крест-накрест.
Шаблоны: а) в каждой строке и столбце равное количество единиц и нулей; б) каждая строка и каждый столбец являются «палиндромными»; в) левая и правая половины зеркально отражены; и d) верхняя и нижняя половины являются зеркальными изображениями (c и d подразумевают б). Таблицу шаблонов для простоты можно обозначить шестнадцатеричными числами как (9, 6, 6, 9) (1 полубайт на строку, 4 строки). Самый простой метод создания требуемого шаблона для дважды четных квадратов более высокого порядка — это копирование общего шаблона для квадрата четвертого порядка в каждом подквадрате размером четыре на четыре.
Для M = 8 возможные варианты шаблона: (99, 66, 66, 99, 99, 66, 66, 99); (3С, 3С, С3, С3, С3, С3, 3С, 3С); (A5, 5A, A5, 5A, 5A, A5, 5A, A5) (2 полубайта в строке, 8 строк).
Для M = 12 таблица шаблонов (E07, E07, E07, 1F8, 1F8, 1F8, 1F8, 1F8, 1F8, E07, E07, E07) дает магический квадрат (3 полубайта на строку, 12 строк). Это можно подсчитать количество вариантов выбора на основе таблицы шаблонов с учетом вращательной симметрии.
Самое раннее открытие метода суперпозиции было сделано индийским математиком Нараяной в 14 веке. Тот же метод позже был вновь открыт и изучен в Европе в начале 18 века де ла Лубером, Пуаньаром, де Ла Гиром и Совером; и этот метод обычно называют методом де ла Гира. Хотя работа Эйлера по магическому квадрату не была оригинальной, он, как известно, высказал гипотезу о невозможности построения равномерно нечетно упорядоченных взаимно ортогональных греко-латинских квадратов . Эта гипотеза была опровергнута в середине 20 века. Для ясности изложения можно выделить две важные разновидности этого метода.
Этот метод заключается в построении двух предварительных квадратов, которые при сложении дают магический квадрат. В качестве рабочего примера рассматривается магический квадрат 3×3. Каждое число натурального квадрата 3×3, состоящее из пары чисел, можно обозначить как
где каждая пара греческого и латинского алфавитов, например αa , предназначена для сложения, т.е. αa = α + a . Здесь ( α , β , γ ) = (0, 3, 6) и ( a , b , c ) = (1, 2, 3). Числа 0, 3 и 6 называются корневыми числами , а числа 1, 2 и 3 — первичными числами . Важным общим ограничением здесь является
Таким образом, исходный квадрат теперь можно разделить на два более простых квадрата:
Квадраты с буквами называются греческим квадратом или латинским квадратом , если они заполнены греческими или латинскими буквами соответственно. Магический квадрат можно построить, гарантируя, что греческий и латинский квадраты также являются магическими квадратами. Обратное утверждение также часто, но не всегда (например, магические квадраты с рамкой), верно: магический квадрат можно разложить на греческий и латинский квадраты, которые сами являются магическими квадратами. Таким образом, метод полезен как для синтеза, так и для анализа магического квадрата. Наконец, исследуя шаблон, по которому числа расположены в готовом квадрате, часто можно придумать более быстрый алгоритм построения квадратов более высокого порядка, повторяющих заданный шаблон, без необходимости создания предварительных греческих и латинских символов. квадраты.
При построении магического квадрата 3×3 гораздо проще иметь дело с греческими и латинскими квадратами, содержащими всего три уникальных термина, чем с исходным квадратом с девятью различными терминами. Сумма строки и сумма столбца греческого квадрата будут одинаковыми, α + β + γ , если
Этого можно достичь путем циклической перестановки α , β и γ . Удовлетворение этих двух условий гарантирует, что полученный квадрат будет полумагическим; и такие греческие и латинские квадраты называются взаимно ортогональными друг другу. Для данного порядка n в наборе взаимно ортогональных квадратов имеется не более n - 1 квадратов, не считая изменений, вызванных перестановкой символов. Эта верхняя граница точна, когда n — простое число.
Чтобы построить магический квадрат, мы также должны убедиться, что сумма диагоналей равна магической константе. Для этого у нас есть третье условие:
Взаимно ортогональные греческие и латинские квадраты, удовлетворяющие первой части третьего условия (что все буквы появляются в обеих диагоналях), называются взаимно ортогональными двудиагональными греко-латинскими квадратами .
Нечетные квадраты: для нечетного квадрата 3×3, поскольку α , β и γ находятся в арифметической прогрессии, их сумма равна произведению порядка квадрата и среднего члена, т.е. α + β + γ = 3 β . Таким образом, диагональные суммы будут равны, если у нас есть β s на главной диагонали и α , β , γ на косой диагонали. Аналогично и для латинского квадрата. Полученные греческие и латинские квадраты и их комбинации будут такими, как показано ниже. Латинский квадрат — это всего лишь поворот греческого квадрата на 90 градусов против часовой стрелки (или, что то же самое, поворот вокруг вертикальной оси) с заменой соответствующих букв. Замена значений греческих и латинских букв даст магический квадрат 3х3.
Для нечетных квадратов этот метод объясняет, почему работает сиамский метод (метод Де ла Лубера) и его варианты. Этот базовый метод можно использовать для построения магических квадратов нечетного порядка более высоких порядков. Обобщить:
Особенностью приведенного выше метода построения нечетных магических квадратов является то, что среднее число ( n 2 + 1)/2 всегда будет находиться в центральной ячейке магического квадрата. Так как их ( n - 1)! способов расположить косодиагональные члены, мы можем получить ( n - 1)! Греческие квадраты таким образом; то же самое и с латинскими квадратами. Кроме того, поскольку каждому греческому квадрату можно поставить пару ( n - 1)! латинских квадратов, и поскольку для каждого греческого квадрата средний член может быть произвольно помещен в главную диагональ или косую диагональ (и соответственно вдоль косой диагонали или главной диагонали для латинских квадратов), мы можем построить в общей сложности 2 × ( н - 1)! × ( n - 1)! магические квадраты с помощью этого метода. Для n = 3, 5 и 7 это даст 8, 1152 и 1 036 800 различных магических квадратов соответственно. Разделив на 8, пренебрегая эквивалентными квадратами, возникающими из-за вращения и отражения, мы получаем соответственно 1, 144 и 129 600 существенно различных магических квадратов.
В качестве другого примера приведено построение магического квадрата 5×5. Числа записываются непосредственно вместо букв. Пронумерованные квадраты называются первичными квадратами или корневыми квадратами , если они заполнены первичными числами или корневыми числами соответственно. Числа располагаются по косой диагонали в корневом квадрате так, чтобы в среднем столбце полученного корневого квадрата были 0, 5, 10, 15, 20 (снизу вверх). Первичный квадрат получается поворотом корневого квадрата против часовой стрелки на 90 градусов и заменой чисел. Полученный квадрат представляет собой ассоциативный магический квадрат, в котором каждая пара чисел, симметрично противоположных центру, в сумме дает одно и то же значение — 26. Например, 16+10, 3+23, 6+20 и т. д. В готовом квадрате , 1 помещается в центральную ячейку нижнего ряда, а последовательные числа размещаются с помощью удлиненного хода коня (две клетки вправо, две клетки вниз) или, что то же самое, хода слона (две клетки по диагонали вниз вправо). Когда происходит столкновение, ход разрыва заключается в перемещении на одну ячейку вверх. Все нечетные числа встречаются внутри центрального ромба, образованного цифрами 1, 5, 25 и 21, а четные числа расположены по углам. О появлении четных чисел можно узнать, скопировав квадрат на соседние стороны. Четные числа из четырех соседних квадратов образуют крест.
Вариант приведенного выше примера, в котором косая диагональная последовательность берется в другом порядке, приведен ниже. Полученный магический квадрат представляет собой перевернутую версию знаменитого магического квадрата Марса Агриппы. Это ассоциативный магический квадрат, аналогичный квадрату, полученному методом Мосхопулоса. Здесь полученный квадрат начинается с 1, помещенной в ячейку, которая находится справа от центральной ячейки, и продолжается по методу Де ла Лубера с движением вниз-вправо. Когда происходит столкновение, движение разрыва заключается в сдвиге на две ячейки вправо.
В предыдущих примерах для греческого квадрата вторую строку можно получить из первой строки, сдвинув ее по кругу вправо на одну клетку. Аналогично, третья строка представляет собой версию второй строки, сдвинутую по кругу на одну ячейку вправо; и так далее. Аналогично строки латинского квадрата смещаются по кругу влево на одну клетку. Сдвиги строк греческого и латинского квадратов направлены во взаимно противоположные стороны. Можно сдвинуть строки по кругу более чем на одну ячейку, чтобы получился греческий и латинский квадрат.
По сути, это воссоздает ход коня. Все буквы появятся на обеих диагоналях, обеспечивая правильную сумму диагоналей. Поскольку существует n ! перестановок греческих букв, с помощью которых мы можем создать первую строку греческого квадрата, таким образом, существует n ! Греческие квадраты, которые можно создать, сдвигая первый ряд в одном направлении. Аналогично, существует n ! такие латинские квадраты создаются путем сдвига первой строки в противоположную сторону. Поскольку греческий квадрат можно объединить с любым латинским квадратом со смещением строк в противоположные стороны, существует n ! × н ! такие комбинации. Наконец, поскольку греческий квадрат можно создать, сдвигая строки влево или вправо, всего их получается 2 × n ! × н ! магические квадраты, которые можно сформировать этим методом. Для n = 5 и 7, поскольку они являются простыми числами, этот метод создает 28 800 и 50 803 200 пандиагональных магических квадратов. Разделив на 8, чтобы пренебречь эквивалентными квадратами из-за вращения и отражений, мы получим 3600 и 6350400 эквивалентных квадратов. Далее разделив на n 2 , пренебрегая эквивалентными панмагическими квадратами из-за циклического сдвига строк или столбцов, получим 144 и 129 600 существенно различных панмагических квадратов. Для квадратов порядка 5 это единственный панмагический квадрат. Условие того, что порядок квадрата не делится на 3, означает, что мы не можем построить квадраты порядков 9, 15, 21, 27 и т. д. этим методом.
В приведенном ниже примере квадрат построен так, что 1 находится в центральной ячейке. В готовом квадрате числа можно непрерывно пересчитывать ходом коня (две клетки вверх, одна клетка вправо). Когда происходит столкновение, ход разрыва заключается в перемещении на одну клетку вверх и на одну клетку влево. Полученный квадрат представляет собой пандиагональный магический квадрат. У этого квадрата также есть еще одно дьявольское свойство: любые пять ячеек в образце квинкунса , образованные любым нечетным подквадратом, включая обертку, дают в сумме магическую константу 65. Например, 13+7+1+20+24, 23+ 1+9+15+17, 13+21+10+19+2 и т. д. Также четыре угла любого квадрата 5×5 и центральная клетка, а также средние клетки каждой стороны вместе с центральной клеткой, в том числе заверните, дайте волшебную сумму: 13+10+19+22+1 и 20+24+12+8+1. Наконец, четыре ромба, образующие вытянутые кресты, также дают магическую сумму: 23+1+9+24+8, 15+1+17+20+12, 14+1+18+13+19, 7+1+25+. 22+10.
Мы также можем комбинировать греческие и латинские квадраты, построенные разными методами. В приведенном ниже примере основное поле создается с помощью хода коня. Мы воссоздали магический квадрат, полученный методом Де ла Лубера. Как и раньше, мы можем составить 8 × ( n - 1)! × н ! магические квадраты по этой комбинации. Для n = 5 и 7 это создаст 23 040 и 29 030 400 магических квадратов. После деления на 8, чтобы пренебречь эквивалентными квадратами из-за вращения и отражения, получаем 2880 и 3628800 квадратов.
Для квадратов пятого порядка эти три метода дают полную оценку количества магических квадратов, которые можно построить методом суперпозиции. Если пренебречь вращением и отражениями, общее количество магических квадратов пятого порядка, полученных методом суперпозиции, составит 144 + 3600 + 2880 = 6624.
Четные квадраты: таким способом мы также можем построить даже упорядоченные квадраты. Поскольку в греческом и латинском алфавитах нет среднего термина для четных квадратов, в дополнение к первым двум ограничениям, чтобы диагональные суммы давали магическую константу, все буквы алфавита должны появляться на главной диагонали и на перекос по диагонали.
Ниже приведен пример квадрата 4×4. Для заданной диагонали и наклонной диагонали в греческом квадрате остальные ячейки можно заполнить, используя условие, чтобы каждая буква появлялась только один раз в строке и столбце.
Используя эти два греко-латинских квадрата, мы можем построить 2 × 4! × 4! = 1152 магических квадрата. Разделив на 8, чтобы исключить эквивалентные квадраты вследствие вращения и отражения, получим 144 существенно различных магических квадрата порядка 4. Это единственные магические квадраты, которые можно построить методом Эйлера, поскольку существует только два взаимно ортогональных двоякодиагональных греко-латинских квадрата заказ 4.
Аналогичным образом можно построить магический квадрат 8×8, как показано ниже. Здесь порядок появления цифр не важен; однако квадранты имитируют схему расположения греко-латинских квадратов 4×4.
Метод Эйлера дал начало изучению греко-латинских квадратов . Метод Эйлера для построения магических квадратов справедлив для любого порядка, кроме 2 и 6.
Вариации : Магические квадраты, построенные из взаимно ортогональных двудиагональных греко-латинских квадратов, интересны сами по себе, поскольку магическое свойство возникает из относительного положения алфавитов в квадрате, а не из-за какого-либо арифметического свойства присвоенного им значения. Это означает, что мы можем присвоить алфавитам таких квадратов любое значение и все равно получить магический квадрат. Это основа для построения квадратов, отображающих в квадрате некоторую информацию (например, дни рождения, годы и т. д.), а также для создания «обратимых квадратов». Например, мы можем отобразить число π ≈3.141 592 в нижнем ряду магического квадрата 4×4, используя греко-латинский квадрат, указанный выше, путем присвоения ( α , β , γ , δ ) = (10, 0, 90, 15) и ( a , b , c , г ) = (0, 2, 3, 4). Мы получим следующий ненормальный магический квадрат с магической суммой 124:
Метод Нараяны-Де ла Гира для нечетного квадрата такой же, как метод Эйлера. Однако для четных квадратов мы опускаем второе требование, согласно которому каждая греческая и латинская буква встречается только один раз в данной строке или столбце. Это позволяет воспользоваться тем, что сумма арифметической прогрессии с четным числом членов равна сумме двух противоположных симметричных членов, умноженной на половину общего количества членов. Таким образом, при построении греческих или латинских квадратов
В качестве примера, если мы возьмем квадрат 4×4, где греческие и латинские термины имеют значения ( α , β , γ , δ ) = (0, 4, 8, 12) и ( a , b , c , d ) = (1, 2, 3, 4) соответственно, то α + β + γ + δ = 2 ( α + δ ) = 2 ( β + γ ). Аналогично, a + b + c + d = 2 ( a + d ) = 2 ( b + c ). Это означает, что дополнительная пара α и δ (или β и γ ) может появиться дважды в столбце (или строке) и при этом дать искомую магическую сумму. Таким образом, мы можем построить:
В примере, приведенном ниже, главная диагональ (слева сверху вниз справа) заполнена последовательностью, упорядоченной как α , β , γ , δ , а наклонная диагональ (слева снизу вверх справа) заполнена в том же порядке. Остальные ячейки затем заполняются по столбцам так, что дополнительные буквы появляются только один раз в строке и дважды в столбце. В первом столбце, поскольку α появляется в 1-й и 4-й строках, оставшиеся ячейки заполняются дополнительным к нему членом δ . Аналогичным образом пустые ячейки во втором столбце заполняются значением γ ; в третьем столбце β ; и 4-й столбец α . Каждая греческая буква появляется в строках только один раз, а в столбцах — дважды. Таким образом, суммы строк равны α + β + γ + δ , а суммы столбцов равны либо 2 ( α + δ ), либо 2 ( β + γ ). Аналогично и с латинским квадратом, который получается переворачиванием греческого квадрата по главной диагонали и перестановкой соответствующих букв.
Приведенный выше пример объясняет, почему работает метод «крест-накрест» для дважды четного магического квадрата. Другой возможный магический квадрат 4 × 4, который также является пандиагональным и наиболее совершенным, построен ниже с использованием того же правила. Однако диагональная последовательность выбирается такой, чтобы все четыре буквы α , β , γ , δ появлялись внутри центрального подквадрата 2×2. Остальные ячейки заполняются по столбцам так, что каждая буква появляется в строке только один раз. В 1-м столбце пустые клетки нужно заполнить одной из букв, выбранных из дополнительной пары α и δ . Учитывая 1-й столбец, запись во 2-й строке может быть только δ , поскольку α уже присутствует во 2-й строке; в то время как в 3-й строке запись может быть только α , поскольку δ уже присутствует в 3-й строке. Действуем аналогично, пока все ячейки не будут заполнены. Приведенный ниже латинский квадрат получен путем переворачивания греческого квадрата по главной диагонали и замены греческих алфавитов соответствующими латинскими алфавитами.
Мы можем использовать этот подход и для построения одиночных четных магических квадратов. Однако в этом случае нам следует быть более осторожными, поскольку критерии однозначного сочетания греческого и латинского алфавитов не выполняются автоматически. Нарушение этого условия приводит к тому, что в конечном квадрате одних чисел не хватает, а другие дублируются. Поэтому есть важная оговорка:
Ниже представлена конструкция магического квадрата 6×6, где непосредственно заданы цифры, а не буквы алфавита. Второй квадрат строится путем переворачивания первого квадрата по главной диагонали. Здесь в первом столбце квадрата корня 3-я клетка соединена с дополнением в 4-х ячейках. Таким образом, в основном квадрате числа в 1-й и 6-й ячейке 3-й строки совпадают. Аналогично с другими столбцами и строками. В этом примере перевернутая версия квадратного корня удовлетворяет этому условию.
Ниже приведен еще один пример построенного таким образом магического квадрата 6×6. Здесь диагональные записи расположены по-другому. Первичный квадрат строится путем переворачивания корневого квадрата вокруг главной диагонали. Во втором квадрате условие об единственном четном квадрате не выполняется, что приводит к ненормальному магическому квадрату (третий квадрат), в котором числа 3, 13, 24 и 34 дублируются, но отсутствуют числа 4, 18, 19 и 33.
Последнее условие является немного произвольным и не всегда может нуждаться в его вызове, как в этом примере, где в корневом квадрате каждая ячейка вертикально соединена со своим дополнением:
Еще один пример: мы создали магический квадрат 8×8. В отличие от рисунка крест-накрест из предыдущего раздела для равномерных квадратов, здесь мы имеем клетчатый узор для измененных и неизмененных ячеек. Кроме того, в каждом квадранте нечетные и четные числа появляются в чередующихся столбцах.
Вариации . Возможны различные вариации основной идеи: дополнительная пара может появляться в столбце n /2 или менее раз . То есть столбец греческого квадрата можно построить, используя более чем одну дополнительную пару. Этот метод позволяет нам наделить магический квадрат гораздо более богатыми свойствами. Эту идею можно распространить и на диагонали. Ниже приведен пример магического квадрата 8×8. В готовом квадрате каждый из четырех квадрантов также является панмагическим квадратом, причем каждый квадрант имеет одинаковую магическую константу 130.
Целью этого метода является обертывание границы вокруг меньшего магического квадрата, который служит ядром. Возьмем, к примеру, квадрат 3×3. Вычитая среднее число 5 из каждого числа 1, 2, ..., 9, мы получаем 0, ± 1, ± 2, ± 3 и ± 4, что мы и будем, за неимением лучших слов, вслед за С. Гарри Уайтом. , называются номерами костей. Магическая константа магического квадрата, который мы будем называть скелетным квадратом, составленным из этих чисел костей, будет равна нулю, поскольку сложение всех строк магического квадрата даст nM = Σ k = 0; таким образом, М = 0.
Нетрудно доказать, что среднее число должно располагаться в центральной ячейке: пусть x — число, помещенное в среднюю клетку, тогда сумма среднего столбца, средней строки и двух диагоналей дает Σ k + 3 x = 4 М . Поскольку Σ k = 3 M , имеем x = M / 3. Здесь M = 0, поэтому x = 0.
Поместив среднее число 0 в центральную ячейку, мы хотим построить границу так, чтобы полученный квадрат был магическим. Пусть граница задана формулой:
Поскольку сумма каждой строки, столбца и диагоналей должна быть постоянной (т.е. нулевой), мы имеем
Теперь, если мы выбрали a , b , u и v , то у нас есть a* = - a , b* = - b , u* = - u и v* = - v . Это означает, что если мы присвоим переменной заданное число, скажем a = 1, то ее дополнение будет присвоено a* , т.е. a* = - 1. Таким образом, из восьми неизвестных переменных достаточно указать значение всего четыре переменных. Мы будем рассматривать a , b , u и v как независимые переменные, а a* , b* , u* и v* как зависимые переменные. Это позволяет нам рассматривать число костей ± x как одно число независимо от знака, поскольку (1) его присвоение данной переменной, скажем, a , автоматически означает, что такое же количество противоположных знаков будет использоваться совместно с его дополнением a* , и (2) двум независимым переменным, скажем a и b , не может быть присвоен один и тот же номер кости. Но как нам выбрать a , b , u и v ? У нас есть сумма верхней строки и сумма правого столбца как
Поскольку 0 — четное число, существует только два способа, которыми сумма трех целых чисел даст четное число: 1) если все три были четными или 2) если два из них были нечетными, а одно — четным. Поскольку в нашем выборе чисел у нас есть только два четных ненулевых числа (± 2 и ± 4), первое утверждение неверно. Следовательно, должно быть так, что второе утверждение верно: два числа нечетные, а одно четное.
Единственный способ, которым оба приведенных выше уравнения могут одновременно удовлетворять этому условию четности и при этом оставаться совместимыми с имеющимся у нас набором чисел, — это когда u и v нечетны. Напротив, если бы мы предположили, что и и а нечетны, а v — четно в первом уравнении, то и* = — и будет нечетным во втором уравнении, делая b также нечетным, чтобы удовлетворить условие паритета. Но для этого требуются три нечетных числа ( u , a и b ), что противоречит тому факту, что у нас есть только два нечетных числа (± 1 и ± 3), которые мы можем использовать. Это доказывает, что нечетные номера костей занимают угловые ячейки. При преобразовании в обычные числа путем добавления 5 это означает, что все углы магического квадрата 3×3 заняты четными числами.
Таким образом, взяв u = 1 и v = 3, мы получим a = - 4 и b = - 2. Следовательно, готовый квадрат скелета будет таким, как слева. Прибавляя к каждому числу по 5, получаем готовый магический квадрат.
Аналогичный аргумент можно использовать для построения более крупных квадратов. Поскольку не существует магического квадрата 2×2, вокруг которого мы могли бы обернуть границу, чтобы построить магический квадрат 4×4, следующим наименьшим порядком, для которого мы можем построить квадрат с рамкой, является порядок 5.
Рассмотрим квадрат пятого порядка. Для этого у нас есть магическое ядро 3х3, вокруг которого мы обернем магическую рамку. Номера костей, которые будут использоваться, будут составлять ± 5, ± 6, ± 7, ± 8, ± 9, ± 10, ± 11 и ± 12. Без учета знаков у нас есть 8 номеров костей, 4 из которых четные и 4. из них странные. В общем, для квадрата любого порядка n будет 4( n -1) граничных ячеек, которые необходимо заполнить 2( n -1) числами костей. Пусть магическая граница задана как
Как и прежде, нам следует
Для описания магической границы достаточно определить числа u, v, a, b, c, d, e, f . Как и раньше, у нас есть два уравнения ограничений для верхней строки и правого столбца:
Возможны несколько решений. Стандартная процедура заключается в
Существует 28 способов выбрать два числа из набора 8 чисел костей для угловых ячеек u и v . Однако не все пары допустимы. Среди 28 пар 16 пар состоят из четных и нечетных чисел, в 6 парах оба числа имеют четные числа, а в 6 парах оба числа состоят из нечетных чисел.
Мы можем доказать, что угловые клетки u и v не могут иметь четное и нечетное число. Это потому, что если бы это было так, то суммы u + v и v + u* были бы нечетными, а поскольку 0 — четное число, то суммы a + b + c и d + e + f также должны быть нечетными. Единственный случай, когда сумма трех целых чисел даст нечетное число, — это когда 1) два из них четные, а одно нечетное, или 2) когда все три нечетные. Поскольку предполагается, что угловые клетки являются нечетными и четными, ни одно из этих двух утверждений не совместимо с тем фактом, что в нашем распоряжении есть только 3 четных и 3 нечетных числа костей. Это доказывает, что u и v не могут иметь разную четность. Это исключает 16 возможностей.
Используя рассуждения аналогичного типа, мы также можем сделать некоторые выводы о множествах { a , b , c } и { d , e , f }. Если u и v оба четные, то оба набора должны иметь два нечетных числа и одно четное число. Если u и v оба нечетные, то в одном из наборов должно быть три четных числа, а в другом — одно четное и два нечетных числа.
В качестве рабочего примера рассмотрим случай, когда и u , и v четные. Возможные 6 пар: (6, 8), (6, 10), (6, 12), (8, 10), (8, 12) и (10, 12). Поскольку суммы u + v и v + u* четные, суммы a + b + c и d + e + f также должны быть четными. Единственный способ, при котором сумма трех целых чисел даст четное число, — это когда 1) два из них нечетные, а одно четное, или 2) когда все три четные. Тот факт, что две угловые клетки четные, означает, что в нашем распоряжении только два четных числа. Таким образом, второе утверждение не совместимо с этим фактом. Следовательно, должно быть так, что первое утверждение верно: два из трех чисел должны быть нечетными, а одно — четным.
Теперь пусть a, b, d, e — нечетные числа, а c и f — четные числа. Учитывая нечетное количество костей, находящихся в нашем распоряжении: ± 5, ± 7, ± 9 и ± 11, их различия варьируются от D = { ± 2, ± 4, ± 6}, а их суммы варьируются от S = {± 12, ± 6}. 14, ± 16, ± 18, ± 20}. Также полезно иметь таблицу их суммы и разностей для дальнейшего использования. Теперь, учитывая угловые ячейки ( u , v ), мы можем проверить ее допустимость, проверив, попадают ли суммы u + v + c и v + u* + f в набор D или S . Допустимость угловых чисел является необходимым, но не достаточным условием существования решения.
Например, если мы рассмотрим пару ( u , v ) = (8, 12), то u + v = 20 и v + u* = 6; и в нашем распоряжении будет ±6 и ±10 четных чисел костей. Принимая c = ± 6, мы получаем, что сумма u + v + c равна 26 и 14, в зависимости от взятого знака ± 6 , оба из которых не попадают в множества D или S . Аналогично, принимая c = ± 10, мы получаем, что сумма u + v + c равна 30 и 10, оба из которых снова не попадают в множества D или S . Таким образом, пара (8, 12) недопустима. Аналогичным образом мы можем исключить и пару (6, 12).
В качестве другого примера, если мы рассмотрим пару ( u , v ) = (10, 12), то u + v = 22 и v + u* = 2; и в нашем распоряжении будет ±6 и ±8 четных чисел костей. Принимая c = ± 6, мы получаем, что сумма u + v + c равна 28 и 16. Хотя 28 не попадает в наборы D или S , 16 попадает в набор S. При проверке мы обнаруживаем, что если ( a , b ) = (-7, -9), то a + b = -16; и он будет удовлетворять первому уравнению ограничений. Кроме того, принимая f = ± 8, мы получаем, что сумма v + u* + f равна 10 и -6. Хотя 10 не входит в наборы D или S , -6 попадает в набор D. Поскольку -7 и -9 уже присвоены a и b , очевидно ( d , e ) = (-5, 11), так что d + e = 6; и оно будет удовлетворять второму уравнению ограничений.
Аналогично, взяв c = ± 8, мы получим сумму u + v + c , равную 30 и 14. Хотя 30 не попадает в наборы D или S , 14 попадает в набор S. При проверке мы обнаруживаем, что если ( a , b ) = (-5, -9), то a + b = -14. Кроме того, принимая f = ± 6, мы получаем, что сумма v + u* + f равна 8 и -4. Хотя 8 не входит в наборы D или S , -4 попадает в набор D. Очевидно, ( d , e ) = (-7, 11), так что d + e = 4, и второе уравнение ограничения будет удовлетворено.
Следовательно, угловая пара ( u , v ) = (10, 12) допустима; и оно допускает два решения: (a, b, c, d, e, f) = (-7, -9, -6, -5, 11, -8) и (a, b, c, d, e, е) = (-5, -9, -8, -7, 11, -6). Готовые каркасные квадраты представлены ниже. Магический квадрат получается путем прибавления 13 к каждой ячейке.
Используя аналогичный процесс рассуждения, мы можем построить следующую таблицу для значений u, v, a, b, c, d, e, f, выраженных как числа костей, как указано ниже. Существует только 6 возможных вариантов угловых ячеек, что приводит к 10 возможным решениям границ.
Имея эту группу из 10 границ, мы можем построить 10×8×(3!) 2 = 2880 магических квадратов с совершенно разными границами. Здесь номера костей ±5,...,±12 были последовательными. Можно построить больше квадратов с рамкой, если числа не являются последовательными. Если также использовались непоследовательные номера костей, то всего получается 605 магических границ. Таким образом, общее количество магических квадратов 5-го порядка с существенно разными границами (с последовательными и непоследовательными номерами) равно 174 240. [74] [75] См. историю. [76] Число магических квадратов пятого порядка, которые можно построить методом окантовки, примерно в 26 раз больше, чем методом суперпозиции.
Исчерпывающее перечисление всех границ магического квадрата заданного порядка, как это делалось ранее, очень утомительно. Часто желательно такое структурированное решение, позволяющее построить границу для квадрата любого порядка. Ниже мы приведем три алгоритма построения границы для нечетных, дважды четных и одинарно-четных квадратов. Эти алгоритмы непрерывного подсчета были открыты в 10 веке арабскими учеными; и их самое раннее из сохранившихся изложений взято из двух трактатов аль-Бузджани и аль-Антаки, хотя они сами не были первооткрывателями. [24] С тех пор было открыто еще много таких алгоритмов.
Нечетные квадраты : Ниже приводится алгоритм, предложенный аль-Бузджани для построения границы для нечетных квадратов. Особенность этого метода в том, что для квадрата порядка n два соседних угла имеют номера n - 1 и n + 1 .
Начиная с ячейки над левым нижним углом, ставим числа поочередно в левый столбец и нижнюю строку, пока не дойдем до средней ячейки. Следующее число записываем в среднюю ячейку только что достигнутого нижнего ряда, после чего заполняем ячейку в левом верхнем углу, затем среднюю ячейку правого столбца, затем правый верхний угол. После этого, начиная с уже заполненной ячейки выше средней ячейки правого столбца, возобновляем поочередное размещение чисел в правом столбце и верхней строке. Как только половина граничных ячеек заполнена, другая половина заполняется числами, дополнительными к противоположным ячейкам. Последующие внутренние границы заполняются таким же образом, пока не заполнится квадрат третьего порядка. [24]
Ниже приведен пример квадрата 9-го порядка.
Вдвойне четный порядок : Ниже приводится метод, данный аль-Антаки. Рассмотрим пустую границу порядка n = 4 k с k ≥ 3. Особенность этого алгоритма в том, что соседние угловые ячейки заняты числами n и n - 1 .
Начиная с левой верхней угловой ячейки, раскладываем последовательные числа группами по четыре: первое рядом с углом, второе и третье внизу, четвертое вверху и так далее, пока не останется в верхний ряд (без учета углов) шесть пустых ячеек. Затем мы пишем следующие два числа сверху и следующие четыре снизу. Затем заполняем верхние углы, сначала левый, затем правый. Следующее число размещаем ниже правого верхнего угла в правом столбце, следующее число с другой стороны в левом столбце. Затем мы возобновляем размещение групп из четырех последовательных чисел в двух столбцах, как и раньше. Как только половина граничных ячеек заполнена, другая половина заполняется числами, дополнительными к противоположным ячейкам. [24]
В примере ниже показана граница для квадрата порядка 16.
Для квадрата порядка 8 мы просто начинаем с шести ячеек.
Одинарно-четный порядок : Для одинарно-четного порядка у нас есть алгоритм, данный аль-Антаки. Здесь угловые ячейки заняты n и n - 1. Ниже приведен пример квадрата 10-го порядка.
Начните с размещения 1 в нижнем ряду рядом с левой угловой ячейкой, затем поместите 2 в верхний ряд. После этого поместите 3 в нижний ряд и поверните вокруг границы против часовой стрелки, помещая следующие цифры, пока в правом столбце не будет достигнуто n - 2. Следующие два числа располагаются в верхних углах ( n - 1 в левом верхнем углу и n в правом верхнем углу). Затем следующие два числа помещаются в левый столбец, после чего возобновляем циклическое размещение чисел до тех пор, пока не будет заполнена половина всех граничных ячеек. Как только половина граничных ячеек заполнена, другая половина заполняется числами, дополнительными к противоположным ячейкам. [24]
Это метод, напоминающий произведение Кронекера двух матриц, который строит магический квадрат nm × nm из магического квадрата n × n и магического квадрата m × m . [77] «Произведение» двух магических квадратов создает магический квадрат более высокого порядка, чем два множимых. Пусть два магических квадрата имеют порядки m и n . Последний квадрат будет иметь порядок m × n . Разделите квадрат порядка m × n на m × m подквадратов так, чтобы всего таких подквадратов было n 2 . В квадрате порядка n уменьшите на 1 значение всех чисел. Умножьте эти уменьшенные значения на m 2 и поместите результаты в соответствующие подквадраты целого квадрата m × n . К подквадратам последнего квадрата добавляются n 2 раза квадраты порядка m . Особенность этого метода построения в том, что каждый магический подквадрат будет иметь разные магические суммы. Квадрат, составленный из таких магических сумм каждого магического подквадрата, снова будет магическим квадратом. Ниже приведен наименьший составной магический квадрат 9-го порядка, состоящий из двух квадратов 3-го порядка.
Поскольку каждый из подквадратов 3×3 можно независимо вращать и отражать в 8 разных квадратов, из этого одного составного квадрата 9×9 мы можем получить 8 9 = 134 217 728 существенно разных составных квадратов 9×9. Можно также получить гораздо больше составных магических квадратов, если мы выберем непоследовательные числа в магических подквадратах, как в версии Ян Хуэя составного магического квадрата 9×9. Следующие наименьшие составные магические квадраты 12-го порядка, состоящие из магических квадратов 3-го и 4-го порядка, приведены ниже.
Для базовых квадратов существует только один существенно отличающийся квадрат 3-го порядка, в то время как существует 880 существенно различных квадратов 4-го порядка, из которых мы можем выбирать. Каждая пара может дать два разных составных квадрата. Поскольку каждый магический подквадрат в каждом составном квадрате может быть выражен в 8 различных формах благодаря вращениям и отражениям, может быть 1×880×8 9 + 880×1×8 16 ≈ 2,476×10 17 существенно отличающихся составных 12×12. магические квадраты, созданные таким образом, с последовательными числами в каждом подквадрате. В общем случае , если существуют cm и cn существенно разные магические квадраты порядка m и n , то мы можем образовать cm × cn × (8 m 2 + 8 n 2 ) составные квадраты порядка mn , при условии , что m ≠ n . Если m = n , то мы можем сформировать ( cm ) 2 × 8m2 составные квадраты порядка m2 .
Когда квадраты имеют вдвойне четный порядок, мы можем построить составной магический квадрат более элегантным способом, чем описанный выше процесс, в том смысле, что каждый магический подквадрат будет иметь одну и ту же магическую константу. Пусть n — порядок главного квадрата, а m — порядок равных подквадратов. Подквадраты заполняются один за другим, в любом порядке, непрерывной последовательностью m 2 /2 меньших чисел (т.е. чисел, меньших или равных n 2 /2) вместе с их дополнениями до n 2 + 1. Каждый подквадрат как целое даст ту же волшебную сумму. Преимущество этого типа составного квадрата в том, что каждый подквадрат заполняется одинаково и их расположение произвольно. Таким образом, знания одной конструкции четного порядка будет достаточно, чтобы заполнить весь квадрат. Более того, если подквадраты заполнить в естественной последовательности, то полученный квадрат будет пандиагональным. Магическая сумма подквадратов связана с магической суммой всего квадрата соотношением n = km . [24]
В приведенных ниже примерах мы разделили квадрат 12-го порядка на девять подквадратов 4-го порядка, заполненных восемью меньшими числами каждый, и в соответствующих ячейках слона (две клетки по диагонали, включая закругления, в подквадрате 4×4) их дополняется до n 2 + 1 = 145. Каждый подквадрат является пандиагональным с магической константой 290; в то время как весь квадрат слева также является пандиагональным с магической константой 870.
В другом примере ниже мы разделили квадрат порядка 12 на четыре квадрата порядка 6. Каждый из квадратов порядка 6 заполнен восемнадцатью маленькими числами и их дополнениями с использованием техники окантовки, данной аль-Антаки. Если убрать заштрихованные границы подквадратов 6-го порядка и образовать квадрат 8-го порядка, то этот квадрат 8-го порядка снова станет магическим квадратом. В полной общности мы можем взять любые m 2 /2 меньших чисел вместе с их дополнениями к n 2 + 1 для заполнения подквадратов, не обязательно в непрерывной последовательности.
В этом методе магический квадрат «умножается» на меджиг-квадрат, чтобы создать магический квадрат большего размера. Тезка этого метода происходит от математической игры под названием «Меджиг», созданной Виллемом Баринком в 2006 году, хотя сам метод намного старше. [ нужна цитация ] Ранний пример магического квадрата, построенного с использованием этого метода, встречается в тексте Ян Хуэя для магического квадрата 6-го порядка. [ нужна цитация ] Метод LUX для построения одиночных четных магических квадратов является частным случаем метода меджига, где только 3 из 24 шаблонов используются для построения квадрата меджига. [ нужна цитата ]
Детали головоломки «Меджиг» представляют собой квадраты 2х2, на которых расположены цифры 0, 1, 2 и 3. Существует три основных шаблона, с помощью которых числа 0, 1, 2 и 3 можно разместить в квадрате 2×2, где 0 находится в верхнем левом углу:
Каждый узор можно отразить и повернуть, чтобы получить 8 эквивалентных узоров, что дает нам в общей сложности 3×8 = 24 узора. Цель головоломки состоит в том, чтобы взять n 2 частей меджига и расположить их в квадрате меджига размером n × n таким образом, чтобы каждая строка, столбец, а также две длинные диагонали, образованные квадратом меджига, в сумме давали 3 n , магическая константа квадрата Меджиг. Меджиг -квадрат n × n может создать магический квадрат 2 n × 2 n , где n > 2.
Учитывая меджиг-квадрат n × n и основу магического квадрата n × n , магический квадрат порядка 2 n × 2 n можно построить следующим образом:
Если предположить, что у нас есть исходная основа магического квадрата, задача состоит в построении квадрата меджига. Для справки суммы каждого куска меджига по строкам, столбцам и диагоналям, обозначенным курсивом, составляют:
Дважды четные квадраты : наименьший четный меджиг-квадрат имеет порядок 2 с магической константой 6. Хотя можно построить меджиг-квадрат 2×2, мы не можем построить из него магический квадрат 4×4, поскольку требуются магические квадраты 2×2. «умножить» его не существует. Тем не менее, построить эти меджиг-квадраты 2×2 стоит. Магическую константу 6 можно разделить на две части тремя способами: 6 = 5 + 1 = 4 + 2 = 3 + 3. Существует 96 таких меджиг-квадратов 2×2. [ нужна цитация ] В приведенных ниже примерах каждый квадрат меджига 2 × 2 создается путем комбинирования разных ориентаций одного куска меджига.
Мы можем использовать меджиг-квадраты 2×2, чтобы построить более крупные, даже упорядоченные меджиг-квадраты. Один из возможных подходов — просто объединить квадраты меджига 2×2 вместе. Другая возможность — обернуть меньшую квадратную сердцевину меджига рамкой. Части квадрата меджига 2х2 могут образовывать угловые части границы. Еще одна возможность — добавить строку и столбец к нечетному упорядоченному квадрату. Пример магического квадрата 8×8 построен ниже путем объединения четырех копий самого левого меджиг-квадрата 2×2, приведенного выше:
Следующий пример построен путем окантовки квадратного ядра меджига 2×2.
Одиночные четные квадраты : квадрата Меджига первого порядка не существует. Таким образом, наименьший нечетный квадрат меджига имеет порядок 3 с магической константой 9. Есть только 7 способов разделить целое число 9, нашу магическую константу, на три части. [ нужна цитация ] Если эти три части соответствуют трем частям меджига в ряду, столбце или диагонали, то соответствующими разделами для нас являются:
Меджиг-квадрат 3х3 можно построить методом проб и ошибок, как показано в крайнем левом квадрате ниже. Другой подход — добавить строку и столбец в квадрат меджига 2×2. В среднем квадрате ниже были добавлены левый столбец и нижняя строка, образуя L-образную границу медджига, к квадрату медджига 2 × 2, указанному ранее. Самый правый квадрат ниже по сути такой же, как средний квадрат, за исключением того, что строка и столбец были добавлены в середине, чтобы сформировать крест, а части квадрата меджига 2 × 2 расположены по углам.
После того как меджиг-квадрат 3х3 построен, его можно преобразовать в магический квадрат 6х6. Например, используя крайний левый меджиг-квадрат 3×3, указанный выше:
Таких меджиг-квадратов 3×3 1 740 800. [78] Самый простой способ построить нечетный меджиг-квадрат более высокого порядка - это обернуть меньший нечетный меджиг-квадрат рамкой, так же, как и в случае с четно-упорядоченными меджиг-квадратами. Другой подход — добавить строку и столбец к четному квадрату меджига. Также можно использовать такие подходы, как метод LUX. В приведенном ниже примере квадрат меджига 5×5 создается путем обертывания границы меджига вокруг квадрата меджига 3×3, заданного ранее:
Решение частично заполненных магических квадратов — популярное математическое занятие. Необходимые методы аналогичны тем, которые используются в головоломках судоку или KenKen , и включают в себя вычисление значений незаполненных квадратов с использованием логики и теории групп перестановок (сетки судоку не являются магическими квадратами, но основаны на родственной идее, называемой греко-латинскими квадратами ). [67]
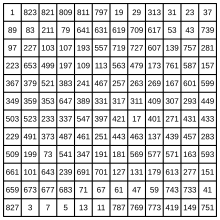
На магические квадраты могут быть наложены некоторые дополнительные ограничения.
Если возведение каждого числа в n- ю степень дает еще один магический квадрат, результатом будет бимагический (n = 2), тримагический (n = 3) или, вообще, мультимагический квадрат .
Магический квадрат, в котором количество букв в названии каждого числа в квадрате порождает другой магический квадрат, называется альфа-магическим квадратом .
Существуют магические квадраты, полностью состоящие из простых чисел. Рудольф Ондрейка (1928–2001) обнаружил следующий магический квадрат простых чисел 3 × 3 , в данном случае девяти простых чисел Чена :
Теорема Грина -Тао подразумевает, что существуют сколь угодно большие магические квадраты, состоящие из простых чисел.
Следующий «обратимый магический квадрат» имеет магическую константу 264 как в перевернутом, так и в прямом направлении: [79]

Когда дополнительным ограничением является отображение какой-либо даты, особенно даты рождения, такие магические квадраты называются магическими квадратами дней рождения. Ранний пример такого магического квадрата дня рождения был создан Шринивасой Рамануджаном . Он создал квадрат 4×4, в который ввел дату своего рождения в формате D–M–CY в верхнем ряду, и произошло волшебство со сложением и вычитанием чисел в квадратах. Не только строки, столбцы и диагонали в сумме дают одно и то же число, но и четыре угла, четыре средних квадрата (17, 9, 24, 89), первая и последняя строки, два средних числа (12, 18, 86). , 23), а в первом и последнем столбцах два средних числа (88, 10, 25, 16) в сумме дают сумму 139.
Вместо сложения чисел в каждой строке, столбце и диагонали можно применить какую-нибудь другую операцию. Например, мультипликативный магический квадрат имеет постоянное произведение чисел. Мультипликативный магический квадрат можно получить из аддитивного магического квадрата, возведя 2 (или любое другое целое число) в степень каждого элемента, поскольку логарифм произведения двух чисел представляет собой сумму логарифмов каждого из них. В качестве альтернативы, если любые 3 числа в строке равны 2 a , 2 b и 2 c , их произведение равно 2 a + b + c , что является постоянным, если a + b + c является постоянным, как это было бы, если бы a , b и c были взяты из обычного (аддитивного) магического квадрата. [80] Например, исходный магический квадрат Ло-Шу выглядит следующим образом:
Другие примеры мультипликативных магических квадратов включают:
По-прежнему используя неитеративный метод Али Скалли, можно получить бесконечное количество мультипликативных магических квадратов комплексных чисел [81] , принадлежащих множеству. В примере ниже действительная и мнимая части являются целыми числами, но они также могут принадлежать всему множеству действительных чисел . Произведение: −352 507 340 640 − 400 599 719 520 i .
Аддитивно-мультипликативные магические квадраты и полумагические квадраты удовлетворяют свойствам как обычных, так и мультипликативных магических квадратов и полумагических квадратов соответственно. [82]
Неизвестно, существуют ли какие-либо аддитивно-мультипликативные магические квадраты размером меньше 7 × 7, но было доказано, что не существует аддитивно-мультипликативных магических квадратов 3 × 3 или 4 × 4, а также не существует аддитивно-мультипликативных полумагических квадратов 3 × 3. [83]

Можно построить магические квадраты, содержащие вместо чисел геометрические фигуры. Такие квадраты, известные как геометрические магические квадраты , были изобретены и названы Ли Саллоузом в 2001 году. [84]
В показанном примере фигуры являются двухмерными. Сэллоуз открыл, что все магические квадраты являются геометрическими; числа, которые появляются в числовых магических квадратах, можно интерпретировать как сокращенное обозначение, указывающее длины отрезков прямых линий, которые представляют собой геометрические «фигуры», встречающиеся в квадрате. То есть числовые магические квадраты представляют собой особый случай геометрического магического квадрата, использующего одномерные формы. [85]

В 2017 году, следуя первоначальным идеям Уильяма Уокингтона и Индера Танехи, Уолтер Трамп построил первый магический квадрат линейной площади (L-AMS) . [86]
Можно рассмотреть и другие двумерные формы, кроме квадратов. В общем случае дизайн, состоящий из N частей, можно считать волшебным, если N частей помечены цифрами от 1 до N , а количество идентичных подпроектов дает одинаковую сумму. Примеры включают магические круги , магические прямоугольники, магические треугольники [87] , магические звезды , магические шестиугольники , магические ромбы. Подъем в измерение приводит к появлению магических сфер, магических цилиндров, магических кубов , магических параллелепипедов, магических тел и других магических гиперкубов .
Возможные магические формы ограничены количеством подмножеств одинакового размера и равной суммы выбранного набора меток. Например, если кто-то предлагает сформировать волшебную фигуру, помечая части {1, 2, 3, 4}, подпроекты должны быть помечены {1,4} и {2,3}. [87]

В 1992 году Демирёрс, Рафраф и Таник опубликовали метод преобразования некоторых магических квадратов в решения с n -ферзями и наоборот. [89]
Магические квадраты порядка 3-9, присвоенные семи планетам и описанные как средства привлечения влияния планет и их ангелов (или демонов) во время магических практик, можно найти в нескольких рукописях по всей Европе, начиная по крайней мере с 15-го века. век. Среди наиболее известных — Liber de Angelis , магическое руководство, написанное около 1440 года и включенное в Кембриджский университет. Либ. МС Дд.xi.45. [90] Текст Liber de Angelis очень близок к тексту De septem Quadaturis Planetarum seu Quadati Magici , еще одного справочника по магии планетарных образов, содержащегося в Кодексе 793 Библиотеки Ягеллонской (Ms BJ 793). [91] Магические операции включают в себя гравировку соответствующего квадрата на пластине, сделанной из металла, присвоенного соответствующей планете, [92] , а также выполнение различных ритуалов. Например, квадрат 3х3, принадлежащий Сатурну, нужно вписать на свинцовую пластину. Оно, в частности, поможет женщинам во время тяжелых родов.
Примерно в 1510 году Генрих Корнелиус Агриппа написал «Оккультную философию» , опираясь на герметические и магические труды Марсилио Фичино и Пико делла Мирандола . В издании 1531 года он разъяснил магические свойства семи магических квадратов 3-9 порядков, каждый из которых связан с одной из астрологических планет, во многом так же, как это делали в более старых текстах. Эта книга имела большое влияние во всей Европе до контрреформации , и магические квадраты Агриппы, иногда называемые камеями, продолжают использоваться в современной церемониальной магии во многом так же, как он предписывал впервые. [93]

Чаще всего эти камеи используются для создания образца, на основе которого можно построить символы духов, ангелов или демонов ; буквы имени сущности преобразуются в цифры, а линии прорисовываются по узору, который эти последовательные цифры образуют на камее. В магическом контексте термин «магический квадрат» также применяется к множеству словесных квадратов или числовых квадратов, встречающихся в магических гримуарах , включая те, которые не следуют какому-либо очевидному шаблону, и даже те, которые имеют разное количество строк и столбцов. Обычно они предназначены для использования в качестве талисманов. Например, следующие квадраты: Квадрат Сатора , один из самых известных магических квадратов, встречающийся во многих гримуарах, включая « Ключ Соломона» ; квадрат «для преодоления зависти» из «Книги силы» ; [94] и два квадрата из «Книги Священной Магии Абрамелина Мага» , первый вызывает иллюзию великолепного дворца, а второй нужно носить на голове ребенка во время ангельского призыва :

Магический квадрат в музыкальной композиции – это не блок цифр – это порождающий принцип, который нужно изучить и познать близко, воспринимать внутренне как многомерную проекцию в эту обширную (хаотичную!) область внутреннего уха – пространство. /time тигель – место, где зарождается музыка. ... Проецируемый на страницу магический квадрат представляет собой мертвое черное скопление цифр; настройтесь, и вы услышите мощное вращающееся динамо музыкальных образов, сияющее нуменом и люменом. [98]
Исомура Киттоку.
Исомура Киттоку.
Исомура Киттоку.
Исомура Киттоку.
Два соответствующих приза еще предстоит выиграть!
Паркер-сквер — талисман для людей, которые пытаются, но в конечном итоге терпят неудачу.
Более того, это магический квадрат, образец, согласно которому Бог предположительно поручил древним евреям черпать силу из имен или их числовых эквивалентов.
Мне нравится, когда они приводят занудного парня из ФБР, чтобы объяснить концепцию «магического квадрата», и он делает это, рассказывая нам, что магические квадраты существуют уже какое-то время, и больше ничего.
Если я ничего не пропустил, то на данный момент у меня есть только то, что магические квадраты — это квадраты, которые люди когда-то считали магическими.