Сила

Влияние, которое может изменить движение объекта

Сила — это влияние, которое может заставить объект изменить свою скорость, если оно не уравновешено другими силами. Концепция силы делает повседневное понятие толкания или притягивания математически точным. Поскольку важны как величина , так и направление силы, сила является векторной величиной. Единицей силы в системе СИ является ньютон (Н) , а сила часто обозначается символом F.

Сила играет важную роль в классической механике. Концепция силы является центральной для всех трех законов движения Ньютона . Типы сил, часто встречающиеся в классической механике, включают упругие , фрикционные , контактные или «нормальные» силы и гравитационные . Вращательная версия силы — это крутящий момент , который вызывает изменения скорости вращения объекта. В протяженном теле каждая часть часто прикладывает силы к соседним частям; распределение таких сил по телу — это внутреннее механическое напряжение . В равновесии эти напряжения не вызывают ускорения тела, поскольку силы уравновешивают друг друга. Если они не находятся в равновесии, они могут вызвать деформацию твердых материалов или течение в жидкостях .

В современной физике , которая включает в себя теорию относительности и квантовую механику , законы, управляющие движением, пересмотрены, чтобы полагаться на фундаментальные взаимодействия как на конечный источник силы. Однако понимание силы, предоставляемое классической механикой, полезно для практических целей. ^[1]

Разработка концепции

Философы древности использовали концепцию силы при изучении неподвижных и движущихся объектов и простых машин , но такие мыслители, как Аристотель и Архимед, сохранили фундаментальные ошибки в понимании силы. Отчасти это было связано с неполным пониманием иногда неочевидной силы трения и, следовательно, неадекватным взглядом на природу естественного движения. ^[2] Фундаментальной ошибкой было убеждение, что сила необходима для поддержания движения, даже с постоянной скоростью. Большинство предыдущих заблуждений о движении и силе были в конечном итоге исправлены Галилео Галилеем и сэром Исааком Ньютоном . Благодаря своей математической проницательности Ньютон сформулировал законы движения , которые не улучшались более двухсот лет. ^[3]

К началу 20 века Эйнштейн разработал теорию относительности , которая правильно предсказала действие сил на объекты с увеличивающимися импульсами около скорости света, а также дала представление о силах, создаваемых гравитацией и инерцией . С современным пониманием квантовой механики и технологий, которые могут ускорять частицы до скорости, близкой к скорости света, физика элементарных частиц разработала Стандартную модель для описания сил между частицами, меньшими, чем атомы. Стандартная модель предсказывает, что обменивающиеся частицы, называемые калибровочными бозонами, являются фундаментальными средствами, с помощью которых силы испускаются и поглощаются. Известно только четыре основных взаимодействия: в порядке убывания силы это: сильное , электромагнитное , слабое и гравитационное . ^{[4] : 2–10  [5] : 79} Наблюдения физики частиц высоких энергий, проведенные в 1970-х и 1980-х годах, подтвердили, что слабые и электромагнитные силы являются выражениями более фундаментального электрослабого взаимодействия. ^[6]

Доньютоновские концепции

Аристотель описал силу как нечто, заставляющее объект совершать «неестественное движение».

С античности концепция силы признавалась неотъемлемой частью функционирования каждой из простых машин . Механическое преимущество, даваемое простой машиной, позволяло использовать меньшую силу в обмен на силу, действующую на большем расстоянии за тот же объем работы . Анализ характеристик сил в конечном итоге достиг кульминации в работе Архимеда , который был особенно известен тем, что сформулировал трактовку выталкивающих сил, присущих жидкостям . ^[2]

Аристотель дал философское обсуждение концепции силы как неотъемлемой части аристотелевской космологии . По мнению Аристотеля, земная сфера содержала четыре элемента , которые останавливались в разных «естественных местах» в ней. Аристотель считал, что неподвижные объекты на Земле, состоящие в основном из элементов земли и воды, находились на своем естественном месте, когда находились на земле, и что они остаются такими, если их оставить в покое. Он различал врожденную тенденцию объектов находить свое «естественное место» (например, падение тяжелых тел), что приводило к «естественному движению», и неестественное или вынужденное движение, которое требовало постоянного приложения силы. ^[7] Эта теория, основанная на повседневном опыте того, как движутся объекты, например, постоянное приложение силы, необходимое для поддержания движения тележки, имела концептуальные проблемы с объяснением поведения снарядов , например, полета стрел. Лучник заставляет стрелу двигаться в начале полета, и затем она летит по воздуху, хотя на нее не действует никакая различимая эффективная причина. Аристотель знал об этой проблеме и предположил, что воздух, вытесняемый по пути снаряда, переносит снаряд к цели. Это объяснение требует наличия непрерывной среды, такой как воздух, для поддержания движения. ^[8]

Хотя физика Аристотеля подвергалась критике еще в VI веке, ^{[9] [10]} ее недостатки не были исправлены до работы Галилео Галилея в XVII веке , на которого повлияла идея позднего Средневековья о том, что объекты в вынужденном движении обладают внутренней силой импульса . Галилей построил эксперимент, в котором камни и пушечные ядра катились вниз по наклонной плоскости, чтобы опровергнуть теорию движения Аристотеля . Он показал, что тела ускоряются под действием силы тяжести до степени, которая не зависит от их массы, и утверждал, что объекты сохраняют свою скорость, если на них не действует сила, например трение . ^[11] Идея Галилея о том, что сила нужна для изменения движения, а не для его поддержания, далее улучшенная Исааком Бекманом , Рене Декартом и Пьером Гассенди , стала ключевым принципом физики Ньютона. ^[12]

В начале 17 века, до «Начал» Ньютона , термин «сила» ( лат . vis ) применялся ко многим физическим и нефизическим явлениям, например, для ускорения точки. Произведение массы точки на квадрат ее скорости было названо Лейбницем vis viva (живая сила) . Современное понятие силы соответствует ньютоновскому vis motrix (ускоряющая сила). ^[13]

Ньютоновская механика

Сэр Исаак Ньютон описал движение всех объектов, используя концепции инерции и силы. В 1687 году Ньютон опубликовал свой главный труд Philosophiæ Naturalis Principia Mathematica . ^{[3] [14]} В этой работе Ньютон изложил три закона движения, которые до сих пор доминируют в описании сил в физике. ^[14] Точные способы выражения законов Ньютона развивались в ногу с новыми математическими подходами. ^[15]

Первый закон

Первый закон движения Ньютона гласит, что естественное поведение объекта, находящегося в состоянии покоя, заключается в том, чтобы продолжать оставаться в состоянии покоя, а естественное поведение объекта, движущегося с постоянной скоростью по прямой линии, заключается в том, чтобы продолжать двигаться с этой постоянной скоростью вдоль этой прямой линии. ^[14] Последнее следует из первого из-за принципа, что законы физики одинаковы для всех инерциальных наблюдателей , т. е. всех наблюдателей, которые не чувствуют себя находящимися в движении. Наблюдатель, движущийся в тандеме с объектом, будет видеть его находящимся в состоянии покоя. Таким образом, его естественным поведением будет оставаться в состоянии покоя по отношению к этому наблюдателю, что означает, что наблюдатель, который видит его движущимся с постоянной скоростью по прямой линии, будет видеть его продолжающим это делать. ^{[16] : 1–7}

Сэр Исаак Ньютон в 1689 году. Его «Начала» изложили три закона движения на геометрическом языке, тогда как современная физика использует дифференциальное исчисление и векторы .

Второй закон

Согласно первому закону, движение с постоянной скоростью по прямой линии не нуждается в причине. Изменение движения требует причины, и второй закон Ньютона дает количественное соотношение между силой и изменением движения. Второй закон Ньютона гласит, что чистая сила, действующая на объект, равна скорости , с которой его импульс изменяется со временем . Если масса объекта постоянна, этот закон подразумевает, что ускорение объекта прямо пропорционально чистой силе, действующей на объект, направлено в направлении чистой силы и обратно пропорционально массе объекта . ^{[17] : 204–207}

Современное изложение второго закона Ньютона представляет собой векторное уравнение: F = d p d t , {\displaystyle \mathbf {F} ={\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}},} где — импульс системы, а — чистая ( векторная сумма ) сила. ^{[17] : 399} Если тело находится в равновесии, то по определению чистая сила равна нулю (уравновешенные силы тем не менее могут присутствовать). Напротив, второй закон гласит, что если на объект действует неуравновешенная сила , то это приведет к изменению импульса объекта с течением времени. ^[14] ${\displaystyle \mathbf {p} }$ ${\displaystyle \mathbf {F} }$

В обычных инженерных приложениях масса в системе остается постоянной, что позволяет использовать простую алгебраическую форму для второго закона. По определению импульса, где m — масса , а — скорость . ^{[4] : 9-1,9-2} Если второй закон Ньютона применяется к системе с постоянной массой , m можно вынести за пределы оператора производной. Тогда уравнение становится таким: Подставляя определение ускорения , выводится алгебраическая версия второго закона Ньютона : F = m a . {\displaystyle \mathbf {F} =m\mathbf {a} .} $${\displaystyle \mathbf {F} ={\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}={\frac {\mathrm {d} \left(m\mathbf {v} \right)}{\mathrm {d} t}},}$$ ${\displaystyle \mathbf {v} }$ $${\displaystyle \mathbf {F} =m{\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}.}$$

Третий закон

Всякий раз, когда одно тело оказывает силу на другое, последнее одновременно оказывает равную и противоположную силу на первое. В векторной форме, если - сила тела 1 на тело 2 и сила тела 2 на тело 1, то Этот закон иногда называют законом действия-противодействия , с называемыми действием и реакцией . ${\displaystyle \mathbf {F} _{1,2}}$ ${\displaystyle \mathbf {F} _{2,1}}$ $${\displaystyle \mathbf {F} _{1,2}=-\mathbf {F} _{2,1}.}$$ ${\displaystyle \mathbf {F} _{1,2}}$ ${\displaystyle -\mathbf {F} _{2,1}}$

Третий закон Ньютона является результатом применения симметрии к ситуациям, где силы могут быть приписаны присутствию различных объектов. Третий закон означает, что все силы являются взаимодействиями между различными телами. ^{[18] [19]} и, таким образом, не существует такого понятия, как однонаправленная сила или сила, которая действует только на одно тело.

В системе, состоящей из объекта 1 и объекта 2, чистая сила, действующая на систему из-за их взаимного взаимодействия, равна нулю: В более общем смысле, в замкнутой системе частиц все внутренние силы уравновешены. Частицы могут ускоряться относительно друг друга, но центр масс системы не будет ускоряться. Если на систему действует внешняя сила, она заставит центр масс ускоряться пропорционально величине внешней силы, деленной на массу системы. ^{[4] : 19-1  [5]} $${\displaystyle \mathbf {F} _{1,2}+\mathbf {F} _{2,1}=0.}$$

Объединяя Второй и Третий законы Ньютона, можно показать, что линейный импульс системы сохраняется в любой замкнутой системе . В системе из двух частиц, если есть импульс объекта 1 и импульс объекта 2, то Используя аналогичные аргументы, это можно обобщить на систему с произвольным числом частиц. В общем, пока все силы обусловлены взаимодействием объектов с массой, можно определить систему таким образом, что чистый импульс никогда не теряется и не приобретается. ^{[4] : гл.12  [5]} ${\displaystyle \mathbf {p} _{1}}$ ${\displaystyle \mathbf {p} _{2}}$ $${\displaystyle {\frac {\mathrm {d} \mathbf {p} _{1}}{\mathrm {d} t}}+{\frac {\mathrm {d} \mathbf {p} _{2}}{\mathrm {d} t}}=\mathbf {F} _{1,2}+\mathbf {F} _{2,1}=0.}$$

Определение «силы»

Некоторые учебники используют второй закон Ньютона в качестве определения силы. ^{[20] [21] [22] [23]} Однако для того, чтобы уравнение для постоянной массы имело какое-либо предсказательное содержание, его необходимо объединить с дополнительной информацией. ^{[24] [4] : 12-1} Более того, вывод о наличии силы из-за ускорения тела справедлив только в инерциальной системе отсчета. ^{[5] : 59} На вопрос о том, какие аспекты законов Ньютона следует принимать в качестве определений, а какие следует считать содержащими физическое содержание, отвечали разными способами, ^{[25] [26] : vii} которые в конечном итоге не влияют на то, как теория используется на практике. ^[25] Известные физики, философы и математики, которые стремились к более четкому определению концепции силы, включают Эрнста Маха и Уолтера Нолла . ^{[27] [28]} ${\displaystyle \mathbf {F} =m\mathbf {a} }$ ${\displaystyle m}$

Объединение сил

Сложение векторов и результаты в ${\displaystyle v_{1}}$ ${\displaystyle v_{2}}$ ${\displaystyle v}$

Силы действуют в определенном направлении и имеют размеры, зависящие от того, насколько сильным является толчок или тяга. Из-за этих характеристик силы классифицируются как « векторные величины ». Это означает, что силы следуют другому набору математических правил, чем физические величины, которые не имеют направления (обозначаемые скалярными величинами). Например, при определении того, что происходит, когда две силы действуют на один и тот же объект, необходимо знать как величину, так и направление обеих сил, чтобы вычислить результат . Если обе эти части информации неизвестны для каждой силы, ситуация неоднозначна. ^{[17] : 197}

Исторически силы впервые количественно исследовались в условиях статического равновесия , когда несколько сил уравновешивали друг друга. Такие эксперименты демонстрируют важнейшие свойства того, что силы являются аддитивными векторными величинами : они имеют величину и направление. ^[3] Когда две силы действуют на точечную частицу , результирующая сила, равнодействующая (также называемая чистой силой ), может быть определена с помощью правила параллелограмма сложения векторов : сложение двух векторов, представленных сторонами параллелограмма, дает эквивалентный результирующий вектор, который по величине и направлению равен поперечной оси параллелограмма. Величина равнодействующей варьируется от разности величин двух сил до их суммы в зависимости от угла между их линиями действия. ^{[4] : гл.12  [5]}

Диаграммы свободного тела блока на плоской поверхности и наклонной плоскости . Силы разрешаются и суммируются для определения их величин и чистой силы.

Диаграммы свободного тела можно использовать как удобный способ отслеживания сил, действующих на систему. В идеале эти диаграммы рисуются с сохранением углов и относительных величин векторов силы, чтобы можно было выполнить графическое сложение векторов для определения чистой силы. ^[29]

Помимо сложения, силы также могут быть разложены на независимые компоненты под прямым углом друг к другу. Горизонтальная сила, направленная на северо-восток, может быть разделена на две силы, одна из которых направлена ​​на север, а другая — на восток. Суммирование этих компонентных сил с помощью векторного сложения дает исходную силу. Разложение векторов силы на компоненты набора базисных векторов часто является более математически чистым способом описания сил, чем использование величин и направлений. ^[30] Это происходит потому, что для ортогональных компонентов компоненты векторной суммы однозначно определяются скалярным сложением компонентов отдельных векторов. Ортогональные компоненты независимы друг от друга, поскольку силы, действующие под углом девяносто градусов друг к другу, не оказывают влияния на величину или направление друг друга. Выбор набора ортогональных базисных векторов часто осуществляется путем рассмотрения того, какой набор базисных векторов сделает математику наиболее удобной. Желательно выбрать базисный вектор, который имеет то же направление, что и одна из сил, поскольку тогда эта сила будет иметь только один ненулевой компонент. Ортогональные векторы силы могут быть трехмерными, причем третий компонент находится под прямым углом к ​​двум другим. ^{[4] : гл.12  [5]}

Равновесие

Когда все силы, действующие на объект, уравновешены, то объект находится в состоянии равновесия . ^{[17] : 566} Следовательно, равновесие наступает, когда результирующая сила, действующая на точечную частицу, равна нулю (то есть векторная сумма всех сил равна нулю). Когда мы имеем дело с протяженным телом, также необходимо, чтобы чистый крутящий момент был равен нулю. Тело находится в статическом равновесии относительно системы отсчета, если оно покоится и не ускоряется, тогда как тело в динамическом равновесии движется с постоянной скоростью по прямой линии, то есть движется, но не ускоряется. То, что один наблюдатель видит как статическое равновесие, другой может видеть как динамическое равновесие и наоборот. ^{[17] : 566}

Статичный

Статическое равновесие было понято задолго до изобретения классической механики. Объекты, которые не ускоряются, имеют нулевую чистую силу, действующую на них. ^[31]

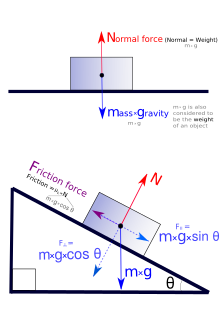
Простейший случай статического равновесия происходит, когда две силы равны по величине, но противоположны по направлению. Например, объект на ровной поверхности тянется (притягивается) вниз к центру Земли силой тяжести. В то же время, сила прикладывается поверхностью, которая сопротивляется силе, направленной вниз, с равной силой, направленной вверх (называемой нормальной силой ). Ситуация создает нулевую чистую силу и, следовательно, отсутствие ускорения. ^[3]

Надавливание на объект, который лежит на фрикционной поверхности, может привести к ситуации, когда объект не будет двигаться, поскольку приложенная сила противостоит статическому трению , возникающему между объектом и поверхностью стола. В ситуации без движения статическая сила трения точно уравновешивает приложенную силу, что приводит к отсутствию ускорения. Статическое трение увеличивается или уменьшается в ответ на приложенную силу до верхнего предела, определяемого характеристиками контакта между поверхностью и объектом. ^[3]

Статическое равновесие между двумя силами является наиболее обычным способом измерения сил с использованием простых устройств, таких как весы и пружинные весы . Например, объект, подвешенный на вертикальных пружинных весах, испытывает силу тяжести, действующую на объект, уравновешенную силой, приложенной «силой реакции пружины», которая равна весу объекта. Используя такие инструменты, были открыты некоторые количественные законы силы: сила тяжести пропорциональна объему для объектов постоянной плотности (широко используется на протяжении тысячелетий для определения стандартных весов); принцип Архимеда для плавучести; анализ рычага Архимедом ; закон Бойля для давления газа; и закон Гука для пружин. Все они были сформулированы и экспериментально проверены до того, как Исаак Ньютон изложил свои Три закона движения . ^{[3] [4] : гл.12  [5]}

Динамичный

Галилео Галилей был первым, кто указал на внутренние противоречия, содержащиеся в описании сил Аристотелем.

Динамическое равновесие было впервые описано Галилеем, который заметил, что некоторые предположения аристотелевской физики противоречат наблюдениям и логике . Галилей понял, что простое сложение скоростей требует, чтобы концепция «абсолютной системы отсчета покоя » не существовала. Галилей пришел к выводу, что движение с постоянной скоростью полностью эквивалентно покою. Это противоречило понятию Аристотеля о «естественном состоянии» покоя, к которому естественным образом приближаются объекты с массой. Простые эксперименты показали, что понимание Галилеем эквивалентности постоянной скорости и покоя было правильным. Например, если бы моряк сбросил пушечное ядро ​​с вороньего гнезда корабля, движущегося с постоянной скоростью, аристотелевская физика заставила бы пушечное ядро ​​падать прямо вниз, пока корабль двигался бы под ним. Таким образом, в аристотелевской вселенной падающее пушечное ядро ​​приземлилось бы позади подножия мачты движущегося корабля. Когда этот эксперимент проводится на самом деле, пушечное ядро ​​всегда падает у подножия мачты, как будто пушечное ядро ​​знает, что нужно плыть вместе с кораблем, несмотря на то, что оно отделено от него. Поскольку к пушечному ядру не прикладывается никакая горизонтальная сила, направленная вперед, когда оно падает, остается только одно заключение: пушечное ядро ​​продолжает двигаться с той же скоростью, что и лодка, когда она падает. Таким образом, не требуется никакой силы, чтобы поддерживать движение пушечного ядра с постоянной скоростью. ^[11]

Более того, любой объект, движущийся с постоянной скоростью, должен подвергаться воздействию нулевой чистой силы (результирующей силы). Это определение динамического равновесия: когда все силы на объекте уравновешиваются, но он все еще движется с постоянной скоростью. Простой случай динамического равновесия происходит при движении с постоянной скоростью по поверхности с кинетическим трением . В такой ситуации сила прикладывается в направлении движения, в то время как сила кинетического трения точно противодействует приложенной силе. Это приводит к нулевой чистой силе, но поскольку объект начал движение с ненулевой скоростью, он продолжает двигаться с ненулевой скоростью. Аристотель неверно истолковал это движение как вызванное приложенной силой. Если принять во внимание кинетическое трение, то станет ясно, что нет чистой силы, вызывающей движение с постоянной скоростью. ^{[4] : гл.12  [5]}

Примеры сил в классической механике

Некоторые силы являются следствиями фундаментальных сил. В таких ситуациях идеализированные модели могут быть использованы для получения физического понимания. Например, каждый твердый объект считается жестким телом . ^{[ необходима цитата ]}

Гравитационная сила или Гравитация

Изображения свободно падающего баскетбольного мяча, снятые стробоскопом с частотой 20 вспышек в секунду. Единицы расстояния справа кратны примерно 12 миллиметрам. Баскетбольный мяч начинает движение в состоянии покоя. В момент первой вспышки (расстояние равно нулю) его отпускают, после чего количество упавших единиц равно квадрату количества вспышек.

То, что мы сейчас называем гравитацией, не было идентифицировано как универсальная сила до работы Исаака Ньютона. До Ньютона тенденция объектов падать к Земле не понималась как связанная с движениями небесных объектов. Галилей сыграл важную роль в описании характеристик падающих объектов, определив, что ускорение каждого объекта в свободном падении было постоянным и независящим от массы объекта. Сегодня это ускорение, вызванное гравитацией к поверхности Земли, обычно обозначается как и имеет величину около 9,81 метра в секунду в квадрате (это измерение берется от уровня моря и может меняться в зависимости от местоположения) и указывает на центр Земли. ^[32] Это наблюдение означает, что сила гравитации на объект на поверхности Земли прямо пропорциональна массе объекта. Таким образом, объект, имеющий массу будет испытывать силу: ${\displaystyle \mathbf {g} }$ ${\displaystyle m}$ $${\displaystyle \mathbf {F} =m\mathbf {g} .}$$

Для объекта в свободном падении эта сила не встречает сопротивления, и чистая сила на объекте равна его весу. Для объектов, не находящихся в свободном падении, сила тяжести противостоит силам реакции, приложенным их опорами. Например, человек, стоящий на земле, испытывает нулевую чистую силу, поскольку нормальная сила (сила реакции) прикладывается землей вверх к человеку, которая уравновешивает его вес, направленный вниз. ^{[4] : гл.12  [5]}

Вклад Ньютона в теорию гравитации состоял в объединении движений небесных тел, которые, как предполагал Аристотель, находились в естественном состоянии постоянного движения, с падающим движением, наблюдаемым на Земле. Он предложил закон гравитации , который мог бы объяснить небесные движения, описанные ранее с использованием законов Кеплера о движении планет . ^[33]

Ньютон пришел к выводу, что эффекты гравитации могут наблюдаться по-разному на больших расстояниях. В частности, Ньютон определил, что ускорение Луны вокруг Земли можно приписать той же силе гравитации, если ускорение, вызванное гравитацией, уменьшается как закон обратных квадратов . Кроме того, Ньютон понял, что ускорение тела, вызванное гравитацией, пропорционально массе другого притягивающего тела. ^[33] Объединение этих идей дает формулу, которая связывает массу ( ) и радиус ( ) Земли с гравитационным ускорением: g = − G m ⊕ R ⊕ 2 r ^ , {\displaystyle \mathbf {g} =-{\frac {Gm_{\oplus }}{{R_{\oplus }}^{2}}}{\hat {\mathbf {r} }},} где направление вектора задается как , — единичный вектор, направленный наружу от центра Земли. ^[14] ${\displaystyle m_{\oplus }}$ ${\displaystyle R_{\oplus }}$ ${\displaystyle {\hat {\mathbf {r} }}}$

В этом уравнении размерная константа используется для описания относительной силы гравитации. Эта константа стала известна как ньютоновская постоянная гравитации , хотя ее значение было неизвестно при жизни Ньютона. Только в 1798 году Генри Кавендиш смог провести первое измерение с использованием крутильных весов ; это широко освещалось в прессе как измерение массы Земли, поскольку знание могло позволить решить для массы Земли, учитывая приведенное выше уравнение. Ньютон понял, что поскольку все небесные тела следуют одним и тем же законам движения , его закон гравитации должен быть универсальным. Кратко говоря, закон тяготения Ньютона гласит, что сила, действующая на сферический объект массы из-за гравитационного притяжения массы, равна F = − G m 1 m 2 r 2 r ^ , {\displaystyle \mathbf {F} =-{\frac {Gm_{1}m_{2}}{r^{2}}}{\hat {\mathbf {r} }},} где — расстояние между центрами масс двух объектов, а — единичный вектор, направленный от центра первого объекта к центру второго объекта. ^[14] ${\displaystyle G}$ ${\displaystyle G}$ ${\displaystyle G}$ ${\displaystyle m_{1}}$ ${\displaystyle m_{2}}$ ${\displaystyle r}$ ${\displaystyle {\hat {\mathbf {r} }}}$

Эта формула была достаточно мощной, чтобы стать основой для всех последующих описаний движения в Солнечной системе вплоть до 20-го века. В то время были изобретены сложные методы анализа возмущений ^[34] для расчета отклонений орбит из-за влияния нескольких тел на планету , луну , комету или астероид . Формализм был достаточно точным, чтобы позволить математикам предсказать существование планеты Нептун до того, как она была обнаружена. ^[35]

Электромагнитный

Электростатическая сила была впервые описана в 1784 году Кулоном как сила, которая существует между двумя зарядами . ^{[36] : 519} Свойства электростатической силы заключались в том, что она изменялась по закону обратных квадратов, направленному в радиальном направлении , была как притягивающей, так и отталкивающей (имела внутреннюю полярность ), не зависела от массы заряженных объектов и следовала принципу суперпозиции . Закон Кулона объединяет все эти наблюдения в одно краткое утверждение. ^[37]

Последующие математики и физики обнаружили, что конструкция электрического поля полезна для определения электростатической силы, действующей на электрический заряд в любой точке пространства. Электрическое поле было основано на использовании гипотетического « тестового заряда » в любой точке пространства, а затем на использовании закона Кулона для определения электростатической силы. ^{[38] : 4-6–4-8} Таким образом, электрическое поле в любой точке пространства определяется как , где — величина гипотетического тестового заряда. Аналогично, идея магнитного поля была введена для выражения того, как магниты могут влиять друг на друга на расстоянии. Закон силы Лоренца дает силу, действующую на тело с зарядом из-за электрических и магнитных полей: F = q ( E + v × B ) , {\displaystyle \mathbf {F} =q\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right),} где — электромагнитная сила, — электрическое поле в месте расположения тела, — магнитное поле, — скорость частицы. Магнитный вклад в силу Лоренца — это векторное произведение вектора скорости на магнитное поле. ^{[39] [40] : 482} $${\displaystyle \mathbf {E} ={\mathbf {F} \over {q}},}$$ ${\displaystyle q}$ ${\displaystyle q}$ ${\displaystyle \mathbf {F} }$ ${\displaystyle \mathbf {E} }$ ${\displaystyle \mathbf {B} }$ ${\displaystyle \mathbf {v} }$

Происхождение электрических и магнитных полей не было полностью объяснено до 1864 года, когда Джеймс Клерк Максвелл объединил ряд более ранних теорий в набор из 20 скалярных уравнений, которые позже были переформулированы в 4 векторных уравнения Оливером Хевисайдом и Джозайей Уиллардом Гиббсом . ^[41] Эти « уравнения Максвелла » полностью описывали источники полей как неподвижные и движущиеся заряды, а также взаимодействие самих полей. Это привело Максвелла к открытию того, что электрические и магнитные поля могут «самогенерироваться» посредством волны , которая распространяется со скоростью, которую он вычислил как скорость света . Это понимание объединило зарождающиеся поля электромагнитной теории с оптикой и привело непосредственно к полному описанию электромагнитного спектра . ^[42]

Нормальный

F _N представляет собой нормальную силу, действующую на объект.

Когда объекты находятся в контакте, сила, действующая непосредственно между ними, называется нормальной силой, составляющей полной силы в системе, приложенной нормально к интерфейсу между объектами. ^{[36] : 264} Нормальная сила тесно связана с третьим законом Ньютона. Нормальная сила, например, отвечает за структурную целостность столов и полов, а также является силой, которая реагирует всякий раз, когда внешняя сила толкает твердый объект. Примером нормальной силы в действии является сила удара объекта, врезающегося в неподвижную поверхность. ^{[4] : гл.12  [5]}

Трение

Трение — это сила, которая препятствует относительному движению двух тел. В макроскопическом масштабе сила трения напрямую связана с нормальной силой в точке контакта. Существуют две широкие классификации сил трения: статическое трение и кинетическое трение . ^{[17] : 267}

Сила трения покоя ( ) будет точно противодействовать силам, приложенным к объекту параллельно поверхности, до предела, определяемого коэффициентом трения покоя ( ), умноженным на нормальную силу ( ). Другими словами, величина силы трения покоя удовлетворяет неравенству: ${\displaystyle \mathbf {F} _{\mathrm {sf} }}$ ${\displaystyle \mu _{\mathrm {sf} }}$ ${\displaystyle \mathbf {F} _{\text{N}}}$ $${\displaystyle 0\leq \mathbf {F} _{\mathrm {sf} }\leq \mu _{\mathrm {sf} }\mathbf {F} _{\mathrm {N} }.}$$

Сила кинетического трения ( ) обычно не зависит ни от приложенных сил, ни от движения объекта. Таким образом, величина силы равна: ${\displaystyle F_{\mathrm {kf} }}$ $${\displaystyle \mathbf {F} _{\mathrm {kf} }=\mu _{\mathrm {kf} }\mathbf {F} _{\mathrm {N} },}$$

где - коэффициент кинетического трения . Коэффициент кинетического трения обычно меньше коэффициента статического трения. ^{[17] : 267–271} ${\displaystyle \mu _{\mathrm {kf} }}$

Напряжение

Силы натяжения можно моделировать с помощью идеальных струн, которые не имеют массы, трения, не ломаются и не растягиваются. Их можно комбинировать с идеальными блоками , которые позволяют идеальным струнам менять физическое направление. Идеальные струны передают силы натяжения мгновенно в парах действия-противодействия, так что если два объекта соединены идеальной струной, любая сила, направленная вдоль струны первым объектом, сопровождается силой, направленной вдоль струны в противоположном направлении вторым объектом. ^[43] Соединяя одну и ту же струну несколько раз с одним и тем же объектом с помощью конфигурации, которая использует подвижные блоки, силу натяжения на грузе можно умножить. Для каждой струны, которая действует на груз, другой фактор силы натяжения в струне действует на груз. Такие машины обеспечивают механическое преимущество для соответствующего увеличения длины смещенной струны, необходимой для перемещения груза. Эти тандемные эффекты в конечном итоге приводят к сохранению механической энергии, поскольку работа, выполняемая над грузом, одинакова независимо от того, насколько сложна машина. ^{[4] : гл.12  [5] [44]}

Весна

F _k — сила, действующая на пружину при нагрузке

Простая упругая сила действует, чтобы вернуть пружину к ее естественной длине. Идеальная пружина считается невесомой, не подверженной трению, неломкой и бесконечно растягиваемой. Такие пружины оказывают силы, которые толкают при сжатии или тянут при растяжении пропорционально смещению пружины от ее положения равновесия. ^[45] Эта линейная зависимость была описана Робертом Гуком в 1676 году, в честь которого и назван закон Гука . Если — смещение, то сила, оказываемая идеальной пружиной, равна: F = − k Δ x , {\displaystyle \mathbf {F} =-k\Delta \mathbf {x} ,} где — константа пружины (или силовая константа), которая является частной для пружины. Знак минус учитывает тенденцию силы действовать в противовес приложенной нагрузке. ^{[4] : гл.12  [5]} ${\displaystyle \Delta x}$ ${\displaystyle k}$

Центростремительный

Для объекта, совершающего равномерное круговое движение , чистая сила, действующая на объект, равна: ^[46] F = − m v 2 r r ^ , {\displaystyle \mathbf {F} =-{\frac {mv^{2}}{r}}{\hat {\mathbf {r} }},} где — масса объекта, — скорость объекта, — расстояние до центра круговой траектории, — единичный вектор, направленный в радиальном направлении наружу от центра. Это означает, что чистая сила, ощущаемая объектом, всегда направлена ​​к центру криволинейной траектории. Такие силы действуют перпендикулярно вектору скорости, связанному с движением объекта, и, следовательно, не изменяют скорость объекта (величину скорости), а только направление вектора скорости. В более общем смысле, чистая сила, ускоряющая объект, может быть разложена на компонент, перпендикулярный траектории, и компонент, касательный к траектории. Это дает как тангенциальную силу, которая ускоряет объект, либо замедляя его, либо ускоряя, так и радиальную (центростремительную) силу, которая изменяет его направление. ^{[4] : гл.12  [5]} ${\displaystyle m}$ ${\displaystyle v}$ ${\displaystyle r}$ ${\displaystyle {\hat {\mathbf {r} }}}$

Механика сплошной среды

Когда сила сопротивления ( ), связанная с сопротивлением воздуха, становится равной по величине силе тяжести падающего объекта ( ), объект достигает состояния динамического равновесия при конечной скорости . ${\displaystyle \mathbf {F} _{\text{d}}}$ ${\displaystyle \mathbf {F} _{\text{g}}}$

Законы Ньютона и ньютоновская механика в целом были впервые разработаны для описания того, как силы влияют на идеализированные точечные частицы, а не на трехмерные объекты. В реальной жизни материя имеет протяженную структуру, и силы, которые действуют на одну часть объекта, могут влиять на другие части объекта. Для ситуаций, когда решетка, удерживающая вместе атомы в объекте, способна течь, сжиматься, расширяться или иным образом изменять форму, теории механики сплошных сред описывают, как силы влияют на материал. Например, в протяженных жидкостях различия в давлении приводят к тому, что силы направляются вдоль градиентов давления следующим образом: $${\displaystyle {\frac {\mathbf {F} }{V}}=-\mathbf {\nabla } P,}$$

где - объем объекта в жидкости, а - скалярная функция , описывающая давление во всех точках пространства. Градиенты и перепады давления приводят к выталкивающей силе для жидкостей, взвешенных в гравитационных полях, ветрам в атмосферной науке и подъемной силе , связанной с аэродинамикой и полетом . ^{[4] : гл.12  [5]} ${\displaystyle V}$ ${\displaystyle P}$

Конкретным примером такой силы, связанной с динамическим давлением, является сопротивление жидкости: сила тела, которая сопротивляется движению объекта через жидкость из-за вязкости . Для так называемого « сопротивления Стокса » сила приблизительно пропорциональна скорости, но противоположна по направлению: F d = − b v , {\displaystyle \mathbf {F} _{\mathrm {d} }=-b\mathbf {v} ,} где:

• ${\displaystyle b}$— константа, зависящая от свойств жидкости и размеров объекта (обычно площади поперечного сечения ), и
• ${\displaystyle \mathbf {v} }$это скорость объекта. ^{[4] : гл.12  [5]}

Более формально, силы в механике сплошной среды полностью описываются тензором напряжений с членами, которые примерно определяются как σ = F A , {\displaystyle \sigma ={\frac {F}{A}},} где - соответствующая площадь поперечного сечения для объема, для которого вычисляется тензор напряжений. Этот формализм включает в себя члены давления, связанные с силами, которые действуют нормально к площади поперечного сечения ( диагонали матрицы тензора), а также члены сдвига , связанные с силами, которые действуют параллельно площади поперечного сечения (внедиагональные элементы). Тензор напряжений учитывает силы, которые вызывают все напряжения (деформации), включая также растягивающие напряжения и сжатия . ^{[3] [5] : 133–134  [38] : 38-1–38-11} ${\displaystyle A}$

Вымышленный

Существуют силы, зависящие от системы отсчета , то есть они появляются из-за принятия неньютоновских (то есть неинерциальных ) систем отсчета . К таким силам относятся центробежная сила и сила Кориолиса . ^[47] Эти силы считаются фиктивными, поскольку они не существуют в системах отсчета, которые не ускоряются. ^{[4] : гл.12  [5]} Поскольку эти силы не являются подлинными, их также называют «псевдосилами». ^{[4] : 12-11}

В общей теории относительности гравитация становится фиктивной силой, которая возникает в ситуациях, когда пространство-время отклоняется от плоской геометрии. ^[48]

Концепции, полученные от силы

Вращение и крутящий момент

Соотношение между силой ( F ), крутящим моментом ( τ ) и векторами импульса ( p и L ) во вращающейся системе.

Силы, которые заставляют протяженные объекты вращаться, связаны с крутящими моментами . Математически крутящий момент силы определяется относительно произвольной точки отсчета как векторное произведение : τ = r × F , {\displaystyle {\boldsymbol {\tau }}=\mathbf {r} \times \mathbf {F} ,} где — радиус-вектор точки приложения силы относительно точки отсчета. ^{[17] : 497} ${\displaystyle \mathbf {F} }$ ${\displaystyle \mathbf {r} }$

Крутящий момент является эквивалентом вращения силы таким же образом, как угол является эквивалентом вращения для положения , угловая скорость для скорости , а угловой момент для импульса . Как следствие первого закона движения Ньютона, существует инерция вращения , которая гарантирует, что все тела сохраняют свой угловой момент, если на них не действует несбалансированный крутящий момент. Аналогично, второй закон движения Ньютона может быть использован для вывода аналогичного уравнения для мгновенного углового ускорения твердого тела: где $${\displaystyle {\boldsymbol {\tau }}=I{\boldsymbol {\alpha }},}$$

• ${\displaystyle I}$это момент инерции тела
• ${\displaystyle {\boldsymbol {\alpha }}}$— угловое ускорение тела. ^{[17] : 502}

Это дает определение для момента инерции, который является вращательным эквивалентом массы. В более продвинутых трактовках механики, где описывается вращение в течение временного интервала, момент инерции должен быть заменен тензором , который при правильном анализе полностью определяет характеристики вращений, включая прецессию и нутацию . ^{[26] : 96–113}

Эквивалентно, дифференциальная форма второго закона Ньютона дает альтернативное определение крутящего момента: ^[49] где — момент импульса частицы. $${\displaystyle {\boldsymbol {\tau }}={\frac {\mathrm {d} \mathbf {L} }{\mathrm {dt} }},}$$ ${\displaystyle \mathbf {L} }$

Третий закон движения Ньютона требует, чтобы все объекты, создающие крутящие моменты, сами испытывали равные и противоположные крутящие моменты ^[50], и, следовательно, также напрямую подразумевает сохранение момента импульса для замкнутых систем, которые испытывают вращения и обороты под действием внутренних крутящих моментов.

Янки

Рывок определяется как скорость изменения силы ^[51] : ¹³¹

${\displaystyle \mathbf {Y} ={\frac {\mathrm {d} \mathbf {F} }{\mathrm {d} t}}}$

Термин используется в биомеханическом анализе, ^[52] спортивной оценке ^[53] и роботизированном управлении. ^[54] Вторая («рывок»), третья («рывок»), четвертая («встряхивание») и более высокие производные используются редко. ^[51]

Кинематические интегралы

Силы могут быть использованы для определения ряда физических понятий путем интегрирования по кинематическим переменным . Например, интегрирование по времени дает определение импульса : ^[55] который по второму закону Ньютона должен быть эквивалентен изменению импульса (что дает теорему об импульсе ). $${\displaystyle \mathbf {J} =\int _{t_{1}}^{t_{2}}{\mathbf {F} \,\mathrm {d} t},}$$

Аналогично, интегрирование по положению дает определение для работы, совершаемой силой: ^{[4] : 13-3} W = ∫ x 1 x 2 F ⋅ d x , {\displaystyle W=\int _{\mathbf {x} _{1}}^{\mathbf {x} _{2}}{\mathbf {F} \cdot {\mathrm {d} \mathbf {x} }},} что эквивалентно изменению кинетической энергии (что дает теорему об энергии работы ). ^{[4] : 13-3}

Мощность P — это скорость изменения d W /d t работы W , поскольку траектория удлиняется за счет изменения положения за интервал времени d t : ^{[4] : 13-2} поэтому при v = d x / d t {\displaystyle \mathbf {v} =\mathrm {d} \mathbf {x} /\mathrm {d} t } скорость . ${\displaystyle d\mathbf {x} }$ $${\displaystyle \mathrm {d} W={\frac {\mathrm {d} W}{\mathrm {d} \mathbf {x} }}\cdot \mathrm {d} \mathbf {x} =\mathbf {F} \cdot \mathrm {d} \mathbf {x} ,}$$ $${\displaystyle P={\frac {\mathrm {d} W}{\mathrm {d} t}}={\frac {\mathrm {d} W}{\mathrm {d} \mathbf {x} }}\cdot {\frac {\mathrm {d} \mathbf {x} }{\mathrm {d} t}}=\mathbf {F} \cdot \mathbf {v} ,}$$

Потенциальная энергия

Вместо силы часто используется математически связанное понятие потенциального энергетического поля. Например, гравитационную силу, действующую на объект, можно рассматривать как действие гравитационного поля , которое присутствует в месте расположения объекта. Перефразируя математически определение энергии (через определение работы ), потенциальное скалярное поле определяется как поле, градиент которого равен и противоположен силе, производимой в каждой точке: ${\displaystyle U(\mathbf {r} )}$ $${\displaystyle \mathbf {F} =-\mathbf {\nabla } U.}$$

Силы можно классифицировать как консервативные и неконсервативные. Консервативные силы эквивалентны градиенту потенциала , а неконсервативные — нет. ^{[4] : гл.12  [5]}

Сохранение

Консервативная сила, действующая на замкнутую систему , имеет связанную с ней механическую работу, которая позволяет энергии преобразовываться только между кинетической и потенциальной формами. Это означает, что для замкнутой системы чистая механическая энергия сохраняется всякий раз, когда на систему действует консервативная сила. Таким образом, сила напрямую связана с разницей в потенциальной энергии между двумя различными точками в пространстве, ^[56] и может считаться артефактом потенциального поля таким же образом, как направление и количество потока воды можно считать артефактом контурной карты возвышения области. ^{[4] : гл.12  [5]}

Консервативные силы включают гравитацию , электромагнитную силу и силу пружины . Каждая из этих сил имеет модели, которые зависят от положения, часто заданного как радиальный вектор, исходящий из сферически симметричных потенциалов. ^[57] Вот примеры этого: ${\displaystyle \mathbf {r} }$

Для гравитации: где — гравитационная постоянная , а — масса объекта n . $${\displaystyle \mathbf {F} _{\text{g}}=-{\frac {Gm_{1}m_{2}}{r^{2}}}{\hat {\mathbf {r} }},}$$ ${\displaystyle G}$ ${\displaystyle m_{n}}$

Для электростатических сил: где — электрическая проницаемость свободного пространства , а — электрический заряд объекта n . $${\displaystyle \mathbf {F} _{\text{e}}={\frac {q_{1}q_{2}}{4\pi \varepsilon _{0}r^{2}}}{\hat {\mathbf {r} }},}$$ ${\displaystyle \varepsilon _{0}}$ ${\displaystyle q_{n}}$

Для пружинных сил: где - коэффициент жесткости пружины . ^{[4] : гл.12  [5]} $${\displaystyle \mathbf {F} _{\text{s}}=-kr{\hat {\mathbf {r} }},}$$ ${\displaystyle k}$

Для некоторых физических сценариев невозможно моделировать силы как возникающие из-за простого градиента потенциалов. Это часто происходит из-за макроскопического статистического среднего микросостояний . Например, статическое трение вызвано градиентами многочисленных электростатических потенциалов между атомами , но проявляется как модель силы, которая не зависит от любого макромасштабного вектора положения. Неконсервативные силы, отличные от трения, включают другие контактные силы , растяжение , сжатие и сопротивление . Для любого достаточно подробного описания все эти силы являются результатами консервативных, поскольку каждая из этих макроскопических сил является чистым результатом градиентов микроскопических потенциалов. ^{[4] : гл.12  [5]}

Связь между макроскопическими неконсервативными силами и микроскопическими консервативными силами описывается с помощью детального рассмотрения статистической механики . В макроскопических замкнутых системах неконсервативные силы действуют, изменяя внутреннюю энергию системы, и часто связаны с передачей тепла. Согласно Второму закону термодинамики , неконсервативные силы обязательно приводят к преобразованиям энергии в замкнутых системах из упорядоченных в более случайные состояния по мере увеличения энтропии . ^{[4] : гл.12  [5]}

Единицы

Единицей силы в системе СИ является ньютон (символ Н), который представляет собой силу, необходимую для ускорения массы в один килограмм со скоростью один метр в секунду в квадрате, или кг·м·с ⁻² . Соответствующей единицей СГС является дина , сила, необходимая для ускорения массы в один грамм на один сантиметр в секунду в квадрате, или г·см·с ⁻² . Таким образом, ньютон равен 100 000 дин. ^[58]

Гравитационная английская единица силы фут-фунт-секунда — фунт-сила (lbf), определяемая как сила, действующая под действием силы тяжести на массу фунт в стандартном гравитационном поле 9,80665 м·с ⁻² . ^[58] Фунт-сила представляет собой альтернативную единицу массы: один слаг — это масса, которая будет ускоряться на один фут в секунду в квадрате при воздействии на нее силы в один фунт. ^[58] Альтернативной единицей силы в другой системе фут-фунт-секунда, абсолютной системе fps, является паундал , определяемый как сила, необходимая для ускорения массы в один фунт со скоростью один фут в секунду в квадрате. ^[58]

Фунт-сила имеет метрический аналог, менее используемый, чем ньютон: килограмм-сила (кгс) (иногда килопонд) — это сила, оказываемая стандартной гравитацией на один килограмм массы. Килограмм-сила приводит к альтернативной, но редко используемой единице массы: метрический слаг (иногда мюг или хил) — это масса, которая ускоряется со скоростью 1 м·с ⁻² при воздействии силы в 1 кгс. Килограмм-сила не является частью современной системы СИ и, как правило, не рекомендуется, иногда используется для выражения веса самолета, реактивной тяги, натяжения спиц велосипеда, настроек динамометрического ключа и выходного крутящего момента двигателя. ^[58]

См. также Тонна-сила .

Пересмотр концепции силы

В начале 20-го века появились новые физические идеи, объясняющие экспериментальные результаты в астрономических и субмикроскопических областях. Как обсуждается ниже, относительность изменяет определение импульса, а квантовая механика повторно использует концепцию «силы» в микроскопических контекстах, где законы Ньютона не применяются напрямую.

Специальная теория относительности

В специальной теории относительности масса и энергия эквивалентны (как можно увидеть, вычислив работу, необходимую для ускорения объекта). Когда скорость объекта увеличивается, увеличивается и его энергия, а следовательно, и его эквивалент массы (инерция). Таким образом, требуется больше силы, чтобы ускорить его на ту же величину, чем при более низкой скорости. Второй закон Ньютона остается в силе, поскольку это математическое определение. ^{[36] : 855–876} Но для сохранения импульса при релятивистской относительной скорости, импульс должен быть переопределен как: где — масса покоя , а скорость света . $${\displaystyle \mathbf {F} ={\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}},}$$ ${\displaystyle v}$ $${\displaystyle \mathbf {p} ={\frac {m_{0}\mathbf {v} }{\sqrt {1-v^{2}/c^{2}}}},}$$ ${\displaystyle m_{0}}$ ${\displaystyle c}$

Выражение, связывающее силу и ускорение для частицы с постоянной ненулевой массой покоя , движущейся в направлении со скоростью, имеет вид: ^{[59] : 216} , где γ = 1 1 − v 2 / c 2 . {\displaystyle \gamma ={\frac {1}{\sqrt {1-v^{2}/c^{2}}}}.} называется фактором Лоренца . Фактор Лоренца резко увеличивается по мере того, как относительная скорость приближается к скорости света. Следовательно, для создания того же ускорения при экстремальной скорости необходимо прикладывать все большую и большую силу. Относительная скорость не может достичь . ^{[59] : 26  [4] : §15–8} Если очень мало по сравнению с , то очень близко к 1 и является близким приближением. Даже для использования в теории относительности можно восстановить форму с помощью четырехвекторов . Это соотношение справедливо в теории относительности, когда — 4-сила , — инвариантная масса , — 4-ускорение . ^[60] ${\displaystyle m}$ ${\displaystyle x}$ ${\displaystyle v}$ $${\displaystyle \mathbf {F} =\left(\gamma ^{3}ma_{x},\gamma ma_{y},\gamma ma_{z}\right),}$$ ${\displaystyle c}$ ${\displaystyle v}$ ${\displaystyle c}$ ${\displaystyle \gamma }$ $${\displaystyle \mathbf {F} =m\mathbf {a} }$$ $${\displaystyle F^{\mu }=mA^{\mu }}$$ ${\displaystyle F^{\mu }}$ ${\displaystyle m}$ ${\displaystyle A^{\mu }}$

Общая теория относительности включает в себя более радикальный отход от ньютоновского способа мышления о силе , в частности, о гравитационной силе. Это переосмысление природы гравитации более полно описано ниже.

Квантовая механика

Квантовая механика — это теория физики, изначально разработанная для понимания микроскопических явлений: поведения в масштабах молекул, атомов или субатомных частиц. В общем и целом, чем меньше система, тем больше адекватная математическая модель потребует понимания квантовых эффектов. Концептуальная основа квантовой физики отличается от классической физики. Вместо того чтобы думать о таких величинах, как положение, импульс и энергия, как о свойствах, которыми обладает объект , мы рассматриваем, какой результат может появиться при выполнении измерения выбранного типа. Квантовая механика позволяет физику вычислить вероятность того, что выбранное измерение вызовет определенный результат. ^{[61] [62]} Ожидаемое значение для измерения — это среднее значение возможных результатов, которые оно может дать, взвешенное по их вероятностям появления. ^[63]

В квантовой механике взаимодействия обычно описываются в терминах энергии, а не силы. Теорема Эренфеста устанавливает связь между квантовыми ожидаемыми значениями и классическим понятием силы, связь, которая обязательно неточна, поскольку квантовая физика принципиально отличается от классической. В квантовой физике правило Борна используется для вычисления ожидаемых значений измерения положения или измерения импульса. Эти ожидаемые значения, как правило, будут меняться со временем; то есть, в зависимости от времени, в которое (например) выполняется измерение положения, вероятности его различных возможных результатов будут различаться. Теорема Эренфеста, грубо говоря, гласит, что уравнения, описывающие, как эти ожидаемые значения изменяются со временем, имеют форму, напоминающую второй закон Ньютона, с силой, определяемой как отрицательная производная потенциальной энергии. Однако, чем более выражены квантовые эффекты в данной ситуации, тем сложнее вывести осмысленные выводы из этого сходства. ^{[64] [65]}

Квантовая механика также вводит два новых ограничения, которые взаимодействуют с силами в субмикроскопическом масштабе и которые особенно важны для атомов. Несмотря на сильное притяжение ядра, принцип неопределенности ограничивает минимальную степень распределения вероятности электронов ^[66] , а принцип исключения Паули не позволяет электронам разделять одно и то же распределение вероятности. ^[67] Это приводит к возникновению давления, известного как давление вырождения . Динамическое равновесие между давлением вырождения и притягивающей электромагнитной силой придает атомам, молекулам, жидкостям и твердым телам устойчивость . ^[68]

Квантовая теория поля

Диаграмма Фейнмана для распада нейтрона в протон. Бозон W находится между двумя вершинами, что указывает на отталкивание.

В современной физике элементарных частиц силы и ускорение частиц объясняются как математический побочный продукт обмена калибровочными бозонами , переносящими импульс . С развитием квантовой теории поля и общей теории относительности было осознано, что сила является избыточной концепцией, возникающей из сохранения импульса ( 4-импульс в теории относительности и импульс виртуальных частиц в квантовой электродинамике ). Сохранение импульса может быть напрямую выведено из однородности или симметрии пространства и поэтому обычно считается более фундаментальным, чем концепция силы. Таким образом, известные в настоящее время фундаментальные силы более точно считаются « фундаментальными взаимодействиями ». ^{[6] : 199–128}

Хотя для детального предсказания результата таких взаимодействий необходимы сложные математические описания, существует концептуально простой способ их описания с помощью диаграмм Фейнмана . На диаграмме Фейнмана каждая частица материи представлена ​​в виде прямой линии (см. мировая линия ), движущейся во времени, которая обычно увеличивается вверх или вправо на диаграмме. Частицы материи и антиматерии идентичны, за исключением направления их распространения через диаграмму Фейнмана. Мировые линии частиц пересекаются в вершинах взаимодействия , и диаграмма Фейнмана представляет любую силу, возникающую в результате взаимодействия, как происходящую в вершине с соответствующим мгновенным изменением направления мировых линий частицы. Калибровочные бозоны испускаются из вершины в виде волнистых линий и, в случае обмена виртуальными частицами, поглощаются в соседней вершине. ^[69] Полезность диаграмм Фейнмана заключается в том, что другие типы физических явлений, которые являются частью общей картины фундаментальных взаимодействий , но концептуально отделены от сил, также могут быть описаны с использованием тех же правил. Например, диаграмма Фейнмана может описать в сжатых деталях, как нейтрон распадается на электрон , протон и антинейтрино , взаимодействие, опосредованное тем же калибровочным бозоном, который отвечает за слабое ядерное взаимодействие . ^[69]

Фундаментальные взаимодействия

Все известные силы Вселенной классифицируются на четыре фундаментальных взаимодействия . Сильные и слабые взаимодействия действуют только на очень коротких расстояниях и отвечают за взаимодействия между субатомными частицами , включая нуклоны и составные ядра . Электромагнитная сила действует между электрическими зарядами , а гравитационная сила действует между массами . Все другие силы в природе вытекают из этих четырех фундаментальных взаимодействий, действующих в рамках квантовой механики , включая ограничения, введенные уравнением Шредингера и принципом исключения Паули . ^[67] Например, трение является проявлением электромагнитной силы, действующей между атомами двух поверхностей. Силы в пружинах , моделируемые законом Гука , также являются результатом электромагнитных сил. Центробежные силы являются силами ускорения , которые возникают просто из-за ускорения вращающихся систем отсчета . ^{[4] : 12-11  [5] : 359}

Фундаментальные теории сил развивались из объединения различных идей. Например, универсальная теория тяготения Ньютона показала, что сила, ответственная за падение объектов вблизи поверхности Земли , также является силой, ответственной за падение небесных тел вокруг Земли ( Луны ) и вокруг Солнца (планет). Майкл Фарадей и Джеймс Клерк Максвелл продемонстрировали, что электрические и магнитные силы были объединены посредством теории электромагнетизма. В 20 веке развитие квантовой механики привело к современному пониманию того, что первые три фундаментальные силы (все, кроме гравитации) являются проявлениями материи ( фермионов ), взаимодействующей путем обмена виртуальными частицами, называемыми калибровочными бозонами . ^[70] Эта Стандартная модель физики элементарных частиц предполагает сходство между силами и привела ученых к предсказанию объединения слабых и электромагнитных сил в электрослабой теории, что впоследствии было подтверждено наблюдением. ^[71]

Гравитационный

Такие приборы, как GRAVITY, представляют собой мощный зонд для обнаружения силы тяжести. ^[73]

Закон тяготения Ньютона является примером действия на расстоянии : одно тело, например Солнце, оказывает влияние на любое другое тело, например Землю, независимо от того, насколько далеко они находятся друг от друга. Более того, это действие на расстоянии происходит мгновенно. Согласно теории Ньютона, изменение положения одного тела изменяет гравитационное притяжение, ощущаемое всеми другими телами, все в один и тот же момент времени. Альберт Эйнштейн осознал, что это несовместимо со специальной теорией относительности и ее предсказанием о том, что влияния не могут распространяться быстрее скорости света . Поэтому он искал новую теорию гравитации, которая была бы релятивистски последовательной. ^{[74] [75] Орбита} Меркурия не соответствовала предсказанной законом тяготения Ньютона. Некоторые астрофизики предсказывали существование неоткрытой планеты ( Вулкан ), которая могла бы объяснить эти расхождения. Когда Эйнштейн сформулировал свою общую теорию относительности (ОТО), он сосредоточился на проблемной орбите Меркурия и обнаружил, что его теория добавила поправку, которая могла бы объяснить несоответствие . Это был первый случай, когда было показано, что теория гравитации Ньютона неточна. ^[76]

С тех пор общая теория относительности была признана теорией, которая наилучшим образом объясняет гравитацию. В ОТО гравитация не рассматривается как сила, а скорее объекты, свободно движущиеся в гравитационных полях, движутся под действием собственной инерции по прямым линиям через искривленное пространство-время , определяемое как кратчайший путь пространства-времени между двумя событиями пространства-времени. С точки зрения объекта все движение происходит так, как если бы гравитации вообще не было. Только при наблюдении за движением в глобальном смысле можно наблюдать кривизну пространства-времени, и сила выводится из искривленного пути объекта. Таким образом, прямой путь в пространстве-времени рассматривается как искривленная линия в пространстве, и она называется баллистической траекторией объекта. Например, баскетбольный мяч, брошенный с земли, движется по параболе , как и в однородном гравитационном поле. Его пространственно-временная траектория представляет собой почти прямую линию, слегка искривленную (с радиусом кривизны порядка нескольких световых лет ). Производная по времени изменяющегося импульса объекта – это то, что мы называем «гравитационной силой» ^{[5] .}

Электромагнитный

Уравнения Максвелла и набор методов, построенных вокруг них, адекватно описывают широкий спектр физики, включающий силу в электричестве и магнетизме. Эта классическая теория уже включает эффекты относительности. ^[77] Понимание квантованных электромагнитных взаимодействий между элементарными частицами требует квантовой электродинамики (или КЭД). В КЭД фотоны являются фундаментальными обменными частицами, описывающими все взаимодействия, связанные с электромагнетизмом, включая электромагнитную силу. ^[78]

Сильный ядерный

Существуют две «ядерные силы», которые сегодня обычно описываются как взаимодействия, происходящие в квантовых теориях физики элементарных частиц. Сильная ядерная сила — это сила, ответственная за структурную целостность атомных ядер , и получила свое название из-за своей способности преодолевать электромагнитное отталкивание между протонами. ^{[36] : 940  [79]}

Сегодня сильное взаимодействие понимается как взаимодействие между кварками и глюонами , как это подробно описано в теории квантовой хромодинамики (КХД). ^[80] Сильное взаимодействие является фундаментальной силой , опосредованной глюонами, действующей на кварки, антикварки и сами глюоны. Сильное взаимодействие действует только непосредственно на элементарные частицы. Остаточное взаимодействие наблюдается между адронами (в частности, нуклонами в атомных ядрах), известное как ядерное взаимодействие . Здесь сильное взаимодействие действует косвенно, передаваясь в виде глюонов, которые образуют часть виртуальных пи- и ро- мезонов , классических передатчиков ядерного взаимодействия. Неудачи многих поисков свободных кварков показали, что затронутые элементарные частицы не поддаются непосредственному наблюдению. Это явление называется ограничением цвета . ^{[81] : 232}

Слабое ядерное

Уникальное среди фундаментальных взаимодействий, слабое ядерное взаимодействие не создает связанных состояний. ^[82] Слабое взаимодействие обусловлено обменом тяжелыми W- и Z-бозонами . Поскольку слабое взаимодействие опосредуется двумя типами бозонов, его можно разделить на два типа взаимодействия или « вершин » — заряженный ток , включающий электрически заряженные W ⁺ и W ^−- бозоны, и нейтральный ток , включающий электрически нейтральные Z0 ^- бозоны. Наиболее известным эффектом слабого взаимодействия является бета-распад (нейтронов в атомных ядрах) и связанная с ним радиоактивность . ^{[36] : 951} Это тип взаимодействия заряженного тока. Слово «слабое» происходит от того факта, что напряженность поля примерно в 1013 ^раз меньше, чем у сильного взаимодействия . Тем не менее, оно сильнее гравитации на коротких расстояниях. Также была разработана последовательная электрослабая теория, которая показывает, что электромагнитные силы и слабое взаимодействие неразличимы при температурах, превышающих приблизительно10 ¹⁵  К. ^[83] Такие температуры возникали при столкновениях плазмы в первые моменты Большого взрыва . [ ^{82] : 201}

Смотрите также

• Физический портал

• Сила контакта  – сила между двумя объектами, находящимися в физическом контакте.
• Управление силой  – Управление силой осуществляется машиной.
• Силомер  – прибор для измерения силы
• Порядки величин (сил)  – Сравнение широкого спектра физических сил.
• Система параллельных сил  – Ситуация в машиностроении
• Твёрдое тело  – Физический объект, который не деформируется при воздействии на него сил или моментов.
• Удельная сила  – Понятие в физике

Ссылки

1. Коэн, Майкл. "Классическая механика: критическое введение" (PDF) . Университет Пенсильвании . Архивировано (PDF) из оригинала 3 июля 2022 г. . Получено 9 января 2024 г. .
2. Heath, Thomas L. (1897). Труды Архимеда. Cambridge University Press . Получено 2007-10-14 – через интернет-архив .
3. Сирс, Фрэнсис В .; Земански, Марк В .; Янг, Хью Д. (1982). University Physics (6-е изд.). Addison-Wesley. стр. 18–38. ISBN 0-201-07199-1.
4. Фейнман, Ричард П.; Лейтон , Роберт Б .; Сэндс, Мэтью (2010). Лекции Фейнмана по физике. Том I: Главным образом механика, излучение и тепло (ред. New millennium). Нью-Йорк: Basic Books. ISBN 978-0465024933.
5. Клеппнер, Дэниел; Коленков, Роберт Дж. (2014). «Глава 3: Силы и уравнения движения». Введение в механику (2-е изд.). Кембридж: Издательство Кембриджского университета. ISBN 978-0521198110.
6. Weinberg, S. (1994). Мечты об окончательной теории . Винтажные книги. ISBN 978-0-679-74408-5.
7. Ланг, Хелен С. (1998). Порядок природы в физике Аристотеля: место и элементы . Кембридж: Cambridge Univ. Press. ISBN 978-0521624534.
8. Хетерингтон, Норрис С. (1993). Космология: исторические, литературные, философские, религиозные и научные перспективы. Справочная библиотека Гарленда по гуманитарным наукам. стр. 100. ISBN 978-0-8153-1085-3.
9. Сорабджи, Ричард (2010). «Иоанн Филопон». Филопон и отказ от аристотелевской науки (2-е изд.). Институт классических исследований Лондонского университета. п. 47. ИСБН 978-1-905-67018-5. JSTOR  44216227. OCLC  878730683.
10. Майер, Аннелиз (1982). Сарджент, Стивен Д. (ред.). На пороге точной науки . Издательство Пенсильванского университета. стр. 79. ISBN 978-0-812-27831-6. OCLC  495305340.
11. Drake, Stillman (1978). Galileo At Work . Чикаго: Издательство Чикагского университета. ISBN 0-226-16226-5.
12. ЛоЛордо, Антония (2007). Пьер Гассенди и рождение ранней современной философии. Нью-Йорк: Cambridge University Press. С. 175–180. ISBN 978-0-511-34982-9. OCLC  182818133.
13. Арнольд, VI ; Козлов В.В.; Нейштадт, А.И. (1988). «Математические аспекты классической и небесной механики». Энциклопедия математических наук, Динамические системы III. Том. 3. Аносов, Д.В. Берлин: Springer-Verlag. ISBN 0-387-17002-2. OCLC  16404140.
14. Ньютон, Исаак (1999). Principia Математические начала натуральной философии . Беркли: Издательство Калифорнийского университета. ISBN 978-0-520-08817-7.Это недавний перевод на английский язык, выполненный Бернардом Коэном и Энн Уитмен при содействии Джулии Буденц.
15. Хауленд, РА (2006). Промежуточная динамика: линейный алгебраический подход (Online-Ausg. ed.). Нью-Йорк: Springer. С. 255–256. ISBN 978-0387280592.
16. Мермин, Н. Дэвид (2005). Время пришло: понимание теории относительности Эйнштейна . Princeton University Press. ISBN 978-0-691-21877-9.
17. Ling, Samuel J.; Sanny, Jeff; Moebs, William; et al. (2021). Университетская физика, том 1. OpenStax . ISBN 978-1-947-17220-3.
18. Хеллингман, К. (1992). «Ньютонов третий закон пересматривается». Phys. Educ . 27 (2): 112–115. Bibcode :1992PhyEd..27..112H. doi :10.1088/0031-9120/27/2/011. S2CID  250891975. Цитата из «Начал» Ньютона : «Это не одно действие, посредством которого Солнце притягивает Юпитер, и другое, посредством которого Юпитер притягивает Солнце; но это одно действие, посредством которого Солнце и Юпитер взаимно стремятся приблизиться друг к другу».
19. Резник, Роберт; Холлидей, Дэвид; Крейн, Кеннет С. (2002). Физика. 1 (5-е изд.). ISBN 978-0-471-32057-9. Любая отдельная сила представляет собой лишь один аспект взаимодействия двух тел.
20. Ландау, Л. Д .; Ахиезер, А. И.; Лифшиц , А. М. (1967). Общая физика; механика и молекулярная физика . Оксфорд: Pergamon Press. ISBN 978-0-08-003304-4.Перевод: JB Sykes, AD Petford и CL Petford. LCCN  67--30260. В разделе 7, стр. 12–14, эта книга определяет силу как dp/dt .
21. Киббл, Том У. Б.; Беркшир, Фрэнк Х. (2004). Классическая механика (5-е изд.). Лондон: Imperial College Press. ISBN 1860944248.Согласно странице 12, «[Силу] можно, конечно, ввести, определив ее через второй закон Ньютона».
22. de Lange, OL; Pierrus, J. (2010). Решенные задачи классической механики . Оксфорд: Oxford University Press. ISBN 978-0-19-958252-5.Согласно странице 3, «[второй закон движения Ньютона] можно рассматривать как определяющий силу».
23. Хосе, Хорхе В .; Салетан, Юджин Дж. (1998). Классическая динамика: современный подход. Кембридж [Англия]: Cambridge University Press. стр. 9. ISBN 978-1-139-64890-5. OCLC  857769535.
24. Фраучи, Стивен К .; Оленик, Ричард П.; Апостол, Том М.; Гудштейн , Дэвид Л. (2007). Механическая вселенная: механика и тепло (расширенное издание). Кембридж [Кембриджшир]: Cambridge University Press. стр. 134. ISBN 978-0-521-71590-4. OCLC  227002144.
25. Thornton, Stephen T.; Marion, Jerry B. (2004). Классическая динамика частиц и систем (5-е изд.). Thomson Brooks/Cole. стр. 49–50. ISBN 0-534-40896-6.
26. Ландау, Лев Д. ; Лифшиц, Евгений М. (1969). Механика . Курс теоретической физики . Том 1. Перевод Сайкса, Дж. Б.; Белла, Дж. С. (2-е изд.). Pergamon Press . ISBN 978-0-080-06466-6.
27. Джаммер, Макс (1999). Концепции силы: исследование основ динамики (Facsim. ed.). Минеола, Нью-Йорк: Dover Publications. стр. 220–222. ISBN 978-0486406893.
28. Нолл, Уолтер (апрель 2007 г.). «О концепции силы» (PDF) . Университет Карнеги-Меллона . Получено 28 октября 2013 г.
29. "Введение в диаграммы свободных тел". Меню учебника по физике . Университет Гвельфа . Архивировано из оригинала 2008-01-16 . Получено 2008-01-02 .
30. Хендерсон, Том (2004). "The Physics Classroom". The Physics Classroom и Mathsoft Engineering & Education, Inc. Архивировано из оригинала 2008-01-01 . Получено 2008-01-02 .
31. "Статическое равновесие". Физика Статическое равновесие (силы и моменты) . Университет Виргинских островов . Архивировано из оригинала 19 октября 2007 г. . Получено 2008-01-02 .
32. Кук, AH (1965). «Новое абсолютное определение ускорения силы тяжести в Национальной физической лаборатории». Nature . 208 (5007): 279. Bibcode :1965Natur.208..279C. doi : 10.1038/208279a0 . S2CID  4242827.
33. Янг, Хью; Фридман, Роджер; Сирс, Фрэнсис; и Земанский, Марк (1949) Университетская физика . Pearson Education. стр. 59–82.
34. Уоткинс, Тайер. «Анализ возмущений, регулярных и сингулярных». Экономический факультет . Университет штата Сан-Хосе. Архивировано из оригинала 2011-02-10 . Получено 2008-01-05 .
35. Коллерстром, Ник (2001). «Открытие Нептуна. Британский случай совместного прогнозирования». Университетский колледж Лондона. Архивировано из оригинала 2005-11-11 . Получено 2007-03-19 .
36. Катнелл, Джон Д.; Джонсон, Кеннет В. (2004). Физика (6-е изд.). Хобокен, Нью-Джерси: Wiley. ISBN 978-0-471-44895-2.
37. Куломб, Чарльз (1784). «Теоретические и экспериментальные исследования по силе кручения и эластичности металлических листов». История Королевской академии наук : 229–269.
38. Фейнман, Ричард П .; Лейтон, Роберт Б.; Сэндс , Мэтью (2010). Лекции Фейнмана по физике. Том II: Главным образом электромагнетизм и материя (ред. New millennium). Нью-Йорк: Basic Books. ISBN 978-0465024940.
39. Тоннелат, Мария-Антуанетта (1966). Принципы электромагнитной теории и теории относительности. Дордрехт: D. Reidel. стр. 85. ISBN 90-277-0107-5. OCLC  844001.
40. Линг, Сэмюэл Дж.; Санни, Джефф; Моебс, Уильям (2021). Университетская физика, Том 2. OpenStax . ISBN 978-1-947-17221-0.
41. Шарф, Торальф (2007). "Глава 2". Поляризованный свет в жидких кристаллах и полимерах . John Wiley and Sons. стр. 19. ISBN 978-0-471-74064-3.
42. Даффин, Уильям (1980). Электричество и магнетизм (3-е изд.). McGraw-Hill. стр. 364–383. ISBN 978-0-07-084111-6.
43. "Сила натяжения". Non-calculus Based Physics I. Архивировано из оригинала 2007-12-27 . Получено 2008-01-04 .
44. Фицпатрик, Ричард (2006-02-02). "Струны, блоки и наклонные плоскости" . Получено 04.01.2008 .
45. Nave, Carl Rod. "Эластичность". HyperPhysics . University of Guelph . Получено 28.10.2013 .
46. Nave, Carl Rod. "Centripetal Force". HyperPhysics . University of Guelph . Получено 28 октября 2013 г.
47. Маллетт, Винсент (1982–2008). «Сила Кориолиса». Публикации по науке и математике, вычислительной технике и гуманитарным наукам . Inwit Publishing, Inc. Получено 04.01.2008 .
48. Шоке-Брюа, Ивонн (2009). Общая теория относительности и уравнения Эйнштейна. Оксфорд: Oxford University Press. стр. 39. ISBN 978-0-19-155226-7. OCLC  317496332.
49. Nave, Carl Rod. "Второй закон Ньютона: вращение". HyperPhysics . University of Guelph . Получено 28 октября 2013 г.
50. Фицпатрик, Ричард (2007-01-07). "Третий закон движения Ньютона" . Получено 2008-01-04 .
51. Jazar, Reza N. (2011). Расширенная динамика: твердое тело, многотельные системы и аэрокосмические приложения . Hoboken, NJ: Wiley. ISBN 978-0-470-39835-7.
52. Лин, Дэвид К.; Макгоуэн, Крейг П.; Блюм, Кайл П.; Тинг, Лена Х. (2019-09-12). «Янк: производная силы по времени является важной биомеханической переменной в сенсомоторных системах». Журнал экспериментальной биологии . 222 (18): jeb180414. doi :10.1242/jeb.180414. ISSN  0022-0949. PMC 6765171. PMID 31515280  . 
53. Гарри, Джон Р.; Баркер, Леланд А.; Тинсли, Грант М.; Кшишковски, Джон; Чоунинг, Люк Д.; Макмахон, Джон Дж.; Лейк, Джейсон (2021-05-05). «Связь между показателями эффективности вертикального прыжка с контрдвижением, переменными стратегии и асимметрией между конечностями у женщин». Спортивная биомеханика : 1–19. doi :10.1080/14763141.2021.1908412. ISSN  1476-3141. PMID  33947320.
54. Росендо, Андре; Танака, Такаюки; Канеко, Шуничи (2012-04-20). «Метод переменного коэффициента на основе янкинга для маломощной полуактивной системы усиления мощности». Журнал робототехники и мехатроники . 24 (2): 291–297. doi : 10.20965/jrm.2012.p0291 .
55. Хиббелер, Рассел К. (2010). Инженерная механика (12-е изд.). Pearson Prentice Hall. стр. 222. ISBN 978-0-13-607791-6.
56. Сингх, Сунил Кумар (2007-08-25). "Консервативная сила". Связи . Получено 2008-01-04 .
57. Дэвис, Дуг. "Закон сохранения энергии". Общая физика . Получено 2008-01-04 .
58. Вандмахер, Корнелиус; Джонсон, Арнольд (1995). Метрические единицы в машиностроении. ASCE Publications. стр. 15. ISBN 978-0-7844-0070-8.
59. French, AP (1972). Специальная теория относительности . Вводная серия по физике Массачусетского технологического института (переиздание). Лондон: Chapman & Hall. ISBN 978-0-17-771075-9.
60. Уилсон, Джон Б. "Четырехвекторы (4-векторы) специальной теории относительности: исследование элегантной физики". The Science Realm: John's Virtual Sci-Tech Universe . Архивировано из оригинала 26 июня 2009 года . Получено 2008-01-04 .
61. Mermin, N. David (1993). «Скрытые переменные и две теоремы Джона Белла». Reviews of Modern Physics . 65 (3): 803–815. arXiv : 1802.10119 . Bibcode :1993RvMP...65..803M. doi :10.1103/RevModPhys.65.803. S2CID  119546199. Фундаментальная квантовая доктрина заключается в том, что измерение, как правило, не раскрывает ранее существовавшее значение измеряемого свойства.
62. Шаффер, Кэтрин; Баррето Лемос, Габриэла (24 мая 2019 г.). «Уничтожение вещности: введение в «Что» и «Ну и что» квантовой физики». Основы науки . 26 : 7–26. arXiv : 1908.07936 . doi : 10.1007/s10699-019-09608-5. ISSN  1233-1821. S2CID  182656563.
63. Маршман, Эмили; Сингх, Чандралекха (2017-03-01). «Исследование и улучшение понимания студентами вероятностных распределений для измерения физических наблюдаемых в квантовой механике». Европейский журнал физики . 38 (2): 025705. Bibcode : 2017EJPh...38b5705M. doi : 10.1088/1361-6404/aa57d1 . ISSN  0143-0807. S2CID  126311599.
64. Коэн-Таннуджи, Клод ; Диу, Бернар; Лалоэ, Франк (2005). Квантовая механика . Перевод Хемли, Сьюзен Рид; Островский, Николь; Островский, Дэн. Джон Уайли и сыновья. п. 242. ИСБН 0-471-16433-X.
65. Перес, Эшер (1993). Квантовая теория: концепции и методы . Kluwer . стр. 302. ISBN 0-7923-2549-4. OCLC  28854083.
66. Либ, Эллиотт Х. (1976-10-01). "Устойчивость материи". Reviews of Modern Physics . 48 (4): 553–569. Bibcode :1976RvMP...48..553L. doi :10.1103/RevModPhys.48.553. ISSN  0034-6861. тот факт, что если попытаться сжать волновую функцию в любом месте , то кинетическая энергия увеличится. Этот принцип был предложен Соболевым (1938)...
67. Lieb, Elliott H. (1990). "The stable of matter: from atoms to stars". Bulletin of the American Mathematical Society . 22 (1): 1–49. doi : 10.1090/S0273-0979-1990-15831-8 . ISSN  0273-0979. основная масса материи стабильна и имеет объем, пропорциональный числу частиц, из-за принципа исключения Паули для фермионов (т. е. электронов). Фактически электроны ведут себя как жидкость с плотностью энергии , и это ограничивает сжатие, вызванное притягивающими электростатическими силами. ${\displaystyle \rho ^{5/3}}$
68. Гриффитс (2005). Введение в квантовую механику, второе издание . Лондон, Великобритания: Prentice Hall . стр. 221–223. ISBN 0131244051.
69. Шифман, Михаил (1999). Лекции ИТЭФ по физике элементарных частиц и теории поля . World Scientific. ISBN 978-981-02-2639-8.
70. "Фермионы и бозоны". Приключение частиц . Архивировано из оригинала 2007-12-18 . Получено 2008-01-04 .
71. Ярлског, Сесилия (1999-10-12). "Дополнительные справочные материалы о Нобелевской премии по физике 1999 года". Нобелевская премия . Получено 2023-07-26 .
72. "Стандартная модель частиц и взаимодействий". Contemporary Physics Education Project. 2000. Архивировано из оригинала 2 января 2017 года . Получено 2 января 2017 года .
73. "Мощный новый зонд для исследования черной дыры прибыл в Паранал" . Получено 13 августа 2015 г.
74. Мизнер, Чарльз В .; Торн, Кип С.; Уилер , Джон Арчибальд (1973). Гравитация . Сан-Франциско: WH Freeman . С. 3–5. ISBN 978-0-7167-0344-0.
75. Choquet-Bruhat, Yvonne (2009). Общая теория относительности и уравнения Эйнштейна. Оксфорд: Oxford University Press. С. 37–39. ISBN 978-0-19-155226-7. OCLC  317496332.
76. Siegel, Ethan (20 мая 2016 г.). «Когда Исаак Ньютон окончательно потерпел неудачу?». Forbes . Получено 3 января 2017 г.
77. Панофски, Вольфганг К.; Филлипс, Мельба (2005). Классическое электричество и магнетизм (2-е изд.). Минеола, Нью-Йорк: Dover Publ. ISBN 978-0-486-43924-2.
78. Зи, Энтони (2010). Квантовая теория поля в двух словах (2-е изд.). Princeton University Press. стр. 29. ISBN 978-0-691-14034-6.
79. "strong, 7.g physics" . Оксфордский словарь английского языка (Электронная правка). Oxford University Press . doi :10.1093/OED/1058721983. (Требуется подписка или членство в участвующем учреждении.)
80. Стивенс, Таб (10 июля 2003 г.). "Квантовая хромодинамика: определение – научные статьи". Архивировано из оригинала 2011-10-16 . Получено 2008-01-04 .
81. Голдберг, Дэйв (2017). Стандартная модель в двух словах . Princeton University Press. ISBN 978-0-691-16759-6.
82. Greiner, Walter; Müller, Berndt; Greiner, Walter (2009). Калибровочная теория слабых взаимодействий: с 75 проработанными примерами и упражнениями (4-е изд.). Гейдельберг: Springer. ISBN 978-3-540-87842-1.
83. Даррер, Рут (2008). Космический микроволновый фон . Cambridge Pniversity Press. стр. 41–42. ISBN 978-0-521-84704-9.

Внешние ссылки

• «Классическая механика, неделя 2: Законы Ньютона». MIT OpenCourseWare . Получено 2023-08-09 .
• "Основы физики I, Лекция 3: Законы движения Ньютона". Открытые курсы Йельского университета . Получено 09.08.2023 .