Равномерный 4-многогранник

Класс 4-мерных многогранников

Диаграмма Шлегеля для усеченной 120-ячеечной ячейки с видимыми тетраэдрическими ячейками.

Ортографическая проекция усеченных 120 ячеек в плоскости Кокстера H ₃ ( симметрия D ₁₀ ). Рисуются только вершины и ребра.

В геометрии однородный 4-многогранник (или однородный многогранник ) ^[1] — это 4-мерный многогранник , который является вершинно-транзитивным и ячейки которого представляют собой однородные многогранники , а грани — правильные многоугольники .

Имеется 47 непризматических выпуклых однородных 4-многогранников. Существует два бесконечных множества выпуклых призматических форм, а также 17 случаев, возникающих как призмы выпуклых однородных многогранников. Существует также неизвестное количество невыпуклых звездных форм.

История открытия

• Выпуклые правильные многогранники :
  • 1852 : Людвиг Шлефли доказал в своей рукописи Theorie der vielfachen Kontinuität , что существует ровно 6 правильных многогранников в 4 измерениях и только 3 в 5 или более измерениях.
• Правильные звездчатые 4-многогранники ( ячейки звездчатых многогранников и/или вершинные фигуры )
  • 1852 : Людвиг Шлефли также нашел 4 из 10 правильных звездчатых 4-многогранников, не считая 6 с ячейками или вершинными фигурами { 5 ^/ 2,5 _} и { 5 , 5/2 } .
  • 1883 : Эдмунд Гесс завершил список 10 невыпуклых правильных 4-многогранников в своей книге (на немецком языке) Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder Einleitung in die Lehre von. der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder, von Dr. Эдмунд Хесс. Mit sechzehn Litographierten Tafeln..
• Выпуклые полуправильные многогранники : (Различные определения до однородной категории Коксетера )
  • 1900 : Торольд Госсет перечислил список непризматических полуправильных выпуклых многогранников с правильными ячейками ( платоновых тел ) в своей публикации «О правильных и полуправильных фигурах в пространстве n измерений ». В четырех измерениях это дает выпрямленный 5-элементный , выпрямленный 600-элементный и курносый 24-элементный . ^[2]
  • 1910 : Алисия Буль Стотт в своей публикации «Геометрический вывод полуправильных чисел из правильных многогранников и заполнений пространства » расширила определение, также допустив архимедовы твердые тела и призматические ячейки. Эта конструкция насчитывала 45 полуправильных 4-многогранников, соответствующих перечисленным ниже непризматическим формам. В ее списке не было курносой 24-клеточной камеры и большой антипризмы . ^[3]
  • 1911 : Питер Хендрик Шоут опубликовал «Аналитическое лечение многогранников, регулярно полученных из правильных многогранников» , следуя обозначениям Буля-Стота, перечисляя выпуклые однородные многогранники по симметрии на основе 5-ячеечных , 8- / 16-ячеечных и 24-ячеечных .
  • 1912 : Э.Л.Эльте независимо расширил список Госсета публикацией « Полуправильные многогранники гиперпространств» , многогранники с одним или двумя типами полуправильных граней. ^[4]
• Выпуклые однородные многогранники :
  • 1940 : Поиск систематически расширялся Х.С.М. Коксетером в его публикации « Регулярные и полуправильные многогранники» .
  • Выпуклые однородные 4-многогранники :
    • 1965 : Полный список выпуклых форм был наконец перечислен Джоном Хортоном Конвеем и Майклом Гаем в их публикации « Четырехмерные архимедовы многогранники» , установленной с помощью компьютерного анализа, с добавлением только одного не витоффова выпуклого 4-многогранника, большой антипризмы.
    • 1966 Норман Джонсон защищает докторскую диссертацию. диссертация «Теория однородных многогранников и сот» под руководством Коксетера завершает основную теорию однородных многогранников для размерностей 4 и выше.
    • В 1986 году Коксетер опубликовал статью «Регулярные и полуправильные многогранники II» , в которой был проведен анализ уникальной курносой 24-клеточной структуры и симметрии аномальной большой антипризмы.
    • 1998 ^[5] -2000 : 4-многогранники были систематически названы Норманом Джонсоном и даны с помощью онлайн-индексированного перечисления Джорджа Ольшевского (использованного в качестве основы для этого списка). Джонсон назвал 4-многогранники полихорами, как и многогранники для 3-многогранников, от греческих корней поли («много») и choros («комната» или «пространство»). ^[6] Названия единой полихоры начинались с шести правильных полихор с префиксами, основанными на кольцах в диаграммах Кокстера; усечение t _0,1 , кантелляция t _0,2 , прорезание t _0,3 с однокольцевыми формами, называемыми выпрямленными, и би-, три-префиксами, добавляемыми, когда первое кольцо находилось на втором или третьем узлах. ^{[7] [8]}
    • 2004 : Доказательство полноты множества Конвея-Гая было опубликовано Марко Мёллером в его диссертации « Vier Dimensione Archimedische Polytope» . Мёллер воспроизвел систему именования Джонсона в своем списке. ^[9]
    • 2008 : Книга «Симметрии вещей» ^[10] была опубликована Джоном Х. Конвеем и содержит первый опубликованный в печати список выпуклых однородных 4-многогранников и многогранников более высокой размерности семейства групп Кокстера, с общими диаграммами вершинных фигур для каждой кольцевой диаграммы Кокстера . перестановки — курносые, большие антипризмы и дуопризмы — которые он назвал пропризмами вместо продуктовых призм. Он использовал свою собственную схему именования ijk -ambo для перестановок индексированных колец, помимо усечения и побитового усечения, и все имена Джонсона были включены в указатель книги.
• Неправильные однородные звездчатые 4-многогранники : (аналогично невыпуклым однородным многогранникам )
  • 1966 : Джонсон описывает в своей диссертации три невыпуклые однородные антипризмы в четырехмерном пространстве. ^[11]
  • 1990-2006 : В ходе совместных поисков до 2005 года Джонатаном Бауэрсом и Джорджем Ольшевским было идентифицировано в общей сложности 1845 однородных 4-многогранников (выпуклых и невыпуклых) ^[12] , а в 2006 году было обнаружено еще четыре, всего 1849. В подсчет входят 74 призмы из 75 непризматических однородных многогранников (поскольку это конечное множество — кубическая призма исключена, поскольку она дублирует тессеракт), но не бесконечные категории дуопризм или призм антипризм. ^[13]
  • 2020–2023 гг .: обнаружено 342 новых полихоры, в результате чего общее количество известных однородных 4-многогранников достигло 2191. Список не является полным. ^{[13] [14]}

Правильные 4-многогранники

Правильные 4-многогранники — это подмножество однородных 4-многогранников, удовлетворяющее дополнительным требованиям. Правильные 4-многогранники могут быть выражены с помощью символа Шлефли { p , q , r } и имеют ячейки типа { p , q }, грани типа { p }, реберные фигуры { r } и вершинные фигуры { q , r }.

Существование правильного 4-многогранника { p , q , r } ограничено существованием правильных многогранников { p , q }, которые становятся ячейками, и { q , r }, которые становятся вершинной фигурой .

Существование конечного 4-многогранника зависит от неравенства: ^[15]

${\displaystyle \sin \left({\frac {\pi }{p}}\right)\sin \left({\frac {\pi }{r}}\right)>\cos \left({\frac {\pi }{q}}\right).}$

16 правильных 4-многогранников со свойством конгруэнтности всех ячеек, граней, ребер и вершин:

• 6 правильных выпуклых 4-многогранников : 5-клеточный {3,3,3}, 8-клеточный {4,3,3}, 16-клеточный {3,3,4}, 24-клеточный {3,4,3} , 120 ячеек {5,3,3} и 600 ячеек {3,3,5}.
• 10 правильных звездчатых 4-многогранников : икосаэдрический 120-клеточный {3,5, ^5/2 }, малый звездчатый 120-клеточный { ^5/2 ,5,3}, _{большой} 120-клеточный _{ 5, ^5/2 , ₅ }, большой 120 _- ячеечный {5,3, 5/2 ^} , большой звездчатый ₁₂₀ - ячеечный _{ ⁵ / 2,3,5}, большой звездчатый 120-ячеечный { ⁵ / _2,5 , ^5/2 } , большой большой 120- ячейка {5, ^5/2 , 3}, большая икосаэдрическая 120-ячеечная { ₃ , ^5/2 , 5 }, большая 600-ячеечная {3,3, ^5/2 _} и большая звёздчатая 120-ячеечная { ⁵ _{/ 2,3,3} }.

Выпуклые однородные 4-многогранники

Симметрия однородных 4-многогранников в четырех измерениях

Существует 5 основных семейств точечных групп зеркальной симметрии в 4-х измерениях: A ₄ =, В ₄ =, Д ₄ =, Ф ₄ =, Ч ₄ =. ^[7] Также существуют 3 призматические группы A ₃ A ₁ =, В ₃ А ₁ =, ЧАС ₃ А ₁ =, и дуопризматические группы: I ₂ (p)×I ₂ (q) =. Каждая группа определяется фундаментальной областью тетраэдра Гурса , ограниченной зеркальными плоскостями.

Каждый отражающий однородный 4-многогранник может быть построен в одной или нескольких отражающих точечных группах в 4 измерениях с помощью конструкции Витхоффа , представленной кольцами вокруг перестановок узлов на диаграмме Коксетера . Зеркальные гиперплоскости можно группировать, как видно по цветным узлам, разделенным четными ветвями. Группы симметрии вида [a,b,a] имеют расширенную симметрию [[a,b,a]], удваивая порядок симметрии. Сюда входят [3,3,3], [3,4,3] и [ p ,2, p ]. Однородные многогранники в этой группе с симметричными кольцами содержат эту расширенную симметрию.

Если все зеркала данного цвета не имеют кольца (неактивны) в данном однородном многограннике, он будет иметь конструкцию с более низкой симметрией за счет удаления всех неактивных зеркал. Если все узлы данного цвета окольцованы (активны), операция чередования может создать новый 4-многогранник с киральной симметрией, показанный как «пустые» узлы в кружке», но геометрия обычно не настраивается для создания единых решений.

Перечисление

Существует 64 выпуклых однородных 4-многогранника, включая 6 правильных выпуклых 4-многогранников, исключая бесконечные множества дуопризм и антипризматических призм .

• 5 — многогранные призмы на основе Платоновых тел (1 перекрывается с регулярной, поскольку кубическая гиперпризма — это тессеракт )
• 13 — многогранные призмы на основе архимедовых тел.
• 9 принадлежат к самодуальному регулярному семейству A ₄ [3,3,3] группы ( 5-клеток ).
• 9 принадлежат к самодуальному регулярному семейству F ₄ [3,4,3] группы ( 24 ячейки ). (исключая курносый 24-элементный)
• 15 входят в обычную группу B ₄ [3,3,4] ( тессеракт / 16-клеточное семейство) (3 перекрываются с 24-клеточным семейством)
• 15 относятся к обычной группе H _{4 [} 3,3,5 ] ( 120/600 ячеек ).
• 1 специальная курносая форма в семействе групп [3,4,3] ( 24 ячейки ).
• 1 специальный невитоффов 4-многогранник, большая антипризма.
• ИТОГО: 68 − 4 = 64

Эти 64 однородных 4-многогранника пронумерованы ниже Георгием Ольшевским. Повторяющиеся формы симметрии указаны в скобках.

В дополнение к 64, указанным выше, существует 2 бесконечных призматических набора, которые порождают все оставшиеся выпуклые формы:

• Набор однородных антипризматических призм — sr{ p ,2}×{ } — Многогранные призмы из двух антипризм .
• Набор однородных дуопризм - { p }×{ q } - Декартово произведение двух многоугольников.

Семья А 4

5-ячейка имеет диплоидную пентахорную [3,3,3] симметрию , [7] порядка 120 ^, изоморфную перестановкам пяти элементов, поскольку все пары вершин связаны одинаковым образом.

Фасеты (ячейки) задаются, сгруппированные в своих местоположениях на диаграмме Кокстера путем удаления указанных узлов.

Три однородные формы 4-многогранников , отмеченные звездочкой * , имеют более высокую расширенную пентахорную симметрию порядка 240, [[3,3,3]], поскольку элемент, соответствующий любому элементу базовой 5-ячейки, можно поменять местами. с одним из тех, которые соответствуют элементу его двойника. Существует одна небольшая индексная подгруппа [3,3,3] ⁺ , порядок 60 или ее удвоение [[3,3,3]] ⁺ , порядок 120, определяющая 5-ячейку omnisnub , которая указана для полноты, но не униформа.

Семья Б 4

Это семейство имеет диплоидную гексадекахорную симметрию , ^[7] [4,3,3], порядка 24 ×16=384: 4!=24 перестановки четырёх осей, 2 ⁴ =16 для отражения по каждой оси. Существует 3 небольшие индексные подгруппы, первые две из которых порождают однородные 4-многогранники, которые также повторяются в других семействах: [1 ⁺ ,4,3,3], [4,(3,3) ⁺ ] и [4, 3,3] ⁺ , всего порядка 192.

Усечение Тессеракта

16-ячеечные усечения

(*) Точно так же, как при выпрямлении тетраэдра образуется октаэдр , при выпрямлении 16-ячеечного получается 24-ячеечный, обычный член следующего семейства.

Курносый 24-элементный элемент повторяется в этом семействе для полноты картины. Это чередование кантиусеченной 16-клеточной или усеченной 24-клеточной с полугруппой симметрии [(3,3) ⁺ ,4]. Усеченные октаэдрические ячейки превращаются в икосаэдры. Кубы становятся тетраэдрами, а в промежутках из удаленных вершин создается 96 новых тетраэдров.

Семья Ф 4

Это семейство обладает диплоидной икоситетрахорической симметрией ^[7] [3,4,3] порядка 24 ×48 = 1152: 48 симметрий октаэдра для каждой из 24 ячеек. Существует 3 небольшие индексные подгруппы, причем первые две изоморфные пары порождают однородные 4-многогранники, которые также повторяются в других семействах: [3 ⁺ ,4,3], [3,4,3 ⁺ ] и [3,4, 3] ⁺ , всего порядка 576.

(†) Курносый 24-клеточный здесь, несмотря на свое общее название, не является аналогом курносого куба ; скорее, он получается путем чередования усеченных 24 ячеек. Его число симметрии всего 576 ( ионная уменьшенная икоситетрахорная группа, [3 ⁺ ,4,3]).

Подобно 5-клеточной, 24-клеточная является самодвойственной, поэтому следующие три формы имеют в два раза больше симметрий, в результате чего их общее количество достигает 2304 ( расширенная икоситетрахорическая симметрия [[3,4,3]]).

Семья H 4

Это семейство имеет диплоидную гексакосихорную симметрию , ^[7] [5,3,3], порядка 120×120=24×600=14400: по 120 на каждый из 120 додекаэдров или по 24 на каждый из 600 тетраэдров. Есть одна небольшая индексная подгруппа [5,3,3] ⁺ всего порядка 7200.

Усечение 120 ячеек

Усечение 600 ячеек

Семья Д 4

Это семейство демитессерактов [3 ^1,1,1 ] не вводит новых однородных 4-многогранников, но стоит повторить эти альтернативные конструкции. Это семейство имеет порядок 12×16=192: 4!/2=12 перестановок четырех осей, половина из которых чередуется, 2 ⁴ =16 для отражения по каждой оси. Существует одна небольшая индексная подгруппа, порождающая однородные 4-многогранники, [3 ^1,1,1 ] ⁺ , порядок 96.

Когда три узла раздвоенной ветки одинаково окольцованы, симметрия может быть увеличена на 6, так как [3[3 ^1,1,1 ]] = [3,4,3], и, таким образом, эти многогранники повторяются из 24-клеточного многогранника. семья.

Здесь снова курносая 24-ячейка с группой симметрии [3 ^1,1,1 ] ⁺ на этот раз представляет собой поочередное усечение усеченной 24-ячейки, создающее 96 новых тетраэдров в положениях удаленных вершин. В отличие от его внешнего вида в прежних группах как частично курносого 4-многогранника, только внутри этой группы симметрии он имеет полную аналогию с курносыми кеплерами, т. е. курносым кубом и курносым додекаэдром .

Великая антипризма

Существует один не витоффов однородный выпуклый 4-многогранник, известный как большая антипризма , состоящий из 20 пятиугольных антипризм , образующих два перпендикулярных кольца, соединенных 300 тетраэдрами . Это во многом аналогично трехмерным антипризмам , которые состоят из двух параллельных многоугольников , соединенных полосой треугольников . Однако в отличие от них большая антипризма не является членом бесконечного семейства однородных многогранников.

Его симметрия - ионная уменьшенная группа Коксетера , [[10,2 ⁺ ,10]], порядка 400.

Призматические однородные 4-многогранники

Призматический многогранник — это декартово произведение двух многогранников меньшей размерности; знакомыми примерами являются трехмерные призмы , которые представляют собой произведения многоугольника и отрезка . Призматические однородные 4-многогранники состоят из двух бесконечных семейств:

• Многогранные призмы : произведения отрезка и однородного многогранника. Это семейство бесконечно, поскольку в него входят призмы, построенные на основе трехмерных призм и антипризм .
• Дуопризмы : произведения двух многоугольников.

Выпуклые многогранные призмы

Наиболее очевидным семейством призматических 4-многогранников являются многогранные призмы, т.е. произведения многогранника с отрезком . Ячейками такого 4-многогранника являются два одинаковых однородных многогранника, лежащие в параллельных гиперплоскостях ( ячейки основания ) и соединяющий их слой призм ( боковые ячейки). В это семейство входят призмы для 75 непризматических однородных многогранников (из них 18 выпуклых; одна из них, куб-призма, указана выше как тессеракт ) . ^{[ нужна цитата ]}

Существует 18 выпуклых многогранных призм , созданных из 5 платоновых тел и 13 архимедовых тел , а также для бесконечных семейств трехмерных призм и антипризм . ^{[ нужна цитата ]} Число симметрии многогранной призмы в два раза больше, чем у базового многогранника.

Четырехгранные призмы: А ₃ × А ₁

Эта призматическая тетраэдральная симметрия равна [3,3,2], порядок 48. Есть две подгруппы индекса 2, [(3,3) ⁺ ,2] и [3,3,2] ⁺ , но вторая не порождает однородный 4-многогранник.

Октаэдрические призмы: Б ₃ × А ₁

Симметрия этого призматического октаэдрического семейства равна [4,3,2], порядок 96. Существует 6 подгрупп индекса 2, порядок 48, которые выражены в чередующихся 4-многогранниках ниже. Симметрии : [(4,3) ⁺ ,2], [1 ⁺ ,4,3,2], [4,3,2 ⁺ ], [4,3 ⁺ ,2], [4,(3,2) ⁺ ] и [4,3,2] ⁺ .

Икосаэдрические призмы: H ₃ × A ₁

Эта призматическая икосаэдральная симметрия равна [5,3,2], порядок 240. Есть две подгруппы индекса 2, [(5,3) ⁺ ,2] и [5,3,2] ⁺ , но вторая не порождает однородный полихорон.

Дуопризмы: [p] × [q]

Самая простая из дуопризм, 3,3-дуопризма, на диаграмме Шлегеля , одна из 6 показанных ячеек треугольной призмы .

Второе — бесконечное семейство однородных дуопризм , произведений двух правильных многоугольников . Диаграмма Кокстера-Динкина дуопризмы :. Его вершинная фигура — дисфеноидный тетраэдр ,.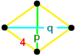

Это семейство пересекается с первым: когда один из двух «факторных» многоугольников является квадратом, произведение эквивалентно гиперпризме, основанием которой является трехмерная призма. Число симметрии дуопризмы, факторами которой являются p -угольник и q -угольник (« p,q -дуопризма»), равно 4 pq , если p ≠ q ; если оба фактора являются p -угольниками, число симметрии равно 8 p ² . Тессеракт также можно считать 4,4-дуопризмой.

Расширенный f-вектор { p }×{ q } равен ( p , p ,1)*( q , q ,1) = ( pq ,2 pq , pq + p + q , p + q ).

• Ячейки: pq - гональные призмы, qp - гональные призмы.
• Грани: pq квадраты, p q -угольники, q p -угольники
• Края: 2 шт.
• Вершины: pq

Не существует единого четырехмерного аналога бесконечного семейства трехмерных антипризм .

Бесконечный набор дуопризм pq -- p q -угольные призмы, q p -угольные призмы:

Возможны чередования."="дает семейство дуоантипризм , но их вообще нельзя сделать однородными. p=q=2 — единственный выпуклый случай, который можно сделать однородным, получив правильные 16 ячеек. p=5, q=5/3 — единственный невыпуклый случай, который можно сделать однородным, давая так называемую большую дуоантипризму .дает p-2q-гональную призмантипризму (чередование краев дуопризмы 2p-4q), но ее ни в коем случае нельзя сделать однородной. ^[20]

Многоугольные призматические призмы: [p] × [ ] × [ ]

Бесконечное множество однородных призматических призм перекрывается с 4-p дуопризмами: (p≥3) -- p кубов и 4 p -угольных призмы - (Все такие же, как 4-p дуопризма ) Второй многогранник в серии представляет собой более низкую симметрию правильного тессеракта , {4}×{4}.

Многоугольные антипризматические призмы: [p] × [ ] × [ ]

Бесконечные множества однородных антипризматических призм построены из двух параллельных однородных антипризм : (p≥2) -- 2 p -угольные антипризмы, соединенные 2 p -угольными призмами и 2p- треугольными призмами.

P -угольная антипризматическая призма имеет треугольник 4p , квадрат 4p и грани 4 p-угольника. Он имеет ребра 10p и вершины 4p .

Неравномерные чередования

Как трехмерный курносый куб ,чередование удаляет половину вершин в двух киральных наборах вершин из кольцевой формы, однако единообразное решение требует, чтобы позиции вершин были отрегулированы на одинаковую длину. В четырех измерениях такая регулировка возможна только для двух чередующихся фигур, а остальные существуют только как неравносторонние чередующиеся фигуры.

Коксетер показал только два равномерных решения для групп Кокстера ранга 4 со всеми чередующимися кольцами (показаны пустыми узлами в виде кружков). Первое - это, s{2 ^1,1,1 } который представлял подгруппу индекса 24 ( симметрия [2,2,2] ⁺ , порядок 8) форму демитессеракта ,, h{4,3,3} (симметрия [1 ⁺ ,4,3,3] = [3 ^1,1,1 ], порядок 192). Второй, s{3 ^1,1,1 }, которая является подгруппой индекса 6 (симметрия [3 ^1,1,1 ] ⁺ , порядок 96) формой курносой 24-клетки ,, s{3,4,3}, (симметрия [3 ⁺ ,4,3], порядок 576).

Другие варианты, например, как альтернатива всеусеченному тессеракту , не может быть сделан равномерным, поскольку решение для равных длин ребер, как правило, переопределено (есть шесть уравнений, но только четыре переменных). Такие неоднородные чередующиеся фигуры могут быть построены как вершинно-транзитивные 4-многогранники путем удаления одного из двух полумножеств вершин полнокольцевой фигуры, но они будут иметь неравную длину ребер. Как и равномерные чередования, они будут иметь половину симметрии однородной фигуры, например [4,3,3] ⁺ порядок 192 — это симметрия чередующегося всеусеченного тессеракта . ^[21]

Конструкции Витхоффа с чередованиями создают транзитивные по вершинам фигуры, которые можно сделать равносторонними, но не однородными, поскольку чередующиеся промежутки (вокруг удаленных вершин) создают ячейки, которые не являются регулярными или полуправильными. Предлагаемое название таких фигур — чешуйчатые многогранники . ^[22] Эта категория допускает подмножество твердых тел Джонсона в виде ячеек, например треугольный купол .

Каждая конфигурация вершин внутри тела Джонсона должна существовать внутри фигуры вершин. Например, квадратная пирамида имеет две конфигурации вершин: 3.3.4 вокруг основания и 3.3.3.3 на вершине.

Ниже приведены сети и фигуры вершин четырех выпуклых равносторонних случаев, а также список ячеек вокруг каждой вершины.

Геометрические выводы для 46 непризматических однородных полихор Витоффа

46 витоффовых 4-многогранников включают шесть выпуклых правильных 4-многогранников . Остальные сорок могут быть получены из регулярной полихоры с помощью геометрических операций, которые сохраняют большую часть или все их симметрии , и, следовательно, могут быть классифицированы по группам симметрии , которые у них общие.

Геометрические операции, которые производят 40 однородных 4-многогранников из правильных 4-многогранников, являются операциями усечения . 4-многогранник может быть усечен по вершинам, ребрам или граням, что приводит к добавлению ячеек, соответствующих этим элементам, как показано в столбцах таблиц ниже.

На диаграмме Коксетера -Динкина четыре зеркала калейдоскопа Витоффа показаны как узлы, а края между узлами помечены целым числом, показывающим угол между зеркалами ( π / n радиан или 180/ n градусов). Узлы в кружке показывают, какие зеркала активны для каждой формы; зеркало активно по отношению к вершине, не лежащей на нем.

См. также выпуклые однородные соты , некоторые из которых иллюстрируют эти операции применительно к обычным кубическим сотам .

Если два многогранника являются двойственными друг другу (например, тессеракт и 16-ячеечный или 120-ячеечный и 600-ячеечный), то побитовое усечение , прогонка или всеусечение либо дает ту же фигуру, что и та же операция для другого. Таким образом, если в таблице встречается только причастие, следует понимать, что оно применимо к любому из родителей.

Краткое изложение конструкций расширенной симметрии

46 однородных полихор, построенных на основе симметрии A ₄ , B ₄ , F ₄ , H ₄ , представлены в этой таблице в виде их полной расширенной симметрии и диаграмм Кокстера. Симметрия D ₄ также включена, но она создает только дубликаты. Чередования сгруппированы по их киральной симметрии. Приведены все чередования, хотя курносая 24-клетка с тремя конструкциями из разных семейств является единственной однородной. В скобках указано либо повторение, либо неравномерность. Диаграммы Кокстера даны с индексами индексов от 1 до 46. Включено дуопризматическое семейство 3-3 и 4-4, второе по отношению к семейству B ₄ .

Равномерная звездчатая полихора

Помимо вышеупомянутых семейств бесконечных дуопризм и антипризм, которые имеют бесконечное количество невыпуклых членов, было обнаружено множество однородных звездных полихор. В 1852 году Людвиг Шлефли открыл четыре правильных звездчатых полихоры: {5,3,5/2}, {5/2,3,5}, {3,3,5/2} и {5/2,3,3. }. В 1883 году Эдмунд Гесс нашел остальные шесть: {3,5,5/2}, {5/2,5,3}, {5,5/2,5}, {5/2,5,5/2. }, {5,5/2,3} и {3,5/2,5}. Норман Джонсон описал три однородных звездчатых полихора, похожих на антипризмы, в своей докторской диссертации 1966 года: они основаны на трех дитригональных многогранниках , разделяющих ребра и вершины правильного додекаэдра. С тех пор другие исследователи, в том числе Джонатан Бауэрс и Джордж Ольшевский, обнаружили гораздо больше, в результате чего в настоящее время насчитывается 2127 известных однородных звездных полихор (не считая бесконечного набора дуопризм, основанных на звездных многоугольниках). В настоящее время нет доказательств полноты набора.

Смотрите также

• Конечные правильные косые многогранники 4-пространства
• Выпуклые однородные соты - связанные бесконечные 4-многогранники в евклидовом 3-мерном пространстве.
• Выпуклые однородные соты в гиперболическом пространстве - связанные бесконечные 4-многогранники в гиперболическом 3-пространстве.
• Паракомпактные однородные соты

Рекомендации

1. Н. В. Джонсон : Геометрии и преобразования , (2018) ISBN  978-1-107-10340-5 Глава 11: Группы конечной симметрии , 11.1 Многогранники и соты , стр.224
2. Т. Госсет : О правильных и полуправильных фигурах в пространстве n измерений , Вестник математики, Макмиллан, 1900 г.
3. «Архивная копия» (PDF) . Архивировано из оригинала (PDF) 29 декабря 2009 г. Проверено 13 августа 2010 г.{{cite web}}: CS1 maint: архивная копия в заголовке ( ссылка )
4. Эльте (1912)
5. Однородные многогранники в четырех измерениях, 6 декабря 1998 г., самый старый архив.
6. Универсальная книга по математике: от абракадабры до парадоксов Зенона Дэвида Дарлинга, (2004) ASIN: B00SB4TU58
7. Johnson (2015), Глава 11, раздел 11.5 Сферические группы Кокстера, 11.5.5 полные полихорические группы
8. Однородные многогранники в четырех измерениях, Джордж Ольшевский.
9. Мёллер, Марко (2004). Viersizede Archimedische Polytope (PDF) (Докторская диссертация) (на немецком языке). Университет Гамбурга.
10. Конвей (2008)
11. Многомерный глоссарий, Джордж Ольшевский
12. https://www.mit.edu/~hlb/Associahedron/program.pdf Семинар по выпуклым и абстрактным многогранникам (2005), Н.Джонсон - аннотация «Равномерная полихора».
13. "Равномерная Полихора". www.polytope.net . Проверено 20 февраля 2020 г.
14. «Однородный многогранник». Политоп Wiki . 6 ноября 2023 г. Проверено 11 ноября 2023 г.
15. Коксетер, Правильные многогранники, 7.7 Критерий Шлефли, уравнение 7.78, стр.135
16. "S3s3s3s" .
17. "S3s3s4s".
18. "S3s4s3s" .
19. "S3s3s5s".
20. sns2s2mx, Ричард Клитцинг
21. HSM Коксетер, Правильные и полуправильные многогранники II, [Math. Зейт. 188 (1985) с. 582-588 2.7 Четырехмерные аналоги курносого куба
22. "Многогранник-дерево".
23. "Тута".
24. Категория S1: Тутпап Simple Scaliforms
25. "Присси".
26. Категория S3: Особые чешуйчатые присси
27. _ Bendwavevy.org . Проверено 11 ноября 2023 г.
28. Категория S3: Специальный бидекс Scaliforms.
29. Би-икозитетрадиминишированный 600-ячеечный
30. "Спидрокс". Bendwavevy.org . Проверено 11 ноября 2023 г.
31. Категория S4: Чешуйчатые вихревые призмы spidrox

• А. Буль Стотт : Геометрический вывод полуправильных многогранников из правильных многогранников и пространственного заполнения , Verhandelingen из Koninklijke academy van Wetenschappen, единица ширины Амстердам, Eerste Sectie 11,1, Амстердам, 1910 г.
• Б. Грюнбаум «Выпуклые многогранники» , Нью-Йорк; Лондон: Спрингер, 2003 г. ISBN 0-387-00424-6 . Второе издание подготовили Фолькер Кайбель, Виктор Клее и Гюнтер М. Циглер. 
  
• Эльте, EL (1912), Полуправильные многогранники гиперпространств , Гронинген: Гронингенский университет, ISBN 1-4181-7968-ХПолуправильные многогранники гиперпространств. Полуправильные многогранники гиперпространств.
• ХСМ Коксетер :
  • HSM Коксетер, М. С. Лонге-Хиггинс и Дж. К. П. Миллер: однородные многогранники , Философские труды Лондонского королевского общества, Лондон, 1954 г.
  • HSM Coxeter, Правильные многогранники , 3-е издание, Дувр, Нью-Йорк, 1973 г.
• Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Асии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 
  • (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380-407, МР 2,10]
  • (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559-591]
  • (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
• HSM Coxeter и WOJ Moser. Генераторы и отношения для дискретных групп. 4-е изд., Springer-Verlag. Нью-Йорк. 1980 р. 92, с. 122.
• Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус , Симметрии вещей 2008, ISBN 978-1-56881-220-5 (глава 26) 
• Джон Х. Конвей и Гай MJT : Четырехмерные архимедовы многогранники , Материалы коллоквиума по выпуклости в Копенгагене, стр. 38 и 39, 1965 г.
• Н. В. Джонсон : Теория однородных многогранников и сот , доктор философии. Диссертация, Университет Торонто, 1966 г.
• Н. В. Джонсон: Геометрии и преобразования , (2015) Глава 11: Конечные группы симметрии
• Ричард Клитцинг, Снубс, чередующиеся грани и диаграммы Стотта-Коксетера-Динкина , Симметрия: Культура и наука, Том. 21, №4, 329-344, (2010) [1]
• Шуте, Питер Хендрик (1911), «Аналитическая обработка многогранников, регулярно полученных из правильных многогранников», Verhandelingen der Koninklijke Akademie van Wetenschappen te Amsterdam , 11 (3): 87 стр.Гуглбук, 370–381

Внешние ссылки

• Выпуклые однородные 4-многогранники
  • Однородные выпуклые многогранники в четырех измерениях, Марко Мёллер (на немецком языке) . Включает альтернативные имена этих фигур, в том числе имена Джонатана Бауэрса, Джорджа Ольшевского и Нормана Джонсона.
  • Правильные и полуправильные выпуклые многогранники: краткий исторический обзор
  • Java3D-апплеты с исходниками
• Невыпуклые однородные 4-многогранники
  • Равномерная полихора Джонатана Бауэрса
  • Stella4D Stella (программное обеспечение) создает интерактивные изображения известных однородных полихор, включая 64 выпуклые формы и бесконечные призматические семейства.
• Клитцинг, Ричард. «4D однородные многогранники».
• 4D-многогранники и их двойственные многогранники группы Коксетера W(A4), представленные кватернионами Международный журнал геометрических методов в современной физике, Vol. 9, № 4 (2012) Мехмет Коджа, Назифе Оздес Коджа, Мудхахир Аль-Аджми (2012) [2]