лента Мёбиуса

Неориентируемая поверхность с одним краем

Лента Мёбиуса, сделанная из бумаги и клейкой ленты

В математике лента Мёбиуса , лента Мёбиуса или петля Мёбиуса ^[a] — это поверхность , которую можно образовать, соединив концы полоски бумаги полуоборотом. Как математический объект она была открыта Иоганном Бенедиктом Листингом и Августом Фердинандом Мёбиусом в 1858 году, но уже появлялась в римских мозаиках с третьего века нашей эры . Лента Мёбиуса — это неориентируемая поверхность, что означает, что внутри нее нельзя последовательно отличить повороты по часовой стрелке от поворотов против часовой стрелки. Каждая неориентируемая поверхность содержит ленту Мёбиуса.

Как абстрактное топологическое пространство , лента Мёбиуса может быть вложена в трехмерное евклидово пространство многими различными способами: полуповорот по часовой стрелке отличается от полуповорота против часовой стрелки, и она также может быть вложена с нечетным числом поворотов, большим одного, или с завязанной центральной линией. Любые два вложения с одним и тем же узлом для центральной линии и одинаковым числом и направлением поворотов топологически эквивалентны . Все эти вложения имеют только одну сторону, но при вложении в другие пространства лента Мёбиуса может иметь две стороны. Она имеет только одну граничную кривую .

Несколько геометрических конструкций ленты Мёбиуса придают ей дополнительную структуру. Она может быть выметена как линейчатая поверхность отрезком прямой, вращающимся во вращающейся плоскости, с самопересечениями или без них. Тонкая бумажная полоска, концы которой соединены в ленту Мёбиуса, может плавно изгибаться как развертывающаяся поверхность или быть сложенной плоско ; сплющенные ленты Мёбиуса включают тригексафлексагон . Суданская лента Мёбиуса является минимальной поверхностью в гиперсфере , а лента Мёбиуса Микса является самопересекающейся минимальной поверхностью в обычном евклидовом пространстве. Как суданская лента Мёбиуса, так и другая самопересекающаяся лента Мёбиуса, кросс-шапка, имеют круговую границу. Лента Мёбиуса без своей границы, называемая открытой лентой Мёбиуса, может образовывать поверхности постоянной кривизны . Некоторые высокосимметричные пространства, точки которых представляют линии на плоскости, имеют форму ленты Мёбиуса.

Многочисленные применения лент Мёбиуса включают механические ремни , которые изнашиваются равномерно с обеих сторон, двухпутные американские горки , вагончики которых чередуются между двумя путями, и карты мира, напечатанные таким образом, что антиподы появляются друг напротив друга. Ленты Мёбиуса появляются в молекулах и устройствах с новыми электрическими и электромеханическими свойствами и использовались для доказательства невозможности результатов в теории социального выбора . В популярной культуре ленты Мёбиуса появляются в произведениях искусства М. К. Эшера , Макса Билла и других, а также в дизайне символа переработки . Многие архитектурные концепции были вдохновлены лентой Мёбиуса, включая проект здания для Зала славы NASCAR . Такие исполнители, как Гарри Блэкстоун-старший и Томас Нельсон Даунс, основывали сценические фокусы на свойствах ленты Мёбиуса. Каноны И. С. Баха были проанализированы с использованием лент Мёбиуса. Во многих произведениях спекулятивной фантастики есть ленты Мёбиуса; В более общем плане в художественной литературе распространена структура сюжета, основанная на ленте Мёбиуса, то есть на повторяющихся с неожиданным поворотом событиях.

История

Открытие ленты Мёбиуса как математического объекта приписывается независимо друг от друга немецким математикам Иоганну Бенедикту Листингу и Августу Фердинанду Мёбиусу в 1858 году. ^[2] Однако она была известна задолго до этого, как физический объект, так и в художественных изображениях; в частности, ее можно увидеть на нескольких римских мозаиках третьего века н. э. ^{[3] [4]} Во многих случаях они просто изображают свернутые ленты в качестве границ. Когда число витков нечетное, эти ленты являются лентами Мёбиуса, но для четного числа витков они топологически эквивалентны раскрученным кольцам . Поэтому то, является ли лента лентой Мёбиуса, может быть совпадением, а не преднамеренным выбором. По крайней мере в одном случае лента с разными цветами на разных сторонах была нарисована с нечетным числом витков, заставив художника сделать неуклюжее исправление в точке, где цвета не совпадали. ^[3] Другая мозаика из города Сентинум ( изображена) показывает зодиак , который держит бог Эон , как полосу с единственным поворотом. Нет четких доказательств того, что односторонность этого визуального представления небесного времени была преднамеренной; она могла быть выбрана просто как способ заставить все знаки зодиака появиться на видимой стороне полосы. Некоторые другие древние изображения уробороса или украшений в форме восьмерки также предположительно изображают ленты Мёбиуса, но неясно, были ли они предназначены для изображения плоских полос любого типа. ^[4]

Независимо от математической традиции, машинисты давно знали, что механические ремни изнашиваются вдвое медленнее, когда они образуют ленты Мёбиуса, потому что они используют всю поверхность ремня, а не только внутреннюю поверхность некрученого ремня. ^[3] Кроме того, такой ремень может быть менее склонен к закручиванию из стороны в сторону. Раннее письменное описание этой техники датируется 1871 годом, то есть после первых математических публикаций, касающихся ленты Мёбиуса. Гораздо раньше изображение цепного насоса в работе Исмаила аль-Джазари от 1206 года изображает конфигурацию ленты Мёбиуса для его приводной цепи. ^[4] Другое использование этой поверхности было сделано швеями в Париже (в неустановленную дату): они инициировали новичков, требуя от них пришивать ленту Мёбиуса в качестве воротника к одежде . ^[3]

Характеристики

Двумерный объект, проходящий один раз по ленте Мёбиуса, возвращается в зеркальном отображении.

Лента Мёбиуса обладает несколькими любопытными свойствами. Это неориентируемая поверхность : если асимметричный двумерный объект скользит один раз по ленте, он возвращается в исходное положение как свое зеркальное отражение. В частности, изогнутая стрелка, указывающая по часовой стрелке (↻), вернется как стрела, указывающая против часовой стрелки (↺), подразумевая, что внутри ленты Мёбиуса невозможно последовательно определить, что значит быть по часовой стрелке или против часовой стрелки. Это простейшая неориентируемая поверхность: любая другая поверхность неориентируема тогда и только тогда, когда она имеет ленту Мёбиуса в качестве подмножества. ^[5] Соответственно, при встраивании в евклидово пространство лента Мёбиуса имеет только одну сторону. Трехмерный объект, который скользит один раз по поверхности ленты, не отражается, а вместо этого возвращается в ту же точку ленты на том, что локально кажется ее другой стороной, показывая, что оба положения на самом деле являются частью одной стороны. Такое поведение отличается от поведения знакомых ориентируемых поверхностей в трех измерениях, таких как те, которые моделируются плоскими листами бумаги, цилиндрическими соломинками для питья или полыми шарами, у которых одна сторона поверхности не соединена с другой. ^[6] Однако это свойство ее вложения в пространство, а не внутреннее свойство самой ленты Мёбиуса: существуют другие топологические пространства, в которые лента Мёбиуса может быть вложена так, что у нее будут две стороны. ^[7] Например, если передняя и задняя грани куба склеены друг с другом с левым-правым зеркальным отражением, результатом будет трехмерное топологическое пространство (декартово произведение ленты Мёбиуса с интервалом), в котором верхняя и нижняя половины куба могут быть отделены друг от друга двусторонней лентой Мёбиуса. ^[b] В отличие от дисков, сфер и цилиндров, для которых возможно одновременное вложение несчетного множества непересекающихся копий в трехмерное пространство, только счетное число лент Мёбиуса может быть одновременно вложено. ^{[9] [10] [11]}

Путь вдоль края ленты Мёбиуса, проложенный до тех пор, пока он не вернется в свою начальную точку на краю, включает все граничные точки ленты Мёбиуса в одну непрерывную кривую. Для ленты Мёбиуса, образованной склеиванием и скручиванием прямоугольника, она имеет длину, вдвое большую средней линии ленты. В этом смысле лента Мёбиуса отличается от нескрученного кольца и, как и круглый диск, имеет только одну границу. ^[6] Лента Мёбиуса в евклидовом пространстве не может быть перемещена или растянута в свое зеркальное отображение; это хиральный объект с правым или левым направлением. ^[12] Ленты Мёбиуса с нечетным числом полуповоротов больше одного или которые завязаны перед склеиванием, различаются как вложенные подмножества трехмерного пространства, хотя все они эквивалентны как двумерные топологические поверхности. ^[13] Точнее, две ленты Мёбиуса эквивалентно вложены в трехмерное пространство, когда их центральные линии определяют один и тот же узел, и они имеют одинаковое количество поворотов . ^[14] Однако при четном количестве поворотов получается другая топологическая поверхность, называемая кольцом . ^[15]

Ленту Мёбиуса можно непрерывно преобразовывать в её центральную линию, делая её уже, фиксируя точки на центральной линии. Это преобразование является примером деформационного ретракции , и его существование означает, что лента Мёбиуса имеет многие из тех же свойств, что и её центральная линия, которая топологически является окружностью. В частности, её фундаментальная группа совпадает с фундаментальной группой окружности, бесконечной циклической группой . Поэтому пути на ленте Мёбиуса, которые начинаются и заканчиваются в одной и той же точке, можно топологически различить (с точностью до гомотопии ) только по количеству раз, которое они обходят ленту. ^[16]

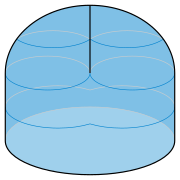
Разрезание ленты Мёбиуса вдоль центральной линии ножницами дает одну длинную ленту с четырьмя полуоборотами в ней (относительно нескрученного кольца или цилиндра), а не две отдельные ленты. Два полуоборота возникают из-за того, что эта более тонкая лента проходит два раза через полуоборот в исходной ленте Мёбиуса, а два других возникают из-за того, как две половины более тонкой ленты оборачиваются вокруг друг друга. Результат не является лентой Мёбиуса, а вместо этого топологически эквивалентен цилиндру. Разрезание этой дважды скрученной ленты снова вдоль ее центральной линии дает две связанные дважды скрученные ленты. Если вместо этого ленту Мёбиуса разрезать вдоль, на треть поперек ее ширины, то получатся две связанные ленты. Одна из двух является центральной, более тонкой лентой Мёбиуса, в то время как другая имеет два полуоборота. ^[6] Эти взаимосвязанные формы, образованные продольными срезами лент Мёбиуса различной ширины, иногда называют парадромными кольцами . ^{[17] [18]}

Ленту Мёбиуса можно разрезать на шесть смежных областей, что показывает, что карты на поверхности ленты Мёбиуса иногда могут потребовать шесть цветов, в отличие от теоремы о четырех цветах для плоскости. ^[19] Шести цветов всегда достаточно. Этот результат является частью теоремы Рингеля–Юнгса , которая устанавливает, сколько цветов требуется каждой топологической поверхности. ^[20] Рёбра и вершины этих шести областей образуют граф Титце , который является двойственным графом на этой поверхности для шестивершинного полного графа , но не может быть нарисован без пересечений на плоскости . Другое семейство графов, которые можно вложить в ленту Мёбиуса, но не в плоскость, — это лестницы Мёбиуса , границы подразделений ленты Мёбиуса на прямоугольники, встречающиеся концом в конец. ^[21] К ним относится граф полезности, полный двудольный граф с шестью вершинами , вложение которого в ленту Мёбиуса показывает, что, в отличие от плоскости, задача о трех полезностях может быть решена на прозрачной ленте Мёбиуса. ^[22] Эйлерова характеристика ленты Мёбиуса равна нулю , что означает, что для любого подразделения ленты вершинами и ребрами на области, числа , , и вершин, ребер и областей удовлетворяют . Например, граф Титце имеет вершины, ребра и области; . ^[19] ${\displaystyle V}$ ${\displaystyle E}$ ${\displaystyle F}$ ${\displaystyle V-E+F=0}$ ${\displaystyle 12}$ ${\displaystyle 18}$ ${\displaystyle 6}$ ${\displaystyle 12-18+6=0}$

Конструкции

Существует множество различных способов определения геометрических поверхностей с топологией ленты Мёбиуса, что приводит к реализациям с дополнительными геометрическими свойствами.

Зачистка сегмента линии

Один из способов встроить ленту Мёбиуса в трехмерное евклидово пространство — вымести ее отрезком прямой, вращающимся в плоскости, который, в свою очередь, вращается вокруг одной из своих линий. ^[23] Чтобы выметаемая поверхность встретилась сама с собой после полуоборота, отрезок прямой должен вращаться вокруг своего центра с половинной угловой скоростью вращения плоскости. Это можно описать как параметрическую поверхность, определяемую уравнениями для декартовых координат ее точек, для и , где один параметр описывает угол поворота плоскости вокруг ее центральной оси, а другой параметр описывает положение точки вдоль вращающегося отрезка прямой. Это создает ленту Мёбиуса шириной 1, центральная окружность которой имеет радиус 1, лежит в -плоскости и центрирована в . ^[24] Тем же методом можно создавать ленты Мёбиуса с любым нечетным числом полуоборотов, вращая отрезок быстрее в его плоскости. Вращающийся сегмент выметает круглый диск в плоскости, в которой он вращается, а лента Мёбиуса, которую он генерирует, образует срез через сплошной тор, выметаемый этим диском. Из-за односторонности этого среза, нарезанный тор остается связанным. ^[25] $${\displaystyle {\begin{aligned}x(u,v)&=\left(1+{\frac {v}{2}}\cos {\frac {u}{2}}\right)\cos u\\y(u,v)&=\left(1+{\frac {v}{2}}\cos {\frac {u}{2}}\right)\sin u\\z(u,v)&={\frac {v}{2}}\sin {\frac {u}{2}}\\\end{aligned}}}$$ ${\displaystyle 0\leq u<2\pi }$ ${\displaystyle -1\leq v\leq 1}$ ${\displaystyle u}$ ${\displaystyle v}$ ${\displaystyle xy}$ ${\displaystyle (0,0,0)}$

Линия или сегмент линии, совершающий иное движение, вращающийся в горизонтальной плоскости вокруг начала координат при движении вверх и вниз, образует коноид или цилиндроид Плюккера , алгебраическую линейчатую поверхность в форме самопересекающейся ленты Мёбиуса. ^[26] Он применяется в проектировании зубчатых передач . ^[27]

Многогранные поверхности и плоские складчатые поверхности

Тригексафлексагон сгибается

Полоску бумаги можно сформировать в плоскости сплющенной лентой Мёбиуса, сложив ее под углами так, чтобы ее центральная линия лежала вдоль равностороннего треугольника , и соединив концы. Самая короткая полоска, для которой это возможно, состоит из трех равносторонних треугольников, сложенных по краям, где встречаются два треугольника. Ее соотношение сторон  — отношение длины полоски ^[c] к ее ширине — равно , и тот же метод складывания работает для любого большего соотношения сторон. ^{[28] [29]} Для полосы из девяти равносторонних треугольников результатом является тригексафлексагон , который можно сгибать, чтобы обнажить различные части его поверхности. ^[30] Для полосок, слишком коротких, чтобы применить этот метод напрямую, можно сначала «сложить гармошкой» полоску в ее широком направлении вперед и назад, используя четное количество складок. Например, при двух сгибах полоска станет сложенной полоской, поперечное сечение которой имеет форму буквы «N», и останется «N» после полуоборота. Более узкая сложенная гармошкой полоска затем может быть сложена и соединена таким же образом, как и более длинная полоска . ^{[28] [29]} ${\displaystyle 60^{\circ }}$ ${\displaystyle {\sqrt {3}}\approx 1.73}$ ${\displaystyle 1\times 1}$ ${\displaystyle 1\times {\tfrac {1}{3}}}$

Пятивершинные многогранные и плоские сложенные ленты Мёбиуса

Лента Мёбиуса также может быть вложена в пространство как многогранная поверхность или сложена на плоскости, при этом только пять треугольных граней имеют пять общих вершин. В этом смысле она проще цилиндра , которому требуется шесть треугольников и шесть вершин, даже если представить его более абстрактно как симплициальный комплекс . ^{[31] [d]} Пятитреугольная лента Мёбиуса может быть представлена ​​наиболее симметрично пятью из десяти равносторонних треугольников четырехмерного правильного симплекса . Эта четырехмерная многогранная лента Мёбиуса является единственной плотной лентой Мёбиуса, которая полностью четырехмерна и для которой все разрезы гиперплоскостями разделяют ее на две части, которые топологически эквивалентны дискам или окружностям. ^[32]

Другие многогранные вложения лент Мёбиуса включают одно с четырьмя выпуклыми четырехугольниками в качестве граней, другое с тремя невыпуклыми четырехугольными гранями ^[33] и одно, использующее вершины и центральную точку правильного октаэдра с треугольной границей. ^[34] Каждая абстрактная триангуляция проективной плоскости может быть вложена в 3D как многогранная лента Мёбиуса с треугольной границей после удаления одной из ее граней; ^[35] примером является шестивершинная проективная плоскость, полученная путем добавления одной вершины к пятивершинной ленте Мёбиуса, соединенной треугольниками с каждым из ее граничных ребер. ^[31] Однако не каждая абстрактная триангуляция ленты Мёбиуса может быть представлена ​​геометрически, как многогранная поверхность. ^[36] Для того, чтобы быть реализуемым, необходимо и достаточно, чтобы в триангуляции не было двух непересекающихся несократимых 3-циклов. ^[37]

Плавно вложенные прямоугольники

Прямоугольная лента Мёбиуса, сделанная путем скрепления концов бумажного прямоугольника, может быть гладко вложена в трехмерное пространство всякий раз, когда ее соотношение сторон больше , то же самое соотношение, что и для плоско сложенной версии ленты Мёбиуса в виде равностороннего треугольника. ^[38] Это плоское треугольное вложение может быть поднято до гладкого ^[e] вложения в трех измерениях, в котором полоса лежит плоско в трех параллельных плоскостях между тремя цилиндрическими роликами, каждый из которых касается двух плоскостей . ^[38] Математически гладко вложенный лист бумаги может быть смоделирован как развертываемая поверхность , которая может сгибаться, но не может растягиваться. ^{[39] [40]} По мере того, как его соотношение сторон уменьшается к , все гладкие вложения, по-видимому, приближаются к той же треугольной форме. ^[41] ${\displaystyle {\sqrt {3}}\approx 1.73}$ ${\displaystyle {\sqrt {3}}}$

Продольные складки сложенной гармошкой плоской ленты Мёбиуса не позволяют ей образовывать трехмерное вложение, в котором слои отделены друг от друга и плавно изгибаются, не сминаясь и не растягиваясь от складок. ^[29] Вместо этого, в отличие от случая плоского сложения, существует нижний предел соотношения сторон гладких прямоугольных лент Мёбиуса. Их соотношение сторон не может быть меньше , даже если допускаются самопересечения. Самопересекающиеся гладкие ленты Мёбиуса существуют для любого соотношения сторон выше этого предела. ^{[29] [42]} Без самопересечений соотношение сторон должно быть не менее ^[43] ${\displaystyle \pi /2\approx 1.57}$ $${\displaystyle {\frac {2}{3}}{\sqrt {3+2{\sqrt {3}}}}\approx 1.695.}$$

Нерешенная задача по математике :

Можно ли склеить бумажный прямоугольник встык, чтобы получилась гладкая лента Мёбиуса, врезанная в пространство?  ^[f] ${\displaystyle 12\times 7}$

(еще нерешенные проблемы по математике)

Для соотношений сторон между этой границей и оставалась открытой проблема ${\displaystyle {\sqrt {3}}}$существования гладких вложений без самопересечения . ^{[29] [42] [43]} В 2023 году Ричард Шварц объявил о доказательстве того, что они не существуют, но этот результат все еще ждет рецензирования и публикации. ^{[44] [45]} Если требование гладкости ослабить, чтобы разрешить непрерывно дифференцируемые поверхности, теорема Нэша–Койпера подразумевает, что любые два противоположных края любого прямоугольника можно склеить, чтобы сформировать вложенную ленту Мёбиуса, независимо от того, насколько малым становится соотношение сторон . ^[g] Предельный случай, поверхность, полученная из бесконечной полосы плоскости между двумя параллельными линиями, склеенными с противоположной ориентацией друг к другу, называется неограниченной лентой Мёбиуса или действительным тавтологическим линейным расслоением . ^[46] Хотя она не имеет гладкого замкнутого вложения в трехмерное пространство, ее можно гладко вложить как замкнутое подмножество четырехмерного евклидова пространства. ^[47]

Форма с минимальной энергией гладкой ленты Мёбиуса, склеенной из прямоугольника, не имеет известного аналитического описания, но может быть рассчитана численно и была предметом большого изучения в теории пластин с момента первой работы по этой теме в 1930 году Майкла Садовски . ^{[39] [40]} Также можно найти алгебраические поверхности , которые содержат прямоугольные развертывающиеся ленты Мёбиуса. ^{[48] [49]}

Делаем границу круглой

Край, или граница , ленты Мёбиуса топологически эквивалентна кругу . В обычных формах ленты Мёбиуса она имеет форму, отличную от круга, но она не завязана , и поэтому всю ленту можно растянуть, не пересекая саму себя, чтобы сделать край идеально круглым . ^[50] Один из таких примеров основан на топологии бутылки Клейна , односторонней поверхности без границы, которая не может быть встроена в трехмерное пространство, но может быть погружена (позволяя поверхности пересекать саму себя определенными ограниченными способами). Бутылка Клейна — это поверхность, которая получается, когда две ленты Мёбиуса склеиваются вместе край к краю, и — обращая этот процесс — бутылку Клейна можно разрезать вдоль тщательно выбранного разреза, чтобы получить две ленты Мёбиуса. ^[51] Для формы бутылки Клейна, известной как бутылка Клейна Лоусона, кривая, по которой она разрезается, может быть сделана круглой, в результате чего получатся ленты Мёбиуса с круглыми краями. ^[52]

Бутылка Клейна Лоусона — это самопересекающаяся минимальная поверхность в единичной гиперсфере 4-мерного пространства, множество точек вида для . ^[53] Половина этой бутылки Клейна, подмножество с , дает ленту Мёбиуса, вложенную в гиперсферу как минимальную поверхность с большим кругом в качестве ее границы. ^[54] Это вложение иногда называют «Суданской лентой Мёбиуса» в честь топологов Сью Гудман и Дэниела Азимова, которые открыли его в 1970-х годах. ^[55] Геометрически бутылка Клейна Лоусона может быть построена путем заметания большого круга посредством движения по большой окружности в 3-сфере, а суданская лента Мёбиуса получается путем заметания полукруга вместо круга или, что эквивалентно, путем разрезания бутылки Клейна вдоль круга, который перпендикулярен всем заметаемым кругам . ^{[52] [56]} Стереографическая проекция преобразует эту форму из трехмерного сферического пространства в трехмерное евклидово пространство, сохраняя кругообразность его границы. ^[52] Наиболее симметричная проекция получается с использованием точки проекции, которая лежит на большом круге, проходящем через середину каждого из полукругов, но производит неограниченное вложение с точкой проекции, удаленной от ее центральной линии. ^[54] Вместо этого, оставляя суданскую ленту Мёбиуса непроецированной, в 3-сфере, оставляет ее с бесконечной группой симметрий, изоморфной ортогональной группе , группе симметрий круга . ^[53] $${\displaystyle (\cos \theta \cos \phi ,\sin \theta \cos \phi ,\cos 2\theta \sin \phi ,\sin 2\theta \sin \phi )}$$ ${\displaystyle 0\leq \theta <\pi ,0\leq \phi <2\pi }$ ${\displaystyle 0\leq \phi <\pi }$ ${\displaystyle \mathrm {O} (2)}$

Схематическое изображение крестообразной крышки с открытым дном, показывающее ее уровни . Эта поверхность пересекает сама себя по вертикальному отрезку.

Суданская лента Мёбиуса простирается на все стороны своего граничного круга, что неизбежно, если поверхность должна избегать пересечения с собой. Другая форма ленты Мёбиуса, называемая кросс-шапкой или кросс-шапкой , также имеет круглую границу, но в остальном остается только на одной стороне плоскости этого круга, ^[57] что делает ее более удобной для прикрепления к круглым отверстиям в других поверхностях. Для этого она пересекает себя. Ее можно сформировать, удалив четырехугольник с вершины полусферы, ориентируя края четырехугольника в чередующихся направлениях, а затем склеив противоположные пары этих краев последовательно с этой ориентацией. ^[58] Две части поверхности, образованные двумя склеенными парами краев, пересекают друг друга с точкой защемления, подобной точке зонтика Уитни на каждом конце пересекающегося сегмента, ^[59] та же топологическая структура, что и в коноиде Плюккера . ^[26]

Поверхности постоянной кривизны

Открытая лента Мёбиуса — это относительная внутренняя часть стандартной ленты Мёбиуса, образованная путем исключения точек на ее граничном крае. Ей может быть задана риманова геометрия постоянной положительной, отрицательной или нулевой гауссовой кривизны . Случаи отрицательной и нулевой кривизны образуют геодезически полные поверхности, что означает, что все геодезические («прямые линии» на поверхности) могут быть продолжены неограниченно в любом направлении.

Нулевая кривизна

Открытая полоса с нулевой кривизной может быть построена путем склеивания противоположных сторон плоской полосы между двумя параллельными линиями, описанными выше как тавтологическое линейное расслоение. ^[46] Полученная метрика превращает открытую ленту Мёбиуса в (геодезически) полную плоскую поверхность (т. е. имеющую нулевую гауссову кривизну везде). Это единственная метрика на ленте Мёбиуса, с точностью до равномерного масштабирования, которая является как плоской, так и полной. Это факторпространство плоскости по скользящему отражению , и (вместе с плоскостью, цилиндром , тором и бутылкой Клейна ) является одним из пяти двумерных полных плоских многообразий . ^[60]

Отрицательная кривизна

Открытая лента Мёбиуса также допускает полную метрику постоянной отрицательной кривизны. Один из способов увидеть это — начать с модели верхней полуплоскости (Пуанкаре) гиперболической плоскости , геометрии постоянной кривизны, линии которой представлены в модели полуокружностями, которые встречаются с осью под прямым углом. Возьмите подмножество верхней полуплоскости между любыми двумя вложенными полуокружностями и отождествите внешнюю полуокружность с лево-правым обращением внутренней полуокружности. Результатом является топологически полная и некомпактная лента Мёбиуса с постоянной отрицательной кривизной. Это «нестандартная» полная гиперболическая поверхность в том смысле, что она содержит полную гиперболическую полуплоскость (на самом деле две, по разные стороны от оси скользящего отражения), и является одной из всего лишь 13 нестандартных поверхностей. ^[61] Опять же, это можно понимать как фактор гиперболической плоскости по скользящему отражению. ^[62] ${\displaystyle x}$

Положительная кривизна

Лента Мёбиуса постоянной положительной кривизны не может быть полной, поскольку известно, что единственными полными поверхностями постоянной положительной кривизны являются сфера и проективная плоскость . ^[60] Однако в некотором смысле она находится всего в одной точке от полной поверхности, поскольку открытая лента Мёбиуса гомеоморфна однажды проколотой проективной плоскости, поверхности, полученной путем удаления любой одной точки из проективной плоскости. ^[63]

Минимальные поверхности описываются как имеющие постоянную нулевую среднюю кривизну вместо постоянной гауссовой кривизны. Суданская лента Мёбиуса была построена как минимальная поверхность, ограниченная большим кругом в 3-сфере, но существует также уникальная полная (безграничная) минимальная поверхность, погруженная в евклидово пространство, имеющая топологию открытой ленты Мёбиуса. Она называется лентой Мёбиуса Микса [ ^64] после ее описания в 1982 году Уильямом Гамильтоном Миксом, III . ^[65] Хотя она глобально нестабильна как минимальная поверхность, ее небольшие участки, ограниченные нестягиваемыми кривыми внутри поверхности, могут образовывать устойчивые вложенные ленты Мёбиуса как минимальные поверхности. ^[66] Как лента Мебиуса Микса, так и любая многомерная минимальная поверхность с топологией ленты Мебиуса могут быть построены с использованием решений задачи Бьёрлинга , которая определяет минимальную поверхность однозначно из ее граничной кривой и касательных плоскостей вдоль этой кривой. ^[67]

Пространства линий

Семейству прямых на плоскости можно придать структуру гладкого пространства, причем каждая прямая представлена ​​как точка в этом пространстве. Полученное пространство прямых топологически эквивалентно открытой ленте Мёбиуса. ^[68] Один из способов увидеть это — расширить евклидову плоскость до действительной проективной плоскости, добавив еще одну прямую, прямую на бесконечности . По проективной двойственности пространство прямых на проективной плоскости эквивалентно ее пространству точек, самой проективной плоскости. Удаление прямой на бесконечности для получения пространства евклидовых прямых прокалывает это пространство проективных прямых. ^[69] Следовательно, пространство евклидовых прямых является проколотой проективной плоскостью, которая является одной из форм открытой ленты Мёбиуса. ^[63] Пространство прямых на гиперболической плоскости можно параметризовать неупорядоченными парами различных точек на окружности, парами точек на бесконечности каждой прямой. Это пространство, опять же, имеет топологию открытой ленты Мёбиуса. ^[70]

Эти пространства прямых высоко симметричны. Симметрии евклидовых прямых включают аффинные преобразования , а симметрии гиперболических прямых включают преобразования Мёбиуса . ^[71] Аффинные преобразования и преобразования Мёбиуса образуют 6-мерные группы Ли , топологические пространства, имеющие совместимую алгебраическую структуру, описывающую композицию симметрий. ^{[72] [73]} Поскольку каждая прямая на плоскости симметрична любой другой прямой, открытая лента Мёбиуса является однородным пространством , пространством с симметриями, которые переводят каждую точку в любую другую точку. Однородные пространства групп Ли называются солвмногообразиями , а лента Мёбиуса может быть использована в качестве контрпримера , показывающего, что не каждое солвмногообразие является нильмногообразием , и что не каждое солвмногообразие может быть разложено на множители в прямое произведение компактного солвмногообразия с . ${\displaystyle \mathbb {R} ^{n}}$ Эти симметрии также предоставляют другой способ построения самой ленты Мёбиуса как групповой модели этих групп Ли. Групповая модель состоит из группы Ли и подгруппы стабилизатора ее действия; стягивание смежных классов подгруппы в точки создает пространство с той же топологией, что и лежащее в основе однородное пространство. В случае симметрий евклидовых прямых стабилизатор -оси состоит из всех симметрий, которые переводят ось в себя. Каждая линия соответствует смежному классу, набору симметрий, которые отображаются на -ось. Следовательно, фактор-пространство , пространство, которое имеет одну точку на смежный класс и наследует свою топологию от пространства симметрий, совпадает с пространством прямых и снова является открытой лентой Мёбиуса. ^[74] ${\displaystyle x}$ ${\displaystyle \ell }$ ${\displaystyle \ell }$ ${\displaystyle x}$

Приложения

Электрический поток в резисторе Мёбиуса

Помимо уже обсуждавшихся применений лент Мёбиуса для проектирования механических ремней, которые изнашиваются равномерно по всей поверхности, и коноида Плюккера для проектирования зубчатых передач, существуют и другие применения лент Мёбиуса:

• Графеновые ленты, скрученные в ленты Мёбиуса с новыми электронными характеристиками, включая спиральный магнетизм ^[75]
• Ароматичность Мёбиуса , свойство органических химических веществ , молекулярная структура которых образует цикл, с молекулярными орбиталями , выстроенными вдоль цикла в виде ленты Мёбиуса ^{[76] [77]}
• Резистор Мёбиуса , полоска проводящего материала, покрывающая одну сторону диэлектрической ленты Мёбиуса таким образом, что нейтрализует ее собственную индуктивность ^{[78] [79]}
• Резонаторы с компактной конструкцией и резонансной частотой, которая вдвое меньше, чем у линейных катушек идентичной конструкции ^{[80] [81]}
• Паттерны поляризации света, выходящего из q -пластины ^[82]
• Доказательство невозможности непрерывных, анонимных и единогласных правил двухпартийной агрегации в теории общественного выбора ^[83]
• Американские горки с петлей Мёбиуса — разновидность двухпутных американских горок, в которых два пути закручиваются вокруг друг друга нечетное число раз, так что вагончики возвращаются на другой путь, а не на тот, с которого они начали движение ^{[84] [85]}
• Карты мира, спроецированные на ленту Мёбиуса с удобными свойствами, заключающимися в том, что не существует границ восток-запад и что антипод любой точки на карте можно найти на другой печатной стороне поверхности в той же точке ленты Мёбиуса ^{[86] [87]}

Ученые также изучали энергетику мыльных пленок , имеющих форму лент Мёбиуса, ^[88] [ ^89], химический синтез молекул в форме лент Мёбиуса, ^{[90] [91]} и формирование более крупных наноразмерных лент Мёбиуса с использованием ДНК-оригами . ^[92]

В популярной культуре

«Бесконечный поворот» , Макс Билл , 1956, из Музея скульптур под открытым небом Мидделхейм

Двумерные произведения искусства, изображающие ленту Мёбиуса, включают безымянную картину 1947 года Коррадо Кальи (увековеченную в стихотворении Чарльза Олсона ) ^{[93] [94]} и две гравюры М. К. Эшера : «Лента Мёбиуса I» (1961), изображающая трех сложенных камбал, кусающих друг друга за хвосты; и «Лента Мёбиуса II» (1963), изображающая муравьев, ползающих по ленте Мёбиуса в форме лемнискаты . ^{[95] [96]} Это также популярный предмет математической скульптуры , включая работы Макса Билла ( «Бесконечная лента» , 1953), Хосе де Риверы ( «Бесконечность» , 1967) и Себастьяна . ^[93] Завязанная трилистником лента Мёбиуса была использована в «Бессмертии » Джона Робинсона ( 1982). ^{[97] «} Континуум » Чарльза О. Перри (1976) — одна из нескольких работ Перри, исследующих вариации ленты Мёбиуса. ^[98]

Благодаря своей легко узнаваемой форме ленты Мёбиуса являются распространенным элементом графического дизайна . ^[97] Знакомый логотип с тремя стрелками для переработки отходов , разработанный в 1970 году, основан на гладкой треугольной форме ленты Мёбиуса , ^[99] как и логотип для тематической выставки Expo '74, посвященной окружающей среде . ^[100] Некоторые вариации символа переработки отходов используют другое вложение с тремя полуоборотами вместо одного, ^[99] а оригинальная версия логотипа Google Drive использовала сложенную пополам трехоборотную ленту Мёбиуса, как и другие подобные дизайны. ^[101] Бразильский Национальный институт чистой и прикладной математики (IMPA) использует стилизованную гладкую ленту Мёбиуса в качестве своего логотипа и имеет соответствующую большую скульптуру ленты Мёбиуса, выставленную в его здании. ^[102] Лента Мёбиуса также была представлена ​​в оформлении почтовых марок таких стран, как Бразилия, Бельгия, Нидерланды и Швейцария. ^{[103] [104]}

Вход в Зал славы NASCAR

Ленты Мёбиуса часто служили источником вдохновения для архитектурного проектирования зданий и мостов. Однако многие из них являются проектами или концептуальными конструкциями, а не построенными объектами, или расширяют свою интерпретацию ленты Мёбиуса за пределы ее узнаваемости как математической формы или функциональной части архитектуры. ^{[105] [106]} Примером является Национальная библиотека Казахстана , для которой было запланировано здание в форме утолщенной ленты Мёбиуса, но переделанное с другим дизайном после того, как первоначальные архитекторы вышли из проекта. ^[107] Одним из примечательных зданий, включающих ленту Мёбиуса, является Зал славы NASCAR , который окружен большой витой лентой из нержавеющей стали, выступающей в качестве фасада и навеса и вызывающей в памяти изогнутые формы гоночных трасс. ^[108] В меньшем масштабе кресло Мёбиуса (2006) Педро Рейеса представляет собой скамейку для ухаживания, основание и стороны которой имеют форму ленты Мёбиуса. ^[109] Как форма математики и волокнистого искусства , шарфы вяжутся в ленты Мёбиуса со времен работ Элизабет Циммерманн в начале 1980-х годов. [ ^110] В стилистике еды ленты Мёбиуса используются для нарезки бубликов , ^[111] изготовления петель из бекона , ^[112] и создания новых форм для пасты . ^[113]

Хотя математически лента Мёбиуса и четвертое измерение являются чисто пространственными концепциями, они часто использовались в спекулятивной фантастике в качестве основы для временной петли , в которой могут оказаться неосторожные жертвы. Примерами этого тропа являются «No-Sided Professor» Мартина Гарднера ( 1946), « A Subway Named Mobius » Армина Джозефа Дойча ( 1950) и основанный на ней фильм «Moebius» (1996). Весь мир, имеющий форму ленты Мёбиуса, является местом действия «The Wall of Darkness» Артура Кларка (1946), в то время как обычные ленты Мёбиуса используются в качестве остроумных изобретений в нескольких рассказах Уильяма Хазлетта Апсона 1940-х годов. ^[114] Другие произведения художественной литературы были проанализированы как имеющие структуру, подобную ленте Мёбиуса, в которой элементы сюжета повторяются с изюминкой; К ним относятся « В поисках утраченного времени» Марселя Пруста ( 1913–1927), «Шесть персонажей в поисках автора» Луиджи Пиранделло (1921), « Эта прекрасная жизнь » Фрэнка Капры (1946), «Заблудившиеся в комнате смеха» Джона Барта ( 1968), « Дальгрен » Сэмюэля Р. Делани ( 1975) и фильм «Донни Дарко» (2001). ^[115]

Один из музыкальных канонов И. С. Баха , пятый из 14 канонов ( BWV 1087 ), обнаруженный в 1974 году в копии Гольдберг-вариаций Баха , характеризуется симметрией скольжения-отражения , в которой каждый голос в каноне повторяет с перевернутыми нотами тот же мотив из двух тактов ранее. Из-за этой симметрии этот канон можно рассматривать как имеющий свою партитуру, записанную на ленте Мёбиуса. ^{[116] [h]} В теории музыки тоны, которые отличаются на октаву, обычно считаются эквивалентными нотами, а пространство возможных нот образует круг, хроматический круг . Поскольку лента Мёбиуса является конфигурационным пространством двух неупорядоченных точек на окружности, пространство всех двухнотных аккордов принимает форму ленты Мёбиуса. Эта концепция и обобщения на большее количество точек являются значительным приложением орбифолдов к теории музыки . ^{[117] [118]} Современные музыкальные группы, получившие свое название от ленты Мёбиуса, включают американское электронное рок-трио Mobius Band ^[119] и норвежскую прогрессивную рок-группу Ring Van Möbius . ^[120]

Ленты Мёбиуса и их свойства использовались в дизайне сценической магии . Один из таких трюков, известный как «афганские ленты», использует тот факт, что лента Мёбиуса остается целой как одна полоса, если ее разрезать вдоль. Он возник в 1880-х годах и был очень популярен в первой половине двадцатого века. Существует много версий этого трюка, и они были выполнены известными иллюзионистами, такими как Гарри Блэкстоун-старший и Томас Нельсон Даунс . ^{[121] [122]}

Смотрите также

• Счетчик Мёбиуса , сдвиговый регистр, выходной бит которого дополняется перед подачей обратно во входной бит.
• Треугольник Пенроуза — невозможная фигура, граница которой, кажется, обертывается вокруг нее в ленту Мёбиуса.
• Теория лент , математическая теория бесконечно тонких полосок, которые следуют запутанным пространственным кривым.
• Аттрактор Смейла–Вильямса , фрактал, образованный путем многократного утолщения пространственной кривой до ленты Мёбиуса с последующей заменой ее граничным краем
• Пупочный тор

Примечания

1. Произносится в США : / ˈm oʊb iəs , ˈm eɪ - / MOH -bee-əs, MAY - , в Великобритании : / ˈm ɜːb iəs / ; [ 1 ] ^в Германии : [ˈmøːbi̯ʊs] . Как и в случае со словами, содержащими умлаут , его также часто пишут как Mobius или Moebius .
2. По сути, этот пример, но для бутылки Клейна , а не для ленты Мёбиуса, приводит Блэкетт (1982). ^[8]
3. Длину ленты можно измерить по ее средней линии или разрезав полученную ленту Мёбиуса перпендикулярно ее границе так, чтобы она образовала прямоугольник.
4. Плоская сложенная лента Мёбиуса, образованная тремя равносторонними треугольниками, не получается из абстрактного симплициального комплекса , поскольку все три треугольника имеют одни и те же три вершины, в то время как абстрактные симплициальные комплексы требуют, чтобы каждый треугольник имел разный набор вершин.
5. Это кусочно-плоское и цилиндрическое вложение имеет класс гладкости и может быть аппроксимировано произвольно точно бесконечно дифференцируемыми (класс ) вложениями. ^[39] ${\displaystyle C^{2}}$ ${\displaystyle C^{\infty }}$
6. 12/7 — простейшее рациональное число в диапазоне соотношений сторон от 1,695 до 1,73, для которого существование гладкого вложения неизвестно.
7. Эти поверхности имеют класс гладкости . Для более тонкого анализа предположений о гладкости, которые заставляют вложение быть развертываемым, по сравнению с предположениями, при которых теорема Нэша–Койпера допускает произвольно гибкие вложения, см. замечания Бартельса и Хорнунга (2015), стр. 116, после теоремы 2.2. ^[39] ${\displaystyle C^{1}}$
8. Ленты Мёбиуса также использовались для анализа многих других канонов Баха и других, но в большинстве этих случаев другие петлевые поверхности, такие как цилиндр, могли бы быть использованы с таким же успехом. ^[116]

Ссылки

1. Уэллс, Джон С. (2008). Словарь произношения Longman (3-е изд.). Longman. ISBN 978-1-4058-8118-0.
2. Пиковер, Клиффорд А. (2005). Лента Мёбиуса: Чудесная лента доктора Августа Мёбиуса в математике, играх, литературе, искусстве, технологии и космологии. Thunder's Mouth Press. С. 28–29. ISBN 978-1-56025-826-1.
3. Larison, Lorraine L. (1973). «Лента Мёбиуса в римских мозаиках». American Scientist . 61 (5): 544–547. Bibcode : 1973AmSci..61..544L. JSTOR  27843983.
4. Cartwright, Julian HE ; González, Diego L. (2016). «Ленты Мёбиуса до Мёбиуса: топологические намеки в древних представлениях». The Mathematical Intelligencer . 38 (2): 69–76. arXiv : 1609.07779 . Bibcode :2016arXiv160907779C. doi :10.1007/s00283-016-9631-8. MR  3507121. S2CID  119587191.
5. Флапан, Эрика (2000). Когда топология встречается с химией: топологический взгляд на молекулярную хиральность . Перспективы. Вашингтон, округ Колумбия: Математическая ассоциация Америки. стр. 82–83. doi :10.1017/CBO9780511626272. ISBN 0-521-66254-0. МР  1781912.
6. Pickover (2005), стр. 8–9.
7. Woll, John W. Jr. (весна 1971 г.). «Односторонние поверхности и ориентируемость». The Two-Year College Mathematics Journal . 2 (1): 5–18. doi :10.2307/3026946. JSTOR  3026946.
8. Блэкетт, Дональд В. (1982). Элементарная топология: комбинаторный и алгебраический подход . Academic Press. стр. 195. ISBN 9781483262536.
9. Фролкина, Ольга Д. (2018). "Pairwise disjoint Moebius bands in space". Journal of Knot Theory and Its Ramifications . 27 (9): 1842005, 9. arXiv : 2212.02983 . doi :10.1142/S0218216518420051. MR  3848635. S2CID  126421578.
10. Лэмб, Эвелин (20 февраля 2019 г.). «Ленты Мёбиуса бросают вызов связи с бесконечностью». Журнал Quanta .
11. Мелихов, Сергей А. (2019). "Заметка о статье О. Фролкиной "Попарно непересекающиеся ленты Мёбиуса в пространстве"". Журнал теории узлов и ее разветвлений . 28 (7): 1971001, 3. arXiv : 1810.04089 . doi : 10.1142/s0218216519710019. MR  3975576. S2CID  119179202.
12. Пиковер (2005), стр. 52.
13. Пиковер (2005), стр. 12.
14. Кайл, Р. Х. (1955). «Вложения лент Мёбиуса в трехмерное пространство». Труды Королевской Ирландской Академии, Раздел A. 57 : 131–136. JSTOR  20488581. MR  0091480.
15. Пиковер (2005), стр. 11.
16. Мэсси, Уильям С. (1991). Базовый курс алгебраической топологии. Graduate Texts in Mathematics. Т. 127. Нью-Йорк: Springer-Verlag. С. 49. ISBN 0-387-97430-X. МР  1095046.
17. Рауз Болл, WW (1892). «Парадромные кольца». Математические воссоздания и проблемы прошлого и настоящего времени (2-е изд.). Лондон и Нью-Йорк: Macmillan and co. стр. 53–54. ISBN 9780608377803.
18. Беннетт, Г. Т. (июнь 1923 г.). «Парадромные кольца». Nature . 111 (2800): 882. Bibcode :1923Natur.111R.882B. doi : 10.1038/111882b0 . S2CID  4099647.
19. Титце, Генрих (1910). «Einige Bemerkungen zum Issue des Kartenfärbens auf einseitigen Flächen» (PDF) . Jahresbericht der Deutschen Mathematiker-Vereinigung . 19 : 155–159.
20. Рингель, Г.; Янгс, Дж. У. Т. (1968). «Решение проблемы раскраски карт Хивуда». Труды Национальной академии наук Соединенных Штатов Америки . 60 (2): 438–445. Bibcode : 1968PNAS...60..438R. doi : 10.1073 /pnas.60.2.438 . MR  0228378. PMC 225066. PMID  16591648. 
21. Яблан, Славик; Радович, Лилиана; Сазданович, Радмила (2011). «Непланарные графы, полученные из кодов Гаусса виртуальных узлов и связей». Журнал математической химии . 49 (10): 2250–2267. doi :10.1007/s10910-011-9884-6. MR  2846715. S2CID  121332704.
22. Larsen, Mogens Esrom (1994). «Непонимание моих запутанных лабиринтов может сделать меня несчастным». В Guy, Richard K. ; Woodrow, Robert E. (ред.). Труды конференции памяти Эжена Стрэнса по занимательной математике и ее истории, состоявшейся в Университете Калгари, Калгари, Альберта, август 1986 г. MAA Spectrum. Вашингтон, округ Колумбия: Математическая ассоциация Америки. стр. 289–293. ISBN 0-88385-516-X. МР  1303141., См. Рисунок 7, стр. 292.
23. Машке, Генрих (1900). «Заметка об односторонней поверхности Мёбиуса». Труды Американского математического общества . 1 (1): 39. doi : 10.2307/1986401 . JSTOR  1986401. MR  1500522.
24. Юнгхенн, Хьюго Д. (2015). Курс реального анализа. Бока-Ратон, Флорида: CRC Press. п. 430. ИСБН 978-1-4822-1927-2. МР  3309241.
25. Séquin, Carlo H. (2005). «Расщепление торов, узлов и полос Мёбиуса». В Sarhangi, Reza; Moody, Robert V. (ред.). Renaissance Banff: Mathematics, Music, Art, Culture . Southwestern College, Winfield, Kansas: Bridges Conference. стр. 211–218. ISBN 0-9665201-6-5.
26. Francis, George K. (1987). "Plücker conoid". Топологическая иллюстрированная книга . Springer-Verlag, Нью-Йорк. С. 81–83. ISBN 0-387-96426-6. МР  0880519.
27. Дунер, Дэвид Б.; Сейрег, Али (1995). "3.4.2 Цилиндроид". Кинематическая геометрия зубчатых передач: параллельный инженерный подход . Серия Wiley по проектированию. Том 3. John Wiley & Sons. С. 135–137. ISBN 9780471045977.
28. Barr, Stephen (1964). Эксперименты по топологии. Нью-Йорк: Thomas Y. Crowell Company. С. 40–49, 200–201. ISBN 9780690278620.
29. Фукс, Дмитрий ; Табачников, Сергей (2007). "Лекция 14: Бумага Мёбиуса". Математический омнибус: Тридцать лекций по классической математике (PDF) . Провиденс, Род-Айленд: Американское математическое общество. стр. 199–206. doi :10.1090/mbk/046. ISBN 978-0-8218-4316-1. MR  2350979. Архивировано из оригинала (PDF) 24.04.2016.
30. Пук, Лес (2003). "4.2: Тригексафлексагон снова". Флексагоны изнутри наружу . Кембридж, Великобритания: Cambridge University Press. стр. 33–36. doi : 10.1017/CBO9780511543302. ISBN 0-521-81970-9. МР  2008500.
31. Kühnel, W.; Banchoff, TF (1983). "9-вершинная комплексная проективная плоскость" (PDF) . The Mathematical Intelligencer . 5 (3): 11–22. doi :10.1007/BF03026567. MR  0737686. S2CID  120926324.
32. Кёйпер, Николас Х. (1972). «Плотные топологические вложения ленты Мёбиуса». Журнал дифференциальной геометрии . 6 (3): 271–283. doi : 10.4310/jdg/1214430493 . MR  0314057.
33. Szilassi, Lajos (2008). "Многогранная модель в евклидовом 3-пространстве шестипентагональной карты проективной плоскости". Дискретная и вычислительная геометрия . 40 (3): 395–400. doi : 10.1007/s00454-007-9033-y . MR  2443291. S2CID  38606607.
34. Такерман, Брайант (1948). «Неособая многогранная лента Мёбиуса, граница которой — треугольник». American Mathematical Monthly . 55 (5): 309–311. doi :10.2307/2305482. JSTOR  2305482. MR  0024138.
35. Боннингтон, К. Пол; Накамото, Ацухиро (2008). «Геометрическая реализация триангуляции на проективной плоскости с одной удаленной гранью». Дискретная и вычислительная геометрия . 40 (1): 141–157. doi : 10.1007/s00454-007-9035-9 . MR  2429652. S2CID  10887519.
36. Брем, Ульрих (1983). «Неполиэдральная триангулированная лента Мёбиуса». Труды Американского математического общества . 89 (3): 519–522. doi :10.2307/2045508. JSTOR  2045508. MR  0715878.
37. Накамото, Ацухиро; Цутия, Сёичи (2012). «О геометрически реализуемых триангуляциях Мёбиуса». Дискретная математика . 312 (14): 2135–2139. doi : 10.1016/j.disc.2011.06.007 . MR  2921579.
38. Hinz, Denis F.; Fried, Eliot (2015). "Перевод статьи Майкла Садовски "Элементарное доказательство существования развертывающейся ленты Мёбиуса и отнесение геометрической задачи к вариационной задаче"". Журнал эластичности . 119 (1–2): 3–6. arXiv : 1408.3034 . doi :10.1007/s10659-014-9490-5. MR  3326180. S2CID  119733903.Перепечатано в Fosdick, Roger; Fried, Eliot (2016). Механика лент и лент Мёбиуса (PDF) . Springer, Dordrecht. стр. 3–6. doi :10.1007/978-94-017-7300-3. ISBN 978-94-017-7299-0. МР  3381564.
39. Бартельс, Сёрен; Хорнунг, Питер (2015). «Изгиб бумаги и лента Мёбиуса». Журнал эластичности . 119 (1–2): 113–136. doi :10.1007/s10659-014-9501-6. MR  3326187. S2CID  119782792.Перепечатано в Fosdick & Fried (2016), стр. 113–136. См. в частности Раздел 5.2, стр. 129–130.
40. Starostin, EL; van der Heijden, GHM (2015). "Формы равновесия с локализацией напряжений для нерастяжимой эластичной ленты Мёбиуса и других лент". Journal of Elasticity . 119 (1–2): 67–112. doi : 10.1007/s10659-014-9495-0 . MR  3326186. S2CID  53462568.Перепечатано в Fosdick & Fried (2016), стр. 67–112.
41. Шварц, Гидеон Э. (1990). «Темная сторона ленты Мёбиуса». The American Mathematical Monthly . 97 (10): 890–897. doi :10.1080/00029890.1990.11995680. JSTOR  2324325. MR  1079975.
42. Halpern, B.; Weaver, C. (1977). «Обращение цилиндра посредством изометрических погружений и изометрических вложений». Труды Американского математического общества . 230 : 41–70. doi : 10.2307/1997711 . JSTOR  1997711. MR  0474388.
43. Шварц, Ричард Эван (2021). «Улучшенная граница оптимальной бумажной ленты Мёбиуса». Geometriae Dedicata . 215 : 255–267. arXiv : 2008.11610 . doi :10.1007/s10711-021-00648-5. MR  4330341. S2CID  220279013.
44. Шварц, Ричард (2023). «Оптимальная бумажная лента Мёбиуса». arXiv : 2308.12641 [math.MG].
45. Кроуэлл, Рэйчел (12 сентября 2023 г.). «Математики решают 50-летнюю головоломку с лентой Мёбиуса». Scientific American .
46. Dundas, Bjørn Ian (2018). "Пример 5.1.3: Неограниченная лента Мёбиуса". Краткий курс дифференциальной топологии . Cambridge Mathematical Textbooks. Cambridge University Press, Кембридж. стр. https://books.google.com/books?id=7a1eDwAAQBAJ&pg=PA101. doi :10.1017/9781108349130. ISBN 978-1-108-42579-7. MR  3793640. S2CID  125997451.
47. Блануша, Данило (1954). «Изометрическое удлинение бесконечной ленты Мёбиуса, большой евклид в пространстве сферы, параболическое или гиперболическое в четырех измерениях». Международный бюллетень Югославской академии наук и изящных искусств . 12 :19–23. МР  0071060.
48. Вундерлих, В. (1962). «Über ein abwickelbares Möbiusband». Монашефте по математике . 66 (3): 276–289. дои : 10.1007/BF01299052. MR  0143115. S2CID  122215321.
49. Шварц, Гидеон (1990). «Претендент на звание „канонической ленты Мёбиуса“». Pacific Journal of Mathematics . 143 (1): 195–200. doi : 10.2140/pjm.1990.143.195 . MR  1047406.
50. Гильберт, Дэвид ; Кон-Фоссен, Стефан (1952). Геометрия и воображение (2-е изд.). Челси. С. 315–316. ISBN 978-0-8284-1087-8.
51. Спивак, Майкл (1979). Всестороннее введение в дифференциальную геометрию, том I (2-е изд.). Уилмингтон, Делавэр: Опубликуй или погибни. стр. 591.
52. Knöppel, Felix (лето 2019 г.). "Учебник 3: Минимальные поверхности Лоусона и суданская лента Мёбиуса". DDG2019: Курс визуализации в Техническом университете Берлина .
53. Lawson, H. Blaine Jr. (1970). "Полные минимальные поверхности в ". Annals of Mathematics . Вторая серия. 92 (3): 335–374. doi :10.2307/1970625. JSTOR  1970625. MR  0270280. ${\displaystyle S^{3}}$См. раздел 7, стр. 350–353, где бутылка Клейна обозначена . ${\displaystyle \tau _{1,2}}$
54. Шлеймер, Сол; Сегерман, Генри (2012). «Скульптуры в S3». В Bosch, Роберт; Маккенна, Дуглас; Сарханги, Реза (ред.). Труды Bridges 2012: Математика, Музыка, Искусство, Архитектура, Культура . Финикс, Аризона: Tessellations Publishing. стр. 103–110. arXiv : 1204.4952 . ISBN 978-1-938664-00-7.
55. Ганн, Чарльз (23 августа 2018 г.). «Суданская лента Мёбиуса». Vimeo . Получено 17.03.2022 .
56. Franzoni, Gregorio (2012). «Бутылка Клейна: вариации на тему». Notices of the American Mathematical Society . 59 (8): 1076–1082. doi : 10.1090/noti880 . MR  2985809.
57. Хаггетт, Стивен; Джордан, Дэвид (2009). Топологический аперитив (переработанная ред.). Спрингер-Верлаг. п. 57. ИСБН 978-1-84800-912-7. МР  2483686.
58. Флапан, Эрика (2016). Узлы, молекулы и Вселенная: введение в топологию. Провиденс, Род-Айленд: Американское математическое общество. стр. 99–100. doi :10.1090/mbk/096. ISBN 978-1-4704-2535-7. МР  3443369.
59. Ричесон, Дэвид С. (2008). Драгоценный камень Эйлера: Формула многогранника и рождение топологии . Принстон, Нью-Джерси: Princeton University Press. стр. 171. ISBN 978-0-691-12677-7. МР  2440945.
60. Godinho, Leonor; Natário, José (2014). Введение в риманову геометрию: с приложениями к механике и теории относительности. Universitext. Springer, Cham. стр. 152–153. doi :10.1007/978-3-319-08666-8. ISBN 978-3-319-08665-1. МР  3289090.
61. Кантуэлл, Джон; Конлон, Лоуренс (2015). «Гиперболическая геометрия и гомотопические гомеоморфизмы поверхностей». Geometriae Dedicata . 177 : 27–42. arXiv : 1305.1379 . doi :10.1007/s10711-014-9975-1. MR  3370020. S2CID  119640200.
62. Стиллвелл, Джон (1992). "4.6 Классификация изометрий". Геометрия поверхностей . Universitext. Cham: Springer. стр. 96–98. doi :10.1007/978-1-4612-0929-4. ISBN 0-387-97743-0. МР  1171453.
63. Seifert, Herbert ; Threlfall, William (1980). Учебник топологии. Чистая и прикладная математика. Т. 89. Перевод Goldman, Michael A. New York & London: Academic Press. стр. 12. ISBN 0-12-634850-2. МР  0575168.
64. Лопес, Франциско Х.; Мартин, Франциско (1997). «Полные неориентируемые минимальные поверхности с наивысшей группой симметрии». American Journal of Mathematics . 119 (1): 55–81. doi :10.1353/ajm.1997.0004. MR  1428058. S2CID  121366986.
65. Микс, Уильям Х. III (1981). «Классификация полных минимальных поверхностей в с полной кривизной, большей, чем ». Duke Mathematical Journal . 48 (3): 523–535. doi :10.1215/S0012-7094-81-04829-8. MR  0630583. ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle -8\pi }$
66. Pesci, Adriana I. ; Goldstein, Raymond E. ; Alexander, Gareth P.; Moffatt, H. Keith (2015). "Неустойчивость минимальной поверхности ленты Мёбиуса и связь с систолической геометрией" (PDF) . Physical Review Letters . 114 (12): 127801. Bibcode :2015PhRvL.114l7801P. doi :10.1103/PhysRevLett.114.127801. MR  3447638. PMID  25860771.
67. Мира, Пабло (2006). «Полные минимальные ленты Мёбиуса в и проблема Бьёрлинга». Журнал геометрии и физики . 56 (9): 1506–1515. Bibcode : 2006JGP....56.1506M. doi : 10.1016/j.geomphys.2005.08.001. MR  2240407. ${\displaystyle \mathbb {R} ^{n}}$
68. Паркер, Филипп Э. (1993). «Пространства геодезических». В Дель Риего, Л. (ред.). Семинар по дифференциальной геометрии по геометрическим пространствам (Гуанахуато, 1992) . Апортационный мат. Notas Investigación. Том. 8. Соц. Мат. Мексикана, Мексика. стр. 67–79. MR  1304924. Архивировано из оригинала 13 марта 2016 г. Проверено 21 марта 2022 г.{{cite book}}: CS1 maint: bot: original URL status unknown (link)
69. Бикель, Хольгер (1999). «Двойственность в стабильных плоскостях и связанные с ними операции замыкания и ядра». Журнал геометрии . 64 (1–2): 8–15. doi :10.1007/BF01229209. MR  1675956. S2CID  122209943.
70. Mangahas, Johanna (июль 2017 г.). «Office Hour Five: The Ping-Pong Lemma». В Clay, Matt; Margalit, Dan (ред.). Office Hours with a Geometric Group Theorist . Princeton University Press. стр. 85–105. doi : 10.1515/9781400885398. ISBN 9781400885398.См. в частности Проект 7, стр. 104–105.
71. Рамирес Галарса, Ана Ирен; Сид, Хосе (2007). Введение в классическую геометрию . Базель: Birkhäuser Verlag. стр. 83–88, 157–163. ISBN 978-3-7643-7517-1. МР  2305055.
72. Фоменко, Анатолий Т.; Куний, Тосиясу Л. (2013). Топологическое моделирование для визуализации. Springer. стр. 269. ISBN 9784431669562.
73. Ишем, Крис Дж. (1999). Современная дифференциальная геометрия для физиков. World Scientific lecture notes in physics. Vol. 61 (2nd ed.). World Scientific. p. 269. ISBN 981-02-3555-0. МР  1698234.
74. Горбацевич, В. В.; Онищик, А. Л.; Винберг, Э. Б. (1993). Группы Ли и алгебры Ли I: Основы теории Ли; Группы преобразований Ли. Энциклопедия математических наук. Т. 20. Springer-Verlag, Берлин. С. 164–166. doi :10.1007/978-3-642-57999-8. ISBN 3-540-18697-2. МР  1306737.
75. Ямасиро, Ацуши; Симои, Юкихиро; Харигая, Кикуо; Вакабаяси, Кацунори (2004). «Новые электронные состояния в графеновых лентах: конкурирующие порядки спина и заряда». Физика Э. 22 (1–3): 688–691. arXiv : cond-mat/0309636 . Бибкод : 2004PhyE...22..688Y. дои : 10.1016/j.physe.2003.12.100. S2CID  17102453.
76. Rzepa, Henry S. (сентябрь 2005 г.). «Ароматичности Мебиуса и делокализация». Chemical Reviews . 105 (10): 3697–3715. doi :10.1021/cr030092l. PMID  16218564.
77. Yoon, Zin Seok; Osuka, Atsuhiro; Kim, Dongho (май 2009). «Ароматичности Мёбиуса и антиароматичности в расширенных порфиринах». Nature Chemistry . 1 (2): 113–122. Bibcode : 2009NatCh...1..113Y. doi : 10.1038/nchem.172. PMID  21378823.
78. "Изготовление резисторов с помощью математики". Time . Т. 84, № 13. 25 сентября 1964 г.
79. Пиковер (2005), стр. 45–46.
80. Понд, Дж. М. (2000). «Двухмодовые резонаторы Мёбиуса и полосовые фильтры». Труды IEEE по теории и технике СВЧ . 48 (12): 2465–2471. Bibcode : 2000ITMTT..48.2465P. doi : 10.1109/22.898999.
81. Роде, Ульрих Л.; Поддар, Аджай; Сундарараджан, Д. (ноябрь 2013 г.). «Печатные резонаторы: теория ленты Мёбиуса и ее применение» (PDF) . Microwave Journal . 56 (11).
82. Бауэр, Томас; Банцер, Питер; Карими, Эбрагим; Орлов, Сергей; Рубано, Андреа; Марруччи, Лоренцо; Сантамато, Энрико; Бойд, Роберт В.; Лейхс, Герд (февраль 2015 г.). «Наблюдение оптической поляризации лент Мёбиуса». Science . 347 (6225): 964–966. Bibcode :2015Sci...347..964B. doi :10.1126/science.1260635. PMID  25636796. S2CID  206562350.
83. Кандил, Хуан Карлос; Индурайн, Эстебан (январь 1994 г.). «Лента Мебиуса и парадокс социального выбора». Письма по экономике . 45 (3): 407–412. дои : 10.1016/0165-1765(94)90045-0.
84. Исдаун, Мартин (2012). Аттракционы в парке развлечений. Bloomsbury Publishing. стр. 43. ISBN 9781782001522.
85. Хук, Патрик (2019). Билет на поездку: путеводитель по лучшим в мире американским горкам и захватывающим аттракционам. Chartwell Books. стр. 20. ISBN 9780785835776.
86. Тоблер, Уолдо Р. (1961). «Карта мира на ленте Мёбиуса». Геодезия и картография . 21 : 486.
87. Кумлер, Марк П.; Тоблер, Уолдо Р. (январь 1991 г.). «Три карты мира на ленте Мёбиуса». Картография и географические информационные системы . 18 (4): 275–276. doi :10.1559/152304091783786781.
88. Курант, Ричард (1940). «Эксперименты с мыльной пленкой и минимальными поверхностями». The American Mathematical Monthly . 47 (3): 167–174. doi :10.1080/00029890.1940.11990957. JSTOR  2304225. MR  0001622.
89. Goldstein, Raymond E. ; Moffatt, H. Keith ; Pesci, Adriana I. ; Ricca, Renzo L. (декабрь 2010 г.). «Мыльная пленка ленты Мёбиуса меняет топологию с сингулярностью поворота». Труды Национальной академии наук . 107 (51): 21979–21984. Bibcode :2010PNAS..10721979G. doi : 10.1073/pnas.1015997107 . PMC 3009808 . 
90. Walba, David M.; Richards, Rodney M.; Haltiwanger, R. Curtis (июнь 1982 г.). «Полный синтез первой молекулярной ленты Мёбиуса». Журнал Американского химического общества . 104 (11): 3219–3221. doi :10.1021/ja00375a051.
91. Пиковер (2005), стр. 52–58.
92. Gitig, Diana (18 октября 2010 г.). «Химическое оригами, используемое для создания ДНК-ленты Мёбиуса». Ars Technica . Получено 28.03.2022 .
93. Эммер, Мишель (весна 1980 г.). «Изобразительное искусство и математика: лента Мёбиуса». Leonardo . 13 (2): 108–111. doi :10.2307/1577979. JSTOR  1577979. S2CID  123908555.
94. Байерс, Марк (2018). Чарльз Олсон и американский модернизм: практика себя. Oxford University Press. С. 77–78. ISBN 9780198813255.
95. Crato, Nuno (2010). «Эшер и лента Мёбиуса». Figureuring It Out: Entertaining Encounters with Everyday Math . Springer. С. 123–126. doi :10.1007/978-3-642-04833-3_29.
96. Керстен, Эрик (13 марта 2017 г.). «Лента Мёбиуса I». Эшер во дворце . Получено 17 апреля 2022 г.
97. Pickover (2005), стр. 13.
98. Брехер, Кеннет (2017). «Искусство бесконечности». В Сварт, Дэвид; Сейкин, Карло Х.; Феньвеси, Кристоф (ред.). Труды Bridges 2017: Математика, Искусство, Музыка, Архитектура, Образование, Культура . Финикс, Аризона: Tessellations Publishing. стр. 153–158. ISBN 978-1-938664-22-9.
99. Peterson, Ivars (2002). «Recycling topology». Mathematical Treks: From Surreal Numbers to Magic Circles . MAA Spectrum. Математическая ассоциация Америки, Вашингтон, округ Колумбия. С. 31–35. ISBN 0-88385-537-2. МР  1874198.
100. "Выбран символ Expo '74". The Spokesman-Review . 12 марта 1972 г. стр. 1.
101. Миллворд, Стивен (30 апреля 2012 г.). «Скопировал ли Google Drive свой значок из китайского приложения?». Tech in Asia . Получено 27.03.2022 – через Yahoo! News.
102. "Символ IMPA" . Для того, чтобы стать IMPA, любопытными экспонатами нашего института . ИМПА. 7 мая 2020 г. Проверено 27 марта 2022 г.
103. Пиковер (2005), стр. 156–157.
104. Декер, Хайнц; Старк, Эберхард (1983). «Мёбиус-Бендер: ... und natürlich auch auf Briefmarken». Практика математики . 25 (7): 207–215. МР  0720681.
105. Туласидас, Джолли; Кравчик, Роберт Дж. (2003). «Концепции Мёбиуса в архитектуре». В Барралло, Хавьер; Фридман, Натаниэль; Мальдонадо, Хуан Антонио; Мартинес-Ароза, Хосе; Сарханги, Реза; Секен, Карло (ред.). Встреча с Альгамброй, Материалы конференции ISAMA-BRIDGES . Гранада, Испания: Университет Гранады. стр. 353–360. ISBN 84-930669-1-5.
106. Séquin, Carlo H. (январь 2018 г.). «Мосты Мёбиуса». Журнал математики и искусств . 12 (2–3): 181–194. doi :10.1080/17513472.2017.1419331. S2CID  216116708.
107. Уэйнрайт, Оливер (17 октября 2017 г.). «Норман сказал, что президент хочет пирамиду»: как звездные архитекторы построили Астану». The Guardian .
108. Мюре, Дон (17 мая 2010 г.). «Зал славы NASCAR выглядит быстрым, даже не двигаясь с места». Sports Business Journal .
109. Гопник, Блейк (17 октября 2014 г.). «Педро Рейес создает бесконечный диванчик для любви». Новости Artnet .
110. Томас, Нэнси Дж. (4 октября 1998 г.). «Превращая Мёбиус в вопрос математики». The Times (Трентон) . стр. aa3 – через NewsBank .
111. Пашман, Дэн (6 августа 2015 г.). «Разрежьте бублик математически правильным способом». The Salt . NPR.
112. Миллер, Росс (5 сентября 2014 г.). «Как сделать математически бесконечную полоску бекона». The Verge .
113. Чанг, Кеннет (9 января 2012 г.). «Паста переходит от алфавитного супа к продвинутой геометрии». The New York Times .
114. Пиковер (2005), стр. 174–177.
115. Пиковер (2005), стр. 179–187.
116. Филлипс, Тони (25 ноября 2016 г.). «Бах и музыкальная лента Мёбиуса». Plus Magazine .Перепечатано из рубрики Американского математического общества.
117. Московиц, Клара (6 мая 2008 г.). «Музыка, сведенная к красивой математике». Live Science . Получено 21.03.2022 .
118. Тимочко, Дмитрий (7 июля 2006 г.). «Геометрия музыкальных аккордов» (PDF) . Science . 313 (5783): 72–4. Bibcode :2006Sci...313...72T. doi :10.1126/science.1126287. JSTOR  3846592. PMID  16825563. S2CID  2877171.
119. Паркс, Эндрю (30 августа 2007 г.). «Лента Мёбиуса: Дружественный огонь». Магнит .
120. Лоусон, Дом (9 февраля 2021 г.). «Кольцо Ван Мёбиуса». Prog .
121. Превос, Питер (2018). Лента Мёбиуса в магии: Трактат об афганских лентах. Кенгуру Флэт: Третье полушарие.
122. Гарднер, Мартин (1956). «Афганские отряды». Математика, магия и тайна . Нью-Йорк: Dover Books. С. 70–73.

Внешние ссылки

• Медиа, связанные с лентой Мёбиуса на Wikimedia Commons
• Вайсштейн, Эрик В. «Лента Мёбиуса». Математический мир .