В математике теорема Пифагора или теорема Пифагора — это фундаментальное соотношение в евклидовой геометрии между тремя сторонами прямоугольного треугольника . Она гласит, что площадь квадрата , сторона которого является гипотенузой (стороной, противолежащей прямому углу ), равна сумме площадей квадратов на двух других сторонах.
Теорему можно записать в виде уравнения, связывающего длины сторон a , b и гипотенузы c , иногда называемого уравнением Пифагора : [1]
Теорема названа в честь греческого философа Пифагора , родившегося около 570 г. до н. э. Теорема была доказана множество раз многими различными методами — возможно, больше, чем любая другая математическая теорема. Доказательства разнообразны, включая как геометрические , так и алгебраические доказательства , некоторые из которых датируются тысячелетиями.
Когда евклидово пространство представлено декартовой системой координат в аналитической геометрии , евклидово расстояние удовлетворяет пифагорейскому соотношению: квадрат расстояния между двумя точками равен сумме квадратов разности каждой координаты между точками.
Теорему можно обобщить различными способами: на пространства более высокой размерности , на пространства, не являющиеся евклидовыми , на объекты, не являющиеся прямоугольными треугольниками, и на объекты, которые вообще не являются треугольниками, а являются n -мерными телами.
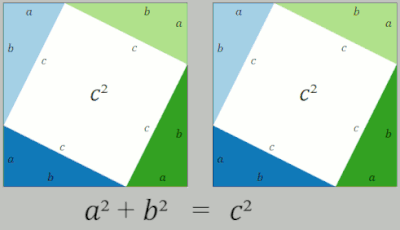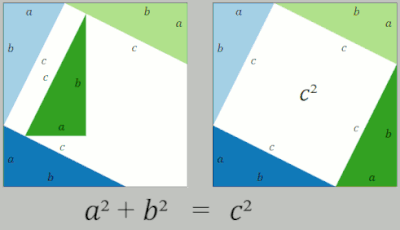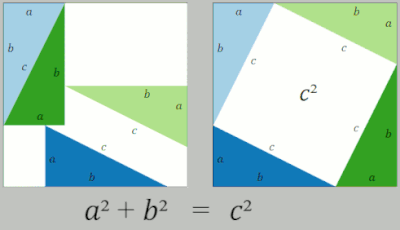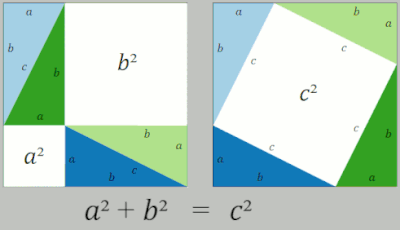
В одном доказательстве перестановки используются два квадрата, стороны которых имеют меру и которые содержат четыре прямоугольных треугольника со сторонами a , b и c , с гипотенузой, равной c . В квадрате с правой стороны треугольники размещены таким образом, что углы квадрата соответствуют углам прямого угла в треугольниках, образуя квадрат в центре, стороны которого имеют длину c . Каждый внешний квадрат имеет площадь, а также , причем представляет собой общую площадь четырех треугольников. Внутри большого квадрата с левой стороны четыре треугольника перемещаются, образуя два подобных прямоугольника со сторонами длиной a и b . Эти прямоугольники в своем новом положении теперь очерчивают два новых квадрата, один со стороной длиной a образован в нижнем левом углу, а другой квадрат со стороной длиной b образован в верхнем правом углу. В этом новом положении эта левая сторона теперь имеет квадрат площади, а также . Поскольку оба квадрата имеют площадь, следует, что другая мера площади квадрата также равна друг другу, так что = . Если из обеих частей уравнения вычесть площади четырех треугольников, то останется [2]
В другом доказательстве прямоугольники во втором поле также могут быть размещены так, что оба имеют один угол, который соответствует последовательным углам квадрата. Таким образом, они также образуют два поля, на этот раз в последовательных углах, с площадями и которые снова приведут ко второму квадрату с площадью .
Английский математик сэр Томас Хит приводит это доказательство в своем комментарии к предложению I.47 в «Началах » Евклида и упоминает предложения немецких математиков Карла Антона Бретшнайдера и Германа Ганкеля о том, что Пифагор мог знать это доказательство. Сам Хит выступает за другое предложение о пифагорейском доказательстве, но признает с самого начала своего обсуждения, «что греческая литература, которой мы обладаем и которая относится к первым пяти векам после Пифагора, не содержит никаких утверждений, указывающих на это или какое-либо другое конкретное великое геометрическое открытие, сделанное им». [3] Недавние исследования все больше подвергают сомнению какую-либо роль Пифагора как создателя математики, хотя споры по этому поводу продолжаются. [4]

Теорему можно доказать алгебраически, используя четыре копии одного и того же треугольника, расположенные симметрично вокруг квадрата со стороной c , как показано в нижней части диаграммы. [5] Это приводит к большему квадрату со стороной a + b и площадью ( a + b ) 2 . Четыре треугольника и квадратная сторона c должны иметь ту же площадь, что и больший квадрат,
давая
Аналогичное доказательство использует четыре копии прямоугольного треугольника со сторонами a , b и c , расположенные внутри квадрата со стороной c, как в верхней половине диаграммы. [6] Треугольники подобны с площадью , в то время как маленький квадрат имеет сторону b − a и площадь ( b − a ) 2 . Площадь большого квадрата, таким образом, равна
Но это квадрат со стороной c и площадью c 2 , поэтому
Эта теорема, возможно, имеет больше известных доказательств, чем любая другая ( закон квадратичной взаимности является еще одним претендентом на это звание); книга «Предложение Пифагора» содержит 370 доказательств. [7]

Это доказательство основано на пропорциональности сторон трех подобных треугольников, то есть на том факте, что отношение любых двух соответствующих сторон подобных треугольников одинаково независимо от размеров треугольников.
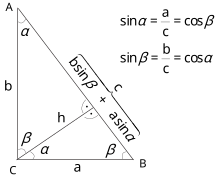
Пусть ABC представляет собой прямоугольный треугольник с прямым углом , расположенным в точке C , как показано на рисунке. Проведите высоту из точки C и назовите ее пересечением со стороной AB . Точка H делит длину гипотенузы c на части d и e. Новый треугольник ACH подобен треугольнику ABC , потому что они оба имеют прямой угол (по определению высоты), и они разделяют угол в точке A , что означает, что третий угол будет одинаковым в обоих треугольниках, обозначенный на рисунке как θ . По аналогичным рассуждениям треугольник CBH также подобен ABC . Доказательство подобия треугольников требует постулата треугольника : сумма углов в треугольнике равна двум прямым углам, и это эквивалентно постулату о параллельности . Подобие треугольников приводит к равенству отношений соответствующих сторон:
Первый результат уравнивает косинусы углов θ , тогда как второй результат уравнивает их синусы .
Эти соотношения можно записать как
Суммируя эти два равенства, получаем
что после упрощения демонстрирует теорему Пифагора:
Роль этого доказательства в истории является предметом множества спекуляций. Основной вопрос заключается в том, почему Евклид не использовал это доказательство, а придумал другое. Одна из гипотез заключается в том, что доказательство с помощью подобных треугольников включало теорию пропорций, тему, не обсуждавшуюся до более поздних моментов в « Началах» , и что теория пропорций нуждалась в дальнейшем развитии в то время. [8]
Альберт Эйнштейн дал доказательство путем разрезания, в котором части не нужно перемещать. [9] Вместо использования квадрата на гипотенузе и двух квадратов на катетах, можно использовать любую другую фигуру, которая включает гипотенузу, и две подобные фигуры, каждая из которых включает один из двух катетов вместо гипотенузы (см. Подобные фигуры на трех сторонах). В доказательстве Эйнштейна фигура, которая включает гипотенузу, является самим прямоугольным треугольником. Разрез состоит в опускании перпендикуляра из вершины прямого угла треугольника на гипотенузу, таким образом разделяя весь треугольник на две части. Эти две части имеют ту же форму, что и исходный прямоугольный треугольник, и имеют катеты исходного треугольника в качестве своих гипотенуз, а сумма их площадей равна сумме площадей исходного треугольника. Поскольку отношение площади прямоугольного треугольника к квадрату его гипотенузы одинаково для подобных треугольников, соотношение между площадями трех треугольников справедливо и для квадратов сторон большого треугольника.

В общих чертах, вот как проходит доказательство в «Началах » Евклида . Большой квадрат делится на левый и правый прямоугольники. Строится треугольник, площадь которого равна половине площади левого прямоугольника. Затем строится другой треугольник, площадь которого равна половине площади квадрата с самой левой стороны. Показано, что эти два треугольника равны , что доказывает, что этот квадрат имеет ту же площадь, что и левый прямоугольник. За этим аргументом следует аналогичная версия для правого прямоугольника и оставшегося квадрата. Соединяя два прямоугольника вместе, чтобы восстановить квадрат на гипотенузе, его площадь равна сумме площадей двух других квадратов. Подробности следуют.
Пусть A , B , C — вершины прямоугольного треугольника с прямым углом A . Опустим перпендикуляр из A на сторону, противоположную гипотенузе в квадрате на гипотенузе. Эта линия разделит квадрат на гипотенузе на два прямоугольника, каждый из которых имеет ту же площадь, что и один из двух квадратов на катетах.
Для формального доказательства нам потребуются четыре элементарные леммы :
Далее, каждый верхний квадрат связан с треугольником, конгруэнтным другому треугольнику, связанному в свою очередь с одним из двух прямоугольников, составляющих нижний квадрат. [10]

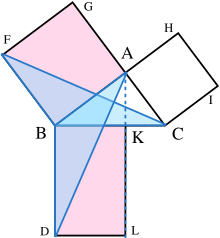
Доказательство следующее:
Это доказательство, которое появляется в «Началах » Евклида как предложение 47 в книге 1, показывает, что площадь квадрата, построенного на гипотенузе, равна сумме площадей двух других квадратов. [12] [13] Это совершенно отличается от доказательства с помощью подобия треугольников, которое, как предполагается, использовал Пифагор. [14] [15]
Другой перестановкой дается средней анимацией. Большой квадрат формируется площадью c 2 из четырех одинаковых прямоугольных треугольников со сторонами a , b и c , расположенных вокруг маленького центрального квадрата. Затем путем перемещения треугольников формируются два прямоугольника со сторонами a и b . Объединение меньшего квадрата с этими прямоугольниками дает два квадрата с площадями a 2 и b 2 , которые должны иметь ту же площадь, что и исходный большой квадрат. [16]
Третье, самое правое изображение также дает доказательство. Верхние два квадрата разделены, как показано синей и зеленой штриховкой, на части, которые при перестановке могут быть сделаны так, чтобы соответствовать нижнему квадрату на гипотенузе – или наоборот, большой квадрат может быть разделен, как показано, на части, которые заполняют другие два. Этот способ разрезания одной фигуры на части и перестановки их для получения другой фигуры называется рассечением . Это показывает, что площадь большого квадрата равна площади двух меньших. [17]

Как показано в прилагаемой анимации, сохраняющие площадь сдвиговые отображения и переносы могут преобразовать квадраты на сторонах, прилегающих к прямому углу, в квадрат на гипотенузе, вместе полностью покрывая его. [18] Каждый сдвиг оставляет основание и высоту неизменными, таким образом, оставляя площадь неизменной. Переносы также оставляют площадь неизменной, поскольку они вообще не изменяют формы. Каждый квадрат сначала сдвигается в параллелограмм, а затем в прямоугольник, который может быть перенесен на одну часть квадрата на гипотенузе.
Связанное доказательство было опубликовано будущим президентом США Джеймсом А. Гарфилдом (тогда представителем США ) (см. диаграмму). [19] [20] [21] Вместо квадрата он использует трапецию , которую можно построить из квадрата во втором из приведенных выше доказательств путем деления пополам по диагонали внутреннего квадрата, чтобы получить трапецию, показанную на диаграмме. Площадь трапеции можно вычислить как половину площади квадрата, то есть
Внутренний квадрат аналогичным образом делится пополам, и остается только два треугольника, поэтому доказательство проводится так же, как и выше, за исключением множителя , который удаляется путем умножения на два, чтобы получить результат.
К теореме Пифагора можно прийти, изучая, как изменения длины стороны приводят к изменению длины гипотенузы, и применяя исчисление . [22] [23] [24]
Треугольник ABC является прямоугольным треугольником, как показано в верхней части диаграммы, с гипотенузой BC . В то же время длины треугольника измеряются, как показано, с гипотенузой длиной y , стороной AC длиной x и стороной AB длиной a , как показано в нижней части диаграммы.

Если x увеличивается на небольшую величину dx путем небольшого удлинения стороны AC до D , то y также увеличивается на dy . Они образуют две стороны треугольника CDE , который (при выборе E так, чтобы CE была перпендикулярна гипотенузе) является прямоугольным треугольником, приблизительно похожим на ABC . Следовательно, соотношения их сторон должны быть одинаковыми, то есть:
Это можно переписать как , что является дифференциальным уравнением , которое можно решить путем прямого интегрирования:
давая
Константу можно вывести из x = 0, y = a, получив уравнение
Это скорее интуитивное доказательство, чем формальное: его можно сделать более строгим, если вместо dx и dy использовать соответствующие пределы .
Обратное утверждение теоремы также верно: [25]
Дан треугольник со сторонами длиной a , b и c , если a 2 + b 2 = c 2 , то угол между сторонами a и b является прямым углом .
Для любых трех положительных действительных чисел a , b и c, таких что a2 + b2 = c2 , существует треугольник со сторонами a , b и c, как следствие обратного неравенства треугольника .
Это обратное утверждение появляется в «Началах » Евклида (книга I, предложение 48): «Если в треугольнике квадрат одной из сторон равен сумме квадратов двух оставшихся сторон треугольника, то угол, образованный двумя оставшимися сторонами треугольника, прямой». [26]
Это можно доказать с помощью теоремы косинусов или следующим образом:
Пусть ABC — треугольник со сторонами длиной a , b и c , причем a 2 + b 2 = c 2 . Постройте второй треугольник со сторонами длиной a и b, содержащий прямой угол. По теореме Пифагора следует, что гипотенуза этого треугольника имеет длину c = √ a 2 + b 2 , такую же, как гипотенуза первого треугольника. Поскольку стороны обоих треугольников имеют одинаковую длину a , b и c , треугольники равны и должны иметь одинаковые углы. Следовательно, угол между сторонами длиной a и b в исходном треугольнике является прямым углом.
Вышеприведенное доказательство обратного утверждения использует саму теорему Пифагора. Обратное утверждение можно доказать и без предположения теоремы Пифагора. [27] [28]
Следствием обратной теоремы Пифагора является простой способ определения того, является ли треугольник прямоугольным, тупоугольным или остроугольным, следующим образом. Пусть c выбрано как самая длинная из трех сторон и a + b > c (иначе треугольника нет согласно неравенству треугольника ). Применимы следующие утверждения: [29]
Эдсгер В. Дейкстра сформулировал следующее положение об остроугольных, прямоугольных и тупоугольных треугольниках на этом языке:
где α — угол, противолежащий стороне a , β — угол, противолежащий стороне b , γ — угол, противолежащий стороне c , а sgn — функция знака . [30]
Пифагорова тройка имеет три положительных целых числа a , b , и c , таких что a 2 + b 2 = c 2 . Другими словами, пифагорова тройка представляет длины сторон прямоугольного треугольника, где все три стороны имеют целые длины. [1] Такая тройка обычно записывается как ( a , b , c ). Некоторые известные примеры — (3, 4, 5) и (5, 12, 13).
Примитивная пифагорова тройка — это тройка, в которой a , b и c взаимно просты ( наибольший общий делитель a , b и c равен 1).
Ниже приведен список примитивных пифагорейских троек со значениями меньше 100:
Дан прямоугольный треугольник со сторонами и высотой (прямая, проходящая через прямой угол и перпендикулярная гипотенузе ) . Теорема Пифагора имеет,
в то время как обратная теорема Пифагора связывает две стороны с высотой , [31]
Уравнение можно преобразовать к виду,
где для любого ненулевого действительного . Если должны быть целыми числами , наименьшее решение тогда
с использованием наименьшей пифагорейской тройки . Обратная теорема Пифагора является частным случаем оптического уравнения
где знаменатели являются квадратами, а также для семиугольного треугольника , стороны которого являются квадратными числами.

Одним из следствий теоремы Пифагора является то, что отрезки прямых, длины которых несоизмеримы (то есть отношение которых не является рациональным числом ), можно построить с помощью линейки и циркуля . Теорема Пифагора позволяет строить несоизмеримые длины, поскольку гипотенуза треугольника связана со сторонами посредством операции извлечения квадратного корня .
На рисунке справа показано, как построить отрезки прямых, длины которых находятся в соотношении квадратного корня любого положительного целого числа. [32] Каждый треугольник имеет сторону (обозначенную «1»), которая является выбранной единицей измерения. В каждом прямоугольном треугольнике теорема Пифагора устанавливает длину гипотенузы в терминах этой единицы. Если гипотенуза связана с единицей квадратным корнем положительного целого числа, которое не является полным квадратом, то это реализация длины, несоизмеримой с единицей, например √ 2 , √ 3 , √ 5 . Более подробно см. Квадратичные иррациональные .
Несоизмеримые длины противоречили концепции пифагорейской школы о числах как о целых числах. Пифагорейская школа рассматривала пропорции путем сравнения целых кратных общей субъединицы. [33] Согласно одной легенде, Гиппас из Метапонта ( ок. 470 г. до н. э.) утонул в море за то, что сообщил о существовании иррационального или несоизмеримого. [34] Подробное обсуждение вклада Гиппаса можно найти у Фрица . [35]

Для любого комплексного числа
абсолютная величина или модуль определяется как
Итак, три величины r , x и y связаны уравнением Пифагора:
Обратите внимание, что r определяется как положительное число или ноль, но x и y могут быть как отрицательными, так и положительными. Геометрически r — это расстояние z от нуля или начала координат O в комплексной плоскости .
Это можно обобщить, чтобы найти расстояние между двумя точками, скажем, z 1 и z 2. Требуемое расстояние определяется как
поэтому они снова связаны версией уравнения Пифагора,
Формула расстояния в декартовых координатах выводится из теоремы Пифагора. [36] Если ( x 1 , y 1 ) и ( x 2 , y 2 ) — точки на плоскости, то расстояние между ними, также называемое евклидовым расстоянием , определяется как
В более общем смысле, в евклидовом n -пространстве евклидово расстояние между двумя точками и определяется обобщением теоремы Пифагора следующим образом:
Если вместо евклидова расстояния использовать квадрат этого значения ( квадрат евклидова расстояния , или SED), то полученное уравнение избегает квадратных корней и представляет собой просто сумму SED координат:
Квадратичная форма представляет собой гладкую, выпуклую функцию обеих точек и широко используется в теории оптимизации и статистике , составляя основу метода наименьших квадратов .
Если декартовы координаты не используются, например, если используются полярные координаты в двух измерениях или, в более общих чертах, если используются криволинейные координаты , формулы, выражающие евклидово расстояние, сложнее теоремы Пифагора, но могут быть выведены из нее. Типичный пример, когда расстояние по прямой между двумя точками преобразуется в криволинейные координаты, можно найти в приложениях полиномов Лежандра в физике . Формулы можно найти, используя теорему Пифагора с уравнениями, связывающими криволинейные координаты с декартовыми координатами. Например, полярные координаты ( r , θ ) можно ввести как:
Тогда две точки с местоположениями ( r 1 , θ 1 ) и ( r 2 , θ 2 ) разделены расстоянием s :
Выполняя возведение в квадрат и объединение членов, формула Пифагора для расстояния в декартовых координатах дает разделение в полярных координатах как:
с использованием тригонометрических формул произведения в сумму . Эта формула является законом косинусов, иногда называемым обобщенной теоремой Пифагора. [37] Из этого результата, для случая, когда радиусы к двум точкам находятся под прямым углом, заключенный в нем угол Δ θ = π /2, и форма, соответствующая теореме Пифагора, восстанавливается: Теорема Пифагора, верная для прямоугольных треугольников, следовательно, является частным случаем более общего закона косинусов, верного для произвольных треугольников.

В прямоугольном треугольнике со сторонами a , b и гипотенузой c тригонометрия определяет синус и косинус угла θ между стороной a и гипотенузой как:
Из этого следует:
где последний шаг применяет теорему Пифагора. Это соотношение между синусом и косинусом иногда называют фундаментальным тригонометрическим тождеством Пифагора. [38] В подобных треугольниках соотношения сторон одинаковы независимо от размера треугольников и зависят от углов. Следовательно, на рисунке треугольник с гипотенузой единичного размера имеет противолежащую сторону размером sin θ и прилежащую сторону размером cos θ в единицах гипотенузы.

Теорема Пифагора связывает векторное произведение и скалярное произведение аналогичным образом: [39]
Это можно увидеть из определений векторного произведения и скалярного произведения, как
где n — единичный вектор, нормальный как к a, так и к b . Соотношение следует из этих определений и тригонометрического тождества Пифагора.
Это также можно использовать для определения перекрестного произведения. Переставляя, получаем следующее уравнение
Это можно рассматривать как условие для векторного произведения и, таким образом, часть его определения, например, в семи измерениях . [40] [41]
Если предположить, что первые четыре аксиомы евклидовой геометрии истинны, то теорема Пифагора эквивалентна пятой. То есть пятый постулат Евклида подразумевает теорему Пифагора и наоборот.
Теорема Пифагора обобщает за пределы площадей квадратов по трем сторонам на любые подобные фигуры . Это было известно Гиппократу Хиосскому в V веке до н. э. [42] и было включено Евклидом в его Элементы : [43]
Если на сторонах прямоугольного треугольника построить подобные фигуры (см. Евклидову геометрию ) с соответствующими сторонами, то сумма площадей фигур на двух меньших сторонах будет равна площади фигуры на большей стороне.
Это расширение предполагает, что стороны исходного треугольника являются соответствующими сторонами трех конгруэнтных фигур (поэтому общие соотношения сторон между подобными фигурами равны a:b:c ). [44] В то время как доказательство Евклида применимо только к выпуклым многоугольникам, теорема также применима к вогнутым многоугольникам и даже к подобным фигурам, имеющим изогнутые границы (но все еще с частью границы фигуры, являющейся стороной исходного треугольника). [44]
Основная идея этого обобщения заключается в том, что площадь плоской фигуры пропорциональна квадрату любого линейного измерения, и в частности пропорциональна квадрату длины любой стороны. Таким образом, если подобные фигуры с площадями A , B и C возведены на сторонах с соответствующими длинами a , b и c, то:
Но по теореме Пифагора a 2 + b 2 = c 2 , поэтому A + B = C .
Наоборот, если мы можем доказать, что A + B = C для трех подобных фигур без использования теоремы Пифагора, то мы можем работать в обратном направлении, чтобы построить доказательство теоремы. Например, исходный центральный треугольник можно воспроизвести и использовать как треугольник C на его гипотенузе, и два подобных прямоугольных треугольника ( A и B ), построенных на двух других сторонах, образованных делением центрального треугольника на его высоту . Сумма площадей двух меньших треугольников, таким образом, равна сумме площадей третьего, таким образом, A + B = C , и обращение вышеприведенной логики приводит к теореме Пифагора a 2 + b 2 = c 2 . ( См. также доказательство Эйнштейна путем рассечения без перестановки )

Теорема Пифагора является частным случаем более общей теоремы, связывающей длины сторон в любом треугольнике, закона косинусов, который гласит, что где — угол между сторонами и . [45]
Когда — радианы или 90°, то , и формула сводится к обычной теореме Пифагора.

В любой выбранный угол общего треугольника со сторонами a, b, c впишите равнобедренный треугольник так, чтобы равные углы при его основании θ были такими же, как выбранный угол. Предположим, что выбранный угол θ находится напротив стороны, обозначенной c . Вписывание равнобедренного треугольника образует треугольник CAD с углом θ, противолежащим стороне b , и со стороной r вдоль c . Второй треугольник образован с углом θ, противолежащим стороне a , и стороной длиной s вдоль c , как показано на рисунке. Сабит ибн Курра утверждал, что стороны трех треугольников были связаны следующим образом: [47] [48]
По мере того, как угол θ приближается к π /2, основание равнобедренного треугольника сужается, а длины r и s перекрываются все меньше и меньше. Когда θ = π /2, ADB становится прямоугольным треугольником, r + s = c , и исходная теорема Пифагора восстанавливается.
Одно доказательство показывает, что треугольник ABC имеет те же углы, что и треугольник CAD , но в противоположном порядке. (Два треугольника разделяют угол при вершине A, оба содержат угол θ, и поэтому также имеют один и тот же третий угол по постулату треугольника .) Следовательно, ABC подобен отражению CAD , треугольнику DAC на нижней панели. Принимая соотношение сторон, противолежащих и примыкающих к θ,
Аналогично, для отражения другого треугольника,
Очищаем дроби и добавляем эти два соотношения:
требуемый результат.
Теорема остается справедливой, если угол тупой, поэтому длины r и s не перекрываются.
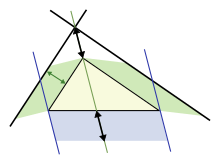

Теорема Паппа о площадях является дальнейшим обобщением, которое применяется к треугольникам, которые не являются прямоугольными треугольниками, используя параллелограммы на трех сторонах вместо квадратов (квадраты, конечно, являются особым случаем). Верхний рисунок показывает, что для разностороннего треугольника площадь параллелограмма на самой длинной стороне равна сумме площадей параллелограммов на двух других сторонах, при условии, что параллелограмм на длинной стороне построен так, как указано (измерения, отмеченные стрелками, одинаковы и определяют стороны нижнего параллелограмма). Эта замена квадратов параллелограммами имеет явное сходство с исходной теоремой Пифагора и считалась обобщением Паппа Александрийского в 4 г. н. э. [49] [50]
На нижнем рисунке показаны элементы доказательства. Сосредоточьтесь на левой стороне рисунка. Левый зеленый параллелограмм имеет ту же площадь, что и левая, синяя часть нижнего параллелограмма, потому что у обоих одинаковое основание b и высота h . Однако левый зеленый параллелограмм также имеет ту же площадь, что и левый зеленый параллелограмм верхнего рисунка, потому что у них одинаковое основание (верхняя левая сторона треугольника) и одинаковая высота, перпендикулярная этой стороне треугольника. Повторяя рассуждение для правой стороны рисунка, нижний параллелограмм имеет ту же площадь, что и сумма двух зеленых параллелограммов.


В терминах стереометрии теорема Пифагора может быть применена к трем измерениям следующим образом. Рассмотрим кубоид , показанный на рисунке. Длина диагонали грани AC находится из теоремы Пифагора как:
где эти три стороны образуют прямоугольный треугольник. Используя диагональ AC и горизонтальное ребро CD , длина диагонали тела AD затем находится вторым применением теоремы Пифагора как:
или, сделав все это за один шаг:
Этот результат представляет собой трехмерное выражение для величины вектора v (диагонали AD) через его ортогональные компоненты { v k } (три взаимно перпендикулярные стороны):
Эту одношаговую формулировку можно рассматривать как обобщение теоремы Пифагора на более высокие измерения. Однако этот результат на самом деле является всего лишь повторным применением исходной теоремы Пифагора к последовательности прямоугольных треугольников в последовательности ортогональных плоскостей.
Существенным обобщением теоремы Пифагора на три измерения является теорема де Гуа , названная в честь Жана Поля де Гуа де Мальвеса : если тетраэдр имеет прямой угол (как угол куба ) , то квадрат площади грани, противоположной прямому углу, равен сумме квадратов площадей трех других граней. Этот результат можно обобщить, как в « n -мерной теореме Пифагора»: [51]
Пусть — ортогональные векторы в R n . Рассмотрим n -мерный симплекс S с вершинами . (Думайте о ( n − 1)-мерном симплексе с вершинами, не включая начало координат, как о «гипотенузе» S , а об оставшихся ( n − 1)-мерных гранях S как о его «катетах».) Тогда квадрат объема гипотенузы S равен сумме квадратов объемов n катетов.
Это утверждение проиллюстрировано в трех измерениях тетраэдром на рисунке. «Гипотенуза» — это основание тетраэдра на задней стороне рисунка, а «ноги» — это три стороны, исходящие из вершины на переднем плане. По мере увеличения глубины основания от вершины площадь «ног» увеличивается, в то время как площадь основания остается фиксированной. Теорема предполагает, что когда эта глубина достигает значения, создающего прямую вершину, применяется обобщение теоремы Пифагора. В другой формулировке: [52]
Для n -прямоугольного n -мерного симплекса квадрат ( n − 1)-содержимого грани, противолежащей правой вершине, будет равен сумме квадратов ( n − 1)-содержимого остальных граней.

Теорема Пифагора может быть обобщена на пространства внутреннего произведения , [53] которые являются обобщениями знакомых 2-мерных и 3-мерных евклидовых пространств . Например, функцию можно рассматривать как вектор с бесконечным числом компонентов в пространстве внутреннего произведения, как в функциональном анализе . [54]
В пространстве скалярного произведения понятие перпендикулярности заменяется понятием ортогональности : два вектора v и w ортогональны, если их скалярное произведение равно нулю. Скалярное произведение является обобщением скалярного произведения векторов. Скалярное произведение называется стандартным скалярным произведением или евклидовым скалярным произведением. Однако возможны и другие скалярные произведения. [55]
Понятие длины заменяется понятием нормы ‖ v ‖ вектора v , определяемой как: [56]
В пространстве внутренних произведений теорема Пифагора утверждает, что для любых двух ортогональных векторов v и w мы имеем
Здесь векторы v и w подобны сторонам прямоугольного треугольника с гипотенузой, заданной векторной суммой v + w . Эта форма теоремы Пифагора является следствием свойств внутреннего произведения :
где из-за ортогональности.
Дальнейшим обобщением теоремы Пифагора в пространстве скалярного произведения на неортогональные векторы является закон параллелограмма : [56]
что говорит, что удвоенная сумма квадратов длин сторон параллелограмма равна сумме квадратов длин диагоналей. Любая норма, удовлетворяющая этому равенству, является ipso facto нормой, соответствующей внутреннему произведению. [56]
Тождество Пифагора можно распространить на суммы более двух ортогональных векторов. Если v 1 , v 2 , ..., v n являются попарно ортогональными векторами в пространстве внутреннего произведения, то применение теоремы Пифагора к последовательным парам этих векторов (как описано для 3-мерного пространства в разделе о стереометрии) приводит к уравнению [57]
Другое обобщение теоремы Пифагора применимо к измеримым по Лебегу множествам объектов в любом количестве измерений. В частности, квадрат меры m -мерного множества объектов в одной или нескольких параллельных m -мерных плоскостях в n -мерном евклидовом пространстве равен сумме квадратов мер ортогональных проекций объекта(ов) на все m -мерные координатные подпространства. [58]
В математических терминах:
где:
Теорема Пифагора выводится из аксиом евклидовой геометрии , и на самом деле, если бы теорема Пифагора не выполнялась для некоторого прямоугольного треугольника, то плоскость, в которой содержится этот треугольник, не могла бы быть евклидовой. Точнее, теорема Пифагора подразумевает и следует из постулата о параллельных (пятом) треугольниках Евклида . [59] [60] Таким образом, прямоугольные треугольники в неевклидовой геометрии [61] не удовлетворяют теореме Пифагора. Например, в сферической геометрии все три стороны прямоугольного треугольника (скажем, a , b и c ), ограничивающие октант единичной сферы, имеют длину, равную π /2, и все его углы являются прямыми, что нарушает теорему Пифагора, поскольку .
Здесь рассматриваются два случая неевклидовой геометрии — сферическая геометрия и гиперболическая плоская геометрия ; в каждом случае, как и в евклидовом случае для непрямоугольных треугольников, результат, заменяющий теорему Пифагора, следует из соответствующего закона косинусов.
Однако теорема Пифагора остается верной в гиперболической и эллиптической геометрии, если условие, что треугольник должен быть прямым, заменить условием, что два угла в сумме дают третий, скажем, A + B = C. Тогда стороны связаны следующим образом: сумма площадей кругов с диаметрами a и b равна площади круга с диаметром c . [62]

Для любого прямоугольного треугольника на сфере радиуса R (например, если γ на рисунке — прямой угол) со сторонами a , b , c соотношение между сторонами принимает вид: [63]
Это уравнение можно вывести как частный случай сферического закона косинусов , который применим ко всем сферическим треугольникам:
Для бесконечно малых треугольников на сфере (или, что эквивалентно, для конечных сферических треугольников на сфере бесконечного радиуса) сферическое соотношение между сторонами прямоугольного треугольника сводится к евклидовой форме теоремы Пифагора. Чтобы увидеть, как это сделать, предположим, что у нас есть сферический треугольник с фиксированными длинами сторон a , b , и c на сфере с расширяющимся радиусом R . Когда R стремится к бесконечности, величины a/R , b/R , и c/R стремятся к нулю, а сферическое пифагорейское тождество сводится к , поэтому мы должны рассмотреть его асимптотическое расширение .
Ряд Маклорена для функции косинуса можно записать как с остаточным членом в большой нотации O. Пусть будет стороной треугольника, и выражение рассматривается как асимптотическое разложение в терминах R для фиксированного c ,
и аналогично для a и b . Подстановка асимптотического разложения для каждого из косинусов в сферическое соотношение для прямоугольного треугольника дает
Вычитаем 1 и затем отрицаем каждую сторону,
Умножая на 2 R 2 , асимптотическое разложение для c в терминах фиксированных a , b и переменной R равно
Соотношение Евклида и Пифагора восстанавливается в пределе, поскольку остаток исчезает, когда радиус R стремится к бесконечности.
Для практических вычислений в сферической тригонометрии с малыми прямоугольными треугольниками косинусы можно заменить синусами, используя тождество двойного угла, чтобы избежать потери значимости . Тогда сферическая теорема Пифагора может быть альтернативно записана как

В гиперболическом пространстве с равномерной гауссовой кривизной −1/ R 2 для прямоугольного треугольника с катетами a , b и гипотенузой c соотношение между сторонами принимает вид: [64]
где cosh — гиперболический косинус . Эта формула — особая форма гиперболического закона косинусов , которая применяется ко всем гиперболическим треугольникам: [65]
где γ — угол при вершине, противолежащей стороне c .
Используя ряд Маклорена для гиперболического косинуса, cosh x ≈ 1 + x 2 /2 , можно показать, что когда гиперболический треугольник становится очень маленьким (то есть когда a , b , и c стремятся к нулю), гиперболическое соотношение для прямоугольного треугольника приближается к форме теоремы Пифагора.
Для небольших прямоугольных треугольников ( a , b << R ) гиперболические косинусы можно исключить, чтобы избежать потери значимости , что дает
Для любой равномерной кривизны K (положительной, нулевой или отрицательной) в очень маленьких прямоугольных треугольниках (| K | a 2 , | K | b 2 << 1) с гипотенузой c можно показать, что

Теорема Пифагора применима к бесконечно малым треугольникам, рассматриваемым в дифференциальной геометрии . В трехмерном пространстве расстояние между двумя бесконечно малыми точками удовлетворяет условию
где ds — элемент расстояния, а ( dx , dy , dz ) — компоненты вектора, разделяющего две точки. Такое пространство называется евклидовым пространством . Однако в римановой геометрии обобщение этого выражения, полезное для общих координат (не только декартовых) и общих пространств (не только евклидовых), принимает вид: [66]
который называется метрическим тензором . (Иногда, из-за злоупотребления языком, тот же термин применяется к набору коэффициентов g ij .) Он может быть функцией положения и часто описывает искривленное пространство . Простым примером является евклидово (плоское) пространство, выраженное в криволинейных координатах . Например, в полярных координатах :

Ведутся споры о том, была ли теорема Пифагора открыта один раз или много раз во многих местах, и дата первого открытия неизвестна, как и дата первого доказательства. Историки месопотамской математики пришли к выводу, что правило Пифагора широко использовалось в древневавилонский период (20-16 вв. до н. э.), более чем за тысячу лет до рождения Пифагора . [68] [69] [70] [71] Историю теоремы можно разделить на четыре части: знание пифагорейских троек , знание отношений между сторонами прямоугольного треугольника, знание отношений между смежными углами и доказательства теоремы в рамках некоторой дедуктивной системы .
Написанный около 1800 г. до н. э., египетский папирус Среднего царства Берлин 6619 включает задачу, решением которой является пифагорейская тройка 6:8:10, но в задаче не упоминается треугольник. Месопотамская табличка Plimpton 322 , написанная около Ларсы также около 1800 г. до н. э., содержит много записей, тесно связанных с пифагорейскими тройками. [72]
В Индии Баудхаяна Шульба Сутра , даты которой указываются по-разному, между VIII и V веками до н. э., [73] содержит список пифагорейских троек и формулировку теоремы Пифагора, как в частном случае равнобедренного прямоугольного треугольника , так и в общем случае, как и Апастамба Шульба Сутра ( ок. 600 г. до н. э. ). [a]
Византийский неоплатоник и математик Прокл , писавший в пятом веке нашей эры, излагает два арифметических правила, «одно из них приписывается Платону , другое — Пифагору», [76] для создания специальных пифагорейских троек. Правило, приписываемое Пифагору ( ок. 570 — ок. 495 до н. э. ), начинается с нечетного числа и производит тройку с катетом и гипотенузой, отличающимися на одну единицу; правило, приписываемое Платону (428/427 или 424/423 — 348/347 до н. э.), начинается с четного числа и производит тройку с катетом и гипотенузой, отличающимися на две единицы. По словам Томаса Л. Хита (1861–1940), в сохранившейся греческой литературе за пять столетий после жизни Пифагора не существует конкретного приписывания теоремы Пифагору. [77] Однако, когда такие авторы, как Плутарх и Цицерон, приписывали теорему Пифагору, они делали это таким образом, который предполагает, что атрибуция была широко известна и не вызывала сомнений. [78] [79] Классицист Курт фон Фриц писал: «Если эта формула справедливо приписывается лично Пифагору... можно с уверенностью предположить, что она принадлежит к древнейшему периоду пифагорейской математики ». [35] Около 300 г. до н. э. в « Началах » Евклида представлено старейшее из сохранившихся аксиоматических доказательств теоремы. [80]
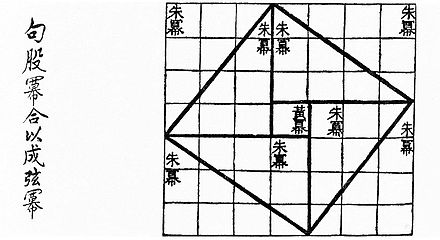
С содержанием, известным гораздо раньше, но в сохранившихся текстах, датируемых примерно I в. до н. э., китайский текст Чжоуби Суаньцзин (周髀算经), ( Арифметическая классика гномона и круговых путей неба ) дает обоснование теоремы Пифагора для треугольника (3, 4, 5) — в Китае она называется « теорема Гоугу » (勾股定理). [81] [82] Во времена династии Хань (202 г. до н. э. — 220 г. н. э.) пифагорейские тройки появляются в «Девяти главах о математическом искусстве » [83] вместе с упоминанием прямоугольных треугольников. [84] Некоторые полагают, что теорема впервые возникла в Китае в 11 веке до нашей эры, [85] где она также известна как « теорема Шан Гао » (商高定理), [86] названная в честь астронома и математика герцога Чжоу , чьи рассуждения составили большую часть того, что было в « Чжоуби Суаньцзин» . [87]
эквивалентен постулату равноудалённости , аксиоме Плейфера , аксиоме Прокла , постулату треугольника и теореме Пифагора .
Мы могли бы включить... постулат о параллельных и вывести теорему Пифагора. Или мы могли бы вместо этого включить теорему Пифагора в число других аксиом и вывести постулат о параллельных.
Цитата: [В Sulba-sutras] мы находим правила построения прямых углов с помощью троек шнуров, длины которых образуют пифагорейские триажи, такие как 3, 4 и 5, или 5, 12 и 13, или 8, 15 и 17, или 12, 35 и 37. Хотя месопотамское влияние в Sulvasũtras не является маловероятным, мы не знаем никаких убедительных доказательств за или против этого. Аспастамба знал, что квадрат на диагонали прямоугольника равен сумме квадратов на двух смежных сторонах. Менее легко объяснить другое правило, данное Апастамбой, — то, которое сильно напоминает часть геометрической алгебры во второй книге « Начал» Евклида . (...)
только у Евклида мы находим логическую последовательность общих теорем с надлежащими доказательствами.
Пифагорейцы утрояют вавилонских писцов ван дер Вардена.