Теория игр — это изучение математических моделей стратегических взаимодействий. [1] Она имеет приложения во многих областях социальных наук и широко используется в экономике , логике , системной науке и информатике . [2] Первоначально теория игр рассматривала игры двух лиц с нулевой суммой , в которых выигрыши или проигрыши одного участника точно уравновешиваются проигрышами и выигрышами другого участника. В 1950-х годах она была расширена до изучения игр с ненулевой суммой и в конечном итоге была применена к широкому спектру поведенческих отношений . Сейчас это обобщающий термин для науки о рациональном принятии решений людьми, животными и компьютерами.
Современная теория игр началась с идеи равновесий со смешанными стратегиями в играх двух лиц с нулевой суммой и ее доказательства Джоном фон Нейманом . Первоначальное доказательство фон Неймана использовало теорему Брауэра о неподвижной точке для непрерывных отображений в компактные выпуклые множества , которая стала стандартным методом в теории игр и математической экономике . За его работой последовала работа «Теория игр и экономическое поведение» (1944), написанная совместно с Оскаром Моргенштерном , в которой рассматривались кооперативные игры нескольких игроков. [3] Второе издание представило аксиоматическую теорию ожидаемой полезности , которая позволила математическим статистикам и экономистам рассматривать принятие решений в условиях неопределенности. [4]
Теория игр получила широкое развитие в 1950-х годах и была явно применена к эволюции в 1970-х годах, хотя подобные разработки восходят, по крайней мере, к 1930-м годам. Теория игр была широко признана важным инструментом во многих областях. Джон Мейнард Смит был награжден премией Крафорда за свое применение эволюционной теории игр в 1999 году, и пятнадцать теоретиков игр получили Нобелевскую премию по экономике по состоянию на 2020 год, включая совсем недавно Пола Милгрома и Роберта Б. Уилсона .
Теоретико-игровая стратегия в зафиксированной истории восходит по крайней мере к руководству Сунь Цзы по военной стратегии . [5] [6] В «Искусстве войны » он писал:
Зная другого и зная себя, В сотне битв нет опасности,
Не зная другого и не зная себя, Одна победа за одно поражение,
Не зная другого и не зная себя, В каждой битве неизбежное поражение.
— Сунь Цзы
Обсуждения математики игр начались задолго до возникновения современной математической теории игр. Работа Кардано Liber de ludo aleae ( Книга об азартных играх ), написанная около 1564 года, но опубликованная посмертно в 1663 году, набрасывает некоторые основные идеи об азартных играх. В 1650-х годах Паскаль и Гюйгенс разработали концепцию ожидания в рассуждениях о структуре азартных игр. Паскаль выступал за равное деление, когда шансы равны, в то время как Гюйгенс расширил аргумент, рассмотрев стратегии для игрока, который может сделать любую ставку с любым противником, пока ее условия равны. [7] Позднее Гюйгенс опубликовал свое игорное исчисление как De ratiociniis in ludo aleaæ ( О рассуждениях в азартных играх ) в 1657 году.
В 1713 году в письме, приписываемом Чарльзу Уолдегрейву, активному якобиту и дяде британского дипломата Джеймса Уолдегрейва , был проанализирован матч под названием « le her ». [8] [9] Уолдегрейв предоставил решение минимаксной смешанной стратегии для версии карточной игры для двух человек, и эта задача теперь известна как задача Уолдегрейва . В 1838 году Антуан Огюстен Курно рассмотрел дуополию и представил решение, которое является равновесием Нэша игры в его Recherches sur les principes mathématiques de la théorie des richesses ( Исследования математических принципов теории богатства ).
В 1913 году Эрнст Цермело опубликовал работу Über eine Anwendung der Mengenlehre auf die Theorie des Schachspiels ( О применении теории множеств к теории шахматной игры ), в которой доказал, что оптимальная шахматная стратегия строго определена . Это проложило путь для более общих теорем. [10]
В 1938 году датский математик-экономист Фредерик Цойтен доказал, что математическая модель имеет выигрышную стратегию, используя теорему Брауэра о неподвижной точке . [11] В своей книге 1938 года Applications aux Jeux de Hasard и более ранних заметках Эмиль Борель доказал теорему минимакса для двухсторонних матричных игр с нулевой суммой только в том случае, когда матрица выплат симметрична, и предоставил решение нетривиальной бесконечной игры (известной в английском языке как игра Блотто ). Борель выдвинул гипотезу об отсутствии равновесий со смешанными стратегиями в конечных двухсторонних играх с нулевой суммой , гипотеза, которая была опровергнута фон Нейманом.

Теория игр возникла как уникальная область, когда Джон фон Нейман опубликовал статью «О теории стратегических игр» в 1928 году. [12] [13] Первоначальное доказательство фон Неймана использовало теорему Брауэра о неподвижной точке для непрерывных отображений в компактные выпуклые множества , которая стала стандартным методом в теории игр и математической экономике . Работа фон Неймана в области теории игр достигла кульминации в его книге 1944 года «Теория игр и экономическое поведение» , написанной в соавторстве с Оскаром Моргенштерном . [14] Второе издание этой книги представило аксиоматическую теорию полезности , которая возродила старую теорию полезности (денег) Даниэля Бернулли в качестве независимой дисциплины. Эта основополагающая работа содержит метод поиска взаимно согласованных решений для игр двух лиц с нулевой суммой. Последующие работы были сосредоточены в основном на кооперативной теории игр , которая анализирует оптимальные стратегии для групп людей, предполагая, что они могут обеспечить соблюдение соглашений между собой о надлежащих стратегиях. [15]

В 1950 году появилось первое математическое обсуждение дилеммы заключенного , и был проведен эксперимент известными математиками Мерриллом М. Флудом и Мелвином Дрешером в рамках исследований RAND Corporation в области теории игр. RAND продолжила исследования из-за возможных приложений к глобальной ядерной стратегии . [16] Примерно в это же время Джон Нэш разработал критерий взаимной согласованности стратегий игроков, известный как равновесие Нэша , применимый к более широкому спектру игр, чем критерий, предложенный фон Нейманом и Моргенштерном. Нэш доказал, что каждая конечная некооперативная игра с n игроками и ненулевой суммой (а не только с двумя игроками и нулевой суммой) имеет то, что сейчас известно как равновесие Нэша в смешанных стратегиях.
Теория игр пережила всплеск активности в 1950-х годах, в течение которых были разработаны концепции ядра , игры в развернутой форме , фиктивной игры , повторяющихся игр и значения Шепли . В 1950-х годах также появились первые приложения теории игр к философии и политологии .
В 1965 году Райнхард Сельтен представил свою концепцию решения подигровых идеальных равновесий , которая еще больше усовершенствовала равновесие Нэша. Позже он также ввел понятие дрожащей руки совершенства . В 1994 году Нэш, Сельтен и Харсани стали лауреатами Нобелевской премии по экономике за вклад в экономическую теорию игр.
В 1970-х годах теория игр широко применялась в биологии , в основном благодаря работам Джона Мейнарда Смита и его эволюционно стабильной стратегии . Кроме того, были введены и проанализированы концепции коррелированного равновесия , совершенства дрожащей руки и общего знания [a] .
В 1994 году Джон Нэш был удостоен Нобелевской премии по экономике за вклад в теорию игр. Самым известным вкладом Нэша в теорию игр является концепция равновесия Нэша, которая является концепцией решения для некооперативных игр . Равновесие Нэша — это набор стратегий, по одной для каждого игрока, такой, что ни один игрок не может улучшить свой выигрыш, односторонне изменив свою стратегию.
В 2005 году теоретики игр Томас Шеллинг и Роберт Ауманн последовали за Нэшем, Селтеном и Харсани в качестве лауреатов Нобелевской премии. Шеллинг работал над динамическими моделями, ранними примерами эволюционной теории игр . Ауманн внес больший вклад в школу равновесия, введя огрубление равновесия и коррелированные равновесия, а также разработав обширный формальный анализ предположения об общем знании и его следствий.
В 2007 году Леонид Гурвиц , Эрик Маскин и Роджер Майерсон были удостоены Нобелевской премии по экономике «за создание основ теории дизайна механизмов ». Вклад Майерсона включает в себя понятие надлежащего равновесия и важный дипломный текст: Теория игр, анализ конфликта . [1] Гурвиц ввел и формализовал концепцию совместимости стимулов .
В 2012 году Элвин Э. Рот и Ллойд С. Шепли были удостоены Нобелевской премии по экономике «за теорию стабильного распределения и практику проектирования рынков». В 2014 году Нобелевская премия досталась теоретику игр Жану Тиролю .
Игра является кооперативной, если игроки способны формировать связывающие обязательства, принудительно исполняемые извне (например, через договорное право ). Игра является некооперативной, если игроки не могут формировать альянсы или если все соглашения должны быть самоподкрепляемыми (например, через реальные угрозы ). [17]
Кооперативные игры часто анализируются через рамки кооперативной теории игр , которая фокусируется на прогнозировании того, какие коалиции будут сформированы, совместных действий, которые группы предпринимают, и итоговых коллективных выплат. Это отличается от некооперативной теории игр , которая фокусируется на прогнозировании действий и выплат отдельных игроков путем анализа равновесий Нэша . [18] [19]
Кооперативная теория игр обеспечивает высокоуровневый подход, поскольку она описывает только структуру и выигрыши коалиций, тогда как некооперативная теория игр также рассматривает, как стратегическое взаимодействие повлияет на распределение выигрышей. Поскольку некооперативная теория игр является более общей, кооперативные игры можно анализировать с помощью подхода некооперативной теории игр (обратное не выполняется), при условии, что сделаны достаточные предположения, чтобы охватить все возможные стратегии, доступные игрокам из-за возможности внешнего принуждения к сотрудничеству.
Симметричная игра — это игра, в которой каждый игрок получает одинаковый выигрыш, делая одинаковый выбор. Другими словами, личность игрока не меняет итоговую игру, с которой сталкивается другой игрок. [20] Многие из обычно изучаемых игр 2×2 симметричны. Стандартные представления курицы , дилеммы заключенного и охоты на оленя — все это симметричные игры.
Наиболее часто изучаемые асимметричные игры — это игры, в которых нет идентичных наборов стратегий для обоих игроков. Например, игра ультиматум и, аналогично, игра диктатор имеют разные стратегии для каждого игрока. Однако возможно, что игра имеет идентичные стратегии для обоих игроков, но при этом является асимметричной. Например, игра, изображенная на графике этого раздела, является асимметричной, несмотря на идентичные наборы стратегий для обоих игроков.
Игры с нулевой суммой (в более общем смысле, игры с постоянной суммой) — это игры, в которых выбор игроков не может ни увеличить, ни уменьшить доступные ресурсы. В играх с нулевой суммой общая выгода достается всем игрокам в игре, для каждой комбинации стратегий, и всегда добавляется к нулю (более неформально, игрок получает выгоду только за счет других). [21] Покер является примером игры с нулевой суммой (игнорируя возможность сокращения казино), поскольку игрок выигрывает ровно столько, сколько проигрывают его противники. Другие игры с нулевой суммой включают в себя сопоставление пенни и большинство классических настольных игр, включая го и шахматы .
Многие игры, изучаемые теоретиками игр (включая знаменитую дилемму заключенного), являются играми с ненулевой суммой, поскольку исход имеет чистые результаты больше или меньше нуля. Неформально, в играх с ненулевой суммой выигрыш одного игрока не обязательно соответствует проигрышу другого.
Более того, игры с постоянной суммой соответствуют таким видам деятельности, как воровство и азартные игры, но не фундаментальной экономической ситуации, в которой есть потенциальные выгоды от торговли . Можно преобразовать любую игру с постоянной суммой в (возможно, асимметричную) игру с нулевой суммой, добавив подставного игрока (часто называемого «доской»), чьи потери компенсируют чистый выигрыш игроков.
Одновременные игры — это игры, в которых оба игрока двигаются одновременно, или вместо этого более поздние игроки не знают о действиях более ранних игроков (что делает их фактически одновременными). Последовательные игры (или динамические игры) — это игры, в которых игроки не принимают решения одновременно, и более ранние действия игрока влияют на результат и решения других игроков. [22] Это не обязательно должна быть идеальная информация о каждом действии более ранних игроков; это может быть очень мало знаний. Например, игрок может знать, что более ранний игрок не выполнил одно конкретное действие, в то время как он не знает, какие из других доступных действий первый игрок фактически выполнил.
Разница между одновременными и последовательными играми отражена в различных представлениях, обсуждавшихся выше. Часто для представления одновременных игр используется нормальная форма , а для представления последовательных — развернутая . Преобразование развернутой формы в нормальную является односторонним, что означает, что несколько игр развернутой формы соответствуют одной и той же нормальной форме. Следовательно, понятия равновесия для одновременных игр недостаточны для рассуждений о последовательных играх; см. subgame perfection .
Короче говоря, различия между последовательными и одновременными играми заключаются в следующем:

Важное подмножество последовательных игр состоит из игр с полной информацией. Игра с полной информацией означает, что все игроки на каждом ходу в игре знают предыдущую историю игры и ходы, сделанные ранее всеми другими игроками. Игра с неполной информацией играется, когда игроки не знают все ходы, уже сделанные противником, например, игра с одновременными ходами. [23] Примерами игр с полной информацией являются крестики-нолики , шашки , шахматы и го . [24] [25] [26]
Многие карточные игры являются играми с неполной информацией, например, покер и бридж . [27] Полную информацию часто путают с полной информацией , которая является схожей концепцией, относящейся к общему знанию последовательности, стратегий и выплат каждого игрока на протяжении всего игрового процесса. [28] Полная информация требует, чтобы каждый игрок знал стратегии и выплаты, доступные другим игрокам, но не обязательно предпринятые действия, тогда как полная информация - это знание всех аспектов игры и игроков. [29] Однако игры с неполной информацией можно свести к играм с несовершенной информацией, введя « ходы по природе ». [30]
Одно из предположений равновесия Нэша заключается в том, что каждый игрок имеет правильные убеждения относительно действий других игроков. Однако в теории игр существует множество ситуаций, когда участники не полностью понимают характеристики своих оппонентов. Переговорщики могут не знать об оценке оппонентом объекта переговоров, компании могут не знать о функциях затрат оппонента, воюющие стороны могут не знать о сильных сторонах оппонента, а присяжные могут не знать об интерпретации доказательств на суде их коллегами. В некоторых случаях участники могут хорошо знать характер своего оппонента, но не знать, насколько хорошо оппонент знает свой собственный характер. [31]
Байесовская игра означает стратегическую игру с неполной информацией. Для стратегической игры лица, принимающие решения, являются игроками, и у каждого игрока есть группа действий. Основная часть спецификации несовершенной информации — это набор состояний. Каждое состояние полностью описывает набор характеристик, относящихся к игроку, таких как его предпочтения и подробности о нем. Должно быть состояние для каждого набора характеристик, которые, по мнению некоторого игрока, могут существовать. [32]

Например, когда Игрок 1 не уверен, предпочтет ли Игрок 2 встречаться с ней или уйти от нее, в то время как Игрок 2 понимает предпочтения Игрока 1, как и прежде. Для определенности, предположим, что Игрок 1 считает, что Игрок 2 хочет встречаться с ней при вероятности 1/2 и уйти от нее при вероятности 1/2 (эта оценка, вероятно, исходит из опыта Игрока 1: в таком случае она сталкивается с игроками, которые хотят встречаться с ней половину времени, и игроками, которые хотят избегать ее половину времени). Из-за вовлеченной вероятности анализ этой ситуации требует понимания предпочтения игрока в отношении ничьей, даже несмотря на то, что людей интересует только чистое стратегическое равновесие.
Игры, в которых сложность поиска оптимальной стратегии вытекает из множественности возможных ходов, называются комбинаторными играми. Примерами являются шахматы и го . Игры, в которых задействована несовершенная информация , также могут иметь ярко выраженный комбинаторный характер, например, нарды . Не существует единой теории, рассматривающей комбинаторные элементы в играх. Однако существуют математические инструменты, которые могут решать некоторые частные проблемы и отвечать на некоторые общие вопросы. [33]
Игры с полной информацией изучались в комбинаторной теории игр , которая разработала новые представления, например, сюрреалистические числа , а также комбинаторные и алгебраические (а иногда и неконструктивные ) методы доказательства для решения игр определенных типов, включая «петлевые» игры, которые могут приводить к бесконечно длинным последовательностям ходов. Эти методы рассматривают игры с более высокой комбинаторной сложностью, чем те, которые обычно рассматриваются в традиционной (или «экономической») теории игр. [34] [35] Типичная игра, которая была решена таким образом, — это Hex . Связанная область исследования, опирающаяся на теорию вычислительной сложности , — это сложность игр , которая занимается оценкой вычислительной сложности поиска оптимальных стратегий. [36]
Исследования в области искусственного интеллекта затрагивали как игры с совершенной, так и с несовершенной информацией, которые имеют очень сложные комбинаторные структуры (например, шахматы, го или нарды), для которых не было найдено доказуемых оптимальных стратегий. Практические решения включают вычислительную эвристику, например, альфа-бета-отсечение или использование искусственных нейронных сетей, обученных с помощью обучения с подкреплением , что делает игры более поддающимися обработке в вычислительной практике. [33] [37]
Большая часть теории игр касается конечных, дискретных игр, в которых есть конечное число игроков, ходов, событий, результатов и т. д. Однако многие концепции могут быть расширены. Непрерывные игры позволяют игрокам выбирать стратегию из непрерывного набора стратегий. Например, соревнование Курно обычно моделируется со стратегиями игроков, представляющими собой любые неотрицательные величины, включая дробные величины.
Дифференциальные игры, такие как игра непрерывного преследования и уклонения, являются непрерывными играми, в которых эволюция переменных состояния игроков регулируется дифференциальными уравнениями . Проблема поиска оптимальной стратегии в дифференциальной игре тесно связана с теорией оптимального управления . В частности, существует два типа стратегий: стратегии открытого цикла находятся с использованием принципа максимума Понтрягина , а стратегии замкнутого цикла находятся с использованием метода динамического программирования Беллмана .
Частным случаем дифференциальных игр являются игры со случайным временным горизонтом . [38] В таких играх конечное время является случайной величиной с заданной функцией распределения вероятностей . Поэтому игроки максимизируют математическое ожидание функции стоимости. Было показано, что модифицированную задачу оптимизации можно переформулировать как дисконтированную дифференциальную игру на бесконечном интервале времени.
Эволюционная теория игр изучает игроков, которые корректируют свои стратегии с течением времени в соответствии с правилами, которые не обязательно являются рациональными или дальновидными. [39] В общем, эволюция стратегий с течением времени в соответствии с такими правилами моделируется как цепь Маркова с переменной состояния, такой как текущий профиль стратегии или то, как игра велась в недавнем прошлом. Такие правила могут включать имитацию, оптимизацию или выживание наиболее приспособленных.
В биологии такие модели могут представлять эволюцию , в которой потомство перенимает стратегии своих родителей, а родители, которые играют в более успешные стратегии (т. е. соответствующие более высоким выплатам), имеют большее количество потомков. В социальных науках такие модели обычно представляют стратегическую корректировку игроками, которые играют в игру много раз в течение своей жизни и, сознательно или бессознательно, время от времени корректируют свои стратегии. [40]
Индивидуальные проблемы принятия решений со стохастическими результатами иногда считаются «играми одного игрока». Их можно моделировать с использованием аналогичных инструментов в смежных дисциплинах теории принятия решений , исследования операций и областях искусственного интеллекта , в частности, планирования ИИ (с неопределенностью) и многоагентных систем . Хотя эти области могут иметь разные мотиваторы, задействованная математика по существу одинакова, например, с использованием марковских процессов принятия решений (MDP). [41]
Стохастические результаты также можно смоделировать в терминах теории игр, добавив случайно действующего игрока, который делает «случайные ходы» (« ходы по своей природе »). [42] Этот игрок обычно не считается третьим игроком в игре, которая в противном случае является игрой для двух игроков, а просто служит для броска костей, когда этого требует игра.
Для некоторых проблем разные подходы к моделированию стохастических результатов могут приводить к разным решениям. Например, разница в подходе между MDP и минимаксным решением заключается в том, что последнее рассматривает наихудший случай из набора состязательных ходов, а не рассуждает об этих ходах с учетом фиксированного распределения вероятностей. Минимаксный подход может быть выгоден, когда стохастические модели неопределенности недоступны, но также может переоценивать крайне маловероятные (но дорогостоящие) события, резко меняя стратегию в таких сценариях, если предполагается, что противник может заставить такое событие произойти. [43] (См. теорию черного лебедя для более подробного обсуждения этого вида проблемы моделирования, особенно в том, что касается прогнозирования и ограничения потерь в инвестиционном банкинге.)
Общие модели, включающие все элементы стохастических результатов, противников и частичную или шумную наблюдаемость (ходов других игроков), также были изучены. « Золотым стандартом » считается частично наблюдаемая стохастическая игра (POSG), но лишь немногие реалистичные задачи вычислительно осуществимы в представлении POSG. [43]
Это игры, в которых игра представляет собой разработку правил для другой игры, целевой или предметной игры. Метаигры стремятся максимизировать ценность полезности разработанного набора правил. Теория метаигр связана с теорией проектирования механизмов .
Термин метаигровой анализ также используется для обозначения практического подхода, разработанного Найджелом Говардом [44] , в котором ситуация представлена как стратегическая игра, в которой заинтересованные стороны пытаются реализовать свои цели с помощью доступных им вариантов. Последующие разработки привели к формулировке анализа конфронтации .
Теория игр среднего поля — это изучение принятия стратегических решений в очень больших популяциях малых взаимодействующих агентов. Этот класс проблем рассматривался в экономической литературе Бояном Йовановичем и Робертом В. Розенталем , в инженерной литературе Питером Э. Кейнсом , а также математиками Пьером-Луи Лионсом и Жаном-Мишелем Ласри.
Игры, изучаемые в теории игр, являются четко определенными математическими объектами. Чтобы быть полностью определенной, игра должна указывать следующие элементы: игроков игры, информацию и действия, доступные каждому игроку в каждой точке принятия решения, и выигрыши за каждый результат. (Эрик Расмусен называет эти четыре «основных элемента» аббревиатурой «PAPI».) [45] [46] [47] [48] Теоретик игр обычно использует эти элементы вместе с концепцией решения по своему выбору, чтобы вывести набор равновесных стратегий для каждого игрока таким образом, что при использовании этих стратегий ни один игрок не может получить прибыль, односторонне отклоняясь от своей стратегии. Эти равновесные стратегии определяют равновесие в игре — стабильное состояние, в котором происходит либо один результат, либо набор результатов с известной вероятностью.
Большинство кооперативных игр представлены в форме характеристической функции, тогда как для определения некооперативных игр используются экстенсивная и нормальная формы.

Расширенная форма может использоваться для формализации игр с временной последовательностью ходов. Игры в расширенной форме могут быть визуализированы с помощью игровых деревьев (как показано здесь). Здесь каждая вершина (или узел) представляет собой точку выбора для игрока. Игрок указывается числом, указанным вершиной. Линии, выходящие из вершины, представляют собой возможное действие для этого игрока. Выигрыши указываются в нижней части дерева. Расширенную форму можно рассматривать как многопользовательское обобщение дерева решений . [49] Чтобы решить любую игру в расширенной форме, необходимо использовать обратную индукцию . Она включает в себя работу в обратном направлении вверх по игровому дереву, чтобы определить, что сделал бы рациональный игрок в последней вершине дерева, что сделал бы игрок с предыдущим ходом, учитывая, что игрок с последним ходом является рациональным, и так далее, пока не будет достигнута первая вершина дерева. [50]
В игре, изображенной на рисунке, участвуют два игрока. Согласно структуре этой конкретной игры (т. е. с последовательным принятием решений и полной информацией), Игрок 1 «ходит» первым, выбирая либо F , либо U (честно или нечестно). Далее в последовательности Игрок 2 , который теперь наблюдал за ходом Игрока 1 , может выбрать либо A , либо R (принять или отклонить). Как только Игрок 2 сделал свой выбор, игра считается завершенной, и каждый игрок получает свой соответствующий выигрыш, представленный на рисунке в виде двух чисел, где первое число представляет собой выигрыш Игрока 1, а второе число представляет собой выигрыш Игрока 2. Предположим, что Игрок 1 выбирает U , а затем Игрок 2 выбирает A : Игрок 1 затем получает выигрыш «восемь» (что в реальных терминах можно интерпретировать многими способами, самый простой из которых — в денежном выражении, но может означать такие вещи, как восемь дней отпуска или восемь завоеванных стран или даже восемь дополнительных возможностей сыграть в ту же игру против других игроков), а Игрок 2 получает выигрыш «два».
Расширенная форма может также охватывать игры с одновременными ходами и игры с неполной информацией. Чтобы представить ее, либо пунктирная линия соединяет разные вершины, чтобы представить их как часть одного и того же информационного множества (т. е. игроки не знают, в какой точке они находятся), либо их обводит замкнутая линия. (См. пример в разделе неполной информации.)
Обычная (или стратегическая форма) игра обычно представлена матрицей , которая показывает игроков, стратегии и выигрыши (см. пример справа). В более общем виде ее можно представить любой функцией, которая связывает выигрыш для каждого игрока с каждой возможной комбинацией действий. В прилагаемом примере есть два игрока: один выбирает строку, а другой выбирает столбец. У каждого игрока есть две стратегии, которые определяются количеством строк и количеством столбцов. Выигрыши указаны внутри. Первое число — это выигрыш, полученный игроком строки (Игрок 1 в нашем примере); второе — это выигрыш для игрока столбца (Игрок 2 в нашем примере). Предположим, что Игрок 1 играет Вверх , а Игрок 2 играет Влево . Тогда Игрок 1 получает выигрыш 4, а Игрок 2 получает 3.
Когда игра представлена в нормальной форме, предполагается, что каждый игрок действует одновременно или, по крайней мере, не зная действий другого. Если у игроков есть некоторая информация о выборе других игроков, игра обычно представлена в развернутой форме.
Каждая игра в расширенной форме имеет эквивалентную игру в нормальной форме, однако преобразование в нормальную форму может привести к экспоненциальному увеличению размера представления, что делает его вычислительно непрактичным. [51]
В кооперативной теории игр характеристическая функция перечисляет выигрыш каждой коалиции. Происхождение этой формулировки — в книге Джона фон Неймана и Оскара Моргенштерна. [ необходима цитата ]
Формально характеристическая функция — это функция [52] от множества всех возможных коалиций игроков к множеству выплат, а также удовлетворяет . Функция описывает, какой коллективный выигрыш может получить множество игроков, сформировав коалицию.
Альтернативные формы представления игр используются для некоторых подклассов игр или адаптированы к потребностям междисциплинарных исследований. [53] В дополнение к классическим представлениям игр, некоторые из альтернативных представлений также кодируют аспекты, связанные со временем.
Как метод прикладной математики , теория игр использовалась для изучения широкого спектра поведения людей и животных. Первоначально она была разработана в экономике для понимания большого количества экономических поведений, включая поведение фирм, рынков и потребителей. Первое использование теоретико-игрового анализа было сделано Антуаном Огюстеном Курно в 1838 году с его решением дуополии Курно . Использование теории игр в социальных науках расширилось, и теория игр также была применена к политическому, социологическому и психологическому поведению. [68]
Хотя натуралисты до двадцатого века, такие как Чарльз Дарвин, делали утверждения теоретико-игрового типа, использование теоретико-игрового анализа в биологии началось с исследований Рональда Фишера поведения животных в 1930-х годах. Эта работа предшествовала названию «теория игр», но она разделяет многие важные черты с этой областью. Разработки в экономике были позже применены к биологии в значительной степени Джоном Мейнардом Смитом в его книге 1982 года « Эволюция и теория игр» . [69]
Помимо использования для описания, прогнозирования и объяснения поведения, теория игр также использовалась для разработки теорий этического или нормативного поведения и для предписания такого поведения. [70] В экономике и философии ученые применяли теорию игр для помощи в понимании хорошего или надлежащего поведения. Игровые теоретико-подходы также были предложены в философии языка и философии науки . [71] Игровые теоретико-аргументы такого типа можно найти еще у Платона . [72] Альтернативная версия теории игр, называемая химической теорией игр , представляет выбор игрока в виде метафорических молекул химических реагентов, называемых «knowlecules». [73] Затем химическая теория игр вычисляет результаты как равновесные решения для системы химических реакций.

Основное применение теории игр — описание и моделирование поведения человеческих популяций. [ необходима цитата ] Некоторые [ кто? ] ученые полагают, что, находя равновесия игр, они могут предсказать, как будут вести себя реальные человеческие популяции, столкнувшись с ситуациями, аналогичными изучаемой игре. Этот конкретный взгляд на теорию игр подвергся критике. Утверждается, что предположения, сделанные теоретиками игр, часто нарушаются при применении к ситуациям реального мира. Теоретики игр обычно предполагают, что игроки действуют рационально, но на практике человеческая рациональность и/или поведение часто отклоняются от модели рациональности, используемой в теории игр. Теоретики игр отвечают, сравнивая свои предположения с теми, которые используются в физике . Таким образом, хотя их предположения не всегда верны, они могут рассматривать теорию игр как разумный научный идеал, родственный моделям, используемым физиками . Однако эмпирическая работа показала, что в некоторых классических играх, таких как игра в многоножку , угадай 2/3 средней игры и игра в диктатора , люди регулярно не играют в равновесия Нэша. Продолжаются споры относительно важности этих экспериментов и того, в полной ли мере анализ экспериментов охватывает все аспекты соответствующей ситуации. [b]
Некоторые теоретики игр, следуя работам Джона Мейнарда Смита и Джорджа Р. Прайса , обратились к эволюционной теории игр, чтобы разрешить эти проблемы. Эти модели предполагают либо отсутствие рациональности, либо ограниченную рациональность со стороны игроков. Несмотря на название, эволюционная теория игр не обязательно предполагает естественный отбор в биологическом смысле. Эволюционная теория игр включает как биологическую, так и культурную эволюцию, а также модели индивидуального обучения (например, фиктивную игровую динамику).
Некоторые ученые рассматривают теорию игр не как предсказательный инструмент для поведения людей, а как предложение того, как люди должны себя вести. Поскольку стратегия, соответствующая равновесию Нэша в игре, представляет собой наилучший ответ на действия других игроков — при условии, что они находятся в (том же) равновесии Нэша — игра по стратегии, которая является частью равновесия Нэша, кажется целесообразной. Это нормативное использование теории игр также подверглось критике. [75]
Теория игр является основным методом, используемым в математической экономике и бизнесе для моделирования конкурирующего поведения взаимодействующих агентов . [c] [76] [77] [78] Приложения включают широкий спектр экономических явлений и подходов, таких как аукционы , торги , ценообразование при слияниях и поглощениях , [79] справедливое разделение , дуополии , олигополии , формирование социальных сетей , вычислительная экономика на основе агентов , [80] [81] общее равновесие , проектирование механизмов, [82] [83] [84] [85] [86] и системы голосования ; [87] и в таких широких областях, как экспериментальная экономика, [88] [89] [90] [91] [92] поведенческая экономика , [93] [94] [95] [96] [97] [98] информационная экономика , [45] [46] [47] [48] промышленная организация , [99] [100] [101] [102] и политическая экономия . [103] [104] [105] [47]
Это исследование обычно фокусируется на определенных наборах стратегий, известных как «концепции решения» или «равновесия» . Распространенное предположение заключается в том, что игроки действуют рационально. В некооперативных играх наиболее известным из них является равновесие Нэша. Набор стратегий является равновесием Нэша, если каждая представляет собой наилучший ответ на другие стратегии. Если все игроки играют в стратегии в равновесии Нэша, у них нет одностороннего стимула отклоняться, поскольку их стратегия является лучшей из возможных, учитывая то, что делают другие. [106] [107]
Выигрыши в игре обычно рассматриваются как показатель полезности отдельных игроков.
Прототипическая статья по теории игр в экономике начинается с представления игры, которая является абстракцией конкретной экономической ситуации. Выбирается одна или несколько концепций решения, и автор демонстрирует, какие наборы стратегий в представленной игре являются равновесиями соответствующего типа. Экономисты и профессора бизнеса предлагают два основных использования (отмеченных выше): описательное и предписывающее . [70]
Теория игр также широко используется в определенной отрасли или направлении экономики – управленческой экономике . Одним из важных применений ее в области управленческой экономики является анализ стратегических взаимодействий между фирмами. [108] Например, фирмы могут конкурировать на рынке с ограниченными ресурсами, и теория игр может помочь менеджерам понять, как их решения влияют на их конкурентов и общие рыночные результаты. Теория игр также может использоваться для анализа сотрудничества между фирмами, например, при формировании стратегических альянсов или совместных предприятий. Другое применение теории игр в управленческой экономике – анализ стратегий ценообразования. Например, фирмы могут использовать теорию игр для определения оптимальной стратегии ценообразования на основе того, как они ожидают, что их конкуренты отреагируют на их ценовые решения. В целом, теория игр служит полезным инструментом для анализа стратегических взаимодействий и принятия решений в контексте управленческой экономики.
Институт дипломированных специалистов по закупкам и поставкам (CIPS) продвигает знания и использование теории игр в контексте бизнес- закупок . [109] CIPS и партнеры TWS провели ряд опросов, направленных на изучение понимания, осведомленности и применения теории игр среди специалистов по закупкам . Некоторые из основных результатов их третьего ежегодного опроса (2019) включают:
Разумное принятие решений имеет решающее значение для успеха проектов. В управлении проектами теория игр используется для моделирования процесса принятия решений игроками, такими как инвесторы, менеджеры проектов, подрядчики, субподрядчики, правительства и клиенты. Довольно часто эти игроки имеют конкурирующие интересы, а иногда их интересы напрямую наносят ущерб другим игрокам, что делает сценарии управления проектами хорошо подходящими для моделирования с помощью теории игр.
Пиравинан (2019) [111] в своем обзоре приводит несколько примеров, где теория игр используется для моделирования сценариев управления проектами. Например, у инвестора обычно есть несколько вариантов инвестиций, и каждый вариант, скорее всего, приведет к другому проекту, и, таким образом, один из вариантов инвестиций должен быть выбран до того, как может быть составлен устав проекта. Аналогично, любой крупный проект с участием субподрядчиков, например, строительный проект, имеет сложное взаимодействие между главным подрядчиком (менеджером проекта) и субподрядчиками или между самими субподрядчиками, которое обычно имеет несколько точек принятия решений. Например, если в контракте между подрядчиком и субподрядчиком есть двусмысленность, каждый должен решить, насколько сильно проталкивать свою позицию, не ставя под угрозу весь проект и, следовательно, свою собственную долю в нем. Аналогично, когда запускаются проекты от конкурирующих организаций, маркетинговый персонал должен решить, какие сроки и стратегия являются наилучшими для маркетинга проекта или его конечного продукта или услуги, чтобы он мог получить максимальную поддержку в условиях конкуренции. В каждом из этих сценариев требуемые решения зависят от решений других игроков, чьи интересы в некотором роде противоречат интересам лица, принимающего решения, и поэтому их в идеале можно смоделировать с помощью теории игр.
Пиравинан [111] подводит итог, что игры с двумя игроками в основном используются для моделирования сценариев управления проектами, и на основе личности этих игроков в управлении проектами используются пять различных типов игр.
С точки зрения типов игр, для моделирования различных сценариев управления проектами используются как кооперативные, так и некооперативные, как в нормальной, так и в расширенной форме, как с нулевой, так и с ненулевой суммой.
Применение теории игр в политической науке сосредоточено в пересекающихся областях справедливого разделения , политической экономики , общественного выбора , военных переговоров , позитивной политической теории и теории общественного выбора . В каждой из этих областей исследователи разработали игровые теоретико-модели, в которых игроками часто являются избиратели, государства, группы особых интересов и политики. [112]
Ранние примеры теории игр, применяемой к политической науке, предоставлены Энтони Даунсом . В своей книге 1957 года «Экономическая теория демократии » [113] он применяет модель расположения фирм Хотеллинга к политическому процессу. В модели Даунса политические кандидаты придерживаются идеологий в одномерном политическом пространстве. Сначала Даунс показывает, как политические кандидаты будут сходиться к идеологии, предпочитаемой средним избирателем, если избиратели полностью информированы, но затем утверждает, что избиратели предпочитают оставаться рационально неосведомленными, что допускает расхождение кандидатов. Теория игр была применена в 1962 году к Карибскому кризису во время президентства Джона Ф. Кеннеди. [114]
Также было высказано предположение, что теория игр объясняет стабильность любой формы политического правления. Взяв, например, простейший случай монархии, король, будучи всего лишь одним человеком, не поддерживает и не может поддерживать свою власть, лично осуществляя физический контроль над всеми или даже значительным числом своих подданных. Вместо этого суверенный контроль объясняется признанием каждым гражданином того, что все другие граждане ожидают друг от друга, что король (или другое установленное правительство) будет рассматриваться как лицо, чьи приказы будут выполняться. Координация коммуникации между гражданами с целью замены суверена фактически запрещена, поскольку заговор с целью замены суверена, как правило, наказывается как преступление. [115] Таким образом, в процессе, который можно смоделировать с помощью вариантов дилеммы заключенного, в периоды стабильности ни один гражданин не сочтет рациональным предпринять действия для замены суверена, даже если все граждане знают, что им будет лучше, если они будут действовать коллективно. [ требуется цитата ]
Игровое объяснение демократического мира заключается в том, что публичные и открытые дебаты в демократиях посылают другим государствам ясную и надежную информацию об их намерениях. Напротив, трудно узнать намерения недемократических лидеров, какой эффект будут иметь уступки и будут ли выполнены обещания. Таким образом, будет недоверие и нежелание идти на уступки, если хотя бы одна из сторон в споре не является демократией. [116]
Однако теория игр предсказывает, что две страны все равно могут начать войну, даже если их лидеры осознают стоимость боевых действий. Война может возникнуть из-за асимметричной информации; две страны могут иметь стимулы для искажения объема имеющихся у них военных ресурсов, что делает их неспособными разрешать споры мирным путем, не прибегая к боевым действиям. Более того, война может возникнуть из-за проблем с обязательствами: если две страны хотят урегулировать спор мирным путем, но каждая хочет вернуться к условиям этого урегулирования, у них может не быть выбора, кроме как прибегнуть к войне. Наконец, война может возникнуть из-за неделимости вопросов. [117]
Теория игр также может помочь предсказать реакцию страны, когда к ней применяется новое правило или закон. Одним из примеров является исследование Питера Джона Вуда (2013), посвященное тому, что страны могут сделать, чтобы помочь уменьшить изменение климата. Вуд считал, что этого можно достичь, заключив договоры с другими странами о сокращении выбросов парниковых газов . Однако он пришел к выводу, что эта идея не может работать, поскольку она создаст дилемму заключенного для стран. [118]
Теория игр широко использовалась для моделирования сценариев принятия решений, имеющих отношение к оборонным приложениям. [119] Большинство исследований, в которых применялась теория игр в оборонных условиях, касаются войны командования и управления и могут быть далее классифицированы на исследования, посвященные (i) войне за распределение ресурсов, (ii) информационной войне, (iii) войне за контроль над оружием и (iv) войне с мониторингом противника. [119] Многие из изучаемых проблем связаны с обнаружением и отслеживанием, например, надводный корабль, пытающийся отслеживать вражескую подводную лодку, и подводная лодка, пытающаяся уклониться от отслеживания, и взаимозависимым принятием решений, которое происходит в отношении пеленга, скорости и сенсорной технологии, активируемой обоими судами. Хо и др. [119] дают краткое резюме современного состояния дел в отношении использования теории игр в оборонных приложениях и подчеркивают преимущества и ограничения теории игр в рассматриваемых сценариях.
В отличие от экономики, выигрыши в играх в биологии часто интерпретируются как соответствующие приспособленности . Кроме того, внимание уделялось не столько равновесиям, которые соответствуют понятию рациональности, сколько тем, которые будут поддерживаться эволюционными силами. Наиболее известное равновесие в биологии известно как эволюционно стабильная стратегия (ESS), впервые введенная в (Maynard Smith & Price 1973). Хотя его первоначальная мотивация не включала никаких ментальных требований равновесия Нэша, каждое ESS является равновесием Нэша.
В биологии теория игр использовалась в качестве модели для понимания множества различных явлений. Впервые она была использована для объяснения эволюции (и стабильности) приблизительного соотношения полов 1:1 . (Фишер, 1930) предположил, что соотношение полов 1:1 является результатом эволюционных сил, действующих на индивидуумов, которых можно рассматривать как пытающихся максимизировать число своих внуков.
Кроме того, биологи использовали эволюционную теорию игр и ESS для объяснения возникновения коммуникации у животных . [120] Анализ сигнальных игр и других коммуникационных игр дал представление об эволюции коммуникации среди животных. Например, поведение толпы у многих видов, когда большое количество животных-жертв нападает на более крупного хищника, по-видимому, является примером спонтанной возникающей организации. Было также показано, что муравьи демонстрируют поведение прямой связи, родственное моде (см. « Butterfly Economics » Пола Ормерода ) .
Биологи использовали игру «Курица» для анализа боевого поведения и территориальности. [121]
По словам Мейнарда Смита в предисловии к «Эволюции и теории игр» , «парадоксальным образом оказалось, что теория игр легче применима к биологии, чем к области экономического поведения, для которой она изначально была разработана». Эволюционная теория игр использовалась для объяснения многих, казалось бы, нелепых явлений в природе. [122]
Одно из таких явлений известно как биологический альтруизм . Это ситуация, в которой организм, по-видимому, действует таким образом, что приносит пользу другим организмам и вредит себе. Это отличается от традиционных представлений об альтруизме, поскольку такие действия не являются осознанными, а, по-видимому, являются эволюционными адаптациями для повышения общей приспособленности. Примеры можно найти у видов, начиная от летучих мышей-вампиров, которые отрыгивают кровь, полученную ими во время ночной охоты, и отдают ее членам группы, которые не смогли поесть, до рабочих пчел, которые заботятся о пчелиной матке всю свою жизнь и никогда не спариваются, до мартышек-верветок , которые предупреждают членов группы о приближении хищника, даже если это ставит под угрозу шансы этой особи на выживание. [123] Все эти действия повышают общую приспособленность группы, но происходят за счет особи.
Эволюционная теория игр объясняет этот альтруизм идеей родственного отбора . Альтруисты различают особей, которым они помогают, и отдают предпочтение родственникам. Правило Гамильтона объясняет эволюционное обоснование этого отбора с помощью уравнения c < b × r , где стоимость c для альтруиста должна быть меньше, чем выгода b для получателя, умноженная на коэффициент родства r . Более тесное родство двух организмов приводит к увеличению случаев альтруизма, поскольку они разделяют многие из тех же аллелей. Это означает, что альтруистичная особь, гарантируя, что аллели ее близкого родственника передаются через выживание ее потомства, может отказаться от возможности иметь потомство сама, поскольку передается то же количество аллелей. Например, помощь брату или сестре (у диплоидных животных) имеет коэффициент 1 ⁄ 2 , потому что (в среднем) особь разделяет половину аллелей с потомством своего брата или сестры. Обеспечение того, чтобы достаточное количество потомков брата или сестры дожило до взрослого возраста, исключает необходимость альтруистичного индивидуума производить потомство. [123] Значения коэффициентов в значительной степени зависят от масштаба игрового поля; например, если выбор того, кому отдать предпочтение, включает все генетические живые существа, а не только всех родственников, мы предполагаем, что расхождение между всеми людьми составляет только приблизительно 1% разнообразия на игровом поле, коэффициент, который был 1 ⁄ 2 на меньшем поле, становится 0,995. Аналогично, если считать, что информация, отличная от информации генетического характера (например, эпигенетика, религия, наука и т. д.), сохраняется с течением времени, игровое поле становится еще больше, а расхождения меньше.
Теория игр стала играть все более важную роль в логике и информатике . Несколько логических теорий имеют основу в игровой семантике . Кроме того, специалисты по информатике использовали игры для моделирования интерактивных вычислений . Кроме того, теория игр обеспечивает теоретическую основу для области многоагентных систем . [124]
Отдельно теория игр сыграла свою роль в онлайн-алгоритмах ; в частности, в задаче k -сервера , которую в прошлом называли играми с движущимися затратами и играми типа «запрос-ответ» . [125] Принцип Яо — это метод теории игр для доказательства нижних границ вычислительной сложности рандомизированных алгоритмов , особенно онлайн-алгоритмов.
Появление Интернета мотивировало разработку алгоритмов для поиска равновесия в играх, рынках, вычислительных аукционах, одноранговых системах, а также рынках безопасности и информации. Алгоритмическая теория игр [86] и в ее рамках алгоритмическое проектирование механизмов [85] объединяют вычислительное проектирование алгоритмов и анализ сложных систем с экономической теорией. [126] [127] [128]
Теория игр нашла несколько применений в философии . Отвечая на две статьи У. В. О. Куайна (1960, 1967), Льюис (1969) использовал теорию игр для разработки философского описания конвенции . При этом он предоставил первый анализ общих знаний и применил его при анализе игры в координационных играх . Кроме того, он первым предположил, что можно понимать значение в терминах сигнальных игр . Это более позднее предположение было продолжено несколькими философами после Льюиса. [129] [130] После теоретико-игрового описания конвенций Льюиса (1969) Эдна Ульманн-Маргалит (1977) и Биккьери (2006) разработали теории социальных норм , которые определяют их как равновесия Нэша, которые возникают в результате преобразования игры со смешанными мотивами в координационную игру. [131] [132]
Теория игр также бросила вызов философам, чтобы они мыслили в терминах интерактивной эпистемологии : что означает для коллектива иметь общие убеждения или знания, и каковы последствия этого знания для социальных результатов, возникающих в результате взаимодействия агентов. Философы, которые работали в этой области, включают Bicchieri (1989, 1993), [133] [134] Skyrms (1990), [135] и Stalnaker (1999). [136]
Синтез теории игр с этикой отстаивал Р. Б. Брейтуэйт . [137] Была надежда, что строгий математический анализ теории игр поможет формализовать более неточные философские дискуссии. Однако это ожидание оправдалось лишь в ограниченной степени. [138]
В этике некоторые (в частности, Дэвид Готье, Грегори Кавка и Джин Хэмптон) [ кто? ] авторы пытались продолжить проект Томаса Гоббса по выведению морали из личной выгоды. Поскольку игры, подобные дилемме заключенного, представляют собой очевидный конфликт между моралью и личной выгодой, объяснение того, почему личная выгода требует сотрудничества, является важным компонентом этого проекта. Эта общая стратегия является компонентом общего взгляда на общественный договор в политической философии (например, см. Готье (1986) и Кавка (1986)). [d]
Другие авторы пытались использовать эволюционную теорию игр для объяснения возникновения человеческих установок относительно морали и соответствующего поведения животных. Эти авторы рассматривают несколько игр, включая дилемму заключенного, охоту на оленя и игру в переговоры Нэша , как объяснение возникновения установок относительно морали (см., например, Skyrms (1996, 2004) и Sober and Wilson (1998)).
Поскольку решение о вакцинации от конкретного заболевания часто принимается отдельными лицами, которые могут учитывать ряд факторов и параметров при принятии этого решения (таких как заболеваемость и распространенность заболевания, предполагаемые и реальные риски, связанные с заражением заболеванием, уровень смертности, предполагаемые и реальные риски, связанные с вакцинацией, и финансовая стоимость вакцинации), теория игр использовалась для моделирования и прогнозирования вакцинации в обществе. [139] [140]
Теория игр имеет множество приложений в области ИИ/МО. Она часто используется при разработке автономных систем, которые могут принимать сложные решения в неопределенной среде. [141] Некоторые другие области применения теории игр в контексте ИИ/МО: формирование многоагентных систем, обучение с подкреплением, [142] проектирование механизмов и т. д. [143] Используя теорию игр для моделирования поведения других агентов и предвидения их действий, системы ИИ/МО могут принимать лучшие решения и работать более эффективно. [144]
Уильям Паундстоун описал игру в своей книге 1993 года «Дилемма заключенного»: [145]
Двое членов преступной банды, А и Б, арестованы и заключены в тюрьму. Каждый заключенный находится в одиночной камере без возможности общения со своим партнером. Основное обвинение приведет к десяти годам тюремного заключения; однако у полиции нет доказательств для осуждения. Они планируют приговорить обоих к двум годам тюремного заключения по менее серьезному обвинению, но предлагают каждому заключенному сделку Фауста: если один из них признается в преступлении по основному обвинению, предав другого, они будут помилованы и смогут свободно выйти, в то время как другой должен будет отбыть весь срок наказания вместо двух лет по менее серьезному обвинению.
Доминирующая стратегия ( и, следовательно, лучший ответ на любую возможную стратегию противника) — предать другого, что соответствует принципу «надежности» . [146] Однако молчание обоих заключенных принесло бы им обоим большую награду, чем взаимное предательство.
«Битва полов» — это термин, используемый для описания воспринимаемого конфликта между мужчинами и женщинами в различных областях жизни, таких как отношения, карьера и социальные роли. Этот конфликт часто изображается в популярной культуре, например, в фильмах и телешоу, как юмористическое или драматическое соревнование между полами. Этот конфликт можно изобразить в рамках теории игр. Это пример некооперативных игр.
Пример «битвы полов» можно увидеть в изображении отношений в популярных СМИ, где мужчины и женщины часто изображаются как принципиально разные и конфликтующие друг с другом. Например, в некоторых романтических комедиях главные герои мужского и женского пола показаны имеющими противоположные взгляды на любовь и отношения, и им приходится преодолевать эти различия, чтобы быть вместе. [147]
В этой игре есть два равновесия Нэша в чистой стратегии: одно, где оба игрока выбирают одну и ту же стратегию, и другое, где игроки выбирают разные варианты. Если игра ведется в смешанных стратегиях, где каждый игрок выбирает свою стратегию случайным образом, то существует бесконечное количество равновесий Нэша. Однако в контексте игры «битва полов» обычно делается предположение, что игра ведется в чистых стратегиях. [148]
Игра в ультиматум — это игра, которая стала популярным инструментом экономических экспериментов . Раннее описание принадлежит лауреату Нобелевской премии Джону Харсани в 1961 году. [149]
Один игрок, предлагающий, наделен суммой денег. Предлагающий должен разделить ее с другим игроком, отвечающим (который знает, какова общая сумма). Как только предлагающий сообщает свое решение, отвечающий может принять его или отклонить. Если отвечающий принимает, деньги делятся в соответствии с предложением; если отвечающий отклоняет, оба игрока не получают ничего. Оба игрока заранее знают последствия принятия или отклонения предложения отвечающим. Игра демонстрирует, как социальное принятие, справедливость и щедрость влияют на решения игроков. [150]
У игры «Ультиматум» есть вариант — игра «Диктатор». Они в основном идентичны, за исключением того, что в игре «Диктатор» у отвечающего нет полномочий отклонить предложение предлагающего.
Trust Game — это эксперимент, разработанный для измерения доверия в экономических решениях. Его также называют «инвестиционной игрой», и он разработан для исследования доверия и демонстрации его важности, а не «рациональности» личной заинтересованности. Игра была разработана Бергом Джойсом, Джоном Дикхаутом и Кевином МакКейбом в 1995 году. [151]
В игре одному игроку (инвестору) дается сумма денег, и он должен решить, какую часть отдать другому игроку (доверительному управляющему). Затем экспериментатор утраивает данную сумму. Затем доверенное лицо решает, какую часть утроенной суммы вернуть инвестору. Если получатель полностью заинтересован в себе, то он/она не должен ничего возвращать. Однако это не так, поскольку эксперимент проводится. Результат предполагает, что люди готовы оказать доверие, рискуя некоторой суммой денег, веря, что будет взаимность. [152]
Модель конкуренции Курно предполагает, что игроки выбирают количество однородного продукта для производства независимо и одновременно, где предельные издержки могут быть разными для каждой фирмы, а выигрыш фирмы — прибыль. Издержки производства являются общедоступной информацией, и фирма стремится найти свое максимизирующее прибыль количество на основе того, что, по их мнению, будет производить другая фирма и вести себя как монополии. В этой игре фирмы хотят производить в монопольном количестве, но есть высокий стимул отклониться и производить больше, что снижает равновесную цену рынка. [23] Например, фирмы могут поддаться соблазну отклониться от монопольного количества, если есть низкое монопольное количество и высокая цена, с целью увеличения производства для максимизации прибыли. [23] Однако этот вариант не обеспечивает наивысшего выигрыша, поскольку способность фирмы максимизировать прибыль зависит от ее доли на рынке и эластичности рыночного спроса. [153] Равновесие Курно достигается, когда каждая фирма действует на основе своей функции реакции без стимула отклоняться, поскольку у них есть наилучший ответ на основе выпуска других фирм. [23] В игре фирмы достигают равновесия Нэша, когда достигается равновесие Курно.
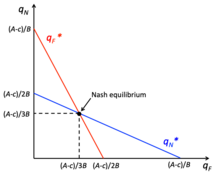
Конкуренция Бертрана предполагает однородные продукты и постоянную предельную стоимость, а игроки выбирают цены. [23] Равновесие ценовой конкуренции — это когда цена равна предельным издержкам, предполагая полную информацию о затратах конкурентов. Поэтому у фирм есть стимул отклоняться от равновесия, поскольку однородный продукт с более низкой ценой получит всю долю рынка, что известно как преимущество по издержкам. [154]
Списки
Тем не менее, математические методы, используемые в теории игр, направлены на достижение единственной цели: максимизации «уровня безопасности», где уровень безопасности — это наименьшая сумма, которую игрок может получить от выбора стратегии.
... заключается в том, что весь смысл машины Судного дня теряется, если вы держите его в секрете!