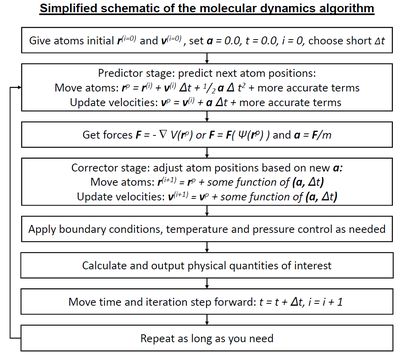
Молекулярная динамика

Компьютерное моделирование для открытия и понимания химических свойств

Пример моделирования молекулярной динамики в простой системе: осаждение одного атома меди (Cu) на холодный кристалл меди ( индекс Миллера (001) поверхность ). Каждый круг представляет положение одного атома. Кинетическая энергия атома, приближающегося сверху, перераспределяется между другими атомами, поэтому вместо того, чтобы отскочить, он остается прикрепленным из-за сил притяжения между атомами.

Молекулярно-динамическое моделирование часто используется для изучения биофизических систем. Здесь изображено 100-пс моделирование воды.

Упрощенное описание стандартного алгоритма моделирования молекулярной динамики, когда используется интегратор типа предиктор-корректор. Силы могут исходить либо из классических межатомных потенциалов (математически описываемых как ), либо из квантово-механических (математически описываемых как ) методов. Между различными интеграторами существуют большие различия; некоторые не имеют точно таких же членов высшего порядка, как указано в блок-схеме, многие также используют производные по времени высшего порядка, а некоторые используют как текущий, так и предыдущий временной шаг в схемах с переменным временным шагом. ${\displaystyle F=-\nabla V({\vec {r}})}$ ${\displaystyle F=F(\Psi ({\vec {r}}))}$

Молекулярная динамика ( МД ) — это метод компьютерного моделирования для анализа физических движений атомов и молекул . Атомам и молекулам разрешено взаимодействовать в течение фиксированного периода времени, что дает представление о динамической «эволюции» системы. В наиболее распространенной версии траектории атомов и молекул определяются путем численного решения уравнений движения Ньютона для системы взаимодействующих частиц, где силы между частицами и их потенциальные энергии часто рассчитываются с использованием межатомных потенциалов или молекулярных механических силовых полей . Метод применяется в основном в химической физике , материаловедении и биофизике .

Поскольку молекулярные системы обычно состоят из огромного числа частиц, невозможно определить свойства таких сложных систем аналитически; моделирование МД обходит эту проблему, используя численные методы. Однако длительные моделирования МД математически плохо обусловлены , генерируя кумулятивные ошибки в численном интегрировании, которые можно минимизировать с помощью правильного выбора алгоритмов и параметров, но не устранить.

Для систем, которые подчиняются эргодической гипотезе , эволюция одной молекулярно-динамической симуляции может быть использована для определения макроскопических термодинамических свойств системы: временные средние значения эргодической системы соответствуют микроканоническим ансамблевым средним. МД также называют « статистической механикой чисел» и « видением Лапласа ньютоновской механики » предсказания будущего путем оживления сил природы ^[1] и предоставления возможности проникновения в молекулярное движение в атомном масштабе.

История

Первоначально МД была разработана в начале 1950-х годов после более ранних успехов симуляций Монте-Карло , которые сами по себе относятся к восемнадцатому веку, например , в задаче об игле Бюффона , но была популяризирована для статистической механики в Лос-Аламосской национальной лаборатории Маршаллом Розенблютом и Николасом Метрополисом в том, что сегодня известно как алгоритм Метрополиса–Гастингса . Интерес к временной эволюции систем N-тел восходит к гораздо более раннему семнадцатому веку, начиная с Исаака Ньютона , и продолжался в следующем столетии в основном с акцентом на небесную механику и такие вопросы, как устойчивость Солнечной системы . Многие из численных методов, используемых сегодня, были разработаны в этот период времени, который предшествовал использованию компьютеров; например, наиболее распространенный алгоритм интегрирования, используемый сегодня, алгоритм интегрирования Верле , был использован еще в 1791 году Жаном Батистом Жозефом Деламбре . Численные вычисления с этими алгоритмами можно считать МД, выполненными «вручную».

Еще в 1941 году интеграция уравнений движения многих тел была выполнена с помощью аналоговых компьютеров . Некоторые взяли на себя трудоемкую работу по моделированию атомного движения, построив физические модели, например, используя макроскопические сферы. Цель состояла в том, чтобы расположить их таким образом, чтобы воспроизвести структуру жидкости и использовать это для изучения ее поведения. Дж. Д. Бернал описывает этот процесс в 1962 году, написав: ^[2]

... Я взял несколько резиновых шариков и склеил их вместе с помощью стержней разной длины от 2,75 до 4 дюймов. Я пытался сделать это в первую очередь как можно более небрежно, работая в своем собственном офисе, прерываясь каждые пять минут или около того и не помня, что я делал до прерывания.

После открытия микроскопических частиц и развития компьютеров интерес вышел за рамки испытательного полигона гравитационных систем и перешел к статистическим свойствам материи. В попытке понять происхождение необратимости Энрико Ферми предложил в 1953 году и опубликовал в 1955 году ^[3] использование раннего компьютера MANIAC I , также в Лос-Аламосской национальной лаборатории , для решения временной эволюции уравнений движения для системы многих тел, подчиняющейся нескольким выборам законов силы. Сегодня эта основополагающая работа известна как проблема Ферми–Пасты–Улама–Цингоу . Временная эволюция энергии из оригинальной работы показана на рисунке справа.

Одно из самых ранних симуляций системы N-тел было проведено на MANIAC-I Ферми и его коллегами с целью понять истоки необратимости в природе. Здесь показана энергия против времени для системы из 64 частиц.

В 1957 году Берни Олдер и Томас Уэйнрайт использовали компьютер IBM 704 для моделирования идеально упругих столкновений между твердыми сферами . ^[4] В 1960 году, возможно, в первой реалистичной симуляции материи, Дж. Б. Гибсон и др . смоделировали радиационное повреждение твердой меди , используя отталкивающее взаимодействие типа Борна-Майера вместе с когезионными поверхностными силами. ^[5] В 1964 году Анесур Рахман опубликовал моделирование жидкого аргона , в котором использовался потенциал Леннарда-Джонса ; расчеты свойств системы, таких как коэффициент самодиффузии , хорошо сопоставлялись с экспериментальными данными. ^[6] Сегодня потенциал Леннарда-Джонса по-прежнему является одним из наиболее часто используемых межмолекулярных потенциалов . ^{[7] [8]} Он используется для описания простых веществ (также известных как Леннард-Джонсиум ^{[9] [10] [11]} ) для концептуальных и модельных исследований и в качестве строительного блока во многих силовых полях реальных веществ. ^{[12] [13]}

Области применения и ограничения

Впервые использованный в теоретической физике , метод молекулярной динамики вскоре приобрел популярность в материаловедении , а с 1970-х годов он также широко используется в биохимии и биофизике . МД часто используется для уточнения трехмерных структур белков и других макромолекул на основе экспериментальных ограничений из рентгеновской кристаллографии или ЯМР-спектроскопии . В физике МД используется для изучения динамики явлений на атомном уровне, которые невозможно наблюдать напрямую, таких как рост тонких пленок и ионная субплантация, а также для изучения физических свойств нанотехнологических устройств, которые еще не созданы или не могут быть созданы. В биофизике и структурной биологии метод часто применяется для изучения движений макромолекул, таких как белки и нуклеиновые кислоты , что может быть полезно для интерпретации результатов определенных биофизических экспериментов и для моделирования взаимодействий с другими молекулами, как при стыковке лигандов . В принципе, МД можно использовать для ab initio прогнозирования структуры белка путем моделирования сворачивания полипептидной цепи из случайного клубка .

Результаты моделирования МД можно проверить путем сравнения с экспериментами, измеряющими молекулярную динамику, из которых популярным методом является ЯМР-спектроскопия. Предсказания структуры, полученные с помощью МД, можно проверить с помощью экспериментов в масштабах всего сообщества в рамках критической оценки предсказания структуры белка ( CASP ), хотя этот метод исторически имел ограниченный успех в этой области. Майкл Левитт , который разделил Нобелевскую премию отчасти за применение МД к белкам, писал в 1999 году, что участники CASP обычно не использовали этот метод из-за «... центрального затруднения молекулярной механики , а именно того, что минимизация энергии или молекулярная динамика обычно приводит к модели, которая меньше похожа на экспериментальную структуру». ^[14] Улучшения в вычислительных ресурсах, позволяющие использовать больше и более длинных траекторий МД, в сочетании с современными улучшениями в качестве параметров силового поля , дали некоторые улучшения как в прогнозировании структуры, так и в уточнении модели гомологии , не достигнув точки практической полезности в этих областях; многие определяют параметры силового поля как ключевую область для дальнейшего развития. ^{[15] [16] [17]}

Моделирование МД было описано для разработки фармакофоров и дизайна лекарств . ^[18] Например, Пинто и др . реализовали моделирование МД комплексов Bcl-xL для расчета средних положений критических аминокислот, участвующих в связывании лиганда. ^[19] Карлсон и др . реализовали моделирование молекулярной динамики для идентификации соединений, которые дополняют рецептор, вызывая при этом минимальное нарушение конформации и гибкости активного сайта. Снимки белка с постоянными временными интервалами во время моделирования накладывались для идентификации консервативных областей связывания (консервированных по крайней мере в трех из одиннадцати кадров) для разработки фармакофоров. Спиракис и др . полагались на рабочий процесс моделирования МД, отпечатки пальцев для лигандов и белков (FLAP) и линейный дискриминантный анализ (LDA) для идентификации наилучших конформаций лиганд-белок, которые будут действовать как шаблоны фармакофоров на основе ретроспективного ROC- анализа полученных фармакофоров. В попытке улучшить моделирование открытия лекарств на основе структуры, в связи с необходимостью множества моделируемых соединений, Хатмал и др . предложили комбинацию моделирования МД и анализа межмолекулярных контактов лиганд-рецептор для различения критических межмолекулярных контактов (взаимодействий связывания) от избыточных в одном комплексе лиганд-белок. Критические контакты затем могут быть преобразованы в модели фармакофоров, которые могут быть использованы для виртуального скрининга. ^[20]

Важным фактором являются внутримолекулярные водородные связи [ ^21] , которые явно не включены в современные силовые поля, но описываются как кулоновские взаимодействия атомных точечных зарядов . ^{[ требуется ссылка ]} Это грубое приближение, поскольку водородные связи имеют частично квантово-механическую и химическую природу. Кроме того, электростатические взаимодействия обычно рассчитываются с использованием диэлектрической проницаемости вакуума , хотя окружающий водный раствор имеет гораздо более высокую диэлектрическую проницаемость. Таким образом, использование макроскопической диэлектрической проницаемости на коротких межатомных расстояниях сомнительно. Наконец, ван-дер-ваальсовы взаимодействия в МД обычно описываются потенциалами Леннарда-Джонса ^{[22] [23],} основанными на теории Фрица Лондона , которая применима только в вакууме. ^{[ требуется ссылка ]} Однако все типы ван-дер-ваальсовых сил в конечном итоге имеют электростатическое происхождение и, следовательно, зависят от диэлектрических свойств окружающей среды . ^[24] Прямое измерение сил притяжения между различными материалами (как константа Гамакера ) показывает, что «взаимодействие между углеводородами через воду составляет около 10% от взаимодействия через вакуум». ^[24] Зависимость сил Ван-дер-Ваальса от окружающей среды не учитывается в стандартных моделях, но может быть учтена путем разработки поляризуемых силовых полей.

Ограничения дизайна

Проектирование моделирования молекулярной динамики должно учитывать доступную вычислительную мощность. Размер моделирования ( n = число частиц), временной шаг и общая продолжительность времени должны быть выбраны таким образом, чтобы расчет мог быть завершен в течение разумного периода времени. Однако моделирование должно быть достаточно продолжительным, чтобы соответствовать временным масштабам изучаемых естественных процессов. Чтобы сделать статистически обоснованные выводы из моделирования, моделируемый временной промежуток должен соответствовать кинетике естественного процесса. В противном случае это аналогично заключению о том, как человек ходит, когда он смотрит только на менее чем один шаг. Большинство научных публикаций о динамике белков и ДНК ^{[25] [26]} используют данные из моделирования, охватывающего наносекунды (10−9 ^с ) до микросекунд (10−6 ^с ). Для получения этих моделирования требуется от нескольких CPU-дней до CPU-лет. Параллельные алгоритмы позволяют распределять нагрузку между CPU ; примером является пространственный или силовой алгоритм разложения. ^[27]

Во время классического моделирования МД наиболее ресурсоемкой задачей является оценка потенциала как функции внутренних координат частиц. В рамках этой оценки энергии наиболее затратной является не связанная или нековалентная часть. В нотации big O общие моделирования молекулярной динамики масштабируются на , если все парные электростатические и ван-дер-ваальсовы взаимодействия должны быть учтены явно. Эти вычислительные затраты можно уменьшить, используя методы электростатики, такие как суммирование Эвальда сетки частиц ( ), сетка частица-частица-частица ( P 3 M ) или хорошие методы сферического отсечения ( ). ^{[ необходима цитата ]} ${\displaystyle O(n^{2})}$ ${\displaystyle O(n\log(n))}$ ${\displaystyle O(n)}$

Другим фактором, влияющим на общее время ЦП, необходимое для моделирования, является размер временного шага интеграции. Это временной интервал между оценками потенциала. Временной шаг должен быть выбран достаточно малым, чтобы избежать ошибок дискретизации (т. е. меньше периода, связанного с самой быстрой частотой колебаний в системе). Типичные временные шаги для классической МД составляют порядка 1 фемтосекунды (10 ⁻¹⁵ с). Это значение может быть увеличено с помощью алгоритмов, таких как алгоритм ограничения SHAKE , который фиксирует колебания самых быстрых атомов (например, водорода) на месте. Также были разработаны методы с несколькими временными шкалами, которые позволяют увеличить время между обновлениями более медленных дальнодействующих сил. ^{[28] [29] [30]}

Для моделирования молекул в растворителе следует сделать выбор между явным и неявным растворителем . Явные частицы растворителя (такие как модели воды TIP3P , SPC/E и SPC-f ) должны рассчитываться с большими затратами с помощью силового поля, в то время как неявные растворители используют подход среднего поля . Использование явного растворителя является вычислительно затратным, требуя включения примерно в десять раз большего количества частиц в моделирование. Но гранулярность и вязкость явного растворителя необходимы для воспроизведения определенных свойств молекул растворенного вещества. Это особенно важно для воспроизведения химической кинетики .

Во всех видах моделирования молекулярной динамики размер блока моделирования должен быть достаточно большим, чтобы избежать артефактов граничных условий . Граничные условия часто обрабатываются путем выбора фиксированных значений на краях (что может вызвать артефакты) или путем использования периодических граничных условий , в которых одна сторона моделирования возвращается к противоположной стороне, имитируя объемную фазу (что также может вызвать артефакты).

Схематическое изображение выборки поверхности потенциальной энергии системы с помощью молекулярной динамики (красным цветом) в сравнении с методами Монте-Карло (синим цветом)

Микроканонический ансамбль (NVE)

В микроканоническом ансамбле система изолирована от изменений молей (N), объема (V) и энергии (E). Это соответствует адиабатическому процессу без теплообмена. Микроканоническая молекулярно-динамическая траектория может рассматриваться как обмен потенциальной и кинетической энергией, при этом полная энергия сохраняется. Для системы из N частиц с координатами и скоростями следующая пара дифференциальных уравнений первого порядка может быть записана в обозначениях Ньютона как ${\displaystyle X}$ ${\displaystyle V}$

${\displaystyle F(X)=-\nabla U(X)=M{\dot {V}}(t)}$

${\displaystyle V(t)={\dot {X}}(t).}$

Функция потенциальной энергии системы является функцией координат частиц . В физике ее называют просто потенциалом , а в химии — силовым полем . Первое уравнение вытекает из законов движения Ньютона ; сила, действующая на каждую частицу в системе, может быть рассчитана как отрицательный градиент . ${\displaystyle U(X)}$ ${\displaystyle X}$ ${\displaystyle F}$ ${\displaystyle U(X)}$

Для каждого временного шага положение и скорость каждой частицы можно интегрировать с помощью метода симплектического интегратора , например, метода Верле . Эволюция во времени и называется траекторией. Зная начальные положения (например, из теоретических знаний) и скорости (например, рандомизированные гауссовы ), мы можем вычислить все будущие (или прошлые) положения и скорости. ${\displaystyle X}$ ${\displaystyle V}$ ${\displaystyle X}$ ${\displaystyle V}$

Одним из частых источников путаницы является значение температуры в МД. Обычно мы имеем дело с макроскопическими температурами, которые включают огромное количество частиц, но температура является статистической величиной. Если имеется достаточно большое количество атомов, статистическую температуру можно оценить из мгновенной температуры , которая находится путем приравнивания кинетической энергии системы к nk _B T /2, где n — число степеней свободы системы.

Температурно-связанное явление возникает из-за небольшого числа атомов, которые используются в моделировании МД. Например, рассмотрим моделирование роста медной пленки, начиная с подложки, содержащей 500 атомов, и энергии осаждения 100 эВ . В реальном мире 100 эВ от осажденного атома будут быстро переноситься и распределяться между большим количеством атомов ( или более) без большого изменения температуры. Однако, когда имеется всего 500 атомов, подложка почти немедленно испаряется при осаждении. Нечто подобное происходит в биофизических симуляциях. Температура системы в NVE естественным образом повышается, когда макромолекулы, такие как белки, претерпевают экзотермические конформационные изменения и связывание. ${\displaystyle 10^{10}}$

Канонический ансамбль (НВТ)

В каноническом ансамбле сохраняются количество вещества (N), объем (V) и температура (T). Иногда его также называют молекулярной динамикой при постоянной температуре (CTMD). В NVT происходит обмен энергией эндотермических и экзотермических процессов с термостатом .

Доступны различные алгоритмы термостата для добавления и удаления энергии из границ моделирования МД более или менее реалистичным способом, приближаясь к каноническому ансамблю . Популярные методы управления температурой включают масштабирование скорости, термостат Нозе-Гувера , цепи Нозе-Гувера, термостат Берендсена , термостат Андерсена и динамику Ланжевена . Термостат Берендсена может вводить эффект летающего кубика льда , который приводит к нефизическим перемещениям и вращениям моделируемой системы.

Нетривиально получить каноническое ансамблевое распределение конформаций и скоростей с помощью этих алгоритмов. То, как это зависит от размера системы, выбора термостата, параметров термостата, временного шага и интегратора, является предметом многих статей в этой области.

Изотермически-изобарический (NPT) ансамбль

В изотермически-изобарическом ансамбле сохраняются количество вещества (N), давление (P) и температура (T). Помимо термостата необходим баростат . Он наиболее точно соответствует лабораторным условиям с колбой, открытой для температуры и давления окружающей среды.

При моделировании биологических мембран изотропный контроль давления не подходит. Для липидных бислоев контроль давления происходит при постоянной площади мембраны (NPAT) или постоянном поверхностном натяжении «гамма» (NPγT).

Обобщенные ансамбли

Метод обмена репликами представляет собой обобщенный ансамбль. Первоначально он был создан для работы с медленной динамикой неупорядоченных спиновых систем. Его также называют параллельным закаливанием. Формулировка обмена репликами MD (REMD) ^[31] пытается преодолеть проблему множественных минимумов путем обмена температурой невзаимодействующих реплик системы, работающих при нескольких температурах.

Потенциалы в моделировании МД

Молекулярно-динамическое моделирование требует определения потенциальной функции или описания условий, с помощью которых будут взаимодействовать частицы в моделировании. В химии и биологии это обычно называют силовым полем , а в физике материалов — межатомным потенциалом . Потенциалы могут быть определены на многих уровнях физической точности; те, которые чаще всего используются в химии, основаны на молекулярной механике и воплощают классическую механическую трактовку взаимодействий частица-частица, которая может воспроизводить структурные и конформационные изменения , но обычно не может воспроизводить химические реакции .

Сведение от полностью квантового описания к классическому потенциалу влечет за собой два основных приближения. Первое — это приближение Борна–Оппенгеймера , которое утверждает, что динамика электронов настолько быстра, что можно считать, что они мгновенно реагируют на движение своих ядер. Как следствие, их можно рассматривать отдельно. Второе рассматривает ядра, которые намного тяжелее электронов, как точечные частицы, которые следуют классической ньютоновской динамике. В классической молекулярной динамике эффект электронов аппроксимируется как одна поверхность потенциальной энергии, обычно представляющая основное состояние.

Когда требуются более тонкие уровни детализации, используются потенциалы, основанные на квантовой механике ; некоторые методы пытаются создать гибридные классические/квантовые потенциалы, где основная часть системы рассматривается классически, но небольшая область рассматривается как квантовая система, обычно претерпевающая химическое превращение.

Эмпирические потенциалы

Эмпирические потенциалы, используемые в химии, часто называются силовыми полями , тогда как те, которые используются в физике материалов, называются межатомными потенциалами .

Большинство силовых полей в химии являются эмпирическими и состоят из суммы связанных сил, связанных с химическими связями , углами связей и двугранными углами связей , а также несвязанных сил, связанных с силами Ван-дер-Ваальса и электростатическим зарядом . ^[32] Эмпирические потенциалы представляют квантово-механические эффекты ограниченным образом посредством специальных функциональных приближений. Эти потенциалы содержат свободные параметры, такие как атомный заряд , параметры Ван-дер-Ваальса, отражающие оценки атомного радиуса и равновесной длины связи , угла и двугранного угла; они получаются путем подгонки подробных электронных расчетов (квантово-химическое моделирование) или экспериментальных физических свойств, таких как упругие константы , параметры решетки и спектроскопические измерения.

Из-за нелокальной природы не связанных взаимодействий они включают по крайней мере слабые взаимодействия между всеми частицами в системе. Его расчет обычно является узким местом в скорости моделирования МД. Чтобы снизить вычислительные затраты, силовые поля используют численные аппроксимации, такие как смещенные радиусы отсечки, алгоритмы поля реакции , суммирование Эвальда для сетки частиц или более новую сетку частица-частица-частица ( P3M ).

Химические силовые поля обычно используют предустановленные схемы связей (исключением является динамика ab initio ) и, таким образом, не могут явно моделировать процесс разрыва химических связей и реакций. С другой стороны, многие потенциалы, используемые в физике, такие как основанные на формализме порядка связей, могут описывать несколько различных координаций системы и разрыва связей. ^{[33] [34]} Примерами таких потенциалов являются потенциал Бреннера ^[35] для углеводородов и его дальнейшие разработки для систем C-Si-H ^[36] и COH ^[37] . Потенциал ReaxFF ^[38] можно считать полностью реактивным гибридом между потенциалами порядка связей и химическими силовыми полями.

Парные потенциалы против многочастичных потенциалов

Потенциальные функции, представляющие несвязанную энергию, формулируются как сумма по взаимодействиям между частицами системы. Простейшим выбором, используемым во многих популярных силовых полях , является «парный потенциал», в котором полная потенциальная энергия может быть рассчитана из суммы энергетических вкладов между парами атомов. Поэтому эти силовые поля также называются «аддитивными силовыми полями». Примером такого парного потенциала является несвязанный потенциал Леннарда-Джонса (также называемый потенциалом 6–12), используемый для расчета сил Ван-дер-Ваальса.

${\displaystyle U(r)=4\varepsilon \left[\left({\frac {\sigma }{r}}\right)^{12}-\left({\frac {\sigma }{r}}\right)^{6}\right]}$

Другим примером является борновская (ионная) модель ионной решетки. Первый член в следующем уравнении — закон Кулона для пары ионов, второй член — отталкивание на малых расстояниях, объясняемое принципом исключения Паули, а последний член — член дисперсионного взаимодействия. Обычно моделирование включает только дипольный член, хотя иногда включается и квадрупольный член. ^{[39] [40]} Когда n _l = 6, этот потенциал также называется потенциалом Кулона–Бекингема .

${\displaystyle U_{ij}(r_{ij})={\frac {z_{i}z_{j}}{4\pi \epsilon _{0}}}{\frac {1}{r_{ij}}}+A_{l}\exp {\frac {-r_{ij}}{p_{l}}}+C_{l}r_{ij}^{-n_{l}}+\cdots }$

В многочастичных потенциалах потенциальная энергия включает эффекты трех или более частиц, взаимодействующих друг с другом. ^[41] В моделировании с парными потенциалами глобальные взаимодействия в системе также существуют, но они происходят только через парные члены. В многочастичных потенциалах потенциальная энергия не может быть найдена суммой по парам атомов, поскольку эти взаимодействия вычисляются явно как комбинация членов более высокого порядка. В статистическом представлении зависимость между переменными в общем случае не может быть выражена с использованием только парных произведений степеней свободы. Например, потенциал Терсоффа ^[42] , который изначально использовался для моделирования углерода , кремния и германия , а с тех пор использовался для широкого спектра других материалов, включает сумму по группам из трех атомов, причем углы между атомами являются важным фактором в потенциале. Другими примерами являются метод внедренного атома (EAM) ^[43] , EDIP ^[41] и потенциалы приближения второго момента сильной связи (TBSMA) ^[44] , где плотность электронных состояний в области атома рассчитывается из суммы вкладов окружающих атомов, а вклад потенциальной энергии затем является функцией этой суммы.

Полуэмпирические потенциалы

Полуэмпирические потенциалы используют матричное представление из квантовой механики. Однако значения матричных элементов находятся с помощью эмпирических формул, которые оценивают степень перекрытия определенных атомных орбиталей. Затем матрица диагонализуется для определения занятости различных атомных орбиталей, а эмпирические формулы снова используются для определения энергетических вкладов орбиталей.

Существует большое разнообразие полуэмпирических потенциалов, называемых потенциалами сильной связи , которые различаются в зависимости от моделируемых атомов.

Поляризующиеся потенциалы

Большинство классических силовых полей неявно включают эффект поляризуемости , например, путем масштабирования частичных зарядов, полученных из квантово-химических расчетов. Эти частичные заряды стационарны по отношению к массе атома. Но моделирование молекулярной динамики может явно моделировать поляризуемость с введением индуцированных диполей с помощью различных методов, таких как частицы Друде или флуктуирующие заряды. Это позволяет осуществлять динамическое перераспределение заряда между атомами, которое реагирует на локальное химическое окружение.

В течение многих лет поляризуемые МД-симуляции рекламировались как следующее поколение. Для однородных жидкостей, таких как вода, повышенная точность была достигнута за счет включения поляризуемости. ^{[45] [46] [47]} Некоторые многообещающие результаты были также достигнуты для белков. ^{[48] [49]} Однако все еще неясно, как лучше всего аппроксимировать поляризуемость в моделировании. ^{[ необходима цитата ]} Этот момент становится более важным, когда частица сталкивается с различными средами во время своей траектории моделирования, например, транслокация лекарства через клеточную мембрану. ^[50]

Потенциалы вab initioметоды

В классической молекулярной динамике одна потенциальная энергетическая поверхность (обычно основное состояние) представлена ​​в силовом поле. Это является следствием приближения Борна–Оппенгеймера . В возбужденных состояниях, химических реакциях или когда требуется более точное представление, электронное поведение может быть получено из первых принципов с использованием квантово-механического метода, такого как теория функционала плотности . Это называется Ab Initio Molecular Dynamics (AIMD). Из-за стоимости обработки электронных степеней свободы вычислительная нагрузка этих симуляций намного выше, чем в классической молекулярной динамике. По этой причине AIMD обычно ограничивается меньшими системами и более короткими временами.

Ab initio квантово-механические и химические методы могут использоваться для расчета потенциальной энергии системы «на лету», как это необходимо для конформаций на траектории. Этот расчет обычно выполняется в непосредственной близости от координаты реакции . Хотя могут использоваться различные приближения, они основаны на теоретических соображениях, а не на эмпирической подгонке. Ab initio вычисления дают огромное количество информации, которая недоступна из эмпирических методов, такой как плотность электронных состояний или другие электронные свойства. Значительным преимуществом использования ab initio методов является возможность изучать реакции, которые включают разрыв или образование ковалентных связей, которые соответствуют нескольким электронным состояниям. Более того, ab initio методы также позволяют восстанавливать эффекты за пределами приближения Борна–Оппенгеймера, используя такие подходы, как смешанная квантово-классическая динамика .

Гибридный QM/MM

Методы QM (квантово-механические) очень мощные. Однако они требуют больших вычислительных затрат, в то время как методы MM (классическая или молекулярная механика) быстры, но страдают от нескольких ограничений (требуют обширной параметризации; полученные оценки энергии не очень точны; не могут использоваться для моделирования реакций, в которых ковалентные связи разрываются/образуются; и ограничены в своих возможностях предоставления точных данных относительно химической среды). Появился новый класс методов, который сочетает в себе хорошие стороны расчетов QM (точность) и MM (скорость). Эти методы называются смешанными или гибридными методами квантовой механики и молекулярной механики (гибридные QM/MM). ^[51]

Самым важным преимуществом гибридного метода QM/MM является скорость. Стоимость выполнения классической молекулярной динамики (MM) в самом прямом случае масштабируется O(n ² ), где n — число атомов в системе. Это в основном из-за электростатического взаимодействия (каждая частица взаимодействует с каждой другой частицей). Однако использование радиуса обрезания, периодических обновлений парного списка и, в последнее время, вариаций метода Эвальда (PME) для сетки частиц уменьшили это до O(n) до O(n ² ). Другими словами, если моделируется система с вдвое большим числом атомов, то это потребует от двух до четырех раз больше вычислительной мощности. С другой стороны, самые простые вычисления ab initio обычно масштабируются O(n ³ ) или хуже ( было предложено масштабировать ограниченные вычисления Хартри–Фока ~O(n ^2.7 )). Чтобы преодолеть это ограничение, небольшая часть системы обрабатывается квантово-механически (обычно активный центр фермента), а оставшаяся часть системы обрабатывается классически.

В более сложных реализациях существуют методы QM/MM для обработки как легких ядер, восприимчивых к квантовым эффектам (таких как водороды), так и электронных состояний. Это позволяет генерировать волновые функции водорода (похожие на электронные волновые функции). Эта методология оказалась полезной при исследовании таких явлений, как туннелирование водорода. Одним из примеров, где методы QM/MM обеспечили новые открытия, является расчет переноса гидрида в ферменте алкогольдегидрогеназе печени . В этом случае квантовое туннелирование важно для водорода, поскольку оно определяет скорость реакции. ^[52]

Грубая зернистость и сокращенные представления

На другом конце шкалы детализации находятся крупнозернистые и решетчатые модели. Вместо того, чтобы явно представлять каждый атом системы, для представления групп атомов используются «псевдоатомы». Моделирование МД на очень больших системах может потребовать таких больших компьютерных ресурсов, что их нельзя легко изучить традиционными методами всех атомов. Аналогично, моделирование процессов на больших временных масштабах (более 1 микросекунды) является непомерно дорогим, поскольку требует очень много временных шагов. В этих случаях иногда можно решить проблему, используя сокращенные представления, которые также называются крупнозернистыми моделями . ^[53]

Примерами методов грубой зернистости (CG) являются методы прерывистой молекулярной динамики (CG-DMD) ^{[54] [55]} и модели Go. ^[56] Грубая зернистость иногда выполняется с использованием более крупных псевдоатомов. Такие приближения объединенных атомов использовались в моделировании биологических мембран методом МД. Реализация такого подхода в системах, где интерес представляют электрические свойства, может быть сложной из-за сложности использования надлежащего распределения заряда на псевдоатомах. ^[57] Алифатические хвосты липидов представлены несколькими псевдоатомами путем объединения от 2 до 4 метиленовых групп в каждый псевдоатом.

Параметризация этих очень грубозернистых моделей должна быть выполнена эмпирически, путем сопоставления поведения модели с соответствующими экспериментальными данными или моделированием всех атомов. В идеале эти параметры должны учитывать как энтальпийный , так и энтропийный вклад в свободную энергию неявным образом. ^[58] Когда грубозернистость выполняется на более высоких уровнях, точность динамического описания может быть менее надежной. Но очень грубозернистые модели успешно использовались для изучения широкого круга вопросов в структурной биологии, организации жидких кристаллов и полимерных стеклах.

Примеры применения грубой зернистости:

• Исследования по сворачиванию белков и прогнозированию структуры белков часто проводятся с использованием одного или нескольких псевдоатомов на аминокислоту; ^[53]
• Фазовые переходы жидких кристаллов были исследованы в ограниченных геометриях и/или во время течения с использованием потенциала Гая-Берна, который описывает анизотропные виды;
• Полимерные стекла во время деформации изучались с использованием простых гармонических или FENE- пружин для соединения сфер, описываемых потенциалом Леннарда-Джонса ;
• Суперспирализация ДНК исследовалась с использованием 1–3 псевдоатомов на пару оснований и при еще более низком разрешении;
• Упаковка двухспиральной ДНК в бактериофаг была исследована с помощью моделей, в которых один псевдоатом представляет один виток (около 10 пар оснований) двойной спирали;
• Структура РНК в рибосоме и других крупных системах была смоделирована с использованием одного псевдоатома на нуклеотид.

Простейшей формой грубой зернистости является объединенный атом (иногда называемый расширенным атомом ) и он использовался в большинстве ранних MD-моделирований белков, липидов и нуклеиновых кислот. Например, вместо того, чтобы явно рассматривать все четыре атома метильной группы CH3 (или все три атома метиленовой группы CH2 _{) ,} всю группу представляют одним псевдоатомом. Он, конечно, должен быть правильно параметризован, чтобы его ван-дер-ваальсовы взаимодействия с другими группами имели надлежащую зависимость от расстояния. Аналогичные соображения применимы к связям, углам и кручениям, в которых участвует псевдоатом. В этом виде представления объединенного атома обычно исключают все явные атомы водорода, за исключением тех, которые имеют возможность участвовать в водородных связях ( полярные водороды ). Примером этого является силовое поле CHARMM 19.

Полярные водороды обычно сохраняются в модели, поскольку правильная обработка водородных связей требует достаточно точного описания направленности и электростатических взаимодействий между донорными и акцепторными группами. Гидроксильная группа, например, может быть как донором водородной связи, так и акцептором водородной связи, и было бы невозможно обработать это одним псевдоатомом ОН. Около половины атомов в белке или нуклеиновой кислоте являются неполярными водородами, поэтому использование объединенных атомов может обеспечить существенную экономию машинного времени.

Силовые поля машинного обучения

[Силовые поля машинного обучения] (MLFF) представляют собой один из подходов к моделированию межатомных взаимодействий в симуляциях молекулярной динамики. ^[59] MLFF могут достигать точности, близкой к точности методов ab initio . После обучения MLFF намного быстрее прямых квантово-механических расчетов. MLFF устраняют ограничения традиционных силовых полей, изучая сложные поверхности потенциальной энергии непосредственно из квантово-механических данных высокого уровня. Несколько программных пакетов теперь поддерживают MLFF, включая VASP ^[60] и библиотеки с открытым исходным кодом, такие как DeePMD-kit ^{[61] [62]} и SchNetPack. ^{[63] [64]}

Включение эффектов растворителя

Во многих симуляциях системы растворенное вещество-растворитель основное внимание уделяется поведению растворенного вещества с небольшим интересом к поведению растворителя, особенно в тех молекулах растворителя, которые находятся в областях, удаленных от молекулы растворенного вещества. ^[65] Растворители могут влиять на динамическое поведение растворенных веществ посредством случайных столкновений и путем наложения фрикционного сопротивления на движение растворенного вещества через растворитель. Использование непрямоугольных периодических граничных условий, стохастических границ и оболочек растворителя может помочь уменьшить количество требуемых молекул растворителя и позволить вместо этого потратить большую часть вычислительного времени на моделирование растворенного вещества. Также возможно включить эффекты растворителя без необходимости явного присутствия молекул растворителя. Одним из примеров такого подхода является использование потенциальной средней силы (PMF), которая описывает, как изменяется свободная энергия при изменении определенной координаты. Изменение свободной энергии, описываемое PMF, содержит усредненные эффекты растворителя.

Без учета эффектов растворителя моделирование макромолекул (таких как белки) может привести к нереалистичному поведению, и даже небольшие молекулы могут принимать более компактные конформации из-за благоприятных сил Ван-дер-Ваальса и электростатических взаимодействий, которые будут ослаблены в присутствии растворителя. ^[66]

Силы дальнего действия

Дальнодействующее взаимодействие — это взаимодействие, при котором пространственное взаимодействие спадает не быстрее, чем где — размерность системы. Примерами служат заряд-зарядовые взаимодействия между ионами и диполь-дипольные взаимодействия между молекулами. Моделирование этих сил представляет собой сложную задачу, поскольку они значительны на расстоянии, которое может быть больше половины длины ящика при моделировании многих тысяч частиц. Хотя одним из решений было бы значительное увеличение размера длины ящика, этот подход грубой силы не идеален, поскольку моделирование стало бы очень затратным в вычислительном отношении. Сферическое усечение потенциала также не рассматривается, поскольку может наблюдаться нереалистичное поведение, когда расстояние близко к расстоянию отсечки. ^[67] ${\displaystyle r^{-d}}$ ${\displaystyle d}$

Управляемая молекулярная динамика (SMD)

Моделирование управляемой молекулярной динамики (SMD) или моделирование силового зонда прикладывает силы к белку, чтобы манипулировать его структурой, перемещая его вдоль желаемых степеней свободы. Эти эксперименты можно использовать для выявления структурных изменений в белке на атомном уровне. SMD часто используется для моделирования таких событий, как механическое развертывание или растяжение. ^[68]

Существует два типичных протокола SMD: один, в котором скорость вытягивания поддерживается постоянной, и один, в котором приложенная сила является постоянной. Обычно часть изучаемой системы (например, атом в белке) ограничивается гармоническим потенциалом. Затем силы прикладываются к определенным атомам либо с постоянной скоростью, либо с постоянной силой. Зонтичная выборка используется для перемещения системы вдоль желаемой координаты реакции путем изменения, например, сил, расстояний и углов, манипулируемых в моделировании. С помощью зонтичной выборки все конфигурации системы — как высокоэнергетические, так и низкоэнергетические — адекватно отбираются. Затем изменение свободной энергии каждой конфигурации может быть рассчитано как потенциал средней силы . ^[69] Популярным методом вычисления PMF является метод анализа взвешенной гистограммы (WHAM), который анализирует ряд симуляций зонтичной выборки. ^{[70] [71]}

Множество важных приложений SMD находятся в области открытия лекарств и биомолекулярных наук. Например, SMD использовался для исследования стабильности протофибрилл Альцгеймера ^[72] , для изучения взаимодействия белка и лиганда в циклин-зависимой киназе 5 ^[73] и даже для демонстрации влияния электрического поля на тромбин (белок) и аптамер (нуклеотид) комплекс ^[74] среди многих других интересных исследований.

Примеры применения

Молекулярно-динамическое моделирование синтетического молекулярного мотора, состоящего из трех молекул в нанопоре (внешний диаметр 6,7 нм) при 250 К ^[75]

Молекулярная динамика используется во многих областях науки.

• Первая МД-симуляция упрощенного биологического процесса сворачивания была опубликована в 1975 году. Ее моделирование, опубликованное в журнале Nature, проложило путь для обширной области современного вычислительного сворачивания белков. ^[76]
• Первая МД-симуляция биологического процесса была опубликована в 1976 году. Ее моделирование, опубликованное в журнале Nature, проложило путь к пониманию движения белка как неотъемлемой части функции, а не просто вспомогательного процесса. ^[77]
• МД является стандартным методом обработки каскадов столкновений в режиме теплового пика, т. е. эффектов, которые облучение энергичными нейтронами и ионами оказывает на твердые тела и твердые поверхности. ^[78]

Следующие биофизические примеры иллюстрируют заметные усилия по созданию симуляций систем очень большого размера (целый вирус) или очень длительного времени моделирования (до 1,112 миллисекунд):

• Моделирование MD полного сателлитного вируса табачной мозаики (STMV) (2006, Размер: 1 миллион атомов, Время моделирования: 50 нс, Программа: NAMD ) Этот вирус представляет собой небольшой икосаэдрический вирус растений, который ухудшает симптомы заражения вирусом табачной мозаики (TMV). Молекулярно-динамическое моделирование использовалось для исследования механизмов сборки вируса . Вся частица STMV состоит из 60 идентичных копий одного белка, которые составляют вирусный капсид (оболочку), и одноцепочечного генома РНК из 1063 нуклеотидов . Одним из ключевых выводов является то, что капсид очень нестабилен, когда внутри нет РНК. Моделирование заняло бы около 35 лет для одного настольного компьютера 2006 года выпуска. Таким образом, оно было выполнено на многих процессорах параллельно с непрерывной связью между ними. ^[79]
• Моделирование сворачивания головки Виллина в подробностях всех атомов (2006, размер: 20 000 атомов; время моделирования: 500 мкс = 500 000 нс, программа: Folding@home ) Это моделирование было запущено на 200 000 ЦП участвующих персональных компьютеров по всему миру. На этих компьютерах была установлена ​​программа Folding@home, крупномасштабная распределенная вычислительная работа, координируемая Виджаем Панде из Стэнфордского университета. Кинетические свойства белка головки Виллина были исследованы с использованием множества независимых коротких траекторий, запущенных ЦП без непрерывной связи в реальном времени. Одним из использованных методов был анализ значения Pfold, который измеряет вероятность сворачивания до развертывания определенной начальной конформации. Pfold дает информацию о структурах переходного состояния и упорядочении конформаций вдоль пути сворачивания . Каждая траектория в расчете Pfold может быть относительно короткой, но необходимо много независимых траекторий. ^[80]
• Длинные непрерывные траекторные симуляции были выполнены на Anton , массивно-параллельном суперкомпьютере, разработанном и построенном на основе специализированных интегральных схем (ASIC) и межсоединений компанией DE Shaw Research . Самый длинный опубликованный результат симуляции, выполненной с использованием Anton, — это 1,112-миллисекундная симуляция NTL9 при 355 К; также была выполнена вторая, независимая 1,073-миллисекундная симуляция этой конфигурации (и множество других симуляций более 250 мкс непрерывного химического времени). ^[81] В статье How Fast-Folding Proteins Fold исследователи Крестен Линдорфф-Ларсен, Стефано Пиана, Рон О. Дрор и Дэвид Э. Шоу обсуждают «результаты симуляций молекулярной динамики на атомном уровне в течение периодов от 100 мкс до 1 мс, которые раскрывают набор общих принципов, лежащих в основе сворачивания 12 структурно разнообразных белков». Изучение этих разнообразных длинных траекторий, осуществляемое с помощью специализированного, индивидуального оборудования, позволило им сделать вывод, что «в большинстве случаев сворачивание следует одному доминирующему маршруту, в котором элементы нативной структуры появляются в порядке, тесно связанном с их склонностью к формированию в развернутом состоянии». ^[81] В отдельном исследовании Антон был использован для проведения 1,013-миллисекундной симуляции динамики нативного состояния бычьего панкреатического ингибитора трипсина (BPTI) при 300 К. ^[82]

Другое важное применение метода МД основано на его способности трехмерной характеристики и анализа микроструктурной эволюции в атомном масштабе.

• Моделирование МД используется для характеристики эволюции размера зерна, например, при описании износа и трения нанокристаллических материалов Al и Al(Zr). ^[83] Эволюция дислокаций и эволюция размера зерна анализируются в процессе трения в этом моделировании. Поскольку метод МД предоставил полную информацию о микроструктуре, эволюция размера зерна была рассчитана в 3D с использованием методов сопоставления полиэдральных шаблонов, ^[84] сегментации зерен ^[85] и кластеризации графов ^[86] . В таком моделировании метод МД обеспечил точное измерение размера зерна. Используя эту информацию, были извлечены, измерены и представлены фактические структуры зерен. По сравнению с традиционным методом использования СЭМ с одним 2-мерным срезом материала, МД обеспечивает 3-мерный и точный способ характеризовать эволюцию микроструктуры в атомном масштабе.

Алгоритмы молекулярной динамики

• Экранированные кулоновские потенциалы неявной модели растворителя

Интеграторы

• Симплектический интегратор
• Интеграция Верле-Штермера
• Интеграция Рунге-Кутта
• Алгоритм Бимана
• Алгоритмы ограничений (для систем с ограничениями)

Алгоритмы ближнего взаимодействия

• Списки ячеек
• Список Верле
• Связанные взаимодействия

Алгоритмы дальнего взаимодействия

• суммирование Эвальда
• Суммирование Эвальда для сетки частиц (PME)
• Частица–частица–частица–сетка ( P3M )
• Метод смещенной силы

Стратегии распараллеливания

• Метод декомпозиции домена (Распределение системных данных для параллельных вычислений )

Молекулярная динамика ab-initio

• Молекулярная динамика Кар-Парринелло

Специализированное оборудование для моделирования МД

• Антон – специализированный, массивно-параллельный суперкомпьютер, предназначенный для выполнения моделирования МД.
• MDGRAPE – Специальная система, созданная для моделирования молекулярной динамики, в частности, прогнозирования структуры белков.

Видеокарта как аппаратное обеспечение для моделирования МД

Моделирование ионной жидкости на GPU ( Abalone )

Молекулярное моделирование на GPU — это метод использования графического процессора (GPU) для молекулярного моделирования. ^[87]

В 2007 году NVIDIA представила видеокарты, которые можно было использовать не только для отображения графики, но и для научных расчетов. Эти карты включают в себя множество арифметических блоков (по состоянию на 2016 год ^{[обновлять]}до 3584 в Tesla P100), работающих параллельно. Задолго до этого события вычислительная мощность видеокарт использовалась исключительно для ускорения графических расчетов. Новым было то, что NVIDIA сделала возможной разработку параллельных программ в высокоуровневом интерфейсе прикладного программирования (API) под названием CUDA . Эта технология существенно упростила программирование, позволив писать программы на C / C++ . Совсем недавно OpenCL обеспечил кроссплатформенное ускорение GPU.

Смотрите также

• Молекулярное моделирование
• Вычислительная химия
• Силовое поле (химия)
• Сравнение реализаций силового поля
• Метод Монте-Карло
• Программное обеспечение для молекулярного дизайна
• Молекулярная механика
• Многомасштабная функция Грина
• Метод Кар–Парринелло
• Сравнение программного обеспечения для моделирования молекулярной механики
• Квантовая химия
• Метод дискретных элементов
• Сравнение программного обеспечения для моделирования нуклеиновых кислот
• Редактор молекул
• Смешанная квантово-классическая динамика

Ссылки

1. Schlick T (1996). «Pursuing Laplace's Vision on Modern Computers». Математические подходы к биомолекулярной структуре и динамике . Тома IMA по математике и ее приложениям. Том 82. С. 219–247. doi :10.1007/978-1-4612-4066-2_13. ISBN 978-0-387-94838-6.
2. Bernal JD (январь 1997 г.). «Бейкерианская лекция, 1962 г. Структура жидкостей». Труды Лондонского королевского общества. Серия A. Математические и физические науки . 280 (1382): 299–322. Bibcode : 1964RSPSA.280..299B. doi : 10.1098/rspa.1964.0147. S2CID  178710030.
3. Ферми Э., Паста Дж., Улам С., отчет Лос-Аламоса о Лос-Аламосе LA-1940 (1955).
4. Alder BJ, Wainwright T (август 1959). «Исследования по молекулярной динамике. I. Общий метод». Журнал химической физики . 31 (2): 459–466. Bibcode : 1959JChPh..31..459A. doi : 10.1063/1.1730376.
5. Гибсон Дж. Б., Голанд АН, Милгрэм М., Виньярд Г. (1960). «Динамика радиационного повреждения». Phys. Rev. 120 ( 4): 1229–1253. Bibcode : 1960PhRv..120.1229G. doi : 10.1103/PhysRev.120.1229.
6. Рахман А (19 октября 1964 г.). «Корреляции в движении атомов в жидком аргоне». Physical Review . 136 (2A): A405–A411. Bibcode : 1964PhRv..136..405R. doi : 10.1103/PhysRev.136.A405.
7. Stephan S, Thol M, Vrabec J, Hasse H (октябрь 2019 г.). «Теплофизические свойства жидкости Леннарда-Джонса: база данных и оценка данных». Журнал химической информации и моделирования . 59 (10): 4248–4265. doi :10.1021/acs.jcim.9b00620. PMID  31609113. S2CID  204545481.
8. Ван X, Рамирес-Хинестроса С, Добникар Дж, Френкель Д (май 2020 г.). «Потенциал Леннарда-Джонса: когда (не) его использовать». Физическая химия Химическая физика . 22 (19): 10624–10633. arXiv : 1910.05746 . Bibcode :2020PCCP...2210624W. doi :10.1039/C9CP05445F. PMID  31681941. S2CID  204512243.
9. Мик Дж., Хайлат Э., Руссо В., Рушаидат К., Швиберт Л., Потофф Дж. (декабрь 2013 г.). «Моделирование ансамбля Гиббса Монте-Карло с использованием GPU для Леннарда-Джонсиума». Computer Physics Communications . 184 (12): 2662–2669. Bibcode : 2013CoPhC.184.2662M. doi : 10.1016/j.cpc.2013.06.020.
10. Чапела Г.А., Скривен Л.Е., Дэвис Х.Т. (октябрь 1989 г.). «Молекулярная динамика разрывного потенциала. IV. Леннард-Джонезиум». Журнал химической физики . 91 (7): 4307–4313. Бибкод : 1989JChPh..91.4307C. дои : 10.1063/1.456811. ISSN  0021-9606.
11. Lenhard J, Stephan S, Hasse H (февраль 2024 г.). «Дитя предсказания. Об истории, онтологии и вычислениях Леннарда-Джонсиума». Исследования по истории и философии науки . 103 : 105–113. doi : 10.1016/j.shpsa.2023.11.007. PMID  38128443. S2CID  266440296.
12. Eggimann BL, Sunnarborg AJ, Stern HD, Bliss AP, Siepmann JI (2013-12-24). "Онлайн-база данных параметров и свойств для силового поля TraPPE". Molecular Simulation . 40 (1–3): 101–105. doi :10.1080/08927022.2013.842994. ISSN  0892-7022. S2CID  95716947.
13. Stephan S, Horsch MT, Vrabec J, Hasse H (2019-07-03). "MolMod – открытая база данных силовых полей для молекулярного моделирования жидкостей". Molecular Simulation . 45 (10): 806–814. arXiv : 1904.05206 . doi :10.1080/08927022.2019.1601191. ISSN  0892-7022. S2CID  119199372.
14. Koehl P, Levitt M (февраль 1999). «Более светлое будущее для предсказания структуры белка». Nature Structural Biology . 6 (2): 108–111. doi :10.1038/5794. PMID  10048917. S2CID  3162636.
15. Raval A, Piana S, Eastwood MP, Dror RO, Shaw DE (август 2012 г.). «Уточнение моделей гомологии белковой структуры с помощью длительных симуляций молекулярной динамики на всех атомах». Proteins . 80 (8): 2071–2079. doi :10.1002/prot.24098. PMID  22513870. S2CID  10613106.
16. Beauchamp KA, Lin YS, Das R, Pande VS (апрель 2012 г.). «Улучшаются ли силовые поля белков? Систематический бенчмарк на основе 524 различных измерений ЯМР». Journal of Chemical Theory and Computation . 8 (4): 1409–1414. doi :10.1021/ct2007814. PMC 3383641 . PMID  22754404. 
17. Piana S, Klepeis JL, Shaw DE (февраль 2014 г.). «Оценка точности физических моделей, используемых в моделировании сворачивания белков: количественные доказательства из длительных симуляций молекулярной динамики». Current Opinion in Structural Biology . 24 : 98–105. doi : 10.1016/j.sbi.2013.12.006 . PMID  24463371.
18. Choudhury C, Priyakumar UD, Sastry GN (апрель 2015 г.). «Модели фармакофоров на основе динамики для скрининга потенциальных ингибиторов микобактериальной циклопропансинтазы». Журнал химической информации и моделирования . 55 (4): 848–60. doi :10.1021/ci500737b. PMID  25751016.
19. Pinto M, Perez JJ, Rubio-Martinez J (январь 2004 г.). «Молекулярно-динамическое исследование пептидных сегментов домена BH3 проапоптотических белков Bak, Bax, Bid и Hrk, связанных с белками Bcl-xL и Bcl-2». Журнал компьютерного молекулярного дизайна . 18 (1): 13–22. Bibcode : 2004JCAMD..18...13P. doi : 10.1023/b:jcam.0000022559.72848.1c. PMID  15143800. S2CID  11339000.
20. Хатмал ММ, Джабер С, Таха МО (декабрь 2016 г.). «Объединение моделирования молекулярной динамики и анализа контактов лиганд-рецептор как новый подход к моделированию фармакофора: бета-секретаза 1 и киназа контрольных точек 1 как примеры». Журнал компьютерного молекулярного дизайна . 30 (12): 1149–1163. Bibcode : 2016JCAMD..30.1149H. doi : 10.1007/s10822-016-9984-2. PMID  27722817. S2CID  11561853.
21. Myers JK, Pace CN (октябрь 1996). «Водородные связи стабилизируют глобулярные белки». Biophysical Journal . 71 (4): 2033–2039. Bibcode :1996BpJ....71.2033M. doi :10.1016/s0006-3495(96)79401-8. PMC 1233669 . PMID  8889177. 
22. Lenhard J, Stephan S, Hasse H (июнь 2024 г.). «Об истории потенциала Леннарда-Джонса». Annalen der Physik . 536 (6). doi :10.1002/andp.202400115. ISSN  0003-3804.
23. Фишер Дж., Вендланд М. (октябрь 2023 г.). «Об истории ключевых эмпирических межмолекулярных потенциалов». Fluid Phase Equilibria . 573 : 113876. Bibcode : 2023FlPEq.57313876F. doi : 10.1016/j.fluid.2023.113876 .
24. Israelachvili J (1992). Межмолекулярные и поверхностные силы . Сан-Диего: Academic Press.
25. Cruz FJ, de Pablo JJ, Mota JP (июнь 2014 г.). «Эндоэдральное ограничение додекамера ДНК на чистых углеродных нанотрубках и стабильность канонической формы B». Журнал химической физики . 140 (22): 225103. arXiv : 1605.01317 . Bibcode : 2014JChPh.140v5103C. doi : 10.1063/1.4881422. PMID  24929415. S2CID  15149133.
26. Cruz FJ, Mota JP (2016). «Конформационная термодинамика цепей ДНК в гидрофильных нанопорах». J. Phys. Chem. C. 120 ( 36): 20357–20367. doi :10.1021/acs.jpcc.6b06234.
27. Плимптон С. «Молекулярная динамика — параллельные алгоритмы». sandia.gov .
28. Streett WB, Tildesley DJ, Saville G (1978). «Множественные временные методы в молекулярной динамике». Mol Phys . 35 (3): 639–648. Bibcode : 1978MolPh..35..639S. doi : 10.1080/00268977800100471.
29. Tuckerman ME, Berne BJ, Martyna GJ (1991). «Алгоритм молекулярной динамики для множественных временных масштабов: системы с дальнодействующими силами». J Chem Phys . 94 (10): 6811–6815. Bibcode : 1991JChPh..94.6811T. doi : 10.1063/1.460259.
30. Tuckerman ME, Berne BJ, Martyna GJ (1992). «Обратимая многомасштабная молекулярная динамика». J Chem Phys . 97 (3): 1990–2001. Bibcode :1992JChPh..97.1990T. doi :10.1063/1.463137. S2CID  488073.
31. Sugita Y, Okamoto Y (ноябрь 1999). «Метод молекулярной динамики обмена репликами для сворачивания белков». Chemical Physics Letters . 314 (1–2): 141–151. Bibcode : 1999CPL...314..141S. doi : 10.1016/S0009-2614(99)01123-9.
32. Rizzuti B (2022). «Молекулярное моделирование белков: от упрощенных физических взаимодействий к сложным биологическим явлениям». Biochimica et Biophysica Acta (BBA) - Белки и протеомика . 1870 (3): 140757. doi :10.1016/j.bbapap.2022.140757. PMID  35051666. S2CID  263455009.
33. Синнотт СБ , Бреннер ДВ (2012). «Три десятилетия многочастичных потенциалов в исследовании материалов». Бюллетень MRS . 37 (5): 469–473. Bibcode : 2012MRSBu..37..469S. doi : 10.1557/mrs.2012.88 .
34. Albe K, Nordlund K, Averback RS (2002). "Моделирование взаимодействия металл-полупроводник: аналитический потенциал порядка связи для платины-углерода". Phys. Rev. B. 65 ( 19): 195124. Bibcode : 2002PhRvB..65s5124A. doi : 10.1103/physrevb.65.195124.
35. Brenner DW (ноябрь 1990 г.). «Эмпирический потенциал углеводородов для использования при моделировании химического осаждения алмазных пленок из паровой фазы» (PDF) . Physical Review B. 42 ( 15): 9458–9471. Bibcode : 1990PhRvB..42.9458B. doi : 10.1103/physrevb.42.9458. PMID  9995183. Архивировано из оригинала 22 сентября 2017 г.
36. Бирдмор К, Смит Р (1996). «Эмпирические потенциалы для систем C-Si-H с применением к взаимодействиям C ₆₀ с поверхностями кристаллов Si». Philosophical Magazine A . 74 (6): 1439–1466. Bibcode :1996PMagA..74.1439B. doi :10.1080/01418619608240734.
37. Ni B, Lee KH, Sinnott SB (2004). "Реактивный эмпирический потенциал порядка связи (rebo) для взаимодействия углеводородов и кислорода". Journal of Physics: Condensed Matter . 16 (41): 7261–7275. Bibcode : 2004JPCM...16.7261N. doi : 10.1088/0953-8984/16/41/008. S2CID  250760409.
38. Ван Дуин AC, Дасгупта С, Лорант Ф, Годдард В.А. (октябрь 2001 г.). «ReaxFF: Поле реактивной силы для углеводородов». Журнал физической химии А. 105 (41): 9396–9409. Бибкод : 2001JPCA..105.9396V. CiteSeerX 10.1.1.507.6992 . дои : 10.1021/jp004368u. 
39. Cruz FJ, Lopes JN, Calado JC, Minas da Piedade ME (декабрь 2005 г.). «Исследование термодинамических свойств апатитов кальция методом молекулярной динамики. 1. Гексагональные фазы». The Journal of Physical Chemistry B. 109 ( 51): 24473–24479. doi :10.1021/jp054304p. PMID  16375450.
40. Cruz FJ, Lopes JN, Calado JC (март 2006 г.). «Моделирование молекулярной динамики расплавленного гидроксиапатита кальция». Fluid Phase Equilibria . 241 (1–2): 51–58. Bibcode : 2006FlPEq.241...51C. doi : 10.1016/j.fluid.2005.12.021.
41. Justo JF, Bazant MZ, Kaxiras E, Bulatov VV, Yip S (1998). "Межатомный потенциал для дефектов кремния и неупорядоченных фаз". Phys. Rev. B . 58 (5): 2539–2550. arXiv : cond-mat/9712058 . Bibcode :1998PhRvB..58.2539J. doi :10.1103/PhysRevB.58.2539. S2CID  14585375.
42. Tersoff J (март 1989). «Моделирование химии твердого тела: межатомные потенциалы для многокомпонентных систем». Physical Review B. 39 ( 8): 5566–5568. Bibcode : 1989PhRvB..39.5566T. doi : 10.1103/physrevb.39.5566. PMID  9948964.
43. Daw MS , Foiles SM, Baskes MI (март 1993 г.). «Метод внедренных атомов: обзор теории и приложений». Materials Science Reports . 9 (7–8): 251–310. doi : 10.1016/0920-2307(93)90001-U .
44. Клери Ф., Розато В. (июль 1993 г.). "Потенциалы сильной связи для переходных металлов и сплавов". Physical Review B. 48 ( 1): 22–33. Bibcode : 1993PhRvB..48...22C. doi : 10.1103/physrevb.48.22. PMID  10006745.
45. Lamoureux G, Harder E, Vorobyov IV, Roux B, MacKerell AD (2006). "Поляризуемая модель воды для моделирования молекулярной динамики биомолекул". Chem Phys Lett . 418 (1): 245–249. Bibcode :2006CPL...418..245L. doi :10.1016/j.cplett.2005.10.135.
46. Sokhan VP, Jones AP, Cipcigan FS, Crain J, Martyna GJ (май 2015 г.). «Сигнатурные свойства воды: их молекулярно-электронное происхождение». Труды Национальной академии наук Соединенных Штатов Америки . 112 (20): 6341–6346. Bibcode : 2015PNAS..112.6341S. doi : 10.1073/pnas.1418982112 . PMC 4443379. PMID  25941394 . 
47. Cipcigan FS, Sokhan VP, Jones AP, Crain J, Martyna GJ (апрель 2015 г.). «Водородные связи и молекулярная ориентация на границе раздела жидкость-пар в воде». Physical Chemistry Chemical Physics . 17 (14): 8660–8669. Bibcode :2015PCCP...17.8660C . doi : 10.1039/C4CP05506C . hdl : 20.500.11820/0bd0cd1a-94f1-4053-809c-9fb68bbec1c9 . PMID  25715668.
48. Mahmoudi M, Lynch I, Ejtehadi MR, Monopoli MP, Bombelli FB, Laurent S (сентябрь 2011 г.). «Взаимодействие белков и наночастиц: возможности и проблемы». Chemical Reviews . 111 (9): 5610–5637. doi :10.1021/cr100440g. PMID  21688848.
49. Patel S, Mackerell AD, Brooks CL (сентябрь 2004 г.). «CHARMM флуктуирующее поле силы заряда для белков: II свойства белка/растворителя из моделирования молекулярной динамики с использованием неаддитивной электростатической модели». Журнал вычислительной химии . 25 (12): 1504–1514. doi : 10.1002/jcc.20077 . PMID  15224394. S2CID  16741310.
50. Najla Hosseini A, Lund M, Ejtehadi MR (май 2022 г.). «Эффекты электронной поляризации при мембранной транслокации противораковых препаратов». Physical Chemistry Chemical Physics . 24 (20): 12281–12292. Bibcode :2022PCCP...2412281N. doi :10.1039/D2CP00056C. PMID  35543365. S2CID  248696332.
51. Методология таких методов была введена Уоршелем и его коллегами. В последние годы их пионерами стали несколько групп, в том числе: Арье Уоршел ( Университет Южной Калифорнии ), Вэйтао Ян ( Университет Дьюка ), Шэрон Хаммес-Шиффер ( Университет штата Пенсильвания ), Дональд Трулар и Цзяли Гао ( Университет Миннесоты ) и Кеннет Мерц ( Университет Флориды ).
52. Billeter SR, Webb SP, Agarwal PK, Iordanov T, Hammes-Schiffer S (ноябрь 2001 г.). «Перенос гидрида в алкогольдегидрогеназе печени: квантовая динамика, кинетические изотопные эффекты и роль движения фермента». Журнал Американского химического общества . 123 (45): 11262–11272. doi :10.1021/ja011384b. PMID  11697969.
53. Кмиецик С., Гронт Д., Колински М., Витеска Л., Давид А.Е., Колински А. (июль 2016 г.). «Крупнозернистые белковые модели и их применение». Химические обзоры . 116 (14): 7898–7936. doi : 10.1021/acs.chemrev.6b00163 . ПМИД  27333362.
54. Voegler Smith A, Hall CK (август 2001 г.). «Формирование альфа-спирали: прерывистая молекулярная динамика на модели белка промежуточного разрешения». Белки . 44 (3): 344–360. doi :10.1002/prot.1100. PMID  11455608. S2CID  21774752.
55. Ding F, Borreguero JM, Buldyrey SV, Stanley HE, Dokholyan NV (ноябрь 2003 г.). «Механизм перехода альфа-спирали в бета-шпильку». Proteins . 53 (2): 220–228. doi :10.1002/prot.10468. PMID  14517973. S2CID  17254380.
56. Paci E, Vendruscolo M, Karplus M (декабрь 2002 г.). «Достоверность моделей Gō: сравнение с эмпирическим разложением энергии, защищенным растворителем». Biophysical Journal . 83 (6): 3032–3038. Bibcode :2002BpJ....83.3032P. doi :10.1016/S0006-3495(02)75308-3. PMC 1302383 . PMID  12496075. 
57. Чакрабарти А., Кагин Т. (май 2010 г.). «Крупнозернистое моделирование полиимидных сополимеров». Polymer . 51 (12): 2786–2794. doi :10.1016/j.polymer.2010.03.060.
58. Foley TT, Shell MS, Noid WG (декабрь 2015 г.). «Влияние разрешения на энтропию и информацию в крупнозернистых моделях». Журнал химической физики . 143 (24): 243104. Bibcode : 2015JChPh.143x3104F. doi : 10.1063/1.4929836. PMID  26723589.
59. Unke OT, Chmiela S, Sauceda HE, Gastegger M, Poltavsky I, Schütt KT и др. (август 2021 г.). «Силовые поля машинного обучения». Chemical Reviews . 121 (16): 10142–10186. doi :10.1021/acs.chemrev.0c01111. PMC 8391964 . PMID  33705118. 
60. Хафнер Дж (октябрь 2008 г.). «Ab-initio моделирование материалов с использованием VASP: теория функционала плотности и далее». Журнал вычислительной химии . 29 (13): 2044–78. doi :10.1002/jcc.21057. PMID  18623101.
61. Wang H, Zhang L, Han J, Weinan E (июль 2018 г.). «DeePMD-kit: пакет глубокого обучения для представления потенциальной энергии многих тел и молекулярной динамики». Computer Physics Communications . 228 : 178–184. doi :10.1016/j.cpc.2018.03.016.
62. Zeng J, Zhang D, Lu D, Mo P, Li Z, Chen Y и др. (август 2023 г.). «DeePMD-kit v2: программный пакет для моделей глубокого потенциала». Журнал химической физики . 159 (5). doi : 10.1063/5.0155600. PMC 10445636. PMID  37526163 . 
63. Schütt KT, Kessel P, Gastegger M, Nicoli KA, Tkatchenko A, Müller KR (январь 2019 г.). «SchNetPack: набор инструментов глубокого обучения для атомистических систем». Journal of Chemical Theory and Computation . 15 (1): 448–455. doi :10.1021/acs.jctc.8b00908. PMID  30481453.
64. Schütt KT, Hessmann SS, Gebauer NW, Lederer J, Gastegger M (апрель 2023 г.). «SchNetPack 2.0: набор инструментов нейронной сети для атомистического машинного обучения». Журнал химической физики . 158 (14): 144801. doi : 10.1063/5.0138367.
65. Лич А. (30 января 2001 г.). Молекулярное моделирование: принципы и приложения (2-е изд.). Harlow: Prentice Hall. ISBN 9780582382107. ASIN  0582382106.
66. Leach AR (2001). Молекулярное моделирование: принципы и приложения (2-е изд.). Харлоу, Англия: Prentice Hall. стр. 320. ISBN 0-582-38210-6. OCLC  45008511.
67. Аллен MP, Тилдесли DJ (2017-08-22). Компьютерное моделирование жидкостей (2-е изд.). Oxford University Press. стр. 216. ISBN 9780198803201. ASIN  0198803206.
68. Ниенхаус ГУ (2005). Белково-лигандные взаимодействия: методы и приложения . Хумана Пресс. стр. 54–56. ISBN 978-1-61737-525-5.
69. Leszczyński J (2005). Вычислительная химия: обзоры современных тенденций, том 9. World Scientific. стр. 54–56. ISBN 978-981-256-742-0.
70. Kumar S, Rosenberg JM, Bouzida D, Swendsen RH, Kollman PA (октябрь 1992 г.). «Метод анализа взвешенной гистограммы для расчетов свободной энергии биомолекул. I. Метод». Journal of Computational Chemistry . 13 (8): 1011–1021. doi :10.1002/jcc.540130812. S2CID  8571486.
71. Bartels C (декабрь 2000 г.). «Анализ смещенных Монте-Карло и моделирования молекулярной динамики». Chemical Physics Letters . 331 (5–6): 446–454. Bibcode : 2000CPL...331..446B. doi : 10.1016/S0009-2614(00)01215-X.
72. Lemkul JA, Bevan DR (февраль 2010 г.). «Оценка стабильности протофибрилл амилоида болезни Альцгеймера с использованием молекулярной динамики». Журнал физической химии B. 114 ( 4): 1652–1660. doi :10.1021/jp9110794. PMID  20055378.
73. Patel JS, Berteotti A, Ronsisvalle S, Rocchia W, Cavalli A (февраль 2014 г.). «Моделирование управляемой молекулярной динамики для изучения взаимодействия белок-лиганд в циклин-зависимой киназе 5». Journal of Chemical Information and Modeling . 54 (2): 470–480. doi :10.1021/ci4003574. PMID  24437446.
74. Gosai A, Ma X, Balasubramanian G, Shrotriya P (ноябрь 2016 г.). "Связывание/расцепление комплекса человеческий тромбин-аптамер, контролируемое электрическим стимулом". Scientific Reports . 6 (1): 37449. Bibcode :2016NatSR...637449G. doi :10.1038/srep37449. PMC 5118750 . PMID  27874042. 
75. Palma CA, Björk J, Rao F, Kühne D, Klappenberger F, Barth JV (август 2014 г.). «Топологическая динамика в супрамолекулярных роторах». Nano Letters . 14 (8): 4461–4468. Bibcode : 2014NanoL..14.4461P. doi : 10.1021/nl5014162. PMID  25078022.
76. Левитт М., Уоршел А. (февраль 1975 г.). «Компьютерное моделирование сворачивания белков». Nature . 253 (5494): 694–698. Bibcode :1975Natur.253..694L. doi :10.1038/253694a0. PMID  1167625. S2CID  4211714.
77. Warshel A (апрель 1976). «Модель велосипедной педали для первого шага в процессе зрения». Nature . 260 (5553): 679–683. Bibcode :1976Natur.260..679W. doi :10.1038/260679a0. PMID  1264239. S2CID  4161081.
78. Смит, Р., ред. (1997). Атомные и ионные столкновения в твердых телах и на поверхностях: теория, моделирование и приложения . Кембридж, Великобритания: Cambridge University Press.^{[ нужна страница ]}
79. Фреддолино П., Архипов А., Ларсон С.Б., Макферсон А., Шультен К. «Моделирование молекулярной динамики вируса табачной мозаики (STMV)». Группа теоретической и вычислительной биофизики . Иллинойсский университет в Урбане-Шампейне.
80. Jayachandran G, Vishal V, Pande VS (апрель 2006 г.). «Использование массового параллельного моделирования и марковских моделей для изучения сворачивания белка: изучение динамики головки виллина». Журнал химической физики . 124 (16): 164902. Bibcode : 2006JChPh.124p4902J. doi : 10.1063/1.2186317 . PMID  16674165.
81. Lindorff-Larsen K, Piana S, Dror RO, Shaw DE (октябрь 2011 г.). «Как быстро сворачиваются белки». Science . 334 (6055): 517–520. Bibcode :2011Sci...334..517L. CiteSeerX 10.1.1.1013.9290 . doi :10.1126/science.1208351. PMID  22034434. S2CID  27988268. 
82. Shaw DE, Maragakis P, Lindorff-Larsen K, Piana S, Dror RO, Eastwood MP и др. (октябрь 2010 г.). «Характеристика структурной динамики белков на атомном уровне». Science . 330 (6002): 341–346. Bibcode :2010Sci...330..341S. doi :10.1126/science.1187409. PMID  20947758. S2CID  3495023.
83. Shi Y, Szlufarska I (ноябрь 2020 г.). «Износоиндуцированная микроструктурная эволюция нанокристаллического алюминия и роль легирующих добавок циркония». Acta Materialia . 200 : 432–441. Bibcode : 2020AcMat.200..432S. doi : 10.1016/j.actamat.2020.09.005 . S2CID  224954349.
84. Larsen PM, Schmidt S, Schiøtz J (1 июня 2016 г.). "Надежная структурная идентификация с помощью сопоставления полиэдральных шаблонов". Моделирование и имитация в материаловедении и машиностроении . 24 (5): 055007. arXiv : 1603.05143 . Bibcode : 2016MSMSE..24e5007M. doi : 10.1088/0965-0393/24/5/055007. S2CID  53980652.
85. Hoffrogge PW, Barrales-Mora LA (февраль 2017 г.). «Кинетика и вращение с разрешением зерен во время роста зерен нанокристаллического алюминия методом молекулярной динамики». Computational Materials Science . 128 : 207–222. arXiv : 1608.07615 . doi :10.1016/j.commatsci.2016.11.027. S2CID  118371554.
86. Бональд Т., Шарпантье Б., Галланд А., Холлоку А. (22 июня 2018 г.). «Иерархическая кластеризация графов с использованием выборки пар узлов». arXiv : 1806.01664 [cs.SI].
87. Stone JE, Phillips JC, Freddolino PL, Hardy DJ, Trabuco LG, Schulten K (декабрь 2007 г.). «Ускорение приложений молекулярного моделирования с помощью графических процессоров». Журнал вычислительной химии . 28 (16): 2618–2640. CiteSeerX 10.1.1.466.3823 . doi :10.1002/jcc.20829. PMID  17894371. S2CID  15313533. 

Общие ссылки

• Allen MP, Tildesley DJ (1989). Компьютерное моделирование жидкостей . Oxford University Press. ISBN 0-19-855645-4.
• McCammon JA, Harvey SC (1987). Динамика белков и нуклеиновых кислот . Cambridge University Press. ISBN 0-521-30750-3.
• Рапапорт Д.К. (1996). Искусство моделирования молекулярной динамики . ISBN 0-521-44561-2.
• Грибель М. , Кнапек С., Зумбуш Г. (2007). Численное моделирование в молекулярной динамике . Берлин, Гейдельберг: Springer. ISBN 978-3-540-68094-9.
• Френкель Д. , Смит Б. (2002) [2001]. Понимание молекулярного моделирования: от алгоритмов к приложениям . Сан-Диего: Academic Press. ISBN 978-0-12-267351-1.
• Haile JM (2001). Моделирование молекулярной динамики: элементарные методы . Wiley. ISBN 0-471-18439-X.
• Садус Р. Дж. (2002). Молекулярное моделирование жидкостей: теория, алгоритмы и объектная ориентация . Elsevier. ISBN 0-444-51082-6.
• Беккер OM, Макерелл Jr AD, Ру Б, Ватанабе М (2001). Вычислительная биохимия и биофизика . Марсель Деккер. ISBN 0-8247-0455-X.
• Лич А. (2001). Молекулярное моделирование: принципы и приложения (2-е изд.). Prentice Hall. ISBN 978-0-582-38210-7.
• Шлик Т. (2002). Молекулярное моделирование и симуляция . Спрингер. ISBN 0-387-95404-X.
• Hoover WB (1991). Вычислительная статистическая механика . Elsevier. ISBN 0-444-88192-1.
• Эванс ДЖ, Моррис Г (2008). Статистическая механика неравновесных жидкостей (второе издание). Cambridge University Press. ISBN 978-0-521-85791-8.

Внешние ссылки

• Проект GPUGRID.net ( GPUGRID.net )
• Проект Blue Gene ( IBM ) JawBreakers.org
• Моделирование материалов и коды компьютерного моделирования
• Несколько советов по молекулярной динамике
• Фильм MD моделирования воды (YouTube)