Кватернион

Некоммутативное расширение комплексных чисел

График Кэли Q8 , показывающий шесть циклов умножения на i , j и k . (Если изображение открывается на Wikimedia Commons двойным щелчком по нему, циклы можно выделить, наведя на них курсор или щелкнув по ним.)

В математике система счисления кватернионов расширяет комплексные числа . Кватернионы были впервые описаны ирландским математиком Уильямом Роуэном Гамильтоном в 1843 году ^{[1] [2]} и применены к механике в трехмерном пространстве . Алгебра кватернионов часто обозначается буквой H (от Гамильтона ) или жирным шрифтом на доске : Хотя умножение кватернионов некоммутативно , оно дает определение фактора двух векторов в трехмерном пространстве. ^{[3] [4]} Кватернионы обычно представляются в виде ${\displaystyle \mathbb {H} .}$

$${\displaystyle a+b\ \mathbf {i} +c\ \mathbf {j} +d\ \mathbf {k} ,}$$

где коэффициенты a , b , c , d — действительные числа , а 1, i , j , k — базисные векторы или базисные элементы . ^[5]

Кватернионы используются в чистой математике , но также имеют практическое применение в прикладной математике , особенно для вычислений, включающих трехмерное вращение , например, в трехмерной компьютерной графике , компьютерном зрении и анализе кристаллографических текстур . ^[6] Их можно использовать наряду с другими методами вращения, такими как углы Эйлера и матрицы вращения , или в качестве альтернативы им, в зависимости от приложения.

Говоря современным языком, кватернионы образуют четырехмерную ассоциативную нормированную алгебру с телом над действительными числами и, следовательно, кольцо, а также тело и область определения . Это частный случай алгебры Клиффорда , классифицированный как «Это была первая открытая некоммутативная алгебра с делением». ${\displaystyle \operatorname {Cl} _{0,2}(\mathbb {R} )\cong \operatorname {Cl} _{3,0}^{+}(\mathbb {R} ).}$

Согласно теореме Фробениуса , алгебра — одно из двух конечномерных тел , содержащих собственное подкольцо , изоморфное действительным числам; другой - комплексные числа. Эти кольца также являются евклидовыми алгебрами Гурвица , из которых кватернионы являются самой большой ассоциативной алгеброй (и, следовательно, самым большим кольцом). Дальнейшее расширение кватернионов дает неассоциативные октонионы , которые являются последней нормированной алгеброй с делением над действительными числами. Следующее расширение дает седенионы , которые имеют делители нуля и поэтому не могут быть нормированной алгеброй с делением. ^[7] ${\displaystyle \mathbb {H} }$

Единичные кватернионы задают групповую структуру на 3-сфере S ³ , изоморфную группам Spin(3) и SU(2) , т.е. универсальную накрывающую группу SO(3) . Положительные и отрицательные базисные векторы образуют группу кватернионов из восьми элементов .

Графическое представление произведений единиц кватернионов в виде поворотов на 90° в плоскостях 4-мерного пространства, охватываемых двумя из {1, i , j , k }. Левый фактор можно рассматривать как вращаемый правым фактором для получения продукта. Визуально я  ⋅  j знак равно - ( j  ⋅  я ) .

• В синем :
  • 1  ⋅ i = i    (1/ i плоскость)
  • я  ⋅ j = k    (плоскость i / k )
• В красном :
  • 1  ⋅ j = j    ( плоскость 1/ j )
  • j  ⋅ i = − k    (плоскость j / k )

История

Мемориальная доска кватерниона на мосту Брум (Брум) в Дублине , на которой написано:

     Здесь, проходя мимо
16 октября 1843 года,
сэр Уильям Роуэн Гамильтон
в вспышке гениальности открыл
фундаментальную формулу
умножения кватернионов
     i ² = j ² = k ² = i  j  k = −1
и вырезал ее на камне из этого камня. мост

Кватернионы были введены Гамильтоном в 1843 году. ^[8] Важными предшественниками этой работы были четырехквадратное тождество Эйлера (1748 год) и параметризация общих вращений Олинде Родригеса четырьмя параметрами (1840 год), но ни один из этих авторов не рассматривал четырехпараметрическое тождество. вращения как алгебра. ^{[9] [10]} Карл Фридрих Гаусс также открыл кватернионы в 1819 году, но эта работа не была опубликована до 1900 года. ^{[11] [12]}

Гамильтон знал, что комплексные числа можно интерпретировать как точки на плоскости , и искал способ сделать то же самое для точек в трехмерном пространстве . Точки в пространстве могут быть представлены их координатами, которые представляют собой тройки чисел, и в течение многих лет он знал, как складывать и вычитать тройки чисел. Однако долгое время он зацикливался на проблеме умножения и деления. Он не мог понять, как вычислить частное координат двух точек пространства. Фактически, Фердинанд Георг Фробениус позже доказал в 1877 году, что для того, чтобы тело алгебры над действительными числами было конечномерным и ассоциативным, оно не может быть трехмерным, и существует только три таких тела алгебры: (комплексные числа) и (кватернионы ), которые имеют размерность 1, 2 и 4 соответственно. ${\displaystyle \mathbb {R,C} }$ ${\displaystyle \mathbb {H} }$

Великий прорыв в области кватернионов наконец произошел в понедельник 16 октября 1843 года в Дублине , когда Гамильтон направлялся в Королевскую ирландскую академию , чтобы председательствовать на заседании совета. Пока он шел со своей женой по тропинке Королевского канала , в его голове формировались концепции, лежащие в основе кватернионов. Когда ответ осенил его, Гамильтон не смог устоять перед желанием вырезать формулу для кватернионов:

$${\displaystyle \mathbf {i} ^{2}=\mathbf {j} ^{2}=\mathbf {k} ^{2}=\mathbf {i\,j\,k} =-1}$$

в камень Брумского моста , когда он остановился на нем. Хотя с тех пор резьба исчезла, с 1989 года проводится ежегодное паломничество под названием « Прогулка Гамильтона» для ученых и математиков, которые идут от обсерватории Дансинк к мосту через Королевский канал в память об открытии Гамильтона.

На следующий день Гамильтон написал письмо своему другу и коллеге-математику Джону Т. Грейвсу , описывая ход мыслей, которые привели к его открытию. Это письмо было позже опубликовано в письме в Лондонский, Эдинбургский и Дублинский философский журнал и журнал науки ; ^[13] Гамильтон утверждает:

И тут меня осенила мысль, что надо допустить в каком-то смысле четвертое измерение пространства для вычислений с тройками... Электрическая цепь как будто замкнулась, и вспыхнула искра. ^[13]

Гамильтон назвал четверку с этими правилами умножения кватернионом и посвятил большую часть оставшейся жизни их изучению и обучению. Подход Гамильтона более геометрический , чем современный подход, который подчеркивает алгебраические свойства кватернионов. Он основал школу «кватернионов» и в нескольких книгах пытался популяризировать кватернионы. Последняя и самая длинная из его книг « Элементы кватернионов » ^[14] имела длину 800 страниц; он был отредактирован его сыном и опубликован вскоре после его смерти.

После смерти Гамильтона шотландский физик-математик Питер Тейт стал главным сторонником кватернионов. В то время кватернионы были обязательной темой экзамена в Дублине. Темы физики и геометрии, которые теперь описывались с помощью векторов, такие как кинематика в пространстве и уравнения Максвелла , полностью описывались с помощью кватернионов. Существовала даже профессиональная исследовательская ассоциация Quaternion Society , занимавшаяся изучением кватернионов и других гиперкомплексных систем счисления.

С середины 1880-х годов кватернионы начали вытесняться векторным анализом , который был разработан Джозайей Уиллардом Гиббсом , Оливером Хевисайдом и Германом фон Гельмгольцем . Векторный анализ описывал те же явления, что и кватернионы, поэтому некоторые идеи и терминологию он обильно заимствовал из литературы по кватернионам. Однако векторный анализ был концептуально проще и понятнее, и в конечном итоге кватернионам отводилась второстепенная роль в математике и физике . Побочным эффектом этого перехода является то, что работу Гамильтона трудно понять многим современным читателям. Первоначальные определения Гамильтона незнакомы, а его стиль письма был многословным и трудным для понимания.

Однако с конца 20-го века кватернионы возродились, в первую очередь из-за их полезности для описания пространственного вращения . Представления вращений кватернионами более компактны и быстрее вычисляются, чем представления матрицами . Кроме того, в отличие от углов Эйлера, они не подвержены « карданному запиранию ». По этой причине кватернионы используются в компьютерной графике , ^{[15] [16]} компьютерном зрении , робототехнике , ^[17] теории управления , обработке сигналов , управлении ориентацией , физике , биоинформатике , молекулярной динамике , компьютерном моделировании и орбитальной механике . Например, системы управления ориентацией космического корабля обычно управляются в терминах кватернионов. Кватернионы получили еще один импульс от теории чисел из-за их связи с квадратичными формами . ^[18]

Кватернионы в физике

В эссе П.Р. Жирара 1984 года « Группа кватернионов и современная физика» ^[19] обсуждаются некоторые роли кватернионов в физике. В эссе показано, как различные физические ковариационные группы, а именно SO(3) , группа Лоренца, группа общей теории относительности, алгебра Клиффорда SU(2) и конформная группа, могут быть легко связаны с группой кватернионов в современной алгебре . Жирар начал с обсуждения представлений групп и представления некоторых пространственных групп кристаллографии . Он перешел к кинематике движения твердого тела . Затем он использовал комплексные кватернионы ( бикватернионы ) для представления группы Лоренца специальной теории относительности, включая прецессию Томаса . Он процитировал пять авторов, начиная с Людвика Зильберштейна , который использовал потенциальную функцию одной кватернионной переменной для выражения уравнений Максвелла в одном дифференциальном уравнении . Что касается общей теории относительности, он выразил вектор Рунге-Ленца . Он упомянул бикватернионы Клиффорда ( сплит-бикватернионы ) как пример алгебры Клиффорда. Наконец, ссылаясь на обратную величину бикватерниона, Жирар описал конформные отображения пространства -времени . Среди пятидесяти ссылок Жирар включил Александра Макфарлейна и его «Бюллетень Общества кватернионов » . В 1999 году он показал, как уравнения общей теории относительности Эйнштейна могут быть сформулированы в рамках алгебры Клиффорда, напрямую связанной с кватернионами. ^[20]

Открытие 1924 года о том, что в квантовой механике спин электрона и других частиц материи (известных как спиноры ) можно описать с помощью кватернионов (в форме знаменитых спиновых матриц Паули), усилило их интерес; кватернионы помогли понять, как можно отличить вращение электронов на 360° от вращения на 720° (« трюк с тарелкой »). ^{[21] [22]} По состоянию на 2018 год их использование не обогнало группы ротации . ^{[а][обновлять]}

Определение

Кватернион — это выражение формы

$${\displaystyle a+b\,\mathbf {i} +c\,\mathbf {j} +d\,\mathbf {k} \ ,}$$

где a , b , c , d — действительные числа, а i , j , k — символы , которые можно интерпретировать как единичные векторы, указывающие вдоль трех пространственных осей. На практике, если один из a , b , c , d равен 0, соответствующий член опускается; если a , b , c , d все равны нулю, кватернион является нулевым кватернионом , обозначаемым 0; если один из b , c , d равен 1, соответствующий термин записывается просто i , j или k .

Гамильтон описывает кватернион как состоящий из скалярной части и векторной части. Кватернион называется векторной частью (иногда мнимой частью ) q , а a — скалярной частью (иногда вещественной частью ) q . Кватернион, равный своей действительной части (то есть его векторная часть равна нулю), называется скалярным или действительным кватернионом и отождествляется с соответствующим действительным числом. То есть действительные числа встроены в кватернионы. (Точнее, поле действительных чисел изоморфно подмножеству кватернионов. Поле комплексных чисел также изоморфно трем подмножествам кватернионов.) ^[23] Кватернион, равный своей векторной части, называется векторным кватернионом . ${\displaystyle q=a+b\,\mathbf {i} +c\,\mathbf {j} +d\,\mathbf {k} }$ ${\displaystyle b\,\mathbf {i} +c\,\mathbf {j} +d\,\mathbf {k} }$

Набор кватернионов представляет собой 4-мерное векторное пространство над действительными числами с базисом путем покомпонентного сложения ${\displaystyle \left\{1,\mathbf {i} ,\mathbf {j} ,\mathbf {k} \right\}}$

$${\displaystyle {\begin{aligned}&(a_{1}+b_{1}\,\mathbf {i} +c_{1}\,\mathbf {j} +d_{1}\,\mathbf {k} )+(a_{2}+b_{2}\,\mathbf {i} +c_{2}\,\mathbf {j} +d_{2}\,\mathbf {k} )\\[3mu]&\qquad =(a_{1}+a_{2})+(b_{1}+b_{2})\,\mathbf {i} +(c_{1}+c_{2})\,\mathbf {j} +(d_{1}+d_{2})\,\mathbf {k} ,\end{aligned}}}$$

и покомпонентное скалярное умножение

$${\displaystyle \lambda (a+b\,\mathbf {i} +c\,\mathbf {j} +d\,\mathbf {k} )=\lambda a+(\lambda b)\,\mathbf {i} +(\lambda c)\,\mathbf {j} +(\lambda d)\,\mathbf {k} .}$$

Мультипликативная групповая структура, называемая произведением Гамильтона и обозначаемая сопоставлением, может быть определена на кватернионах следующим образом:

• Реальный кватернион 1 является единичным элементом .
• Реальные кватернионы коммутируют со всеми другими кватернионами, то есть aq = qa для каждого кватерниона q и каждого реального кватерниона a . В алгебраической терминологии это означает, что поле действительных кватернионов является центром этой алгебры кватернионов.
• Произведение сначала задается для базисных элементов (см. следующий подраздел), а затем распространяется на все кватернионы с использованием свойства дистрибутивности и свойства центра действительных кватернионов. Произведение Гамильтона не коммутативно , но ассоциативно , поэтому кватернионы образуют ассоциативную алгебру над действительными числами.
• Кроме того, каждый ненулевой кватернион имеет обратный по отношению к гамильтоновому произведению:
  $${\displaystyle (a+b\,\mathbf {i} +c\,\mathbf {j} +d\,\mathbf {k} )^{-1}={\frac {1}{a^{2}+b^{2}+c^{2}+d^{2}}}\,(a-b\,\mathbf {i} -c\,\mathbf {j} -d\,\mathbf {k} ).}$$

Таким образом, кватернионы образуют алгебру с делением.

Умножение базисных элементов

Умножение на 1 базовых элементов i , j и k определяется тем фактом, что 1 является мультипликативным тождеством , то есть

$${\displaystyle \mathbf {i} \,1=1\,\mathbf {i} =\mathbf {i} ,\qquad \mathbf {j} \,1=1\,\mathbf {j} =\mathbf {j} ,\qquad \mathbf {k} \,1=1\,\mathbf {k} =\mathbf {k} \,.}$$

Произведения других базисных элементов

$${\displaystyle {\begin{aligned}\mathbf {i} ^{2}&=\mathbf {j} ^{2}=\mathbf {k} ^{2}=-1,\\[5mu]\mathbf {i\,j} &=-\mathbf {j\,i} =\mathbf {k} ,\qquad \mathbf {j\,k} =-\mathbf {k\,j} =\mathbf {i} ,\qquad \mathbf {k\,i} =-\mathbf {i\,k} =\mathbf {j} .\end{aligned}}}$$

Объединив эти правила,

$${\displaystyle {\begin{aligned}\mathbf {i\,j\,k} &=-1.\end{aligned}}}$$

Центр

Центром некоммутативного кольца является подкольцо элементов c такое, что cx = xc для каждого x . Центр алгебры кватернионов — это подполе вещественных кватернионов. Фактически, частью определения является принадлежность реальных кватернионов центру. Обратно, если q = a + b i + c j + d k принадлежит центру, то

$${\displaystyle 0=\mathbf {i} \,q-q\,\mathbf {i} =2c\,\mathbf {ij} +2d\,\mathbf {ik} =2c\,\mathbf {k} -2d\,\mathbf {j} \,,}$$

и с знак равно d знак равно 0 . Аналогичное вычисление с j вместо i показывает, что также имеет место b = 0 . Таким образом, q = a — действительный кватернион.

Кватернионы образуют алгебру с делением. Это означает, что некоммутативность умножения — единственное свойство, отличающее кватернионы от поля. Эта некоммутативность имеет некоторые неожиданные последствия, в том числе то, что полиномиальное уравнение над кватернионами может иметь более различные решения, чем степень полинома. Например, уравнение z 2 ⁺ 1 = 0 имеет бесконечно много решений кватернионов, которыми являются кватернионы z = b i + c j + d k такие, что b ² + c ² + d ² = 1 . Таким образом, эти «корни из –1» образуют единичную сферу в трехмерном пространстве векторных кватернионов.

Продукт Гамильтона

Для двух элементов a ₁ + b ₁ i + c ₁ j + d ₁ k и a ₂ + b ₂ i + c ₂ j + d ₂ k их произведение называется гамильтоновым произведением ( a ₁ + b ₁ i + c ₁ j + d ₁ k ) ( a ₂ + b ₂ i + c ₂ j + d ₂ k ), определяется произведениями базисных элементов и распределительным законом . Распределительный закон позволяет разложить продукт так, чтобы он представлял собой сумму произведений базисных элементов. Это дает следующее выражение:

$${\displaystyle {\begin{alignedat}{4}&a_{1}a_{2}&&+a_{1}b_{2}\mathbf {i} &&+a_{1}c_{2}\mathbf {j} &&+a_{1}d_{2}\mathbf {k} \\{}+{}&b_{1}a_{2}\mathbf {i} &&+b_{1}b_{2}\mathbf {i} ^{2}&&+b_{1}c_{2}\mathbf {ij} &&+b_{1}d_{2}\mathbf {ik} \\{}+{}&c_{1}a_{2}\mathbf {j} &&+c_{1}b_{2}\mathbf {ji} &&+c_{1}c_{2}\mathbf {j} ^{2}&&+c_{1}d_{2}\mathbf {jk} \\{}+{}&d_{1}a_{2}\mathbf {k} &&+d_{1}b_{2}\mathbf {ki} &&+d_{1}c_{2}\mathbf {kj} &&+d_{1}d_{2}\mathbf {k} ^{2}\end{alignedat}}}$$

Теперь базовые элементы можно умножить, используя приведенные выше правила, и получить: ^[8]

$${\displaystyle {\begin{alignedat}{4}&a_{1}a_{2}&&-b_{1}b_{2}&&-c_{1}c_{2}&&-d_{1}d_{2}\\{}+{}(&a_{1}b_{2}&&+b_{1}a_{2}&&+c_{1}d_{2}&&-d_{1}c_{2})\mathbf {i} \\{}+{}(&a_{1}c_{2}&&-b_{1}d_{2}&&+c_{1}a_{2}&&+d_{1}b_{2})\mathbf {j} \\{}+{}(&a_{1}d_{2}&&+b_{1}c_{2}&&-c_{1}b_{2}&&+d_{1}a_{2})\mathbf {k} \end{alignedat}}}$$

Произведение двух кватернионов вращения ^[24] будет эквивалентно вращению a ₂ + b ₂ i + c ₂ j + d ₂ k , за которым следует вращение a ₁ + b ₁ i + c ₁ j + d ₁ k .

Скалярные и векторные части

Кватернион вида a + 0 i + 0 j + 0 k , где a — действительное число, называется скалярным , а кватернион вида 0 + b i + c j + d k , где b , c , и d — действительные числа, и хотя бы одно из b , c или d не равно нулю, называется векторным кватернионом . Если a + b i + c j + d k — любой кватернион, то a называется его скалярной частью , а b i + c j + d k называется его векторной частью . Несмотря на то, что каждый кватернион можно рассматривать как вектор в четырехмерном векторном пространстве, векторную часть принято называть векторами в трехмерном пространстве. Согласно этому соглашению, вектор — это то же самое, что элемент векторного пространства ^[b] ${\displaystyle \mathbb {R} ^{3}.}$

Гамильтон также называл векторные кватернионы правыми кватернионами ^{[26] [27]} и действительные числа (рассматриваемые как кватернионы с нулевой векторной частью) скалярными кватернионами .

Если кватернион разделен на скалярную часть и векторную часть, то есть

$${\displaystyle \mathbf {q} =(r,\ {\vec {v}}),~~\mathbf {q} \in \mathbb {H} ,~~r\in \mathbb {R} ,~~{\vec {v}}\in \mathbb {R} ^{3},}$$

тогда формулы сложения, умножения и обратного мультипликативного преобразования будут иметь вид

$${\displaystyle {\begin{aligned}(r_{1},\ {\vec {v}}_{1})+(r_{2},\ {\vec {v}}_{2})&=(r_{1}+r_{2},\ {\vec {v}}_{1}+{\vec {v}}_{2})\,,\\[5mu](r_{1},\ {\vec {v}}_{1})(r_{2},\ {\vec {v}}_{2})&=(r_{1}r_{2}-{\vec {v}}_{1}\cdot {\vec {v}}_{2},\ r_{1}{\vec {v}}_{2}+r_{2}{\vec {v}}_{1}+{\vec {v}}_{1}\times {\vec {v}}_{2})\,,\\[5mu](r,{\vec {v}})^{-1}&=\left({\frac {r}{r^{2}+{\vec {v}}\cdot {\vec {v}}}},{\frac {-{\vec {v}}}{r^{2}+{\vec {v}}\cdot {\vec {v}}}}\right)\,,\end{aligned}}}$$

где " " и " " обозначают соответственно скалярное произведение и векторное произведение . ${\displaystyle \cdot }$ ${\displaystyle \times }$

Конъюгация, норма и реципрокное

Сопряжение кватернионов аналогично сопряжению комплексных чисел и транспозиции (также известной как обращение) элементов алгебр Клиффорда. Чтобы определить это, пусть это будет кватернион. Сопряженным с q является кватернион . Он обозначается q ^∗ , qt ^, или q . ^[8] Сопряжение — это инволюция , то есть оно является обратным самому себе , поэтому сопряжение элемента дважды возвращает исходный элемент. Сопряженное произведение двух кватернионов — это произведение сопряженных в обратном порядке . То есть, если p и q — кватернионы, то ( pq ) ^∗ = q ^∗ p ^∗ , а не p ^∗ q ^∗ . ${\displaystyle q=a+b\,\mathbf {i} +c\,\mathbf {j} +d\,\mathbf {k} }$ ${\displaystyle q^{*}=a-b\,\mathbf {i} -c\,\mathbf {j} -d\,\mathbf {k} }$ ${\displaystyle {\tilde {q}}}$

Сопряжение кватерниона, в отличие от сложной ситуации, может быть выражено умножением и сложением кватернионов:

$${\displaystyle q^{*}=-{\frac {1}{2}}(q+\,\mathbf {i} \,q\,\mathbf {i} +\,\mathbf {j} \,q\,\mathbf {j} +\,\mathbf {k} \,q\,\mathbf {k} ).}$$

Сопряжение можно использовать для извлечения скалярной и векторной частей кватерниона. Скалярная часть p равна1/2( p + p ^∗ ) , а векторная часть p равна1/2( п - п ^* ) .

Квадратный корень из произведения кватерниона на сопряженный ему называется его нормой и обозначается ‖q‖ (Гамильтон называл эту величину тензором q , но это противоречит современному значению слова « тензор » ) . В формулах это выражается следующим образом:

$${\displaystyle \lVert q\rVert ={\sqrt {\,qq^{*}~}}={\sqrt {\,q^{*}q~}}={\sqrt {\,a^{2}+b^{2}+c^{2}+d^{2}~}}}$$

Это всегда неотрицательное действительное число, и оно совпадает с евклидовой нормой в векторном пространстве . Умножение кватерниона на действительное число масштабирует его норму на абсолютное значение числа. То есть, если α действительно, то ${\displaystyle \mathbb {H} }$ ${\displaystyle \mathbb {R} ^{4}}$

$${\displaystyle \lVert \alpha q\rVert =\left|\alpha \right|\,\lVert q\rVert ~.}$$

Это частный случай того факта, что норма мультипликативна , то есть

$${\displaystyle \lVert pq\rVert =\lVert p\rVert \,\lVert q\rVert }$$

для любых двух кватернионов p и q . Мультипликативность является следствием формулы сопряжения произведения. Альтернативно это следует из тождества

$${\displaystyle \det {\begin{pmatrix}a+ib&id+c\\id-c&a-ib\end{pmatrix}}=a^{2}+b^{2}+c^{2}+d^{2},}$$

(где i обозначает обычную мнимую единицу ) и, следовательно, из мультипликативного свойства определителей квадратных матриц.

Эта норма позволяет определить расстояние d ( p , q ) между p и q как норму их разности:

$${\displaystyle d(p,q)=\lVert p-q\rVert ~.}$$

Это создает метрическое пространство . Сложение и умножение непрерывны относительно соответствующей метрической топологии . Это следует из того же доказательства, что и для действительных чисел, из того факта, что это нормированная алгебра. ${\displaystyle \mathbb {H} }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {H} }$

Единичный кватернион

Единичный кватернион — это кватернион первой нормы. Деление ненулевого кватерниона q на его норму дает единичный кватернион U q , называемый версором q :

$${\displaystyle \mathbf {U} q={\frac {q}{\lVert q\rVert }}.}$$

Каждый ненулевой кватернион имеет уникальное полярное разложение , а нулевой кватернион может быть образован из любого единичного кватерниона. ${\displaystyle q=\lVert q\rVert \cdot \mathbf {U} q}$

Использование сопряжения и нормы позволяет определить обратную величину ненулевого кватерниона. Произведение кватерниона на обратное значение должно равняться 1, а из приведенных выше соображений следует, что произведение и равно 1 (для любого порядка умножения). Таким образом, обратная величина q определяется как ${\displaystyle q}$ ${\displaystyle q^{*}/\left\Vert q\right\|^{2}}$

$${\displaystyle q^{-1}={\frac {q^{*}}{\lVert q\rVert ^{2}}}.}$$

Поскольку умножение некоммутативно, частные величины p q ⁻¹ или q ⁻¹ p   различны (за исключением случаев, когда p и q являются скалярными кратными друг другу или если один из них является скаляром): обозначениеп/днеоднозначен и не должен использоваться.

Алгебраические свойства

Граф Кэли Q8 _. _ Красные стрелки представляют собой умножение справа на i , а зеленые стрелки представляют умножение справа на j .

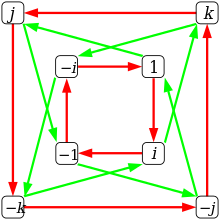
Набор всех кватернионов представляет собой векторное пространство над действительными числами размерности  4. ^[c] Умножение кватернионов ассоциативно и распределяется по сложению векторов, но, за исключением скалярного подмножества, оно не является коммутативным. Следовательно, кватернионы представляют собой некоммутативную ассоциативную алгебру над действительными числами. Несмотря на то, что она содержит копии комплексных чисел, она не является ассоциативной алгеброй комплексных чисел. ${\displaystyle \mathbb {H} }$ ${\displaystyle \mathbb {H} }$ ${\displaystyle \mathbb {H} }$

Поскольку кватернионы можно разделить, они образуют алгебру с делением. Это структура, похожая на поле, за исключением некоммутативности умножения. Конечномерные ассоциативные алгебры с делением над действительными числами встречаются очень редко. Теорема Фробениуса утверждает, что их ровно три: , , и . Норма превращает кватернионы в нормированную алгебру , а нормированные алгебры с делением над действительными числами также очень редки: теорема Гурвица гласит, что их только четыре: , , и (октонионы). Кватернионы также являются примером композиционной алгебры и банаховой алгебры с единицей . ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {H} }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {H} }$ ${\displaystyle \mathbb {O} }$

Трехмерный график Q ₈ . Красные, зеленые и синие стрелки обозначают умножение на i , j и k соответственно. Умножение на отрицательные числа опущено для ясности.

Поскольку произведение любых двух базисных векторов равно плюс или минус другому базисному вектору, набор {±1, ± i , ± j , ± k } образует группу при умножении. Эта неабелева группа называется группой кватернионов и обозначается Q ₈ . ^[28] Вещественное групповое кольцо Q 8 _- это кольцо , которое также является восьмимерным векторным пространством. Оно имеет один базисный вектор для каждого элемента Кватернионы изоморфны фактор - кольцу идеала, порожденного элементами 1 + (-1) , я + (- я ) , j + (- j ) и k + (- k ) . Здесь первый член в каждом из разностей — это один из базисных элементов 1, i , j и k , а второй член — один из базисных элементов −1, — i , — j и — k , а не аддитивные обратные элементы. из 1, i , j и k . ${\displaystyle \mathbb {R} [\mathrm {Q} _{8}]}$ ${\displaystyle \mathbb {R} .}$ ${\displaystyle \mathrm {Q} _{8}.}$ ${\displaystyle \mathbb {R} [\mathrm {Q} _{8}]}$

Кватернионы и трехмерная геометрия

Векторную часть кватерниона можно интерпретировать как координатный вектор , поэтому алгебраические операции над кватернионами отражают геометрию таких операций, как векторная точка и векторные произведения, которые могут быть определены в терминах кватернионов, и это позволяет применять кватернионные методы везде, где возникают пространственные векторы. Полезным применением кватернионов была интерполяция ориентации ключевых кадров в компьютерной графике. ^[15] ${\displaystyle \mathbb {R} ^{3};}$ ${\displaystyle \mathbb {R} ^{3}.}$

В оставшейся части этого раздела i , j и k будут обозначать как три воображаемых ^[29] базисных вектора, так и основу для замены i на − i , j на − j , а k на − k отправляет вектор в его аддитивный инверсный , поэтому аддитивный инверсный вектор совпадает с его сопряженным кватернионом. По этой причине сопряжение иногда называют пространственной инверсией . ${\displaystyle \mathbb {H} }$ ${\displaystyle \mathbb {R} ^{3}.}$

Для двух векторных кватернионов p = b ₁ i + c ₁ j + d ₁ k и q = b ₂ i + c ₂ j + d ₂ k их скалярное произведение по аналогии с векторами в ${\displaystyle \mathbb {R} ^{3},}$

$${\displaystyle p\cdot q=b_{1}b_{2}+c_{1}c_{2}+d_{1}d_{2}~.}$$

Это также можно выразить без компонентов как

$${\displaystyle p\cdot q=\textstyle {\frac {1}{2}}(p^{*}q+q^{*}p)=\textstyle {\frac {1}{2}}(pq^{*}+qp^{*}).}$$

Это равно скалярным частям произведений pq ^∗ , qp ^∗ , p ^∗ q и q ^∗ p . Обратите внимание, что их векторные части различны.

Перекрестное произведение p и q относительно ориентации , определяемой упорядоченным базисом i , j и k , равно

$${\displaystyle p\times q=(c_{1}d_{2}-d_{1}c_{2})\mathbf {i} +(d_{1}b_{2}-b_{1}d_{2})\mathbf {j} +(b_{1}c_{2}-c_{1}b_{2})\mathbf {k} \,.}$$

(Напомним, что ориентация необходима для определения знака.) Это равно векторной части произведения pq (как кватернионы), а также векторной части − q ^∗ p ^∗ . Также имеется формула

$${\displaystyle p\times q=\textstyle {\tfrac {1}{2}}(pq-qp).}$$

Для коммутатора [ p , q ] = pq − qp двух векторных кватернионов получаем

$${\displaystyle [p,q]=2p\times q.}$$

В общем, пусть p и q — кватернионы, и пишут

$${\displaystyle {\begin{aligned}p&=p_{\text{s}}+p_{\text{v}},\\[5mu]q&=q_{\text{s}}+q_{\text{v}},\end{aligned}}}$$

где ps и qs — _{скалярные} части, а _{pv и} qv _— векторные части p и q . Тогда у нас есть формула

$${\displaystyle pq=(pq)_{\text{s}}+(pq)_{\text{v}}=(p_{\text{s}}q_{\text{s}}-p_{\text{v}}\cdot q_{\text{v}})+(p_{\text{s}}q_{\text{v}}+q_{\text{s}}p_{\text{v}}+p_{\text{v}}\times q_{\text{v}}).}$$

Это показывает, что некоммутативность умножения кватернионов возникает из-за умножения векторных кватернионов. Это также показывает, что два кватерниона коммутируют тогда и только тогда, когда их векторные части коллинеарны. Гамильтон ^[30] показал, что это произведение вычисляет третью вершину сферического треугольника по двум заданным вершинам и связанным с ними длинам дуг, что также является алгеброй точек в эллиптической геометрии .

Единичные кватернионы можно отождествить с вращением внутрь, и Гамильтон назвал их версорами . ^[30] Также см. «Кватернионы и пространственное вращение» для получения дополнительной информации о моделировании трехмерных вращений с использованием кватернионов. ${\displaystyle \mathbb {R} ^{3}}$

См. Hanson (2005) ^[31] для визуализации кватернионов.

Матричные представления

Кватернионы могут быть представлены в виде матриц так же , как комплексные числа. Существует по крайней мере два способа представления кватернионов в виде матриц таким образом, чтобы сложение и умножение кватернионов соответствовало сложению и умножению матриц . Один из них — использовать комплексные матрицы 2 × 2, а другой — действительные матрицы 4 × 4. В каждом случае данное представление является одним из семейства линейно связанных представлений. В терминологии абстрактной алгебры это инъективные гомоморфизмы из в кольца матриц M(2, C ) и M(4, R ) соответственно. ${\displaystyle \mathbb {H} }$

Кватернион a + b i + c j + d k можно представить с помощью комплексной матрицы 2 × 2 как

${\displaystyle \left[{\begin{array}{rr}a+bi&c+di\\-c+di&a-bi\end{array}}\right].}$

Это представление имеет следующие свойства:

• Ограничение любых двух из b , c и d нулем дает представление комплексных чисел. Например, установка c = d = 0 создает диагональное комплексное матричное представление комплексных чисел, а установка b = d = 0 создает вещественное матричное представление.
• Норма кватерниона (квадратный корень из произведения на сопряженное ему число, как и в случае с комплексными числами) — это квадратный корень из определителя соответствующей матрицы. ^[32]
• Сопряжение кватерниона соответствует сопряженному транспонированию матрицы.
• Путем ограничения это представление дает изоморфизм между подгруппой единичных кватернионов и их образом SU(2) . Топологически единичные кватернионы представляют собой 3-сферу, поэтому основное пространство SU (2) также является 3-сферой. Группа SU(2) важна для описания спина в квантовой механике; см. матрицы Паули .
• Существует сильная связь между единицами кватернионов и матрицами Паули. Получите восемь единичных матриц кватернионов, взяв a , b , c и d , установите три из них в ноль, а четвертый в 1 или -1. Умножение любых двух матриц Паули всегда дает единичную матрицу кватернионов, все они, кроме -1. Получаем −1 через i ² = j ² = k ² = ijk = −1 ; например, последнее равенство
  $${\displaystyle ijk=\sigma _{1}\sigma _{2}\sigma _{3}\sigma _{1}\sigma _{2}\sigma _{3}=-1.}$$

Используя вещественные матрицы 4 × 4, тот же кватернион можно записать как

$${\displaystyle {\begin{aligned}\left[{\begin{array}{rrrr}a&-b&-c&-d\\b&a&-d&c\\c&d&a&-b\\d&-c&b&a\end{array}}\right]&=a\left[{\begin{array}{rrrr}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{array}}\right]+b\left[{\begin{array}{rrrr}0&-1&0&0\\1&0&0&0\\0&0&0&-1\\0&0&1&0\end{array}}\right]\\[10mu]&\qquad +c\left[{\begin{array}{rrrr}0&0&-1&0\\0&0&0&1\\1&0&0&0\\0&-1&0&0\end{array}}\right]+d\left[{\begin{array}{rrrr}0&0&0&-1\\0&0&-1&0\\0&1&0&0\\1&0&0&0\end{array}}\right].\end{aligned}}}$$

Однако представление кватернионов в M(4, R ) не является единственным. Например, тот же кватернион можно представить как

$${\displaystyle {\begin{aligned}\left[{\begin{array}{rrrr}a&d&-b&-c\\-d&a&c&-b\\b&-c&a&-d\\c&b&d&a\end{array}}\right]&=a\left[{\begin{array}{rrrr}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{array}}\right]+b\left[{\begin{array}{rrrr}0&0&-1&0\\0&0&0&-1\\1&0&0&0\\0&1&0&0\end{array}}\right]\\[10mu]&\qquad +c\left[{\begin{array}{rrrr}0&0&0&-1\\0&0&1&0\\0&-1&0&0\\1&0&0&0\end{array}}\right]+d\left[{\begin{array}{rrrr}0&1&0&0\\-1&0&0&0\\0&0&0&-1\\0&0&1&0\end{array}}\right].\end{aligned}}}$$

Существует 48 различных матричных представлений этой формы, в которых одна из матриц представляет скалярную часть, а все три другие кососимметричны. Точнее, существует 48 наборов четверок матриц с этими ограничениями симметрии, так что функция, передающая 1, i , j и k матрицам в четверке, является гомоморфизмом, то есть она переводит суммы и произведения кватернионов в суммы и произведения матриц. ^[33] В этом представлении сопряжение кватерниона соответствует транспонированию матрицы . Четвертая степень нормы кватерниона является определителем соответствующей матрицы. Как и в случае с комплексным представлением 2 × 2, приведенным выше, комплексные числа снова можно получить, соответствующим образом ограничив коэффициенты; например, как блочные диагональные матрицы с двумя блоками 2 × 2, установив c = d = 0 .

Каждое матричное представление кватернионов 4×4 соответствует таблице умножения единичных кватернионов. Например, последнее приведенное выше матричное представление соответствует таблице умножения.

который изоморфен — через — ${\displaystyle \{a\mapsto 1,b\mapsto i,c\mapsto j,d\mapsto k\}}$

Ограничивая любую такую ​​таблицу умножения таким образом, чтобы она имела идентичность в первой строке и столбце и чтобы знаки заголовков строк были противоположны знакам заголовков столбцов, тогда есть 3 возможных варианта для второго столбца (игнорируя знак), 2 возможных варианта варианты выбора для третьего столбца (знак игнорирования) и 1 возможный вариант выбора для четвертого столбца (знак игнорирования); это дает 6 возможностей. Затем второй столбец можно выбрать как положительный или отрицательный, третий столбец можно выбрать как положительный или отрицательный, а четвертый столбец можно выбрать как положительный или отрицательный, что дает 8 возможностей для знака. Умножение возможностей положения букв и их знаков дает 48. Затем замена 1 на a , i на b , j на c и k на d и удаление заголовков строк и столбцов дает матричное представление a + b i + c. j + d k .

Теорема Лагранжа о четырех квадратах

Кватернионы также используются в одном из доказательств теоремы Лагранжа о четырёх квадратах в теории чисел , которая утверждает, что каждое неотрицательное целое число является суммой четырёх целых квадратов. Теорема Лагранжа о четырех квадратах не только сама по себе является элегантной теоремой, но и имеет полезные применения в областях математики за пределами теории чисел, таких как комбинаторная теория замысла. Доказательство на основе кватернионов использует кватернионы Гурвица — подкольцо кольца всех кватернионов, для которого существует аналог алгоритма Евклида .

Кватернионы как пары комплексных чисел

Кватернионы можно представить как пары комплексных чисел. С этой точки зрения кватернионы являются результатом применения конструкции Кэли-Диксона к комплексным числам. Это обобщение конструкции комплексных чисел как пар действительных чисел.

Пусть — двумерное векторное пространство над комплексными числами. Выберите базис, состоящий из двух элементов 1 и j . Вектор in можно записать через базисные элементы 1 и j как ${\displaystyle \mathbb {C} ^{2}}$ ${\displaystyle \mathbb {C} ^{2}}$

$${\displaystyle (a+bi)1+(c+di)\mathbf {j} \,.}$$

Если мы определим j ² = −1 и i j = − j i , то мы сможем умножить два вектора, используя закон распределения. Использование k в качестве сокращенного обозначения произведения i j приводит к тем же правилам умножения, что и обычные кватернионы. Следовательно, приведенный выше вектор комплексных чисел соответствует кватерниону a + bi + c j + d k . Если мы запишем элементы как упорядоченные пары, а кватернионы как четверки, то соответствие будет таким: ${\displaystyle \mathbb {C} ^{2}}$

$${\displaystyle (a+bi,\ c+di)\leftrightarrow (a,b,c,d).}$$

Квадратные корни

Квадратные корни из −1

В комплексных числах есть ровно два числа, i и − i , которые в квадрате дают −1. В существует бесконечно много квадратных корней из минус единицы: кватернионное решение для квадратного корня из −1 представляет собой единичную сферу в . Чтобы убедиться в этом, пусть q = a + b i + c j + d k будет кватернионом и предположим, что его квадрат равен −1. С точки зрения a , b , c и d это означает ${\displaystyle \mathbb {C} ,}$ ${\displaystyle \mathbb {H} }$ ${\displaystyle \mathbb {R} ^{3}.}$

$${\displaystyle {\begin{aligned}a^{2}-b^{2}-c^{2}-d^{2}&=-1,{\vphantom {x^{|}}}\\[3mu]2ab&=0,\\[3mu]2ac&=0,\\[3mu]2ad&=0.\end{aligned}}}$$

Чтобы удовлетворить последним трем уравнениям, либо a = 0 , либо все b , c и d равны 0. Последнее невозможно, поскольку a — действительное число, а из первого уравнения следует, что a ² = −1 . Следовательно, a = 0 и b ² + c ² + d ² = 1 . Другими словами: кватернион имеет квадратуру −1 тогда и только тогда, когда он является векторным кватернионом с нормой 1. По определению набор всех таких векторов образует единичную сферу.

Только отрицательные вещественные кватернионы имеют бесконечно много квадратных корней. У всех остальных их всего два (или один в случае 0). ^{[ нужна ссылка ] [d]}

Как объединение сложных плоскостей

Каждая антиподальная пара квадратных корней из −1 создает отдельную копию комплексных чисел внутри кватернионов. Если q ² = −1 , то копия является образом функции

$${\displaystyle a+bi\mapsto a+bq\,.}$$

Это инъективный гомоморфизм колец из в , который определяет изоморфизм поля из на его образ . Образы вложений, соответствующие q и − q , идентичны. ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {H} ,}$ ${\displaystyle \mathbb {C} }$

Каждый невещественный кватернион порождает подалгебру кватернионов , которая изоморфна и, таким образом, является плоским подпространством записи q как сумма его скалярной части и векторной части: ${\displaystyle \mathbb {C} ,}$ ${\displaystyle \mathbb {H} \colon }$

$${\displaystyle q=q_{s}+{\vec {q}}_{v}.}$$

Разложим векторную часть как произведение ее нормы и ее версора :

$${\displaystyle q=q_{s}+\lVert {\vec {q}}_{v}\rVert \cdot \mathbf {U} {\vec {q}}_{v}=q_{s}+\|{\vec {q}}_{v}\|\,{\frac {{\vec {q}}_{v}}{\|{\vec {q}}_{v}\|}}.}$$

(Это не то же самое, что .) Версор векторной части q , , является правым версором с –1 в качестве его квадрата. Непосредственная проверка показывает, что ${\displaystyle q_{s}+\lVert q\rVert \cdot \mathbf {U} q}$ ${\displaystyle \mathbf {U} {\vec {q}}_{v}}$

$${\displaystyle a+bi\mapsto a+b\mathbf {U} {\vec {q}}_{v}}$$

гомоморфизмалгебрq ${\displaystyle \mathbb {C} }$ ${\displaystyle q_{s}+\lVert {\vec {q}}_{v}\rVert i}$

Как и объединение образов всех этих гомоморфизмов, кватернионы можно рассматривать как пучок плоскостей, пересекающихся на вещественной прямой . Каждая из этих комплексных плоскостей содержит ровно одну пару противоположных точек сферы квадратных корней из минус единицы. ${\displaystyle \mathbb {H} }$

Коммутативные подкольца

Отношения кватернионов друг к другу внутри комплексных подплоскостей также могут быть идентифицированы и выражены в терминах коммутативных подколец . В частности, поскольку два кватерниона p и q коммутируют (т. е. pq = qp ), только если они лежат в одной и той же комплексной подплоскости , профиль как объединения комплексных плоскостей возникает, когда кто-то пытается найти все коммутативные подкольца кольца кватернионов . ${\displaystyle \mathbb {H} }$ ${\displaystyle \mathbb {H} }$ ${\displaystyle \mathbb {H} }$

Квадратные корни произвольных кватернионов

Любой кватернион (представленный здесь в скалярно-векторном представлении) имеет хотя бы один квадратный корень, который решает уравнение . Рассмотрение скалярной и векторной частей в этом уравнении по отдельности дает два уравнения, которые при решении дают решения ${\displaystyle \mathbf {q} =(r,\,{\vec {v}})}$ ${\displaystyle {\sqrt {\mathbf {q} }}=(x,\,{\vec {y}})}$ ${\displaystyle {\sqrt {\mathbf {q} }}^{2}=(x,\,{\vec {y}})^{2}=\mathbf {q} }$

$${\displaystyle {\sqrt {\mathbf {q} }}={\sqrt {(r,\,{\vec {v}}\,)}}=\pm \left({\sqrt {\frac {\|\mathbf {q} \|+r}{2}}},\ {\frac {\vec {v}}{\|{\vec {v}}\|}}{\sqrt {\frac {\|\mathbf {q} \|-r}{2}}}\right),}$$

где норма и норма . Для любого скалярного кватерниона это уравнение дает правильные квадратные корни, если интерпретируется как произвольный единичный вектор. ${\textstyle \|{\vec {v}}\|={\sqrt {{\vec {v}}\cdot {\vec {v}}}}={\sqrt {-{\vec {v}}^{2}}}}$ ${\displaystyle {\vec {v}}}$ ${\textstyle \|\mathbf {q} \|={\sqrt {\mathbf {q} ^{*}\mathbf {q} }}=r^{2}+\|{\vec {v}}\|^{2}}$ ${\displaystyle \mathbf {q} }$ ${\displaystyle \mathbf {q} }$ ${\textstyle {\frac {\vec {v}}{\|{\vec {v}}\|}}}$

Следовательно, ненулевые, нескалярные кватернионы или положительные скалярные кватернионы имеют ровно два корня, в то время как 0 имеет ровно один корень (0), а отрицательные скалярные кватернионы имеют бесконечно много корней, которые представляют собой векторные кватернионы, расположенные на , т. е. там, где скалярная часть равна нулю, а векторная часть расположена на 2-сфере радиусом . ${\displaystyle \{0\}\times S^{2}({\sqrt {-r}})}$ ${\displaystyle {\sqrt {-r}}}$

Функции переменной кватерниона

Наборы Джулии и наборы Мандельброта можно расширить до кватернионов, но для визуальной визуализации в трех измерениях они должны использовать поперечные сечения. Этот набор Джулии имеет поперечное сечение в плоскости xy .

Подобно функциям комплексной переменной , функции кватернионной переменной предлагают полезные физические модели. Например, первоначальные электрические и магнитные поля, описанные Максвеллом, были функциями кватернионной переменной. Примеры других функций включают расширение множества Мандельброта и множеств Жюлиа в 4-мерное пространство. ^[37]

Экспоненциальные, логарифмические и степенные функции

Учитывая кватернион,

$${\displaystyle q=a+b\mathbf {i} +c\mathbf {j} +d\mathbf {k} =a+\mathbf {v} ,}$$

экспонента вычисляется как ^[38]

$${\displaystyle \exp(q)=\sum _{n=0}^{\infty }{\frac {q^{n}}{n!}}=e^{a}\left(\cos \|\mathbf {v} \|+{\frac {\mathbf {v} }{\|\mathbf {v} \|}}\sin \|\mathbf {v} \|\right),}$$

а логарифм равен ^[38]

$${\displaystyle \ln(q)=\ln \|q\|+{\frac {\mathbf {v} }{\|\mathbf {v} \|}}\arccos {\frac {a}{\|q\|}}.}$$

Отсюда следует, что полярное разложение кватерниона можно записать

$${\displaystyle q=\|q\|e^{{\hat {n}}\varphi }=\|q\|\left(\cos(\varphi )+{\hat {n}}\sin(\varphi )\right),}$$

где угол ^[е] ${\displaystyle \varphi }$

$${\displaystyle a=\|q\|\cos(\varphi )}$$

а единичный вектор определяется как: ${\displaystyle {\hat {n}}}$

$${\displaystyle \mathbf {v} ={\hat {n}}\|\mathbf {v} \|={\hat {n}}\|q\|\sin(\varphi )\,.}$$

Любой единичный кватернион может быть выражен в полярной форме как:

$${\displaystyle q=\exp {({\hat {n}}\varphi )}.}$$

Степень кватерниона, возведенная в произвольную (действительную) степень x , определяется выражением:

$${\displaystyle q^{x}=\|q\|^{x}e^{{\hat {n}}x\varphi }=\|q\|^{x}\left(\cos(x\varphi )+{\hat {n}}\,\sin(x\varphi )\right)~.}$$

Геодезическая норма

Геодезическое расстояние d _g ( p , q ) между единичными кватернионами p и q определяется как: ^[40]

$${\displaystyle d_{\text{g}}(p,q)=\lVert \ln(p^{-1}q)\rVert .}$$

и составляет абсолютную величину половины угла, образованного p и q вдоль большой дуги сферы S ³ . Этот угол также можно вычислить из скалярного произведения кватернионов без логарифма как:

$${\displaystyle \arccos(2(p\cdot q)^{2}-1).}$$

Трехмерные и четырехмерные группы вращения

Слово « сопряжение », помимо значения, данного выше, может также означать преобразование элемента a в r a r ⁻¹ , где r — некоторый ненулевой кватернион. Все элементы, сопряженные с данным элементом (в этом смысле слова сопряженные), имеют одну и ту же действительную часть и одну и ту же норму векторной части. (Таким образом, сопряженное в другом смысле является одним из сопряженных в этом смысле.) ^[41]

Таким образом, мультипликативная группа ненулевых кватернионов действует путем сопряжения на копию, состоящую из кватернионов с вещественной частью, равной нулю. Сопряжение единичным кватернионом (кватернионом по модулю 1) с действительной частью cos( φ ) представляет собой поворот на угол 2 φ , причем осью вращения является направление векторной части. Преимущества кватернионов: ^[42] ${\displaystyle \mathbb {R} ^{3}}$

• Избегание блокировки подвеса , проблемы с такими системами, как углы Эйлера.
• Быстрее и компактнее матриц.
• Несингулярное представление (по сравнению, например, с углами Эйлера).
• Пары единичных кватернионов представляют вращение в 4D- пространстве (см. Вращения в 4-мерном евклидовом пространстве: Алгебра 4D-вращений ).

Набор всех единичных кватернионов ( версоров ) образует 3-сферу S ³ и группу ( группу Ли ) при умножении, дважды покрывающую группу вещественных ортогональных  матриц 3×3 определителя  1, поскольку два единичных кватерниона соответствуют каждому вращению при вышеуказанная переписка. Смотрите трюк с тарелкой . ${\displaystyle {\text{SO}}(3,\mathbb {R} )}$

Образ подгруппы версоров является точечной группой и, наоборот, прообразом точечной группы является подгруппа версоров. Прообраз конечной точечной группы называется тем же именем с префиксом двоичный . Например, прообразом группы икосаэдра является бинарная группа икосаэдра .

Группа версоров изоморфна SU(2) , группе комплексных унитарных матриц размера 2×2 с определителем 1.

Пусть A — набор кватернионов вида a + b i + c j + d k , где a, b, c и d — либо все целые числа , либо все полуцелые числа . Множество A представляет собой кольцо (фактически область ) и решетку и называется кольцом кватернионов Гурвица. В этом кольце 24 единичных кватерниона, и они являются вершинами правильной 24-клетки с символом Шлефли {3,4,3}. Они соответствуют двойному покрытию вращательной группы симметрии правильного тетраэдра . Аналогично, вершины правильной ячейки 600 с символом Шлефли {3,3,5 } можно взять за единичные икосианы , соответствующие двойному покрытию группы вращательной симметрии правильного икосаэдра . Двойное покрытие группы вращательной симметрии правильного октаэдра соответствует кватернионам, представляющим вершины дисфеноидальной 288-ячейки . ^[43]

Кватернионные алгебры

Кватернионы могут быть обобщены на дополнительные алгебры, называемые алгебрами кватернионов . Возьмем F любое поле с характеристикой, отличной от 2, а a и b — элементами F ; четырехмерная унитарная ассоциативная алгебра может быть определена над F с базисом 1, i , j и ij , где i ² = a , j ² = b и ij = - ji (так что (ij) ² = - ab ).

Алгебры кватернионов изоморфны алгебре матриц 2×2 над F или образуют алгебры с делением над F , в зависимости от выбора a и b .

Кватернионы как четная часть Cl 3,0 (R)

Полезность кватернионов для геометрических вычислений можно распространить на другие измерения, определив кватернионы как четную часть алгебры Клиффорда. Это ассоциативная многовекторная алгебра, построенная из фундаментальных базисных элементов σ 1 , σ 2 , σ 3 с использованием правил произведения. ${\displaystyle \operatorname {Cl} _{3,0}^{+}(\mathbb {R} )}$ ${\displaystyle \operatorname {Cl} _{3,0}(\mathbb {R} ).}$

$${\displaystyle \sigma _{1}^{2}=\sigma _{2}^{2}=\sigma _{3}^{2}=1,}$$

$${\displaystyle \sigma _{i}\sigma _{j}=-\sigma _{j}\sigma _{i}\qquad (j\neq i).}$$

Если эти фундаментальные базисные элементы принять за представление векторов в трехмерном пространстве, то окажется, что отражение вектора r в плоскости, перпендикулярной единичному вектору w , можно записать:

$${\displaystyle r^{\prime }=-w\,r\,w.}$$

Два отражения совершают поворот на угол, в два раза превышающий угол между двумя плоскостями отражения, поэтому

$${\displaystyle r^{\prime \prime }=\sigma _{2}\sigma _{1}\,r\,\sigma _{1}\sigma _{2}}$$

соответствует повороту на 180° в плоскости, содержащей σ ₁ и σ ₂ . Это очень похоже на соответствующую формулу кватернионов:

$${\displaystyle r^{\prime \prime }=-\mathbf {k} \,r\,\mathbf {k} .}$$

Действительно , две структуры и изоморфны . Одной из естественных идентификаций является ${\displaystyle \operatorname {Cl} _{3,0}^{+}(\mathbb {R} )}$ ${\displaystyle \mathbb {H} }$

$${\displaystyle 1\mapsto 1\,,\quad \mathbf {k} \mapsto \sigma _{2}\sigma _{1}\,,\quad \mathbf {i} \mapsto \sigma _{3}\sigma _{2}\,,\quad \mathbf {j} \mapsto \sigma _{1}\sigma _{3}\,,}$$

и несложно убедиться, что при этом сохраняются гамильтоновы соотношения

$${\displaystyle \mathbf {i} ^{2}=\mathbf {j} ^{2}=\mathbf {k} ^{2}=\mathbf {i\,j\,k} =-1~.}$$

В этой картине так называемые «векторные кватернионы» (то есть чисто мнимые кватернионы) соответствуют не векторам, а бивекторам – величинам и ориентациям, связанным с конкретными двумерными  плоскостями , а не с одномерными  направлениями . Отношение к комплексным числам также становится более ясным: в 2D с двумя векторными направлениями σ ₁ и σ ₂ существует только один бивекторный базисный элемент σ ₁ σ ₂ , то есть только один мнимый. Но в 3D с тремя векторными направлениями существует три базисных элемента бивекторов σ ₁ σ ₂ , σ ₂ σ ₃ , σ ₃ σ ₁ , то есть три мнимых.

Это рассуждение простирается дальше. В алгебре Клиффорда есть шесть базисных элементов бивекторов, поскольку с четырьмя различными основными векторными направлениями можно определить шесть разных пар и, следовательно, шесть разных линейно независимых плоскостей. Вращения в таких пространствах с использованием этих обобщений кватернионов, называемых роторами , могут быть очень полезны для приложений, включающих однородные координаты . Но только в 3D количество базисных бивекторов равно количеству базисных векторов, и каждый бивектор можно идентифицировать как псевдовектор . ${\displaystyle \operatorname {Cl} _{4,0}(\mathbb {R} ),}$

Есть несколько преимуществ размещения кватернионов в этой более широкой ситуации: ^[44]

• Роторы являются естественной частью геометрической алгебры и легко понимаются как кодирование двойного отражения.
• В геометрической алгебре ротор и объекты, на которые он действует, живут в одном пространстве. Это устраняет необходимость изменять представления и кодировать новые структуры данных и методы, что традиционно требуется при дополнении линейной алгебры кватернионами.
• Роторы универсально применимы к любому элементу алгебры, не только к векторам и другим кватернионам, но также к линиям, плоскостям, кругам, сферам, лучам и так далее.
• В конформной модели евклидовой геометрии роторы позволяют кодировать вращение, перемещение и масштабирование в одном элементе алгебры, универсально действуя на любой элемент. В частности, это означает, что роторы могут представлять вращение вокруг произвольной оси, тогда как кватернионы ограничены осью, проходящей через начало координат.
• Преобразования, закодированные ротором, делают интерполяцию особенно простой.
• Роторы естественным образом переходят в псевдоевклидовы пространства , например, в пространство Минковского специальной теории относительности . В таких пространствах роторы могут использоваться для эффективного представления повышения Лоренца и для интерпретации формул, включающих гамма-матрицы .

Для получения дополнительной информации о геометрическом использовании алгебр Клиффорда см. Геометрическую алгебру .

Группа Брауэра

Кватернионы «по сути» являются единственной (нетривиальной) центральной простой алгеброй (CSA) над действительными числами в том смысле, что каждая CSA над действительными числами Брауэровски эквивалентна либо действительным числам, либо кватернионам. Явно группа Брауэра действительных чисел состоит из двух классов, представленных действительными числами и кватернионами, где группа Брауэра представляет собой набор всех CSA, с точностью до отношения эквивалентности одного CSA, являющегося кольцом матриц над другим. Согласно теореме Артина-Веддерберна (в частности, части Веддерберна), все CSA являются матричными алгебрами над алгеброй с делением, и, таким образом, кватернионы являются единственной нетривиальной алгеброй с делением над действительными числами.

CSA — конечномерные кольца над полем, являющиеся простыми алгебрами (не имеющими нетривиальных двусторонних идеалов, как и поля), центром которых является именно поле, — являются некоммутативным аналогом расширенных полей и являются более ограничительными, чем общие удлинители колец. Тот факт, что кватернионы являются единственным нетривиальным CSA над действительными числами (с точностью до эквивалентности), можно сравнить с тем фактом, что комплексные числа являются единственным нетривиальным конечным расширением действительных чисел.

Котировки

Я рассматриваю это как неизящность или несовершенство кватернионов или, скорее, того состояния, в котором они до сих пор были развернуты, всякий раз, когда становится или кажется необходимым прибегнуть к помощи x, y, z и т. д.

-  Уильям Роуэн Гамильтон (около 1848 г.) ^[45]

Говорят, что время имеет только одно измерение, а пространство — три измерения. ... Математический кватернион включает в себя оба этих элемента; на техническом языке его можно назвать «время плюс пространство» или «пространство плюс время»: и в этом смысле оно имеет или, по крайней мере, предполагает ссылку на четыре измерения. ... И как Единый Времени, Пространственный Трой, Мог бы быть опоясанным Цепью Символов .

-  Уильям Роуэн Гамильтон (около 1853 г.) ^[46]

Кватернионы пришли от Гамильтона после того, как была проделана его действительно хорошая работа; и, хотя они были удивительно изобретательны, они были настоящим злом для тех, кто каким-либо образом их касался, включая клерка Максвелла .

-  В. Томпсон, лорд Кельвин (1892) ^[47]

Действительно, было время, когда я, хотя и признавал уместность векторного анализа в теории электромагнетизма (и в математической физике в целом), все же думал, что его труднее понимать и работать, чем картезианский анализ. Но это было до того, как я сбросил с себя кватернионного старика-морехода, который вцепился мне в плечи, когда я читал единственный доступный трактат на эту тему – «Кватернионы» профессора Тейта. Но позже я понял, что для векторного анализа, который мне требовался, кватернион не только не требовался, но был положительным злом немалой величины; и что из-за его отказа создание векторного анализа стало довольно простым, а его работа также упростилась, и что его можно было удобно гармонизировать с обычной картезианской работой. Ни в одной из моих статей (за исключением одной, предназначенной для специальных целей) нет и тени кватерниона. Векторный анализ, который я использую, можно описать либо как удобное и систематическое сокращение декартова анализа; или иначе, как кватернионы без кватернионов... «Кватернион», я думаю, была определена американской школьницей как «древняя религиозная церемония». Однако это было полной ошибкой. Древние – в отличие от профессора Тейта – не знали и не поклонялись кватернионам.

-  Оливер Хевисайд (1893) ^[48]

Ни матрицы, ни кватернионы, ни обычные векторы не были изгнаны из этих десяти [дополнительных] глав. Ибо, несмотря на неоспоримую мощь современного тензорного исчисления, эти старые математические языки, по моему мнению, продолжают предлагать заметные преимущества в ограниченной области специальной теории относительности. Более того, в науке, как и в повседневной жизни, владение более чем одним языком также ценно, поскольку оно расширяет наши взгляды, способствует критике и предохраняет от ипостаси [слабообоснованности] выражаемого предмета. словами или математическими символами.

-  Людвик Зильберштейн (1924) ^[49]

... кватернионы, кажется, источают атмосферу распада девятнадцатого века как довольно неудачный вид в борьбе за жизнь математических идей. Математики, по общему признанию, до сих пор хранят в своих сердцах теплые чувства к замечательным алгебраическим свойствам кватернионов, но, увы, такой энтузиазм мало что значит для более твердолобых ученых-физиков.

-  Саймон Л. Альтманн (1986) ^[50]

Смотрите также

• Преобразование между кватернионами и углами Эйлера  - Математическая стратегия
• Двойной кватернион  - Восьмимерная алгебра над действительными числами
• Двойственное комплексное число  - Четырехмерная алгебра над действительными числами.Pages displaying short descriptions of redirect targets
• Внешняя алгебра  - алгебра векторного пространства.
• Порядок кватернионов Гурвица  - Понятие в математике
• Гиперболический кватернион  - мутация кватернионов, при которой единичные векторы имеют квадрат +1.
• Сфера Ленарта  - прозрачная сфера, которую можно стереть сухим стиранием, используемая для обучения сферической геометрии.
• Матрицы Паули  - Матрицы, важные в квантовой механике и изучении спина.
• Кватернионное многообразие  - Понятие в геометрии
• Кватернионная матрица  - понятие в линейной алгебре
• Кватернионный многогранник  - Понятие в геометрии
• Кватернионное проективное пространство  - Понятие в математике
• Вращения в 4-мерном евклидовом пространстве  - Специальная ортогональная группа
• Слерп  - Сферическая линейная интерполяция в компьютерной графике.
• Сплит-кватернион  - Четырехмерная ассоциативная алгебра над действительными числами.
• Тессеракт  – четырехмерный аналог куба.

Примечания

1. Более личный взгляд на кватернионы был написан Иоахимом Ламбеком в 1995 году. В своем эссе «Если бы Гамильтон победил: кватернионы в физике » он написал : «Мой собственный интерес как аспиранта был вызван вдохновляющей книгой Зильберштейна». В заключение он заявил: «Я твердо верю, что кватернионы могут помочь чистым математикам, желающим ознакомиться с определенными аспектами теоретической физики». Ламбек, Дж. (1995). «Если бы Гамильтон победил: кватернионы в физике». Математика. Интеллигент . Том. 17, нет. 4. стр. 7–15. дои : 10.1007/BF03024783.
2. Важно отметить, что векторная часть кватерниона на самом деле является «осевым» вектором или « псеввектором », а не обычным или «полярным» вектором, как было формально доказано Альтманном (1986). ^[25] Полярный вектор может быть представлен в вычислениях (например, для вращения с помощью «преобразования подобия» кватерниона) чистым мнимым кватернионом без потери информации, но их не следует путать. В таком случае ось кватерниона «бинарного» (180°) вращения соответствует направлению изображаемого полярного вектора.
3. Для сравнения, действительные числа имеют размерность 1, комплексные числа имеют размерность 2, а октонионы имеют размерность 8. ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {O} }$
4. Идентификация квадратных корней из минус единицы была дана Гамильтоном ^[34] , но часто опускалась в других текстах. К 1971 году сфера была включена Сэмом Перлисом в его трехстраничную экспозицию, включенную в журнал « Исторические темы алгебры» , опубликованный Национальным советом учителей математики . ^[35] Совсем недавно сфера квадратных корней из минус единицы описана в книге Яна Р. Портеуса « Алгебры Клиффорда и классические группы» (Кембридж, 1995) в предложении 8.13. ^[36] ${\displaystyle \mathbb {H} }$
5. В книгах по прикладной математике, таких как Corke (2017) ^[39], часто используются разные обозначения с φ  :=1/2θ — то есть другая переменная θ = 2 φ .

Рекомендации

1. «О кватернионах; или о новой системе воображений в алгебре». Письмо Джону Т. Грейвсу . 17 октября 1843 г.
2. Розенфельд, Борис Абрамович (1988). История неевклидовой геометрии: Эволюция понятия геометрического пространства. Спрингер. п. 385. ИСБН 9780387964584.
3. Гамильтон. Ходжес и Смит. 1853. с. 60. Факторлинии кватернионов трехмерного пространства-времени
4. Харди 1881. Джинн, Хит и компания. 1881. с. 32. ISBN 9781429701860.
5. Кертис, Мортон Л. (1984), Матричные группы (2-е изд.), Нью-Йорк: Springer-Verlag , стр. 10, ISBN 978-0-387-96074-6
6. Кунце, Карстен; Шебен, Гельмут (ноябрь 2004 г.). «Распределение Бингама кватернионов и его сферическое преобразование радона в текстурном анализе». Математическая геология . 36 (8): 917–943. дои :10.1023/Б:МАТГ.0000048799.56445.59. S2CID  55009081.
7. Смит, Фрэнк (Тони). «Почему не седенион?» . Проверено 8 июня 2018 г.
8. См. Хазевинкель, Губарени и Кириченко 2004, с. 12
9. Конвей и Смит 2003, с. 9
10. Брэдли, Роберт Э.; Сандифер, Чарльз Эдвард (2007). Леонард Эйлер: жизнь, творчество и наследие. Эльзевир. п. 193. ИСБН 978-0-444-52728-8.Они упоминают утверждение Вильгельма Бляшке в 1959 году о том, что «кватернионы были впервые идентифицированы Л. Эйлером в письме Гольдбаху, написанном 4 мая 1748 года», и отмечают, что «нет никакого смысла говорить, что Эйлер «идентифицировал» кватернионы в этом письме... это утверждение абсурдно».
11. Пужоль, Дж., «Гамильтон, Родригес, Гаусс, кватернионы и вращения: историческая переоценка» Коммуникации в математическом анализе (2012), 13 (2), 1–14
12. Гаусс, CF (1900). «Mutationen des Raumes [Преобразования пространства] (ок. 1819 г.)». В Мартине Бренделе (ред.). Карл Фридрих Гаусс Верке [ Труды Карла Фридриха Гаусса ]. Том. 8. статья под редакцией профессора Штекеля из Киля, Германия. Геттинген, Германия: Königlichen Gesellschaft der Wissenschaften [Королевское общество наук]. стр. 357–361.
13. Гамильтон, WR (1844). "Письмо". Философский журнал и журнал науки Лондона, Эдинбурга и Дублина . Том. XXV. стр. 489–495.
14. Гамильтон, сэр WR (1866). Гамильтон, МЫ (ред.). Элементы кватернионов. Лондон: Longmans, Green & Co.
15. Шумейк, Кен (1985). «Анимация вращения с помощью кватернионных кривых» (PDF) . Компьютерная графика . 19 (3): 245–254. дои : 10.1145/325165.325242.Представлено на SIGGRAPH '85.
16. Tomb Raider (1996) часто называют первой компьютерной игрой для массового рынка, в которой кватернионы использовались для достижения плавного трехмерного вращения. См., например, Ника Бобика (июль 1998 г.). «Вращение объектов с помощью кватернионов». Разработчик игр .
17. Маккарти, Дж. М. (1990). Введение в теоретическую кинематику. МТИ Пресс. ISBN 978-0-262-13252-7.
18. Гурвиц, А. (1919), Vorlesungen über die Zahlentheorie der Quaternionen , Берлин: J. Springer, JFM  47.0106.01, относительно кватернионов Гурвица
19. Жирар, PR (1984). «Группа кватернионов и современная физика». Европейский журнал физики . 5 (1): 25–32. Бибкод : 1984EJPh....5...25G. дои : 10.1088/0143-0807/5/1/007. S2CID  250775753.
20. Жирар, Патрик Р. (1999). «Уравнения Эйнштейна и алгебра Клиффорда» (PDF) . Достижения в области прикладной алгебры Клиффорда . 9 (2): 225–230. дои : 10.1007/BF03042377. S2CID  122211720. Архивировано из оригинала (PDF) 17 декабря 2010 года.
21. Уэрта, Джон (27 сентября 2010 г.). «Представляем кватернионы» (PDF) . Архивировано (PDF) из оригинала 21 октября 2014 г. Проверено 8 июня 2018 г.
22. Вуд, Чарли (6 сентября 2018 г.). «Странные числа, породившие современную алгебру». Блог абстракций . Журнал Кванта.
23. Евс (1976, стр. 391)
24. «Математика - Преобразования с использованием кватернионов» . Евклидово пространство . Вращение q1 , за которым следует вращение q2 , эквивалентно одному повороту q2 q1 . Обратите внимание на обратный порядок: мы помещаем первое вращение в правую часть умножения.
25. Альтманн, Вращения SL, кватернионы и двойные группы . Ч. 12.
26. Гамильтон, сэр Уильям Роуэн (1866). «Статья 285». Элементы кватернионов. Лонгманс, Грин и компания. п. 310.
27. Харди (1881). «Элементы кватернионов». Наука . библиотека.cornell.edu. 2 (75): 65. doi :10.1126/science.os-2.75.564. ПМИД  17819877.
28. «Группа кватернионов». Wolframalpha.com .
29. Гиббс, Дж. Уиллард; Уилсон, Эдвин Бидвелл (1901). Векторный анализ. Издательство Йельского университета. п. 428. правый тензор двоичный
30. Гамильтон, WR (1844–1850). «О кватернионах или новой системе воображаемых в алгебре». Коллекция Дэвида Р. Уилкинса. Философский журнал . Тринити-колледж Дублина .
31. «Визуализация кватернионов». Морган-Кауфманн/Эльзевир. 2005.
32. «[название не указано; определяющая оценка]». Wolframalpha.com .
33. Фарбратер, Ричард Уильям; Гросс, Юрген; Трошке, Свен-Оливер (2003). «Матричное представление кватернионов». Линейная алгебра и ее приложения . 362 : 251–255. дои : 10.1016/s0024-3795(02)00535-9 .
34. Гамильтон, WR (1899). Элементы кватернионов (2-е изд.). Издательство Кембриджского университета. п. 244. ИСБН 1-108-00171-8.
35. Перлис, Сэм (1971). «Капсула 77: Кватернионы». Исторические темы в алгебре . Исторические темы для математического класса. Том. 31. Рестон, В.А.: Национальный совет учителей математики . п. 39. ИСБН 9780873530583. ОСЛК  195566.
36. Портеус, Ян Р. (1995). «Глава 8: Кватернионы». Алгебры Клиффорда и классические группы (PDF) . Кембриджские исследования по высшей математике. Том. 50. Кембридж: Издательство Кембриджского университета . п. 60. дои : 10.1017/CBO9780511470912.009. ISBN 9780521551779. МР  1369094. OCLC  32348823.
37. «[название не указано]» (PDF) . Bridgesmathart.org . архив . Проверено 19 августа 2018 г.
38. Сярккя, Симо (28 июня 2007 г.). «Заметки о кватернионах» (PDF) . Lce.hut.fi. _ Архивировано из оригинала (PDF) 5 июля 2017 года.
39. Корк, Питер (2017). Робототехника, зрение и управление – фундаментальные алгоритмы в MATLAB . Спрингер . ISBN 978-3-319-54413-7.
40. Парк, ФК; Равани, Бахрам (1997). «Гладкая инвариантная интерполяция вращений». Транзакции ACM с графикой . 16 (3): 277–295. дои : 10.1145/256157.256160 . S2CID  6192031.
41. Хэнсон, Джейсон (2011). «Вращения в трех, четырех и пяти измерениях». arXiv : 1103.5263 [math.MG].
42. Гюнашти, Гёкмен (2016). Алгебра кватернионов, их приложения в вращениях и за пределами кватернионов (BS). Университет Линнея.
43. «Трёхмерные точечные группы». www.classe.cornell.edu . Проверено 9 декабря 2022 г.
44. «Кватернионы и геометрическая алгебра». геометрическая алгебра.нет . Проверено 12 сентября 2008 г.См. также: Дорст, Лео; Фонтейн, Дэниел; Манн, Стивен (2007). Геометрическая алгебра для информатики. Морган Кауфманн . ISBN 978-0-12-369465-2.
45. Гамильтон, Уильям Роуэн (1853). Лекции по кватернионам. Дублин: Ходжес и Смит. п. 522.
46. Грейвс, RP Жизнь сэра Уильяма Роуэна Гамильтона. Дублин Ходжес, Фиггис. стр. 635–636.
47. Томпсон, Сильванус Филлипс (1910). Жизнь Уильяма Томсона (Том 2). Лондон, Макмиллан. п. 1138.
48. Хевисайд, Оливер (1893). Электромагнитная теория. Том. I. Лондон, Великобритания: Полиграфическая и издательская компания Electrician. стр. 134–135.
49. Людвик Зильберштейн (1924). Предисловие ко второму изданию Теории Относительности.
50. Альтманн, Саймон Л. (1986). Вращения, кватернионы и двойные группы . Кларендон Пресс. ISBN 0-19-855372-2. LCCN  85013615.

дальнейшее чтение

Книги и публикации

• Гамильтон, Уильям Роуэн (1844). «О кватернионах, или о новой системе мнимых в алгебре». Философский журнал . 25 (3): 489–495. дои : 10.1080/14786444408645047.
• Гамильтон, Уильям Роуэн (1853), « Лекции по кватернионам ». Королевская ирландская академия.
• Гамильтон (1866) Элементы кватернионов Дублинского университета . Под редакцией Уильяма Эдвина Гамильтона, сына покойного автора.
• Гамильтон (1899) Элементы кватернионов, том I, (1901), том II. Под редакцией Чарльза Джаспера Джоли ; опубликовано Longmans, Green & Co.
• Тейт, Питер Гатри (1873), « Элементарный трактат о кватернионах ». 2-е изд., Кембридж, [англ.]: The University Press.
• Максвелл, Джеймс Клерк (1873), « Трактат об электричестве и магнетизме ». Кларендон Пресс, Оксфорд.
• Тейт, Питер Гатри (1886), « Архивная копия». Архивировано из оригинала 8 августа 2014 года . Проверено 26 июня 2005 года .{{cite web}}: CS1 maint: archived copy as title (link) CS1 maint: unfit URL (link)". MA Sec. Британская энциклопедия RSE , девятое издание, 1886 г., том XX, стр. 160–164. ( Файл PostScript в сжатом формате )
• Жоли, Чарльз Джаспер (1905). Руководство по кватернионам . Макмиллан. LCCN  05036137.
• Макфарлейн, Александр (1906). Векторный анализ и кватернионы (4-е изд.). Уайли. LCCN  16000048.
• Чисхолм, Хью , изд. (1911). «Алгебра»  . Британская энциклопедия (11-е изд.). Издательство Кембриджского университета.( См. раздел о кватернионах. )
• Финкельштейн, Дэвид; Яух, Йозеф М.; Шиминович, Самуэль; Спейзер, Дэвид (1962). «Основы кватернионной квантовой механики». Дж. Математика. Физ . 3 (2): 207–220. Бибкод : 1962JMP.....3..207F. дои : 10.1063/1.1703794. S2CID  121453456.
• Дю Валь, Патрик (1964). Гомографии, кватернионы и вращения . Оксфордские математические монографии. Кларендон Пресс. LCCN  64056979.
• Майкл Дж. Кроу (1967), История векторного анализа : эволюция идеи векторной системы , University of Notre Dame Press. Рассматриваются основные и второстепенные векторные системы XIX века (Гамильтон, Мёбиус, Беллавитис, Клиффорд, Грассман, Тейт, Пирс, Максвелл, Макфарлейн, Маколи, Гиббс, Хевисайд).
• Альтманн, Саймон Л. (1989). «Гамильтон, Родригес и скандал с кватернионами». Журнал «Математика» . 62 (5): 291–308. дои : 10.1080/0025570X.1989.11977459.
• Пужоль, Хосе (2014). «О почти забытой ранней работе Гамильтона о связи между вращениями и кватернионами и о составе вращений». Американский математический ежемесячник . 121 (6): 515–522. doi : 10.4169/amer.math.monthly.121.06.515. S2CID  1543951.
• Адлер, Стивен Л. (1995). Кватернионная квантовая механика и квантовые поля . Международная серия монографий по физике. Том. 88. Издательство Оксфордского университета. ISBN 0-19-506643-Х. LCCN  94006306.
• Уорд, JP (1997). Кватернионы и числа Кэли: алгебра и приложения . Клювер Академик. ISBN 0-7923-4513-4.
• Кантор, Иллинойс; Солодников А.С. (1989). Гиперкомплексные числа, элементарное введение в алгебры . Спрингер-Верлаг. ISBN 0-387-96980-2.
• Гюрлебек, Клаус; Спрёссиг, Вольфганг (1997). Кватернионное и Клиффордовое исчисление для физиков и инженеров . Математические методы на практике. Том. 1. Уайли. ISBN 0-471-96200-7. LCCN  98169958.
• Койперс, Джек (2002). Кватернионы и последовательности вращения: учебник по применению в орбитах, аэрокосмической отрасли и виртуальной реальности . Издательство Принстонского университета . ISBN 0-691-10298-8.
• Конвей, Джон Хортон ; Смит, Дерек А. (2003). О кватернионах и октонионах: их геометрия, арифметика и симметрия . АК Петерс. ISBN 1-56881-134-9.(обзор).
• Джек, премьер-министр (2003). «Физическое пространство как кватернионная структура, I: Уравнения Максвелла. Краткое примечание». arXiv : math-ph/0307038 .
• Кравченко, Владислав (2003). Прикладной кватернионный анализ . Хельдерманн Верлаг. ISBN 3-88538-228-8.
• Хазевинкель, Михель ; Губарени, Надежда; Кириченко, Владимир В. (2004). Алгебры, кольца и модули. Том. 1. Спрингер. ISBN 1-4020-2690-0.
• Хэнсон, Эндрю Дж. (2006). Визуализация кватернионов. Эльзевир. ISBN 0-12-088400-3.
• Бинц, Эрнст; Стручки, Соня (2008). «1. Тело кватернионов». Геометрия групп Гейзенберга . Американское математическое общество . ISBN 978-0-8218-4495-3.
• Доран, Крис Дж.Л .; Ласенби, Энтони Н. (2003). Геометрическая алгебра для физиков . Издательство Кембриджского университета. ISBN 978-0-521-48022-2.
• Винс, Джон А. (2008). Геометрическая алгебра для компьютерной графики . Спрингер. ISBN 978-1-84628-996-5.
• Для молекул, которые можно рассматривать как классические твердые тела, компьютерное моделирование молекулярной динамики использует кватернионы. Впервые они были представлены для этой цели диджеем Эвансом (1977). «О представлении ориентационного пространства». Мол. Физ . 34 (2): 317–325. Бибкод : 1977MolPh..34..317E. дои : 10.1080/00268977700101751.
• Чжан, Фучжэнь (1997). «Кватернионы и матрицы кватернионов». Линейная алгебра и ее приложения . 251 : 21–57. дои : 10.1016/0024-3795(95)00543-9 .
• Рон Голдман (2010). Переосмысление кватернионов: теория и вычисления . Морган и Клейпул. ISBN 978-1-60845-420-4.
• Ивс, Ховард (1976), Введение в историю математики (4-е изд.), Нью-Йорк: Холт, Райнхарт и Уинстон , ISBN 0-03-089539-1
• Войт, Джон (2021). Кватернионные алгебры . Тексты для аспирантов по математике. Том. 288. Спрингер. дои : 10.1007/978-3-030-56694-4 . ISBN 978-3-030-57467-3.

Ссылки и монографии

• «Уведомления о кватернионах».Уведомления и материалы, связанные с презентациями конференции Quaternion
• «Кватернион», Математическая энциклопедия , EMS Press , 2001 [1994]
• "Часто задаваемые вопросы". Матрица и кватернион . 1.21.
• Свитзер, Дуг. «Занимаемся физикой с кватернионами».
• Кватернионы для компьютерной графики и механики (Гернот Хоффман)
• Гспонер, Андре; Хурни, Жан-Пьер (2002). «Физическое наследие сэра В. Р. Гамильтона». arXiv : math-ph/0201058 .
• Уилкинс, Д.Р. «Исследование Гамильтона кватернионов».
• Гроссман, Дэвид Дж. «Фракталы Кватерниона Джулии».3D-кватернион Джулии с трассировкой лучей
• «Кватернионная математика и преобразования».Отличная страница, объясняющая основы математики, со ссылками на простые формулы преобразования вращения.
• Мэтьюз, Джон Х. «Библиография кватернионов». Архивировано из оригинала 2 сентября 2006 г.
• «Степень кватерниона». GameDev.net.
• Хэнсон, Эндрю. «Визуализация домашней страницы кватернионов». Архивировано из оригинала 5 ноября 2006 г.
• Карни, Чарльз Ф.Ф. (январь 2007 г.). «Кватернионы в молекулярном моделировании». Дж. Мол. График. Мод . 25 (5): 595–604. arXiv : физика/0506177 . дои : 10.1016/j.jmgm.2006.04.002. PMID  16777449. S2CID  6690718.
• Мебиус, Йохан Э. (2005). «Матричное доказательство теоремы о представлении кватернионов для четырехмерных вращений». arXiv : math/0501249 .
• Мебиус, Йохан Э. (2007). «Вывод формулы Эйлера-Родригеса для трехмерных вращений из общей формулы для четырехмерных вращений». arXiv : math/0701759 .
• «Гамильтон Уок». Департамент математики NUI Мейнут .
• «Использование кватернионов для представления вращения». OpenGL: Учебники . Архивировано из оригинала 15 декабря 2007 г.
• Дэвид Эриксон, Министерство оборонных исследований и разработок Канады (DRDC), Полный вывод матрицы вращения из унитарного представления кватернионов в документе DRDC TR 2005-228.
• Мартинес, Альберто. «Негативная математика, как можно изменить математические правила в положительную сторону». Исторический факультет Техасского университета. Архивировано из оригинала 24 сентября 2011 г.
• Штальке, Д. «Кватернионы в классической механике» (PDF) .
• Морье-Жену, Софи; Овсиенко, Валентин (2008). «Ну, папа, а тройки умеешь?». arXiv : 0810.5562 [math.AC].описывает, как кватернионы можно превратить в косокоммутативную алгебру, градуированную Z /2 × Z /2 × Z /2 .
• Джойс, Хелен (ноябрь 2004 г.). «Любопытные кватернионы». ведущий Джон Баэз .
• Ибаньес, Луис. «Учебник по кватернионам. Часть I» (PDF) . Архивировано из оригинала (PDF) 4 февраля 2012 г. Проверено 5 декабря 2011 г.Часть II (PDF; используется терминология Гамильтона, которая отличается от современного использования)
• Гилони, Р.; Моретти, В.; Перотти, А. (2013). «Непрерывное функциональное исчисление срезов в кватернионных гильбертовых пространствах». Преподобный Матем. Физ . 25 (4): 1350006–126. arXiv : 1207.0666 . Бибкод : 2013RvMaP..2550006G. дои : 10.1142/S0129055X13500062. S2CID  119651315.
  Гилони, Р.; Моретти, В.; Перотти, А. (2017). «Спектральные представления нормальных операторов посредством переплетающихся кватернионных проекционных мер». Преподобный Матем. Физ . 29 : 1750034. arXiv : 1602.02661 . дои : 10.1142/S0129055X17500349. S2CID  124709652.две пояснительные статьи о непрерывном функциональном исчислении и спектральной теории в кватернионных гильбертовых пространствах, полезные в строгой кватернионной квантовой механике.
• Кватернионы Приложение для Android отображает кватернионы, соответствующие ориентации устройства.
• Статья о вращении объектов с использованием кватернионов, в которой рассказывается об использовании кватернионов для вращения в видеоиграх/компьютерной графике.

Внешние ссылки

• СМИ, связанные с кватернионами, на Викискладе?
• Полсон, Лоуренс К. Кватернионы (разработка формальных доказательств в Isabelle/HOL, Архив формальных доказательств)
• Кватернионы — Визуализация