
Деление — одно из четырех основных действий арифметики . Другие действия — сложение , вычитание и умножение . То, что делится, называется делимым , которое делится на делитель , а результат называется частным .
На элементарном уровне деление двух натуральных чисел , помимо прочих возможных интерпретаций , представляет собой процесс вычисления количества раз, которое одно число содержится в другом. [1] : 7 Например, если 20 яблок разделить поровну между 4 людьми, каждый получит по 5 яблок (см. рисунок). Однако это количество раз или содержащееся число (делитель) не обязательно должны быть целыми числами .
Деление с остатком или евклидово деление двух натуральных чисел дает целое частное , которое является числом раз, когда второе число полностью содержится в первом числе, и остаток , который является частью первого числа, которая остается, когда в ходе вычисления частного не может быть выделена никакая дополнительная полная часть размера второго числа. Например, если 21 яблоко разделить между 4 людьми, каждый снова получает по 5 яблок, и остается 1 яблоко.
Чтобы деление всегда давало одно число, а не целое частное плюс остаток, натуральные числа должны быть расширены до рациональных чисел или действительных чисел . В этих расширенных системах счисления деление является обратной операцией умножению, то есть a = c / b означает a × b = c , пока b не равно нулю. Если b = 0 , то это деление на ноль , которое не определено. [a] [4] : 246 В примере с 21 яблоком каждый получил бы 5 яблок и четверть яблока, таким образом избежав остатка.
Обе формы деления появляются в различных алгебраических структурах , различных способах определения математической структуры. Те, в которых определено евклидово деление (с остатком), называются евклидовыми областями и включают кольца полиномов с одним неопределенным (которые определяют умножение и сложение по формулам с одной переменной). Те, в которых определено деление (с одним результатом) на все ненулевые элементы, называются полями и кольцами деления . В кольце элементы, на которые всегда возможно деление, называются единицами (например, 1 и −1 в кольце целых чисел). Другим обобщением деления на алгебраические структуры является фактор-группа , в которой результатом «деления» является группа, а не число.
Самый простой способ рассмотреть деление — с точки зрения цитаты и разбиения : с точки зрения цитаты 20 / 5 означает количество пятерок, которые нужно добавить, чтобы получить 20. С точки зрения разбиения 20 / 5 означает размер каждой из 5 частей, на которые делится набор размером 20. Например, 20 яблок делятся на пять групп по четыре яблока, что означает, что «двадцать разделить на пять равно четырем». Это обозначается как 20 / 5 = 4 , или 20/5 = 4 . [2] В этом примере 20 — делимое, 5 — делитель, а 4 — частное.
В отличие от других основных операций, при делении натуральных чисел иногда возникает остаток , который не входит равномерно в делимое; например, 10 / 3 дает остаток 1, так как 10 не кратно 3. Иногда этот остаток добавляется к частному как дробная часть , поэтому 10 / 3 равно 3+1/3 или 3,33... , но в контексте целочисленного деления, где числа не имеют дробной части, остаток сохраняется отдельно (или в исключительных случаях отбрасывается или округляется ). [5] Когда остаток сохраняется в виде дроби, он приводит к рациональному числу . Множество всех рациональных чисел создается путем расширения целых чисел всеми возможными результатами деления целых чисел.
В отличие от умножения и сложения, деление не является коммутативным , то есть a / b не всегда равно b / a . [6] Деление также, в общем случае, не является ассоциативным , то есть при многократном делении порядок деления может изменить результат. [7] Например, (24/6)/2 = 2 , но 24/(6/2) = 8 (где использование скобок указывает на то, что операции внутри скобок выполняются до операций вне скобок).
Деление традиционно считается левоассоциативным . То есть, если есть несколько делений подряд, порядок вычисления идет слева направо: [8] [9]
Деление является правораспределительным по отношению к сложению и вычитанию в том смысле, что
Это то же самое для умножения , как . Однако деление не является лево-дистрибутивным , как
Это отличается от случая умножения, которое является как лево-, так и право-дистрибутивным, и, следовательно, дистрибутивным .
Деление часто изображается в алгебре и науке путем помещения делимого над делителем с горизонтальной линией, также называемой дробной чертой , между ними. Например, « a деленное на b » можно записать как:
что также можно прочитать вслух как «разделить a на b » или « a на b ». Один из способов выразить деление в одной строке — написать делимое (или числитель), затем косую черту , затем делитель (или знаменатель), как показано ниже:
Это обычный способ задания деления в большинстве языков программирования , поскольку его можно легко набрать как простую последовательность символов ASCII . (Это также единственная нотация, используемая для частных объектов в абстрактной алгебре .) Некоторое математическое программное обеспечение , такое как MATLAB и GNU Octave , позволяет записывать операнды в обратном порядке, используя обратную косую черту в качестве оператора деления:
Типографский вариант, находящийся на полпути между этими двумя формами, использует косую черту (дробь), но при этом делимое возвышается, а делитель опускается:
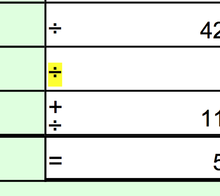
Любая из этих форм может быть использована для отображения дроби . Дробь — это выражение деления, где и делимое, и делитель являются целыми числами (обычно называемыми числителем и знаменателем ), и нет никакого намека на то, что деление должно быть оценено дополнительно. Второй способ показать деление — использовать знак деления (÷, также известный как обелус , хотя этот термин имеет дополнительные значения), распространенный в арифметике, таким образом:
Эта форма встречается редко, за исключением элементарной арифметики. ISO 80000-2 -9.6 гласит, что ее не следует использовать. Этот знак деления также используется отдельно для обозначения самой операции деления, например, в качестве метки на клавише калькулятора . Обелус был введен швейцарским математиком Иоганном Раном в 1659 году в «Тейтской алгебре» . [10] : 211 Символ ÷ используется для обозначения вычитания в некоторых европейских странах, поэтому его использование может быть неправильно понято. [11]
В некоторых неанглоязычных странах для обозначения деления используется двоеточие: [12]
Эта нотация была введена Готфридом Вильгельмом Лейбницем в его Acta eruditorum 1684 года . [10] : 295 Лейбниц не любил иметь отдельные символы для отношения и деления. Однако в английском использовании двоеточие ограничено выражением связанной концепции отношений .
Начиная с 19 века, учебники США использовали или для обозначения a, деленного на b , особенно при обсуждении деления в столбик . История этой нотации не совсем ясна, поскольку она развивалась с течением времени. [13]
Деление часто вводится через понятие «разделения» набора объектов, например, кучки леденцов, на несколько равных частей. Распределение объектов по несколько за раз в каждом раунде деления на каждую часть приводит к идее « разделения » — формы деления, при которой из делимого многократно вычитаются кратные делителя.
Позволяя вычитать больше кратных, чем позволяет частичный остаток на данном этапе, можно разработать более гибкие методы, такие как двунаправленный вариант фрагментации.
Более систематично и эффективно два целых числа можно разделить с помощью карандаша и бумаги методом короткого деления , если делитель мал, или длинного деления , если делитель больше. Если делимое имеет дробную часть (выраженную в виде десятичной дроби ), можно продолжать процедуру после разряда единиц до тех пор, пока делитель не переформулирует задачу, переместив десятичную часть вправо в обоих числах до тех пор, пока делитель не будет иметь дроби, что может облегчить решение задачи (например, 10/2,5 = 100/25 = 4).
Деление можно выполнить с помощью счет . [14]
Таблицы логарифмов можно использовать для деления двух чисел, вычитая логарифмы двух чисел, а затем находя антилогарифм результата.
Деление можно вычислить с помощью логарифмической линейки , совместив делитель на шкале C с делимым на шкале D. Частное можно найти на шкале D, совместив его с левым индексом на шкале C. Однако пользователь несет ответственность за мысленное отслеживание десятичной точки.
Современные калькуляторы и компьютеры выполняют деление либо методами, аналогичными делению в столбик, либо более быстрыми методами; см. Алгоритм деления .
В модульной арифметике (по модулю простого числа) и для действительных чисел ненулевые числа имеют мультипликативную обратную величину . В этих случаях деление на x может быть вычислено как произведение на мультипликативную обратную величину x . Этот подход часто ассоциируется с более быстрыми методами в компьютерной арифметике.
Евклидово деление — это математическая формулировка результата обычного процесса деления целых чисел. Оно утверждает, что для двух целых чисел, a , делимого , и b , делителя , таких, что b ≠ 0, существуют уникальные целые числа q , частное , и r , остаток , такие, что a = bq + r и 0 ≤ r < | b |, где | b | обозначает абсолютное значение b .
Целые числа не замкнуты относительно деления. Помимо того, что деление на ноль не определено, частное не является целым числом, если делимое не является целым числом, кратным делителю. Например, 26 нельзя разделить на 11, чтобы получить целое число. В таком случае используется один из пяти подходов:
Деление целых чисел в компьютерной программе требует особой осторожности. Некоторые языки программирования обрабатывают целочисленное деление как в случае 5 выше, поэтому ответом является целое число. Другие языки, такие как MATLAB и каждая система компьютерной алгебры, возвращают рациональное число в качестве ответа, как в случае 3 выше. Эти языки также предоставляют функции для получения результатов других случаев, либо напрямую, либо из результата случая 3.
Названия и символы, используемые для целочисленного деления, включают div, /, \ и %. Определения различаются относительно целочисленного деления, когда делимое или делитель отрицательны: округление может быть в сторону нуля (так называемое T-деление) или в сторону −∞ (F-деление); могут встречаться и более редкие стили — подробности см. в описании операции по модулю .
Правила делимости иногда можно использовать для быстрого определения, делится ли одно целое число на другое.
Результатом деления двух рациональных чисел является другое рациональное число, если делитель не равен 0. Деление двух рациональных чисел p / q и r / s можно вычислить как
Все четыре величины являются целыми числами, и только p может быть равно 0. Это определение гарантирует, что деление является операцией, обратной умножению .
Деление двух действительных чисел приводит к другому действительному числу (когда делитель не равен нулю). Оно определяется так, что a / b = c тогда и только тогда, когда a = cb и b ≠ 0.
Деление двух комплексных чисел (когда делитель отличен от нуля) приводит к другому комплексному числу, которое находится с помощью сопряжения знаменателя:
Этот процесс умножения и деления на называется «реализацией» или (по аналогии) рационализацией . Все четыре величины p , q , r , s являются действительными числами, а r и s не могут быть оба равны 0.
Деление комплексных чисел, выраженных в полярной форме, проще, чем определение выше:
Опять же, все четыре величины p , q , r , s являются действительными числами, и r может не быть равным 0.
Можно определить операцию деления для многочленов от одной переменной над полем . Тогда, как и в случае целых чисел, есть остаток. См. Евклидово деление многочленов , а для рукописных вычислений — многочленное длинное деление или синтетическое деление .
Можно определить операцию деления для матриц. Обычный способ сделать это — определить A / B = AB −1 , где B −1 обозначает обратную B , но гораздо более распространено явное указание AB −1 , чтобы избежать путаницы. Поэлементное деление также можно определить в терминах произведения Адамара .
Поскольку умножение матриц не является коммутативным , можно также определить левое деление или так называемое обратное слэш-деление как A \ B = A −1 B . Для того, чтобы это было хорошо определено, B −1 не обязательно должно существовать, однако A −1 должно существовать. Чтобы избежать путаницы, деление, определенное как A / B = AB −1, иногда называют правым делением или слэш-делением в этом контексте.
При таком определении левого и правого деления A / ( BC ) в общем случае не то же самое, что ( A / B ) / C , а ( AB ) \ C не то же самое, что A \ ( B \ C ) . Однако верно, что A / ( BC ) = ( A / C ) / B и ( AB ) \ C = B \ ( A \ C ) .
Чтобы избежать проблем, когда A −1 и/или B −1 не существуют, деление можно также определить как умножение на псевдообратное . То есть, A / B = AB + и A \ B = A + B , где A + и B + обозначают псевдообратные элементы A и B .
В абстрактной алгебре , если задана магма с бинарной операцией ∗ (которую можно было бы номинально назвать умножением), левое деление b на a (записывается как a \ b ) обычно определяется как решение x уравнения a ∗ x = b , если оно существует и является единственным. Аналогично, правое деление b на a (записывается как b / a ) является решением y уравнения y ∗ a = b . Деление в этом смысле не требует , чтобы ∗ обладало какими - либо особыми свойствами (такими как коммутативность, ассоциативность или элемент тождества ). Магма, для которой существуют и являются уникальными для всех a и всех b ( свойство латинского квадрата ), является квазигруппой . В квазигруппе деление в этом смысле всегда возможно, даже без элемента тождества и, следовательно, без обратных.
«Деление» в смысле «отмены» может быть выполнено в любой магме элементом со свойством отмены . Примерами служат матричные алгебры, кватернионные алгебры и квазигруппы. В целостной области , где не каждый элемент должен иметь обратный, деление на сокращаемый элемент a все еще может быть выполнено на элементах вида ab или ca путем левого или правого сокращения соответственно. Если кольцо конечно и каждый ненулевой элемент является сокращаемым, то, применяя принцип «ящика» , каждый ненулевой элемент кольца обратим, и деление на любой ненулевой элемент возможно. Чтобы узнать о том, когда алгебры (в техническом смысле) имеют операцию деления, обратитесь к странице об алгебрах деления . В частности, периодичность Ботта можно использовать для того, чтобы показать, что любая действительная нормированная алгебра с делением должна быть изоморфна либо действительным числам R , либо комплексным числам C , либо кватернионам H , либо октонионам O.
Производная частного двух функций определяется по правилу частного :
Деление любого числа на ноль в большинстве математических систем не определено, поскольку ноль, умноженный на любое конечное число, всегда дает произведение нуля . [15] Ввод такого выражения в большинство калькуляторов приводит к сообщению об ошибке. Однако в некоторых высших уровнях математики деление на ноль возможно с помощью нулевого кольца и алгебр, таких как колеса . [16] В этих алгебрах значение деления отличается от традиционных определений.