Многообразие

Топологическое пространство, локально напоминающее евклидово пространство.

Бутылка Клейна погружена в трехмерное пространство

Поверхность Земли требует (как минимум) двух карт, чтобы включить каждую точку. Здесь земной шар разложен на карты вокруг Северного и Южного полюсов .

В математике многообразие — это топологическое пространство , локально напоминающее евклидово пространство вблизи каждой точки. Точнее, -мерное многообразие, или сокращенно -многообразие , представляет собой топологическое пространство со свойством, что каждая точка имеет окрестность, гомеоморфную открытому подмножеству -мерного евклидова пространства . ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle n}$

Одномерные многообразия включают линии и окружности , но не самопересекающиеся кривые, такие как рисунок 8 . Двумерные многообразия также называют поверхностями . Примеры включают плоскость , сферу и тор , а также бутылку Клейна и реальную проективную плоскость .

Концепция многообразия занимает центральное место во многих разделах геометрии и современной математической физики , поскольку позволяет описывать сложные структуры в терминах хорошо понятных топологических свойств более простых пространств. Многообразия естественным образом возникают как множества решений систем уравнений и как графики функций. Эта концепция находит применение в компьютерной графике, поскольку необходимо связать изображения с координатами (например, компьютерная томография ).

Коллекторы могут быть оснащены дополнительной конструкцией. Одним из важных классов многообразий являются дифференцируемые многообразия ; их дифференцируемая структура позволяет проводить исчисления . Риманова метрика на многообразии позволяет измерять расстояния и углы . Симплектические многообразия служат фазовыми пространствами в гамильтоновом формализме классической механики , а четырехмерные лоренцевы многообразия моделируют пространство-время в общей теории относительности .

Изучение многообразий требует практических знаний исчисления и топологии .

Мотивирующие примеры

Круг

Рисунок 1. Каждая из четырех диаграмм отображает часть круга на открытый интервал и вместе покрывает весь круг.

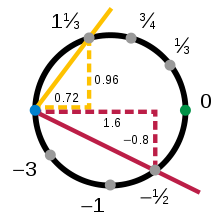
После линии круг является простейшим примером топологического многообразия. Топология игнорирует изгиб, поэтому небольшой участок круга рассматривается так же, как небольшой участок линии. Рассмотрим, например, верхнюю часть единичного круга , x ²  +  y ²  = 1, где координата y положительна (обозначена желтой дугой на рисунке 1 ). Любая точка этой дуги может быть однозначно описана ее координатой x . Итак, проекция на первую координату — это непрерывное и обратимое отображение верхней дуги на открытый интервал (−1, 1):

$${\displaystyle \chi _{\mathrm {top} }(x,y)=x.\,}$$

Такие функции вместе с открытыми областями, которые они отображают, называются диаграммами . Аналогичным образом существуют диаграммы для нижней (красной), левой (синей) и правой (зеленой) частей круга:

$${\displaystyle {\begin{aligned}\chi _{\mathrm {bottom} }(x,y)&=x\\\chi _{\mathrm {left} }(x,y)&=y\\\chi _{\mathrm {right} }(x,y)&=y.\end{aligned}}}$$

Вместе эти части охватывают весь круг, а четыре диаграммы образуют атлас круга.

Верхняя и правая диаграммы соответственно перекрываются в своей области: их пересечение находится в той четверти круга, где обе координаты и -положительны. Оба отображают эту часть в интервал , хотя и по-разному. Таким образом, можно построить функцию , которая принимает значения из ко-области обратно в круг, используя обратное, а затем обратно в интервал. Если a — любое число из , то: ${\displaystyle \chi _{\mathrm {top} }}$ ${\displaystyle \chi _{\mathrm {right} }}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle (0,1)}$ ${\displaystyle T:(0,1)\rightarrow (0,1)=\chi _{\mathrm {right} }\circ \chi _{\mathrm {top} }^{-1}}$ ${\displaystyle \chi _{\mathrm {top} }}$ ${\displaystyle \chi _{\mathrm {right} }}$ ${\displaystyle (0,1)}$

$${\displaystyle {\begin{aligned}T(a)&=\chi _{\mathrm {right} }\left(\chi _{\mathrm {top} }^{-1}\left[a\right]\right)\\&=\chi _{\mathrm {right} }\left(a,{\sqrt {1-a^{2}}}\right)\\&={\sqrt {1-a^{2}}}\end{aligned}}}$$

Такая функция называется картой перехода .

Рисунок 2. Диаграмма кругового многообразия, основанная на наклоне и охватывающая все точки круга, кроме одной.

Верхняя, нижняя, левая и правая диаграммы не образуют единственно возможный атлас. Диаграммы не обязательно должны представлять собой геометрические проекции, а количество диаграмм является вопросом выбора. Рассмотрим графики

$${\displaystyle \chi _{\mathrm {minus} }(x,y)=s={\frac {y}{1+x}}}$$

$${\displaystyle \chi _{\mathrm {plus} }(x,y)=t={\frac {y}{1-x}}}$$

Здесь s — наклон линии, проходящей через точку с координатами ( x ,  y ) и фиксированную точку поворота (−1, 0); аналогично, t является противоположностью наклона линии, проходящей через точки с координатами ( x ,  y ) и (+1, 0). Обратное отображение s в ( x ,  y ) задается формулой

$${\displaystyle {\begin{aligned}x&={\frac {1-s^{2}}{1+s^{2}}}\\[5pt]y&={\frac {2s}{1+s^{2}}}\end{aligned}}}$$

Можно подтвердить, что x ²  +  y ²  = 1 для всех значений s и t . Эти две диаграммы представляют собой второй атлас круга с картой перехода.

$${\displaystyle t={\frac {1}{s}}}$$

stst

На каждой диаграмме отсутствует одна точка: либо (−1, 0) для s , либо (+1, 0) для t , поэтому ни одной диаграммы в отдельности недостаточно, чтобы охватить весь круг. Можно доказать, что невозможно охватить весь круг одной диаграммой. Например, хотя можно построить круг из одного интервала линии, перекрывая и «склеивая» концы, это не создает диаграмму; часть круга будет сопоставлена ​​с обоими концами одновременно, потеряв обратимость.

Сфера

Сфера является примером поверхности . Единичная сфера неявного уравнения

х ² + у ² + z ² – 1 = 0

может быть покрыт атласом из шести карт : плоскость z = 0 делит сферу на две полусферы ( z > 0 и z < 0 ), которые обе могут быть отображены на диске x ² + y ² < 1 с помощью проекции на плоскости координат xy . Это дает две диаграммы; четыре другие карты имеют аналогичную конструкцию с двумя другими координатными плоскостями.

Как и в случае с кругом, можно определить одну карту, охватывающую всю сферу, исключая одну точку. Таким образом, двух карт достаточно, но сфера не может быть охвачена одной картой.

Этот пример исторически значим, поскольку он определил терминологию; стало очевидным, что вся поверхность Земли не может иметь плоское изображение, состоящее из одной карты (называемой также «картой», см. Морскую карту ), и поэтому необходимы атласы для покрытия всей поверхности Земли.

Другие кривые

Четыре многообразия из алгебраических кривых : ■  окружностей, ■  параболы, ■  гиперболы, ■  кубического.

Коллекторы не нужно соединять (все в одном блоке); пример — пара отдельных кругов.

Коллекторы не обязательно должны быть закрыты ; таким образом, отрезок без конечных точек является многообразием. Они никогда не являются счетными , если только размерность многообразия не равна 0. Если объединить эти свободы, то другими примерами многообразий являются парабола , гипербола и геометрическое место точек на кубической кривой y ² = x ³ − x (замкнутая петля кусок и открытый, бесконечный кусок).

Однако исключены такие примеры, как два соприкасающихся круга, которые имеют общую точку, образуя восьмерку; в общей точке удовлетворительную диаграмму создать невозможно. Даже при изгибе, допускаемом топологией, окрестности общей точки выглядят как «+», а не как линия. «+» не гомеоморфен отрезку прямой, поскольку удаление центральной точки из «+» дает пространство с четырьмя компонентами (т.е. частями), тогда как удаление точки из отрезка линии дает пространство, состоящее не более чем из двух частей; топологические операции всегда сохраняют количество частей.

Математическое определение

Неформально многообразие — это пространство , «моделированное» евклидовым пространством.

Существует много различных типов многообразий. В геометрии и топологии все многообразия являются топологическими многообразиями , возможно, с дополнительной структурой. Многообразие можно построить, задав набор координатных карт, то есть покрытие открытыми множествами с гомеоморфизмами евклидова пространства, и функции исправления ^{[ необходимы пояснения ]} : гомеоморфизмы из одной области евклидова пространства в другую область, если они соответствуют одна и та же часть многообразия в двух разных координатных картах. Многообразию можно придать дополнительную структуру, если функции исправления удовлетворяют аксиомам, выходящим за рамки непрерывности. Например, дифференцируемые многообразия имеют гомеоморфизмы в перекрывающихся окрестностях, диффеоморфных друг другу, так что многообразие имеет четко определенный набор функций, которые дифференцируемы в каждой окрестности и, следовательно, дифференцируемы на многообразии в целом.

Формально (топологическое) многообразие — это второе счетное хаусдорфово пространство , локально гомеоморфное евклидову пространству.

Вторая счетная и Хаусдорфа — условия точечного множества ; второе счетное исключает пространства, которые в некотором смысле «слишком велики», такие как длинная линия , в то время как Хаусдорф исключает пространства, такие как «линия с двумя началами» (эти обобщения многообразий обсуждаются в нехаусдорфовых многообразиях ).

Локально гомеоморфно евклидову пространству означает, что каждая точка имеет окрестность , гомеоморфную открытому подмножеству евклидова пространства для некоторого неотрицательного целого числа n . ${\displaystyle \mathbb {R} ^{n},}$

Отсюда следует, что либо точка является изолированной точкой (если ), либо имеет окрестность, гомеоморфную открытому шару ${\displaystyle n=0}$

$${\displaystyle \mathbf {B} ^{n}=\left\{(x_{1},x_{2},\dots ,x_{n})\in \mathbb {R} ^{n}:x_{1}^{2}+x_{2}^{2}+\cdots +x_{n}^{2}<1\right\}.}$$

диффеоморфна ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle n>0}$

Число n , фигурирующее в предыдущем определении, называется локальной размерностью многообразия. Обычно считается, что многообразия имеют постоянную локальную размерность, и тогда локальная размерность называется размерностью многообразия . Это, в частности, имеет место, когда многообразия соединены . Однако некоторые авторы допускают несвязность многообразий, в которых разные точки могут иметь разные размеры . ^[1] Если многообразие имеет фиксированную размерность, это можно подчеркнуть, назвав егочистое многообразие . Например, (поверхность) сферы имеет постоянную размерность 2 и, следовательно, является чистым многообразием, тогда какнепересекающееся объединениесферы и линии в трехмерном пространственечистым многообразием. Поскольку размерность является локальным инвариантом (т. е. карта, отправляющая каждую точку в измерение ее окрестности, в которой определена диаграмма, являетсялокально постоянной), каждыйсвязный компонентимеет фиксированную размерность.

С точки зрения теории пучков многообразие — это локально окольцованное пространство , структурный пучок которого локально изоморфен пучку непрерывных (или дифференцируемых, или комплексно-аналитических и т. д.) функций на евклидовом пространстве. Это определение чаще всего используется при обсуждении аналитических многообразий в алгебраической геометрии .

Диаграммы, атласы и карты перехода

Навигация по сферической Земле осуществляется с помощью плоских карт или схем, собранных в атлас. Аналогично многообразие можно описать с помощью математических карт , называемых координатными картами , собранных в математический атлас . Обычно невозможно описать многообразие с помощью одной карты, поскольку глобальная структура многообразия отличается от простой структуры карт. Например, ни одна плоская карта не может представлять всю Землю без разделения соседних объектов по границам карты или дублирования покрытия. Когда многообразие состоит из нескольких перекрывающихся диаграмм, области, где они перекрываются, несут информацию, необходимую для понимания глобальной структуры.

Графики

Координатная карта , координатная карта или просто карта многообразия — это обратимое отображение между подмножеством многообразия и простым пространством, такое, что и карта, и ее обратная сторона сохраняют желаемую структуру. ^[2] Для топологического многообразия простое пространство является подмножеством некоторого евклидова пространства , и интерес сосредотачивается на топологической структуре. Эта структура сохраняется гомеоморфизмами — обратимыми отображениями, непрерывными в обоих направлениях. ${\displaystyle \mathbb {R} ^{n}}$

В случае дифференцируемого многообразия набор карт , называемый атласом , все функции перехода которого (см. ниже) дифференцируемы, позволяет нам выполнять на нем исчисления. Полярные координаты , например, образуют диаграмму плоскости за вычетом положительной оси X и начала координат. Другим примером диаграммы является упомянутая выше карта χ _top , диаграмма для круга. ${\displaystyle \mathbb {R} ^{2}}$

Атласы

Для описания большинства коллекторов требуется более одной схемы. Определенный набор карт, охватывающий многообразие, называется атласом . Атлас не уникален, поскольку все многообразия можно охватить разными способами, используя разные комбинации карт. Два атласа называются эквивалентными, если их объединение также является атласом.

Атлас, содержащий все возможные карты, совместимые с данным атласом, называется максимальным атласом (т.е. классом эквивалентности, содержащим этот данный атлас). В отличие от обычного атласа максимальный атлас данного многообразия уникален. Хотя он полезен для определений, он является абстрактным объектом и не используется напрямую (например, в вычислениях).

Карты перехода

Диаграммы в атласе могут перекрываться, и одна точка многообразия может быть представлена ​​на нескольких картах. Если две карты перекрываются, части их представляют один и тот же регион многообразия, точно так же, как карта Европы и карта России могут содержать Москву. Учитывая две перекрывающиеся диаграммы, можно определить функцию перехода , которая переходит от открытого шара в многообразие, а затем обратно к другому (или, возможно, тому же самому) открытому шару в . Результирующая карта, как и карта T в приведенном выше примере с кругом, называется изменением координат , преобразованием координат , функцией перехода или картой перехода . ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {R} ^{n}}$

Дополнительная структура

Атлас также можно использовать для определения дополнительной структуры многообразия. Структура сначала определяется на каждой диаграмме отдельно. Если все карты переходов совместимы с этой структурой, структура переносится на многообразие.

Это стандартный способ определения дифференцируемых многообразий. Если функции перехода атласа топологического многообразия сохраняют естественную дифференциальную структуру (т. е. если они являются диффеоморфизмами ), дифференциальная структура переносится на многообразие и превращает его в дифференцируемое многообразие. Аналогичным образом вводятся комплексные многообразия , требующие, чтобы функции перехода атласа были голоморфными функциями . Для симплектических многообразий функции перехода должны быть симплектоморфизмами . ${\displaystyle \mathbb {R} ^{n}}$

Структура многообразия зависит от атласа, но иногда можно сказать, что разные атласы порождают одну и ту же структуру. Такие атласы называются совместимыми .

Эти понятия уточняются в целом за счет использования псевдогрупп .

Многообразие с границей

Многообразие с краем — это многообразие с ребром. Например, лист бумаги представляет собой 2-многообразие с 1-мерной границей. Граница -многообразия с краем является -многообразием . Диск (окружность плюс внутренняя часть ) представляет собой 2-многообразие с краем. Его граница — окружность, 1-многообразие . Квадрат с внутренней частью также является 2-многообразием с краем. Шар ( сфера плюс внутренность) представляет собой 3-многообразие с краем. Его граница — сфера, 2-многообразие. (Не путать с Границей (топологией) ). ${\displaystyle n}$ ${\displaystyle (n-1)}$

Говоря техническим языком, многообразие с краем — это пространство, содержащее как внутренние, так и граничные точки. Каждая внутренняя точка имеет окрестность, гомеоморфную открытому шару . Каждая граничная точка имеет окрестность, гомеоморфную «половине» -шара . Любой гомеоморфизм между полушариками должен отправлять точки с в точки с . Эта инвариантность позволяет «определить» граничные точки; см. следующий абзац. ${\displaystyle n}$ ${\displaystyle \{(x_{1},x_{2},\dots ,x_{n})\vert \Sigma x_{i}^{2}<1\}}$ ${\displaystyle n}$ ${\displaystyle \{(x_{1},x_{2},\dots ,x_{n})\vert \Sigma x_{i}^{2}<1{\text{ and }}x_{1}\geq 0\}}$ ${\displaystyle x_{1}=0}$ ${\displaystyle x_{1}=0}$

Граница и интерьер

Пусть – многообразие с краем. Внутренность , обозначенная , представляет собой множество точек, в которых есть окрестности, гомеоморфные открытому подмножеству . Граница , обозначенная , является дополнением к . _ Граничные точки можно охарактеризовать как точки, которые попадают на граничную гиперплоскость некоторой координатной карты. ${\displaystyle M}$ ${\displaystyle M}$ ${\displaystyle \operatorname {Int} M}$ ${\displaystyle M}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle M}$ ${\displaystyle \partial M}$ ${\displaystyle \operatorname {Int} M}$ ${\displaystyle M}$ ${\displaystyle (x_{n}=0)}$ ${\displaystyle \mathbb {R} _{+}^{n}}$

Если — многообразие с краем размерности , то — многообразие (без края) размерности и многообразие (без края) размерности . ${\displaystyle M}$ ${\displaystyle n}$ ${\displaystyle \operatorname {Int} M}$ ${\displaystyle n}$ ${\displaystyle \partial M}$ ${\displaystyle n-1}$

Строительство

Одно и то же многообразие может быть построено по-разному, каждый из которых подчеркивает разные аспекты многообразия, что приводит к несколько иной точке зрения.

Графики

На диаграмме часть сферы с положительной координатой z отображается на диске.

Возможно, самый простой способ построить многообразие — это тот, который использовался в приведенном выше примере с кругом. Сначала идентифицируется подмножество , а затем строится атлас, охватывающий это подмножество. Концепция многообразия исторически выросла из подобных конструкций. Вот еще один пример применения этого метода к построению сферы: ${\displaystyle \mathbb {R} ^{2}}$

Сфера с графиками

С сферой можно обращаться почти так же, как с кругом. В математике сфера — это просто поверхность (а не внутренняя часть тела), которую можно определить как подмножество : ${\displaystyle \mathbb {R} ^{3}}$

$${\displaystyle S=\left\{(x,y,z)\in \mathbb {R} ^{3}\mid x^{2}+y^{2}+z^{2}=1\right\}.}$$

Сфера двумерна, поэтому каждая диаграмма отображает часть сферы в открытое подмножество . Рассмотрим северное полушарие — часть с положительной координатой z (на рисунке справа она выделена красным). Функция χ, определенная формулой ${\displaystyle \mathbb {R} ^{2}}$

$${\displaystyle \chi (x,y,z)=(x,y),\ }$$

отображает северное полушарие на открытый единичный диск , проецируя его на плоскость ( x , y ). Аналогичная диаграмма существует и для южного полушария. Вместе с двумя картами, проецирующими на плоскость ( x , z ), и двумя картами, проецирующими на плоскость ( y , z ), получается атлас из шести карт, охватывающий всю сферу.

Это можно легко обобщить на сферы более высоких измерений.

Лоскутное шитье

Многообразие можно построить, последовательно склеивая части и превращая их в перекрывающиеся диаграммы. Эта конструкция возможна для любого многообразия и поэтому часто используется в качестве характеристики, особенно для дифференцируемых и римановых многообразий. Основное внимание уделяется атласу, поскольку фрагменты естественным образом представляют собой диаграммы, а поскольку внешнее пространство не задействовано, это приводит к внутреннему представлению многообразия.

Многообразие создается путем указания атласа, который сам определяется картами переходов. Таким образом, точка многообразия представляет собой класс эквивалентности точек, которые отображаются друг в друга посредством отображений перехода. Диаграммы сопоставляют классы эквивалентности с точками одного патча. Обычно предъявляются строгие требования к последовательности карт перехода. Для топологических многообразий они должны быть гомеоморфизмами; если они также являются диффеоморфизмами, полученное многообразие является дифференцируемым многообразием.

Это можно проиллюстрировать с помощью карты перехода t = ¹ ⁄ _с из второй половины примера круга. Начните с двух копий строки. Используйте координату s для первой копии и t для второй копии. Теперь склейте обе копии вместе, отождествив точку t на второй копии с точкой s = ¹ / _t на первой копии (точки t = 0 и s = 0 не отождествляются ни с одной точкой на первой и второй копии, соответственно). Это дает круг.

Внутренний и внешний взгляд

Первая конструкция и эта конструкция очень похожи, но представляют собой достаточно разные точки зрения. В первой конструкции многообразие рассматривается как вложенное в некоторое евклидово пространство. Это внешний взгляд . Когда многообразие рассматривается таким образом, легко использовать интуицию евклидовых пространств для определения дополнительной структуры. Например, в евклидовом пространстве всегда ясно, является ли вектор в некоторой точке касательным или нормальным к некоторой поверхности, проходящей через эту точку.

Лоскутная конструкция не использует никакого вложения, а просто рассматривает многообразие как топологическое пространство само по себе. Эта абстрактная точка зрения называется внутренней точкой зрения . Это может затруднить представление о том, каким может быть касательный вектор, и не существует внутреннего понятия нормального расслоения , но вместо этого существует внутреннее стабильное нормальное расслоение .

n -Sphere как лоскутное одеяло

n - сфера Sn является обобщением идеи круга (1-сферы) и сферы (2-сферы) на более высокие измерения ^. n -сферу Sn можно построить , склеив две копии ^. Карта перехода между ними представляет собой инверсию в сфере , определяемую как ${\displaystyle \mathbb {R} ^{n}}$

$${\displaystyle \mathbb {R} ^{n}\setminus \{0\}\to \mathbb {R} ^{n}\setminus \{0\}:x\mapsto x/\|x\|^{2}.}$$

Эта функция является своей обратной и поэтому может использоваться в обоих направлениях. Поскольку карта перехода является гладкой функцией , этот атлас определяет гладкое многообразие. В случае n = 1 пример упрощается до примера с кругом, приведенного ранее.

Определение точек многообразия

Можно определить разные точки многообразия как одинаковые. Это можно представить как склеивание этих точек в одну точку, образуя факторпространство . Однако нет оснований ожидать, что такие факторпространства будут многообразиями. Среди возможных фактор-пространств, которые не обязательно являются многообразиями, орбифолды и комплексы CW считаются относительно благополучными . Примером фактор-пространства многообразия, которое также является многообразием, является вещественное проективное пространство , идентифицируемое как фактор-пространство соответствующей сферы.

Один из способов идентификации точек (склеивания их) — через правое (или левое) действие группы , действующей на многообразие. Две точки идентифицируются, если одна из них передвинута на другую каким-либо элементом группы. Если M — многообразие, а G — группа, полученное фактор-пространство обозначается M / G (или G \ M ).

Многообразия, которые можно построить путем идентификации точек, включают торы и вещественные проективные пространства (начиная с плоскости и сферы соответственно).

Склеивание по границам

Два многообразия с границами можно склеить по границе. Если все сделано правильно, результатом также будет многообразие. Аналогичным образом можно склеить две границы одного многообразия.

Формально склейка определяется биекцией между двумя границами ^{[ сомнительно ]} . Две точки идентифицируются, когда они сопоставляются друг с другом. Для топологического многообразия эта биекция должна быть гомеоморфизмом, иначе результат не будет топологическим многообразием. Аналогично, для дифференцируемого многообразия оно должно быть диффеоморфизмом. Для других многообразий должны сохраняться другие структуры.

Конечный цилиндр можно построить как многообразие, начав с полосы [0,1] × [0,1] и склеив на границе пару противоположных ребер с помощью подходящего диффеоморфизма. Проективную плоскость можно получить, приклеив сферу с отверстием к ленте Мёбиуса вдоль соответствующих круговых границ.

Декартовы произведения

Декартово произведение многообразий также является многообразием.

Размерность многообразия продуктов равна сумме размерностей его факторов. Его топология — это топология произведения , а декартово произведение диаграмм — это диаграмма многообразия произведений. Таким образом, атлас многообразия произведений может быть построен с использованием атласов его факторов. Если эти атласы определяют дифференциальную структуру факторов, соответствующий атлас определяет дифференциальную структуру многообразия продуктов. То же самое справедливо и для любой другой структуры, определенной на факторах. Если один из факторов имеет границу, то и многообразие произведений тоже имеет границу. Декартовы произведения могут использоваться для построения торов и конечных цилиндров , например, как S ¹  ×  S ¹ и S ¹  × [0,1] соответственно.

Конечный цилиндр — это многообразие с краем.

История

Изучение многообразий объединяет многие важные области математики: оно обобщает такие понятия, как кривые и поверхности, а также идеи линейной алгебры и топологии.

Ранняя разработка

До появления современной концепции многообразия было сделано несколько важных результатов.

Неевклидова геометрия рассматривает пространства, в которых постулат параллельности Евклида не работает. Саккери впервые изучил такую ​​геометрию в 1733 году, но стремился лишь опровергнуть ее. Гаусс , Бояи и Лобачевский независимо открыли их 100 лет спустя. Их исследования выявили два типа пространств, геометрическая структура которых отличается от классической евклидовой структуры; они дали начало гиперболической геометрии и эллиптической геометрии . В современной теории многообразий этим понятиям соответствуют римановы многообразия с постоянной отрицательной и положительной кривизной соответственно.

Карл Фридрих Гаусс, возможно, был первым, кто рассматривал абстрактные пространства как самостоятельные математические объекты. Его теорема egregium дает метод вычисления кривизны поверхности без учета окружающего пространства, в котором находится поверхность. В современной терминологии такую ​​поверхность можно было бы назвать многообразием; и, говоря современным языком, теорема доказала, что кривизна поверхности является внутренним свойством . Теория многообразий сосредоточилась исключительно на этих внутренних свойствах (или инвариантах), в значительной степени игнорируя внешние свойства окружающего пространства.

Другим, более топологическим примером внутреннего свойства многообразия является его эйлерова характеристика . Леонард Эйлер показал, что для выпуклого многогранника в трехмерном евклидовом пространстве с V вершинами (или углами), E ребрами и F гранями:

$${\displaystyle V-E+F=2.\ }$$

топологическую картуVEF^[3]эйлеровой характеристикойторVEFтопологическим инвариантомчисел Беттитеорема Гаусса-Боннегауссовой кривизной

Синтез

Исследования Нильса Хенрика Абеля и Карла Густава Якоби по обращению эллиптических интегралов в первой половине 19 века привели их к рассмотрению особых типов комплексных многообразий, ныне известных как якобианы . Бернхард Риман внес дальнейший вклад в их теорию, прояснив геометрический смысл процесса аналитического продолжения функций комплексных переменных.

Другим важным источником многообразий в математике 19 века была аналитическая механика , разработанная Симеоном Пуассоном , Якоби и Уильямом Роуэном Гамильтоном . Возможными состояниями механической системы считаются точки абстрактного пространства, фазового пространства в лагранжевом и гамильтоновом формализмах классической механики. Это пространство, по сути, представляет собой многомерное многообразие, размерность которого соответствует степеням свободы системы и где точки задаются своими обобщенными координатами . Для неограниченного движения свободных частиц многообразие эквивалентно евклидову пространству, но различные законы сохранения ограничивают его более сложными образованиями, например торами Лиувилля. Теория вращающегося твердого тела, разработанная в 18 веке Леонардом Эйлером и Жозефом-Луи Лагранжем , дает еще один пример нетривиальности многообразия. Геометрические и топологические аспекты классической механики подчеркивал Анри Пуанкаре , один из основоположников топологии.

Риман был первым, кто проделал обширную работу, обобщив идею поверхности на более высокие измерения. Название «многообразие» происходит от оригинального немецкого термина Римана Mannigfaltigkeit , который Уильям Кингдон Клиффорд перевел как «многообразие». В своей вступительной лекции в Гёттингене Риман описал набор всех возможных значений переменной с определёнными ограничениями как Mannigfaltigkeit , поскольку переменная может иметь множество значений. Он различает stetige Mannigfaltigkeit и дискретную Mannigfaltigkeit ( непрерывную многообразность и прерывистую многообразность ), в зависимости от того, меняется ли значение непрерывно или нет. В качестве непрерывных примеров Риман приводит не только цвета и расположение предметов в пространстве, но и возможные формы пространственной фигуры. Используя индукцию , Риман строит n-fach ausgedehnte Mannigfaltigkeit ( n-кратно расширенное многообразие или n-мерное многообразие ) как непрерывный стек (n−1) мерных многообразий. Интуитивное представление Римана о Mannigfaltigkeit развилось в то, что сегодня формализовано как многообразие. Римановы многообразия и римановы поверхности названы в честь Римана.

Определение Пуанкаре

В своей очень влиятельной статье « Анализ положения» [ ^4] Анри Пуанкаре дал определение дифференцируемого многообразия ( variété ), которое послужило предшественником современной концепции многообразия. ^[5]

В первом разделе «Анализ ситуации» Пуанкаре определяет многообразие как множество уровня непрерывно дифференцируемой функции между евклидовыми пространствами, которое удовлетворяет гипотезе невырожденности теоремы о неявной функции . Третий раздел он начинает с замечания, что график непрерывно дифференцируемой функции является многообразием в последнем смысле. Затем он предлагает новое, более общее определение многообразия, основанное на «цепочке многообразий» (une chaîne des variétés ).

Понятие Пуанкаре о цепи многообразий является предшественником современного понятия атласа. В частности, он рассматривает два многообразия, определенные соответственно как графики функций и . Если эти многообразия перекрываются ( a une party commune ), то он требует, чтобы координаты непрерывно дифференцируемо зависели от координат и наоборот (« ...les sont functions analytiques des et inversement »). Таким образом, он вводит предшественник понятия диаграммы и карты перехода. ${\displaystyle \theta (y)}$ ${\displaystyle \theta '\left(y'\right)}$ ${\displaystyle y}$ ${\displaystyle y'}$ ${\displaystyle y}$ ${\displaystyle y'}$

Например, единичный круг на плоскости можно рассматривать как график функции или функцию в окрестности каждой точки, кроме точек (1, 0) и (−1, 0); и в окрестности этих точек его можно рассматривать как график соответственно и . Круг можно представить в виде графика в окрестности каждой точки, поскольку левая часть его определяющего уравнения имеет ненулевой градиент в каждой точке круга. По теореме о неявной функции каждое подмногообразие евклидова пространства является локальным графиком функции. ${\textstyle y={\sqrt {1-x^{2}}}}$ ${\textstyle y=-{\sqrt {1-x^{2}}}}$ ${\textstyle x={\sqrt {1-y^{2}}}}$ ${\textstyle x=-{\sqrt {1-y^{2}}}}$ ${\displaystyle x^{2}+y^{2}-1=0}$

Герман Вейль дал внутреннее определение дифференцируемых многообразий в своем курсе лекций по римановым поверхностям в 1911–1912 годах, открыв дорогу к общей концепции топологического пространства, которая последовала вскоре. В 1930-х годах Хасслер Уитни и другие прояснили фундаментальные аспекты предмета, и, таким образом, интуиция, возникшая во второй половине 19-го века, стала точной и получила развитие посредством дифференциальной геометрии и теории групп Ли . Примечательно, что теорема вложения Уитни ^[6] показала, что внутреннее определение в терминах карт эквивалентно определению Пуанкаре в терминах подмножеств евклидова пространства.

Топология коллекторов: основные моменты

Двумерные многообразия, также известные как двумерные поверхности , встроенные в наше общее трехмерное пространство, рассматривались Риманом под видом римановых поверхностей и строго классифицировались в начале 20-го века Полом Хегором и Максом Деном . Пуанкаре был пионером в изучении трехмерных многообразий и поднял о них фундаментальный вопрос, известный сегодня как гипотеза Пуанкаре . Спустя почти столетие Григорий Перельман доказал гипотезу Пуанкаре (см. Решение гипотезы Пуанкаре ). Программа геометризации Уильяма Тёрстона , сформулированная в 1970-х годах, обеспечила далеко идущее распространение гипотезы Пуанкаре на общие трёхмерные многообразия. Четырехмерные многообразия были выдвинуты на передний план математических исследований в 1980-х годах Майклом Фридманом и, в другом контексте, Саймоном Дональдсоном , который был мотивирован недавним прогрессом в теоретической физике ( теория Янга-Миллса ), где они служат заменитель обычного «плоского» пространства-времени . Андрей Марков-младший показал в 1960 году, что не существует алгоритма классификации четырехмерных многообразий. Важная работа над многомерными многообразиями, включая аналоги гипотезы Пуанкаре , была сделана ранее Рене Томом , Джоном Милнором , Стивеном Смейлом и Сергеем Новиковым . Очень распространенной и гибкой техникой, лежащей в основе многих работ по топологии многообразий, является теория Морса .

Дополнительная структура

Топологические многообразия

Самый простой вид многообразия для определения — это топологическое многообразие, которое локально выглядит как некоторое «обычное» евклидово пространство . По определению, все многообразия являются топологическими многообразиями, поэтому фраза «топологическое многообразие» обычно используется, чтобы подчеркнуть, что в многообразии отсутствует дополнительная структура или что рассматриваются только его топологические свойства. Формально топологическое многообразие — это топологическое пространство, локально гомеоморфное евклидову пространству. Это означает, что каждая точка имеет окрестность, для которой существует гомеоморфизм ( биективная непрерывная функция , обратная которой также непрерывна), отображающий эту окрестность в . Эти гомеоморфизмы являются картами многообразия. ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {R} ^{n}}$

Топологическое многообразие локально выглядит как евклидово пространство, но в довольно слабой форме: хотя для каждой отдельной карты можно различать дифференцируемые функции или измерять расстояния и углы, просто в силу того, что оно является топологическим многообразием, оно не имеет каких- либо конкретных и непротиворечивых выбор таких понятий. ^[7] Чтобы обсудить такие свойства многообразия, необходимо уточнить дополнительную структуру и рассмотреть дифференцируемые многообразия и римановы многообразия, обсуждаемые ниже. В частности, одно и то же топологическое многообразие может иметь несколько взаимно несовместимых классов дифференцируемых функций и бесконечное количество способов задания расстояний и углов.

Обычно для исключения патологических случаев делаются дополнительные технические предположения о топологическом пространстве. Принято требовать, чтобы пространство было хаусдорфовым и вторым счетным .

Размерность многообразия в определенной точке — это размерность евклидова пространства, которому соответствуют карты в этой точке (число n в определении). Все точки связного многообразия имеют одинаковую размерность. Некоторые авторы требуют, чтобы все карты топологического многообразия отображались в евклидовы пространства той же размерности. В этом случае каждое топологическое многообразие имеет топологический инвариант — свою размерность.

Дифференцируемые многообразия

Для большинства приложений используется особый вид топологического многообразия, а именно дифференцируемое многообразие . Если локальные карты на многообразии в определенном смысле совместимы, на этом многообразии можно определить направления, касательные пространства и дифференцируемые функции. В частности, можно использовать исчисление на дифференцируемом многообразии. Каждая точка n -мерного дифференцируемого многообразия имеет касательное пространство . Это n -мерное евклидово пространство, состоящее из касательных векторов кривых, проходящих через точку.

Двумя важными классами дифференцируемых многообразий являются гладкие и аналитические многообразия . Для гладких многообразий отображения переходов гладкие, т. е. бесконечно дифференцируемые. Аналитические многообразия — это гладкие многообразия с дополнительным условием аналитичности отображений переходов (их можно выразить в виде степенных рядов ). Сфере можно придать аналитическую структуру, как и большинству знакомых кривых и поверхностей.

Спрямляемое множество обобщает идею кусочно-гладкой или спрямляемой кривой на более высокие измерения; однако спрямляемые множества не входят в общие многообразия.

Римановы многообразия

Для измерения расстояний и углов на многообразиях многообразие должно быть римановым. Риманово многообразие — это дифференцируемое многообразие, в котором каждое касательное пространство снабжено скалярным произведением , плавно меняющимся от точки к точке. Учитывая два касательных вектора и скалярное произведение дает действительное число. Скалярное (или скалярное) произведение является типичным примером внутреннего продукта. Это позволяет определять различные понятия, такие как длина, углы , площади (или объёмы ), кривизна и дивергенция векторных полей . ${\displaystyle \langle \cdot ,\cdot \rangle }$ ${\displaystyle u}$ ${\displaystyle v}$ ${\displaystyle \langle u,v\rangle }$

Всем дифференцируемым многообразиям (постоянной размерности) можно придать структуру риманова многообразия. Само евклидово пространство имеет естественную структуру риманова многообразия (касательные пространства естественным образом отождествляются с самим евклидовым пространством и несут стандартное скалярное произведение пространства). Многие знакомые кривые и поверхности, включая, например, все n -сферы, заданы как подпространства евклидова пространства и наследуют метрику от их вложения в него.

Финслеровы многообразия

Многообразие Финслера позволяет определять расстояние, но не требует понятия угла; это аналитическое многообразие, в котором каждое касательное пространство снабжено нормой , плавно меняющейся от точки к точке. Эту норму можно расширить до метрики , определяющей длину кривой; но его вообще нельзя использовать для определения внутреннего продукта. ${\displaystyle \|\cdot \|}$

Любое риманово многообразие является финслеровым многообразием.

Группы лжи

Группы Ли , названные в честь Софуса Ли , представляют собой дифференцируемые многообразия, которые также несут структуру группы , которая такова, что групповые операции определяются гладкими отображениями.

Евклидово векторное пространство с групповой операцией сложения векторов является примером некомпактной группы Ли. Простым примером компактной группы Ли является круг: групповая операция — это просто вращение. Эту группу, известную как , можно также охарактеризовать как группу комплексных чисел по модулю 1 с умножением в качестве групповой операции. ${\displaystyle \operatorname {U} (1)}$

Другие примеры групп Ли включают специальные группы матриц , которые являются подгруппами общей линейной группы , группы матриц с ненулевым определителем. Если элементы матрицы — действительные числа , это будет -мерное несвязное многообразие. Ортогональные группы , группы симметрии сферы и гиперсферы , представляют собой размерные многообразия, где – размерность сферы. Дальнейшие примеры можно найти в таблице групп Ли . ${\displaystyle n\times n}$ ${\displaystyle n^{2}}$ ${\displaystyle n(n-1)/2}$ ${\displaystyle n-1}$

Другие типы коллекторов

• Комплексное многообразие — это многообразие, карты которого принимают значения и функции перехода голоморфны на перекрытиях. Эти многообразия являются основными объектами изучения комплексной геометрии . Однокомплексномерное многообразие называется римановой поверхностью . -мерное комплексное многообразие имеет размерность как вещественное дифференцируемое многообразие. ${\displaystyle \mathbb {C} ^{n}}$ ${\displaystyle n}$ ${\displaystyle 2n}$
• CR- многообразие — это многообразие, смоделированное на границах областей в . ${\displaystyle \mathbb {C} ^{n}}$
• «Бесконечномерные многообразия»: чтобы учесть бесконечность измерений, можно рассматривать банаховы многообразия , которые локально гомеоморфны банаховым пространствам . Аналогично многообразия Фреше локально гомеоморфны пространствам Фреше .
• Симплектическое многообразие — это разновидность многообразия, которое используется для представления фазовых пространств в классической механике . Они наделены 2-формой , определяющей скобку Пуассона . Близкий тип коллектора — контактный коллектор .
• Комбинаторное многообразие — это разновидность многообразия, которая представляет собой дискретизацию многообразия. Обычно это означает кусочно-линейное многообразие , составленное из симплициальных комплексов .
• Цифровое многообразие — это особый вид комбинаторного многообразия, определенный в цифровом пространстве. См. цифровую топологию .

Классификация и инварианты

Различные понятия многообразий имеют разные понятия классификации и инварианта; в этом разделе мы сосредоточимся на гладких замкнутых многообразиях.

Классификация гладких замкнутых многообразий в принципе хорошо понятна , за исключением размерности 4 : в малых размерностях (2 и 3) она является геометрической, посредством теоремы униформизации и решения гипотезы Пуанкаре , а в большой размерности (5 и выше) это алгебраично, через теорию хирургии . Это принципиальная классификация: общий вопрос о том, диффеоморфны ли два гладких многообразия, вообще говоря, не вычислим. Кроме того, конкретные расчеты остаются трудными, и остается много открытых вопросов.

Ориентируемые поверхности можно визуализировать, а их классы диффеоморфизма перечислять по родам. Учитывая две ориентируемые поверхности, можно определить, являются ли они диффеоморфными, вычисляя их соответствующие роды и сравнивая: они диффеоморфны тогда и только тогда, когда роды равны, поэтому род образует полный набор инвариантов .

Это гораздо сложнее в более высоких измерениях: многообразия более высокой размерности невозможно визуализировать напрямую (хотя зрительная интуиция полезна для их понимания), нельзя также перечислить их классы диффеоморфизма и вообще невозможно определить, являются ли два разных описания многомерного многообразия более сложными. многообразие относится к одному и тому же объекту.

Однако можно определить, различны ли два многообразия, если существует какая-то внутренняя характеристика, которая их различает. Такие критерии обычно называют инвариантами , поскольку, хотя они и могут быть определены в терминах некоторого представления (например, рода в терминах триангуляции), они одинаковы относительно всех возможных описаний конкретного многообразия: они инвариантны. под разными описаниями.

Можно было бы надеяться разработать арсенал инвариантных критериев, которые окончательно классифицировали бы все многообразия с точностью до изоморфизма. Известно, что для многообразий размерности 4 и выше не существует программы , позволяющей определить, являются ли два многообразия диффеоморфными.

Гладкие многообразия имеют богатый набор инвариантов , происходящих из топологии множества точек , классической алгебраической топологии и геометрической топологии . Наиболее знакомыми инвариантами, видимыми для поверхностей, являются ориентируемость (нормальный инвариант, также обнаруживаемый с помощью гомологии ) и род (гомологический инвариант).

Гладкие замкнутые многообразия не имеют локальных инвариантов (кроме размерности), хотя геометрические многообразия имеют локальные инварианты, в частности, кривизну риманова многообразия и кручение многообразия, снабженного аффинной связностью . Это различие между локальными инвариантами и отсутствием локальных инвариантов является распространенным способом различения геометрии и топологии . Таким образом, все инварианты гладкого замкнутого многообразия глобальны.

Алгебраическая топология является источником ряда важных глобальных инвариантных свойств. Некоторые ключевые критерии включают свойство односвязности и ориентируемость (см. Ниже). Действительно, несколько разделов математики, такие как теория гомологии и гомотопии , а также теория характеристических классов, были основаны с целью изучения инвариантных свойств многообразий.

Поверхности

Ориентируемость

В измерениях два и выше простым, но важным инвариантным критерием является вопрос о том, допускает ли многообразие осмысленную ориентацию. Рассмотрим топологическое многообразие с картами, отображаемыми в . Учитывая упорядоченную основу для , диаграмма приводит к тому, что ее часть многообразия сама по себе приобретает ощущение порядка, который в трехмерном измерении можно рассматривать как правосторонний или левосторонний. Перекрывающиеся диаграммы не обязаны согласовываться в смысле порядка, что дает многообразиям важную свободу. Для некоторых многообразий, таких как сфера, диаграммы могут быть выбраны так, чтобы перекрывающиеся области согласовывали свою «направленность»; это ориентируемые многообразия. Для других это невозможно. Последнюю возможность легко упустить из виду, поскольку любая замкнутая поверхность, вложенная (без самопересечения) в трехмерное пространство, ориентируема. ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {R} ^{n}}$

Некоторые наглядные примеры неориентируемых многообразий включают: (1) полосу Мёбиуса , которая представляет собой многообразие с краем, (2) бутылку Клейна , которая должна пересекать себя в своем трехмерном представлении, и (3) действительную проективную плоскость. , которое естественным образом возникает в геометрии.

Лента Мёбиуса

Лента Мёбиуса

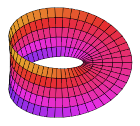
Начните с бесконечного круглого цилиндра, стоящего вертикально, многообразия без границ. Разрежьте его поперек, чтобы получились две круглые границы и цилиндрическая полоса между ними. Это ориентируемое многообразие с краем, над которым будет произведена «хирургия». Разрежьте полоску так, чтобы она могла развернуться в прямоугольник, но держите ее за концы. Поверните один конец на 180°, чтобы внутренняя поверхность была обращена наружу, и плавно склейте концы вместе. В результате получается лента с постоянным полуповоротом: лента Мёбиуса. Его граница — это уже не пара кругов, а (топологически) один круг; и то, что когда-то было его «внутри», слилось с его «внешним», так что теперь у него есть только одна сторона . Подобно бутылке Клейна ниже, эта двумерная поверхность должна будет пересекаться в двух измерениях, но ее легко можно построить в трех или более измерениях.

бутылка Клейна

Возьмите две ленты Мёбиуса; каждый имеет одну петлю в качестве границы. Распрямите эти петли в круги и позвольте полоскам превратиться в перекрещивающиеся шапочки . Склей круги вместе, получим новое замкнутое многообразие без границ — бутылку Клейна. Закрытие поверхности не исправляет отсутствие ориентировки, а просто удаляет границу. Таким образом, бутылка Клейна представляет собой закрытую поверхность, без различия внутреннего и внешнего. В трехмерном пространстве поверхность бутылки Клейна должна проходить сквозь себя. Для создания бутылки Клейна, которая не является самопересекающейся, требуется четыре или более измерений пространства.

Реальная проективная плоскость

Реальная проективная плоскость — это двумерное многообразие, которое невозможно реализовать в трёх измерениях без самопересечения, которое здесь показано как поверхность Боя .

Начните со сферы с центром в начале координат. Каждая линия, проходящая через начало координат, пронзает сферу в двух противоположных точках, называемых антиподами . Хотя физически невозможно сделать это, можно (рассмотрев факторпространство ) математически объединить каждую пару антиподов в одну точку. Полученная таким образом замкнутая поверхность является настоящей проективной плоскостью, еще одной неориентируемой поверхностью. Он имеет ряд эквивалентных описаний и конструкций, но этот маршрут объясняет свое название: все точки на любой заданной линии, проходящей через начало координат, проецируются на одну и ту же «точку» на этой «плоскости».

Род и эйлерова характеристика

Для двумерных многообразий ключевым инвариантным свойством является род или «количество ручек», присутствующих на поверхности. Тор — это сфера с одной ручкой, двойной тор — сфера с двумя ручками и так далее. Действительно, можно полностью охарактеризовать компактные двумерные многообразия на основе рода и ориентируемости. В многомерных многообразиях род заменяется понятием эйлеровой характеристики и, в более общем плане, числами Бетти , гомологиями и когомологиями .

Карты многообразий

Поверхность Морена , погружение , используемое при вывороте сферы.

Точно так же, как существуют различные типы многообразий, существуют и различные типы отображений многообразий . Помимо непрерывных функций и вообще гладких функций, существуют отображения со специальными свойствами. В геометрической топологии основным типом являются вложения , центральным примером которых является теория узлов , и такие обобщения, как погружения , субмерсии , накрывающие пространства и разветвленные накрывающие пространства . Основные результаты включают теорему вложения Уитни и теорему погружения Уитни .

В римановой геометрии можно попросить карты, сохраняющие риманову метрику, что приведет к понятиям изометрических вложений , изометрических погружений и римановых субмерсий ; основным результатом является теорема вложения Нэша .

Скалярные функции

3D цветной график сферических гармоник степени ${\displaystyle n=5}$

Основным примером отображений между многообразиями являются скалярные функции на многообразии.

$${\displaystyle f\colon M\to \mathbb {R} }$$

$${\displaystyle f\colon M\to \mathbb {C} ,}$$

иногда называемые регулярными функциями или функционалами по аналогии с алгебраической геометрией или линейной алгеброй. Они представляют интерес как сами по себе, так и для изучения лежащего в их основе многообразия.

В геометрической топологии чаще всего изучаются функции Морса , которые приводят к разложению тела ручки , в то время как в математическом анализе часто изучается решение уравнений в частных производных , важным примером которого является гармонический анализ , где изучаются гармонические функции : ядро ​​Лапласа . оператор . Это приводит к таким функциям, как сферические гармоники , и к методам изучения многообразий с использованием теплового ядра , таким как прослушивание формы барабана и некоторым доказательствам теоремы об индексе Атьи-Зингера .

Обобщения многообразий

Бесконечномерные многообразия

Определение многообразия можно обобщить, отбросив требование конечномерности. Таким образом, бесконечномерное многообразие представляет собой топологическое пространство, локально гомеоморфное топологическому векторному пространству над вещественными числами. При этом исключаются аксиомы множества точек, что позволяет использовать более высокие мощности и нехаусдорфовые многообразия ; и в нем отсутствует конечная размерность, что позволяет моделировать такие структуры, как гильбертовы многообразия на гильбертовых пространствах , банаховы многообразия моделировать на банаховых пространствах и многообразия Фреше моделировать на пространствах Фреше . Обычно ослабляют то или иное условие: многообразия с аксиомами точечного множества изучаются в общей топологии , а бесконечномерные многообразия изучаются в функциональном анализе .

Орбифолды

Орбифолд — это обобщение многообразия, допускающее определенные виды « особенностей » в топологии. Грубо говоря, это пространство, которое локально выглядит как факторы некоторого простого пространства ( например, евклидова пространства) по действиям различных конечных групп . Особенности соответствуют неподвижным точкам групповых действий, и действия должны быть в определенном смысле совместны.

Алгебраические многообразия и схемы

Несингулярные алгебраические многообразия над действительными или комплексными числами являются многообразиями. Это можно обобщить, во-первых, допуская особенности, во-вторых, допуская различные поля и, в-третьих, эмулируя конструкцию заплаток многообразий: точно так же, как многообразие склеивается из открытых подмножеств евклидова пространства, алгебраическое многообразие склеивается из аффинных алгебраических многообразий, которые являются нулевыми множествами многочленов над алгебраически замкнутыми полями. Схемы склеиваются также из аффинных схем, являющихся обобщением алгебраических многообразий. Оба связаны с многообразиями, но строятся алгебраически с использованием пучков вместо атласов.

Из-за наличия особых точек разнообразие, как правило, не является многообразием, хотя лингвистически французское variété , немецкое Mannigfaltigkeit и английское многообразие во многом являются синонимами . По-французски алгебраическое многообразие называется une variété algébrique ( алгебраическое многообразие ), а гладкое многообразие называется une variété différentielle ( дифференциальное многообразие ).

Расслоенное пространство

«Стратифицированное пространство» - это пространство, которое можно разделить на части («страты»), причем каждый слой представляет собой многообразие, причем страты соединяются друг с другом заданными способами (формально - фильтрация закрытыми подмножествами). Существуют различные технические определения, в частности стратифицированное пространство Уитни (см. Условия Уитни ) для гладких многообразий и топологически стратифицированное пространство для топологических многообразий. Основные примеры включают многообразие с краем (многообразие верхней размерности и граница коразмерности 1) и многообразия с углами (многообразие верхней размерности, граница коразмерности 1, углы коразмерности 2). Стратифицированные пространства Уитни — это широкий класс пространств, включающий алгебраические многообразия, аналитические многообразия, полуалгебраические множества и субаналитические множества .

CW-комплексы

Комплекс КС — это топологическое пространство, образованное склейкой дисков разной размерности. В общем случае полученное пространство является сингулярным и, следовательно, не является многообразием. Однако они представляют центральный интерес в алгебраической топологии, особенно в теории гомотопий .

Гомологические многообразия

Гомологическое многообразие — это пространство, которое ведет себя как многообразие с точки зрения теории гомологии. Это не все многообразия, но (в высокой размерности) их можно анализировать с помощью теории хирургии аналогично многообразиям, а неспособность быть многообразием является локальным препятствием, как и в теории хирургии. ^[8]

Дифференциальные пространства

Пусть - непустое множество. Предположим, что выбрано некоторое семейство действительных функций на . Обозначим его через . Это алгебра относительно поточечного сложения и умножения. Позвольте быть оснащено топологией, индуцированной . Предположим также, что выполнены следующие условия. Первое: для каждого , где , и произвольного состава . Второе: всякая функция, которая в каждой точке локально совпадает с некоторой функцией из , также принадлежит . Пара , для которой выполняются указанные выше условия, называется дифференциальным пространством Сикорского. ^[9] ${\displaystyle M}$ ${\displaystyle M}$ ${\displaystyle C\subseteq \mathbb {R} ^{M}}$ ${\displaystyle M}$ ${\displaystyle C}$ ${\displaystyle H\in C^{\infty }\left(\mathbb {R} ^{n}\right)}$ ${\displaystyle n\in \mathbb {N} }$ ${\displaystyle f_{1},\dots ,f_{n}\in C}$ ${\displaystyle H\circ \left(f_{1},\dots ,f_{n}\right)\in C}$ ${\displaystyle M}$ ${\displaystyle C}$ ${\displaystyle C}$ ${\displaystyle (M,C)}$

Смотрите также

• Геодезическая  - прямой путь на искривленной поверхности или римановом многообразии.
• Направленная статистика  - раздел статистики Pages displaying wikidata descriptions as a fallback: статистика на многообразиях.
• Список коллекторов
• Хронология многообразий  - Хронология математики
• Математика общей теории относительности  - Математические структуры и методы, используемые в общей теории относительности.

По размеру

• 3-многообразие  – Математическое пространство
• 4-многообразие  – Математическое пространство
• 5-многообразие  - Многообразие пятого измерения.
• Многообразия отображений  – локально выпуклые векторные пространства, удовлетворяющие очень мягкому условию полноты.Pages displaying wikidata descriptions as a fallback

Примечания

1. Например, см . Риаза, Рикардо (2008), Дифференциально-алгебраические системы: аналитические аспекты и схемные приложения, World Scientific, p. 110, ISBN 9789812791818; Ганнинг, RC (1990), Введение в голоморфные функции нескольких переменных, том 2, CRC Press, стр. 73, ISBN 9780534133092.
2. Сигэюки Морита; Теруко Нагасе; Кацуми Номидзу (2001). Геометрия дифференциальных форм . Книжный магазин Американского математического общества. п. 12. ISBN 0-8218-1045-6.^{[ мертвая ссылка ]}
3. Понятие карты можно формализовать как разложение ячеек.
4. Пуанкаре, Х. (1895). «Анализ ситуации». Журнал Политехнической школы . Серия 11 (на французском языке). Готье-Виллар.
5. Арнольд, VI (1998). «О преподавании математики». Успехи мат. Наук (на русском языке). 53 (319): 229–234. дои : 10.4213/rm5 .; перевод на русский Матем. Обзоры 53 (1998), вып. 1, 229–236
6. Уитни, Х. (1936). «Дифференцируемые многообразия». Анналы математики . Вторая серия. 37 (3): 645–680. дои : 10.2307/1968482. JSTOR  1968482.
7. Кервэр, М. (1961). «Многообразие, не допускающее никакой дифференцируемой структуры». Комментарий. Математика. Хелв . 35 (1): 1–14. дои : 10.1007/BF02565940. S2CID  120977898.
8. Брайант, Дж.; Ферри, С.; Мио, В.; Вайнбергер, С. (1996). «Топология многообразий гомологии». Анналы математики . Вторая серия. 143 (3): 435–467. arXiv : математика/9304210 . дои : 10.2307/2118532. JSTOR  2118532.
9. Сикорский, Р. (1967). «Абстрактная ковариантная производная». Коллоквиум Математикум . 18 : 251–272. дои : 10,4064/см-18-1-251-272 .

Рекомендации

• Фридман, Майкл Х. и Куинн, Фрэнк (1990) Топология 4-многообразий . Издательство Принстонского университета. ISBN 0-691-08577-3 . 
• Гиймен, Виктор и Поллак, Алан (1974) Дифференциальная топология . Прентис-Холл. ISBN 0-13-212605-2 . Текст для продвинутых студентов/первокурсников, вдохновленный Милнором. 
• Хемпель, Джон (1976) 3-многообразия . Издательство Принстонского университета. ISBN 0-8218-3695-1 . 
• Хирш, Моррис , (1997) Дифференциальная топология . Спрингер Верлаг. ISBN 0-387-90148-5 . Наиболее полный отчет с историческими сведениями и отличными, но трудными задачами. Стандартный справочник для желающих глубоко разобраться в предмете. 
• Кирби, Робион К. и Зибенманн, Лоуренс К. (1977) Основополагающие очерки топологических многообразий. Сглаживания и триангуляции . Издательство Принстонского университета. ISBN 0-691-08190-5 . Детальное изучение категории топологических многообразий. 
• Ли, Джон М. (2000) Введение в топологические многообразия . Спрингер-Верлаг. ISBN 0-387-98759-2 . Подробный и всеобъемлющий текст для выпускников первого года обучения. 
• Ли, Джон М. (2003) Введение в гладкие многообразия . Спрингер-Верлаг. ISBN 0-387-95495-3 . Подробный и всеобъемлющий текст для выпускников первого года обучения; продолжение книги «Введение в топологические многообразия» . 
• Мэсси, Уильям С. (1977) Алгебраическая топология: введение . Спрингер-Верлаг. ISBN 0-387-90271-6 . 
• Милнор, Джон (1997) Топология с дифференцируемой точки зрения . Издательство Принстонского университета. ISBN 0-691-04833-9 . Классическое краткое введение в дифференциальную топологию. 
• Манкрес, Джеймс Р. (1991) Анализ многообразий . Аддисон-Уэсли (перепечатано Westview Press) ISBN 0-201-51035-9 . Текст для студентов, рассматривающий многообразия в формате .  ${\displaystyle \mathbb {R} ^{n}}$
• Манкрес, Джеймс Р. (2000) Топология . Прентис Холл. ISBN 0-13-181629-2 . 
• Нойвирт, LP, изд. (1975) Узлы, группы и 3-многообразия. Статьи, посвященные памяти Р. Х. Фокса . Издательство Принстонского университета. ISBN 978-0-691-08170-0 . 
• Риман, Бернхард , Gesammelte mathematische Werke und wissenschaftlicher Nachlass , Sändig Reprint. ISBN 3-253-03059-8 .  
  • Grundlagen für eine allgemeine Theorie der Functionen einer veränderlichen complexen Grösse. Докторская диссертация 1851 года, в которой впервые появляется слово «многообразие» ( Mannigfaltigkeit ).
  • Ueber die Hypothesen, welche der Geometrie zu Grunde Ligen. Инаугурационная лекция в Гёттингене 1854 года ( Habilitationsschrift ).
• Спивак, Майкл (1965) Исчисление на многообразиях: современный подход к классическим теоремам расширенного исчисления . WA Benjamin Inc. (перепечатано Addison-Wesley и Westview Press). ISBN 0-8053-9021-9 . Знаменитый краткий текст для продвинутых студентов/первокурсников. 
• Спивак, Майкл (1999) Всеобъемлющее введение в дифференциальную геометрию (3-е издание) Publish or Perish Inc. Энциклопедическая пятитомная серия, в первой из которых представлено систематическое рассмотрение теории многообразий, римановой геометрии, классической дифференциальной геометрии и многих других тем. - и уровень выпускников второго года обучения.
• Ту, Лоринг В. (2011). Введение в многообразия (2-е изд.). Нью-Йорк: Спрингер. ISBN 978-1-4419-7399-3.. Краткий текст для выпускников первого курса.

Внешние ссылки

• «Многообразие», Математическая энциклопедия , EMS Press , 2001 [1994]
• Dimensions-math.org (Фильм, объясняющий и визуализирующий многообразия до четвертого измерения.)
• Проект атласа многообразий Математического института Макса Планка в Бонне.