Система рейтинга Эло

Метод расчета относительного уровня мастерства игроков

Арпад Эло , изобретатель рейтинговой системы Эло

Рейтинговая система Эло ^[a] — это метод расчета относительного уровня мастерства игроков в играх с нулевой суммой, таких как шахматы или киберспорт . Она названа в честь своего создателя Арпада Эло , венгерско-американского профессора физики.

Система Эло была изобретена как усовершенствованная система рейтинга шахмат по сравнению с ранее использовавшейся системой Харкнесса [ ^1], но также используется в качестве рейтинговой системы в американском футболе , бейсболе , баскетболе , бильярде , различных настольных играх и киберспорте , а в последнее время и в крупных языковых моделях .

Разница в рейтингах двух игроков служит предиктором исхода матча. Ожидается, что два игрока с одинаковым рейтингом, играющие друг против друга, наберут равное количество побед. Игрок, рейтинг которого на 100 очков больше, чем у соперника, как ожидается, наберет 64%; если разница составляет 200 очков, то ожидаемый счет для более сильного игрока составляет 76%. ^[2]

Рейтинг Эло игрока — это число, которое может меняться в зависимости от результатов сыгранных рейтинговых игр. После каждой игры победитель забирает очки у проигравшего. Разница между рейтингами победителя и проигравшего определяет общее количество очков, полученных или потерянных после игры. Если выигрывает игрок с более высоким рейтингом, то у игрока с более низким рейтингом будет взято всего несколько рейтинговых очков. Однако, если игрок с более низким рейтингом одерживает неожиданную победу , многие рейтинговые очки будут переведены. Игрок с более низким рейтингом также получит несколько очков от игрока с более высоким рейтингом в случае ничьей. Это означает, что эта рейтинговая система является самокорректирующейся. Игроки, рейтинги которых слишком низкие или слишком высокие, должны в долгосрочной перспективе играть лучше или хуже, чем предсказывает рейтинговая система, и, таким образом, получать или терять рейтинговые очки до тех пор, пока рейтинги не отразят их истинную игровую силу.

Рейтинги Эло носят сравнительный характер и действительны только в пределах пула рейтингов, в котором они были рассчитаны, а не являются абсолютной мерой силы игрока.

Хотя системы, подобные Эло, широко используются в соревнованиях с двумя игроками, их вариации также применяются в многопользовательских соревнованиях. ^[3]

История

Арпад Эло был шахматным мастером и активным участником Федерации шахмат США (USCF) с момента ее основания в 1939 году. ^[4] USCF использовала числовую систему рейтингов, разработанную Кеннетом Харкнессом , чтобы позволить членам отслеживать свой индивидуальный прогресс в терминах, отличных от побед и поражений в турнирах. Система Харкнесса была достаточно справедливой, но в некоторых обстоятельствах приводила к рейтингам, которые многие наблюдатели считали неточными.

От имени USCF Эло разработал новую систему с более надежной ^{[ требуется разъяснение ]} статистической основой. ^[5] Примерно в то же время Дьёрдь Карой и Роджер Кук независимо друг от друга разработали систему, основанную на тех же принципах, для Шахматной ассоциации Нового Южного Уэльса. ^[6]

Система Эло заменила более ранние системы соревновательных наград системой, основанной на статистической оценке. Рейтинговые системы для многих видов спорта присуждают очки в соответствии с субъективными оценками «величия» определенных достижений. Например, победа в важном турнире по гольфу может стоить произвольно выбранного в пять раз большего количества очков, чем победа в менее значимом турнире.

Статистический подход, напротив, использует модель, которая связывает результаты игры с базовыми переменными, отражающими способности каждого игрока.

Центральным предположением Эло было то, что шахматная производительность каждого игрока в каждой игре является нормально распределенной случайной величиной . Хотя игрок может играть значительно лучше или хуже от одной игры к другой, Эло предполагал, что среднее значение производительности любого данного игрока меняется лишь медленно с течением времени. Эло считал истинное мастерство игрока средним значением случайной величины производительности этого игрока.

Необходимо еще одно предположение, поскольку шахматная производительность в указанном выше смысле все еще не поддается измерению. Нельзя посмотреть на последовательность ходов и вывести число, представляющее мастерство игрока. Производительность можно вывести только из побед, ничьих и поражений. Поэтому предполагается, что игрок, выигравший игру, выступил на более высоком уровне, чем его противник в этой игре. И наоборот, предполагается, что проигравший игрок выступил на более низком уровне. Если игра заканчивается вничью, предполагается, что оба игрока выступили примерно на одинаковом уровне.

Эло не уточнил, насколько близкими должны быть два выступления, чтобы получить ничью, а не победу или поражение. На самом деле, существует вероятность ничьей, которая зависит от разницы в результатах, поэтому последняя является скорее доверительным интервалом, чем какой-либо детерминированной границей. И хотя он считал, что игроки, вероятно, могут иметь разные стандартные отклонения в своих выступлениях, он сделал упрощающее предположение об обратном.

Чтобы еще больше упростить вычисления, Эло предложил простой метод оценки переменных в своей модели (т. е. истинного мастерства каждого игрока). Можно было относительно легко рассчитать по таблицам, сколько игр игроки, как ожидается, выиграют, на основе сравнения их рейтингов с рейтингами их противников. Рейтинги игрока, который выиграл больше игр, чем ожидалось, будут скорректированы вверх, в то время как рейтинги игрока, который выиграл меньше, чем ожидалось, будут скорректированы вниз. Более того, эта корректировка должна была быть линейно пропорциональна количеству побед, на которое игрок превысил или не дотянул до своего ожидаемого числа. ^[7]

С современной точки зрения, упрощающие предположения Эло не нужны, поскольку вычислительная мощность недорога и широко доступна. Несколько человек, в частности Марк Гликман , предложили использовать более сложную статистическую технику для оценки тех же переменных. С другой стороны, вычислительная простота системы Эло оказалась одним из ее величайших преимуществ. С помощью карманного калькулятора информированный шахматный участник может рассчитать с точностью до одной точки, каким будет его следующий официально опубликованный рейтинг, что помогает создать впечатление, что рейтинги справедливы.

Реализация схемы Эло

USCF внедрила предложения Эло в 1960 году, ^[8] и система быстро получила признание как более справедливая и точная, чем рейтинговая система Харкнесса . Система Эло была принята Всемирной шахматной федерацией (ФИДЕ) в 1970 году. ^[9] Эло подробно описал свою работу в книге «Рейтинг шахматистов прошлого и настоящего» , впервые опубликованной в 1978 году. ^[10]

Последующие статистические тесты показали, что шахматная производительность почти наверняка не распределена как нормальное распределение , поскольку более слабые игроки имеют больше шансов на победу, чем предсказывает модель Эло. ^{[11] [12]} В данных парного сравнения часто очень мало практической разницы в том, предполагается ли, что различия в силе игроков распределены нормально или логистически . Математически, однако, логистическая функция удобнее для работы, чем нормальное распределение. ^[13] ФИДЕ продолжает использовать таблицу разницы рейтингов, предложенную Эло. ^{[14] : таблица 8.1b}

Разработка Таблицы процентного ожидания (таблица 2.11) более подробно описана Эло следующим образом: ^[15]

Нормальные вероятности можно взять непосредственно из стандартных таблиц площадей под нормальной кривой, когда разница в рейтинге выражена как счет z. Поскольку стандартное отклонение σ индивидуальных результатов определяется как 200 баллов, стандартное отклонение σ' различий в результатах становится σ√2 или 282,84. Значение z разницы тогда равно D / 282,84 . Это затем разделит площадь под кривой на две части, большая из которых дает P для игрока с более высоким рейтингом, а меньшая дает P для игрока с более низким рейтингом.

Например, пусть D = 160. Тогда z = 160 / 282,84 = .566 . Таблица дает .7143 и .2857 как площади двух частей под кривой. Эти вероятности округлены до двух цифр в таблице 2.11.

Таблица фактически построена со стандартным отклонением 200(10/7) в качестве приближения для 200√2 . ^{[ требуется ссылка ]}

Нормальное и логистическое распределения, в некотором смысле, являются произвольными точками в спектре распределений, которые будут работать хорошо. На практике оба эти распределения работают очень хорошо для ряда различных игр. ^{[ необходима цитата ]}

Различные системы оценок

Фраза «рейтинг Эло» часто используется для обозначения шахматного рейтинга игрока, рассчитанного ФИДЕ. Однако такое использование может сбивать с толку или вводить в заблуждение, поскольку общие идеи Эло были приняты многими организациями, включая USCF (до ФИДЕ), многими другими национальными шахматными федерациями, недолго просуществовавшей Профессиональной шахматной ассоциацией (PCA) и онлайн-шахматными серверами, включая Internet Chess Club (ICC), Free Internet Chess Server (FICS), Lichess , Chess.com и Yahoo! Games. У каждой организации есть уникальная реализация, и ни одна из них не следует в точности первоначальным предложениям Эло.

Вместо этого можно ссылаться на организацию, присвоившую рейтинг. Например: «По состоянию на апрель 2018 года рейтинг ФИДЕ Татев Абрамян составил 2366, а рейтинг USCF — 2473». Рейтинги Эло этих различных организаций не всегда напрямую сопоставимы, поскольку рейтинги Эло измеряют результаты в закрытом пуле игроков, а не абсолютное мастерство.

Рейтинги ФИДЕ

Для лучших игроков самым важным рейтингом является рейтинг ФИДЕ . ФИДЕ опубликовала следующие списки:

• С 1971 по 1980 год выпускался один список в год.
• С 1981 по 2000 год списки публиковались два раза в год: в январе и июле.
• С июля 2000 года по июль 2009 года ежегодно публиковалось четыре списка: в начале января, апреля, июля и октября.
• С июля 2009 года по июль 2012 года ежегодно публиковалось шесть списков: в начале января, марта, мая, июля, сентября и ноября.
• С июля 2012 года список обновляется ежемесячно.

Следующий анализ рейтинг-листа ФИДЕ за июль 2015 года дает приблизительное представление о том, что означает данный рейтинг ФИДЕ с точки зрения мирового рейтинга:

• 5323 игрока имели активный рейтинг в диапазоне от 2200 до 2299, что обычно соответствует званию кандидата в мастера .
• 2869 игроков имели активный рейтинг в диапазоне от 2300 до 2399, что обычно соответствует званию мастера ФИДЕ .
• 1420 игроков имели активный рейтинг от 2400 до 2499, большинство из них имели звание международного мастера или международного гроссмейстера .
• 542 игрока имели активный рейтинг от 2500 до 2599, большинство из них имели звание международного гроссмейстера .
• 187 игроков имели активный рейтинг от 2600 до 2699, все из них имели звание международного гроссмейстера .
• 40 игроков имели активный рейтинг от 2700 до 2799.
• У 4 игроков активный рейтинг был выше 2800. ( У Магнуса Карлсена рейтинг был 2853, а у 3 игроков — между 2814 и 2816).

Самый высокий рейтинг ФИДЕ был 2882, который был у Магнуса Карлсена в списке за май 2014 года. Список игроков с самым высоким рейтингом за всю историю можно найти на странице Сравнение лучших шахматистов за всю историю .

Рейтинг производительности

Рейтинг производительности или специальный рейтинг — это гипотетический рейтинг, который может быть получен из игр только одного события. Некоторые шахматные организации ^{[16] : стр. 8} используют «алгоритм 400» для расчета рейтинга производительности. Согласно этому алгоритму, рейтинг производительности для события рассчитывается следующим образом:

1. За каждую победу прибавляйте к рейтингу противника 400,
2. За каждое поражение прибавляйте рейтинг противника минус 400,
3. И разделите эту сумму на количество сыгранных игр.

Пример: 2 победы (оппоненты w и x ), 2 поражения (оппоненты y и z )

${\displaystyle {\begin{aligned}&{\frac {w+400+x+400+y-400+z-400}{4}}\\[6pt]&{\frac {w+x+y+z+400(2)-400(2)}{4}}\end{aligned}}}$

Это можно выразить следующей формулой:

${\displaystyle {\text{performance rating}}={\frac {{\text{total of opponents' ratings }}+400\times ({\text{wins}}-{\text{losses}})}{\text{games}}}}$

Пример: Если вы победили игрока с рейтингом Эло 1000,

${\displaystyle {\text{performance rating}}={\frac {1000+400\times (1)}{1}}=1400}$

Если вы победите двух игроков с рейтингом Эло 1000,

${\displaystyle {\text{performance rating}}={\frac {2000+400\times (2)}{2}}=1400}$

Если вы рисуете,

${\displaystyle {\text{performance rating}}={\frac {1000+400\times (0)}{1}}=1000}$

Это упрощение, но оно предлагает простой способ получить оценку PR (рейтинга эффективности).

Однако ФИДЕ вычисляет рейтинг производительности с помощью формулы , где «разница рейтингов» основана на процентном счете игрока в турнире , который затем используется как ключ в таблице поиска, где это просто количество набранных очков, деленное на количество сыгранных партий. Обратите внимание, что в случае идеального или нулевого счета это 800. $${\displaystyle {\text{performance rating}}={\text{average of opponents' ratings}}+d_{p},}$$ ${\displaystyle d_{p}}$ ${\displaystyle p}$ ${\displaystyle p}$ ${\displaystyle d_{p}}$

Текущие рейтинги

FIDE обновляет свой рейтинговый список в начале каждого месяца. Напротив, неофициальные «Live-рейтинги» подсчитывают изменение рейтингов игроков после каждой игры. Эти Live-рейтинги основаны на ранее опубликованных рейтингах FIDE, поэтому Live-рейтинг игрока должен соответствовать тому, каким был бы рейтинг FIDE, если бы FIDE опубликовала новый список в тот день.

Хотя рейтинги Live неофициальны, интерес к ним возник в августе/сентябре 2008 года, когда пять разных игроков заняли первое место в рейтинге «Live». ^[17]

Неофициальные рейтинги игроков выше 2700 публиковались и поддерживались Хансом Арильдом Рунде на сайте Live Rating до августа 2011 года. Другой сайт, 2700chess.com, поддерживается с мая 2011 года Артёмом Цепотаном и охватывает 100 лучших игроков, а также 50 лучших женщин-шахматистов.

Изменения рейтинга можно рассчитать вручную с помощью калькулятора изменения рейтинга ФИДЕ. ^[18] Все ведущие игроки имеют К-фактор 10, что означает, что максимальное изменение рейтинга за одну игру составляет чуть меньше 10 очков.

Рейтинги Федерации шахмат США

Федерация шахмат США (USCF) использует собственную классификацию игроков: ^[19]

• 2400 и выше: Старший магистр
• 2200–2399: Национальный мастер
  • 2200–2399 плюс 300 игр после 2200: Original Life Master ^[20]
• 2000–2199: Эксперт или Кандидат в мастера
• 1800–1999: Класс А
• 1600–1799: Класс B
• 1400–1599: Класс C
• 1200–1399: Класс D
• 1000–1199: Класс E
• 800–999: Класс F
• 600–799: Класс G
• 400–599: Класс H
• 200–399: Класс I
• 100–199: Класс J

K-фактор, используемый USCF

K -фактор в рейтинговой системе USCF можно оценить, разделив 800 на эффективное количество игр, на которых основан рейтинг игрока ( N _e ), плюс количество игр, которые игрок завершил в турнире ( m ). ^[21]

${\displaystyle K={\frac {800}{N_{e}+m}}\,}$

Рейтинг этажей

USCF поддерживает абсолютный рейтинговый минимум 100 для всех рейтингов. Таким образом, ни один член не может иметь рейтинг ниже 100, независимо от их результатов на санкционированных USCF мероприятиях. Однако игроки могут иметь более высокие индивидуальные абсолютные рейтинговые минимумы, рассчитанные по следующей формуле:

${\displaystyle AF=\operatorname {min} \{100+4N_{W}+2N_{D}+N_{R},150\}}$

где — количество выигранных рейтинговых игр, — количество рейтинговых игр, сыгранных вничью, — количество событий, в которых игрок завершил три или более рейтинговых игр. ${\displaystyle N_{W}}$ ${\displaystyle N_{D}}$ ${\displaystyle N_{R}}$

Более высокие рейтинговые полы существуют для опытных игроков, которые достигли значительных рейтингов. Такие более высокие рейтинговые полы существуют, начиная с рейтингов 1200 с шагом в 100 очков до 2100 (1200, 1300, 1400, ..., 2100). Рейтинговый пол рассчитывается путем взятия пикового установленного рейтинга игрока, вычитания 200 очков, а затем округления вниз до ближайшего рейтингового пола. Например, игрок, достигший пикового рейтинга 1464, будет иметь рейтинговый пол 1464 − 200 = 1264 , который будет округлен вниз до 1200. В рамках этой схемы только игроки класса C и выше могут иметь рейтинговый пол выше, чем их абсолютный рейтинг игрока. Все остальные игроки будут иметь пол не более 150.

Есть два способа достичь более высоких рейтинговых уровней, помимо стандартной схемы, представленной выше. Если игрок достиг рейтинга Original Life Master, его рейтинговый уровень устанавливается на уровне 2200. Достижение этого звания уникально тем, что ни один другой признанный титул USCF не приведет к новому уровню. Для игроков с рейтингом ниже 2000 выигрыш денежного приза в размере $2000 или более повышает рейтинговый уровень этого игрока до ближайшего уровня в 100 очков, который дисквалифицировал бы игрока для участия в турнире. Например, если игрок выиграл $4000 в турнире 1750 и ниже, его рейтинговый уровень теперь будет равен 1800.

Теория

Попарные сравнения составляют основу методологии рейтинга Эло. ^[22] Эло ссылался на работы Гуда, ^[23] Дэвида, ^[24] Травински и Дэвида, ^[25] а также Бульмана и Хубера. ^[26]

Математические подробности

Производительность не измеряется абсолютно; она выводится из побед, поражений и ничьих против других игроков. Рейтинги игроков зависят от рейтингов их противников и результатов, набранных против них. Разница в рейтинге между двумя игроками определяет оценку ожидаемого счета между ними. Как среднее значение, так и разброс рейтингов могут быть выбраны произвольно. USCF изначально стремился к тому, чтобы средний клубный игрок имел рейтинг 1500, и Эло предложил масштабировать рейтинги таким образом, чтобы разница в 200 очков рейтинга в шахматах означала, что более сильный игрок имеет ожидаемый счет приблизительно 0,75.

Ожидаемый счет игрока — это вероятность его победы плюс половина вероятности ничьей. Таким образом, ожидаемый счет 0,75 может представлять 75% вероятности победы, 25% вероятности проигрыша и 0% вероятности ничьей. С другой стороны, он может представлять 50% вероятности победы, 0% вероятности проигрыша и 50% вероятности ничьей. Вероятность ничьей, в отличие от решающего результата, не указана в системе Эло. Вместо этого ничья считается половиной победы и половиной поражения. На практике, поскольку истинная сила каждого игрока неизвестна, ожидаемые баллы рассчитываются с использованием текущих рейтингов игрока следующим образом.

Если  рейтинг игрока A равен , а рейтинг игрока  B равен , то точная формула (с использованием логистической кривой с основанием 10 ) ^[27] для ожидаемого счета игрока  A будет следующей: ${\displaystyle \,R_{\mathsf {A}}\,}$ ${\displaystyle \,R_{\mathsf {B}}\,}$

${\displaystyle E_{\mathsf {A}}={\frac {1}{1+10^{(R_{\mathsf {B}}-R_{\mathsf {A}})/400}}}~.}$

Аналогично, ожидаемый счет для игрока  B составляет

${\displaystyle E_{\mathsf {B}}={\frac {1}{1+10^{(R_{\mathsf {A}}-R_{\mathsf {B}})/400}}}~.}$

Это также может быть выражено следующим образом:

${\displaystyle E_{\mathsf {A}}={\frac {Q_{\mathsf {A}}}{Q_{\mathsf {A}}+Q_{\mathsf {B}}}}}$

и

${\displaystyle E_{\mathsf {B}}={\frac {Q_{\mathsf {B}}}{Q_{\mathsf {A}}+Q_{\mathsf {B}}}}~,}$

где и Обратите внимание, что в последнем случае один и тот же знаменатель применяется к обоим выражениям, и очевидно, что Это означает, что, изучая только числители, мы обнаруживаем, что ожидаемый счет для игрока  A в раз больше ожидаемого счета для игрока  B. Из этого следует, что на каждые 400 очков рейтинга преимущества над противником ожидаемый счет увеличивается в десять раз по сравнению с ожидаемым счетом противника. ${\displaystyle \;Q_{\mathsf {A}}=10^{R_{\mathsf {A}}/400}\;,}$ ${\displaystyle \;Q_{\mathsf {B}}=10^{R_{\mathsf {B}}/400}~.}$ ${\displaystyle \;E_{\mathsf {A}}+E_{\mathsf {B}}=1~.}$ ${\displaystyle \;Q_{\mathsf {A}}/Q_{\mathsf {B}}\;}$

Когда фактические результаты игрока на турнире превышают ожидаемые результаты, система Эло воспринимает это как доказательство того, что рейтинг игрока слишком низок и его необходимо скорректировать в сторону повышения. Аналогично, когда фактические результаты игрока на турнире не достигают ожидаемых результатов, рейтинг этого игрока корректируется в сторону понижения. Первоначальное предложение Эло, которое до сих пор широко используется, представляло собой простую линейную корректировку, пропорциональную сумме, на которую игрок переиграл или недоиграл ожидаемый результат. Максимально возможная корректировка за игру, называемая K-фактором, была установлена ​​для мастеров и для более слабых игроков. ${\displaystyle \;K=16\;}$ ${\displaystyle \;K=32\;}$

Предположим, что игрок  A (снова с рейтингом ) должен был набрать очки, но на самом деле набрал очки. Формула для обновления рейтинга этого игрока: ${\displaystyle R_{\mathsf {A}}}$ ${\displaystyle \,E_{\mathsf {A}}\,}$ ${\displaystyle \,S_{\mathsf {A}}\,}$

${\displaystyle R_{\mathsf {A}}'=R_{\mathsf {A}}+K\cdot (S_{\mathsf {A}}-E_{\mathsf {A}})~.}$^[1]

Это обновление можно выполнять после каждой игры или каждого турнира, или после любого подходящего рейтингового периода.

Пример может помочь прояснить ситуацию:

Предположим, что игрок  A имеет рейтинг 1613 и играет в пятираундовом турнире. Они проигрывают игроку с рейтингом 1609, играют вничью с игроком с рейтингом 1477, побеждают игрока с рейтингом 1388, побеждают игрока с рейтингом 1586 и проигрывают игроку с рейтингом 1720. Фактический счет игрока составляет (0 + 0,5 + 1 + 1 + 0) = 2,5 . Ожидаемый счет, рассчитанный по формуле выше, составил (0,51 + 0,69 + 0,79 + 0,54 + 0,35) = 2,88 .

Таким образом, новый рейтинг игрока равен [1613 + 32·(2,5 − 2,88)] = 1601 , предполагая, что используется коэффициент K , равный 32. Эквивалентно, в каждой игре игрок, можно сказать, внес в банк анте в размере K , умноженное на его ожидаемый счет в игре, соперник делает то же самое, и победитель забирает весь банк стоимостью K ; в случае ничьей игроки делят банк и получают очки каждый. ${\displaystyle \;{\tfrac {1}{2}}K\;}$

Обратите внимание, что хотя две победы, два поражения и одна ничья могут показаться нормальным счетом, для игрока  A это хуже, чем ожидалось , поскольку его противники имели более низкий средний рейтинг. Поэтому игрок  A немного наказан. Если бы игрок  A набрал две победы, одно поражение и две ничьи, набрав в общей сложности три очка, это было бы немного лучше, чем ожидалось, и новый рейтинг игрока был бы [1613 + 32·(3 − 2,88)] = 1617 .

Эта процедура обновления лежит в основе рейтингов, используемых FIDE , USCF , Yahoo! Games , Internet Chess Club (ICC) и Free Internet Chess Server (FICS). Однако каждая организация по-своему подходит к решению проблемы неопределенности, присущей рейтингам, особенно рейтингам новичков, и к решению проблемы инфляции/дефляции рейтингов. Новым игрокам присваиваются предварительные рейтинги, которые корректируются более радикально, чем установленные рейтинги.

Принципы, используемые в этих рейтинговых системах, можно использовать для рейтингования других соревнований, например, международных футбольных матчей.

Рейтинги Эло также применялись к играм без возможности ничьей и к играм, в которых результат может иметь не только качество (выигрыш/проигрыш), но и количество (маленький/большой перевес). Подробнее см. в разделе Рейтинг го с Эло .

Предлагаемая модификация

В 2011 году после анализа 1,5 миллионов рейтинговых партий ФИДЕ Джефф Сонас продемонстрировал, что согласно формуле Эло, два игрока с разницей в рейтинге X на самом деле имеют истинную разницу около X (5/6) . Аналогично, можно оставить разницу в рейтинге в покое и разделить на 480 вместо 400. Поскольку формула Эло переоценивает вероятность победы более сильного игрока, более сильные игроки теряют очки против более слабых игроков, несмотря на то, что играют в свою истинную силу. Аналогично, более слабые игроки набирают очки против более сильных игроков. При применении модификации наблюдаемые показатели выигрышей отклоняются менее чем на 0,1% от прогнозируемого показателя, в то время как традиционный Эло может отличаться на 4% от прогнозируемого показателя. ^[28]

Самая точная модель распределения

Первой математической проблемой, рассмотренной USCF, было использование нормального распределения . Они обнаружили, что оно неточно отражает фактические результаты, достигнутые, особенно игроками с низким рейтингом. Вместо этого они перешли на модель логистического распределения , которая, как обнаружила USCF, лучше подходит для фактических результатов. ^{[29] [ необходима цитата ]} ФИДЕ также использует приближение к логистическому распределению. ^[14]

Самый точный К-фактор

Вторая серьезная проблема — это правильность используемого « K -фактора». Шахматный статистик Джефф Сонас считает, что исходное значение (для игроков с рейтингом выше 2400) в работе Эло неточно. Если коэффициент K -фактора установлен слишком большим, то будет слишком большая чувствительность к нескольким недавним событиям с точки зрения большого количества очков, обмененных в каждой игре. А если K-значение слишком низкое, чувствительность будет минимальной, и система не будет достаточно быстро реагировать на изменения фактического уровня игры игрока. ${\displaystyle \;K=10\;}$

Первоначальная оценка К -фактора Эло была сделана без использования огромных баз данных и статистических данных. Сонас указывает, что К -фактор 24 (для игроков с рейтингом выше 2400) может быть как более точным инструментом прогнозирования будущих результатов, так и более чувствительным к результатам. ^[30]

Некоторые шахматные сайты в Интернете, похоже, избегают трехуровневого K-фактора, основанного на диапазоне рейтинга. Например, ICC, похоже, принимает глобальный K = 32, за исключением игр с игроками с предварительным рейтингом.

Ранее USCF (который использует логистическое распределение , а не нормальное ) распределял K-фактор по трем основным рейтинговым диапазонам:

В настоящее время USCF использует формулу, которая вычисляет K -фактор на основе таких факторов, как количество сыгранных игр и рейтинг игрока. K-фактор также уменьшается для игроков с высоким рейтингом, если в событии более короткий контроль времени. ^[16]

ФИДЕ использует следующие диапазоны: ^[31]

До июля 2014 года ФИДЕ использовала следующие диапазоны: ^[32]

Градация К -фактора снижает изменение рейтинга в верхней части диапазона рейтинга, уменьшая возможность быстрого роста или падения рейтинга для тех, чей рейтинг достаточно высок, чтобы достичь низкого К -фактора.

Теоретически это может применяться в равной степени к игрокам в шахматы онлайн и игрокам в шахматы за доской, поскольку всем игрокам сложнее повышать свой рейтинг после того, как их рейтинг стал высоким, а их К -фактор, соответственно, снизился. Однако, играя онлайн, игроки с рейтингом 2800+ могут легче повышать свой рейтинг, просто выбирая соперников с высоким рейтингом — на игровом сайте ICC гроссмейстер может играть с рядом разных соперников, все из которых имеют рейтинг выше 2700. ^[34] В соревнованиях за доской только в очень высоких турнирах all-play-all игрок сможет сразиться с таким количеством соперников 2700+. В обычном открытом турнире по шахматам по швейцарской системе часто будет много соперников с рейтингом ниже 2500, что снижает возможный прирост рейтинга за один поединок для игрока с высоким рейтингом.

Формальный вывод для игр с выигрышем/проигрышем

Вышеуказанные выражения теперь можно формально вывести, используя связь между рейтингом Эло и обновлением стохастического градиента в логистической регрессии. ^{[35] [36]}

Если предположить, что результаты игры являются бинарными , то есть можно наблюдать только победу или поражение, то проблему можно решить с помощью логистической регрессии , где результаты игры являются зависимыми переменными , рейтинги игроков являются независимыми переменными , а модель, связывающая их, является вероятностной: вероятность победы игрока в игре моделируется как ${\displaystyle {\mathsf {A}}}$

${\displaystyle \Pr\{{\mathsf {A}}~{\textrm {wins}}\}=\sigma (r_{\mathsf {A,B}}),\quad \sigma (r)={\frac {1}{1+10^{-r/s}}},}$

где

${\displaystyle r_{\mathsf {A,B}}=(R_{\mathsf {A}}-R_{\mathsf {B}})}$

обозначает разницу рейтингов игроков, и мы используем масштабирующий коэффициент , и, по закону полной вероятности ${\displaystyle s=400}$

${\displaystyle \Pr\{{\mathsf {B}}~{\textrm {wins}}\}=1-\sigma (r_{\mathsf {A,B}})=\sigma (-r_{\mathsf {A,B}}).}$

Логарифмическая потеря затем рассчитывается как

${\displaystyle \ell ={\begin{cases}-\log \sigma (r_{\mathsf {A,B}})&{\textrm {if}}~{\mathsf {A}}~{\textrm {wins}},\\-\log \sigma (-r_{\mathsf {A,B}})&{\textrm {if}}~{\mathsf {B}}~{\textrm {wins}},\end{cases}}}$

и, используя стохастический градиентный спуск, логарифмические потери минимизируются следующим образом:

${\displaystyle R_{\mathsf {A}}\leftarrow R_{\mathsf {A}}-\eta {\frac {{\textrm {d}}\ell }{{\textrm {d}}R_{\mathsf {A}}}}}$,

${\displaystyle R_{\mathsf {B}}\leftarrow R_{\mathsf {B}}-\eta {\frac {{\textrm {d}}\ell }{{\textrm {d}}R_{\mathsf {B}}}}}$.

где находится шаг адаптации. ${\displaystyle \eta }$

Так как , , и , то адаптация записывается следующим образом ${\displaystyle {\frac {\textrm {d}}{{\textrm {d}}r}}\log \sigma (r)={\frac {\log 10}{s}}\sigma (-r)}$ ${\displaystyle {\frac {{\textrm {d}}r_{\mathsf {A,B}}}{{\textrm {d}}R_{\mathsf {A}}}}=1}$ ${\displaystyle {\frac {{\textrm {d}}r_{\mathsf {A,B}}}{{\textrm {d}}R_{\mathsf {B}}}}=-1}$

${\displaystyle R_{\mathsf {A}}\leftarrow {\begin{cases}R_{\mathsf {A}}+K\sigma (-r_{\mathsf {A,B}})&{\textrm {if}}~{\mathsf {A}}~{\textrm {wins}}\\R_{\mathsf {A}}-K\sigma (r_{\mathsf {A,B}})&{\textrm {if}}~{\mathsf {B}}~{\textrm {wins}},\end{cases}}}$

что можно компактно записать как

${\displaystyle R_{\mathsf {A}}\leftarrow R_{\mathsf {A}}+K(S_{\mathsf {A}}-E_{\mathsf {A}})}$

где — новый шаг адаптации, который поглощает и , если выигрывает и , если выигрывает, а ожидаемая оценка определяется как . ${\displaystyle K=\eta \log 10/s}$ ${\displaystyle \eta }$ ${\displaystyle s}$ ${\displaystyle S_{\mathsf {A}}=1}$ ${\displaystyle {\mathsf {A}}}$ ${\displaystyle S_{\mathsf {A}}=0}$ ${\displaystyle {\mathsf {B}}}$ ${\displaystyle E_{\mathsf {A}}=\sigma (r_{\mathsf {A,B}})}$

Аналогично, обновление рейтинга : ${\displaystyle R_{\mathsf {B}}}$

${\displaystyle R_{\mathsf {B}}\leftarrow R_{\mathsf {B}}+K(S_{\mathsf {B}}-E_{\mathsf {B}})}$.

Формальный вывод для игр с выигрышем/ничьей/проигрышем

С самого начала рейтинг Эло также использовался в шахматах, где мы наблюдаем победы, поражения или ничьи, и для решения последней вводится дробное значение счета, . Однако мы отмечаем, что счета и являются лишь индикаторами событий, когда игрок выигрывает или проигрывает игру. Поэтому не сразу ясно, в чем смысл дробного счета. Более того, поскольку мы не указываем явно модель, связывающую значения рейтинга и вероятность исхода игры, мы не можем сказать, какова вероятность победы, поражения или ничьи. ${\displaystyle S_{\mathsf {A}}=0.5}$ ${\displaystyle S_{\mathsf {A}}=1}$ ${\displaystyle S_{\mathsf {A}}=0}$ ${\displaystyle {\mathsf {A}}}$ ${\displaystyle R_{\mathsf {A}}}$ ${\displaystyle R_{\mathsf {B}}}$

Чтобы преодолеть эти трудности и вывести рейтинг Эло в тернарных играх, мы определим явную вероятностную модель результатов. Затем мы минимизируем логарифмические потери с помощью стохастического градиента.

Поскольку проигрыш, ничья и выигрыш являются порядковыми переменными , нам следует принять модель, которая учитывает их порядковую природу, и мы используем так называемую модель смежных категорий, которая может быть прослежена до работы Дэвидсона ^[37].

${\displaystyle \Pr\{{\mathsf {A}}~{\textrm {wins}}\}=\sigma (r_{\mathsf {A,B}};\kappa ),}$

${\displaystyle \Pr\{{\mathsf {B}}~{\textrm {wins}}\}=\sigma (-r_{\mathsf {A,B}};\kappa ),}$

${\displaystyle \Pr\{{\mathsf {A}}~{\textrm {draws}}\}=\kappa {\sqrt {\sigma (r_{\mathsf {A,B}};\kappa )\sigma (-r_{\mathsf {A,B}};\kappa )}},}$

где

${\displaystyle \sigma (r;\kappa )={\frac {10^{r/s}}{10^{-r/s}+\kappa +10^{r/s}}}}$

и является параметром. Введение свободного параметра не должно вызывать удивления, поскольку у нас есть три возможных результата, и, таким образом, в модели должна появиться дополнительная степень свободы. В частности, с помощью мы восстанавливаем модель, лежащую в основе логистической регрессии ${\displaystyle \kappa \geq 0}$ ${\displaystyle \kappa =0}$

${\displaystyle \Pr\{{\mathsf {A}}~{\textrm {wins}}\}=\sigma (r_{\mathsf {A,B}};0)={\frac {10^{r_{\mathsf {A,B}}/s}}{10^{-r_{\mathsf {A,B}}/s}+10^{r_{\mathsf {A,B}}/s}}}={\frac {1}{1+10^{-r_{\mathsf {A,B}}/s'}}},}$

где . ${\displaystyle s'=s/2}$

Используя порядковую модель, определенную выше, логарифмическая потеря теперь рассчитывается как

${\displaystyle \ell ={\begin{cases}-\log \sigma (r_{\mathsf {A,B}};\kappa )&{\textrm {if}}~{\mathsf {A}}~{\textrm {wins}},\\-\log \sigma (-r_{\mathsf {A,B}};\kappa )&{\textrm {if}}~{\mathsf {B}}~{\textrm {wins}},\\-\log \kappa -{\frac {1}{2}}\log \sigma (r_{\mathsf {A,B}};\kappa )-{\frac {1}{2}}\log \sigma (-r_{\mathsf {A,B}};\kappa )&{\textrm {if}}~{\mathsf {A}}~{\textrm {draw}},\end{cases}}}$

что можно компактно записать как

${\displaystyle \ell =-(S_{\mathsf {A}}+{\frac {1}{2}}D)\log \sigma (r_{\mathsf {A,B}};\kappa )-(S_{\mathsf {B}}+{\frac {1}{2}}D)\log \sigma (-r_{\mathsf {A,B}};\kappa )-D\log \kappa }$

где iff выигрывает, iff выигрывает и iff играет вничью. ${\displaystyle S_{\mathsf {A}}=1}$ ${\displaystyle {\mathsf {A}}}$ ${\displaystyle S_{\mathsf {B}}=1}$ ${\displaystyle {\mathsf {B}}}$ ${\displaystyle D=1}$ ${\displaystyle {\mathsf {A}}}$

Как и прежде, нам нужна производная, которая задается выражением ${\displaystyle \log \sigma (r;\kappa )}$

${\displaystyle {\frac {\textrm {d}}{{\textrm {d}}r}}\log \sigma (r;\kappa )={\frac {2\log 10}{s}}[1-g(r;\kappa )]}$,

где

${\displaystyle g(r;\kappa )={\frac {10^{r/s}+\kappa /2}{10^{-r/s}+\kappa +10^{r/s}}}.}$

Таким образом, производная логарифмической потери по отношению к рейтингу определяется выражением ${\displaystyle R_{\mathsf {A}}}$

${\displaystyle {\begin{aligned}{\frac {\textrm {d}}{{\textrm {d}}R_{\mathsf {A}}}}\ell &=-{\frac {2\log 10}{s}}\left((S_{\mathsf {A}}+0.5D)[1-g(r_{\mathsf {A,B}};\kappa )]-(S_{\mathsf {B}}+0.5D)g(r_{\mathsf {A,B}};\kappa )\right)\\&=-{\frac {2\log 10}{s}}\left(S_{\mathsf {A}}+0.5D-g(r_{\mathsf {A,B}};\kappa )\right),\end{aligned}}}$

где мы использовали отношения и . ${\displaystyle S_{\mathsf {A}}+S_{\mathsf {B}}+D=1}$ ${\displaystyle g(-r;\kappa )=1-g(r;\kappa )}$

Затем стохастический градиентный спуск, применяемый для минимизации логарифмических потерь, дает следующее обновление рейтинга: ${\displaystyle R_{\mathsf {A}}}$

${\displaystyle R_{\mathsf {A}}\leftarrow R_{\mathsf {A}}+K({\hat {S}}_{\mathsf {A}}-g(r_{\mathsf {A,B}};\kappa ))}$

где и . Конечно, если выигрывает, если ничья, и если проигрывает. Чтобы распознать происхождение в модели, предложенной Дэвидсоном, это обновление называется рейтингом Эло-Дэвидсона. ^[36] ${\displaystyle K=2\eta \log 10/s}$ ${\displaystyle {\hat {S}}_{\mathsf {A}}=S_{\mathsf {A}}+0.5D}$ ${\displaystyle {\hat {S}}_{\mathsf {A}}=1}$ ${\displaystyle {\textsf {A}}}$ ${\displaystyle {\hat {S}}_{\mathsf {A}}=0.5}$ ${\displaystyle {\textsf {A}}}$ ${\displaystyle {\hat {S}}_{\mathsf {A}}=0}$ ${\displaystyle {\textsf {A}}}$

Обновление для выводится таким же образом, как ${\displaystyle R_{\mathsf {B}}}$

${\displaystyle R_{\mathsf {B}}\leftarrow R_{\mathsf {B}}+K({\hat {S}}_{\mathsf {B}}-g(r_{\mathsf {B,A}};\kappa ))}$,

где . ${\displaystyle r_{\mathsf {B,A}}=R_{\mathsf {B}}-R_{\mathsf {A}}=-r_{\mathsf {A,B}}}$

Мы отмечаем, что

${\displaystyle {\begin{aligned}E[{\hat {S}}_{\mathsf {A}}]&=\Pr\{{\mathsf {A}}~{\text{wins}}\}+0.5\Pr\{{\mathsf {A}}~{\text{draws}}\}\\&=\sigma (r_{\mathsf {A,B}};\kappa )+0.5\kappa {\sqrt {\sigma (r_{\mathsf {A,B}};\kappa )\sigma (-r_{\mathsf {A,B}};\kappa )}}\\&=g(r_{\mathsf {A,B}};\kappa )\end{aligned}}}$

и таким образом, получаем обновление рейтинга, которое можно записать как

${\displaystyle R_{\mathsf {A}}\leftarrow R_{\mathsf {A}}+K({\hat {S}}_{\mathsf {A}}-E_{\mathsf {A}})}$,

где и мы получили практически то же уравнение, что и в рейтинге Эло, за исключением того, что ожидаемый балл дается как вместо . ${\displaystyle E_{\mathsf {A}}=E[{\hat {S}}_{\mathsf {A}}]}$ ${\displaystyle E_{\mathsf {A}}=g(r_{\mathsf {A,B}};\kappa )}$ ${\displaystyle E_{\mathsf {A}}=\sigma (r_{\mathsf {A,B}})}$

Конечно, как отмечено выше, для , мы имеем и, таким образом, рейтинг Эло-Дэвидсона в точности совпадает с рейтингом Эло. Однако это не поможет понять случай, когда наблюдаются ничьи (мы не можем использовать , что означало бы, что вероятность ничьи равна нулю). С другой стороны, если мы используем , мы имеем ${\displaystyle \kappa =0}$ ${\displaystyle g(r;0)=\sigma (r)}$ ${\displaystyle \kappa =0}$ ${\displaystyle \kappa =2}$

${\displaystyle g(r;2)={\frac {10^{r/s}+1}{10^{-r/s}+2+10^{r/s}}}={\frac {1}{1+10^{-r/s}}}=\sigma (r)}$

что означает, что при использовании рейтинг Эло-Дэвидсона в точности совпадает с рейтингом Эло. ^[36] ${\displaystyle \kappa =2}$

Практические вопросы

Игровая активность против защиты своего рейтинга

В некоторых случаях рейтинговая система может препятствовать игровой активности игроков, желающих защитить свой рейтинг. ^[38] Чтобы препятствовать игрокам сидеть на высоком рейтинге, в 2012 году британский гроссмейстер Джон Нанн предложил отобрать участников чемпионата мира по шахматам, включив в него бонус за активность, который должен был быть объединен с рейтингом. ^[39]

За пределами шахматного мира опасения по поводу того, что игроки избегают соревновательной игры, чтобы защитить свои рейтинги, заставили Wizards of the Coast отказаться от системы Эло для турниров Magic: the Gathering в пользу системы собственной разработки под названием «Planeswalker Points». ^{[40] [41]}

Избирательное сопряжение

Более тонкая проблема связана с парами. Когда игроки могут выбирать себе соперников, они могут выбирать соперников с минимальным риском проигрыша и максимальным вознаграждением за победу. Конкретные примеры игроков с рейтингом 2800+, выбирающих соперников с минимальным риском и максимальной возможностью повышения рейтинга, включают: выбор соперников, которых они знают, что могут победить с помощью определенной стратегии; выбор соперников, которые, по их мнению, переоценены; или избегание игры с сильными игроками, рейтинг которых на несколько сотен очков ниже их, но которые могут иметь шахматные звания, такие как IM или GM. В категории выбора переоцененных соперников новые участники рейтинговой системы, которые сыграли менее 50 игр, теоретически являются удобной целью, поскольку они могут быть переоценены в своем предварительном рейтинге. ICC компенсирует эту проблему, назначая более низкий К-фактор устоявшемуся игроку, если он выигрывает у нового участника рейтинга. К-фактор на самом деле является функцией количества рейтинговых игр, сыгранных новым участником.

Таким образом, рейтинги Эло онлайн по-прежнему являются полезным механизмом для предоставления рейтинга на основе рейтинга противника. Однако его общая достоверность должна рассматриваться в контексте по крайней мере двух основных проблем, описанных выше — злоупотребление движком и выборочное составление пар противников.

ICC также недавно ввела рейтинги «автоматического спаривания», которые основаны на случайных парах, но с каждой победой подряд, гарантирующей статистически гораздо более сильного противника, который также выиграл x игр подряд. При потенциальном участии сотен игроков это создает некоторые сложности крупного крупного швейцарского турнира, в котором идет ожесточенная борьба, где победители раундов встречаются с победителями раундов. Такой подход к спариванию, безусловно, максимизирует риск рейтинга участников с более высоким рейтингом, которые могут столкнуться с очень жестким сопротивлением со стороны игроков ниже 3000, например. Это отдельный рейтинг сам по себе и находится в категориях рейтинга «1 минута» и «5 минут». Максимальные рейтинги, достигнутые выше 2500, встречаются исключительно редко.

Рейтинги инфляция и дефляция

Графики вероятностей и изменений рейтинга Эло (для K=16 и 32) ожидаемого результата (сплошная кривая) и неожиданного результата (пунктирная кривая) в зависимости от начальной разницы рейтингов. Например, игрок  A начинает с рейтингом 1400, а B с 1800 в турнире с использованием K = 32 (коричневые кривые). Синяя штрихпунктирная линия обозначает начальную разницу рейтингов 400 ( 1800 − 1400 ). Вероятность победы B , ожидаемый результат, составляет 0,91 (пересечение черной сплошной кривой и синей линии); если это произойдет, рейтинг A уменьшится на 3 (пересечение коричневой сплошной кривой и синей линии) до 1397, а рейтинг B увеличится на ту же величину до 1803. И наоборот, вероятность победы A , неожиданный результат, составляет 0,09 (пересечение черной пунктирной кривой и синей линии); если это произойдет, рейтинг A увеличится на 29 (пересечение коричневой пунктирной кривой и синей линии) до 1429, а рейтинг B уменьшится на ту же величину до 1771.

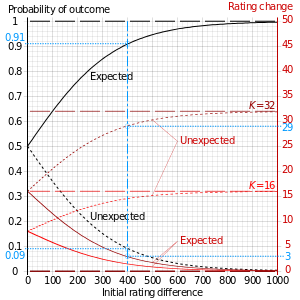
Термин «инфляция», применяемый к рейтингам, подразумевает, что уровень игровой силы, демонстрируемый рейтинговым игроком, со временем снижается; наоборот, «дефляция» предполагает, что уровень повышается. Например, если есть инфляция, современный рейтинг 2500 означает меньше, чем исторический рейтинг 2500, в то время как обратное верно, если есть дефляция. Использование рейтингов для сравнения игроков разных эпох становится более сложным, когда присутствует инфляция или дефляция. (См. также Сравнение лучших шахматистов за всю историю .)

Анализируя рейтинг-листы ФИДЕ с течением времени, Джефф Сонас предполагает, что инфляция могла иметь место примерно с 1985 года. ^[42] Сонас рассматривает игроков с самым высоким рейтингом, а не всех игроков с рейтингом, и признает, что изменения в распределении рейтингов могли быть вызваны повышением стандарта игры на самых высоких уровнях, но ищет и другие причины.

Число людей с рейтингом выше 2700 увеличилось. Около 1979 года был только один активный игрок ( Анатолий Карпов ) с таким высоким рейтингом. В 1992 году Вишванатан Ананд был всего лишь 8-м игроком в истории шахмат, достигшим отметки 2700 на тот момент. ^[43] К 1994 году это число увеличилось до 15 игроков. 33 игрока имели рейтинг 2700+ в 2009 году и 44 по состоянию на сентябрь 2012 года. Только 14 игроков когда-либо превышали рейтинг 2800.

Одной из возможных причин этой инфляции был рейтинговый пол, который долгое время был на уровне 2200, и если игрок опускался ниже этого уровня, он вычеркивался из рейтингового списка. Как следствие, игроки с уровнем мастерства чуть ниже пола могли попасть в рейтинговый список только в том случае, если их переоценивали, и это заставляло их вносить очки в рейтинговый пул. ^[42] В июле 2000 года средний рейтинг топ-100 составлял 2644. К июлю 2012 года он увеличился до 2703. ^[43]

Используя мощный шахматный движок для оценки ходов, сделанных в партиях между рейтинговыми игроками, Риган и Хоуорт анализируют наборы игр из рейтинговых турниров ФИДЕ и приходят к выводу, что с 1976 по 2009 год инфляция была незначительной или отсутствовала вовсе. ^[44]

В чистой системе Эло каждая игра заканчивается равной транзакцией рейтинговых очков. Если победитель получает N рейтинговых очков, проигравший теряет N рейтинговых очков. Это предотвращает попадание или покидание системы очков, когда игры проводятся и оцениваются. Однако игроки, как правило, входят в систему как новички с низким рейтингом и выходят из системы как опытные игроки с высоким рейтингом. Поэтому в долгосрочной перспективе система со строго равными транзакциями имеет тенденцию приводить к дефляции рейтинга. ^[45]

В 1995 году USCF признал, что несколько молодых игроков-школьников прогрессировали быстрее, чем могла отследить рейтинговая система. В результате, признанные игроки со стабильными рейтингами начали терять рейтинговые очки в пользу молодых и недооцененных игроков. Несколько из более старых признанных игроков были разочарованы тем, что они считали несправедливым снижением рейтинга, и некоторые даже бросили шахматы из-за этого. ^[46]

Борьба с дефляцией

Из-за существенной разницы во времени возникновения инфляции и дефляции, а также в целях борьбы с дефляцией, большинство реализаций рейтингов Эло имеют механизм для введения очков в систему для поддержания относительных рейтингов с течением времени. ФИДЕ имеет два инфляционных механизма. Во-первых, выступления ниже «рейтингового пола» не отслеживаются, поэтому игрок с истинным мастерством ниже пола может быть только неоцененным или переоцененным, но никогда не иметь правильного рейтинга. Во-вторых, у признанных и высокорейтинговых игроков более низкий К-фактор. У новых игроков К = 40 , который падает до К = 20 после 30 сыгранных игр и до К = 10 , когда игрок достигает 2400. ^[31] Текущая система в Соединенных Штатах включает схему бонусных очков, которая вводит рейтинговые очки в систему для отслеживания улучшающихся игроков, и различные значения К для разных игроков. ^[46] Некоторые методы, используемые, например, в Норвегии, различают юниоров и ветеранов и используют больший К-фактор для молодых игроков, даже увеличивая прогресс рейтинга на 100%, когда они набирают очки, значительно превышающие их прогнозируемые результаты. ^[47]

Рейтинговые полы в Соединенных Штатах работают, гарантируя, что игрок никогда не опустится ниже определенного предела. Это также борется с дефляцией, но председатель Комитета по рейтингам USCF критиковал этот метод, поскольку он не дает дополнительных очков улучшающимся игрокам. Возможным мотивом для этих рейтинговых полов является борьба с песочницей, т. е. преднамеренным понижением рейтингов для получения права на разделы и призы более низкого рейтингового класса. ^[46]

Рейтинги компьютеров

Матчи человек-компьютер в шахматы между 1997 ( Deep Blue против Гарри Каспарова ) и 2006 годами продемонстрировали, что шахматные компьютеры способны победить даже сильнейших игроков-людей. Однако рейтинги шахматных движков трудно поддаются количественной оценке из-за переменных факторов, таких как контроль времени и оборудование, на котором работает программа, а также тот факт, что шахматы — это нечестная игра. Наличие и величина преимущества первого хода в шахматах становятся очень важными на уровне компьютера. За пределами некоторого порога мастерства движок с белыми должен быть способен форсировать ничью по требованию из начальной позиции даже против идеальной игры, просто потому, что белые начинают со слишком большим преимуществом, чтобы потерять его по сравнению с небольшой величиной ошибок, которые они, вероятно, совершат. Следовательно, такой движок более или менее гарантированно наберет не менее 25% даже против идеальной игры. Различия в мастерстве за пределами определенной точки могут быть обнаружены только в том случае, если не начинать с обычной начальной позиции, а вместо этого выбрать начальную позицию, которая едва ли не проиграна для одной из сторон. Из-за этих факторов рейтинги зависят от пар и выбранных дебютов. ^[48] Опубликованные списки рейтингов движков, такие как CCRL, основаны на играх, сыгранных только на движке на стандартных аппаратных конфигурациях, и их нельзя напрямую сравнивать с рейтингами ФИДЕ.

Оценки некоторых рейтингов см. в разделе Рейтинги шахматного движка .

Использование вне шахмат

Другие настольные и карточные игры

• Го : Европейская федерация го приняла систему рейтинга на основе Эло, первоначально разработанную Чешской федерацией го.
• Backgammon : популярный First Internet Backgammon Server (FIBS) вычисляет рейтинги на основе модифицированной системы Эло. Новым игрокам присваивается рейтинг 1500, а рейтинг лучших людей и ботов превышает 2000. Та же формула была принята несколькими другими сайтами по нардам, такими как Play65 , DailyGammon, GoldToken и VogClub. VogClub устанавливает рейтинг нового игрока на уровне 1600. Федерация нард Великобритании использует формулу FIBS для своих национальных рейтингов Великобритании. ^[49]
• Скрэббл : Национальные организации Скрэббла вычисляют нормально распределенные рейтинги Эло, за исключением Великобритании , где используется другая система. Североамериканская ассоциация игроков в Скрэббл имеет самую большую рейтинговую популяцию активных членов, насчитывающую около 2000 человек по состоянию на начало 2011 года. Lexulous также использует систему Эло.
• Несмотря на вопросы о целесообразности использования системы Эло для оценки игр, в которых удача является фактором, производители карточных игр часто используют рейтинги Эло для своих организованных игровых усилий. DCI (ранее Duelists' Convocation International) использовала рейтинги Эло для турниров по Magic: The Gathering и другим играм Wizards of the Coast . Однако в 2012 году DCI отказалась от этой системы в пользу новой кумулятивной системы «Planeswalker Points», в основном из-за вышеупомянутой обеспокоенности тем, что Эло поощряет игроков с высоким рейтингом избегать игры, чтобы «защитить свой рейтинг». ^{[40] [41]} Pokémon USA использует систему Эло для ранжирования своих участников организованных игр TCG. ^[50] Призы для лучших игроков в различных регионах включали праздники и приглашения на чемпионаты мира до сезона 2011–2012 годов, где награды основывались на системе очков чемпионата, их обоснование было таким же, как у DCI для Magic: The Gathering . Аналогичным образом компания Decipher, Inc. использовала систему Эло для своих рейтинговых игр, таких как Star Trek Customizable Card Game и Star Wars Customizable Card Game .

Спортивные виды спорта

Система рейтинга Эло используется в шахматной части шахбокса . Чтобы иметь право заниматься профессиональным шахбоксом, необходимо иметь рейтинг Эло не менее 1600, а также принять участие в 50 или более матчах любительского бокса или боевых искусств.

Американский студенческий футбол использовал метод Эло как часть своих рейтинговых систем Bowl Championship Series с 1998 по 2013 год, после чего BCS был заменен на College Football Playoff . Джефф Сагарин из USA Today публикует рейтинги команд для большинства американских видов спорта, которые включают рейтинги системы Эло для студенческого футбола. Использование рейтинговых систем было фактически отменено с созданием College Football Playoff в 2014 году.

В других видах спорта рейтинги составляются на основе алгоритма Эло. Обычно они неофициальные и не одобрены руководящим органом вида спорта. Рейтинг Эло мирового футбола является примером метода, применяемого к мужскому футболу . ^[51] В 2006 году рейтинги Эло были адаптированы для команд Главной лиги бейсбола Нейтом Сильвером , тогдашним сотрудником Baseball Prospectus . ^[52] На основе этой адаптации оба также провели моделирование Монте-Карло на основе Эло для вероятности выхода команд в плей-офф. ^[53] В 2014 году Beyond the Box Score, сайт SB Nation , представил систему рейтинга Эло для международного бейсбола. ^[54]

В теннисе рейтинг Universal Tennis Rating (UTR), основанный на Эло, оценивает игроков в глобальном масштабе, независимо от возраста, пола или национальности. Это официальная рейтинговая система крупных организаций, таких как Intercollegiate Tennis Association и World TeamTennis , и часто используется в сегментах на Tennis Channel . Алгоритм анализирует более 8 миллионов результатов матчей более 800 000 теннисистов по всему миру. 8 мая 2018 года Рафаэль Надаль , выиграв 46 последовательных сетов в матчах на грунтовых кортах, имел почти идеальный грунтовый UTR 16,42. ^[55]

В пуле для ранжирования игроков в организованных любительских и профессиональных соревнованиях используется система, основанная на рейтинге Эло, называемая Fargo Rate. ^[56]

Одним из немногих рейтингов на основе Эло, одобренных руководящим органом вида спорта, является женский мировой рейтинг ФИФА , основанный на упрощенной версии алгоритма Эло, который ФИФА использует в качестве официальной рейтинговой системы для национальных сборных по женскому футболу .

Начиная с первого рейтингового списка после чемпионата мира по футболу FIFA 2018 года , ФИФА использовала Эло для своего мирового рейтинга ФИФА . ^[57]

В 2015 году Нейт Сильвер, главный редактор статистического комментаторского сайта FiveThirtyEight , и Рубен Фишер-Баум составили рейтинги Эло для каждой команды Национальной баскетбольной ассоциации и сезона до сезона 2014 года. ^{[58] [59]} В 2014 году FiveThirtyEight создал рейтинги на основе Эло и прогнозы побед для Американской профессиональной Национальной футбольной лиги . ^[60]

Английская ассоциация корфбола составила рейтинг команд на основе рейтинга Эло, чтобы определить гандикапы для их кубковых соревнований в сезоне 2011/12.

Разработан рейтинг игроков Национальной хоккейной лиги на основе индекса Эло. ^[61] Метрика хоккейного Эло оценивает общую двустороннюю игру игрока: результативность И защиту как в равных составах, так и в ситуациях игры в большинстве/убийства штрафных.

Rugbyleagueratings.com использует систему рейтинга Эло для ранжирования международных и клубных команд регбийной лиги .

Hemaratings.com был запущен в 2017 году и использует алгоритм Glicko-2 для ранжирования отдельных исторических европейских фехтовальщиков боевых искусств по всему миру в различных категориях, таких как длинный меч , рапира , историческая сабля и меч и баклер . ^[62]

Видеоигры и онлайн-игры

Многие видеоигры используют модифицированные системы Эло в соревновательном игровом процессе. Игра MOBA League of Legends использовала систему рейтинга Эло до второго сезона соревновательной игры. ^[63] Киберспортивная игра Overwatch , основа уникальной профессиональной спортивной организации Overwatch League , использует производную от системы Эло для ранжирования соревновательных игроков с различными корректировками, вносимыми между соревновательными сезонами. ^[64] World of Warcraft также ранее использовала систему Glicko-2 для объединения в команды и сравнения игроков Арены, но теперь использует систему, похожую на TrueSkill от Microsoft . ^[65] Игра Puzzle Pirates использует систему рейтинга Эло для определения позиций в различных головоломках. Эта система также используется в FIFA Mobile для режимов Division Rivals. Еще одна недавняя игра, которая начала использовать систему рейтинга Эло, — это AirMech , использующая рейтинги Эло ^[66] для случайного/командного подбора игроков 1 на 1, 2 на 2 и 3 на 3. RuneScape 3 использовала систему Эло в переиздании мини-игры охотника за головами в 2016 году. ^[67] Mechwarrior Online ввела систему Эло для своего нового режима «Очередь компов», вступившего в силу с патчем от 20 июня 2017 года. ^[68] Age of Empires II DE и Age of Empires III DE используют систему Эло для своей таблицы лидеров и подбора игроков, при этом новые игроки начинают с Эло 1000. ^[69] Соревновательный классический тетрис ( тетрис, в который играли на Nintendo Entertainment System ) выводит свои рейтинги, используя комбинацию личных лучших результатов игроков и сильно модифицированной системы Эло. ^[70]

Немногие видеоигры используют оригинальную систему рейтинга Эло. Согласно Lichess , онлайн-шахматному серверу, система Эло устарела, и теперь многие шахматные организации используют Glicko-2. ^[71] PlayerUnknown's Battlegrounds — одна из немногих видеоигр, которая использует самую первую систему Эло. В Guild Wars рейтинги Эло используются для записи рейтинга гильдии, полученного и потерянного в сражениях гильдий. В 1998 году была запущена онлайн-игра под названием Clanbase ^[72] , которая использовала систему подсчета очков Эло для ранжирования команд. Первоначальное значение K было 30, но было изменено на 5 в январе 2007 года, затем изменено на 15 в июле 2009 года. ^[73] Позже сайт был закрыт в 2013 году. ^[74] Похожий альтернативный сайт был запущен в 2016 году под названием Scrimbase , ^[75] который также использовал систему подсчета очков Эло для ранжирования команд. С 2005 года Golden Tee Live оценивает игроков на основе системы Эло. Новые игроки начинают с 2100, а рейтинг лучших игроков превышает 3000. ^[76]

Несмотря на то, что во многих видеоиграх используются различные системы подбора игроков , игроки рейтинговых видеоигр часто называют все рейтинги подбора игроков Эло .

Другое использование

Система рейтинга Эло использовалась в мягкой биометрии , ^[77] которая касается идентификации людей с использованием человеческих описаний. Сравнительные описания использовались вместе с системой рейтинга Эло для обеспечения надежных и дискриминационных «относительных измерений», позволяющих проводить точную идентификацию.

Система рейтинга Эло также использовалась в биологии для оценки иерархий доминирования самцов ^[78] , а также в автоматизации и компьютерном зрении для проверки тканей ^[79] .

Более того, сайты онлайн-судей также используют систему рейтинга Эло или ее производные. Например, Topcoder использует модифицированную версию, основанную на нормальном распределении, ^[80] в то время как Codeforces использует другую версию, основанную на логистическом распределении. ^{[81] [82] [83]}

Система рейтинга Эло также была отмечена в приложениях для знакомств, таких как приложение для подбора пар Tinder , которое использует вариант системы рейтинга Эло. ^[84]

YouTuber Marques Brownlee и его команда использовали рейтинговую систему Elo, когда позволили людям голосовать за цифровые фотографии, сделанные с помощью разных моделей смартфонов, выпущенных в 2022 году. ^[85]

Система рейтинга Эло также использовалась в рейтингах колледжей США, составленных , например, компанией Parchment, предоставляющей цифровые сертификаты. ^{[86] [87] [88]}

Система рейтинга Эло также была принята для оценки моделей ИИ. В 2021 году Anthropic использовала систему Эло для ранжирования моделей ИИ в своих исследованиях. ^[89] Таблица лидеров LMSYS недолгое время использовала систему рейтинга Эло для ранжирования моделей ИИ ^[90] перед переходом на модель Брэдли–Терри . ^[91]

Упоминания в СМИ

Система рейтинга Эло была представлена ​​в «Социальной сети» во время сцены алгоритма, где Марк Цукерберг выпустил Facemash . В этой сцене Эдуардо Саверин пишет математические формулы для системы рейтинга Эло на окне общежития Цукерберга. За кулисами, как утверждается в фильме, система Эло используется для ранжирования девушек по их привлекательности. Уравнения, управляющие алгоритмом, показаны кратко, написанными на окне; ^[92] однако они немного неверны. ^{[ необходима цитата ]}

Смотрите также

• Эло ад
• Индекс рейтингового процента (RPI) — еще одна система, учитывающая силу соперников.

Примечания

1. Это пишется как «Эло», а не «ЭЛО», и обычно произносится как / ˈ iː l oʊ / или / ˈ ɛ l oʊ / на английском языке. Настоящее имя Эло произносится [ˈeːløː]. ^ⓘ на венгерском языке.

Ссылки

Примечания

1. Elo, Arpad E. (август 1967 г.). «Предлагаемая система рейтинга USCF, ее развитие, теория и применение» (PDF) . Chess Life . XXII (8): 242–247.
2. Используя формулу 100% / (1 + 10 ^{− D /400} ) для D, равного 100 или 200.
3. Elo-MMR: рейтинговая система для массовых многопользовательских соревнований
4. Редман, Тим (июль 2002 г.). «Вспоминая Ричарда, часть II» (PDF) . Illinois Chess Bulletin. Архивировано (PDF) из оригинала 2020-06-30 . Получено 2020-06-30 .
5. Эло, Арпад Э. (5 марта 1960 г.). «Система рейтинга USCF» (PDF) . Chess Life . XIV (13). USCF : 2.
6. Эло 1986, стр. 4
7. Эло, Арпад Э. (июнь 1961 г.). «Система рейтинга USCF — научное достижение» (PDF) . Chess Life . XVI (6). USCF : 160–161.
8. "About the USCF". Федерация шахмат США. Архивировано из оригинала 2008-09-26 . Получено 2008-11-10 .
9. Эло 1986, Предисловие к первому изданию
10. Эло 1986.
11. Эло 1986, гл. 8.73.
12. Гликман, Марк Э. и Джонс, Олбин К., «Оценка рейтинговой системы шахмат» (1999), Chance, 12, 2, 21-28.
13. Гликман, Марк Э. (1995), "Полное руководство по рейтингам в шахматах". Последующая версия этой статьи появилась в American Chess Journal , 3, стр. 59–102.
14. Правила рейтинга ФИДЕ вступили в силу с 1 июля 2017 года. FIDE Online (fide.com) (Отчет). ФИДЕ . Архивировано из оригинала 2019-11-27 . Получено 2017-09-09 .
15. Эло 1986, стр. 159.
16. Система рейтинга шахмат США (PDF) (Отчет). 24 апреля 2017 г. Архивировано (PDF) из оригинала 7 февраля 2020 г. Получено 16 февраля 2020 г. – через glicko.net.
17. Ананд уступил № 1 Морозевичу (Chessbase, 24 августа 2008 г. Архивировано 10 сентября 2008 г. на Wayback Machine ), затем вернул его, затем Карлсен занял № 1 (Chessbase, 5 сентября 2008 г. Архивировано 09 ноября 2012 г. на Wayback Machine ), затем Иванчук (Chessbase, 11 сентября 2008 г. Архивировано 13 сентября 2008 г. на Wayback Machine ) и, наконец, Топалов (Chessbase, 13 сентября 2008 г. Архивировано 15 сентября 2008 г. на Wayback Machine ).
18. Администратор. "Калькуляторы рейтинга ФИДЕ: Калькулятор изменения рейтинга в шахматах". ratings.fide.com . Архивировано из оригинала 28.09.2017 . Получено 28.09.2017 .
19. Федерация шахмат США Архивировано 18 июня 2012 г. на Wayback Machine
20. Цитата из глоссария USCF: «игрок, который участвует в более чем 300 играх с рейтингом выше 2200». Архивировано 08.03.2013 на Wayback Machine из Федерации шахмат США
21. «Приблизительные формулы для системы рейтинга шахмат США» Архивировано 04.11.2019 в Wayback Machine , Федерация шахмат США , Марк Гликман, апрель 2017 г.
22. Эло 1986, гл. 1.12.
23. Good, IJ (1955). «О маркировке шахматистов». The Mathematical Gazette . 39 (330): 292–296. doi :10.2307/3608567. JSTOR  3608567. S2CID  158885108.
24. Дэвид, HA (1959). «Турниры и парные сравнения». Biometrika . 46 (1/2): 139–149. doi :10.2307/2332816. JSTOR  2332816.
25. Травински, Б. Дж.; Дэвид, HA (1963). «Выбор лучшего лечения в эксперименте по парному сравнению». Annals of Mathematical Statistics . 34 (1): 75–91. doi : 10.1214/aoms/1177704243 .
26. Бульманн, Ганс; Хубер, Питер Дж. (1963). «Попарное сравнение и ранжирование в турнирах». Анналы математической статистики . 34 (2): 501–510. doi : 10.1214/aoms/1177704161 .
27. Эло 1986, стр. 141, гл. 8.4& Логистическая вероятность как основа рейтинга
28. «Система рейтинга Эло – корректировка таблиц ожиданий». 30 марта 2011 г.
29. Эло 1986, гл. 8.73
30. Ключевая статья Sonas — Sonas, Jeff. «Формула рейтинга Sonas — лучше, чем Эло?». chessbase.com . Архивировано из оригинала 2005-03-05 . Получено 2005-05-01 .
31. Правила рейтинга ФИДЕ вступили в силу с 1 июля 2014 года. ФИДЕ Онлайн (fide.com) (Отчет). ФИДЕ . 2014-07-01. Архивировано из оригинала 2014-07-01 . Получено 2014-07-01 .
32. Правила рейтинга ФИДЕ действительны с 1 июля 2013 года по 1 июля 2014 года. ФИДЕ Онлайн (fide.com) (Отчет). 2013-07-01. Архивировано из оригинала 2014-07-15 . Получено 2014-07-01 .
33. "Изменения в Правилах Рейтинга". FIDE Online (fide.com) (Пресс-релиз). FIDE . 2011-07-21. Архивировано из оригинала 2012-05-13 . Получено 2012-02-19 .
34. "K-factor". Chessclub.com . Справка ICC. 2002-10-18. Архивировано из оригинала 2012-03-13 . Получено 2012-02-19 .
35. Кирали, Ф.; Цянь, З. (2017). «Моделирование соревновательных видов спорта: модели Брэдли-Терри-Эло для контролируемого и онлайн-обучения результатам парных соревнований». arXiv : 1701.08055 [stat.ML].
36. Щецинский, Лешек; Джебби, Аймен (2020-09-01). «Понимание ничьих в алгоритме рейтинга Эло». Журнал количественного анализа в спорте . 16 (3): 211–220. doi :10.1515/jqas-2019-0102. ISSN  1559-0410. S2CID  219784913.
37. Дэвидсон, Роджер Р. (1970). «О расширении модели Брэдли-Терри для учета связей в экспериментах по парному сравнению». Журнал Американской статистической ассоциации . 65 (329): 317–328. doi :10.2307/2283595. ISSN  0162-1459. JSTOR  2283595.
38. Руководство для родителей по шахматам. Архивировано 28 мая 2008 г. в Wayback Machine Skittles , Дон Хейсман, Chesscafe.com, 4 августа 2002 г.
39. "Chess News – The Nunn Plan for the World Chess Championship". ChessBase.com. 8 июня 2005 г. Архивировано из оригинала 2011-11-19 . Получено 2012-02-19 .
40. "Introducing Planeswalker Points". 6 сентября 2011 г. Архивировано из оригинала 30 сентября 2011 г. Получено 9 сентября 2011 г.
41. "Getting to the Points". 9 сентября 2011 г. Архивировано из оригинала 18 октября 2016 г. Получено 9 сентября 2011 г.
42. Jeff Sonas (27 июля 2009 г.). "Рейтинговая инфляция – ее причины и возможные методы лечения". chessbase.com . Архивировано из оригинала 23 ноября 2013 г. . Получено 27 августа 2009 г. .
43. "Viswanathan Anand". Chessgames.com. Архивировано из оригинала 2013-03-28 . Получено 2012-08-14 .
44. Regan, Kenneth; Haworth, Guy (2011-08-04). "Intrinsic Chess Ratings". Труды конференции AAAI по искусственному интеллекту . 25 (1): 834–839. doi : 10.1609/aaai.v25i1.7951 . ISSN  2374-3468. S2CID  15489049. Архивировано из оригинала 20.04.2021 . Получено 01.09.2021 .
45. Бергерсен, Пер А. "ELO-SYSTEMET" (на норвежском). Норвежская шахматная федерация. Архивировано из оригинала 8 марта 2013 года . Получено 21 октября 2013 года .
46. Беседа с Марком Гликманом [1] Архивировано 07.08.2011 в Wayback Machine , опубликовано в выпуске Chess Life за октябрь 2006 г.
47. "Эло-системет". Норвежский Сьяккфорбунд . Архивировано из оригинала 5 декабря 2013 года . Проверено 23 августа 2009 г.
48. Ларри Кауфман, Варианты шахматной доски (2021), стр. 179
49. "Объяснение рейтингов игры в нарды". results.ukbgf.com . Архивировано из оригинала 2019-11-14 . Получено 2020-06-01 .
50. "Play! Pokémon Glossary: ​​Elo". Архивировано из оригинала 15 января 2015 г. Получено 15 января 2015 г.
51. Лайонс, Кит (10 июня 2014 г.). «Каковы рейтинги Эло в мировом футболе?». The Conversation . Архивировано из оригинала 15 июня 2019 г. Получено 3 июля 2019 г.
52. Сильвер, Нейт (28.06.2006). «Ложь, проклятая ложь: мы — Эло?». Архивировано из оригинала 22.08.2006 . Получено 13.01.2023 .
53. "Postseason Odds, ELO version". Baseballprospectus.com. Архивировано из оригинала 2012-03-07 . Получено 2012-02-19 .
54. Коул, Брайан (15 августа 2014 г.). "Рейтинги Эло для международного бейсбола". Beyond the Box Score . SB Nation . Архивировано из оригинала 2 января 2016 г. Получено 4 ноября 2015 г.
55. «Is Rafa the GOAT of Clay?». 8 мая 2018 г. Архивировано из оригинала 27 февраля 2021 г. Получено 22 августа 2018 г.
56. "Fargo Rate" . Получено 31 марта 2022 г. .
57. "Пересмотр мирового рейтинга FIFA/Coca-Cola" (PDF) . FIFA. Июнь 2018. Архивировано из оригинала (PDF) 2018-06-12 . Получено 2020-06-30 .
58. Сильвер, Нейт; Фишер-Баум, Рубен (21 мая 2015 г.). «Как мы вычисляем рейтинг Эло НБА». FiveThirtyEight . Архивировано из оригинала 23-05-2015.
59. Рубен Фишер-Баум и Нейт Сильвер, «Полная история НБА», FiveThirtyEight, 21 мая 2015 г.[2] Архивировано 23 мая 2015 г. на Wayback Machine
60. Сильвер, Нейт (4 сентября 2014 г.). «Введение в рейтинг Эло НФЛ». FiveThirtyEight. Архивировано из оригинала 12 сентября 2015 г.
    Пейн, Нил (10 сентября 2015 г.). "Рейтинги Эло НФЛ вернулись". FiveThirtyEight. Архивировано из оригинала 11 сентября 2015 г..
61. "Hockey Stats Revolution – Как команды выбирают игроков?". Hockey Stats Revolution . Архивировано из оригинала 2016-10-02 . Получено 2016-09-29 .
62. "О рейтингах - Hema Ratings". Hemaratings . Получено 2024-01-30 .
63. "Подбор игроков | LoL – League of Legends". Na.leagueoflegends.com. 2010-07-06. Архивировано из оригинала 2012-02-26 . Получено 2012-02-19 .
64. «Добро пожаловать в 8-й сезон соревновательной игры». PlayOverwatch.com . Blizzard Entertainment. Архивировано из оригинала 12 марта 2018 года . Получено 11 марта 2018 года .
65. "World of Warcraft Europe -> Арена". Wow-europe.com. 2011-12-14. Архивировано из оригинала 2010-09-23 . Получено 2012-02-19 .
66. "Разработчик AirMech объясняет, почему они используют Elo". Архивировано из оригинала 17 февраля 2015 г. Получено 15 января 2015 г.
67. [3] ^{[ мертвая ссылка ]}
68. "MWO: News". mwomercs.com . Архивировано из оригинала 2018-08-27 . Получено 2017-06-27 .
69. "Age of Empires II: DE Leaderboards - Age of Empires". 14 ноября 2019 г. Архивировано из оригинала 27 января 2022 г. Получено 27 января 2022 г.
70. "Список лучших игроков в тетрис в мире (NES NTSC)" . Получено 15 июля 2024 г. .
71. "Часто задаваемые вопросы: рейтинги". lichess.org . Архивировано из оригинала 2019-04-02 . Получено 2020-11-11 .
72. "Запись Wayback Machine Clanbase.com". Архивировано из оригинала 2017-11-05 . Получено 2017-10-29 .
73. "Guild ladder". Wiki.guildwars.com. Архивировано из оригинала 2012-03-01 . Получено 2012-02-19 .
74. "Прощальное сообщение Clanbase". Архивировано из оригинала 2013-12-24 . Получено 2017-10-29 .
75. "Scrimbase Gaming Ladder". Архивировано из оригинала 2017-10-30 . Получено 2017-10-29 .
76. "Golden Tee Fan Player Rating Page". 26 декабря 2007 г. Архивировано из оригинала 2014-01-01 . Получено 2013-12-31 .
77. «Использование сравнительных описаний человека для мягкой биометрии». Архивировано 8 марта 2013 г. в Wayback Machine , Д. А. Рейд и М. С. Никсон, Международная совместная конференция по биометрии (IJCB), 2011 г.
78. Pörschmann; et al. (2010). «Успех самцов в репродуктивной сфере и его поведенческие корреляты у полигинного млекопитающего, галапагосского морского льва (Zalophus wollebaeki)». Молекулярная экология . 19 (12): 2574–86. doi :10.1111/j.1365-294X.2010.04665.x. PMID  20497325. S2CID  19595719.
79. Tsang; et al. (2016). «Проверка тканей на основе метода оценки Эло». Pattern Recognition . 51 : 378–394. Bibcode : 2016PatRe..51..378T. doi : 10.1016/j.patcog.2015.09.022. hdl : 10722/229176 . Архивировано из оригинала 2020-11-05 . Получено 2020-05-05 .
80. "Algorithm Competition Rating System". 23 декабря 2009 г. Архивировано из оригинала 2 сентября 2011 г. Получено 16 сентября 2011 г.
81. "FAQ: Что такое рейтинг и подразделения?". Архивировано из оригинала 25 сентября 2011 г. Получено 16 сентября 2011 г.
82. "Rating Distribution". Архивировано из оригинала 13 октября 2011 г. Получено 16 сентября 2011 г.
83. "Rewarding rating: Part 2". Архивировано из оригинала 13 октября 2011 г. Получено 16 сентября 2011 г.
84. «Подбор пар в Tinder больше похож на Warcraft, чем вы могли бы подумать – Kill Screen». Kill Screen . 2016-01-14. Архивировано из оригинала 2017-08-19 . Получено 2017-08-19 .
85. «Лучшая камера смартфона 2022 года!». YouTube . 2022-12-22 . Получено 2023-01-07 .
86. Эвери, Кристофер Н .; Гликман, Марк Э.; Хоксби, Кэролайн М.; Метрик, Эндрю (01.02.2013). «Выявленный рейтинг предпочтений колледжей и университетов США». The Quarterly Journal of Economics . 128 (1): 425–467. doi :10.1093/qje/qjs043.
87. Ирвин, Нил (4 сентября 2014 г.). «Почему колледжи с четкой направленностью имеют скрытое преимущество». The Upshot . The New York Times . Получено 9 мая 2023 г.
88. Селинго, Джеффри Дж. (23 сентября 2015 г.). «Когда у студентов есть выбор среди лучших колледжей, какой из них они выбирают?». The Washington Post . Получено 9 мая 2023 г.
89. Аскелл, Аманда; Бай, Юньтао; Чен, Анна; Слейте, Рассвет; Гангули, Глубокий; Хениган, Том; Джонс, Энди; Джозеф, Николас; Манн, Бен (9 декабря 2021 г.). «Ассистент общего языка как лаборатория выравнивания». arXiv : 2112.00861 [cs.CL].
90. "Chatbot Arena Leaderboard Week 8: Introducing MT-Bench and Vicuna-33B | LMSYS Org". lmsys.org . Получено 28.02.2024 .
91. "Chatbot Arena: Новые модели и обновление системы Elo | LMSYS Org". lmsys.org . Получено 28.02.2024 .
92. Сценарий к фильму «Социальная сеть», Sony Pictures, архив 2012-09-04 на Wayback Machine , стр. 16

Источники

• Эло, Арпад (1986) [1-е изд. 1978]. Рейтинг шахматистов прошлого и настоящего (второе изд.). Нью-Йорк: Arco Publishing, Inc. ISBN 978-0-668-04721-0.

Дальнейшее чтение

• Харкнесс, Кеннет (1967). Официальный шахматный справочник . Маккей.

Внешние ссылки

• Страница исследований Марка Гликмана с рядом ссылок на технические статьи по системам рейтинга шахмат