Теория игр — это изучение математических моделей стратегических взаимодействий между рациональными агентами . [1] Он находит применение во многих областях социальных наук , широко используется в экономике, а также в логике , системных науках и информатике . [2] Традиционная теория игр рассматривает игры с нулевой суммой для двух человек , в которых выигрыши или проигрыши одного участника точно уравновешиваются проигрышами и выигрышами другого участника. В 21 веке теория игр применяется к более широкому спектру поведенческих отношений , и теперь это общий термин для науки о принятии логических решений людьми, животными, а также компьютерами.
Современная теория игр началась с идеи равновесия смешанных стратегий в игре двух лиц с нулевой суммой и ее доказательства Джоном фон Нейманом . В оригинальном доказательстве фон Неймана использовалась теорема Брауэра о неподвижной точке о непрерывных отображениях в компактные выпуклые множества , которая стала стандартным методом в теории игр и математической экономике . За его статьей последовала «Теория игр и экономического поведения» (1944), написанная в соавторстве с Оскаром Моргенштерном , в которой рассматривались совместные игры нескольких игроков. [3] Во втором издании представлена аксиоматическая теория ожидаемой полезности, которая позволила математическим статистикам и экономистам рассматривать процесс принятия решений в условиях неопределенности. [4]
Теория игр получила широкое развитие в 1950-х годах и была открыто применена к эволюции в 1970-х годах, хотя аналогичные разработки начались, по крайней мере, с 1930-х годов. Теория игр получила широкое признание как важный инструмент во многих областях. Джон Мейнард Смит был удостоен премии Крафорда за применение эволюционной теории игр в 1999 году, а пятнадцать теоретиков игр получили Нобелевскую премию по экономике по состоянию на 2020 год, в том числе совсем недавно Пол Милгром и Роберт Б. Уилсон .
Дискуссии по математике игр начались задолго до появления современной математической теории игр. Работа Кардано Liber de ludo aleae ( «Книга об азартных играх »), написанная около 1564 года, но опубликованная посмертно в 1663 году, обрисовывает некоторые основные идеи азартных игр. В 1650-х годах Паскаль и Гюйгенс разработали концепцию ожидания на основе рассуждений о структуре азартных игр. Паскаль выступал за равное разделение, когда шансы равны, в то время как Гюйгенс расширил этот аргумент, рассматривая стратегии для игрока, который может сделать любую ставку с любым противником, при условии, что ее условия равны. [5] Позже Гюйгенс опубликовал свое исчисление азартных игр под названием Deatiociniis in ludo aleæ ( «О рассуждениях в азартных играх ») в 1657 году.
В 1713 году в письме, приписываемом Чарльзу Уолдегрейву, активному якобиту и дяде британского дипломата Джеймса Уолдегрейва , анализировалась игра под названием « ле ее ». [6] [7] Уолдегрейв предложил минимаксное решение смешанной стратегии для версии карточной игры для двух человек, и эта проблема теперь известна как проблема Уолдегрейва . В 1838 году Антуан Огюстен Курно рассмотрел дуополию и представил решение, которое представляет собой равновесие Нэша игры, в своих исследованиях по математическим принципам теории богатства ( Recherches sur les principes mathématiques de la theorie des richesses ).
В 1913 году Эрнст Цермело опубликовал Über eine Anwendung der Mengenlehre auf die Theorie des Schachspiels (« О применении теории множеств к теории игры в шахматы »), в которой доказал, что оптимальная шахматная стратегия строго определена . Это открыло путь к более общим теоремам. [8]
В 1938 году датский экономист-математик Фредерик Цойтен доказал, что математическая модель имеет выигрышную стратегию, используя теорему Брауэра о фиксированной точке . [9] В своей книге 1938 года «Приложения к играм Хасара» и более ранних заметках Эмиль Борель доказал теорему о минимаксе для матричных игр двух лиц с нулевой суммой только тогда, когда матрица выигрышей симметрична, и предоставил решение нетривиальной бесконечной задачи. игра (известная на английском языке как игра Blotto ). Борель выдвинул гипотезу об отсутствии равновесия со смешанными стратегиями в конечных играх двух лиц с нулевой суммой , гипотеза, ложность которой была доказана фон Нейманом.

Теория игр возникла как уникальная область, когда Джон фон Нейман опубликовал статью « Теория стратегических игр» в 1928 году. [10] [11] В оригинальном доказательстве фон Неймана использовалась теорема Брауэра о неподвижной точке о непрерывных отображениях в компактные выпуклые множества , которая стала стандартный метод в теории игр и математической экономике . Работа фон Неймана в области теории игр завершилась в 1944 году его книгой «Теория игр и экономического поведения» , написанной в соавторстве с Оскаром Моргенштерном . [12] Второе издание этой книги представило аксиоматическую теорию полезности , которая реинкарнировала старую теорию полезности (денег) Даниэля Бернулли как независимую дисциплину. Эта основополагающая работа содержит метод поиска взаимно непротиворечивых решений для игр двух лиц с нулевой суммой. Последующая работа была сосредоточена в первую очередь на теории кооперативных игр , которая анализирует оптимальные стратегии для групп людей, предполагая, что они могут обеспечить соблюдение соглашений между собой о правильных стратегиях. [13]

В 1950 году появилось первое математическое обсуждение дилеммы заключённого, и известные математики Меррил М. Флуд и Мелвин Дрешер провели эксперимент в рамках исследований RAND Corporation в области теории игр. РЭНД продолжил исследования из-за возможного применения их в глобальной ядерной стратегии . [14] Примерно в это же время Джон Нэш разработал критерий взаимной согласованности стратегий игроков, известный как равновесие Нэша , применимый к более широкому спектру игр, чем критерий, предложенный фон Нейманом и Моргенштерном. Нэш доказал, что каждая конечная некооперативная игра с n игроками и ненулевой суммой (а не только двумя игроками с нулевой суммой) имеет то, что сейчас известно как равновесие Нэша в смешанных стратегиях.
Теория игр пережила бурную деятельность в 1950-х годах, в ходе которой были разработаны концепции ядра , игры развернутой формы , фиктивной игры , повторяющихся игр и ценности Шепли . В 1950-е годы также появились первые применения теории игр в философии и политической науке .
В 1965 году Рейнхард Зельтен представил свою концепцию решения идеальных равновесий подыгр , которая еще больше уточнила равновесие Нэша. Позже он представит и совершенство дрожащей руки . В 1994 году Нэш, Селтен и Харсаньи стали лауреатами Нобелевской премии по экономике за вклад в теорию экономических игр.
В 1970-е годы теория игр широко применялась в биологии , во многом благодаря работам Джона Мейнарда Смита и его эволюционно стабильной стратегии . Кроме того, были введены и проанализированы понятия коррелированного равновесия , совершенства дрожащей руки и общего знания [а] .
В 1994 году Джон Нэш был удостоен Нобелевской премии по экономике за вклад в теорию игр. Самым известным вкладом Нэша в теорию игр является концепция равновесия Нэша, которая является концепцией решения для некооперативных игр . Равновесие Нэша — это набор стратегий, по одной для каждого игрока, при котором ни один игрок не может улучшить свой выигрыш, изменив в одностороннем порядке свою стратегию.
В 2005 году теоретики игр Томас Шеллинг и Роберт Ауманн последовали за Нэшем, Селтеном и Харсаньи в качестве лауреатов Нобелевской премии. Шеллинг работал над динамическими моделями, ранними примерами эволюционной теории игр . Ауманн внес больший вклад в школу равновесия, введя огрубление равновесия и коррелированные равновесия, а также разработав обширный формальный анализ предположения об общем знании и его последствий.
В 2007 году Леонид Гурвич , Эрик Маскин и Роджер Майерсон были удостоены Нобелевской премии по экономике «за заложение основ теории проектирования механизмов ». Вклад Майерсона включает понятие правильного равновесия и важный дипломный труд: « Теория игр, анализ конфликта» . [1] Гурвич ввел и формализовал концепцию совместимости стимулов .
В 2012 году Элвин Э. Рот и Ллойд С. Шепли были удостоены Нобелевской премии по экономике «за теорию стабильного распределения и практику проектирования рынка». В 2014 году Нобелевская премия досталась теоретику игр Жану Тиролю .
Игра является кооперативной , если игроки могут формировать обязательные обязательства, принудительно реализуемые извне (например, посредством договорного права ). Игра считается некооперативной, если игроки не могут создавать союзы или если все соглашения должны быть самодостаточными (например, посредством реальных угроз ). [15]
Кооперативные игры часто анализируются в рамках теории кооперативных игр , которая фокусируется на прогнозировании того, какие коалиции сформируются, совместные действия, которые предпримут группы, и полученные в результате коллективные выплаты. Она противоположна традиционной теории некооперативных игр , которая фокусируется на прогнозировании действий и выигрышей отдельных игроков и анализе равновесия Нэша . [16] [17] Сосредоточение внимания на индивидуальной выгоде может привести к явлению, известному как «Трагедия общин» , когда ресурсы используются на коллективно неэффективном уровне. Отсутствие официальных переговоров приводит к ухудшению качества общественных благ из-за их чрезмерного использования и недостаточного обеспечения, что обусловлено частными стимулами. [18]
Теория кооперативных игр обеспечивает подход высокого уровня, поскольку она описывает только структуру, стратегии и выигрыши коалиций, тогда как теория некооперативных игр также рассматривает, как процедуры переговоров повлияют на распределение выигрышей внутри каждой коалиции. Поскольку некооперативная теория игр является более общей, кооперативные игры можно анализировать с помощью подхода некооперативной теории игр (обратное утверждение неверно) при условии, что сделаны достаточные предположения, чтобы охватить все возможные стратегии, доступные игрокам, из-за возможности внешнего обеспечения сотрудничества. Хотя использование единой теории может быть желательным, во многих случаях имеется недостаточно информации для точного моделирования формальных процедур, доступных в процессе стратегических переговоров, или полученная модель будет слишком сложной, чтобы предложить практический инструмент в реальном мире. В таких случаях теория кооперативных игр предлагает упрощенный подход, который позволяет анализировать игру в целом без каких-либо предположений о переговорных силах.
Симметричная игра — это игра, в которой каждый игрок получает одинаковый выигрыш, делая один и тот же выбор. Другими словами, личность игрока не меняет исход игры с другим игроком. [19] Многие из широко изучаемых игр 2×2 симметричны. Стандартные представления о курице , дилемме заключенного и охоте на оленя — все это симметричные игры. Некоторые [ кто? ] ученые также рассматривают некоторые асимметричные игры как примеры таких игр. Однако наиболее распространенные выигрыши в каждой из этих игр симметричны.
Наиболее часто изучаемыми асимметричными играми являются игры, в которых у обоих игроков нет одинаковых наборов стратегий. Например, игра «Ультиматум» , как и игра «Диктатор», имеют разные стратегии для каждого игрока. Однако игра может иметь одинаковые стратегии для обоих игроков, но быть асимметричной. Например, игра, изображенная на рисунке в этом разделе, асимметрична, несмотря на идентичные наборы стратегий для обоих игроков.
Игры с нулевой суммой (в более общем смысле, игры с постоянной суммой) — это игры, в которых выбор игроков не может ни увеличить, ни уменьшить доступные ресурсы. В играх с нулевой суммой общая выгода достается всем игрокам в игре для каждой комбинации стратегий и всегда в сумме равна нулю (более неформально, игрок получает выгоду только за равный счет других). [20] Покер является примером игры с нулевой суммой (игнорируя возможность сокращения казино), поскольку каждый выигрывает ровно столько, сколько проигрывают его оппоненты. Другие игры с нулевой суммой включают в себя сопоставление монет и большинство классических настольных игр, включая го и шахматы .
Многие игры, изучаемые теоретиками игр (включая знаменитую дилемму заключенного), являются играми с ненулевой суммой, поскольку конечный результат больше или меньше нуля. Неофициально в играх с ненулевой суммой выигрыш одного игрока не обязательно соответствует проигрышу другого.
Игры с постоянной суммой соответствуют такой деятельности, как воровство и азартные игры, но не фундаментальной экономической ситуации, в которой существуют потенциальные выгоды от торговли . Любую игру с постоянной суммой можно превратить в игру (возможно, асимметричную) с нулевой суммой, добавив фиктивного игрока (часто называемого «доской»), проигрыши которого компенсируют чистый выигрыш игроков.
Одновременные игры — это игры, в которых оба игрока движутся одновременно, или вместо этого более поздние игроки не знают о действиях предыдущих игроков (что делает их фактически одновременными). Последовательные игры (или динамические игры) — это игры, в которых игроки не принимают решения одновременно, а более ранние действия игрока влияют на результат и решения других игроков. [21] Это не обязательно должна быть точная информация о каждом действии предыдущих игроков; это может быть очень мало знаний. Например, игрок может знать, что предыдущий игрок не выполнил одно конкретное действие, но при этом он не знает, какое из других доступных действий фактически выполнил первый игрок.
Разница между одновременными и последовательными играми отражена в различных представлениях, обсуждавшихся выше. Часто нормальная форма используется для представления одновременных игр, а развернутая форма — для представления последовательных. Преобразование развернутой формы в нормальную является одним из способов. Это означает, что одной и той же нормальной форме соответствует несколько игр с развернутой формой. Следовательно, понятия равновесия для одновременных игр недостаточны для рассуждений о последовательных играх; см. совершенство субигры .
Вкратце, различия между последовательными и одновременными играми заключаются в следующем:

Важную подгруппу последовательных игр составляют игры с полной информацией. Игра с полной информацией означает, что все игроки при каждом своем ходе знают предыдущую историю игры и ходы, сделанные ранее всеми остальными игроками. В действительности это можно применить к фирмам и потребителям, имеющим информацию о цене и качестве всех товаров, доступных на рынке. [22] Игра с несовершенной информацией ведется, когда игроки не знают всех ходов, уже сделанных противником, например, игра с одновременными ходами. [23] Примеры игр с совершенной информацией включают крестики-нолики , шашки , шахматы и го . [24] [25] [26]
Многие карточные игры представляют собой игры с несовершенной информацией, например покер и бридж . [27] Совершенную информацию часто путают с полной информацией , которая представляет собой аналогичную концепцию, относящуюся к общему знанию последовательности действий, стратегий и выигрышей каждого игрока на протяжении всего игрового процесса. [28] Полная информация требует, чтобы каждый игрок знал стратегии и выигрыши, доступные другим игрокам, но не обязательно предпринятые действия, тогда как идеальная информация — это знание всех аспектов игры и игроков. [29] Однако игры с неполной информацией можно свести к играм с несовершенной информацией путем введения « естественных ходов ». [30]
Одно из предположений равновесия Нэша состоит в том, что каждый игрок имеет правильные убеждения о действиях других игроков. Однако в теории игр существует множество ситуаций, когда участники не до конца понимают характеристики своих противников. Участники переговоров могут не знать об оценке объекта переговоров своим оппонентом, компании могут не знать о функциях издержек своего оппонента, участники боевых действий могут не знать о сильных сторонах своего оппонента, а присяжные могут не знать о том, как их коллеги интерпретируют доказательства в суде. В некоторых случаях участники могут хорошо знать характер своего оппонента, но могут не знать, насколько хорошо противник знает свой собственный характер. [31]
Байесовская игра означает стратегическую игру с неполной информацией. В стратегической игре лицами, принимающими решения, являются игроки, и у каждого игрока есть группа действий. Основной частью несовершенной информационной спецификации является набор состояний. Каждое состояние полностью описывает набор характеристик, важных для игрока, таких как его предпочтения и подробности о нем. Должно быть состояние для каждого набора функций, которые, по мнению некоторых игроков, могут существовать. [32]

Например, где Игрок 1 не уверен, предпочтет ли Игрок 2 встречаться с ней или уйти от нее, в то время как Игрок 2 понимает предпочтения Игрока 1, как и раньше. Точнее, предположим, что Игрок 1 считает, что Игрок 2 хочет встречаться с ней с вероятностью 1/2 и уйти от нее с вероятностью 1/2 (эта оценка, вероятно, основана на опыте Игрока 1: она сталкивается с игроками, которые хотят встречаться с ней половину времени в таком случае и игроками, которые хотят избегать ее половину времени). Из-за задействованной вероятности анализ этой ситуации требует понимания предпочтения игрока в отношении ничьей, хотя людей интересует только чистое стратегическое равновесие.
Игры, в которых сложность поиска оптимальной стратегии обусловлена множественностью возможных ходов, называются комбинаторными играми. Примеры включают шахматы и Го . Игры, в которых используется несовершенная информация, также могут иметь сильный комбинаторный характер, например нарды . Не существует единой теории комбинаторных элементов в играх. Однако существуют математические инструменты, которые могут решить некоторые частные проблемы и ответить на некоторые общие вопросы. [33]
Игры с совершенной информацией изучались в комбинаторной теории игр , которая разработала новые представления, например, сюрреалистические числа , а также комбинаторные и алгебраические (а иногда и неконструктивные ) методы доказательства для решения игр определенных типов, включая «зацикленные» игры, которые может привести к бесконечно длинным последовательностям ходов. Эти методы относятся к играм с более высокой комбинаторной сложностью, чем те, которые обычно рассматриваются в традиционной (или «экономической») теории игр. [34] [35] Типичная игра, решаемая таким образом, — Hex . Смежной областью исследований, основанной на теории сложности вычислений , является сложность игр , которая занимается оценкой вычислительной сложности поиска оптимальных стратегий. [36]
Исследования в области искусственного интеллекта касаются как совершенных, так и несовершенных информационных игр, имеющих очень сложную комбинаторную структуру (например, шахматы, го или нарды), для которых не найдено доказуемых оптимальных стратегий. Практические решения включают в себя вычислительную эвристику, такую как альфа-бета-обрезка или использование искусственных нейронных сетей, обученных с помощью обучения с подкреплением , что делает игры более удобными для компьютерной практики. [33] [37]
Игры, по мнению экономистов и реальных игроков, обычно заканчиваются за конечное число ходов. Чистые математики не столь ограничены, и теоретики множеств, в частности, изучают игры, которые длятся бесконечно много ходов, в которых победитель (или другой выигрыш) неизвестен до тех пор, пока все эти ходы не будут завершены.
Основное внимание обычно уделяется не столько тому, как лучше вести такую игру, сколько тому, есть ли у одного игрока выигрышная стратегия . (С помощью аксиомы выбора можно доказать , что существуют игры – даже при наличии полной информации и в которых единственным исходом является «выигрыш» или «проигрыш», – в которых ни у одного игрока нет выигрышной стратегии.) Существование таких стратегий. , для умно спроектированных игр, имеет важные последствия в дескриптивной теории множеств .
Большая часть теории игр посвящена конечным дискретным играм с конечным числом игроков, ходов, событий, результатов и т. д. Однако многие концепции можно расширить. Непрерывные игры позволяют игрокам выбирать стратегию из набора непрерывных стратегий. Например, конкуренция по Курно обычно моделируется, когда стратегии игроков представляют собой любые неотрицательные величины, в том числе дробные.
Непрерывные игры дают игрокам возможность общаться друг с другом в соответствии с определенными правилами, в первую очередь соблюдением протокола связи между игроками. Было отмечено, что посредством общения игроки готовы предоставить большее количество товаров в игре общественного блага, чем обычно в дискретной игре, и в результате игроки могут управлять ресурсами более эффективно, чем в дискретной игре. игры, поскольку они делятся друг с другом ресурсами, идеями и стратегиями. Это стимулирует и приводит к тому, что непрерывные игры имеют более высокий средний уровень сотрудничества. [38]
Дифференциальные игры, такие как игра с непрерывным преследованием и уклонением, представляют собой непрерывные игры, в которых эволюция переменных состояния игроков управляется дифференциальными уравнениями . Проблема поиска оптимальной стратегии в дифференциальной игре тесно связана с теорией оптимального управления . В частности, существует два типа стратегий: стратегии разомкнутого цикла находятся с использованием принципа максимума Понтрягина, а стратегии замкнутого цикла находятся с использованием метода динамического программирования Беллмана .
Частным случаем дифференциальных игр являются игры со случайным временным интервалом . [39] В таких играх конечное время является случайной величиной с заданной функцией распределения вероятностей . Следовательно, игроки максимизируют математическое ожидание функции стоимости. Показано, что модифицированную задачу оптимизации можно переформулировать как дифференциальную игру со скидкой на бесконечном интервале времени.
Эволюционная теория игр изучает игроков, которые со временем корректируют свои стратегии в соответствии с правилами, которые не обязательно являются рациональными или дальновидными. [40] В общем, эволюция стратегий во времени в соответствии с такими правилами моделируется как цепь Маркова с переменной состояния, такой как текущий профиль стратегии или то, как игра велась в недавнем прошлом. Такие правила могут включать имитацию, оптимизацию или выживание наиболее приспособленных.
В биологии такие модели могут представлять собой эволюцию , в которой потомство перенимает стратегии своих родителей, а родители, которые применяют более успешные стратегии (т. е. соответствующие более высоким выигрышам), имеют большее количество потомков. В социальных науках такие модели обычно представляют собой стратегическую корректировку игроков, которые играют в игру много раз в течение своей жизни и сознательно или неосознанно время от времени корректируют свои стратегии. [41]
Задачи индивидуального решения со случайными результатами иногда называют «играми для одного игрока». Их можно моделировать с использованием аналогичных инструментов в рамках смежных дисциплин теории принятия решений , исследования операций и областей искусственного интеллекта , в частности планирования ИИ (с неопределенностью) и многоагентных систем . Хотя эти области могут иметь разные мотиваторы, применяемая математика по существу одинакова, например, использование марковских процессов принятия решений (MDP). [42]
Стохастические исходы также можно смоделировать с точки зрения теории игр, добавив случайно действующего игрока, который делает «случайные ходы» (« ходы по своей природе »). [43] Этот игрок обычно не считается третьим игроком в игре для двух игроков, а просто служит для обеспечения броска кубиков там, где этого требует игра.
Для некоторых проблем разные подходы к моделированию стохастических результатов могут привести к разным решениям. Например, разница в подходе между MDP и минимаксным решением заключается в том, что последнее рассматривает наихудший случай из набора состязательных ходов, а не рассуждает в ожидании об этих ходах с учетом фиксированного распределения вероятностей. Минимаксный подход может оказаться выгодным там, где стохастические модели неопределенности недоступны, но он также может приводить к переоценке крайне маловероятных (но дорогостоящих) событий, резко влияя на стратегию в таких сценариях, если предполагается, что противник может заставить такое событие произойти. [44] ( Подробнее об этом виде проблем моделирования, особенно в том, что касается прогнозирования и ограничения убытков в инвестиционно-банковской деятельности, см. в « Теории черного лебедя ».)
Также изучались общие модели, включающие все элементы стохастических исходов, противников и частичную или зашумленную наблюдаемость (ходов других игроков). « Золотым стандартом » считается частично наблюдаемая стохастическая игра (POSG), но в представлении POSG вычислительно осуществимо лишь несколько реалистичных задач. [44]
Это игры, игра в которых представляет собой разработку правил другой игры, целевой или предметной игры. Метаигры стремятся максимизировать полезность разработанного набора правил. Теория метаигр связана с теорией проектирования механизмов .
Термин «метаигровой анализ» также используется для обозначения практического подхода, разработанного Найджелом Ховардом [45] , согласно которому ситуация оформляется как стратегическая игра, в которой заинтересованные стороны пытаются реализовать свои цели посредством доступных им вариантов. Последующие события привели к формулировке анализа конфронтации .
Это игры, господствующие над всеми формами общества. Игры с пулом — это повторяющиеся игры с изменением таблицы выигрышей в целом по опытному пути, и их равновесные стратегии обычно принимают форму эволюционной социальной конвенции и экономической конвенции. Теория объединенных игр возникает для формального признания взаимодействия между оптимальным выбором в одной игре и появлением предстоящего пути обновления таблицы выигрышей, определения существования и устойчивости инвариантности и прогнозирования дисперсии с течением времени. Теория основана на классификации топологических преобразований обновления таблицы выигрышей с течением времени для прогнозирования дисперсии и инвариантности, а также находится в пределах юрисдикции вычислительного закона достижимой оптимальности для упорядоченной системы. [46]
Теория игр среднего поля — это исследование принятия стратегических решений в очень больших популяциях небольших взаимодействующих агентов. Этот класс проблем рассматривался в экономической литературе Бояном Йовановичем и Робертом В. Розенталем , в инженерной литературе Питером Э. Кейнсом , а также математиками Пьером-Луи Лионсом и Жаном-Мишелем Ласри.
Игры, изучаемые в теории игр, представляют собой четко определенные математические объекты. Для полного определения игра должна определять следующие элементы: игроки игры, информация и действия, доступные каждому игроку в каждой точке принятия решения, а также выигрыши для каждого результата. (Эрик Расмусен называет эти четыре «основных элемента» аббревиатурой «PAPI».) [47] [48] [49] [50] Теоретик игр обычно использует эти элементы вместе с концепцией решения по своему выбору, чтобы сделать вывод набор равновесных стратегий для каждого игрока, при котором при использовании этих стратегий ни один игрок не может получить прибыль, отклонившись в одностороннем порядке от своей стратегии. Эти стратегии равновесия определяют равновесие в игре — стабильное состояние, в котором происходит либо один результат, либо набор результатов с известной вероятностью.
В играх у игроков обычно есть «доминирующая стратегия», в которой они заинтересованы в выборе наилучшей возможной стратегии, которая дает им максимальный выигрыш, и придерживаются ее, даже когда другие игроки меняют свои стратегии или выбирают другой вариант. Однако, в зависимости от возможных выигрышей, один из игроков может не обладать «доминирующей стратегией», а другой игрок может. Отсутствие у игрока доминирующей стратегии не является подтверждением того, что у другого игрока не будет собственной доминирующей стратегии, что ставит первого игрока в невыгодное положение.
Однако существует вероятность того, что оба игрока обладают доминирующими стратегиями, когда выбранные ими стратегии и их выигрыши являются доминирующими, а совокупные выигрыши образуют равновесие. Когда это происходит, создается Равновесие Доминирующей Стратегии. Это может вызвать социальную дилемму, когда в игре существует равновесие, созданное двумя или несколькими игроками, у каждого из которых есть доминирующие стратегии, и решение игры отличается от того, каким было бы совместное решение игры. [51]
Также существует вероятность того, что у игрока будет более одной доминирующей стратегии. Это происходит при реакции на несколько стратегий второго игрока, а также при отдельных ответах первого игрока, имеющих разные стратегии друг для друга. Это означает, что в игре невозможно достичь равновесия Нэша. [52]
Большинство кооперативных игр представлены в характеристической функциональной форме, тогда как экстенсивная и нормальная формы используются для определения некооперативных игр.

Развернутая форма может быть использована для формализации игр с временной последовательностью ходов. Игры обширной формы можно визуализировать с помощью деревьев игр (как показано здесь). Здесь каждая вершина (или узел) представляет собой точку выбора для игрока. Игрок определяется числом, указанным в вершине. Линии, выходящие из вершины, представляют собой возможное действие этого игрока. Выплаты указаны в нижней части дерева. Развернутую форму можно рассматривать как многопользовательское обобщение дерева решений . [53] Для решения любой игры с расширенной формой необходимо использовать обратную индукцию . Он включает в себя движение назад вверх по дереву игры, чтобы определить, что бы сделал рациональный игрок в последней вершине дерева, что сделал бы игрок, сделавший предыдущий ход, учитывая, что игрок, сделавший последний ход, является рациональным, и так далее до первого шага. вершина дерева достигнута. [54]
Изображенная игра состоит из двух игроков. В соответствии со структурой этой конкретной игры (т. е. с последовательным принятием решений и точной информацией), Игрок 1 «ходит» первым, выбирая либо F , либо U (честно или несправедливо). Далее в последовательности Игрок 2 , который теперь наблюдает за ходом Игрока 1 , может выбрать ход A или R (принять или отклонить). Как только Игрок 2 сделал свой выбор, игра считается завершенной, и каждый игрок получает соответствующий выигрыш, представленный на изображении в виде двух чисел, где первое число представляет выигрыш Игрока 1, а второе число представляет выигрыш Игрока 2. Предположим, что игрок 1 выбирает U, а затем игрок 2 выбирает A : тогда игрок 1 получает выигрыш в размере «восемь» (что в реальных условиях можно интерпретировать по-разному, самый простой из которых - в терминах денег, но может означать разные вещи). например, восемь дней отпуска или восемь завоеванных стран или даже еще восемь возможностей сыграть в ту же игру против других игроков), и Игрок 2 получает выигрыш «два».
Расширенная форма также может охватывать игры с одновременными ходами и игры с несовершенной информацией. Для этого либо пунктирная линия соединяет разные вершины, чтобы представить их как часть одного и того же набора информации (т. е. игроки не знают, в какой точке они находятся), либо вокруг них рисуется замкнутая линия. (См. пример в разделе несовершенной информации.)
Обычная игра (или стратегическая форма) обычно представляет собой матрицу , показывающую игроков, стратегии и выигрыши (см. пример справа). В более общем смысле ее можно представить любой функцией, которая связывает выигрыш каждого игрока со всеми возможными комбинациями действий. В сопровождающем примере есть два игрока; один выбирает строку, а другой выбирает столбец. У каждого игрока есть две стратегии, которые определяются количеством строк и количеством столбцов. Выплаты предусмотрены внутри. Первое число — это выигрыш, полученный игроком ряда (Игрок 1 в нашем примере); второй — это выигрыш для игрока столбца (Игрок 2 в нашем примере). Предположим, что Игрок 1 играет «Вверх» , а Игрок 2 — «Влево» . Тогда игрок 1 получает выигрыш 4, а игрок 2 — 3.
Когда игра представлена в нормальной форме, предполагается, что каждый игрок действует одновременно или, по крайней мере, не знает действий другого. Если игроки имеют некоторую информацию о выборе других игроков, игра обычно представлена в развернутой форме.
Каждая игра в расширенной форме имеет эквивалентную игру в нормальной форме, однако преобразование в нормальную форму может привести к экспоненциальному увеличению размера представления, что делает его непрактичным с вычислительной точки зрения. [55]
В играх, имеющих съемную утилиту, отдельные награды не выдаются; скорее, характеристическая функция определяет выигрыш каждой единицы. Идея в том, что единство, которое, так сказать, «пустое», вообще не получает награды.
Происхождение этой формы можно найти в книге Джона фон Неймана и Оскара Моргенштерна; рассматривая эти примеры, они догадались, что когда появляется союз, он работает против фракции так, как если бы два индивидуума играли в обычную игру. Сбалансированный выигрыш C является базовой функцией. Хотя существуют разные примеры, которые помогают определить коалиционные суммы из обычных игр, не все они в функциональной форме могут быть получены из них.
Формально характеристическая функция рассматривается как: (N,v), где N представляет группу людей и является нормальной полезностью.
Такие характерные функции расширились для описания игр, где нет съемной утилиты.
Альтернативные формы представления игр используются для некоторых подклассов игр или адаптированы к потребностям междисциплинарных исследований. [56] В дополнение к классическим представлениям игры, некоторые из альтернативных представлений также кодируют аспекты, связанные со временем.
Теория игр как метод прикладной математики использовалась для изучения широкого спектра поведения человека и животных. Первоначально он был разработан в экономике для понимания большого набора экономических моделей поведения, включая поведение фирм, рынков и потребителей. Впервые теоретико-игровой анализ был использован Антуаном Огюстеном Курно в 1838 году, когда он решил дуополию Курно . Использование теории игр в социальных науках расширилось, а теория игр также стала применяться к политическому, социологическому и психологическому поведению. [71]
Хотя натуралисты до двадцатого века, такие как Чарльз Дарвин, делали утверждения, относящиеся к теории игр, использование теоретико-игрового анализа в биологии началось с исследований Рональда Фишера поведения животных в 1930-х годах. Эта работа предшествовала названию «теория игр», но она имеет много общих черт с этой областью. Развитие экономики было позже применено к биологии главным образом Джоном Мейнардом Смитом в его книге 1982 года « Эволюция и теория игр» . [72]
Помимо описания, прогнозирования и объяснения поведения, теория игр также использовалась для разработки теорий этического или нормативного поведения и для предписания такого поведения. [73] В экономике и философии ученые применяли теорию игр, чтобы помочь понять хорошее или правильное поведение. Теоретико-игровые аргументы такого типа можно найти еще у Платона . [74] Альтернативная версия теории игр, называемая химической теорией игр , представляет выбор игрока в виде метафорических химических молекул-реагентов, называемых «нолекулы». [75] Химическая теория игр затем рассчитывает результаты как равновесные решения системы химических реакций.

Основное применение теории игр — описание и моделирование поведения человеческой популяции. [ нужна цитата ] Некоторые [ кто? Ученые полагают, что, находя равновесие в играх, они могут предсказать, как поведет себя реальная человеческая популяция, столкнувшись с ситуациями, аналогичными изучаемой игре. Этот конкретный взгляд на теорию игр подвергся критике. Утверждается, что предположения, сделанные теоретиками игр, часто нарушаются при применении к реальным ситуациям. Теоретики игр обычно предполагают, что игроки действуют рационально, но на практике человеческая рациональность и/или поведение часто отклоняются от модели рациональности, используемой в теории игр. Теоретики игр отвечают, сравнивая свои предположения с предположениями, используемыми в физике . Таким образом, хотя их предположения не всегда верны, они могут рассматривать теорию игр как разумный научный идеал, аналогичный моделям, используемым физиками . Однако эмпирическая работа показала, что в некоторых классических играх, таких как игра «Сороконожка » ( угадай 2/3 средней игры) и игра «Диктатор» , люди регулярно не играют в равновесия Нэша. Продолжаются споры о важности этих экспериментов и о том, полностью ли анализ экспериментов отражает все аспекты соответствующей ситуации. [б]
Некоторые теоретики игр, следуя работам Джона Мейнарда Смита и Джорджа Р. Прайса , обратились к эволюционной теории игр, чтобы решить эти проблемы. Эти модели предполагают либо отсутствие рациональности, либо ограниченную рациональность со стороны игроков. Несмотря на название, эволюционная теория игр не обязательно предполагает естественный отбор в биологическом смысле. Эволюционная теория игр включает как биологическую, так и культурную эволюцию, а также модели индивидуального обучения (например, фиктивную игровую динамику).
Некоторые ученые рассматривают теорию игр не как инструмент прогнозирования поведения людей, а как предложение о том, как людям следует себя вести. Поскольку стратегия, соответствующая равновесию Нэша в игре, представляет собой лучший ответ на действия других игроков – при условии, что они находятся в (одном и том же) равновесии Нэша – игра по стратегии, которая является частью равновесия Нэша, кажется подходящей. Такое нормативное использование теории игр также подверглось критике. [ нужна цитата ]
Теория игр — основной метод, используемый в математической экономике и бизнесе для моделирования конкурирующего поведения взаимодействующих агентов . [c] [77] [78] [79] Приложения включают широкий спектр экономических явлений и подходов, таких как аукционы , переговоры , ценообразование слияний и поглощений , [80] справедливое разделение , дуополии , олигополии , формирование социальных сетей , агент- основанная на вычислительной экономике , [81] [82] общее равновесие , проектирование механизмов, [83] [84] [85] [86] [87] и системы голосования ; [88] и в таких широких областях, как экспериментальная экономика, [89] [90] [91] [92] [93] поведенческая экономика , [94] [95] [96] [97] [98] [99] информационная экономика , [47] [48] [49] [50] промышленная организация , [100] [101] [102] [103] и политическая экономия . [104] [105] [106] [107]
Это исследование обычно фокусируется на определенных наборах стратегий, известных как «концепции решения» или «равновесия» . Распространено предположение, что игроки действуют рационально. В некооперативных играх самым известным из них является равновесие Нэша. Набор стратегий представляет собой равновесие Нэша, если каждая из них представляет собой лучший ответ на другие стратегии. Если все игроки применяют стратегии равновесия Нэша, у них нет одностороннего стимула отклоняться, поскольку их стратегия — лучшее, что они могут сделать, учитывая то, что делают другие. [108] [109]
Выигрыши в игре обычно отражают полезность отдельных игроков.
Прототипическая статья по теории игр в экономике начинается с описания игры, которая представляет собой абстракцию конкретной экономической ситуации. Выбирается одна или несколько концепций решения, и автор демонстрирует, какие множества стратегий в представленной игре являются равновесиями соответствующего типа. Экономисты и профессора бизнеса предлагают два основных варианта использования (отмеченных выше): описательное и предписывающее . [73]
Теория игр также широко используется в определенной отрасли или направлении экономики — управленческой экономике . Одним из важных применений этого метода в области управленческой экономики является анализ стратегических взаимодействий между фирмами. [110] Например, фирмы могут конкурировать на рынке с ограниченными ресурсами, а теория игр может помочь менеджерам понять, как их решения влияют на конкурентов и на общие результаты рынка. Теорию игр также можно использовать для анализа сотрудничества между фирмами, например, при формировании стратегических альянсов или совместных предприятий. Еще одно применение теории игр в экономике управления — анализ стратегий ценообразования. Например, фирмы могут использовать теорию игр для определения оптимальной стратегии ценообразования на основе того, как, по их ожиданиям, конкуренты будут реагировать на их ценовые решения. В целом теория игр служит полезным инструментом для анализа стратегических взаимодействий и принятия решений в контексте экономики управления.
Сертифицированный институт закупок и поставок (CIPS) продвигает знания и использование теории игр в контексте деловых закупок . [111] Партнеры CIPS и TWS провели серию опросов, призванных изучить понимание, осведомленность и применение теории игр среди специалистов по закупкам . Некоторые из основных выводов третьего ежегодного опроса (2019 г.) включают:
Разумное принятие решений имеет решающее значение для успеха проектов. В управлении проектами теория игр используется для моделирования процесса принятия решений участниками, такими как инвесторы, менеджеры проектов, подрядчики, субподрядчики, правительства и клиенты. Довольно часто эти игроки имеют конкурирующие интересы, а иногда их интересы наносят прямой ущерб другим игрокам, что делает сценарии управления проектами хорошо подходящими для моделирования с помощью теории игр.
Пиравинан (2019) [113] в своем обзоре приводит несколько примеров использования теории игр для моделирования сценариев управления проектами. Например, у инвестора обычно есть несколько вариантов инвестирования, и каждый вариант, скорее всего, приведет к созданию отдельного проекта, и, таким образом, один из вариантов инвестирования должен быть выбран до того, как будет составлен устав проекта. Аналогичным образом, любой крупный проект с участием субподрядчиков, например, строительный проект, имеет сложное взаимодействие между главным подрядчиком (менеджером проекта) и субподрядчиками или между самими субподрядчиками, которое обычно имеет несколько точек принятия решений. Например, если в контракте между подрядчиком и субподрядчиком существует двусмысленность, каждый должен решить, насколько сильно продвигать свое дело, не ставя под угрозу весь проект и, следовательно, свою собственную долю в нем. Аналогичным образом, когда запускаются проекты конкурирующих организаций, сотрудники отдела маркетинга должны решить, какие сроки и стратегия лучше всего подходят для продвижения проекта или его результирующего продукта или услуги, чтобы он мог получить максимальную эффективность в условиях конкуренции. В каждом из этих сценариев необходимые решения зависят от решений других игроков, интересы которых каким-то образом конкурируют с интересами лица, принимающего решения, и поэтому в идеале их можно смоделировать с помощью теории игр.
Пиравенан [113] резюмирует, что игры для двух игроков преимущественно используются для моделирования сценариев управления проектами, и в зависимости от личности этих игроков в управлении проектами используются пять различных типов игр.
Что касается типов игр, для моделирования различных сценариев управления проектами используются как кооперативные, так и некооперативные, нормальные и расширенные формы, а также игры с нулевой и ненулевой суммой.
Применение теории игр к политической науке сосредоточено на пересекающихся областях справедливого разделения , политической экономии , общественного выбора , военных переговоров , позитивной политической теории и теории социального выбора . В каждой из этих областей исследователи разработали теоретико-игровые модели, в которых игроками часто являются избиратели, государства, группы с особыми интересами и политики. [114]
Ранние примеры теории игр, примененные к политической науке, предоставлены Энтони Даунсом . В своей книге 1957 года «Экономическая теория демократии» [ 115] он применяет модель местоположения фирмы Хотеллинга к политическому процессу. В модели Даунсиана политические кандидаты придерживаются идеологий в одномерном политическом пространстве. Даунс сначала показывает, как политические кандидаты приблизятся к идеологии, предпочитаемой средним избирателем, если избиратели будут полностью информированы, но затем утверждает, что избиратели предпочитают оставаться рационально невежественными, что допускает расхождения между кандидатами. Теория игр была применена в 1962 году к кубинскому ракетному кризису во время президентства Джона Ф. Кеннеди. [116]
Было также высказано предположение, что теория игр объясняет стабильность любой формы политического правления. Возьмем, к примеру, простейший случай монархии: король, будучи всего лишь одним человеком, не поддерживает и не может поддерживать свою власть, лично осуществляя физический контроль над всеми или даже каким-либо значительным числом своих подданных. Вместо этого суверенный контроль объясняется признанием каждым гражданином того, что все остальные граждане ожидают, что друг от друга будут рассматривать короля (или другое установленное правительство) как человека, приказам которого будут следовать. Координация общения между гражданами с целью замены суверена фактически запрещена, поскольку заговор с целью замены суверена обычно наказуем как преступление. [117] Таким образом, в процессе, который можно смоделировать вариантами дилеммы узника, в периоды стабильности ни один гражданин не сочтет целесообразным заменить суверена, даже если все граждане знают, что им было бы лучше, если бы они были всем действовать сообща. [118]
Теоретико-игровое объяснение демократического мира заключается в том, что публичные и открытые дебаты в демократических странах посылают четкую и надежную информацию об их намерениях другим государствам. Напротив, трудно понять намерения недемократических лидеров, какой эффект окажут уступки и будут ли выполняться обещания. Таким образом, возникнет недоверие и нежелание идти на уступки, если хотя бы одна из сторон в споре — недемократия. [119]
Однако теория игр предсказывает, что две страны все равно могут начать войну, даже если их лидеры осознают цену боевых действий. Война может возникнуть из-за асимметричной информации; У двух стран могут быть стимулы искажать объем имеющихся у них военных ресурсов, что делает их неспособными урегулировать споры мирным путем, не прибегая к боевым действиям. Более того, война может возникнуть из-за проблем с обязательствами: если две страны желают урегулировать спор мирными средствами, но каждая хочет вернуться к условиям этого урегулирования, у них может не быть другого выбора, кроме как прибегнуть к войне. Наконец, война может возникнуть из-за неделимости вопросов. [120]
Теория игр также может помочь предсказать реакцию нации, когда к этой нации будут применяться новые правила или законы. Одним из примеров является исследование Питера Джона Вуда (2013), посвященное тому, что страны могут сделать, чтобы помочь уменьшить изменение климата. Вуд считал, что этого можно достичь, заключив договоры с другими странами о сокращении выбросов парниковых газов . Однако он пришел к выводу, что эта идея не сработает, поскольку создаст для народов дилемму заключенного. [121]
Теория игр широко использовалась для моделирования сценариев принятия решений, имеющих отношение к оборонным приложениям. [122] Большинство исследований, в которых теория игр применялась в оборонных условиях, связаны с войной командования и контроля и могут быть далее классифицированы на исследования, посвященные (i) войне за распределение ресурсов, (ii) информационной войне, (iii) войне за контроль над оружием, и ( iv) Мониторинг противника. [122] Многие из изученных проблем связаны с зондированием и отслеживанием, например, надводный корабль пытается отследить вражескую подводную лодку, а подводная лодка пытается уклониться от слежения, а также с взаимозависимым принятием решений, которые происходят в отношении пеленга, скорости, и сенсорная технология, активируемая обоими судами. Хо и др. [122] дают краткий обзор современного состояния использования теории игр в оборонных приложениях и подчеркивают преимущества и ограничения теории игр в рассматриваемых сценариях.
В отличие от экономических, выигрыши в играх в биологии часто интерпретируются как соответствующие приспособленности . Кроме того, основное внимание уделялось не столько равновесиям, которые соответствуют понятию рациональности, сколько тем, которые будут поддерживаться эволюционными силами. Самое известное равновесие в биологии известно как эволюционно стабильная стратегия (ESS), впервые представленная в (Maynard Smith & Price 1973). Хотя ее первоначальная мотивация не включала в себя какие-либо ментальные требования равновесия Нэша, каждая ESS является равновесием Нэша.
В биологии теория игр использовалась как модель для понимания множества различных явлений. Впервые он был использован для объяснения эволюции (и стабильности) примерного соотношения полов 1:1 . (Fisher 1930) предположил, что соотношение полов 1:1 является результатом эволюционных сил, действующих на людей, которые, как можно рассматривать, пытаются максимизировать количество своих внуков.
Кроме того, биологи использовали эволюционную теорию игр и ESS, чтобы объяснить возникновение общения животных . [123] Анализ сигнальных игр и других коммуникативных игр позволил понять эволюцию общения среди животных. Например, моббинговое поведение многих видов, при котором большое количество животных-жертв нападает на более крупного хищника, по-видимому, является примером спонтанной возникающей организации. Было также показано, что муравьи демонстрируют упреждающее поведение, похожее на моду (см. « Экономика бабочек » Пола Ормерода ).
Биологи использовали игру кур для анализа боевого поведения и территориальности. [124]
По словам Мейнарда Смита в предисловии к книге « Эволюция и теория игр» , «парадоксальным образом оказалось, что теорию игр легче применить к биологии, чем к области экономического поведения, для которой она изначально была разработана». Эволюционная теория игр использовалась для объяснения многих, казалось бы, нелепых явлений в природе. [125]
Одно из таких явлений известно как биологический альтруизм . Это ситуация, в которой организм действует таким образом, который приносит пользу другим организмам и наносит вред самому себе. Это отличается от традиционных представлений об альтруизме, поскольку такие действия не являются сознательными, а кажутся эволюционными адаптациями, направленными на повышение общей приспособленности. Примеры можно найти у самых разных видов: от летучих мышей-вампиров, которые срыгивают кровь, полученную во время ночной охоты, и отдают ее членам группы, которые не смогли накормиться, до рабочих пчел, которые заботятся о пчелиной матке всю свою жизнь и никогда не спариваются. мартышки-верветки , которые предупреждают членов группы о приближении хищника, даже если это ставит под угрозу шансы этого человека на выживание. [126] Все эти действия повышают общую подготовленность группы, но происходят за счет отдельного человека.
Эволюционная теория игр объясняет этот альтруизм идеей родственного отбора . Альтруисты различают людей, которым они помогают, и отдают предпочтение родственникам. Правило Гамильтона объясняет эволюционное обоснование этого выбора уравнением c < b × r , где стоимость c для альтруиста должна быть меньше, чем выгода b для получателя, умноженная на коэффициент родства r . Более близкородственные два организма вызывают увеличение случаев альтруизма, поскольку они имеют много одинаковых аллелей. Это означает, что альтруистический индивидуум, гарантируя, что аллели его близкого родственника передаются через выживание его потомства, может отказаться от возможности иметь потомство самому, поскольку передается такое же количество аллелей. Например, помощь брату или сестре ( у диплоидных животных) имеет коэффициент 1/2 , потому что (в среднем) особь разделяет половину аллелей с потомством своего брата или сестры . Обеспечение того, чтобы достаточное количество потомков брата или сестры дожило до взрослого возраста, исключает необходимость производства потомства у альтруистической личности. [126] Значения коэффициентов сильно зависят от объема игрового поля; например, если выбор, кому отдать предпочтение, включает в себя все генетические живые существа, а не только всех родственников, мы предполагаем, что несоответствие между всеми людьми составляет только примерно 1% разнообразия на игровом поле, коэффициент, который составлял 1 ⁄ 2 в меньшее поле становится 0,995. Аналогичным образом, если принять во внимание, что информация, отличная от генетической природы (например, эпигенетика, религия, наука и т. д.), сохранялась во времени, игровое поле становится еще больше, а расхождения уменьшаются.
Теория игр стала играть все более важную роль в логике и информатике . Несколько логических теорий имеют основу в семантике игр . Кроме того, ученые-компьютерщики использовали игры для моделирования интерактивных вычислений . Кроме того, теория игр обеспечивает теоретическую основу для многоагентных систем . [127]
Отдельно теория игр сыграла роль в онлайн-алгоритмах ; в частности, проблема k -сервера , которую в прошлом называли играми с движущимися издержками и играми запрос-ответ . [128] Принцип Яо — это теоретико-игровой метод доказательства нижних границ вычислительной сложности рандомизированных алгоритмов , особенно онлайн-алгоритмов.
Появление Интернета стимулировало разработку алгоритмов поиска равновесия в играх, рынках, вычислительных аукционах, одноранговых системах, а также на рынках безопасности и информации. Алгоритмическая теория игр [87] и в рамках нее алгоритмическое проектирование механизмов [86] сочетают разработку вычислительных алгоритмов и анализ сложных систем с экономической теорией. [129] [130] [131]
Теория игр нашла несколько применений в философии . Отвечая на две статьи У.В.О. Куайна (1960, 1967), Льюис (1969) использовал теорию игр для разработки философского объяснения конвенции . При этом он провел первый анализ общеизвестных знаний и применил их при анализе координационных игр . Кроме того, он впервые предположил, что понимать смысл можно с точки зрения сигнальных игр . Это более позднее предложение развивалось несколькими философами после Льюиса. [132] [133] Следуя теоретико-игровому описанию конвенций Льюиса (1969), Эдна Ульманн-Маргалит (1977) и Биккьери (2006) разработали теории социальных норм , которые определяют их как равновесия Нэша, возникающие в результате трансформации смешанных мотивов. игра в координационную игру. [134] [135]
Теория игр также заставила философов мыслить в терминах интерактивной эпистемологии : что значит для коллектива иметь общие убеждения или знания и каковы последствия этого знания для социальных результатов, возникающих в результате взаимодействия агентов. Среди философов, работавших в этой области, — Биккьери (1989, 1993), [136] [137] Скирмс (1990), [138] и Сталнакер (1999). [139]
В этике некоторые (особенно Дэвид Готье, Грегори Кавка и Джин Хэмптон) [ кто? ] авторы пытались реализовать проект Томаса Гоббса о выводе морали из личного интереса. Поскольку такие игры, как «Дилемма заключенного», представляют собой очевидный конфликт между моралью и личными интересами, важным компонентом этого проекта является объяснение того, почему сотрудничество необходимо ради собственных интересов. Эта общая стратегия является компонентом общего взгляда на общественный договор в политической философии (см., например, Готье (1986) и Кавку (1986)). [д]
Другие авторы пытались использовать эволюционную теорию игр, чтобы объяснить возникновение человеческих взглядов на мораль и соответствующее поведение животных. Эти авторы рассматривают несколько игр, включая дилемму заключённого, охоту на оленя и торговую игру Нэша , как объясняющие возникновение взглядов на мораль (см., например, Skyrms (1996, 2004) и Sober and Wilson (1998)).
Приложения теории игр часто используются в стратегиях ценообразования на розничных и потребительских рынках, особенно для продажи неэластичных товаров . Поскольку ритейлеры постоянно конкурируют друг с другом за долю на потребительском рынке, для ритейлеров стало довольно распространенной практикой периодически снижать цены на определенные товары в надежде увеличить посещаемость обычных магазинов (посещение веб-сайтов для розничных продавцов электронной коммерции ). или увеличение продаж вспомогательных или дополнительных продуктов. [140]
Черная пятница , популярный праздник шоппинга в США, — это время, когда многие ритейлеры сосредотачивают внимание на оптимальных стратегиях ценообразования, чтобы захватить рынок праздничных покупок. В сценарии «Черной пятницы» ритейлеры, использующие приложения теории игр, обычно спрашивают: «Какова реакция на меня доминирующего конкурента?» [141] В таком сценарии в игре участвуют два игрока: розничный торговец и потребитель. Розничный торговец ориентирован на оптимальную ценовую стратегию, в то время как потребитель ориентирован на лучшее предложение. В этой закрытой системе часто не существует доминирующей стратегии, поскольку у обоих игроков есть альтернативные варианты. То есть розничные продавцы могут найти другого покупателя, а потребители могут делать покупки у другого розничного продавца. [141] Однако, учитывая рыночную конкуренцию в тот день, доминирующая стратегия ритейлеров заключается в том, чтобы превзойти конкурентов. Открытая система предполагает наличие нескольких розничных продавцов, продающих одинаковые товары, и конечного числа потребителей, требующих товары по оптимальной цене. В блоге профессора Корнеллского университета приведен пример такой стратегии: Amazon установил цену на телевизор Samsung на 100 долларов ниже розничной стоимости, что фактически обогнало конкурентов. Amazon частично компенсировал разницу, увеличив цены на кабели HDMI, поскольку было обнаружено, что потребители менее склонны к ценовой дискриминации, когда дело касается продажи второстепенных товаров. [141]
Розничные рынки продолжают развивать стратегии и приложения теории игр, когда дело доходит до ценообразования на потребительские товары. Ключевые выводы, полученные при моделировании в контролируемой среде и реальном опыте розничной торговли, показывают, что применение таких стратегий более сложное, поскольку каждому ритейлеру приходится находить оптимальный баланс между ценообразованием , отношениями с поставщиками , имиджем бренда и потенциалом каннибализации . продажа более выгодных товаров. [142]
Поскольку решение о вакцинации против конкретного заболевания часто принимается отдельными людьми, которые при принятии этого решения могут учитывать ряд факторов и параметров (таких как заболеваемость и распространенность заболевания, предполагаемые и реальные риски, связанные с заражением этим заболеванием). (уровень смертности, предполагаемые и реальные риски, связанные с вакцинацией, а также финансовые затраты на вакцинацию), теория игр использовалась для моделирования и прогнозирования распространения вакцинации в обществе. [143] [144]
Теория игр имеет множество приложений в области искусственного интеллекта и машинного обучения. Его часто используют при разработке автономных систем, способных принимать сложные решения в неопределенной среде. [145] Некоторые другие области применения теории игр в контексте ИИ/МО заключаются в следующем: формирование многоагентных систем, обучение с подкреплением, проектирование механизмов и т. д. [146] Использование теории игр для моделирования поведения других агентов и прогнозирования их действий, системы искусственного интеллекта и машинного обучения могут принимать более обоснованные решения и работать более эффективно. [147]
Уильям Паундстоун описал эту игру в своей книге «Дилемма узника» 1993 года: [148]
Двое членов преступной группировки, А и Б, арестованы и заключены в тюрьму. Каждый заключенный находится в одиночной камере без возможности общения со своим партнером. Основное обвинение влечет за собой наказание в виде десяти лет тюремного заключения; однако у полиции нет доказательств для вынесения обвинительного приговора. Они планируют приговорить обоих к двум годам тюремного заключения по менее серьезному обвинению, но предлагают каждому заключенному фаустовскую сделку: если один из них сознается в преступлении по основному обвинению, предав другого, они будут помилованы и смогут уйти, в то время как другой должен отбыть весь срок наказания вместо двух лет по менее строгому обвинению.
Доминирующая стратегия (и, следовательно, лучший ответ на любую возможную стратегию противника) — предать другого, что соответствует принципу уверенности . [149] Однако молчание обоих заключенных принесет им обоим большую награду, чем взаимное предательство.
«Битва полов» — это термин, используемый для описания предполагаемого конфликта между мужчинами и женщинами в различных сферах жизни, таких как отношения, карьера и социальные роли. Этот конфликт часто изображается в популярной культуре, например, в фильмах и телешоу, как юмористическое или драматическое соревнование между полами. Этот конфликт можно описать в рамках теории игр. Это пример некооперативных игр.
Пример «битвы полов» можно увидеть в изображении отношений в популярных средствах массовой информации, где мужчины и женщины часто изображаются принципиально разными и конфликтующими друг с другом. Например, в некоторых романтических комедиях главные герои мужского и женского пола имеют противоположные взгляды на любовь и отношения, и им приходится преодолевать эти различия, чтобы быть вместе. [150]
В этой игре существуют два равновесия Нэша в чистой стратегии: одно, когда оба игрока выбирают одну и ту же стратегию, и другое, когда игроки выбирают разные варианты. Если игра ведется в смешанных стратегиях, где каждый игрок выбирает свою стратегию случайным образом, то существует бесконечное число равновесий Нэша. Однако в контексте игры «битва полов» обычно делается предположение, что игра ведется в чистых стратегиях. [151]
Игра «Ультиматум» — игра, ставшая популярным инструментом экономических экспериментов . Раннее описание принадлежит нобелевскому лауреату Джону Харсаньи в 1961 году. [152]
Один игрок, предлагающий, получает определенную сумму денег. Предлагающему поручено разделить его с другим игроком, отвечающим (который знает, какова общая сумма). Как только предлагающий сообщает о своем решении, ответчик может принять его или отклонить. Если ответчик соглашается, деньги делятся в зависимости от предложения; если ответчик отклоняет предложение, оба игрока ничего не получают. Оба игрока заранее знают последствия принятия или отклонения предложения ответчиком. Игра демонстрирует, как общественное признание, справедливость и щедрость влияют на решения игроков. [153]
У игры «Ультиматум» есть вариант — игра «Диктатор». Они в основном идентичны, за исключением того, что в игре с диктатором ответчик не имеет права отклонить предложение предлагающего.
«Игра в доверие» — это эксперимент, призванный измерить доверие к экономическим решениям. Ее еще называют «инвестиционной игрой», и она предназначена для исследования доверия и демонстрации его важности, а не «рациональности» личных интересов. Игра была разработана Бергом Джойсом, Джоном Дикхаутом и Кевином Маккейбом в 1995 году. [154]
В игре одному игроку (инвестору) дается определенная сумма денег, и он должен решить, какую часть ее передать другому игроку (попечителю). Затем экспериментатор утраивает данное количество. Затем доверительный управляющий решает, какую часть утроенной суммы вернуть инвестору. Если получатель полностью заинтересован в себе, то он/она не должен ничего возвращать. Однако это не так, как проводится эксперимент. Результаты показывают, что люди готовы оказать доверие, рискуя некоторой суммой денег, полагая, что будет взаимность. [155]
Модель конкуренции Курно предполагает, что игроки выбирают количество однородного продукта для производства независимо и одновременно, при этом предельные издержки могут быть разными для каждой фирмы, а выигрышем фирмы является прибыль. Издержки производства являются общедоступной информацией, и фирма стремится определить объем, максимизирующий прибыль, исходя из того, что, по ее мнению, будет производить другая фирма и вести себя как монополия. В этой игре фирмы хотят производить монопольный объем, но у них есть сильный стимул отклоняться и производить больше, что снижает рыночную цену. [23] Например, у фирм может возникнуть соблазн отклониться от монопольного объема, если существует низкий монопольный объем и высокая цена, с целью увеличения производства для максимизации прибыли. [23] Однако этот вариант не обеспечивает наибольшую отдачу, поскольку способность фирмы максимизировать прибыль зависит от ее доли на рынке и эластичности рыночного спроса. [156] Равновесие Курно достигается, когда каждая фирма действует в соответствии со своей функцией реакции, не имея стимула к отклонению, поскольку у них есть лучший ответ, основанный на выпуске другой фирмы. [23] В игре фирмы достигают равновесия Нэша, когда достигается равновесие Курно.
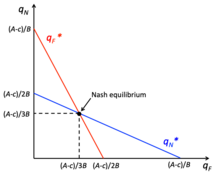
Конкуренция Бертрана предполагает однородность продуктов и постоянные предельные издержки, а цены выбирают игроки. [23] Равновесие ценовой конкуренции – это ситуация, когда цена равна предельным издержкам при условии полной информации о издержках конкурентов. Следовательно, у фирм есть стимул отклоняться от равновесия, поскольку однородный продукт с более низкой ценой получит всю долю рынка, что известно как преимущество в издержках. [157]
Списки
{{cite journal}}: CS1 maint: multiple names: authors list (link){{cite book}}: |journal=игнорируется ( помощь ){{cite book}}: |website=игнорируется ( помощь )... в том, что весь смысл машины судного дня утерян, если держать это в секрете!