Возведение в степень

Арифметическая операция

Графики y = b ^x для различных оснований b :  основание 10,   основание е,   база 2,   база  ⁠1/2⁠ .Каждая кривая проходит через точку(0, 1), поскольку любое ненулевое число, возведенное в степень0, равно1.Приx= 1значениеyравно основанию, поскольку любое число, возведенное в степень1, равно самому числу.

В математике возведение в степень — это операция , включающая два числа : основание и показатель степени или степень . Возведение в степень записывается как b ⁿ , где b — основание , а n — степень ; это произносится как « b (возведенное) в степень n ». ^[1] Когда n — положительное целое число , возведение в степень соответствует повторному умножению основания: то есть b ⁿ — это произведение умножения n оснований: ^[1] $${\displaystyle b^{n}=\underbrace {b\times b\times \dots \times b\times b} _{n{\text{ times}}}.}$$

Экспонента обычно отображается в виде верхнего индекса справа от основания. В этом случае b ⁿ называется « b , возведенное в степень n », « b (возведенное) в степень n », « n -я степень b », « b в n -й степени» ^[2] или, короче, « b в степени n (й)».

Исходя из основного факта, изложенного выше, что для любого положительного целого числа есть вхождения всех умноженных друг на друга, отсюда непосредственно вытекают несколько других свойств возведения в степень. В частности: ^{[nb 1]} ${\displaystyle n}$ ${\displaystyle b^{n}}$ ${\displaystyle n}$ ${\displaystyle b}$

$${\displaystyle {\begin{aligned}b^{n+m}&=\underbrace {b\times \dots \times b} _{n+m{\text{ times}}}\\[1ex]&=\underbrace {b\times \dots \times b} _{n{\text{ times}}}\times \underbrace {b\times \dots \times b} _{m{\text{ times}}}\\[1ex]&=b^{n}\times b^{m}\end{aligned}}}$$

Другими словами, при умножении основания, возведенного в одну степень, на то же основание, возведенное в другую степень, показатели степеней складываются. Из этого основного правила, что показатели степеней складываются, мы можем вывести, что должно быть равно 1 для любого , следующим образом. Для любого , . Разделив обе части на , получаем . ${\displaystyle b^{0}}$ ${\displaystyle b\neq 0}$ ${\displaystyle n}$ ${\displaystyle b^{0}\times b^{n}=b^{0+n}=b^{n}}$ ${\displaystyle b^{n}}$ ${\displaystyle b^{0}=b^{n}/b^{n}=1}$

Тот факт, что можно аналогичным образом вывести из того же правила. Например, . Взяв кубический корень из обеих сторон, получим . ${\displaystyle b^{1}=b}$ ${\displaystyle (b^{1})^{3}=b^{1}\times b^{1}\times b^{1}=b^{1+1+1}=b^{3}}$ ${\displaystyle b^{1}=b}$

Правило, согласно которому умножение заставляет экспоненты складываться, можно использовать и для вывода свойств отрицательных целых экспонент. Рассмотрим вопрос о том, что должно означать. Чтобы соблюсти правило «экспоненты складываются», должно быть так, что . Разделив обе части на , получаем , что можно записать проще как , используя полученный выше результат . Подобным же образом, . ${\displaystyle b^{-1}}$ ${\displaystyle b^{-1}\times b^{1}=b^{-1+1}=b^{0}=1}$ ${\displaystyle b^{1}}$ ${\displaystyle b^{-1}=1/b^{1}}$ ${\displaystyle b^{-1}=1/b}$ ${\displaystyle b^{1}=b}$ ${\displaystyle b^{-n}=1/b^{n}}$

Свойства дробных показателей степени также следуют из того же правила. Например, предположим, что мы рассматриваем и спрашиваем, есть ли некоторая подходящая экспонента, которую мы можем назвать , такая, что . Из определения квадратного корня имеем, что . Следовательно, показатель степени должен быть таким, что . Используя тот факт, что умножение заставляет показатели степени складывать, получаем . С правой стороны можно также записать как , что дает . Приравнивая показатели степени с обеих сторон, имеем . Следовательно, , поэтому . ${\displaystyle {\sqrt {b}}}$ ${\displaystyle r}$ ${\displaystyle b^{r}={\sqrt {b}}}$ ${\displaystyle {\sqrt {b}}\times {\sqrt {b}}=b}$ ${\displaystyle r}$ ${\displaystyle b^{r}\times b^{r}=b}$ ${\displaystyle b^{r+r}=b}$ ${\displaystyle b}$ ${\displaystyle b^{1}}$ ${\displaystyle b^{r+r}=b^{1}}$ ${\displaystyle r+r=1}$ ${\displaystyle r={\tfrac {1}{2}}}$ ${\displaystyle {\sqrt {b}}=b^{1/2}}$

Определение возведения в степень может быть расширено, чтобы разрешить любую действительную или комплексную экспоненту. Возведение в степень целыми экспонентами также может быть определено для широкого спектра алгебраических структур, включая матрицы .

Возведение в степень широко используется во многих областях, включая экономику , биологию , химию , физику и информатику , в таких приложениях, как сложные проценты , рост населения , кинетика химических реакций , волновое поведение и криптография с открытым ключом .

Этимология

Термин exponent происходит от латинского exponentem , настоящего причастия exponere , означающего «выдвигать». ^[3] Термин power ( лат . potentia, potestas, dignitas ) является неправильным переводом ^{[4] [5]} древнегреческого δύναμις ( dúnamis , здесь: «усиление» [ ^{4] ), который} греческий математик Евклид использовал для обозначения квадрата прямой, ^[6] следуя Гиппократу Хиосскому . ^[7]

История

Древность

Песчаный счетовод

В «Песочном счетоводе» Архимед доказал закон степеней, 10a ^· 10b = 10a ^{+ b ,} необходимый для манипулирования степенями числа 10. ^[8] Затем он использовал степени числа 10 ^, чтобы оценить количество песчинок, которые могут содержаться во Вселенной .

Золотой век ислама

МалиКааба(«квадрат» и «куб»)

В IX веке персидский математик Аль-Хорезми использовал термины مَال ( māl , «имущество», «собственность») для квадрата — мусульмане, «как и большинство математиков тех и более ранних времен, думали о квадратном числе как о изображении площади, особенно земли, следовательно, собственности» ^[9] — и كَعْبَة ( Kaʿbah , «куб») для куба , который позднее исламские математики представляли в математической нотации как буквы mīm (m) и kāf (k) соответственно, к XV веку, как видно из работы Абу-ль-Хасана ибн Али аль-Каласади . ^[10]

15–18 век

Введение в экспоненты

Николя Шюке использовал форму экспоненциальной записи в 15 веке, например, 12 ² для представления 12 x ² . ^[11] Позже это использовали Хенрикус Грамматеус и Михаэль Штифель в 16 веке. В конце 16 века Йост Бюрги использовал римские цифры для показателей степени способом, похожим на тот, что использовал Шюке, напримерiii4для 4 x ^3. [ 12 ^]

«Экспонента»; «квадрат» и «куб»

Слово показатель степени было введено в 1544 году Михаэлем Штифелем. ^{[13] [14]} В XVI веке Роберт Рекорд использовал термины квадрат, куб, зензизензик ( четвертая степень ), сурсолид (пятая), зензикуб (шестая), второй сурсолид (седьмая) и зензизензизензик (восьмая). ^[9] Биквадрат также использовался для обозначения четвертой степени.

Современная экспоненциальная запись

В 1636 году Джеймс Юм использовал по существу современную нотацию, когда в L'algèbre de Viète он записал A ⁱⁱⁱ вместо A ³ . ^[15] В начале 17 века первая форма нашей современной экспоненциальной записи была введена Рене Декартом в его тексте под названием La Géométrie ; там эта нотация введена в Книге I. ^[16]

Я обозначаю ... аа , или 2 при умножении а ^на само себя; и ³ при умножении его еще раз на а , и так до бесконечности.

—  Рене Декарт, «Геометрия».

Некоторые математики (например, Декарт) использовали показатели только для степеней больше двух, предпочитая представлять квадраты как повторное умножение. Таким образом, они записывали многочлены , например, как ax + bxx + cx ³ + d .

"Индексы"

Сэмюэл Джик ввел термин «индексы» в 1696 году. ^[6] Термин «инволюция» использовался как синоним термина «индексы» , но со временем его использование сократилось ^[17] и его не следует путать с его более общим значением .

Переменные показатели, нецелые показатели

В 1748 году Леонард Эйлер ввел переменные показатели степени и, неявно, нецелые показатели, написав:

Рассмотрим показательные функции или степени, в которых показатель степени сам по себе является переменной. Ясно, что величины такого рода не являются алгебраическими функциями , поскольку в них показатели степени должны быть постоянными. ^[18]

Терминология

Выражение b ² = b · b называется « квадрат b » или « b в квадрате», потому что площадь квадрата со стороной b равна b ² . (Правда, его можно было бы также назвать « b во второй степени», но «квадрат b » и « b в квадрате» настолько укоренились в традиции и удобстве, что « b во второй степени» имеет тенденцию звучать необычно или неуклюже.)

Аналогично, выражение b ³ = b · b · b называется « кубом b » или « b в кубе», поскольку объем куба со стороной b равен b ³ .

Когда показатель степени является положительным целым числом , этот показатель указывает, сколько копий основания умножаются вместе. Например, 3 ⁵ = 3 · 3 · 3 · 3 · 3 = 243. Основание 3 появляется 5 раз в умножении, потому что показатель степени равен 5. Здесь 243 — это 5-я степень числа 3 , или 3, возведенная в 5-ю степень .

Слово «raised» обычно опускается, а иногда и «power», так что 3 ⁵ можно просто прочитать «3 в 5-й степени» или «3 в 5-й степени». Таким образом, возведение в степень b ⁿ можно выразить как « b в степени n », « b в n- й степени», « b в n-й степени» или, короче, как « b в n-й степени ».

Целые показатели степеней

Операция возведения в степень с целыми показателями может быть определена непосредственно из элементарных арифметических операций .

Положительные показатели степени

Определение возведения в степень как итеративного умножения можно формализовать с помощью индукции ^[19] , и это определение можно использовать, как только появляется ассоциативное умножение:

Базовый вариант:

${\displaystyle b^{1}=b}$

и повторение есть

${\displaystyle b^{n+1}=b^{n}\cdot b.}$

Ассоциативность умножения подразумевает, что для любых положительных целых чисел m и n ,

${\displaystyle b^{m+n}=b^{m}\cdot b^{n},}$

и

${\displaystyle (b^{m})^{n}=b^{mn}.}$

Нулевой показатель степени

Как упоминалось ранее, (ненулевое) число, возведенное в степень 0 , равно 1 : ^{[20] [1]}

${\displaystyle b^{0}=1.}$

Это значение также получается с помощью соглашения о пустом произведении , которое может использоваться в любой алгебраической структуре с умножением, имеющим тождество . Таким образом, формула

${\displaystyle b^{m+n}=b^{m}\cdot b^{n}}$

также справедливо для . ${\displaystyle n=0}$

Случай 0 ⁰ является спорным. В контекстах, где рассматриваются только целые степени, значение 1 обычно присваивается 0 ⁰ , но в противном случае выбор того, присваивать ли ему значение и какое значение присваивать, может зависеть от контекста. Для получения более подробной информации см. Ноль в степени нуля .

Отрицательные показатели степени

Возведение в степень с отрицательными показателями определяется следующим тождеством, которое справедливо для любого целого числа n и ненулевого b :

${\displaystyle b^{-n}={\frac {1}{b^{n}}}}$. ^[1]

Возведение 0 в отрицательную степень не определено, но в некоторых обстоятельствах может интерпретироваться как бесконечность ( ). ^[21] ${\displaystyle \infty }$

Это определение возведения в степень с отрицательными показателями является единственным, которое позволяет распространить тождество на отрицательные показатели (рассмотрим случай ). ${\displaystyle b^{m+n}=b^{m}\cdot b^{n}}$ ${\displaystyle m=-n}$

То же самое определение применимо к обратимым элементам в мультипликативном моноиде , то есть алгебраической структуре , с ассоциативным умножением и мультипликативным тождеством, обозначаемым 1 (например, квадратные матрицы заданной размерности). В частности, в такой структуре обратный элемент обратимого элемента x стандартно обозначается ${\displaystyle x^{-1}.}$

Идентичность и свойства

Следующие идентичности , часто называемыеПравила экспоненты справедливы для всех целочисленных экспонент, при условии, что основание не равно нулю:^[1]

${\displaystyle {\begin{aligned}b^{m+n}&=b^{m}\cdot b^{n}\\\left(b^{m}\right)^{n}&=b^{m\cdot n}\\(b\cdot c)^{n}&=b^{n}\cdot c^{n}\end{aligned}}}$

В отличие от сложения и умножения, возведение в степень не является коммутативным . Например, 2 ³ = 8 ≠ 3 ² = 9. Также в отличие от сложения и умножения, возведение в степень не является ассоциативным . Например, (2 ³ ) ² = 8 ² = 64 , тогда как 2 ^{(3 2 )} = 2 ⁹ = 512. Без скобок общепринятый порядок операций для последовательного возведения в степень в надстрочной нотации — сверху вниз (или правоассоциативный ), а не снизу вверх ^{[22] [23] [24]} (или левоассоциативный ). То есть,

${\displaystyle b^{p^{q}}=b^{\left(p^{q}\right)},}$

что, в общем, отличается от

${\displaystyle \left(b^{p}\right)^{q}=b^{pq}.}$

Степени суммы

Степени суммы обычно можно вычислить из степеней слагаемых по биномиальной формуле

${\displaystyle (a+b)^{n}=\sum _{i=0}^{n}{\binom {n}{i}}a^{i}b^{n-i}=\sum _{i=0}^{n}{\frac {n!}{i!(n-i)!}}a^{i}b^{n-i}.}$

Однако эта формула верна только в том случае, если слагаемые коммутируют (т. е. ab = ba ), что подразумевается, если они принадлежат структуре , которая является коммутативной . В противном случае, если a и b являются, скажем, квадратными матрицами одинакового размера, эту формулу использовать нельзя. Из этого следует, что в компьютерной алгебре многие алгоритмы , включающие целочисленные показатели, должны быть изменены, когда основания возведения в степень не коммутируют. Некоторые системы компьютерной алгебры общего назначения используют другую нотацию (иногда ^^ вместо ^ ) для возведения в степень с некоммутирующими основаниями, что тогда называется некоммутативным возведением в степень .

Комбинаторная интерпретация

Для неотрицательных целых чисел n и m значение n ^m равно числу функций из набора из m элементов в набор из n элементов (см. кардинальное возведение в степень ). Такие функции могут быть представлены в виде m - кортежей из набора из n элементов (или в виде m -буквенных слов из n -буквенного алфавита). Некоторые примеры для конкретных значений m и n приведены в следующей таблице:

Конкретные базы

Степени десяти

В десятичной системе счисления целые степени числа 10 записываются как цифра 1, за которой следует или которой предшествует количество нулей, определяемое знаком и величиной показателя степени. Например,10 ³ =1000 и10 ⁻⁴ =0,0001 .

Возведение в степень с основанием 10 используется в научной записи для обозначения больших или малых чисел. Например,299 792 458  м/с ( скорость света в вакууме, в метрах в секунду ) можно записать как2,997 924 58 × 10 ⁸  м/с и затем аппроксимируется как2,998 × 10 ⁸  м/с .

Префиксы СИ, основанные на степенях числа 10, также используются для описания малых или больших величин. Например, префикс кило означает10 ³ =1000 , поэтому километр равен1000 м .

Степени двойки

Обычно используются первые отрицательные степени числа 2 , которые имеют специальные названия, например: половина и четверть .

Степени числа 2 появляются в теории множеств , поскольку множество с n элементами имеет множество степеней — множество всех его подмножеств , которое имеет 2 ⁿ элементов.

Целые степени числа 2 важны в информатике . Положительные целые степени числа 2 ⁿ дают количество возможных значений для n - битного целого двоичного числа ; например, байт может принимать 2 ⁸ = 256 различных значений. Двоичная система счисления выражает любое число как сумму степеней числа 2 и обозначает его как последовательность 0 и 1 , разделенных двоичной точкой , где 1 указывает на степень числа 2 , которая появляется в сумме; показатель степени определяется местом этой 1 : неотрицательные показатели степени являются рангом 1 слева от точки (начиная с 0 ), а отрицательные показатели степени определяются рангом справа от точки.

Полномочия одного

Каждая степень единицы равна: 1 ⁿ = 1. Это верно, даже если n отрицательно.

Первая степень числа — это само число: n ¹ = n .

Степени нуля

Если показатель степени n положительный ( n > 0 ), то n- я степень нуля равна нулю: 0 ⁿ = 0 .

Если показатель степени n отрицателен ( n < 0 ), то n -я степень нуля 0 ⁿ не определена, поскольку она должна быть равна − n > 0 , и это будет соответствовать вышесказанному. ${\displaystyle 1/0^{-n}}$ ${\displaystyle 1/0}$

Выражение 0 0 либо определяется как 1 , либо остается неопределенным.

Степени отрицательной единицы

Если n — четное целое число, то (−1) ⁿ = 1. Это происходит потому, что отрицательное число, умноженное на другое отрицательное число, отменяет знак и, таким образом, дает положительное число.

Если n — нечетное целое число, то (−1) ⁿ = −1 . Это происходит потому, что после удаления −1 пар останется −1 .

Из-за этого степени −1 полезны для выражения чередующихся последовательностей . Для похожего обсуждения степеней комплексного числа i см. § Корни n-й степени комплексного числа .

Большие показатели степени

Предел последовательности степеней числа, большего единицы, расходится; другими словами, последовательность растет неограниченно:

b ⁿ → ∞ при n → ∞, когда b > 1

Это можно прочитать как « b в степени n стремится к +∞ , когда n стремится к бесконечности, когда b больше единицы».

Степени числа, модуль которого меньше единицы, стремятся к нулю:

b ⁿ → 0 при n → ∞, когда | b | < 1

Любая степень единицы всегда равна единице:

b ⁿ = 1 для всех n , если b = 1

Степени –1 чередуются между 1 и –1 , когда n чередуется между четным и нечетным, и, таким образом, не стремятся к какому-либо пределу по мере роста n .

Если b < –1 , то b ⁿ чередуется между все большими и большими положительными и отрицательными числами, так как n чередуется между четным и нечетным, и, таким образом, не стремится ни к какому пределу по мере роста n .

Если возведенное в степень число стремится к 1 , когда показатель стремится к бесконечности, то предел не обязательно один из приведенных выше. Особенно важным случаем является

(1 + 1/ n ) ⁿ → e при n → ∞

См. § Экспоненциальная функция ниже.

Другие ограничения, в частности, ограничения выражений, принимающих неопределенную форму , описаны в § Ограничения полномочий ниже.

Функции мощности

Степенные функции для n = 1, 3, 5

Степенные функции для n = 2, 4, 6

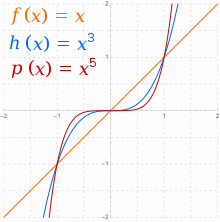
Действительные функции вида , где , иногда называются степенными функциями. ^[25] Когда — целое число и , существуют два основных семейства: для четных и для нечетных. В общем случае для , когда — четное, будет стремиться к положительной бесконечности с увеличением , а также к положительной бесконечности с уменьшением . Все графики из семейства четных степенных функций имеют общую форму , сглаживаясь в середине по мере увеличения. ^[26] Функции с таким видом симметрии ( ) называются четными функциями . ${\displaystyle f(x)=cx^{n}}$ ${\displaystyle c\neq 0}$ ${\displaystyle n}$ ${\displaystyle n\geq 1}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle c>0}$ ${\displaystyle n}$ ${\displaystyle f(x)=cx^{n}}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle y=cx^{2}}$ ${\displaystyle n}$ ${\displaystyle f(-x)=f(x)}$

Когда нечетно, асимптотическое поведение меняется с положительного на отрицательное . Для также будет стремиться к положительной бесконечности с увеличением , но к отрицательной бесконечности с уменьшением . Все графики из семейства нечетных степенных функций имеют общую форму , более уплощаясь в середине по мере увеличения и теряя всю плоскость там на прямой линии для . Функции с таким видом симметрии ( ) называются нечетными функциями . ${\displaystyle n}$ ${\displaystyle f(x)}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle c>0}$ ${\displaystyle f(x)=cx^{n}}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle y=cx^{3}}$ ${\displaystyle n}$ ${\displaystyle n=1}$ ${\displaystyle f(-x)=-f(x)}$

Для в каждом случае справедливо противоположное асимптотическое поведение. ^[26] ${\displaystyle c<0}$

Таблица степеней десятичных цифр

Рациональные показатели степени

Сверху вниз: x ^1/8 , x ^1/4 , x ^1/2 , x ¹ , x ² , x ⁴ , x ⁸ .

Если x — неотрицательное действительное число , а n — положительное целое число, или обозначает единственный положительный действительный корень степени n из x , то есть единственное положительное действительное число y, такое что ${\displaystyle x^{1/n}}$ ${\displaystyle {\sqrt[{n}]{x}}}$ ${\displaystyle y^{n}=x.}$

Если x — положительное действительное число, а также рациональное число , причем p и q > 0 целых чисел, то определяется как ${\displaystyle {\frac {p}{q}}}$ ${\textstyle x^{p/q}}$

${\displaystyle x^{\frac {p}{q}}=\left(x^{p}\right)^{\frac {1}{q}}=(x^{\frac {1}{q}})^{p}.}$

Равенство справа можно вывести, положив и записав ${\displaystyle y=x^{\frac {1}{q}},}$ ${\displaystyle (x^{\frac {1}{q}})^{p}=y^{p}=\left((y^{p})^{q}\right)^{\frac {1}{q}}=\left((y^{q})^{p}\right)^{\frac {1}{q}}=(x^{p})^{\frac {1}{q}}.}$

Если r — положительное рациональное число, то 0 ^r = 0 , по определению.

Все эти определения необходимы для распространения тождества на рациональные показатели степеней. ${\displaystyle (x^{r})^{s}=x^{rs}}$

С другой стороны, существуют проблемы с расширением этих определений на основания, которые не являются положительными действительными числами. Например, отрицательное действительное число имеет действительный корень степени n , который отрицателен, если n нечетно , и не имеет действительного корня, если n четно. В последнем случае, какой бы комплексный корень степени n ни был выбран для тождества, он не может быть удовлетворен. Например, ${\displaystyle x^{\frac {1}{n}},}$ ${\displaystyle (x^{a})^{b}=x^{ab}}$

${\displaystyle \left((-1)^{2}\right)^{\frac {1}{2}}=1^{\frac {1}{2}}=1\neq (-1)^{2\cdot {\frac {1}{2}}}=(-1)^{1}=-1.}$

Подробную информацию о том, как можно решать эти проблемы, см. в разделах § Действительные показатели степени и § Нецелые степени комплексных чисел.

Действительные показатели степени

Для положительных действительных чисел возведение в степень может быть определено двумя эквивалентными способами: либо путем расширения рациональных степеней до действительных чисел по непрерывности ( § Пределы рациональных экспонент , ниже), либо в терминах логарифма основания и показательной функции ( § Степени через логарифмы , ниже). Результатом всегда является положительное действительное число, а тождества и свойства, показанные выше для целых экспонент, остаются верными с этими определениями для действительных экспонент. Второе определение используется чаще, поскольку оно напрямую обобщается на комплексные экспоненты.

С другой стороны, возведение в действительную степень отрицательного действительного числа гораздо сложнее определить последовательно, поскольку оно может быть недействительным и иметь несколько значений. Можно выбрать одно из этих значений, называемое главным значением , но нет выбора главного значения, для которого тождество

${\displaystyle \left(b^{r}\right)^{s}=b^{rs}}$

верно; см. § Несостоятельность тождеств степени и логарифма . Поэтому возведение в степень с основанием, не являющимся положительным действительным числом, обычно рассматривается как многозначная функция .

Пределы рациональных показателей степеней

Предел e ^{1/ n} равен e ⁰ = 1 , когда n стремится к бесконечности.

Поскольку любое иррациональное число можно выразить как предел последовательности рациональных чисел, возведение в степень положительного действительного числа b с произвольным действительным показателем степени x можно определить по непрерывности с помощью правила ^[27]

${\displaystyle b^{x}=\lim _{r(\in \mathbb {Q} )\to x}b^{r}\quad (b\in \mathbb {R} ^{+},\,x\in \mathbb {R} ),}$

где предел берется только по рациональным значениям r . Этот предел существует для каждого положительного b и каждого действительного x .

Например, если x = π , то бесконечное десятичное представление π = 3,14159... и монотонность рациональных степеней можно использовать для получения интервалов, ограниченных рациональными степенями, которые сколь угодно малы и должны содержать ${\displaystyle b^{\pi }:}$

${\displaystyle \left[b^{3},b^{4}\right],\left[b^{3.1},b^{3.2}\right],\left[b^{3.14},b^{3.15}\right],\left[b^{3.141},b^{3.142}\right],\left[b^{3.1415},b^{3.1416}\right],\left[b^{3.14159},b^{3.14160}\right],\ldots }$

Итак, верхние и нижние границы интервалов образуют две последовательности , имеющие один и тот же предел, обозначаемый ${\displaystyle b^{\pi }.}$

Это определяет для каждого положительного b и действительного x как непрерывную функцию b и x . См. также Well -defined expression . ^[28] ${\displaystyle b^{x}}$

Экспоненциальная функция

Экспоненциальная функция часто определяется как , где - число Эйлера . Чтобы избежать круговых рассуждений , это определение не может быть использовано здесь. Поэтому дается определение экспоненциальной функции, обозначенной и числа Эйлера, которые опираются только на возведение в степень с положительными целыми показателями. Затем набрасывается доказательство того, что если использовать определение возведения в степень, данное в предыдущих разделах, то можно получить ${\displaystyle x\mapsto e^{x},}$ ${\displaystyle e\approx 2.718}$ ${\displaystyle \exp(x),}$

${\displaystyle \exp(x)=e^{x}.}$

Существует много эквивалентных способов определения показательной функции , один из них:

${\displaystyle \exp(x)=\lim _{n\rightarrow \infty }\left(1+{\frac {x}{n}}\right)^{n}.}$

Один имеет место и экспоненциальное тождество также выполняется, поскольку ${\displaystyle \exp(0)=1,}$ ${\displaystyle \exp(x+y)=\exp(x)\exp(y)}$

${\displaystyle \exp(x)\exp(y)=\lim _{n\rightarrow \infty }\left(1+{\frac {x}{n}}\right)^{n}\left(1+{\frac {y}{n}}\right)^{n}=\lim _{n\rightarrow \infty }\left(1+{\frac {x+y}{n}}+{\frac {xy}{n^{2}}}\right)^{n},}$

а член второго порядка не влияет на предел, что дает . ${\displaystyle {\frac {xy}{n^{2}}}}$ ${\displaystyle \exp(x)\exp(y)=\exp(x+y)}$

Число Эйлера можно определить как . Из предыдущих уравнений следует, что когда x — целое число (это следует из определения возведения в степень с помощью повторного умножения). Если x — вещественное число, то получается из определений, данных в предыдущих разделах, с использованием показательного тождества, если x — рациональное число, и непрерывности показательной функции в противном случае. ${\displaystyle e=\exp(1)}$ ${\displaystyle \exp(x)=e^{x}}$ ${\displaystyle \exp(x)=e^{x}}$

Предел, определяющий показательную функцию, сходится для каждого комплексного значения x , и поэтому его можно использовать для расширения определения , и, таким образом, от действительных чисел до любого комплексного аргумента z . Эта расширенная показательная функция по-прежнему удовлетворяет показательному тождеству и обычно используется для определения возведения в степень для комплексного основания и показателя. ${\displaystyle \exp(z)}$ ${\displaystyle e^{z},}$

Степени через логарифмы

Определение e ^x как показательной функции позволяет определить b ^x для каждого положительного действительного числа b , в терминах показательной и логарифмической функции. В частности, тот факт, что натуральный логарифм ln( x ) является обратной показательной функцией e ^{x ,} означает, что мы имеем

${\displaystyle b=\exp(\ln b)=e^{\ln b}}$

для любого b > 0. Для сохранения тождества необходимо иметь ${\displaystyle (e^{x})^{y}=e^{xy},}$

${\displaystyle b^{x}=\left(e^{\ln b}\right)^{x}=e^{x\ln b}}$

Итак, можно использовать как альтернативное определение b ^x для любого положительного действительного b . Это согласуется с определением, данным выше с использованием рациональных показателей и непрерывности, с преимуществом прямого распространения на любой комплексный показатель. ${\displaystyle e^{x\ln b}}$

Комплексные показатели с положительным действительным основанием

Если b — положительное действительное число, возведение в степень с основанием b и комплексным показателем z определяется с помощью показательной функции с комплексным аргументом (см. конец § Показательная функция выше) как

${\displaystyle b^{z}=e^{(z\ln b)},}$

где обозначает натуральный логарифм b . ${\displaystyle \ln b}$

Это удовлетворяет тождеству

${\displaystyle b^{z+t}=b^{z}b^{t},}$

В общем случае не определено, так как b ^z не является действительным числом. Если придать значение возведению в степень комплексного числа (см. § Нецелые степени комплексных чисел ниже), то, в общем случае, ${\textstyle \left(b^{z}\right)^{t}}$

${\displaystyle \left(b^{z}\right)^{t}\neq b^{zt},}$

если только z не является действительным числом или t не является целым числом.

Формула Эйлера ,

${\displaystyle e^{iy}=\cos y+i\sin y,}$

позволяет выразить полярную форму через действительную и мнимую части z , а именно ${\displaystyle b^{z}}$

${\displaystyle b^{x+iy}=b^{x}(\cos(y\ln b)+i\sin(y\ln b)),}$

где абсолютное значение тригонометрического множителя равно единице. Это следует из

${\displaystyle b^{x+iy}=b^{x}b^{iy}=b^{x}e^{iy\ln b}=b^{x}(\cos(y\ln b)+i\sin(y\ln b)).}$

Нецелые степени комплексных чисел

В предыдущих разделах возведение в степень с нецелыми показателями было определено только для положительных действительных оснований. Для других оснований трудности возникают уже с, казалось бы, простым случаем корней n- й степени, то есть показателей, где n — положительное целое число. Хотя общая теория возведения в степень с нецелыми показателями применима к корням n - й степени, этот случай заслуживает того, чтобы его рассмотреть в первую очередь, поскольку в нем не требуется использовать сложные логарифмы , и поэтому его легче понять. ${\displaystyle 1/n,}$

нкорни комплексного числа

Каждое ненулевое комплексное число z можно записать в полярной форме как

${\displaystyle z=\rho e^{i\theta }=\rho (\cos \theta +i\sin \theta ),}$

где — абсолютное значение z , а — его аргумент . Аргумент определяется с точностью до целого числа , кратного 2π ; это означает, что если — аргумент комплексного числа, то — также аргумент того же комплексного числа для каждого целого числа . ${\displaystyle \rho }$ ${\displaystyle \theta }$ ${\displaystyle \theta }$ ${\displaystyle \theta +2k\pi }$ ${\displaystyle k}$

Полярная форма произведения двух комплексных чисел получается путем умножения абсолютных значений и сложения аргументов. Отсюда следует, что полярная форма корня n- й степени комплексного числа может быть получена путем взятия корня n -й степени из абсолютного значения и деления его аргумента на n :

${\displaystyle \left(\rho e^{i\theta }\right)^{\frac {1}{n}}={\sqrt[{n}]{\rho }}\,e^{\frac {i\theta }{n}}.}$

Если добавляется к , комплексное число не изменяется, но это добавляется к аргументу корня n -й степени и дает новый корень n- й степени. Это можно сделать n раз и получить корни n - й степени комплексного числа. ${\displaystyle 2\pi }$ ${\displaystyle \theta }$ ${\displaystyle 2i\pi /n}$

Обычно выбирают один из корней n n -й степени в качестве главного корня . Обычным выбором является выбор корня n -й степени, для которого это есть корень n -й степени, имеющий наибольшую действительную часть, и, если их два, тот, у которого положительная мнимая часть. Это делает главный корень n -й степени непрерывной функцией во всей комплексной плоскости, за исключением отрицательных действительных значений подкоренного выражения . Эта функция равна обычному корню n -й степени для положительных действительных подкоренных выражений. Для отрицательных действительных подкоренных выражений и нечетных показателей главный корень n -й степени не является действительным числом, хотя обычный корень n -й степени является действительным числом. Аналитическое продолжение показывает, что главный корень n -й степени является единственной комплексной дифференцируемой функцией, которая расширяет обычный корень n -й степени на комплексную плоскость без неположительных действительных чисел. ${\displaystyle -\pi <\theta \leq \pi ,}$

Если комплексное число перемещается вокруг нуля путем увеличения его аргумента, то после приращения комплексное число возвращается в исходное положение, а его корни n-й степени переставляются по кругу (они умножаются на ). Это показывает, что невозможно определить функцию корня n- й степени, которая была бы непрерывной во всей комплексной плоскости. ${\displaystyle 2\pi ,}$ $e^{2i\pi /n}$

Корни единства

Три третьих корня из 1

Корни n- й степени из единицы — это n комплексных чисел, таких что w ⁿ = 1 , где n — положительное целое число. Они возникают в различных областях математики, например, в дискретном преобразовании Фурье или алгебраических решениях алгебраических уравнений ( резольвента Лагранжа ).

Корни n n- й степени из единицы — это n первых степеней числа , то есть Корни n -й степени из единицы, обладающие этим порождающим свойством, называются примитивными корнями n- й степени из единицы ; они имеют вид с k, взаимно простым с n . Единственный примитивный квадратный корень из единицы — это примитивные корни четвертой степени из единицы и ${\displaystyle \omega =e^{\frac {2\pi i}{n}}}$ ${\displaystyle 1=\omega ^{0}=\omega ^{n},\omega =\omega ^{1},\omega ^{2},\omega ^{n-1}.}$ ${\displaystyle \omega ^{k}=e^{\frac {2k\pi i}{n}},}$ ${\displaystyle -1;}$ ${\displaystyle i}$ ${\displaystyle -i.}$

Корни n- й степени из единицы позволяют выразить все корни n- й степени комплексного числа z в виде n произведений заданных корней n-й степени из z на корень n- й степени из единицы.

Геометрически корни n- й степени из единицы лежат на единичной окружности комплексной плоскости в вершинах правильного n - угольника с одной вершиной на действительном числе 1.

Поскольку число является примитивным корнем n- й степени из единицы с наименьшим положительным аргументом , его называют главным примитивным корнем n-й степени из единицы , иногда сокращают до главного корня n-й степени из единицы , хотя эту терминологию можно спутать с главным значением , которое равно 1. ^{[29] [30] [31]} ${\displaystyle e^{\frac {2k\pi i}{n}}}$ ${\displaystyle 1^{1/n}}$

Комплексное возведение в степень

Определение возведения в степень с комплексными основаниями приводит к трудностям, аналогичным тем, что описаны в предыдущем разделе, за исключением того, что, в общем случае, существует бесконечно много возможных значений для . Таким образом, либо определяется главное значение , которое не является непрерывным для значений z , которые являются действительными и неположительными, либо определяется как многозначная функция . $z^{w}$ $z^{w}$

Во всех случаях комплексный логарифм используется для определения комплексного возведения в степень как

${\displaystyle z^{w}=e^{w\log z},}$

где — вариант комплексного логарифма, который используется, то есть функция или многозначная функция, такая что ${\displaystyle \log z}$

${\displaystyle e^{\log z}=z}$

для каждого z в его области определения .

Основная стоимость

Главное значение комплексного логарифма — это уникальная непрерывная функция, обычно обозначаемая так, что для каждого ненулевого комплексного числа z , ${\displaystyle \log ,}$

${\displaystyle e^{\log z}=z,}$

и аргумент z удовлетворяет​

${\displaystyle -\pi <\operatorname {Arg} z\leq \pi .}$

Главное значение комплексного логарифма не определено, поскольку оно разрывно при отрицательных действительных значениях z и является голоморфным (то есть комплексно дифференцируемым) в других местах. Если z действительно и положительно, главное значение комплексного логарифма — это натуральный логарифм: ${\displaystyle z=0,}$ ${\displaystyle \log z=\ln z.}$

Главное значение определяется как, где — главное значение логарифма. ${\displaystyle z^{w}}$ ${\displaystyle z^{w}=e^{w\log z},}$ ${\displaystyle \log z}$

Функция голоморфна, за исключением окрестности точек, где z является действительным и неположительным. ${\displaystyle (z,w)\to z^{w}}$

Если z действительно и положительно, главное значение равно его обычному значению, определенному выше. Если где n — целое число, это главное значение совпадает с определенным выше. ${\displaystyle z^{w}}$ ${\displaystyle w=1/n,}$

Многозначная функция

В некоторых контекстах возникает проблема с разрывом главных значений и при отрицательных действительных значениях z . В этом случае полезно рассматривать эти функции как многозначные функции . ${\displaystyle \log z}$ ${\displaystyle z^{w}}$

Если обозначает одно из значений многозначного логарифма (обычно его главное значение), другие значения — это где k — любое целое число. Аналогично, если — одно из значений возведения в степень, то другие значения задаются как ${\displaystyle \log z}$ ${\displaystyle 2ik\pi +\log z,}$ ${\displaystyle z^{w}}$

${\displaystyle e^{w(2ik\pi +\log z)}=z^{w}e^{2ik\pi w},}$

где k — любое целое число.

Различные значения k дают различные значения, если только w не является рациональным числом , то есть существует целое число d , такое, что dw является целым числом. Это следует из периодичности экспоненциальной функции, а именно, что тогда и только тогда, когда является целым кратным ${\displaystyle z^{w}}$ ${\displaystyle e^{a}=e^{b}}$ ${\displaystyle a-b}$ ${\displaystyle 2\pi i.}$

Если — рациональное число с m и n взаимно простыми целыми числами , то имеет ровно n значений. В этом случае эти значения совпадают с теми, что описаны в § Корни n-й степени комплексного числа. Если w — целое число, то существует только одно значение, которое согласуется со значением из § Целые показатели степеней. ${\displaystyle w={\frac {m}{n}}}$ ${\displaystyle n>0,}$ ${\displaystyle z^{w}}$ ${\displaystyle m=1,}$

Многозначное возведение в степень голоморфно для в том смысле, что его график состоит из нескольких листов, каждый из которых определяет голоморфную функцию в окрестности каждой точки. Если z непрерывно изменяется вдоль окружности вокруг 0 , то после поворота значение изменилось на листе. ${\displaystyle z\neq 0,}$ ${\displaystyle z^{w}}$

Вычисление

Каноническая форма может быть вычислена из канонической формы z и w . Хотя это можно описать одной формулой, понятнее разделить вычисление на несколько этапов. ${\displaystyle x+iy}$ ${\displaystyle z^{w}}$

• Полярная форма z . Если— каноническая форма z ( a и b — действительные числа), то ее полярная форма имеет вид,гдеи(см. atan2 для определения этой функции). ${\displaystyle z=a+ib}$ $${\displaystyle z=\rho e^{i\theta }=\rho (\cos \theta +i\sin \theta ),}$$ ${\displaystyle \rho ={\sqrt {a^{2}+b^{2}}}}$ ${\displaystyle \theta =\operatorname {atan2} (a,b)}$
• Логарифм z . Главное значение этого логарифма равно , где обозначаетнатуральный логарифм . Остальные значения логарифма получаются путем сложениядля любого целого числа k . ${\displaystyle \log z=\ln \rho +i\theta ,}$ ${\displaystyle \ln }$ ${\displaystyle 2ik\pi }$
• Каноническая форма ${\displaystyle w\log z.}$ Если с c и d действительны, то значения являются главным значением, соответствующим ${\displaystyle w=c+di}$ ${\displaystyle w\log z}$ $${\displaystyle w\log z=(c\ln \rho -d\theta -2dk\pi )+i(d\ln \rho +c\theta +2ck\pi ),}$$ ${\displaystyle k=0.}$
• Конечный результат . Используя тождества и получаем для главного значения. ${\displaystyle e^{x+y}=e^{x}e^{y}}$ ${\displaystyle e^{y\ln x}=x^{y},}$ $${\displaystyle z^{w}=\rho ^{c}e^{-d(\theta +2k\pi )}\left(\cos(d\ln \rho +c\theta +2ck\pi )+i\sin(d\ln \rho +c\theta +2ck\pi )\right),}$$ ${\displaystyle k=0}$

Примеры

• ${\displaystyle i^{i}}$
  Полярная форма i есть и значения есть, таким образом, Отсюда следует, что Итак, все значения действительны, главное из них есть ${\displaystyle i=e^{i\pi /2},}$ ${\displaystyle \log i}$ $${\displaystyle \log i=i\left({\frac {\pi }{2}}+2k\pi \right).}$$ $${\displaystyle i^{i}=e^{i\log i}=e^{-{\frac {\pi }{2}}}e^{-2k\pi }.}$$ ${\displaystyle i^{i}}$ $${\displaystyle e^{-{\frac {\pi }{2}}}\approx 0.2079.}$$
• ${\displaystyle (-2)^{3+4i}}$
  Аналогично, полярная форма −2 имеет вид Таким образом, описанный выше метод дает значения В этом случае все значения имеют один и тот же аргумент и разные абсолютные значения. ${\displaystyle -2=2e^{i\pi }.}$ $${\displaystyle {\begin{aligned}(-2)^{3+4i}&=2^{3}e^{-4(\pi +2k\pi )}(\cos(4\ln 2+3(\pi +2k\pi ))+i\sin(4\ln 2+3(\pi +2k\pi )))\\&=-2^{3}e^{-4(\pi +2k\pi )}(\cos(4\ln 2)+i\sin(4\ln 2)).\end{aligned}}}$$ ${\displaystyle 4\ln 2,}$

В обоих примерах все значения имеют один и тот же аргумент. В более общем случае это верно тогда и только тогда, когда действительная часть w является целым числом. ${\displaystyle z^{w}}$

Несоответствие степенных и логарифмических тождеств

Некоторые тождества для степеней и логарифмов положительных действительных чисел не будут работать для комплексных чисел, независимо от того, как комплексные степени и комплексные логарифмы определены как однозначные функции . Например:

• Тождество log( b ^x ) = x ⋅ log  b справедливо, когда b — положительное действительное число, а x — действительное число. Но для главной ветви комплексного логарифма имеем

  $${\displaystyle \log((-i)^{2})=\log(-1)=i\pi \neq 2\log(-i)=2\log(e^{-i\pi /2})=2\,{\frac {-i\pi }{2}}=-i\pi }$$

  Независимо от того, какая ветвь логарифма используется, будет существовать аналогичный сбой тождества. Лучшее, что можно сказать (используя только этот результат), это то, что: $${\displaystyle \log w^{z}\equiv z\log w{\pmod {2\pi i}}}$$

  Это тождество не выполняется даже при рассмотрении log как многозначной функции. Возможные значения log ( w ^z ) содержат значения z ⋅ log  w как собственное подмножество . Используя Log( w ) для главного значения log( w ) и m , n как любые целые числа, возможные значения обеих сторон следующие:

  $${\displaystyle {\begin{aligned}\left\{\log w^{z}\right\}&=\left\{z\cdot \operatorname {Log} w+z\cdot 2\pi in+2\pi im\mid m,n\in \mathbb {Z} \right\}\\\left\{z\log w\right\}&=\left\{z\operatorname {Log} w+z\cdot 2\pi in\mid n\in \mathbb {Z} \right\}\end{aligned}}}$$
• Тождества ( bc ) ^x = b ^x c ^x и ( b / c ) ^x = b ^x / c ^x справедливы, когда b и c — положительные действительные числа, а x — действительное число. Но для главных значений имеем и С другой стороны, когда x — целое число, тождества справедливы для всех ненулевых комплексных чисел. Если рассматривать возведение в степень как многозначную функцию, то возможными значениями (−1 ⋅ −1) ^1/2 являются {1, −1} . Тождество выполняется, но утверждение {1} = {(−1 ⋅ −1) ^1/2 } неверно. $${\displaystyle (-1\cdot -1)^{\frac {1}{2}}=1\neq (-1)^{\frac {1}{2}}(-1)^{\frac {1}{2}}=-1}$$ $${\displaystyle \left({\frac {1}{-1}}\right)^{\frac {1}{2}}=(-1)^{\frac {1}{2}}=i\neq {\frac {1^{\frac {1}{2}}}{(-1)^{\frac {1}{2}}}}={\frac {1}{i}}=-i}$$
• Тождество ( e ^x ) ^y = e ^xy справедливо для действительных чисел x и y , но предположение его истинности для комплексных чисел приводит к следующему парадоксу , открытому в 1827 году Клаузеном : [ ^32] Для любого целого числа n имеем:
  1. ${\displaystyle e^{1+2\pi in}=e^{1}e^{2\pi in}=e\cdot 1=e}$
  2. ${\displaystyle \left(e^{1+2\pi in}\right)^{1+2\pi in}=e\qquad }$(взяв обе части в -ю степень) ${\displaystyle (1+2\pi in)}$
  3. ${\displaystyle e^{1+4\pi in-4\pi ^{2}n^{2}}=e\qquad }$(используя и расширяя показатель степени) ${\displaystyle \left(e^{x}\right)^{y}=e^{xy}}$
  4. ${\displaystyle e^{1}e^{4\pi in}e^{-4\pi ^{2}n^{2}}=e\qquad }$(с использованием ) ${\displaystyle e^{x+y}=e^{x}e^{y}}$
  5. ${\displaystyle e^{-4\pi ^{2}n^{2}}=1\qquad }$(деление на e )
  но это ложно, когда целое число n не равно нулю. Ошибка заключается в следующем: по определению, является обозначением для истинной функции, а является обозначением, для которого является многозначной функцией. Таким образом, обозначение является неоднозначным, когда x = e . Здесь, перед раскрытием показателя степени, вторая строка должна быть Следовательно, при раскрытии показателя степени неявно предполагалось, что для комплексных значений z , что неверно, так как комплексный логарифм является многозначным. Другими словами, неправильное тождество ( e ^x ) ^y = e ^xy должно быть заменено тождеством, которое является истинным тождеством между многозначными функциями. ${\displaystyle e^{y}}$ ${\displaystyle \exp(y),}$ ${\displaystyle x^{y}}$ ${\displaystyle \exp(y\log x),}$ $${\displaystyle \exp \left((1+2\pi in)\log \exp(1+2\pi in)\right)=\exp(1+2\pi in).}$$ ${\displaystyle \log \exp z=z}$ $${\displaystyle \left(e^{x}\right)^{y}=e^{y\log e^{x}},}$$

Иррациональность и трансцендентность

Если b — положительное действительное алгебраическое число , а x — рациональное число, то b ^x — алгебраическое число. Это следует из теории алгебраических расширений . Это остается верным, если b — любое алгебраическое число, и в этом случае все значения b x (как многозначной функции) являются алгебраическими. Если x иррационально ( то есть ^не рационально ) , а b и x являются алгебраическими , теорема Гельфонда–Шнайдера утверждает, что все значения b ^x являются трансцендентными (то есть не алгебраическими), за исключением случая, когда b равно 0 или 1 .

Другими словами, если x иррационален и тогда хотя бы один из b , x и b ^x является трансцендентным. ${\displaystyle b\not \in \{0,1\},}$

Целые степени в алгебре

Определение возведения в степень с положительными целыми показателями как повторного умножения может применяться к любой ассоциативной операции, обозначенной как умножение. ^{[nb 2]} Определение x ⁰ требует далее существования мультипликативного тождества . ^[33]

Алгебраическая структура , состоящая из множества вместе с ассоциативной операцией, обозначаемой мультипликативно, и мультипликативным тождеством, обозначаемым 1 , является моноидом . В таком моноиде возведение в степень элемента x определяется индуктивно как

• ${\displaystyle x^{0}=1,}$
• ${\displaystyle x^{n+1}=xx^{n}}$для каждого неотрицательного целого числа n .

Если n — отрицательное целое число, то определяется только в том случае, если x имеет мультипликативную обратную величину . ^[34] В этом случае обратная величина x обозначается как x ⁻¹ , а x ⁿ определяется как ${\displaystyle x^{n}}$ ${\displaystyle \left(x^{-1}\right)^{-n}.}$

Возведение в степень с целыми показателями подчиняется следующим законам для x и y в алгебраической структуре и целых чисел m и n :

${\displaystyle {\begin{aligned}x^{0}&=1\\x^{m+n}&=x^{m}x^{n}\\(x^{m})^{n}&=x^{mn}\\(xy)^{n}&=x^{n}y^{n}\quad {\text{if }}xy=yx,{\text{and, in particular, if the multiplication is commutative.}}\end{aligned}}}$

Эти определения широко используются во многих областях математики, в частности для групп , колец , полей , квадратных матриц (которые образуют кольцо). Они также применяются к функциям из множества в себя, которые образуют моноид при композиции функций . Это включает в себя, как конкретные примеры, геометрические преобразования и эндоморфизмы любой математической структуры .

Когда есть несколько операций, которые могут повторяться, принято указывать повторяющуюся операцию, помещая ее символ в верхний индекс перед показателем степени. Например, если f — действительная функция , значение которой можно умножать, обозначает возведение в степень относительно умножения и может обозначать возведение в степень относительно композиции функций . То есть, ${\displaystyle f^{n}}$ ${\displaystyle f^{\circ n}}$

${\displaystyle (f^{n})(x)=(f(x))^{n}=f(x)\,f(x)\cdots f(x),}$

и

${\displaystyle (f^{\circ n})(x)=f(f(\cdots f(f(x))\cdots )).}$

Обычно обозначается как , а обозначается как ${\displaystyle (f^{n})(x)}$ ${\displaystyle f(x)^{n},}$ ${\displaystyle (f^{\circ n})(x)}$ ${\displaystyle f^{n}(x).}$

В группе

Мультипликативная группа — это множество с ассоциативной операцией , обозначаемой умножением, имеющее единичный элемент , и такое, что каждый элемент имеет обратный.

Итак, если G — группа, то определено для каждого целого числа n . ${\displaystyle x^{n}}$ ${\displaystyle x\in G}$

Множество всех степеней элемента группы образует подгруппу . Группа (или подгруппа), состоящая из всех степеней определенного элемента x , является циклической группой, порожденной x . Если все степени x различны, группа изоморфна аддитивной группе целых чисел. В противном случае циклическая группа конечна (она имеет конечное число элементов), а ее число элементов равно порядку x . Если порядок x равен n , то и циклическая группа, порожденная x , состоит из n первых степеней x (начиная безразлично с показателя 0 или 1 ). ${\displaystyle \mathbb {Z} }$ ${\displaystyle x^{n}=x^{0}=1,}$

Порядок элементов играет фундаментальную роль в теории групп . Например, порядок элемента в конечной группе всегда является делителем числа элементов группы (порядка группы ). Возможные порядки элементов группы важны при изучении структуры группы (см. теоремы Силова ), а также при классификации конечных простых групп .

Верхний индекс также используется для сопряжения ; то есть g ^h = h ⁻¹ gh , где g и h являются элементами группы. Это обозначение нельзя путать с возведением в степень, поскольку верхний индекс не является целым числом. Мотивация этого обозначения заключается в том, что сопряжение подчиняется некоторым законам возведения в степень, а именно и ${\displaystyle (g^{h})^{k}=g^{hk}}$ ${\displaystyle (gh)^{k}=g^{k}h^{k}.}$

В ринге

В кольце может случиться так, что некоторые ненулевые элементы удовлетворяют для некоторого целого числа n . Такой элемент называется нильпотентным . В коммутативном кольце нильпотентные элементы образуют идеал , называемый нильрадикалом кольца. ${\displaystyle x^{n}=0}$

Если нильрадикал сводится к нулевому идеалу (то есть, если подразумевает для каждого положительного целого числа n ), то коммутативное кольцо называется редуцированным . Редуцированные кольца важны в алгебраической геометрии , поскольку координатное кольцо аффинного алгебраического множества всегда является редуцированным кольцом. ${\displaystyle x\neq 0}$ ${\displaystyle x^{n}\neq 0}$

В более общем случае, если задан идеал I в коммутативном кольце R , множество элементов R , имеющих степень в I, является идеалом, называемым радикалом I. Нильрадикал — это радикал нулевого идеала . Радикальный идеал — это идеал, равный своему собственному радикалу. В кольце многочленов над полем k идеал является радикальным тогда и только тогда, когда он является множеством всех многочленов, которые равны нулю на аффинном алгебраическом множестве (это следствие Nullstellensatz Гильберта ). ${\displaystyle k[x_{1},\ldots ,x_{n}]}$

Матрицы и линейные операторы

Если A — квадратная матрица, то произведение A на себя n раз называется степенью матрицы . Также определяется как единичная матрица, ^[35] и если A обратима, то . ${\displaystyle A^{0}}$ ${\displaystyle A^{-n}=\left(A^{-1}\right)^{n}}$

Матричные мощности часто появляются в контексте дискретных динамических систем , где матрица A выражает переход от вектора состояния x некоторой системы к следующему состоянию Ax этой системы. ^[36] Это стандартная интерпретация цепи Маркова , например. Тогда — состояние системы после двух временных шагов, и так далее: — состояние системы после n временных шагов. Матричная мощность — это матрица перехода между текущим состоянием и состоянием в момент времени n шагов в будущем. Таким образом, вычисление матричных мощностей эквивалентно решению эволюции динамической системы. Во многих случаях матричные мощности можно целесообразно вычислить, используя собственные значения и собственные векторы . ${\displaystyle A^{2}x}$ ${\displaystyle A^{n}x}$ ${\displaystyle A^{n}}$

Помимо матриц, более общие линейные операторы также могут быть возведены в степень. Примером является производный оператор исчисления, , который является линейным оператором, действующим на функции, чтобы дать новую функцию . n- я степень оператора дифференцирования является n- й производной: ${\displaystyle d/dx}$ ${\displaystyle f(x)}$ ${\displaystyle (d/dx)f(x)=f'(x)}$

${\displaystyle \left({\frac {d}{dx}}\right)^{n}f(x)={\frac {d^{n}}{dx^{n}}}f(x)=f^{(n)}(x).}$

Эти примеры относятся к дискретным показателям линейных операторов, но во многих случаях также желательно определять степени таких операторов с непрерывными показателями. Это отправная точка математической теории полугрупп . ^[37] Так же, как вычисление матричных степеней с дискретными показателями решает дискретные динамические системы, так и вычисление матричных степеней с непрерывными показателями решает системы с непрерывной динамикой. Примеры включают подходы к решению уравнения теплопроводности , уравнения Шредингера , волнового уравнения и других уравнений в частных производных, включая эволюцию во времени. Частный случай возведения оператора производной в степень нецелого числа называется дробной производной , которая вместе с дробным интегралом является одной из основных операций дробного исчисления .

Конечные поля

Поле — это алгебраическая структура, в которой определены умножение, сложение, вычитание и деление, и удовлетворяет свойствам, что умножение ассоциативно, и каждый ненулевой элемент имеет мультипликативную обратную . Это подразумевает, что возведение в степень с целыми показателями определено корректно, за исключением неположительных степеней 0. Распространенными примерами являются поле комплексных чисел , действительных чисел и рациональных чисел , рассмотренные ранее в этой статье, которые все бесконечны .

Конечное поле — это поле с конечным числом элементов. Это число элементов является либо простым числом , либо степенью простого числа ; то есть оно имеет вид , где p — простое число, а k — положительное целое число. Для каждого такого q существуют поля с q элементами. Все поля с q элементами изоморфны , что позволяет, в общем случае, работать так, как если бы было только одно поле с q элементами, обозначаемое ${\displaystyle q=p^{k},}$ ${\displaystyle \mathbb {F} _{q}.}$

Один имеет

${\displaystyle x^{q}=x}$

для каждого ${\displaystyle x\in \mathbb {F} _{q}.}$

Примитивным элементом в является элемент g такой, что множество q − 1 первых степеней g (то есть ) равно множеству ненулевых элементов Существуют примитивные элементы в , где — тотиентная функция Эйлера . ${\displaystyle \mathbb {F} _{q}}$ ${\displaystyle \{g^{1}=g,g^{2},\ldots ,g^{p-1}=g^{0}=1\}}$ ${\displaystyle \mathbb {F} _{q}.}$ ${\displaystyle \varphi (p-1)}$ ${\displaystyle \mathbb {F} _{q},}$ ${\displaystyle \varphi }$

В мечте первокурсника личность ${\displaystyle \mathbb {F} _{q},}$

${\displaystyle (x+y)^{p}=x^{p}+y^{p}}$

верно для показателя p . Как в Из этого следует, что отображение ${\displaystyle x^{p}=x}$ ${\displaystyle \mathbb {F} _{q},}$

${\displaystyle {\begin{aligned}F\colon {}&\mathbb {F} _{q}\to \mathbb {F} _{q}\\&x\mapsto x^{p}\end{aligned}}}$

линейна над и является полевым автоморфизмом , называемым автоморфизмом Фробениуса . Если поле имеет k автоморфизмов, которые являются k первыми степенями (относительно композиции ) F . Другими словами, группа Галуа является циклической порядка k , порожденной автоморфизмом Фробениуса. ${\displaystyle \mathbb {F} _{q},}$ ${\displaystyle q=p^{k},}$ ${\displaystyle \mathbb {F} _{q}}$ ${\displaystyle \mathbb {F} _{q}}$

Обмен ключами Диффи –Хеллмана — это применение возведения в степень в конечных полях, которое широко используется для защищенных коммуникаций . Он использует тот факт, что возведение в степень является вычислительно недорогим, тогда как обратная операция, дискретный логарифм , является вычислительно затратной. Точнее, если g является примитивным элементом в , то может быть эффективно вычислено с возведением в степень путем возведения в квадрат для любого e , даже если q велико, в то время как не существует известного вычислительно практичного алгоритма, который позволяет извлекать e из , если q достаточно велико. ${\displaystyle \mathbb {F} _{q},}$ ${\displaystyle g^{e}}$ ${\displaystyle g^{e}}$

Силы множеств

Декартово произведение двух множеств S и T — это множество упорядоченных пар , таких что и Эта операция не является ни собственно коммутативной , ни ассоциативной , но обладает этими свойствами с точностью до канонических изоморфизмов , что позволяет идентифицировать, например, и ${\displaystyle (x,y)}$ ${\displaystyle x\in S}$ ${\displaystyle y\in T.}$ ${\displaystyle (x,(y,z)),}$ ${\displaystyle ((x,y),z),}$ ${\displaystyle (x,y,z).}$

Это позволяет определить n-ю степень множества S как множество всех n - кортежей элементов S. ${\displaystyle S^{n}}$ ${\displaystyle (x_{1},\ldots ,x_{n})}$

Когда S наделено некоторой структурой, часто естественным образом наделено аналогичной структурой. В этом случае термин « прямое произведение » обычно используется вместо «декартово произведение», а возведение в степень обозначает структуру произведения. Например, (где обозначает действительные числа) обозначает декартово произведение n копий, а также их прямое произведение как векторного пространства , топологических пространств , колец и т. д. ${\displaystyle S^{n}}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} ,}$

Устанавливает как показатели

Набор n элементов S можно рассматривать как функцию от Это обобщается до следующих обозначений. ${\displaystyle (x_{1},\ldots ,x_{n})}$ ${\displaystyle \{1,\ldots ,n\}.}$

При наличии двух множеств S и T множество всех функций из T в S обозначается . Эта экспоненциальная запись оправдывается следующими каноническими изоморфизмами (для первого из них см. Каррирование ): ${\displaystyle S^{T}}$

${\displaystyle (S^{T})^{U}\cong S^{T\times U},}$

${\displaystyle S^{T\sqcup U}\cong S^{T}\times S^{U},}$

где обозначает декартово произведение, а дизъюнктное объединение . ${\displaystyle \times }$ ${\displaystyle \sqcup }$

Можно использовать множества в качестве показателей степеней для других операций над множествами, обычно для прямых сумм абелевых групп , векторных пространств или модулей . Для различения прямых сумм от прямых произведений показатель степени прямой суммы помещается в скобки. Например, обозначает векторное пространство бесконечных последовательностей действительных чисел и векторное пространство тех последовательностей, которые имеют конечное число ненулевых элементов. Последнее имеет базис, состоящий из последовательностей с ровно одним ненулевым элементом, равным 1 , в то время как базисы Гамеля первого не могут быть явно описаны (потому что их существование подразумевает лемму Цорна ). ${\displaystyle \mathbb {R} ^{\mathbb {N} }}$ ${\displaystyle \mathbb {R} ^{(\mathbb {N} )}}$

В этом контексте 2 может представлять множество So, обозначает множество мощности S , то есть множество функций из S , которое можно отождествить с множеством подмножеств S , сопоставив каждую функцию с обратным образом 1 . ${\displaystyle \{0,1\}.}$ ${\displaystyle 2^{S}}$ ${\displaystyle \{0,1\},}$

Это согласуется с возведением в степень кардинальных чисел в том смысле, что | S T ^| = | S | ^{| T |} , где | X | — мощность X.

В теории категорий

В категории множеств морфизмы между множествами X и Y являются функциями из X в Y. Это приводит к тому, что множество функций из X в Y , обозначенное в предыдущем разделе, можно также обозначить Изоморфизм можно переписать ${\displaystyle Y^{X}}$ ${\displaystyle \hom(X,Y).}$ ${\displaystyle (S^{T})^{U}\cong S^{T\times U}}$

${\displaystyle \hom(U,S^{T})\cong \hom(T\times U,S).}$

Это означает, что функтор «возведение в степень T  » является правым сопряженным к функтору «прямое произведение на T  ».

Это обобщается до определения возведения в степень в категории , в которой существуют конечные прямые произведения : в такой категории функтор , если он существует, является правым сопряженным к функтору Категория называется декартово замкнутой категорией , если существуют прямые произведения, и функтор имеет правый сопряженный для каждого T. ${\displaystyle X\to X^{T}}$ ${\displaystyle Y\to T\times Y.}$ ${\displaystyle Y\to X\times Y}$

Повторное возведение в степень

Так же, как возведение в степень натуральных чисел мотивируется повторным умножением, можно определить операцию, основанную на повторном возведении в степень; эта операция иногда называется гипер-4 или тетрацией . Итерация тетрации приводит к другой операции, и так далее, концепции, называемой гипероперацией . Эта последовательность операций выражается функцией Аккермана и обозначением Кнута со стрелкой вверх . Так же, как возведение в степень растет быстрее, чем умножение, которое растет быстрее, чем сложение, тетрация растет быстрее, чем возведение в степень. Оцененные в (3, 3) , функции сложения, умножения, возведения в степень и тетрации дают 6, 9, 27 и7 625 597 484 987 ( =3 ²⁷ = 3 ^{3 3} = ³ 3 ) соответственно.

Пределы полномочий

Ноль в степени нуля дает ряд примеров пределов, которые имеют неопределенный вид 0 ⁰ . Пределы в этих примерах существуют, но имеют разные значения, показывая, что двухпеременная функция x ^y не имеет предела в точке (0, 0) . Можно рассмотреть, в каких точках эта функция имеет предел.

Точнее, рассмотрим функцию, ^{определенную} на . Тогда D можно рассматривать как подмножество R2 (то есть множество всех пар ( x , y ) , где x , y принадлежат расширенной числовой прямой R = [−∞, +∞] , наделенное топологией произведения ), которое будет содержать точки, в которых функция f имеет предел. ${\displaystyle f(x,y)=x^{y}}$ ${\displaystyle D=\{(x,y)\in \mathbf {R} ^{2}:x>0\}}$

Фактически, f имеет предел во всех точках накопления D , за исключением (0, 0) , (+∞, 0) , ( 1, +∞) и (1, −∞) . ^[38] Соответственно, это позволяет определить мощности x ^y по непрерывности всякий раз, когда 0 ≤ x ≤ +∞ , −∞ ≤ y ≤ +∞ , за исключением 0 ⁰ , (+∞) ⁰ , 1 ^+∞ и 1 ^−∞ , которые остаются неопределенными формами.

При этом определении по непрерывности получаем:

• x ^+∞ = +∞ и x ^−∞ = 0 , когда 1 < x ≤ +∞ .
• x ^+∞ = 0 и x ^−∞ = +∞ , когда 0 ≤ x < 1 .
• 0 ^y = 0 и (+∞) ^y = +∞ , когда 0 < y ≤ +∞ .
• 0 ^y = +∞ и (+∞) ^y = 0 , когда −∞ ≤ y < 0 .

Эти мощности получаются путем взятия пределов x ^y для положительных значений x . Этот метод не позволяет определить x ^y , когда x < 0 , поскольку пары ( x , y ) с x < 0 не являются точками накопления D.

С другой стороны, когда n — целое число, степень x ⁿ уже имеет смысл для всех значений x , включая отрицательные. Это может сделать определение 0 ⁿ = +∞ , полученное выше для отрицательного n, проблематичным, когда n нечетно, поскольку в этом случае x ⁿ → +∞ , когда x стремится к 0 через положительные значения, но не через отрицательные.

Эффективные вычисления с целыми показателями степеней

Вычисление b ⁿ с использованием итеративного умножения требует n − 1 операций умножения, но его можно вычислить более эффективно, как показано в следующем примере. Чтобы вычислить 2 ¹⁰⁰ , примените правило Горнера к показателю 100, записанному в двоичном виде:

${\displaystyle 100=2^{2}+2^{5}+2^{6}=2^{2}(1+2^{3}(1+2))}$.

Затем вычислите следующие члены по порядку, читая правило Горнера справа налево.

Эта серия шагов требует всего 8 умножений вместо 99.

В общем случае количество операций умножения, необходимых для вычисления b n , можно сократить до с помощью возведения в степень путем возведения в квадрат , где обозначает количество единиц в двоичном представлении n . ^Для некоторых показателей ( 100 не входит в их число ) количество умножений можно дополнительно сократить, вычислив и используя возведение в степень минимальной цепочки сложения . Нахождение минимальной последовательности умножений (цепочки сложения минимальной длины для показателя степени) для b ⁿ является сложной задачей, для которой в настоящее время не известны эффективные алгоритмы (см. Задача о сумме подмножества ), но доступно много достаточно эффективных эвристических алгоритмов. ^[39] Однако в практических вычислениях возведение в степень путем возведения в квадрат достаточно эффективно и гораздо проще в реализации. ${\displaystyle \sharp n+\lfloor \log _{2}n\rfloor -1,}$ ${\displaystyle \sharp n}$

Итерированные функции

Композиция функций — это бинарная операция , которая определяется над функциями таким образом, что область значений функции, записанной справа, включается в область значений функции, записанной слева. Она обозначается и определяется как ${\displaystyle g\circ f,}$

${\displaystyle (g\circ f)(x)=g(f(x))}$

для каждого x в области определения f .

Если область определения функции f равна ее области определения, можно составить функцию с самой собой произвольное число раз, и это определяет n -ю степень функции при композиции, обычно называемую n- й итерацией функции. Таким образом, обозначает, как правило, n -ю итерацию f ; например, означает ^[40] ${\displaystyle f^{n}}$ ${\displaystyle f^{3}(x)}$ ${\displaystyle f(f(f(x))).}$

Когда умножение определено на области значений функции, это определяет умножение функций, поточечное умножение , которое вызывает другое возведение в степень. При использовании функциональной нотации два вида возведения в степень обычно различаются путем помещения показателя функциональной итерации перед скобками, заключающими аргументы функции, и размещения показателя точечного умножения после скобок. Таким образом, и Когда функциональная нотация не используется, устранение неоднозначности часто осуществляется путем помещения символа композиции перед показателем; например, и По историческим причинам показатель степени повторного умножения помещается перед аргументом для некоторых конкретных функций, как правило, тригонометрических функций . Таким образом, и оба означают и не , что в любом случае редко рассматривается. Исторически сложилось так, что разными авторами использовалось несколько вариантов этих обозначений. ^{[41] [42] [43]} ${\displaystyle f^{2}(x)=f(f(x)),}$ ${\displaystyle f(x)^{2}=f(x)\cdot f(x).}$ ${\displaystyle f^{\circ 3}=f\circ f\circ f,}$ ${\displaystyle f^{3}=f\cdot f\cdot f.}$ ${\displaystyle \sin ^{2}x}$ ${\displaystyle \sin ^{2}(x)}$ ${\displaystyle \sin(x)\cdot \sin(x)}$ ${\displaystyle \sin(\sin(x)),}$

В этом контексте показатель степени всегда обозначает обратную функцию , если она существует. Так что для мультипликативных обратных дробей обычно используются как в ${\displaystyle -1}$ ${\displaystyle \sin ^{-1}x=\sin ^{-1}(x)=\arcsin x.}$ ${\displaystyle 1/\sin(x)={\frac {1}{\sin x}}.}$

В языках программирования

Языки программирования обычно выражают возведение в степень либо как инфиксный оператор , либо как применение функции, поскольку они не поддерживают верхние индексы. Наиболее распространенным символом оператора для возведения в степень является каретка ( ^). Первоначальная версия ASCII включала символ стрелки вверх ( ↑), предназначенный для возведения в степень, но он был заменен кареткой в ​​1967 году, поэтому каретка стала обычной в языках программирования. ^[44] Нотации включают:

• x ^ y: AWK , BASIC , J , MATLAB , Wolfram Language ( Mathematica ), R , Microsoft Excel , Analytica , TeX (и его производные), TI-BASIC , bc (для целых показателей), Haskell (для неотрицательных целых показателей), Lua и большинство систем компьютерной алгебры .
• x ** y. Набор символов Fortran не включал строчные символы или знаки препинания, кроме +-*/()&=.,'и , поэтому использовался **для возведения в степень ^{[45] [46]} (вместо этого использовалась первоначальная версия a xx b. ^[47] ). Многие другие языки последовали его примеру: Ada , Z shell , KornShell , Bash , COBOL , CoffeeScript , Fortran , FoxPro , Gnuplot , Groovy , JavaScript , OCaml , F# , Perl , PHP , PL/I , Python , Rexx , Ruby , SAS , Seed7 , Tcl , ABAP , Mercury , Haskell (для экспонент с плавающей точкой), Turing и VHDL .
• x ↑ y: Справочный язык Algol , Commodore BASIC , TRS-80 Level II/III BASIC . ^{[48] [49]}
• x ^^ y: Haskell (для дробных оснований, целочисленных показателей), D .
• x⋆y: АПЛ .

В большинстве языков программирования с инфиксным оператором возведения в степень он является правоассоциативным , то есть a^b^cинтерпретируется как a^(b^c). ^[50] Это происходит потому, (a^b)^cчто равно a^(b*c)и, следовательно, не так полезно. В некоторых языках он является левоассоциативным, в частности, в Algol , MATLAB и языке формул Microsoft Excel .

Другие языки программирования используют функциональную нотацию:

• (expt x y): Общий Лисп .
• pown x y: F# (для целочисленного основания, целочисленного показателя степени).

Другие же предоставляют возведение в степень только как часть стандартных библиотек :

• pow(x, y): C , C++ (в mathбиблиотеке).
• Math.Pow(x, y): С# .
• math:pow(X, Y): Эрланг .
• Math.pow(x, y): Ява .
• [Math]::Pow(x, y): PowerShell .

В некоторых статически типизированных языках, которые отдают приоритет безопасности типов , таких как Rust , возведение в степень выполняется с помощью множества методов:

• x.pow(y)для xи yкак целые числа
• x.powf(y)для xи yкак чисел с плавающей точкой
• x.powi(y)для xкак числа с плавающей точкой и yкак целого числа

Смотрите также

• Математический портал

• Двойная показательная функция
• Экспоненциальный распад
• Экспоненциальное поле
• Экспоненциальный рост
• Гипероперация
• Тетрация
• Пентацион
• Список экспоненциальных тем
• Модульное возведение в степень
• Научная нотация
• Подстрочные и надстрочные индексы Unicode
• х ^у = у ^х
• Ноль в степени ноль

Примечания

1. Существует три общепринятых обозначения умножения : чаще всего используется для явных чисел и на самом элементарном уровне; чаще всего используется, когда используются переменные ; используется для подчеркивания того, что речь идет об умножении, или когда пропуск знака умножения может вызвать путаницу. ${\displaystyle x\times y}$ ${\displaystyle xy}$ ${\displaystyle x\cdot y}$
2. В более общем смысле для определения достаточно ассоциативности мощности .

Ссылки

1. Найкамп, Дуэйн. "Основные правила возведения в степень". Math Insight . Получено 27.08.2020 .
2. Weisstein, Eric W. "Power". MathWorld . Получено 27.08.2020 .
3. "Экспонента | Этимология показателя степени по etymonline".
4. Rotman, Joseph J. (2015). Advanced Modern Algebra, Part 1. Graduate Studies in Mathematics . Vol. 165 (3rd ed.). Providence, RI: American Mathematical Society . p. 130, fn. 4. ISBN 978-1-4704-1554-9.
5. Сабо, Арпад (1978). Начало греческой математики. Синтезирующая историческая библиотека. Том. 17. Перевод А. М. Унгара. Дордрехт: Д. Рейдель . п. 37. ИСБН 90-277-0819-3.
6. O'Connor, John J.; Robertson, Edmund F. "Этимология некоторых общих математических терминов". Архив истории математики MacTutor . Университет Сент-Эндрюс .
7. Болл, WW Rouse (1915). Краткое изложение истории математики (6-е изд.). Лондон: Macmillan . С. 38.
8. Архимед. (2009). СЧЕТЧИК ПЕСКА. В T. Heath (ред.), Труды Архимеда: отредактировано в современной нотации с вводными главами (Коллекция библиотеки Кембриджа - Математика, стр. 229-232). Кембридж: Издательство Кембриджского университета. doi : 10.1017/CBO9780511695124.017.
9. Quinion, Michael . "Zenzizenzizenzic". World Wide Words . Получено 2020-04-16 .
10. О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. «Абул Хасан ибн Али аль Каласади». Архив истории математики Мактьютора . Университет Сент-Эндрюс .
11. Каджори, Флориан (1928). История математических обозначений. Т. 1. The Open Court Company. стр. 102.
12. Каджори, Флориан (1928). История математических обозначений. Т. 1. Лондон: Open Court Publishing Company . С. 344.
13. «Самые ранние известные случаи использования некоторых слов математики (E)». 2017-06-23.
14. Стифель, Майкл (1544). Интегральная арифметика. Нюрнберг: Йоханнес Петрейус . п. 235В.
15. Каджори, Флориан (1928). История математических обозначений. Т. 1. The Open Court Company. С. 204.
16. Декарт, Рене (1637). « Геометрия ». Дискурс о методе [...]. Лейден: Ян Мэр. п. 299. Et aa , ou a ² , налейте множитель в парное слово; И 3 , для множителя на бис , и снова для бесконечности ^.(И aa , или a2 ^, чтобы умножить a на себя; и a3 ^, чтобы умножить его еще раз на a , и так до бесконечности).
17. Самое последнее использование этого слова в этом смысле, цитируемое в Оксфордском словаре английского языка, относится к 1806 году ( «involution» . Oxford English Dictionary (Online ed.). Oxford University Press . (Требуется подписка или членство в участвующем учреждении.) ).
18. Эйлер, Леонард (1748). Introductio in analysin infinitorum (на латыни). Том. I. Лозанна: Марк-Мишель Буске. стр. 69, 98–99. Primum ergo thinkandæ sunt quantitates exponentiales, seu Potestates, quarum Exponens ipse est quantitas variabilis. Perspicuum enim est hujusmodi количественно оценивает объявление Functiones алгебраические ссылки, не принадлежащие, включая его Expentes non nisi Constantes locum habeant.
19. Ходж, Джонатан К.; Шликер, Стивен; Сандсторм, Тед (2014). Абстрактная алгебра: подход, основанный на исследовании. CRC Press. стр. 94. ISBN 978-1-4665-6706-1.
20. Ахац, Томас (2005). Техническая математика цеха (3-е изд.). Industrial Press. стр. 101. ISBN 978-0-8311-3086-2.
21. Кноблох, Эберхард (1994). «Бесконечность в математике Лейбница – историографический метод понимания в контексте». В Костасе Гавроглу; Жане Кристианидисе; Эфтимиосе Николаидисе (ред.). Тенденции в историографии науки . Бостонские исследования философии науки. Т. 151. Springer Netherlands. стр. 276. doi :10.1007/978-94-017-3596-4_20. ISBN 9789401735964Положительная степень нуля бесконечно мала, отрицательная степень нуля бесконечна.
22. Бронштейн, Илья Николаевич ; Семендяев, Константин Адольфович (1987) [1945]. «2.4.1.1. Определение арифметических выражений». Написано в Лейпциге, Германия. В Гроше, Гюнтер; Зиглер, Виктор; Зиглер, Доротея (ред.). Taschenbuch der Mathematik [ Карманный справочник по математике ] (на немецком языке). Том. 1. Перевод Циглера Виктора. Вайс, Юрген (23-е изд.). Тун, Швейцария / Франкфурт-на-Майне, Германия: Verlag Harri Deutsch (и BG Teubner Verlagsgesellschaft , Лейпциг). стр. 115–120, 802. ISBN. 3-87144-492-8.
23. Olver, Frank WJ; Lozier, Daniel W.; Boisvert, Ronald F.; Clark, Charles W., ред. (2010). Справочник NIST по математическим функциям . Национальный институт стандартов и технологий (NIST), Министерство торговли США , Cambridge University Press . ISBN 978-0-521-19225-5. МР  2723248.[1]
24. Зейдлер, Эберхард [на немецком языке] ; Шварц, Ганс Рудольф; Хакбуш, Вольфганг ; Людерер, Бернд [на немецком языке] ; Блат, Йохен; Шид, Александр; Демпе, Стефан; Ванка, Герт ; Хромкович, Юрай ; Готвальд, Зигфрид (2013) [2012]. Зейдлер, Эберхард [на немецком языке] (ред.). Springer-Handbuch der Mathematik I (на немецком языке). Том. Я (1-е изд.). Берлин/Гейдельберг, Германия: Springer Spektrum , Springer Fachmedien Wiesbaden . п. 590. ИСБН 978-3-658-00284-8.(xii+635 страниц)
25. Хасс, Джоэл Р.; Хейл, Кристофер Э.; Вейр, Морис Д.; Томас, Джордж Б. (2018). Исчисление Томаса (14-е изд.). Пирсон. стр. 7–8. ISBN 9780134439020.
26. Антон, Ховард; Бивенс, Ирл; Дэвис, Стивен (2012). Исчисление: Ранние трансцендентали (9-е изд.). John Wiley & Sons. стр. 28. ISBN 9780470647691.
27. Денлингер, Чарльз Г. (2011). Элементы реального анализа . Джонс и Бартлетт. стр. 278–283. ISBN 978-0-7637-7947-4.
28. Тао, Теренс (2016). «Пределы последовательностей». Анализ I. Тексты и чтения по математике. Т. 37. С. 126–154. doi :10.1007/978-981-10-1789-6_6. ISBN 978-981-10-1789-6.
29. Кормен, Томас Х.; Лейзерсон, Чарльз Э.; Ривест, Рональд Л.; Штейн, Клиффорд (2001). Введение в алгоритмы (второе изд.). МТИ Пресс . ISBN 978-0-262-03293-3.Интернет-ресурс Архивировано 30 сентября 2007 г. на Wayback Machine .
30. Калл, Пол; Флэхайв, Мэри ; Робсон, Робби (2005). Разностные уравнения: от кроликов к хаосу ( Учебники по математике  для студентов). Springer. ISBN 978-0-387-23234-8.Определено на стр. 351.
31. Вайсштейн, Эрик В. «Главный корень из единицы». MathWorld .
32. Штайнер, Дж.; Клаузен, Т.; Абель, Нильс Хенрик (1827). «Aufgaben und Lehrsätze, erstere aufzulösen, letztere zu beweisen» [Проблемы и предложения: первые нужно решить, потом доказать]. Журнал для королевы и математики . 2 : 286–287.
33. Бурбаки, Николя (1970). Алгебра . Спрингер. И.2.
34. Блум, Дэвид М. (1979). Линейная алгебра и геометрия . Cambridge University Press. стр. 45. ISBN 978-0-521-29324-2.
35. Глава 1, Элементарная линейная алгебра, 8E, Говард Антон.
36. Стрэнг, Гилберт (1988). Линейная алгебра и ее приложения (3-е изд.). Брукс-Коул. Глава 5.
37. Э. Хилле, Р. С. Филлипс: Функциональный анализ и полугруппы . Американское математическое общество, 1975.
38. Николя Бурбаки, Общая топология , V.4.2.
39. Gordon, DM (1998). "Обзор методов быстрого возведения в степень" (PDF) . Journal of Algorithms . 27 : 129–146. CiteSeerX 10.1.1.17.7076 . doi :10.1006/jagm.1997.0913. Архивировано из оригинала (PDF) 2018-07-23 . Получено 2024-01-11 . 
40. Пеано, Джузеппе (1903). Formulaire mathématique (на французском языке). Том. IV. п. 229.
41. Гершель, Джон Фредерик Уильям (1813) [1812-11-12]. «О замечательном применении теоремы Котеса». Philosophical Transactions of the Royal Society of London . 103 (часть 1). Лондон: Royal Society of London , напечатано W. Bulmer and Co., Cleveland-Row, St. James's, продано G. and W. Nicol, Pall-Mall: 8–26 [10]. doi :10.1098/rstl.1813.0005. JSTOR  107384. S2CID  118124706.
42. Гершель, Джон Фредерик Уильям (1820). «Часть III. Раздел I. Примеры прямого метода разностей». Сборник примеров приложений исчисления конечных разностей . Кембридж, Великобритания: напечатано Дж. Смитом, продано Дж. Дейтоном и сыновьями. стр. 1–13 [5–6]. Архивировано из оригинала 2020-08-04 . Получено 2020-08-04 .[2] (Примечание. Здесь Гершель ссылается на свою работу 1813 года и упоминает более раннюю работу Ганса Генриха Бюрмана .)
43. Каджори, Флориан (1952) [март 1929]. История математических обозначений. Т. 2 (3-е изд.). Чикаго, США: Open court Publishing Company . С. 108, 176–179, 336, 346. ISBN 978-1-60206-714-1. Получено 18.01.2016 .
44. Ричард Гиллам (2003). Unicode Demystified: A Practical Programmer's Guide to the Encoding Standard . Addison-Wesley Professional. стр. 33. ISBN 0201700522.
45. Backus, John Warner ; Beeber, RJ; Best, Sheldon F.; Goldberg, Richard ; Herrick, Harlan L.; Hughes, RA; Mitchell, LB; Nelson, Robert A.; Nutt, Roy ; Sayre, David ; Sheridan, Peter B.; Stern, Harold; Ziller, Irving (1956-10-15). Sayre, David (ред.). Система автоматического кодирования FORTRAN для IBM 704 EDPM: Справочное руководство программиста (PDF) . Нью-Йорк, США: Отдел прикладных наук и отдел исследований программирования, International Business Machines Corporation . стр. 15. Архивировано (PDF) из оригинала 2022-07-04 . Получено 2022-07-04 .(2+51+1 страницы)
46. Брайс Карнахан; Джеймс О. Уилкс (1968). Введение в цифровые вычисления и FORTRAN IV с приложениями MTS . стр. 2–2, 2–6.
47. Бэкус, Джон Уорнер ; Херрик, Харлан Л.; Нельсон, Роберт А.; Зиллер, Ирвинг (1954-11-10). Бэкус, Джон Уорнер (ред.). Спецификации для: IBM Mathematical FORmula TRANSlating System, FORTRAN (PDF) (Предварительный отчет). Нью-Йорк, США: Programming Research Group, Applied Science Division, International Business Machines Corporation . стр. 4, 6. Архивировано (PDF) из оригинала 29.03.2022 . Получено 04.07.2022 .(29 страниц)
48. Данелюк, Тимоти «Тим» А. (1982-08-09). «BASCOM — компилятор BASIC для TRS-80 I и II». InfoWorld . Software Reviews. Том 4, № 31. Popular Computing, Inc., стр. 41–42. Архивировано из оригинала 2020-02-07 . Получено 2020-02-06 .
49. "80 Contents". 80 Micro (45). 1001001, Inc. : 5. Октябрь 1983. ISSN  0744-7868 . Получено 2020-02-06 .
50. Роберт В. Себеста (2010). Концепции языков программирования . Addison-Wesley. стр. 130, 324. ISBN 978-0136073475.