
В математике динамическая система — это система, в которой функция описывает зависимость точки окружающего пространства от времени , например, параметрической кривой . Примерами служат математические модели , описывающие колебание маятника часов , течение воды в трубе , случайное движение частиц в воздухе и количество рыб в озере каждую весну . Наиболее общее определение объединяет несколько понятий в математике, таких как обыкновенные дифференциальные уравнения и эргодическая теория, допуская различные варианты выбора пространства и способа измерения времени. [ требуется цитирование ] Время может измеряться целыми числами, действительными или комплексными числами или может быть более общим алгебраическим объектом, теряя память о своем физическом происхождении, а пространство может быть многообразием или просто множеством , без необходимости в гладкой структуре пространства-времени, определенной на нем.
В любой момент времени динамическая система имеет состояние, представляющее точку в соответствующем пространстве состояний . Это состояние часто задается кортежем действительных чисел или вектором в геометрическом многообразии. Правило эволюции динамической системы — это функция, которая описывает, какие будущие состояния следуют из текущего состояния. Часто функция является детерминированной , то есть для заданного интервала времени из текущего состояния следует только одно будущее состояние. [1] [2] Однако некоторые системы являются стохастическими , в том смысле, что случайные события также влияют на эволюцию переменных состояния.
В физике динамическая система описывается как «частица или ансамбль частиц, состояние которых изменяется со временем и, таким образом, подчиняется дифференциальным уравнениям, включающим производные по времени». [3] Для того чтобы сделать прогноз о будущем поведении системы, реализуется аналитическое решение таких уравнений или их интегрирование во времени посредством компьютерного моделирования.
Изучение динамических систем является фокусом теории динамических систем , которая имеет приложения к широкому спектру областей, таких как математика, физика, [4] [5] биология , [6] химия , инженерия , [7] экономика , [8] история и медицина . Динамические системы являются фундаментальной частью теории хаоса , динамики логистических карт , теории бифуркаций , процессов самосборки и самоорганизации , а также концепции края хаоса .
Концепция динамической системы берет свое начало в механике Ньютона . Там, как и в других естественных науках и инженерных дисциплинах, правило эволюции динамических систем представляет собой неявное отношение, которое дает состояние системы только на короткое время в будущем. (Отношение представляет собой либо дифференциальное уравнение , либо разностное уравнение , либо другую временную шкалу .) Чтобы определить состояние для всех будущих моментов времени, требуется многократно итерировать отношение — каждое продвижение времени на небольшой шаг. Процедура итерации называется решением системы или интегрированием системы . Если система может быть решена, то, имея начальную точку, можно определить все ее будущие положения, набор точек, известный как траектория или орбита .
До появления компьютеров нахождение орбиты требовало сложных математических методов и могло быть выполнено только для небольшого класса динамических систем. Численные методы, реализованные на электронных вычислительных машинах, упростили задачу определения орбит динамической системы.
Для простых динамических систем часто достаточно знать траекторию, но большинство динамических систем слишком сложны, чтобы их можно было понять в терминах отдельных траекторий. Трудности возникают из-за:
Многие считают французского математика Анри Пуанкаре основателем динамических систем. [9] Пуанкаре опубликовал две ныне классические монографии: «Новые методы небесной механики» (1892–1899) и «Лекции по небесной механике» (1905–1910). В них он успешно применил результаты своих исследований к задаче о движении трех тел и подробно изучил поведение решений (частоту, устойчивость, асимптотику и т. д.). В этих работах была выдвинута теорема Пуанкаре о возвращении , которая гласит, что некоторые системы через достаточно длительное, но конечное время вернутся в состояние, очень близкое к исходному.
Александр Ляпунов разработал много важных методов приближения. Его методы, разработанные им в 1899 году, позволяют определять устойчивость систем обыкновенных дифференциальных уравнений. Он создал современную теорию устойчивости динамической системы.
В 1913 году Джордж Дэвид Биркгоф доказал « Последнюю геометрическую теорему » Пуанкаре , частный случай задачи трех тел , результат, который сделал его всемирно известным. В 1927 году он опубликовал свою работу «Динамические системы» . Самым долговечным результатом Биркгофа стало его открытие в 1931 году того, что сейчас называется эргодической теоремой . Объединив идеи физики об эргодической гипотезе с теорией меры , эта теорема решила, по крайней мере в принципе, фундаментальную проблему статистической механики . Эргодическая теорема также имела последствия для динамики.
Стивен Смейл также добился значительных успехов. Его первым вкладом стала подкова Смейла , которая дала толчок важным исследованиям в области динамических систем. Он также изложил исследовательскую программу, которую проводили многие другие.
Александр Николаевич Шарковский разработал теорему Шарковского о периодах дискретных динамических систем в 1964 году. Одним из следствий теоремы является то, что если дискретная динамическая система на действительной прямой имеет периодическую точку периода 3, то она должна иметь периодические точки любого другого периода.
В конце 20-го века динамическая системная перспектива для уравнений в частных производных начала набирать популярность. Палестинский инженер-механик Али Х. Найфех применил нелинейную динамику в механических и инженерных системах. [10] Его пионерская работа в области прикладной нелинейной динамики оказала влияние на строительство и обслуживание машин и конструкций , которые распространены в повседневной жизни, таких как корабли , краны , мосты , здания , небоскребы , реактивные двигатели , ракетные двигатели , самолеты и космические корабли . [11]
В самом общем смысле [12] [13] динамическая система — это кортеж ( T , X , Φ), где T — моноид , записанный аддитивно, X — непустое множество , а Φ — функция.
с
и для любого x из X :
для и , где мы определили множество для любого x из X .
В частности, в случае, когда для каждого x в X выполняется следующее: и, таким образом, Φ определяет моноидное действие T на X.
Функция Φ( t , x ) называется функцией эволюции динамической системы: она сопоставляет каждой точке x множества X уникальный образ, зависящий от переменной t , называемой параметром эволюции . X называется фазовым пространством или пространством состояний , в то время как переменная x представляет начальное состояние системы.
Мы часто пишем
если мы возьмем одну из переменных как константу. Функция
называется потоком через x , а его график называется траекторией через x . Множество
называется орбитой через x . Орбита через x является образом потока через x . Подмножество S пространства состояний X называется Φ- инвариантным , если для всех x из S и всех t из T
Таким образом, в частности, если S является Φ- инвариантным для всех x в S. То есть поток через x должен быть определен для любого времени для каждого элемента S.
Чаще всего встречаются два класса определений динамической системы: одно основано на обыкновенных дифференциальных уравнениях и имеет геометрический характер; а другое основано на эргодической теории и имеет теоретический характер меры .
В геометрическом определении динамическая система — это кортеж . — область для времени — существует множество вариантов, обычно действительные числа или целые числа, возможно, ограниченные неотрицательными. — многообразие , т. е. локально банахово или евклидово пространство, или в дискретном случае граф . f — это правило эволюции t → f t (с ), такое, что f t — диффеоморфизм многообразия в себя. Таким образом, f — это «гладкое» отображение временной области в пространство диффеоморфизмов многообразия в себя. Другими словами, f ( t ) — это диффеоморфизм для каждого времени t в области .
Реальная динамическая система , динамическая система в реальном времени , динамическая система с непрерывным временем или поток — это кортеж ( T , M , Φ), где T — открытый интервал в действительных числах R , M — многообразие, локально диффеоморфное банахову пространству , а Φ — непрерывная функция . Если Φ непрерывно дифференцируема, мы говорим, что система является дифференцируемой динамической системой . Если многообразие M локально диффеоморфно Rn , динамическая система конечномерна ; в противном случае динамическая система бесконечномерна . Это не предполагает симплектической структуры . Когда T принимается за действительные числа, динамическая система называется глобальной или потоком ; а если T ограничивается неотрицательными действительными числами, то динамическая система является полупотоком .
Дискретная динамическая система , дискретно-временная динамическая система — это кортеж ( T , M , Φ), где M — многообразие , локально диффеоморфное банахову пространству , а Φ — функция. Когда T рассматривается как целые числа, это каскад или отображение . Если T ограничивается неотрицательными целыми числами, мы называем систему полукаскадом . [ 14]
Клеточный автомат — это кортеж ( T , M , Φ), где T — решетка , например, целые числа или целочисленная сетка более высокой размерности , M — набор функций из целочисленной решетки (опять же, с одним или несколькими измерениями) в конечный набор, а Φ — (локально определенная) функция эволюции. Таким образом, клеточные автоматы являются динамическими системами. Решетка в M представляет собой решетку «пространства», а решетка в T — решетку «времени».
Динамические системы обычно определяются по одной независимой переменной, которую мы называем временем. Более общий класс систем определяется по нескольким независимым переменным и поэтому называется многомерными системами . Такие системы полезны для моделирования, например, обработки изображений .
Если задана глобальная динамическая система ( R , X , Φ) на локально компактном и хаусдорфовом топологическом пространстве X , часто бывает полезно изучить непрерывное расширение Φ* системы Φ до одноточечной компактификации X* системы X . Хотя мы теряем дифференциальную структуру исходной системы, теперь мы можем использовать аргументы компактности для анализа новой системы ( R , X* , Φ*).
В компактных динамических системах предельное множество любой орбиты непусто , компактно и односвязно .
Динамическая система может быть формально определена как сохраняющее меру преобразование пространства с мерой , триплета ( T , ( X , Σ, μ ), Φ). Здесь T — моноид (обычно неотрицательные целые числа), X — множество , а ( X , Σ, μ ) — вероятностное пространство , что означает, что Σ — сигма-алгебра на X , а μ — конечная мера на ( X , Σ). Отображение Φ: X → X называется Σ-измеримым тогда и только тогда, когда для каждого σ в Σ выполняется . Отображение Φ выполняется так, чтобы сохраняла меру тогда и только тогда, когда для каждого σ в Σ выполняется . Объединяя вышесказанное, отображение Φ называется сохраняющим меру преобразованием X , если оно является отображением из X в себя, является Σ-измеримым и сохраняет меру. Триплет ( T , ( X , Σ, μ ), Φ) для такого Φ тогда определяется как динамическая система .
Отображение Φ воплощает временную эволюцию динамической системы. Таким образом, для дискретных динамических систем изучаются итерации для каждого целого числа n . Для непрерывных динамических систем отображение Φ понимается как конечное временное отображение эволюции, и его построение более сложное.
Теоретическое определение меры предполагает существование преобразования, сохраняющего меру. С любым правилом эволюции можно связать множество различных инвариантных мер. Если динамическая система задана системой дифференциальных уравнений, то должна быть определена соответствующая мера. Это затрудняет разработку эргодической теории, начиная с дифференциальных уравнений, поэтому становится удобным иметь определение, мотивированное динамическими системами, в рамках эргодической теории, которое обходит стороной выбор меры и предполагает, что выбор уже сделан. Простая конструкция (иногда называемая теоремой Крылова–Боголюбова ) показывает, что для большого класса систем всегда можно построить меру так, чтобы сделать правило эволюции динамической системы преобразованием, сохраняющим меру. В конструкции заданная мера пространства состояний суммируется для всех будущих точек траектории, обеспечивая инвариантность.
Некоторые системы имеют естественную меру, такую как мера Лиувилля в гамильтоновых системах , выбранную вместо других инвариантных мер, таких как меры, поддерживаемые на периодических орбитах гамильтоновой системы. Для хаотических диссипативных систем выбор инвариантной меры технически более сложен. Мера должна поддерживаться на аттракторе , но аттракторы имеют нулевую меру Лебега , а инвариантные меры должны быть сингулярными относительно меры Лебега. Небольшая область фазового пространства сжимается при эволюции во времени.
Для гиперболических динамических систем меры Синая–Рюэля–Боуэна кажутся естественным выбором. Они построены на геометрической структуре устойчивых и неустойчивых многообразий динамической системы; они ведут себя физически при малых возмущениях; и они объясняют многие из наблюдаемых статистик гиперболических систем.
Концепция эволюции во времени является центральной в теории динамических систем, как показано в предыдущих разделах: основная причина этого факта заключается в том, что исходной мотивацией теории было изучение поведения во времени классических механических систем . Но система обыкновенных дифференциальных уравнений должна быть решена, прежде чем она станет динамической системой. Например, рассмотрим задачу начального значения, такую как следующая:
где
Нет необходимости в производных более высокого порядка в уравнении, как и в параметре t в v ( t , x ), поскольку их можно исключить, рассматривая системы более высоких размерностей.
В зависимости от свойств этого векторного поля механическая система называется
Решение можно найти с помощью стандартных методов ОДУ, оно обозначается как функция эволюции, уже введенная выше.
Тогда динамическая система имеет вид ( T , M , Φ).
Некоторые формальные манипуляции с системой дифференциальных уравнений, показанной выше, дают более общую форму уравнений, которым должна удовлетворять динамическая система.
где — функционал из множества эволюционных функций в поле комплексных чисел.
Это уравнение полезно при моделировании механических систем со сложными ограничениями.
Многие концепции динамических систем можно распространить на бесконечномерные многообразия, которые локально являются банаховыми пространствами , и в этом случае дифференциальные уравнения являются уравнениями в частных производных .
Линейные динамические системы могут быть решены в терминах простых функций и поведения всех классифицированных орбит. В линейной системе фазовое пространство является N -мерным евклидовым пространством, поэтому любая точка в фазовом пространстве может быть представлена вектором с N числами. Анализ линейных систем возможен, поскольку они удовлетворяют принципу суперпозиции : если u ( t ) и w ( t ) удовлетворяют дифференциальному уравнению для векторного поля (но не обязательно начальному условию), то также будет удовлетворять u ( t ) + w ( t ).
Для потока векторное поле v( x ) является аффинной функцией положения в фазовом пространстве, то есть,
где A — матрица, b — вектор чисел, а x — радиус-вектор. Решение этой системы можно найти, используя принцип суперпозиции (линейности). Случай b ≠ 0 с A = 0 — это просто прямая линия в направлении b :
Когда b равно нулю и A ≠ 0, начало координат является точкой равновесия (или особой точкой) потока, то есть, если x 0 = 0, то орбита остается там. Для других начальных условий уравнение движения задается экспонентой матрицы : для начальной точки x 0 ,
При b = 0 собственные значения A определяют структуру фазового пространства. Из собственных значений и собственных векторов A можно определить, будет ли начальная точка сходиться или расходиться к точке равновесия в начале координат.
Расстояние между двумя различными начальными условиями в случае A ≠ 0 будет меняться экспоненциально в большинстве случаев, либо сходясь экспоненциально быстро к точке, либо расходясь экспоненциально быстро. Линейные системы демонстрируют чувствительную зависимость от начальных условий в случае расходимости. Для нелинейных систем это одно из (необходимых, но не достаточных) условий хаотического поведения .
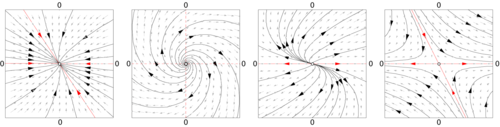
Дискретная по времени аффинная динамическая система имеет форму матричного разностного уравнения :
где A — матрица, а b — вектор. Как и в непрерывном случае, изменение координат x → x + (1 − A ) –1 b удаляет член b из уравнения. В новой системе координат начало координат является фиксированной точкой отображения, а решения являются линейной системой A n x 0 . Решения для отображения больше не являются кривыми, а точками, которые прыгают в фазовом пространстве. Орбиты организованы в кривые, или волокна, которые являются наборами точек, которые отображаются в себя под действием отображения.
Как и в непрерывном случае, собственные значения и собственные векторы A определяют структуру фазового пространства. Например, если u 1 — собственный вектор A с действительным собственным значением, меньшим единицы, то прямые линии, заданные точками вдоль α u 1 , где α ∈ R , являются инвариантной кривой отображения. Точки на этой прямой линии пересекают неподвижную точку.
Существует также множество других дискретных динамических систем .
Качественные свойства динамических систем не меняются при плавном изменении координат (иногда это принимается за определение качественного): особая точка векторного поля (точка, где v ( x ) = 0) останется особой точкой при плавных преобразованиях; периодическая орбита является петлей в фазовом пространстве, и плавные деформации фазового пространства не могут изменить ее как петлю. Именно в окрестности особых точек и периодических орбит можно хорошо понять структуру фазового пространства динамической системы. При качественном изучении динамических систем подход состоит в том, чтобы показать, что существует изменение координат (обычно неопределенное, но вычислимое), которое делает динамическую систему максимально простой.
Поток в большинстве малых участков фазового пространства можно сделать очень простым. Если y — это точка, где векторное поле v ( y ) ≠ 0, то существует изменение координат для области вокруг y , где векторное поле становится серией параллельных векторов одинаковой величины. Это известно как теорема о выпрямлении.
Теорема о выпрямлении гласит, что вдали от особых точек динамика точки в небольшом участке представляет собой прямую линию. Участок иногда можно увеличить, сшивая несколько участков вместе, и когда это работает во всем фазовом пространстве M, динамическая система интегрируема . В большинстве случаев участок не может быть расширен на все фазовое пространство. В векторном поле могут быть особые точки (где v ( x ) = 0); или участки могут становиться все меньше и меньше по мере приближения к некоторой точке. Более тонкая причина — глобальное ограничение, когда траектория начинается в участке и после посещения ряда других участков возвращается к исходному. Если в следующий раз орбита будет описывать петлю вокруг фазового пространства другим образом, то невозможно выпрямить векторное поле во всем ряде участков.
В общем случае в окрестности периодической орбиты теорема о выпрямлении не может быть использована. Пуанкаре разработал подход, который преобразует анализ вблизи периодической орбиты в анализ отображения. Выберите точку x 0 на орбите γ и рассмотрите точки в фазовом пространстве в этой окрестности, которые перпендикулярны v ( x 0 ). Эти точки являются сечением Пуанкаре S ( γ , x 0 ) орбиты. Теперь поток определяет отображение, отображение Пуанкаре F : S → S , для точек, начинающихся в S и возвращающихся в S . Не все эти точки потребуют одинакового количества времени, чтобы вернуться обратно, но времена будут близки ко времени, которое требуется x 0 .
Пересечение периодической орбиты с сечением Пуанкаре является неподвижной точкой отображения Пуанкаре F. При переносе можно предположить, что точка находится в точке x = 0. Ряд Тейлора отображения равен F ( x ) = J · x + O( x 2 ), поэтому можно ожидать, что изменение координат h упростит F только до его линейной части
Это известно как уравнение сопряжения. Нахождение условий для этого уравнения было одной из основных задач исследований динамических систем. Пуанкаре первым подошел к нему, предположив, что все функции являются аналитическими, и в процессе обнаружил нерезонансное условие. Если λ 1 , ..., λ ν являются собственными значениями J , они будут резонансными, если одно собственное значение является целочисленной линейной комбинацией двух или более других. Поскольку члены вида λ i – Σ (кратные других собственных значений) встречаются в знаменателе членов для функции h , нерезонансное условие также известно как проблема малых делителей.
Результаты существования решения уравнения сопряжения зависят от собственных значений J и степени гладкости, требуемой от h . Поскольку J не обязательно должна иметь какие-либо специальные симметрии, ее собственные значения обычно будут комплексными числами. Когда собственные значения J не находятся на единичной окружности, динамика вблизи неподвижной точки x 0 функции F называется гиперболической , а когда собственные значения находятся на единичной окружности и являются комплексными, динамика называется эллиптической .
В гиперболическом случае теорема Хартмана–Гробмана дает условия существования непрерывной функции, которая отображает окрестность неподвижной точки отображения в линейное отображение J · x . Гиперболический случай также структурно устойчив . Небольшие изменения в векторном поле приведут только к небольшим изменениям в отображении Пуанкаре, и эти небольшие изменения отразятся в небольших изменениях в положении собственных значений J в комплексной плоскости, подразумевая, что отображение по-прежнему является гиперболическим.
Теорема Колмогорова –Арнольда–Мозера (КАМ) описывает поведение вблизи эллиптической точки.
Когда эволюционное отображение Φ t (или векторное поле, из которого оно выводится) зависит от параметра μ, структура фазового пространства также будет зависеть от этого параметра. Небольшие изменения могут не вызывать качественных изменений в фазовом пространстве до тех пор, пока не будет достигнуто особое значение μ 0. В этой точке фазовое пространство качественно меняется, и говорят, что динамическая система прошла через бифуркацию.
Теория бифуркации рассматривает структуру в фазовом пространстве (обычно неподвижную точку , периодическую орбиту или инвариантный тор ) и изучает ее поведение как функцию параметра μ . В точке бифуркации структура может изменить свою устойчивость, расколоться на новые структуры или объединиться с другими структурами. Используя аппроксимации рядов Тейлора для отображений и понимание различий, которые могут быть устранены путем изменения координат, можно каталогизировать бифуркации динамических систем.
Бифуркации гиперболической неподвижной точки x 0 семейства систем F μ можно охарактеризовать собственными значениями первой производной системы DF μ ( x 0 ), вычисленными в точке бифуркации. Для отображения бифуркация произойдет, когда на единичной окружности будут собственные значения DF μ . Для потока она произойдет, когда на мнимой оси будут собственные значения. Для получения дополнительной информации см. основную статью о теории бифуркаций .
Некоторые бифуркации могут приводить к очень сложным структурам в фазовом пространстве. Например, сценарий Рюэлля–Такенса описывает, как периодическая орбита бифурцируется в тор, а тор — в странный аттрактор . В другом примере удвоение периода Фейгенбаума описывает, как стабильная периодическая орбита проходит через ряд бифуркаций удвоения периода .
Во многих динамических системах можно выбрать координаты системы так, чтобы объем (на самом деле ν-мерный объем) в фазовом пространстве был инвариантным. Это происходит для механических систем, выведенных из законов Ньютона, пока координатами являются положение и импульс, а объем измеряется в единицах (положение) × (импульс). Поток переводит точки подмножества A в точки Φ t ( A ), а инвариантность фазового пространства означает, что
В гамильтоновом формализме , если задана координата, можно вывести соответствующий (обобщенный) импульс, такой, что связанный с ним объем сохраняется потоком. Говорят, что объем вычисляется с помощью меры Лиувилля .
В гамильтоновой системе не все возможные конфигурации положения и импульса могут быть достигнуты из начального состояния. Из-за сохранения энергии доступны только состояния с той же энергией, что и начальное состояние. Состояния с той же энергией образуют энергетическую оболочку Ω, подмногообразие фазового пространства. Объем энергетической оболочки, вычисленный с использованием меры Лиувилля, сохраняется при эволюции.
Для систем, где объем сохраняется потоком, Пуанкаре открыл теорему о возврате : предположим, что фазовое пространство имеет конечный объем Лиувилля, и пусть F — отображение, сохраняющее объем фазового пространства, а A — подмножество фазового пространства. Тогда почти каждая точка A возвращается в A бесконечно часто. Теорема о возврате Пуанкаре была использована Цермело для возражения против вывода Больцмана об увеличении энтропии в динамической системе сталкивающихся атомов.
Одним из вопросов, поднятых работой Больцмана, было возможное равенство между средними по времени и средними по пространству, что он назвал эргодической гипотезой . Гипотеза утверждает, что продолжительность времени, которую типичная траектория проводит в области A, равна vol( A )/vol(Ω).
Эргодическая гипотеза оказалась не тем существенным свойством, которое необходимо для развития статистической механики , и был введен ряд других свойств, подобных эргодическим, чтобы охватить соответствующие аспекты физических систем. Купман подошел к изучению эргодических систем с помощью функционального анализа . Наблюдаемая a — это функция, которая каждой точке фазового пространства сопоставляет число (например, мгновенное давление или среднюю высоту). Значение наблюдаемой может быть вычислено в другой момент времени с помощью функции эволюции φ t . Это вводит оператор U t , оператор переноса ,
Изучая спектральные свойства линейного оператора U, становится возможным классифицировать эргодические свойства Φ t . При использовании подхода Купмана, рассматривающего действие потока на наблюдаемую функцию, конечномерная нелинейная задача с участием Φ t отображается в бесконечномерную линейную задачу с участием U .
Мера Лиувилля, ограниченная энергетической поверхностью Ω, является основой для средних значений, вычисляемых в равновесной статистической механике . Среднее по времени вдоль траектории эквивалентно среднему значению в пространстве, вычисляемому с помощью фактора Больцмана exp(−β H ) . Эта идея была обобщена Синаем, Боуэном и Рюэллем (SRB) на более широкий класс динамических систем, включающий диссипативные системы. Меры SRB заменяют фактор Больцмана и определяются на аттракторах хаотических систем.
Простые нелинейные динамические системы, включая кусочно-линейные системы, могут демонстрировать сильно непредсказуемое поведение, которое может показаться случайным, несмотря на то, что они в основе своей детерминированы. Это непредсказуемое поведение было названо хаосом . Гиперболические системы — это точно определенные динамические системы, которые демонстрируют свойства, приписываемые хаотическим системам. В гиперболических системах касательные пространства, перпендикулярные орбите, можно разложить на комбинацию из двух частей: одну с точками, которые сходятся к орбите ( устойчивое многообразие ), и другую с точками, которые расходятся с орбиты ( неустойчивое многообразие ).
Эта отрасль математики занимается долгосрочным качественным поведением динамических систем. Здесь внимание сосредоточено не на поиске точных решений уравнений, определяющих динамическую систему (что часто безнадежно), а на ответах на такие вопросы, как «Установится ли система в устойчивом состоянии в долгосрочной перспективе, и если да, то каковы возможные аттракторы ?» или «Зависит ли долгосрочное поведение системы от ее начального состояния?»
Хаотическое поведение сложных систем не является проблемой. Метеорология, как известно, в течение многих лет занимается сложным — даже хаотическим — поведением. Теория хаоса была столь удивительной, потому что хаос можно обнаружить в почти тривиальных системах. Сценарий Помо–Манневиля логистического отображения и проблема Ферми–Паста–Улама–Цингоу возникли только с полиномами второй степени; подковообразное отображение является кусочно-линейным.
Для нелинейных автономных ОДУ при некоторых условиях возможно разработать решения конечной продолжительности, [15] что означает здесь, что в этих решениях система достигнет нулевого значения в некоторый момент времени, называемый конечным временем, и затем останется там навсегда. Это может произойти только тогда, когда траектории системы не определяются однозначно вперед и назад во времени динамикой, таким образом, решения конечной продолжительности подразумевают форму «непредсказуемости назад во времени», тесно связанную с непредсказуемостью хаоса вперед во времени. Такое поведение не может иметь место для непрерывных по Липшицу дифференциальных уравнений согласно доказательству теоремы Пикара-Линделефа . Эти решения являются нелипшицевыми функциями в свои конечные моменты времени и не могут быть аналитическими функциями на всей действительной прямой.
Например, уравнение:
Допускает решение с конечной продолжительностью:
которая равна нулю для и не является непрерывной по Липшицу в момент времени окончания
Работы, обеспечивающие широкий охват:
Вводные тексты с уникальной точки зрения:
{{cite book}}: CS1 maint: multiple names: authors list (link)Учебники
Популяризации: